Monochromatic breast computed tomography with synchrotron radiation: phase-contrast and phase-retrieved image comparison and full-volume reconstruction

Abstract.

A program devoted to performing the first in vivo synchrotron radiation (SR) breast computed tomography (BCT) is ongoing at the Elettra facility. Using the high spatial coherence of SR, phase-contrast (PhC) imaging techniques can be used. The latest high-resolution BCT acquisitions of breast specimens, obtained with the propagation-based PhC approach, are herein presented as part of the SYRMA-3D collaboration effort toward the clinical exam. Images are acquired with a $60\text{-}\mu \mathrm{m}\text{pixel}$ dead-time-free single-photon-counting CdTe detector. The samples are imaged at 32 and 38 keV in a continuous rotating mode, delivering 5 to 20 mGy of mean glandular dose. Contrast-to-noise ratio (CNR) and spatial resolution performances are evaluated for both PhC and phase-retrieved images, showing that by applying the phase-retrieval algorithm a five-time CNR increase can be obtained with a minor loss in spatial resolution across soft tissue interfaces. It is shown that, despite having a poorer CNR, PhC images can provide a sharper visualization of microcalcifications, thus being complementary to phase-retrieved images. Furthermore, the first full-volume scan of a mastectomy sample ($9\times 9\times 3{\mathrm{cm}}^3$) is reported. This investigation into surgical specimens indicates that SR BCT in terms of CNR, spatial resolution, scan duration, and scan volume is feasible.

1. Introduction

In radiological application, the use of tunable monochromatic x-ray sources is highly beneficial for both image quality and dose reduction. In fact, it overcomes beam-hardening effects, avoids the deposition of dose due to the low-energy spectral component of conventional polychromatic sources, allows an optimal use of contrast media in K-edge subtraction imaging, and permits a fine dose/image quality optimization based on both the patient and the detector characteristics. The best performing source of high-flux monochromatic x-rays is synchrotron radiation (SR). In addition to the high-energy resolution, SR typically has a high spatial coherence resulting in detectable phase effects that can be exploited for imaging biological tissues. The simplest phase-sensitive imaging technique is the so-called propagation-based phase-contrast (PhC) configuration, where the object-to-detector distance is increased with respect to the conventional absorption configuration. In this way, having a coherent beam, the collected image will show an enhanced edge contrast (i.e., edge enhancement) due to the interference of the diffracted x-rays, resulting in an increased visibility of the interfaces between different structures.¹ It can be shown that, using simple rules of geometrical optics and if the near-field condition is satisfied, the contrast due to phase effects is proportional to the Laplacian of the phase shift induced by the irradiated object.² This means that, apart from the interfaces where an abrupt change in the phase shift produces a high edge contrast, the PhC image will be similar to a conventional absorption image in terms of signal (i.e., contrast) and noise. This topic has been thoroughly detailed quantitatively by both Cloetens et al.¹ and Gureyev et al.³ The edge-enhanced images can be further processed by applying a phase-retrieval (PhR) algorithm, which allows one to decouple phase and absorption information. Hereinafter, the terms PhC and nonphase-retrieved image are used as synonyms. In this work, it used the well-known algorithm based on the transport of intensity equation, first proposed by Paganin and coworkers.⁴ The key parameter of the algorithm is the ratio between the decrement from unity ($\delta$) and the imaginary part ($\beta$) of the complex refraction index $n=1-\delta +i\beta$ of the object, where $\beta$ is proportional to the absorption coefficient and $\delta$ is proportional to the phase shift. The benefit of a proper application of the phase retrieval is to increase contrast-to-noise ratio (CNR) while preserving spatial resolution, thus enhancing the visibility of low-contrast structures.⁵ In more detail, the PhR is expected to reduce image noise while leaving the image contrast, in regions far from sharp interfaces, unaltered.^3,6 The ultimate goal of the clinical application of this technique is to produce images with a higher diagnostic power delivering a dose comparable with conventional radiological exams.

In this context, the energy range, beam dimension, and experimental setup of the SYRMEP (SR for medical physics) beamline at the Elettra Synchrotron Facility (Trieste, Italy) are well suited for exploiting the advantages of SR for breast imaging. In general, it is well known that x-ray breast imaging is challenging due to the need of resolving low-contrast structures (e.g., tumor/normal tissue interfaces) with an acceptable delivered dose. In this framework, the first x-ray PhC mammographic clinical study performed with SR, involving more than 70 patients, has demonstrated an improvement in the image quality and diagnostic performance when compared with the conventional state-of-the-art mammography.^7–9 The transition of PhC mammography from synchrotron to hospitals is a research topic for several groups.^10–15

At the same time, the advent of more efficient digital detectors and powerful reconstruction algorithms allowed the realization of three-dimensional (3-D) mammographic systems, such as tomosynthesis and tomographic scanners. The aim of these techniques is to overcome the superposition of the structures inherent in planar imaging, which may hinder the detection of massive lesions. Remarkable results obtained with breast tomosynthesis have been published,^16,17 despite the intermediate quality between mammography and tomography in terms of voxel size and contrast. The development of breast computed tomography (BCT) systems is a hot topic for several research groups and companies but, at present, only few cone beam BCT prototypes are in use worldwide, the main challenge being the tradeoff between spatial resolution and delivered dose.^17–21

The convincing results of the SR mammographic study along with the growing interest in the field of BCT have been the driving force for moving toward SR PhC tomographic imaging of the breast. The SYRMA-3D (SR for mammography) collaboration aims to set up the world’s first PhC synchrotron-radiation BCT at the Elettra synchrotron facility. For the sake of high image quality and low delivered dose, both the experimental setup and the data processing include a number of innovative elements: high-efficiency CdTe single-photon-counting detector, dedicated preprocessing procedure, PhR algorithm, and Monte Carlo model for the mean glandular dose (MGD) estimation. A first characterization of the imaging system and the first images of breast specimens, obtained with a detector prototype and step-and-shoot mode, have recently been published showing encouraging results in terms of image quality and delivered dose.^22–25 Given these preliminary results, the detector readout, data processing, and scan mode have been updated and optimized in light of the BCT exam. In this work, the first high-resolution reconstructions of mastectomy samples acquired in a continuous rotation with the detector operated in a dead-time-free mode are reported. Moreover, PhC and phase-retrieved images are compared, focusing both on tumor/adipose tissue interfaces and microcalcifications and, for the first time, a full 3-D reconstruction of a mastectomy is shown.

2. Materials and Methods

2.1. Experimental Setup and Dose Evaluation

The images were acquired at the SYRMEP beamline at Elettra. The x-ray beam is produced by one storage ring bending magnet and monochromatized by means of a Si(111) double-crystal monochromator allowing one to tune the energy in the range of 8.5 to 38 keV, with a resolution of 0.1%. The beam cross section in the patient’s room is 220 (horizontal) × $3{\mathrm{mm}}^2$ [vertical, Gaussian shape, full width half maximum (FWHM)]. The samples were imaged hanging from the patient support, constituted by a rotating table with an ergonomically designed aperture at the rotation center.²⁶ Thanks to the negligible divergence of the beam within the object (i.e., parallel beam geometry), the projections were collected only over 180 deg, thus speeding up the acquisition. Each scan was performed in 40 s in a continuous-rotation mode with an angular speed of $4.5\mathrm{deg}/\mathrm{s}$. Given the small vertical dimension of the beam, 10 scans at different table positions were needed to reconstruct the full-volume mastectomy, corresponding to a total scan time of about 7 min for a 3-cm-thick sample. The photon’s flux is adjusted by means of aluminum filters with a thickness ranging from 5 to 11 mm, located about 10 m upstream with respect to the patient position and coupled with absorbing slits to minimize scattering. To further reduce the total scan duration, the collaboration is developing a beam-flattener filter conforming to the beam vertical profile, which is expected to double the usable beam vertical dimension, thus halving the scan time for a given volume. The object-to-detector distance of 1.6 m (the maximum available in the present configuration) allows one to detect phase effects and, along with the laminar shape of the beam, to work in a scatter-free geometry without the need of antiscattering grids. The dosimetric quantity used for determining the desired photon fluence is the total mean glandular dose (${\mathrm{MGD}}_{\mathrm{t}}$), defined as the ratio between the total energy deposited in the whole breast and the glandular mass in the irradiated volume.²² We remark here that this is a conservative choice since, considering only the energy deposited within the irradiated volume, the dose value would be lower. To calculate ${\mathrm{MGD}}_{\mathrm{t}}$, the air kerma at the breast position is multiplied by a conversion factor accounting for breast size and glandularity, obtained from an ad hoc developed Monte Carlo simulation based on a GEANT4 code optimized for breast dosimetry.²⁷ The breast size (i.e., diameter) is measured when the sample is positioned in the holder, whereas a small glandular fraction (20%) is assumed for both samples, based on the indication of the pathologist and presurgery examinations (see Sec. 2.5). In this context, it is worth noticing that, for energies above 30 keV, a 10% error in glandular fraction estimation would result only in a few percent errors in dose estimation.²² A detailed description of the dosimetric system can be found in Castelli et al.⁷ For the sake of simplicity, hereinafter, we identify the MGD as the total MGD.

2.2. Detector and Data Preprocessing

The detector used in this project is a large-area high-efficiency direct-conversion photon-counting device (PIXIRAD-8). This kind of detector offers substantial advantages over the indirect-conversion and/or charge-integration devices, namely a minimum electronic noise and an energy-based discrimination of photons. Furthermore, unlike indirect-conversion devices that make use of a scintillating screen producing a light blurring inside the layer, direct-conversion detectors allow the use of thick layers of high-Z materials ensuring a high DQE without a significant resolution loss.²⁸ PIXIRAD-8 is consisted of eight modules and the pixels are arranged on a honeycomb matrix with $60\text{-}\mu \mathrm{m}$ pitch. Each block has a hybrid architecture in which the CdTe sensor and the readout electronics are coupled by means of the flip-chip bump-bonding technique.²⁹ The active area of each block is $30.7\times 24.8{\mathrm{mm}}^2$, leading to a global active area of $246\times 25{\mathrm{mm}}^2$, corresponding to $4096\times 476\text{pixels}$ with a gap of three pixels between adjacent modules. Each pixel is associated with two independent 15-bit counters that can be used either in a color mode (two different energy thresholds, useful for chromatic imaging) or in a dead-time-free mode. When the latter is selected, the detector fills one counter while reading the other, thus providing a dead-time-free acquisition.²⁹ The detector shows a linear response up to $2\times {10}^5$ counts per second per pixel (30-keV photons, 5-keV threshold): in this study, the maximum registered count rate was $0.5\times {10}^5$ counts per second per pixel, well below the linearity limit. The projections are first streamed to the control PC via a Gigabit Ethernet connection and then undergo an ad hoc developed preprocessing procedure tailored on the detector characteristics. The procedure consists of the following steps:

• 1.dynamic flat-field equalization, to correct pixel-to-pixel nonuniformity and polarization time-dependent gain variations,³⁰
• 2.seaming, to close the dead space between adjacent blocks. This procedure is based on linear interpolation involving a kernel of $4\times 4\text{pixels}$ next to the edge of the block,
• 3.removal of speckles due to bad pixels by means of an alpha-trimmed mean filter, and
• 4.dynamic ring removal procedure based on a rank filter and 3-D Gaussian smoothing.

A comprehensive discussion on the preprocessing optimization, along with a detailed description of the detector operating conditions, goes beyond the scope of this work and has been recently documented in a separate paper.³¹

2.3. Phase Retrieval Algorithm

The phase extraction from a single distance image of a homogeneous object was first demonstrated starting from the transport of intensity equation, i.e., the equation governing the intensity evolution of a paraxial monochromatic scalar electromagnetic wave, with the additional assumption of large Fresnel number, $N_F=a^2/\lambda d\gg 1$.^4,32 The latter equation relates the smallest feature size $a$ of the object to the wavelength $\lambda$ and the object-to-detector distance $d$. Considering the detector’s pixel size as the smallest detail of interest ($a=60\mu \mathrm{m}$), a 30-keV beam ($\lambda =0.04\mathrm{nm}$), and the distance of the used setup ($d=2\mathrm{m}$), it turns out that $N_F\simeq 45$, so the large Fresnel number assumption holds.

The central step of the PhR algorithm is the application to the projection images of a filter in the two-dimensional (2-D) Fourier domain³³

$$H_{1\mathrm{mat}}(u,\upsilon )={[\pi \lambda d\frac{\delta }{\beta }{|\mathbf{w}|}^2+1]}^{-1},$$ (1)

where $\mathbf{w}=(u,\upsilon )$ is the spatial frequency and $\delta /\beta$ is the key parameter of the filter. As this filter assumes the presence of a single homogeneous material that can be described using only one $\delta$ and one $\beta$ value, hereinafter we define $\delta /\beta \stackrel{\mathrm{def}}{=}{(\delta /\beta )}_1$.

Equation (1) can be slightly modified to account for the presence of interfaces between two different materials (e.g., glandular/fat interfaces in the breast tissue)

$$H_{2\mathrm{mat}}(u,\upsilon )={[\pi \lambda d\frac{{\delta }_1-{\delta }_2}{{\beta }_1-{\beta }_2}{|\mathbf{w}|}^2+1]}^{-1}.$$ (2)

In this case, $\delta /\beta$ is replaced with $({\delta }_1-{\delta }_2)/({\beta }_1-{\beta }_2)\stackrel{\mathrm{def}}{=}{(\delta /\beta )}_{12}$, where the subscripts refer to different materials. If more than two materials are present, several images with different ${(\delta /\beta )}_{12}$, one for each interface, can be obtained. In this perspective, the phase retrieval can be seen as a virtual lens that, tuning the parameter ${(\delta /\beta )}_{12}$, enables one to focus upon a particular interface of interest.³⁴

2.4. Image Reconstruction and Analysis

In this study, the preprocessed was reconstructed via a GPU-based filter back projection (FBP) with a Shepp–Logan filtering.³⁵ To obtain the phase-retrieved images, both the filters presented in Eqs. (1) and (2) were used. When using the single-material approach the selected ${(\delta /\beta )}_1$ was one of the breast equivalent tissues, whereas if the two materials filter were used, an interface between glandular and adipose tissues was considered. The values were extracted from a publicly available database³⁶ and are listed in Table 1. It is worth noticing that the difference in the tabulated ${(\delta /\beta )}_{12}$ values when considering a glandular/adipose or a tumor/adipose interface is of the order of few percent. Moreover, from the images reported in this study, a significant difference in contrast between fibroglandular and tumor tissues cannot be demonstrated (in agreement with a previous study³⁷), thus just one ${(\delta /\beta )}_{12}$ value has been used.

Table 1.

Used values of $\delta /\beta$ as a function of energy.

	${(\delta /\beta )}_1$	${(\delta /\beta )}_{12}$
32 keV	2308	869
38 keV	2321	1083

The whole data processing (i.e., preprocessic about 5 min per scan on an eight core Intel Core i7-6700 CPU @ 3.40 GHz.

For an image to have a high diagnostic significance, it is important that the interfaces between different low-contrast tissues are rendered in a clear and sharp way. Moreover, with the chosen $\delta /\beta$ values, the action of the PhR is focused precisely on these low-contrast interfaces. Therefore, although the standard definition of spatial resolution relies on measures across sharp high-contrast edges, in this work, as done in a previous study,²³ we evaluated the spatial resolution capabilities of our system across a sharp low-contrast interface. In particular, an edge profile across a sharp tumoral-fat step-wedge produced by a surgical cut during the preparation for formalin fixation was used. The profiles were then fitted with an error function (erf) and the resolution is defined as the FWHM of the Gaussian obtained deriving the erf. The error associated with the measured FWHM is derived from the fit parameter uncertainty with the usual error propagation rules. The metric used to evaluate the visibility of low-contrast structures is the contrast-to-noise-ratio (CNR), which is defined as

$$\mathrm{CNR}=\frac{S_1-S_2}{\sqrt{\frac{{\sigma }_1^2+{\sigma }_2^2}{2}}},$$ (3)

where $S$ is the mean voxel value in the selected region of interest (ROI), $\sigma$ is the associated standard deviation, and the subscript number is the ROI index. The CNR was measured taking the average CNR of three nonoverlapping pairs of circular ROIs, where for each pair one ROI is selected within the tumoral tissue and the other within the adipose tissue. The associated error is evaluated as half of the difference between the maximum and minimum CNR. The same ROIs and error estimation are used to determine the tissue contrast ($C$), defined as

$$C=\frac{S_1-S_2}{S_2}.$$ (4)

The ROIs used for the spatial resolution, CNR, and $C$ evaluation are shown in Fig. 1(a).

Fig. 1.

Slice of the high dose acquisition (20-mGy MGD) of sample A obtained (a) without, (b) with two materials, and (c) with the single-material PhR. The sample diameter is about 9 cm. In (a) the ROIs for the evaluation of the CNR (circles) and spatial resolution (rectangle) are reported. The insets on the top right of each image show the edge profiles for FWHM evaluation.

2.5. Samples and Acquisition Parameters

Two breast specimens containing cancer, hereinafter referred to as A and B, were imaged for this work. The samples were fixed in formalin and sealed in a vacuum bag. A few studies suggest that, in the selected energy range, the formalin fixation process does not alter significantly the image contrast.^37–39 The Directive 2004/23/EC of the European Parliament and of the Council of March 31, 2004, on setting standards of quality and safety for the donation, procurement, testing, processing, preservation, storage, and distribution of human tissues were followed. The images reported in this study were acquired to guide the pathologist in the localization of lesions for the histological examination, according to the standard procedures of the Pathology Unit of the Academic Hospital of Cattinara, Trieste University, accredited by Joint Commission International. The samples were derived from surgical material sent to the Pathology Unit according to local guidelines for histological examination. Both samples were imaged in a continuous rotating mode with the detector operated in a dead-time-free mode, with a frame rate of 33 fps corresponding to 1200 equally spaced projections over 180 degrees. Sample A is a lumpectomy containing an infiltrating ductal carcinoma with a wide intratumoral sclerotic component with a diameter of about 2.4 cm. This specimen was imaged at 32 keV and the beam flux was adjusted to deliver optionally 5- or 20-mGy MGD. Sample B is a male mastectomy specimen containing an infiltrating ductal carcinoma with a diameter of about 1.2 cm. In this case, a full-volume scan was acquired with a beam energy of 38 keV and an MGD of 20 mGy. When positioned in the holder, both samples had a diameter of about 9 cm and a height of 3 cm, respectively.

3. Results and Discussion

Figure 1(a) shows the reconstruction of one slice of the sample A irradiated with 20-mGy MGD without phase retrieval. Although the edge enhancement is present and visible especially on the air/tissue interfaces, low-contrast details, such as glandular a tumoral tissue branching, are barely visible due to the poor CNR (about 0.7). In Fig. 1(b), the two materials PhR algorithm [i.e., ${(\delta /\beta )}_{12}$] is used, resulting in a remarkable increase of low-contrast details visibility corresponding to a factor of 5 increment in the CNR (about 3.6). The application of the single-material PhR is reported in Fig. 1(c), further increases CNR by a factor 2 (about 6.8) at the expense of spatial resolution: this additional CNR increment does not significantly enhance the visibility of low-contrast details with respect to Fig. 1(b). Moreover, it is worth noticing that in all the three images, one can appreciate a brighter region in the tumor bulk due to the presence of necrotic tissue and scattered microcalcifications. The spatial resolution for each of the three reconstructions was evaluated starting from the edge profiles shown in the insets of Figs. 1(a)–1(c).

In addition, three common denoising filters (Gaussian, mean, and median filters) were alternatively applied to the nonphase-retrieved image to achieve the same CNR of the phase-retrieved with the two material approaches, then the spatial resolution was measured. The results are shown in Fig. 2: the image reconstructed without PhR yields the highest spatial resolution ($\mathrm{FWHM}\simeq 120\mu \mathrm{m}$), but the difference observed with respect to the two materials PhR approach ($\mathrm{FWHM}\simeq 190\mu \mathrm{m}$) is small and compatible within the fit uncertainty. We remark here that the broad error associated with the FWHM of the nonphase-retrieved image is due to the high noise level of the edge profile. The spatial resolutions obtained from the images filtered with the common denoising filters are significantly worse, all of them being over $270\mu \mathrm{m}$. It is interesting to notice that these resolutions are compatible with the resolution ($\mathrm{FWHM}\simeq 300\mu \mathrm{m}$) of the single-material phase-retrieved image that, in turn, has a CNR of about two times higher. As it should be expected, the application of the two materials PhR is the best choice for minimizing the spatial resolution loss while reducing the noise.

Fig. 2.

FWHM of non-PhR (abs), two materials PhR [ph. retr ${(\delta /\beta )}_{12}$], single-material PhR [ph. retr ${(\delta /\beta )}_1$], and denoising filtered (gauss, mean, and median) images. The values are obtained at a fixed $\mathrm{CNR}=3.6$ except for the non-PhR ($\mathrm{CNR}=0.7$) and the single-material PhR ($\mathrm{CNR}=6.8$) images. Error bars derive from the fit uncertainties.

Figures 3(a)–3(c) show a detail of a microcalcification (size $\sim 300\times 200\times 200\mu {\mathrm{m}}^3$) within the sample A, obtained with the three aforementioned approaches. It can be seen that the application of the PhR algorithm results in a blurring of the microcalcification, which worsens as the $\delta /\beta$ parameter is increased. This fact can be easily understood if we consider that neither ${(\delta /\beta )}_1$ nor ${(\delta /\beta )}_{12}$ refer to a calcification/soft tissue interface. On the contrary, the fibrous tissue surrounding the calcification is clearly visible only when the PhR is applied. In this context, images with and without PhR can be regarded as an complementary information: tiny high-contrast details can be better visualized without the phase retrieval, whereas for low-contrast features the phase retrieval is needed.

Fig. 3.

Detail of a $\sim 300\times 200\times 200\mu {\mathrm{m}}^3$ microcalcification of sample A obtained (a) without, (b) with two materials, and (c) with a single-material PhR. Crop window is $8\times 12{\mathrm{mm}}^2$.

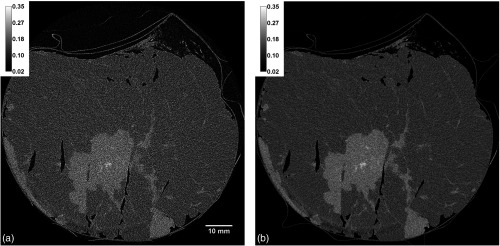
The images of the same slice of the sample A, acquired with 5-mGy MGD and reconstructed without and with the two materials PhR are shown in Figs. 4(a)–4(b). From the figures it is clear that, at low dose, the application of the phase retrieval is even more crucial in terms of low-contrast detail visibility than in the high-dose acquisitions. Spatial resolution, CNR, and contrast were estimated also from these images and the results are shown in Table 2. It can be noticed that, as it is expected, varying the dose the spatial resolution does not change significantly (although, the fit uncertainty for the low dose nonphase-retrieved image increases). The CNR increase associated with the application of the phase retrieval is consistent for high- and low-dose acquisitions: in both cases, the application of the two materials PhR yields an increase by a factor of 5 while the single-material PhR gives about a factor of 10. The fact that reducing the dose by a factor of 4 (from 20 to 5 mGy), the CNR does not decrease by a factor of 2, as it should be expected considering only statistical noise, is due to the structural (i.e., anatomical) noise of the imaged sample that has to be summed to statistical noise. This statement is supported by supplementary CNR measures performed between two homogeneous details inserted in a quality control phantom (images not reported here) and irradiated with the same doses: in this case, changing from 20 to 5 mGy, a factor of 2 reduction in CNR is observed.⁴⁰ Focusing on the contrast, no significant differences in the measured contrast are found when comparing images both with and without PhR (either one or two materials), in agreement with the theory mentioned in Sec. 1. A comprehensive comparison between measured contrasts and the literature is beyond the scope of this work. Anyway, it is noteworthy that the measured contrast ($\sim 0.45$) is compatible, within the experimental uncertainties, with the values inferable by Johns and Yaffe⁴¹ measurements for fibrous adipose interfaces ($\sim 0.42$) and tumoral adipose interfaces ($\sim 0.47$). This study suggests that, especially at low doses, tumor identification should focus on the visualization of tissue structure rather than a contrast discrimination.³⁷ A detailed description of the calibration and accuracy of the system with respect to the quantitative evaluation of attenuation coefficients can be found in Contillo et al.⁴⁰ In addition, it should be noted that given the 1.6-m propagation distance, air attenuation is in the order of 5% to 10% for energy around 30 keV: anyway, the associated CNR loss is significantly smaller than the gain due to phase effects.³⁹ If longer propagation distances are required, the insertion of a vacuum pipe between the object and the detector can be considered to minimize air attenuation.

Fig. 4.

Slice of the low dose acquisition (5-mGy MGD) of sample A obtained (a) without and (b) with two materials PhR. The sample diameter is about 9 cm. The tiny morphological differences with respect to Figs. 1(a)–1(b) are due to the mechanical relaxation of the sample occurred between the two scans.

Table 2.

Summary of the measured values of spatial resolution, CNR, and contrast. The numbers enclosed within round brackets are the uncertainties. The image of the 5-mGy single-material PhR reconstruction is not shown.

MGD [mGy]	Phase retrieval	FWHM [$\mu \mathrm{m}$]	CNR	$C$
20	None	122 (74)	0.67 (0.01)	0.45 (0.02)
	${(\delta /\beta )}_{12}$	195 (26)	3.63 (0.15)	0.44 (0.01)
	${(\delta /\beta )}_1$	299 (19)	6.83 (0.47)	0.45 (< 0.01)
5	None	122 (110)	0.52 (0.03)	0.47 (0.04)
	${(\delta /\beta )}_{12}$	179 (20)	2.60 (0.10)	0.45 (0.03)
	${(\delta /\beta )}_1$	250 (31)	4.18 (0.18)	0.44 (0.02)

In Figs. 5(a)–5(d), a detail of the sample A containing small low-contrast structures is shown at both the delivered doses (5 to 20 mGy) and with or without the two materials PhR, to simultaneously compare the effects of dose and phase retrieval on the image quality. Again, especially when considering the low-dose acquisition, the glandular/tumoral structures cannot be distinguished from the surrounding adipose tissue without the application of the phase retrieval. Noticeably, comparing only the phase-retrieved images, the main features visible in the 20-mGy irradiation can be correctly identified also in the 5-mGy image.

Fig. 5.

A detail of the sample A acquired with (a)–(b) high and (c)–(d) low dose; (a)–(c) are reconstructed without PhR while (b)–(d) with a single-material PhR. The crop window is $15\times 15{\mathrm{mm}}^2$.

The full-volume reconstruction of sample B ($\mathrm{MGD}=20\mathrm{mGy}$, beam energy 38 keV), obtained with the two materials PhR algorithm, is shown in Figs. 6(a)–6(c). The pointers visible both in the axial and lateral views are centered in the tumor mass, whose extension, shape, and boundaries are clearly visible in all the planes. Furthermore, thanks to the laminar beam geometry and the symmetry in the detector pixel matrix, the reconstruction voxel is isotropic and guarantees a constant spatial resolution in all the three orthogonal planes: observing the tiny glandular branchings throughout the sample, one can notice that they are as well defined in the lateral views as in the axial view. We remark here that this is the first full-volume reconstruction of a breast mastectomy obtained by the collaboration.

Fig. 6.

(a) Axial and (b)–(c) lateral views of the full-volume reconstruction of sample B obtained with the two materials PhR. At the crossing of the pointers an infiltrating ductal carcinoma is present. Size of sample $9\times 9\times 3{\mathrm{cm}}^3$.

4. Conclusions

In this study, the latest high-resolution monochromatic CT scans of two breast specimens (about 9 cm in diameter) were acquired, delivering a total MGD in the range of doses delivered in clinical breast-CT (4 to 25 mGy).^18,19,42 The use of a spatially coherent beam, i.e., SR, and a large object-to-detector distance, determines the presence of visible phase effects in the acquired images that can be exploited by applying the PhR algorithm, resulting in a remarkable visibility increase in low-contrast structures. A comparison between the single-material and the two materials PhR was performed, showing that the best way of increasing CNR with a minimal spatial resolution loss is the two materials approach. Seen from another point of view and beyond its physical significance, the PhR can simply be thought of as a filter in the 2-D frequency domain applied to the tomographic projections,³ whereas $\delta /\beta$ can be considered as a reconstruction parameter to be tweaked for privileging either spatial resolution or noise reduction. This approach has been recently used in a study by Baran et al.,³⁹ where a $\delta /\beta$ half than the nominal value is used. When microcalcifications are considered (i.e., tiny high-contrast details), it has been shown that the nonphase-retrieved images yield the minimum blurring and thus can be used as complementary information to the PhR approach. Moreover, we have demonstrated the capability of acquiring high-resolution tomographic images of a thick specimen in a continuous-rotation mode with a delivered dose of 5-mGy MGD: this value has to be compared with the typical dose of a two-view mammography (1 to 2 mGy⁴³) or tomosynthesis exam (1 to 4 mGy⁴⁴). Hence, the minimum dose images presented in this study have a dose slightly higher than, but comparable to, standard screening examinations, possibly offering a higher diagnostic power. In addition, the study reported the first full-volume scan of a breast specimen obtained by the collaboration showing a comparable image quality in the three orthogonal planes. Noticeably, the overall scan time was of about 7 min for a 3-cm-thick sample, thus not incompatible with a clinical exam duration (e.g., comparable with an MRI scan). This is one of the main advantages of the free-propagation-based configuration over other PhC techniques (e.g., grating-based PhC tomography) that, introducing optical elements reducing the x-ray flux, require much longer exposure times.⁴⁵ In this perspective, SR-BCT is feasible in terms of delivered dose, exam duration, and scan volume. Moreover, a great effort is being devoted to further shorten the scan time to ensure patient’s comfort, preventing voluntary motion: the reduction in the number of acquired projections⁴⁶ and the use of a wider portion of the beam thanks to an ad-hoc shaped flattening filter are expected to reduce the scan time by a factor two or more. Furthermore, the effects of involuntary movement (e.g., breathing and heartbeat) on the image quality are now under investigation along with the possible use of a breast-immobilizing system.⁴⁷

This study has to be regarded as a part of a wider framework devoted to the optimization of the acquisition and reconstruction parameters. At present, the collaboration is working on several topics toward the clinical exam: in addition to the scan time reduction, different reconstruction algorithms are currently under evaluation and a systematic study including SIRT, SART, CGLS, MLEM, and MR-FBP is ongoing.⁴⁶ Furthermore, the collaboration is now defining the exam protocol accounting for quality controls, patient safety, security, and comfort.

It is well known that a wide use of SR facilities as diagnostic tools is unfeasible in terms of costs and scale. Anyway, it is the authors’ belief that clinical trials at synchrotrons are important to evaluate the potential impact of x-ray techniques on diagnostic outcomes, possibly stimulating translational research on more compact and less expensive systems suitable for the hospital’s clinical practice. Such studies can provide both a gold-standard, thanks to the ideal experimental conditions (e.g., high-flux, spatial, and temporal coherence) and valuable indications toward the implementation in the clinical practice.

Biography

Biographies for the authors are not available.

Disclosures

No conflicts of interest, financial or otherwise, are declared by the authors.