Metabolic Determinants of Enzyme Evolution in a Genome-Scale Bacterial Metabolic Network

Abstract

Different genes and proteins evolve at very different rates. To identify the factors that explain these differences is an important aspect of research in molecular evolution. One such factor is the role a protein plays in a large molecular network. Here, we analyze the evolutionary rates of enzyme-coding genes in the genome-scale metabolic network of Escherichia coli to find the evolutionary constraints imposed by the structure and function of this complex metabolic system. Central and highly connected enzymes appear to evolve more slowly than less connected enzymes, but we find that they do so as a by-product of their high abundance, and not because of their position in the metabolic network. In contrast, enzymes catalyzing reactions with high metabolic flux—high substrate to product conversion rates—evolve slowly even after we account for their abundance. Moreover, enzymes catalyzing reactions that are difficult to by-pass through alternative pathways, such that they are essential in many different genetic backgrounds, also evolve more slowly. Our analyses show that an enzyme’s role in the function of a metabolic network affects its evolution more than its place in the network’s structure. They highlight the value of a system-level perspective for studies of molecular evolution.

Introduction

Different proteins evolve at very different rates (Zuckerkandl and Pauling 1965; Li et al. 1985; Alvarez-Ponce 2014). Half a century after this observation seeded the field of molecular evolution (Zuckerkandl and Pauling 1965), the reasons are still a subject of active research, and even more so since the genome-era made sequence and functional data about proteins abundantly available. Much of the variation in evolutionary rates stems from variation in selective constraints on proteins, and several factors influence these constraints (for recent reviews, see Alvarez-Ponce 2014; Zhang and Yang 2015). The most important is the amount of a protein that is expressed, and the breadth of its expression across cells or tissues in multicellular organisms (Duret and Mouchiroud 2000; Pál et al. 2001; Drummond et al. 2005). Highly and broadly expressed genes are under strong purifying selection, and therefore evolve slowly. Other factors influence evolutionary rates more weakly. They include protein length (Subramanian and Kumar 2004; Bloom et al. 2006; Ingvarsson 2006; Liao et al. 2006; Kryuchkova and Robinson-Rechavi 2014), essentiality (Hurst and Smith 1999; Jordan et al. 2002; Rocha and Danchin 2004), multifunctionality (Wilson et al. 1977; He and Zhang 2006; Salathé et al. 2006; Podder et al. 2009), subcellular localization (Liao et al. 2010), or being a chaperone client (Bogumil and Dagan 2010; Williams and Fares 2010; Aguilar-Rodríguez et al. 2016; Kadibalban et al. 2016). To gain deeper insights into the determinants of protein evolution, one must go beyond a gene-centered approach and embrace a systems-oriented view of protein evolution.

Inside a cell, proteins often form large and complex networks of interacting molecules. The position of a protein within such a network, as well as its role in the network’s function, can affect the protein’s evolution. In other words, the structure and function of a molecular network can impose selective constraints on its member proteins (Cork and Purugganan 2004). For example, proteins at the center of a protein–protein interaction network evolve more slowly (they are more constrained) than those at the periphery (Fraser et al. 2002; Jordan et al. 2003; Hahn and Kern 2005; Lemos et al. 2005; Alvarez-Ponce 2012; Alvarez-Ponce and Fares 2012). In contrast, in the yeast transcriptional regulation network, more central transcription factors evolve faster than less central ones (Jovelin and Phillips 2009). As these two types of cellular networks have similar topological properties (Barabasi et al. 2004), this difference in selective constraints over the network structure must ultimately be caused by different network functions. Nonetheless, despite being significant and consistent across many different organisms, the effects of network topology on protein evolution are weak. It could be caused by confounding factors such as expression level, and it can be affected by biased and low-quality data (Bloom and Adami 2003; Batada et al. 2006).

Metabolic networks constitute another important class of cellular network. They are well-studied in model organisms such as Escherichia coli (Feist et al. 2007), and comprise hundreds to thousands of chemical reactions, most of them catalyzed by enzymes encoded in genes. In a metabolic network, chemical reactions are organized in a highly reticulate manner to perform two main functions: Energy production and biosynthesis. Specifically, using energy and chemical elements from environmental nutrients, metabolic networks synthetize essential small molecules (i.e., amino acids, ribonucleotides, deoxynucleotides, lipids, and enzyme cofactors). The chemical reactions a metabolic network catalyzes are encoded in a metabolic genotype—a genome’s set of enzyme-encoding genes. The network’s phenotype can be defined as the set of molecules it can synthesize, and the rate at which it does so (Matias Rodrigues and Wagner 2009). Thanks to computational approaches such as flux balance analysis (FBA) (Orth et al. 2010; Bordbar et al. 2014), the relationship between metabolic genotypes and phenotypes can be studied computationally, which also allows us to study how selection for a given metabolic phenotype can constrain metabolic enzyme evolution. This type of analysis is currently not possible in other types of molecular networks, such as protein–protein interaction networks.

Previous work in eukaryotes has revealed that more central and more highly connected enzymes in metabolic networks, that is, those sharing metabolites with many other enzymes, evolve more slowly (Vitkup et al. 2006; Lu et al. 2007; Greenberg et al. 2008; Hudson and Conant 2011; Montanucci et al. 2011). Additionally, enzymes catalyzing reactions with a high metabolic flux—the rate at which a reaction transforms substrates into products—tend to evolve slowly (Vitkup et al. 2006; Colombo et al. 2014), and enzymatic domains with a greater influence on the dynamics of a metabolic pathway also tend to be more selectively constrained (Mannakee and Gutenkunst 2016). In this contribution, we study how the structure and function of a bacterial metabolic network affects the evolution of metabolic genes through point mutations. To our knowledge, this is the first time that such a study is performed using the whole-genome metabolic reconstruction of E. coli (Feist et al. 2007), which is arguably the best-known metabolic network of any living organism. Specifically, we study how quantities such as enzyme connectivity and metabolic flux affect evolutionary rate. To do so, we account for possible flux variation with Markov chain Monte Carlo (MCMC) sampling, a method that has not been used before in this type of evolutionary analysis. Additionally, we also study for the first time the influence of factors such as reaction superessentiality (Samal et al. 2010), which quantifies how easily a reaction can be bypassed in a metabolic network by other reactions or pathways, and the number of different chemical reactions that an enzyme catalyzes (enzyme multifunctionality). In performing these analyses, we comprehensively characterize metabolic determinants of enzyme evolution in E. coli.

Materials and Methods

Metabolic Network

To investigate how the topology of a metabolic network affects the evolution of metabolic genes, we constructed a reaction graph representation of the E. coli metabolic network model iAF1260 (Feist et al. 2007), which includes 2,382 reactions and 1,972 metabolites. In a reaction graph, nodes represent reactions, which are connected by an edge if they share at least one metabolite as either a substrate or a product (Montañez et al. 2010). When constructing this reaction graph, we did not consider the following currency metabolites, which are the most highly connected metabolites: H, H₂O, ATP, orthophosphate, ADP, pyrophosphate, NAD, NADH, AMP, NADP, NADPH, CO₂, and CoA (Vitkup et al. 2006). The inclusion of such metabolites, which participate in many different reactions, would create many reactions that are adjacent in the graph but not otherwise functionally related. Such reactions would come to dominate the structure of the network, and obscure patterns of connections between functionally related reactions. Our results are qualitatively insensitive to the exact number of metabolites removed. The reaction graph thus created comprises 2,382 nodes and 18,953 edges. Its diameter, that is, the longest of the shortest paths between any two nodes, is 15. It has a characteristic path length, that is, the average shortest distance between any pair of nodes, of 4.55. The clustering coefficient, that is, the fraction of a node’s neighbors that are also neighbors themselves, of this graph is 0.54, and its assortativity by degree, that is, the propensity for nodes with a similar number of neighbors to share an edge, is 0.17. In this graph, we computed the connectivity (or degree) of every reaction, which is its number of edges. In other words, the connectivity of a reaction is the number of other reactions that share at least one metabolite with the focal reaction. To determine the centrality of a reaction, we computed its betweenness centrality (Freeman 1977; Newman 2010), which is the number of shortest paths between any two nodes that pass through this reaction, using the Python package “igraph.” Mathematically, the betweenness centrality x_i of node i is defined as $\sum _{st}{n}_{st}^i$, where $n_{st}^i$ is 1 if node i lies on the shortest path between nodes s and t, and 0 otherwise (or if s and t are in different components of the network) (Newman 2010).

To study how different properties of a metabolic reaction may affect the evolution of the enzyme-coding gene whose product catalyzes the reaction, it is preferable to work mostly with reactions that show a one-to-one relationship to enzyme-encoding genes. Therefore, we exclude from our evolutionary analyses reactions catalyzed by large macromolecular complexes that are encoded by multiple genes. Following Vitkup et al. (2006), for enzymes that catalyze more than one reaction, we use the reaction carrying the largest metabolic flux (the rate at which metabolites are converted into products) because it is the reaction imposing a higher evolutionary constraint. In addition, also following Vitkup et al. (2006), wherever different enzymes (isoenzymes) catalyze the same chemical reaction, we use the enzyme with the lowest rate of sequence evolution. The resulting data set comprises 659 enzyme-coding genes associated with the same number of metabolic reactions.

Metabolic Fluxes

We determined the distribution of fluxes that is allowable during growth on glucose for each reaction in the E. coli metabolic model iAF1260 (Feist et al. 2007) using MCMC sampling (Schellenberger and Palsson 2009). We used the artificially centered hit-and-run algorithm (ACHR) (Kaufman and Smith 1998) with minor modification as described by Bordbar et al. (2010) and Lewis, Schramm, et al. (2010). We implemented the ACHR algorithm with the ACHRSampler in COBRA Toolbox v.2.0.5 (Schellenberger, Que, et al. 2011), using the MATLAB (The MathWorks, Natick, MA) environment R2012b. We used a minimal (computational) medium in which glucose was the only carbon source, and set the uptake rate of glucose to the value of 8 millimoles per gram dry cell weight per hour. Following Nam et al. (2012), in order to restrict the sampling to the space of flux values relevant to in vivo E. coli growth on glucose, we established a lower bound to the biomass objective function of 90% of the optimal growth rate predicted by FBA (Orth et al. 2010). The mixed fraction is a metric introduced by Bordbar et al. (2010) to measure the uniformity of the sample from the space of allowed fluxes. We obtained a mixed fraction of 0.5096, which suggests that the space was nearly uniformly sampled (Bordbar et al. 2010). We removed reactions with a median flux value >15 millimoles per gram dry cell weight per hour from further analysis to ensure the exclusion of reactions involved in futile cycles (Beard et al. 2002; Schellenberger, Lewis, et al. 2011).

Reaction Superessentiality, Reaction’s Genome Occurrence, and Enzyme Multifunctionality

We obtained superessentiality indices of metabolic reactions for growth on glucose (SI_glu) and for growth on 54 different sole carbon sources (SI₅₄) from Barve et al. (2012). We obtained data about a reaction’s genome occurrence from the same study. A reaction’s genome occurrence is defined as the fraction of 1,093 prokaryotic species containing a gene encoding an enzyme known to catalyze the reaction.

We followed the classification of E. coli K-12 enzymes in generalists and specialists of Nam et al. (2012). Enzymes that only catalyze a specific chemical reaction were classified as specialists, while enzymes that catalyze more than one reaction were classified as generalists.

Evolutionary Rates

We obtained the values of d_N/d_S, d_N, and d_S in this analysis from the study by Alvarez-Ponce et al. (2016). In that study, orthologs in E. coli and S. enterica genomes were identified as reciprocal best hits (Tatusov et al. 1997) using the protein–protein Basic Local Alignment Search Tool (i.e., BLASTP with an E-value cut-off of 10⁻¹⁰). Each pair of orthologous proteins was aligned using ProbCons 1.2 (Do et al. 2005). The resulting alignments were back-translated into codon-based nucleotide alignments, and the ratio d_N/d_S was estimated using the program codeml from the package PAML 4.7 (one-ratio model M0) (Yang 2007). We removed d_N/d_S values >10 from our analyses.

Gene Expression and Protein Abundance

We obtained gene expression data for E. coli K-12 MG1655 grown in rich medium (LB) at 37°C from Chen and Zhang (2013), who quantified gene expression levels as numbers of RNA-seq reads per gene, normalized by gene length. We retrieved protein abundance data of E. coli K-12 MG1655 from the integrated data set of PaxDb 3.0 (Wang et al. 2012).

Statistical Analyses

We used R for all statistical analyses and plots. We performed the partial correlation analyses using the function “pcor.test” from the R package “ppcor.” We carried out the principal component regression analysis using the package “pls.” We performed a base-10 logarithmic transformation of continuous variables when such transformations lead to a higher percent of the variance in evolutionary rates explained by the model (R²). If data for a continuous variable included values equal to zero, we added a small constant of 0.001 to all values to allow its logarithmic transformation. We scaled the independent variables to zero mean and unit variance.

Results

The Effect of Metabolic Network Topology on Enzyme Evolution

To study how network structure affects enzyme evolution, we constructed a reaction graph representation of the whole-genome E. coli metabolic network, in which the nodes represent reactions. Two reactions are connected by an edge if they share at least one metabolite (Materials and Methods). In such a graph, the connectivity of a reaction corresponds to the number of other reactions that produce or consume the reaction’s substrates or products. The connectivity of an enzyme is equivalent to the connectivity of the reaction catalyzed by the enzyme. The centrality of an enzyme can be measured as the number of shortest pathways passing through the reaction node associated with the enzyme (betweenness centrality).

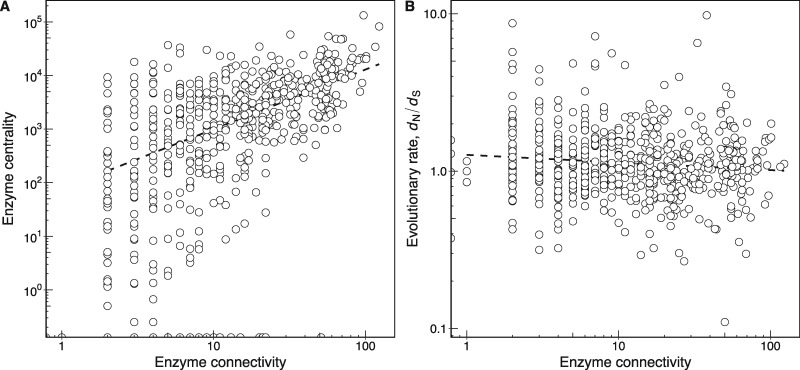
In a metabolic network, highly connected enzymes tend to occupy a central position in the network (as determined by their betweenness centrality, Materials and Methods), while less connected enzymes are more peripheral (fig. 1A; Spearman’s ρ  =  0.524, P < 2.2 × 10⁻¹⁶, n = 635). In other words, enzymes in central metabolic processes, such as central carbon metabolism, tend to be highly connected, while enzymes in peripheral pathways tend to be less connected.

Fig. 1.

—Highly central and connected enzymes in a metabolic network do not evolve slowly. (A) The relationship between enzyme connectivity and centrality in the Escherichia coli metabolic network (Spearman’s ρ  =  0.524, P < 2.2 × 10⁻¹⁶, n = 635). The centrality measure of a reaction is its betweenness centrality determined from the reaction graph (Materials and Methods). (B) The relationship between enzyme connectivity and evolutionary rate measured as d_N/d_S (Spearman’s ρ = −0.088, P = 0.028, n = 635). In both panels, a dashed line shows the best linear fit to the data and is provided as a visual guide. Note the double-logarithmic scale.

One might expect that more highly connected enzymes in a metabolic network are more constrained in their rate of evolution than less connected enzymes. The reason is that the reaction products of highly connected enzymes are substrates of many different reactions, such that any mutation disturbing product formation is bound to be more deleterious in a highly connected enzyme. However, a previous study on E. coli metabolism found no correlation between enzyme connectivity in core intermediary metabolism and evolutionary rate, determined as the rate of amino acid replacements, for 108 pairs of E. coli–Haemophilus influenzae orthologs (Hahn et al. 2004). In contrast, a later study found that highly connected enzymes in the metabolic network of Saccharomyces cerevisiae do evolve more slowly (Vitkup et al. 2006). We suspected that the original negative result in E. coli could be caused by small statistical power resulting from the many fewer enzymes analyzed by Hahn et al. (2004) (n = 108) than by Vitkup et al. (2006) (n = 671). We therefore repeated the E. coli analysis using the much larger whole-genome metabolic reconstruction. We estimated the evolutionary rate of an enzyme as the ratio of nonsynonymous substitutions to synonymous substitutions per nucleotide site (d_N/d_S) in the gene coding for the enzyme. We used values of d_N/d_S obtained by comparing genes in E. coli to orthologs in the closely related genome of Salmonella enterica (Alvarez-Ponce et al. 2016). A small value of d_N/d_S indicates a lower evolutionary rate due to higher constraints on enzyme evolution. Figure 1B shows the relationship between enzyme connectivity and the rate of evolution (Spearman’s ρ = −0.088, P = 0.028, n = 635; table 1). The negative correlation is very small but significant.

Table 1.

Correlations of Various Quantities with d_N/d_S

Quantity	Spearman’s ρ	P Value
Enzyme connectivity	−0.088	2.8 × 10−2
Betweenness centrality	0.074	6.1 × 10−2
Metabolic flux	−0.299	1.1 × 10−13
SIglu	−0.313	6.4 × 10−14
SI54	−0.274	6.7 × 10−11
Gene expression	−0.340	9.4 × 10−15
Protein abundance	−0.488	< 2.2 × 10−16

One potentially important confounding factor in the association between enzyme connectivity and evolutionary constraint is enzyme expression. Highly connected enzymes tend to be highly abundant (Spearman’s ρ  =  0.163, P = 9.5 × 10⁻⁵, n = 565), and in general, abundant proteins tend to evolve more slowly (Pál et al. 2001; Drummond et al. 2005). This association between expression level and evolutionary rate also holds for enzymes. Specifically, we observe that high enzyme expression is associated with slow evolution (low d_N/d_S) regardless of whether expression is measured on the mRNA level (Spearman’s ρ = −0.340, P = 9.4 × 10⁻¹⁵, n = 491; table 1) or on the protein level (Spearman’s ρ = −0.488, P < 2.2 × 10⁻¹⁶, n = 565; table 1). Since expression of enzyme-coding genes is correlated between the mRNA and protein level (Spearman’s ρ  =  0.432, P < 2.2 × 10⁻¹⁶, n = 433), we focus our analysis below on the protein level (Wang et al. 2012), but note that all reported results also hold for the mRNA level. When controlling for enzyme abundance in a partial correlation analysis between enzyme connectivity and evolutionary rate, the correlation loses statistical significance (Spearman’s ρ  =  0.009, P = 0.830, n = 565; table 2). In other words, while highly connected enzymes evolve at slightly lower rates than less connected enzymes, this association is a byproduct of the relationship between evolutionary rate and enzyme abundance.

Table 2.

Partial Correlations of Various Quantities with d_N/d_S

Quantity | Controlled Quantity	Spearman’s ρ	P Value
Enzyme connectivity | Protein abundance	0.009	8.3 × 10−1
Betweenness centrality | Protein abundance	0.082	5.1× 10−2
Metabolic flux | Protein abundance	−0.164	1.5 × 10−4
SIglu | Protein abundance	−0.198	6.9 × 10−6
SIglu | Metabolic flux	−0.197	3.4 × 10−6
SI54 | Protein abundance	−0.187	2.1 × 10−5
SI54 | Metabolic flux	−0.190	7.4 × 10−6

Similarly to enzyme connectivity, one might expect that more central enzymes should be more constrained in their evolution, but this relationship is also not consistent across studies. Some studies in eukaryotic species have found a significant association (Lu et al. 2007; Hudson and Conant 2011), while others have not (Greenberg et al. 2008; Montanucci et al. 2011; Colombo et al. 2014). We find a very weak positive association that is not significant (Spearman’s ρ  =  0.074, P = 0.061, n = 635; table 1), and that is also not significant after controlling for enzyme abundance in a partial correlation analysis (Spearman’s ρ  =  0.082, P = 0.051, n = 565; table 2). Thus, there is no clear association between enzyme centrality and evolutionary rate.

Enzymes Catalyzing Reactions with High Metabolic Flux Evolve Slowly

A reaction’s metabolic flux refers to the rate at which the reaction converts substrates into products. One might expect that enzymes catalyzing high flux reactions may evolve more slowly. The reason is that such enzymes tend to supply products to a large number of reactions and pathways, such that the effects of flux-diminishing mutations may be more deleterious than in low-flux enzymes (Vitkup et al. 2006). To study the relationship between metabolic flux and the rate of enzyme evolution, we applied flux balance analysis (FBA) to the metabolism of E. coli (Feist et al. 2007). FBA is a linear programming method that maximizes the rate of biomass production in a given nutritional environment, simultaneously balancing all the metabolic fluxes under a steady state assumption and a set of flux constraints (Orth et al. 2010). FBA has been extensively used to predict the phenotype of a metabolism from its genotype, that is, to predict the ability of a metabolism to synthetize biomass in a given chemical environment from the genes encoding the metabolism’s enzymes (Matias Rodrigues and Wagner 2009; He et al. 2010; Barve et al. 2012; Barve and Wagner 2013; Harcombe et al. 2013; Bordbar et al. 2014; Hosseini et al. 2015; Plata et al. 2015). FBA predictions are in good agreement with experimental data for model organisms such as E. coli (Edwards and Palsson 2000b; Edwards et al. 2001; Ibarra et al. 2002; Segre et al. 2002; Fong and Palsson 2004; Feist et al. 2007; Lewis, Hixson, et al. 2010).

We applied FBA to the E. coli metabolic network iAF1260 (Feist et al. 2007), maximizing aerobic growth on glucose in an environment where glucose is the only carbon source. Analyzing the association between metabolic flux and evolutionary rate is complicated by the fact many distributions of fluxes through individual enzymes can produce the same maximal biomass synthesis rate. For example, if two different reactions can produce the same biomass molecule at the same maximal rate, one of the two reactions could carry the maximal flux, while the other carries no flux, or both reactions could be active, such that the sum of their individual fluxes produces the metabolite at the maximal rate. In other words, a metabolic network can solve the problem of synthesizing biomass in multiple equivalent ways. To account for this flux variation, we used MCMC sampling to uniformly sample the space of all possible flux values (Schellenberger and Palsson 2009). We then computed a distribution of flux values for each of the reactions in the E. coli metabolic network, and used the median of this distribution as the reaction flux. To our knowledge, this is the first time that the complete flux distribution, as determined by MCMC sampling, is taken into consideration in studying the relationship between metabolic flux and enzyme evolution.

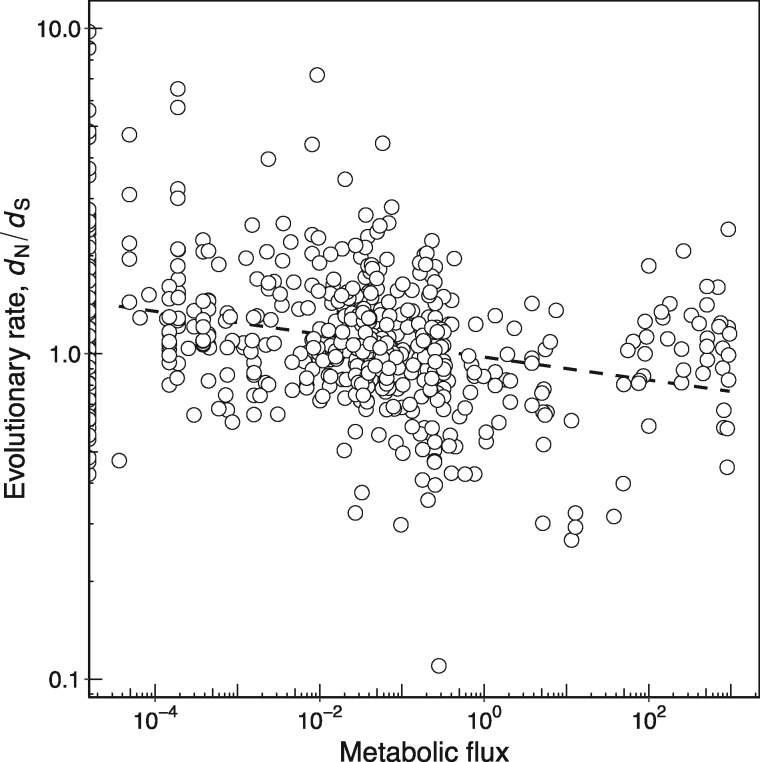
Figure 2 shows that enzymes catalyzing high-flux reactions evolve more slowly (Spearman’s ρ = −0.299, P = 1.1 × 10⁻¹³, n = 592; table 1). Importantly, this association does not disappear if we account for enzyme abundance: While high-flux enzymes tend to be highly abundant (Spearman’s ρ  =  0.370, P < 2.2 × 10⁻¹⁶, n = 529), they still evolve more slowly in a partial correlation analysis that controls for enzyme abundance (Spearman’s ρ = −0.164, P = 1.5 × 10⁻⁴, n = 529; table 2). This observation agrees with a previous finding that high-flux yeast metabolic enzymes are subject to more constrained evolution (Vitkup et al. 2006). A similar association has been found with experimental flux measurements in the human erythrocyte core metabolism (Colombo et al. 2014).

Fig. 2.

—Enzymes catalyzing reactions with high metabolic flux evolve more slowly. The relationship between metabolic flux and enzyme evolutionary rate measured as d_N/d_S (Spearman’s ρ = −0.299, P = 1.1 × 10⁻¹³, n = 592). The dashed line shows the best linear fit to the data and is provided as a visual guide. Flux values <10⁻⁵ are set to zero. Note the logarithmic scale on both axes.

Highly Superessential Enzymes Evolve Slowly

A central function of a metabolic network is to synthetize the small-molecule precursors of biomass (amino acids, nucleotides, and cofactors) that are indispensable for cell growth and survival. In a given chemical environment, a metabolic reaction is essential if its product is needed for viability, that is, for biomass synthesis, and if its removal (“knock-out”) eliminates this ability. Otherwise, the reaction is nonessential. Reaction essentiality depends not only on the environment but also on a network’s genotype, that is, on the genes encoding the enzymes of the network. For example, certain genes are only essential in some strains of Saccharomyces cerevisiae (Dowell et al. 2010). One reason for such variation in essentiality is that different organisms can synthesize the same biomass molecules via alternative metabolic pathways that comprise different biochemical reactions and enzymes, which are encoded by different genes (Edwards and Palsson 1999, 2000a, 2000b; Barve et al. 2012).

While it is easy to manipulate an organism’s environment experimentally to study how reaction essentiality depends on the environment, current technologies limit our ability to systematically alter metabolic genotypes to study how essentiality varies with metabolic genotypes, that is, with the presence or absence of genes encoding alternative metabolic pathways. This limitation calls for computational approaches. One such approach is suited to study comprehensively how the presence or absence of enzyme-coding genes affects the essentiality of other enzyme-coding genes (Barve et al. 2012). It builds on the ability of FBA to efficiently predict a metabolic network’s phenotype—whether the network can produce biomass in a given environment—from its genotype. Briefly, the approach samples the “universe” of >5,000 biochemical reactions known to occur in at least one species, to generate viable metabolic networks with a given phenotype, but an otherwise random complement of reactions (Matias Rodrigues and Wagner 2009). By analyzing large ensembles of such random viable networks, one can determine how difficult it is to bypass a reaction through an alternative metabolic pathway, by computing a reaction’s superessentiality index (SI) (Barve et al. 2012). The SI of a reaction, which ranges from zero to one, is the fraction of random viable networks in which the reaction is essential for viability. In any given environment, reactions with a SI close to zero are easily bypassed, and nonessential for viability in most metabolisms, whereas reactions with the highest SI of one are always essential and cannot be bypassed according to current biochemical knowledge.

It is possible that highly superessential reactions (large SI, not easily by-passed) evolve at lower rates, because they may be subject to stronger purifying selection caused by their greater importance for viability in different genetic backgrounds. This could be especially the case in bacteria, where gene content can evolve very fast via lateral gene transfer, so that a given enzyme may become part of many different metabolic networks during its evolutionary history. To find out whether this is the case, we used superessentiality indices of E.coli metabolic reactions computed for 1) an aerobic minimal environment with glucose as the only carbon source (SI_glu) and 2) 54 minimal environments that contain different unique carbon sources (SI₅₄) (Barve et al. 2012). Enzymes catalyzing highly superessential enzymes tend to be present in most prokaryotic genomes while enzymes catalyzing less superessential enzymes are less common (Barve et al. 2012). There is a positive association between the SI_glu of a metabolic reaction and the fraction of prokaryotic genomes that carry a gene coding for an enzyme known to catalyze the reaction (Spearman’s ρ  =  0.444, P < 2.2 × 10⁻¹⁶, n = 548). This association is also found for SI₅₄ (Spearman’s ρ  =  0.356, P < 2.2 × 10⁻¹⁶, n = 548).

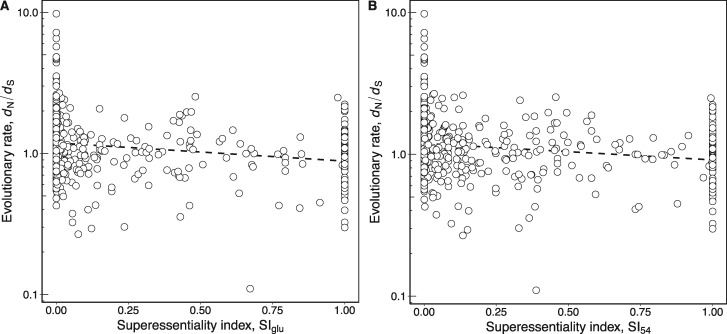
Figure 3A shows that E. coli reactions with high SI_glu evolve more slowly (Spearman’s ρ = −0.313, P = 6.4 × 10⁻¹⁴, n = 548; table 1). It is possible that this association could be explained by enzyme abundance, because superessential enzymes tend to be highly abundant (Spearman’s ρ  =  0.287, P = 3.7 × 10⁻¹¹, n = 510). However, the association between SI_glu and d_N/d_S persists in a partial correlation analysis that controls for protein abundance (Spearman’s ρ = −0.198, P = 6.9 × 10⁻⁶, n = 510; table 2). In other words, enzymes that are difficult to bypass in a glucose minimal environment evolve slowly, and do so independently of their abundance.

Fig. 3.

—Enzymes with high superessentiality evolve more slowly. (A) Scatter-plot showing the negative association between enzyme superessentiality in glucose (SI_glu) and evolutionary rate measured as d_N/d_S (Spearman’s ρ = −0.313, P = 6.4 × 10⁻¹⁴, n = 548). (B) Scatter-plot showing the association between enzyme superessentiality in 54 different carbon sources (SI₅₄) and d_N/d_S (Spearman’s ρ = −0.274, P = 6.7 × 10⁻¹¹, n = 548). In both panels, a dashed line shows the best linear fit to the data and is provided as a visual guide. Note the logarithmic scale of the y axes.

Like SI_glu, SI₅₄ quantifies how difficult it is to bypass a metabolic reaction, but does so for 54 different environments, each containing one of 54 nutrients as its sole carbon source. A reaction or enzyme has a high SI₅₄ if its removal abolishes viability in at least one of the 54 different environments for a large fraction of random networks viable in these 54 environments. Enzymes with a high SI₅₄ also evolve slowly (fig. 3B; Spearman’s ρ = −0.274, P = 6.7 × 10⁻¹¹, n = 548; table 1). While these enzymes also tend to be highly abundant (Spearman’s ρ  =  0.193, P = 1.2 × 10⁻⁵, n = 510), the association persists when we control for enzyme abundance in a partial correlation analysis (Spearman’s ρ = −0.187, P = 2.1 × 10⁻⁵, n = 510; table 2).

Reactions highly superessential in a glucose-minimal environment tend to carry a high metabolic flux in this environment (Spearman’s ρ  =  0.500, P < 2.2 × 10⁻¹⁶, n = 548). Metabolic flux is thus an additional potentially confounding factor for the observed relationship between SI_glu and evolutionary rate. However, a partial correlation analysis shows that enzymes with high SI_glu still evolve more slowly after controlling for metabolic flux (Spearman’s ρ = −0.197, P = 3.4 × 10⁻⁶, n = 548; table 2). Similarly, the effect of SI₅₄ on enzyme evolution still holds after controlling for metabolic flux (Spearman’s ρ = −0.190, P = 7.4 × 10⁻⁶, n = 548; table 2).

The Multifunctionality of an Enzyme Does Not Affect Its Rate of Evolution

Metabolic enzymes can be classified as either specialists or generalists (Nam et al. 2012). A specialist enzyme catalyzes one specific chemical reaction, while a generalist enzyme catalyzes more than one reaction. One might expect that generalist enzymes evolve more slowly than specialist enzymes, since mutations in the genes encoding them may affect more than one metabolic pathway or function. This would at least be predicted by existing work on mutations that are pleiotropic, that is, they affect multiple different phenotypes (Stern and Orgogozo 2008). For example, theoretical considerations (Baatz and Wagner 1997; Orr 2000; Otto 2004), and empirical evidence in yeast suggest that highly pleiotropic mutations tend to be more deleterious than less pleiotropic mutations (Cooper et al. 2007).

For metabolic enzymes in E. coli, we find that generalist enzymes have a lower average evolutionary rate (1.241; n = 216) than specialist enzymes (1.308; n = 424), but the difference between these two enzyme categories is not significant (Wilcoxon rank-sum test, P = 0.804). Thus, there is no connection between multifunctionality or pleiotropy on the one hand, and evolutionary rate on the other hand, at least for E. coli metabolic enzymes.

Principal Component Regression Analysis

Finally, we performed a principal component regression, which is an established method to study the relative contributions of different determinants of protein evolutionary rates (Drummond et al. 2006). Principal component regression computes new variables, called principal components, which are linear combinations of the original predictor variables, and then regresses the response variable against them. We performed principal component regression using protein abundance, enzyme connectivity, betweenness centrality, metabolic flux, SI_glu, SI₅₄, and enzyme multifunctionality as potential predictor variables. Table 3 shows the numerical data from the analysis, while figure 4 shows these data graphically.

Table 3.

Results from the Principal Component Regression Analysis

	Principal Components
	1	2	3	4	5	6	7	All
Percentage of explained variance in
dN/dS	12.55***	3.52***	1.77***	8.51***	0.21	0.01	0.28	26.85
Percent contributions of each variable
Protein abundance	7.3	2.3	5.9	71.9	3.5	8.8	0.1
Enzyme connectivity	3.0	42.2	1.9	10.9	0.0	41.8	0.2
Betweenness centrality	6.4	36.2	8.8	2.2	2.9	42.1	1.4
Superessentiality index, SIglu	32.4	5.0	0.0	2.7	2.5	4.6	52.7
Superessentiality index, SI54	29.6	3.6	0.8	6.2	15.1	1.3	43.3
Metabolic flux	21.2	0.2	5.0	0.4	69.7	1.3	2.3
Enzyme multifunctionality	0.1	10.4	77.5	5.7	6.2	0.0	0.0

Note.—We indicate in bold the contributions of a variable to a principal component when >20%.

Significance levels:

^*P < 0.05, **P < 0.001, ***P < 10⁻⁵.

Fig. 4.

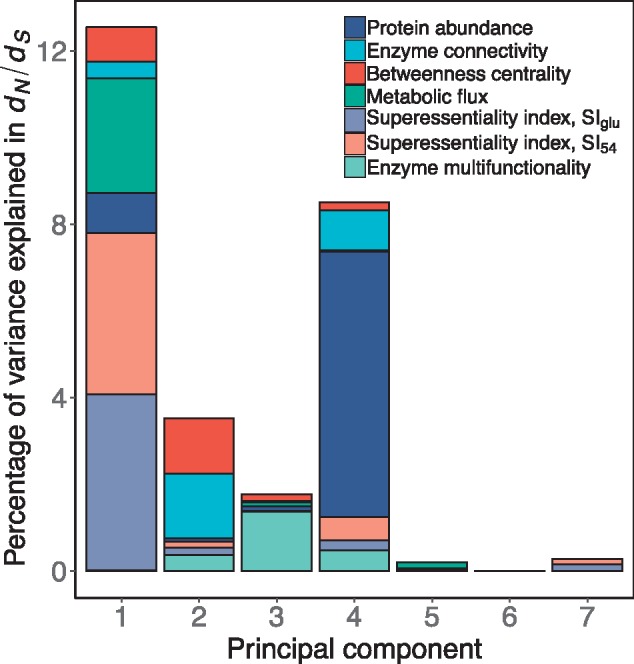
—Principal component regression on the rate of enzyme evolution (d_N/d_S). For each principal component, the height of the bar represents the percent of variance in d_N/d_S explained by the component. The relative contribution of each variable to a principal component is represented with different colors. This analysis was performed with 485 genes for which information for all variables is available. Table 3 contains the numerical data used to draw this figure.

We found four significant principal components. The component explaining the largest fraction of the variance in d_N/d_S (∼13%) was mostly determined (>60%) by roughly equal contributions from both superessentiality indices (SI_glu and SI₅₄). Metabolic flux determined ∼20% of the variance in d_N/d_S explained by this component. Protein abundance contributed ∼70% of the variance explained by a principal component explaining ∼9% of the variance in the rate of enzyme evolution. Network structure (enzyme connectivity and betweenness centrality) was the main contributor (∼78%) to a principal component explaining ∼4% of the variance in d_N/d_S. Finally, enzyme multifunctionality mostly determined (78%) a component explaining just ∼2% of the variance in evolutionary rate.

While protein abundance explained the largest fraction of the total variance in the rate of evolution (7.2%), the two superessentiality indices together explained ∼9% of the variance (table 4). Network topology explained ∼5%, metabolic flux explained ∼3%, and enzyme multifunctionality explained ∼2% of the total variance in d_N/d_S. In summary the main determinant of the rate of enzyme evolution is superessentiality in combination with protein abundance, followed by metabolic network structure. Enzyme multifunctionality has a very minor effect on enzyme evolution.

Table 4.

Percentage of total Variance in d_N/d_S Explained by Each Variable in the Principal Component Regression Analysis

Protein abundance	7.238
Enzyme connectivity	2.825
Betweenness centrality	2.432
Superessentiality index, SIglu	4.623
Superessentiality index, SI54	4.540
Metabolic flux	2.934
Enzyme multifunctionality	2.253

Discussion

Natural selection on the function of a molecular network constrains how the network’s genes evolve. Conversely, changes in network genes affect the function of the whole network. In other words, the evolution of a network’s parts affects the evolution of the whole network, and vice versa. These two types of influence are entangled, because changes in network function that result from changes in network genes can themselves impose new evolutionary constraints on network genes. Here, we study how the structure and function of a large metabolic network (the whole) influences the evolution of its constituent enzymes (the parts). In doing so, we perform a comprehensive exploration of the metabolic determinants of enzyme evolution. Our analysis is part of a research tradition aiming to understand the molecular evolution of living systems by relating the evolutionary rates of genes with their function and position in a biological network (Fraser et al. 2002; Hahn et al. 2004; Vitkup et al. 2006; Alvarez-Ponce 2012, 2014; Alvarez-Ponce and Fares 2012; Zhang and Yang 2015). An advantage of using metabolic systems in such studies is that the relationship between the functions of the enzymes and the network is especially well understood (Papp et al. 2011; Wagner 2012; Bordbar et al. 2014).

First, we show that the position of an enzyme in the E. coli metabolic network does not affect its rate of evolution. Previous studies have found significant but very modest correlations between some topological network parameters and evolutionary rates in other metabolic networks and pathways (Vitkup et al. 2006; Lu et al. 2007; Greenberg et al. 2008; Hudson and Conant 2011). However, in the E. coli metabolic network, central and highly connected enzymes do not evolve at different rates when we control for their abundance. This corroborates previous findings in small-scale metabolic systems of mammals (Hudson and Conant 2011; Colombo et al. 2014) and E. coli (Hahn et al. 2004). Other studies in yeast (Vitkup et al. 2006) and Drosophila (Greenberg et al. 2008) have found that the connectivity of an enzyme influences its rate of evolution. However, even where significant, this association is very weak. Such a weak or absent association is not unreasonable, considering the “bow-tie” architecture of a metabolic network (Csete and Doyle 2004; Friedlander et al. 2015), where numerous input pathways of nutrient conversion feed into a highly interconnected central core metabolism, which feeds many output biosynthetic pathways. Some of these biosynthetic pathways are linear sequences of reactions that produce essential and complex biomass molecules, such as amino acids or enzyme cofactors. A loss-of-function mutation of an enzyme in one such linear and peripheral pathway would be lethal (Wagner 2005), even though the enzyme is not highly connected. In other words, mutations in both central and peripheral enzymes can be deleterious, albeit for different reasons.

Metabolic flux control measures how perturbations to an enzyme’s activity affect the steady-state global flux of a pathway (Kacser and Burns 1973), and it can also explain some variation on enzyme evolutionary rates. Flux control is not uniformly distributed in metabolic networks. Upstream enzymes in linear metabolic pathways and enzymes in bifurcation points of branched pathways tend to have higher flux control (Flowers et al. 2007; Wright and Rausher 2010; Rausher 2013). Over short evolutionary time scales, these enzymes are subjected to higher selective constraints, as well as positive selection (Eanes 2011; Dallolio et al. 2012; Olson-Manning et al. 2013; Hermansen et al. 2015). These observations show how selection on pathway function can constrain the evolution of individual enzymes. However, these evolutionary pressures are not stable because flux control can change considerably over longer evolutionary periods (Orlenko, Hermansen, et al. 2016; Orlenko, Teufel, et al. 2016; Orlenko et al. 2017). Unfortunately, the absence of metabolic-flux control measures for genome-scale metabolic networks prevented us to explore their impact on enzyme evolution in this study.

In agreement with previous studies in other organisms (Vitkup et al. 2006; Colombo et al. 2014), we find that enzyme-specific metabolic flux—the rate at which a reaction converts substrates into products—affects enzyme evolution by itself. We find that enzymes catalyzing reactions with high flux tolerate fewer amino acid substitutions than enzymes catalyzing reactions with lower fluxes. In other words, the function of a metabolic network, that is, biomass production, constrains the evolution of network genes through amino acid substitutions in a nonuniform way: Enzymes with high flux experience greater constraints than enzymes with low flux, since they are more important for network function.

In any one metabolic network, a loss of function mutation in a given enzyme may be lethal (in a specific environment), because it abolishes the network’s ability to produce biomass. In other metabolic networks with the same phenotype but a different metabolic genotype—a different complement of enzyme-coding genes—the enzyme may not be essential, because alternative reactions or pathways can assume its role. The extent to which an enzyme or reaction is easy or difficult to bypass is a function of metabolic biochemistry, and can be quantified through a reaction’s superessentiality index (Barve et al. 2012). Highly superessential reactions (enzymes) are difficult to bypass and their loss would be lethal in many different genetic backgrounds, while the loss of lowly superessential enzymes would be lethal in only a few backgrounds.

We find that highly superessential enzymes evolve more slowly. Relevant for this observation is that the metabolic genotypes of bacteria can evolve very rapidly. That is, bacterial enzymes can rapidly get lost via gene deletion or loss-of-function mutations, and new enzymes may be acquired via horizontal gene transfer (Ochman et al. 2000). For example, closely related E. coli strains may differ in >20% of their genomes, and in hundred or more metabolic genes, a difference that is partly due to horizontal gene transfer and gene deletions (Ochman and Jones 2000; Wagner 2009). On evolutionary time scales, bacterial metabolic enzymes can thus find themselves operating in different genotypic backgrounds, such that differences in superessentiality matter for their rate of evolution, as our data show. Superessentiality might influence the rate of evolution less in organisms whose metabolic genotypes change more slowly.

Finally, we also tested if generalist enzymes, which catalyze many reactions, are subjected to higher selective constraints than enzymes just catalyzing a single chemical reaction, as theoretical expectations would predict (Baatz and Wagner 1997; Orr 2000; Otto 2004). Previous studies have found that multifunctional genes in yeast evolve slowly (He and Zhang 2006; Salathé et al. 2006), corroborating theoretical expectations (Waxman 1998), although the magnitude of this effect is very modest. In mammals, multifunctional proteins also tend to be constrained, and the more functions a protein is involved in, the lower is its rate of evolution (Podder et al. 2009). However, generalist (multifunctional) enzymes do not evolve more slowly, indicating that pleiotropy is not constraining enzyme evolution, at least in E. coli.

We note that myriad other, nonmetabolic factors may influence the evolution of enzyme-coding genes. These include protein structure (Plotkin et al. 2012), chaperone targeting (Bogumil and Dagan 2010; Williams and Fares 2010; Bogumil et al. 2012; Pechmann and Frydman 2014; Aguilar-Rodríguez et al. 2016; Kadibalban et al. 2016), and many others, but the dominant factor is usually gene expression level (Alvarez-Ponce 2014; Zhang and Yang 2015). It is thus remarkable that the associations between evolutionary rate and metabolic flux or superessentiality are moderately high, comparable in strength to that between evolutionary rate and mRNA expression level, and only below the association between evolutionary rate and protein abundance.

In conclusion, our analysis of the rates of evolution of enzyme-coding genes in the E. coli metabolic network shows how a gene’s role in the function of a larger network can affect its evolution. In doing so, we show how a systems-level perspective can help understand the factors that contribute to protein evolution.