Ice Nucleation on a Corrugated Surface

Abstract

Heterogeneous ice nucleation is a key process in many environmental and technical fields and is of particular importance in modeling atmospheric behavior and the Earth’s climate. Despite an improved understanding of how water binds at solid surfaces, no clear picture has emerged to describe how 3D ice grows from the first water layer, nor what makes a particular surface efficient at nucleating bulk ice. This study reports how water at a corrugated, hydrophilic/hydrophobic surface restructures from a complex 2D network, optimized to match the solid surface, to grow into a continuous ice film. Unlike the water networks formed on plane surfaces, the corrugated Cu(511) surface stabilizes a buckled hexagonal wetting layer containing both hydrogen acceptor and donor sites. First layer water is able to relax into an “icelike” arrangement as further water is deposited, creating an array of donor and acceptor sites with the correct spacing and corrugation to stabilize second layer ice and allow continued commensurate multilayer ice growth. Comparison to previous studies of flat surfaces indicates nanoscale corrugation strongly favors ice nucleation, implying surface corrugation will be an important aspect of the surface morphology on other natural or engineered surfaces.

Introduction

Nucleation of bulk ice from pure water is notoriously difficult, inhibited by the large change in density and collective rearrangement required to form ice nuclei able to grow spontaneously. Since homogeneous nucleation is suppressed, occurring only when water is supercooled below −41 °C,¹ ice almost invariably nucleates at an interface, often a dust particle or solid surface. The presence of suitable nucleation sites controls the temperature and rate at which ice forms, influencing behavior in many important systems, ranging from atmospheric precipitation,² where different types of dust lead to different degrees of supercooling during cloud nucleation,³ through to biological interfaces that have evolved to enhance or inhibit freezing.⁴ In addition to the nucleation rate, the mode of ice growth itself can be strongly influenced by the nature of the interface,⁵ influencing the extent of macroscopic ice buildup on surfaces such as aerofoils, for example. Although many experiments reveal changes in the ice nucleation rate at different surfaces,^6,7 the nucleation process itself is difficult to study directly and the particular characteristics that make a good nucleation agent remain unclear. Lattice parameter matching led to the successful use of AgI as a seeding agent, but simulations and experiments on model systems show that having the correct lattice parameter, binding energy, or symmetry alone does not necessarily promote ice growth, with no single parameter emerging as a reliable indicator of a favorable surface.⁸⁻¹³

Water adsorption on well-defined surfaces, particularly metals, provides a convenient arena where experiments can provide sufficient detail to develop molecular models for the water–solid interface.¹⁴ These studies reveal how water binds to simultaneously optimize both the water–water H-bonding and water-surface interaction, creating complex H-bonded water networks with structures quite unlike that of bulk ice.¹⁵ For example, 2D networks made of hexamer, pentamer, and heptamer rings form on close packed metal surfaces,¹⁶⁻¹⁹ with 1D pentamer chains forming on rectangular Cu(110)²⁰ and interlinked tetramers on square NaCl(100).²¹ However, since the first water layer is very different from bulk ice, further multilayer growth requires the density, lateral arrangement, and H orientation of the wetting layer to relax to stabilize a multilayer ice film, inhibiting further growth.^18,22−24 In contrast to these flat surfaces, ice forming proteins, the best nucleation agents known,²⁵ have a very different morphology, typically displaying a corrugated array of hydrophilic and hydrophobic sites, formed for example by stacking protein β-strands to create a corrugated, polar template that matches ice I.²⁶ Molecular dynamics simulations of solid wetting also find corrugation of the contact layer can influence the ice nucleation rate and direct ice growth,²⁷ suggesting surface corrugation may be one key to creating a good nucleation template.

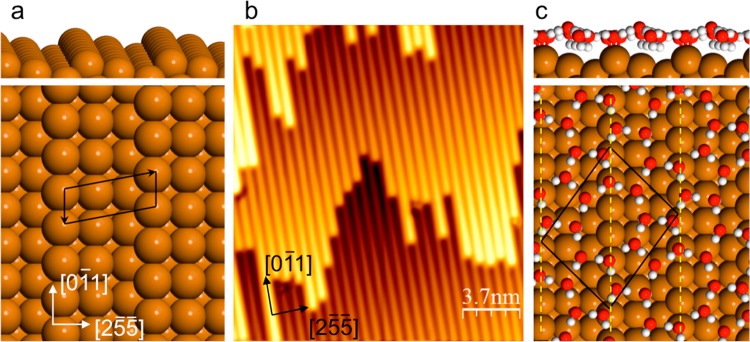
In this study we investigate how multilayer ice forms on a stepped Cu(511) surface, made up from a regular array of close packed steps separated by 3 atom wide terraces, shown in Figure 1. This surface is chosen to create an array of hydrophilic–hydrophobic stripes, 6.6 Å apart, a spacing that can be matched closely to the bulk ice lattice. Water binds tightly at the low coordinate step sites^20,29,30 but weakly on the (100) terraces,³¹ providing a highly corrugated adsorption template for water. Water wets this surface to create monolayer islands with a complex 2D structure,²⁸ shown in Figure 1c. This water network is made from interlinked pentamer, hexamer, and octomer rings, forming an H-bonded network with a coverage of 0.833 ML (where 1 ML is one water per surface Cu atom, or 1.18 × 10¹⁵ cm^–2). All of the molecules in this network have three H-bonds, half of the water donating two H atoms to a neighbor, the other half having one free H atom that points down toward the Cu surface. DFT calculations show that this structure is stabilized by having 4 water molecules bound flat on the Cu step sites and 3 with their free OH groups aligned H-down next to the Cu step, screened by the step dipole, making them particularly good H acceptors.^32,33 The network is completed by just 3 water molecules adsorbed in less favorable sites above the (100) terrace, bridging between water at the steps. This structure is more stable than alternative structures that occupy every step site, but, as for the plane surfaces discussed earlier, provides a poor template for further ice growth, having a completely different symmetry to bulk ice and no free OH groups capable of bonding second layer water.

Figure 1.

Structural model for the bare Cu(511) surface and the low coverage water phase. (a) Model showing the close packed Cu steps separated by (100) terraces and (b) an STM image showing the regular array of steps aligned along the [01̅1] direction. (c) Structural model for the water monolayer formed at low coverage,²⁸ showing the (31, −31) unit cell and Cu steps indicated by the dashed lines.

Multilayer ice growth is investigated using LEED, temperature-programmed desorption (TPD), helium atom scattering (HAS), and STM. We show that the complex 2D wetting layer formed at low coverage²⁸ is unstable to further adsorption, compressing to create a buckled hexagonal network. This structure has a density close to that of ice Ih(0001) and contains OH groups that point both “H-up” away from the surface and “H-down” toward the metal, providing H acceptor and donor sites able to bind effectively to second layer ice. We find that, unlike flat surfaces where multilayer adsorption is inhibited, adsorption on this structure is facile, with water forming a continuous second layer that grows into a commensurate ice multilayer. Based on DFT calculations, we discuss how water relaxes during the transition from single layer to multilayer growth, emphasizing the importance of H donor and acceptor groups in the interface layer relaxing to adopt both the correct periodicity and corrugation to bind bulk ice. These results suggest that surfaces that nucleate ice efficiently will be corrugated, not flat.

Results and Discussion

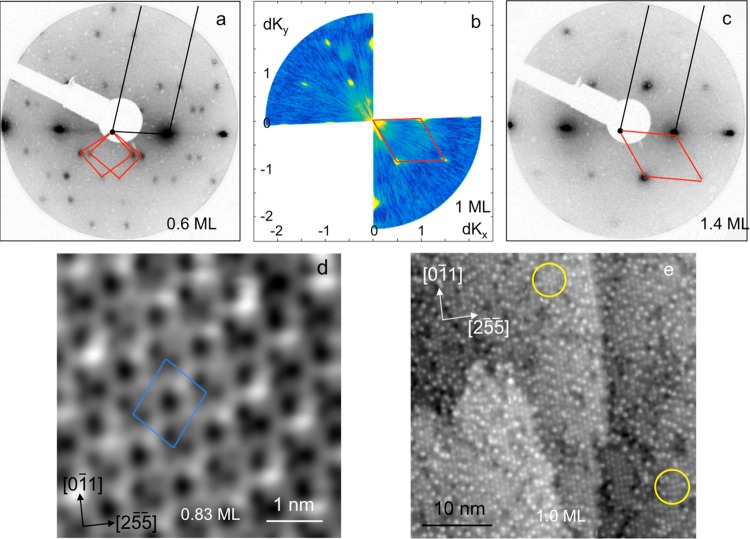
LEED and HAS were used to examine the structures formed as a water multilayer is grown on the Cu(511) surface at 140 K, resulting in the diffraction patterns shown in Figure 2 for increasing water coverage. The (3 1, −3 1) phase formed at low coverage (≤0.83 ML water) disappears as the coverage is increased further, the surface incorporating ca. 25% more water to form an ordered (3 0, −1 1) structure as the coverage reaches 1 ML and the surface saturates to further adsorption. Thermal desorption measurements show the binding energy of this structure is indistinguishable from that of the low coverage phase, the multilayer water TPD peak appearing only as the coverage exceeds 1 ML (see Supporting Information for more details). The high coverage water structure has 6 water molecules per unit cell and a density that is very close to that of the ice Ih(0001) surface. The (3 0, −1 1) LEED pattern persists as the water multilayer grows, indicating this structure is stable to further water adsorption. STM images reproduce this change in surface structure with coverage, with large scale images (Figure 2d,e) showing the complex network of octomer, hexamer, and pentamer rings formed at low coverage being replaced by the (3 0, −1 1) structure at 1 ML coverage.

Figure 2.

Diffraction patterns and STM images showing the change in structure as the first layer saturates with water. (a) LEED pattern (40 eV, 10 nA) showing formation of the (3 1, −3 1) structure for water coverage ≤0.83 ML, (b) HAS (recorded at an energy of 9.69 meV), and (c) LEED (40 eV, 10 nA) showing the formation of an ordered (3 0, −1 1) water film at ≥1 ML water. The Cu(511) reciprocal unit cell is shown by the black lines, while the red lines show that for water. (d) STM image of the (3 1, −3 1) structure (−0.11 V, 100 pA) and (e) the (3 0, −1 1) structure (0.11 V and 21 pA). The yellow circles show regions where the bright features are arranged locally into a hexagonal pattern (top) or a rectangular arrangement (bottom). The water coverage is marked on the images, which are all recorded at 77 K after annealing the surface to 138 K, except (b) which is recorded at 120 K (see Methods for further details).

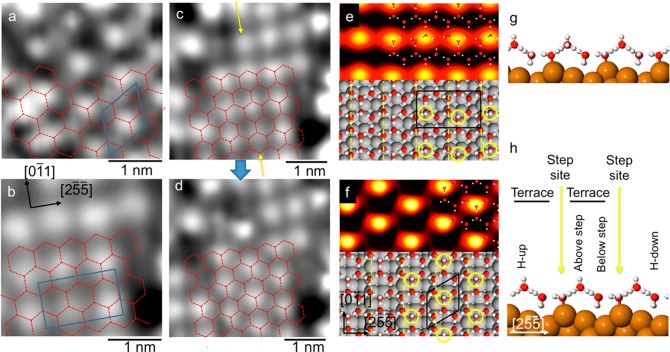
Unlike the low coverage structure shown in Figure 2d, STM images of the high coverage phase (Figure 2e) do not show well resolved rings of water; instead, the images are dominated by individual bright features that align in rows parallel to the Cu steps, separated by the step spacing (6.6 Å). The bright features are typically 7.6 Å (3 Cu atoms) apart along the step direction, with occasional variation by one unit and low contrast sites giving rise to some disorder along the rows. A Fourier transform of the STM image shows weak peaks at the (3 0, −1 1) diffraction positions found in LEED and HAS (see SI and Figure S2 for more information). Detailed STM images shown in Figure 3 reveal two other features of this phase. First, there is some variation in the intensity of the bright features, indicating a slightly different corrugation at different water sites. This variation is attributed to the precise H atom location within the overall water H-bond network modifying the corrugation of individual water sites. Similar behavior is found for the low coverage phase²⁸ and is analogous to the proton disorder found in ice I. Second, the arrangement of bright features sometimes follows a hexagonal ordering, where alternate rows of bright features are out of phase perpendicular to the steps, or else may be roughly aligned (offset by a_Cu/2 on adjacent steps) forming a rectangular arrangement (compare Figure 3a,b and regions circled in Figure 2e). The two different arrangements can interconvert (Figure 3c,d) if the STM tip is moved close and scanned along the [01̅1] direction, with the bright features changing site by one unit along the step direction. This behavior is consistent with both motifs originating from the same underlying hexagonal (3 0, −1 1) water network, shown in Figure 3a–d, with the high contrast site simply switching to the adjacent site along the step direction. Although some structure is visible between the bright sites, we never fully resolve the underlying water network beneath the high contrast features.

Figure 3.

STM images for the 1 ML water structure formed at 138 K showing the formation of a hexagonal network containing water adsorbed with some OH groups pointing away from the surface. (a) Detail of a region with a hexagonal arrangement of bright features in a (3 0, −1 1) repeat and (b) a region with bright features aligned along [25̅5̅] in a doubled, rectangular (3 0, 1 2) repeat that crosses two steps. (c and d) Images of the same region showing a structural change from the rectangular arrangement (c) to hexagonal (d), achieved during scanning by increasing the tunneling current to bring the tip close to the surface. The sites marked by the yellow arrows move up one Cu unit leaving the remaining water network unperturbed, as indicated by the dashed hexagonal network. (e,g and f,h) STM simulations (0.1 V) and DFT structures for arrangements containing one H-up water per unit cell (see SI, structures S4Y and S3D) either in or out of phase on adjacent Cu terraces, with adsorption energies of −75.1 and −75.2 kJ/mol, respectively. The position of the H-up water molecules is indicated by the yellow circles. STM scan direction is vertical with (a) 0.11 V, 41 pA; (b,c) 0.11 V, 21 pA; (d) 53 mV, 21 pA.

The structure of the dense 1 ML water layer was investigated using DFT to explore its minimum energy structure. All the stable structures we found adopted the hexagonal network shown in Figure 3e,f, with a binding energy of 75.5 kJ/mol that is indistinguishable from that of the low coverage structure²⁸ (see SI for details of all the arrangements considered). This binding energy can be compared to the 72.4 kJ/mol calculated for bulk ice using the same functional, with a calculated lattice parameter 3% smaller than the experimental value, which reduces to 71.4 kJ/mol if the structure is constrained to the experimental ice lattice spacing. Entropic contributions to the stability of different solid ice phases are small,^34,35 less than the accuracy of the DFT calculations³⁶ (see SI for more details), so the greater binding energy of water in the (3 0, −1 1) structure is consistent with water wetting the Cu(511) surface.

The hexagonal water network is stabilized by two water molecules that bind flat in a double donor configuration atop the Cu step, separated by one vacant Cu site along the step, as shown in Figure 3e,f and supplementary Figures S3 and S4. The remaining four water molecules complete the H-bond network by bonding as a double donor and three single donors, allowing a number of possible microarrangements. The two water molecules immediately below the step have a weak preference to both align H-down toward the Cu surface, mirroring the arrangement found in the low coverage network, Figure 1c, where water is stabilized H-down next to the Cu step dipole.²⁸ A double donor and single donor species adsorbed on the terrace above the Cu step complete the hexagonal network, with the uncoordinated H atom pointing either toward or away from the surface. DFT calculations find no significant energy difference between arrangements that have all the H atoms pointing down or one water on the terrace aligned H-up, suggesting both orientations will occur within the water network. This behavior is different from flat surfaces where water preferentially aligns H-down toward the surface.^14,15

STM simulations shown in Figure 3e,f provide further insight. Whereas structures containing only H-down water result in low contrast images that resolve the network of hexagonal rings, the presence of H pointing away from the surface creates high contrast sites that dominate all other features in the image (Figure 3e,f and supplementary Figure S5). On this basis we assign the bright features observed in STM to H-up water adsorbed on the Cu terrace above the step (see Figure 3h), creating the rows of bright features parallel to the step edge observed experimentally. The density of bright features in the STM images implies ca. 65% of the (3 0, −1 1) unit cells have one H pointing away from the surface, indicating a slight preference to have one H-up water in the unit cell, rather than all three single donor species H-down toward the surface. Disorder in the location of these sites along the step direction arises from the choice of which of the two adjacent water sites (if any) is H-up. For any particular Cu terrace, a majority of the H-up rows show water adopting the same site, spaced evenly along the row as shown in Figure 3e,f, creating a locally ordered chain along the [01̅1] direction. This arrangement prevents two H-up sites occupying the same water hexagon, something that DFT finds is unfavorable by ∼5 kJ/mol. Hexagonal and rectangular regions result from a different local ordering of the H-up water on adjacent (100) terraces, with the hexagonal patches having the same H-up site on adjacent terraces, whereas the rectangular patches have H-up at opposite sites on adjacent terraces (see Figure 3e,f). The presence of both arrangements implies the choice of which H-up site is occupied on adjacent terraces is decoupled from each other, being in different water rings and therefore not interacting to destabilize the network. The two arrangements can interconvert when the STM tip is moved close to the water layer to exchange the H orientation at sites along the row, as shown in Figure 3c,d. This ability of water in the first layer to adopt an H-down or H-up alignment is critical to further water adsorption and the wetting behavior of this surface.

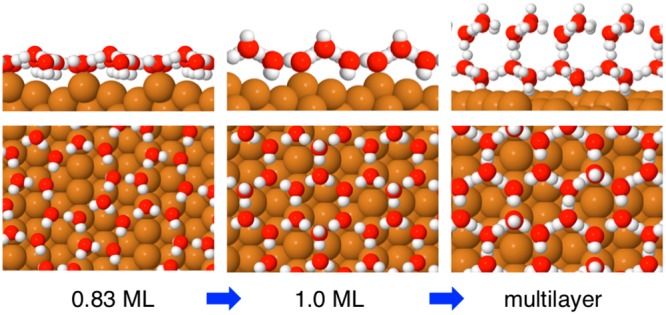
Having understood the compression of the first layer water, we turn our attention to the growth of multilayer ice on this hexagonal network. Whereas water adsorbed on flat metal surfaces, such as Pt(111), forms disordered second layer islands¹⁶ and then dewets to create multilayer islands separated by monolayer water,^22,24,37,38 large scale STM images of Cu(511) (Figure 4a) show second layer water forms a complete layer. The structure is characterized by disordered rows of bright features that are aligned perpendicular to the step direction, the orthogonal direction to those seen in the first layer. Closer inspection of the images reveals the bright features are situated on zigzag chains that run along [25̅5̅] and have a period of twice the Cu step spacing. The density of the bright features in Figure 4 is low, equivalent to just 1 in 30 water sites, and depends on coverage, implying they are not intrinsically associated with the second layer water structure. The bright features image 0.6 Å above the zigzag chains, roughly half the apparent height of the first water layer above Cu(511) and identical to the apparent spacing found between second and third layer water under similar bias conditions on Cu(111).³⁹ We therefore assign the isolated bright features as additional water molecules that are pinned to particular sites above the second layer network, similar to the behavior reported for water adsorbed on top of 2 layer clusters on Cu(111)⁴⁰ and Ru(0001).¹⁶ The diffuse zigzag chains in the underlying second layer water are separated by 4.5 a_Cu (11.5 Å) along the Cu steps, forming a (5 1, −4 1) arrangement that represents a (√3 x √3)R30° superstructure of the hexagonal (3 0, −1 1) first layer, indicated in Figure 4d. The additional long-range order in the second layer implies some ordering of the H location or water corrugation beyond that associated with the hexagonal water network. The zigzag chains have an apparent height ca. 0.5 Å above the dark regions, which is half the apparent height of the first water layer and similar to the corrugation of H-up sites in the first layer. Formation of a complete H-bond network with the first layer would cause the second layer to have the same number of water molecules oriented H-up in the second layer as is present in the first layer, so we tentatively associate the (5 1, −4 1) superstructure as a long-range ordering of H-up water sites in the second layer. This interpretation also explains why additional water molecules are present above the zizgzag chains, as additional water molecules are known to be stabilized by bonding at H donor sites.⁴¹ Although it is not possible to image finer details of the second layer network, the images confirm water forms a complete 2D commensurate network that extends across the surface in registry with the first layer.

Figure 4.

STM images showing second layer water forming a continuous 2D layer across the entire surface. (a) Large scale STM image of ∼2 ML water after annealing at 135 K. (b) Detail showing the bright features preferentially aligning orthogonal to the steps. (c) Portion of the surface with fewer bright features where the second layer water network is visible. (d) Original (3 0, −1 1) first layer network superimposed (red hexagons shown with black unit cell), along with the (5 1, −4 1) unit cell (blue) that represents the commensurate second layer superstructure. (a) 0.1 V, 21 pA; (b–d) 0.1 V, 41 pA.

In order to understand how the first layer relaxes during multilayer growth, we used DFT to explore the binding energy of multilayer structures of this type. Before doing so we note that the deviation in lattice parameter between DFT models for the solid surface and for bulk ice may cause systematic bias in assessing different structures.^42,43 The hexagonal network on Cu(511) is laterally compressed 1.7% compared to bulk ice,⁴⁰ but the optB86b-vdW exchange-correlation functional,^44,45 which includes van der Waals interactions that are important in stabilizing surface adsorption relative to 3D ice formation,^36,46 over binds bulk ice by a similar amount,⁴³ causing strain in the adlayer to be underestimated. We therefore make no attempt to model the detail of the long-range H-bond superstructure observed experimentally; instead, we focus on calculations for the (3 0, −1 1) unit cell to understand how surface corrugation influences the H orientation and buckling of interface water, how the first layer relaxes during growth, and why this particular surface is able to stabilize a commensurate ice film.

Calculations for two layers of water reveal a clear difference in behavior between the stepped Cu(511) surface and previous studies on flat surfaces. Stable two layer structures retain the water molecules adsorbed as double donors on the Cu step, with one of these sites buckling ∼1 Å away from the step and acting as an H-acceptor from second layer water. The first layer is completed by a mixture of H-up and H-down water, as found in the monolayer structure (compare Figures 3 and 5). Several different arrangements of H-donor and acceptor sites lead to stable 2 layer films, with the second layer adopting either an AA or AB stacking. The most stable structures originate from first layer proton arrangements that create a 3-fold arrangement of donor and acceptor sites in next nearest neighbor positions, providing the correct template to bind an “icelike” second layer above. To do this, one of the H-down molecules beneath the step orients H-up to donate to the second layer (circled yellow in Figure 5e), with the third H-bond between the layers made to water on the (100) terrace above the step, in either an H-up or H-down arrangement. The binding energy of the best two layer structure is ca. 4 kJ/mol less than the first layer alone, consistent with the reduced binding energy found for multilayer water from TPD. The structure of the second water layer is very similar to that of bulk ice, with both donor and acceptor sites available to bind third layer water in the ice I structure, Figure 5c,d. We find the adsorption energy for 3 layer ice structures is indistinguishable from 2 water layers, consistent with ice multilayers growing without hindrance. In fact the adsorption energy for 2 and 3 layer structures is the same as we calculate for bulk ice (see SI for more details), implying thick ice films are expected to grow indefinitely on this surface. A full list of all the arrangements considered is given in the Supporting Information; see Figures S6, S7 and additional discussion.

Figure 5.

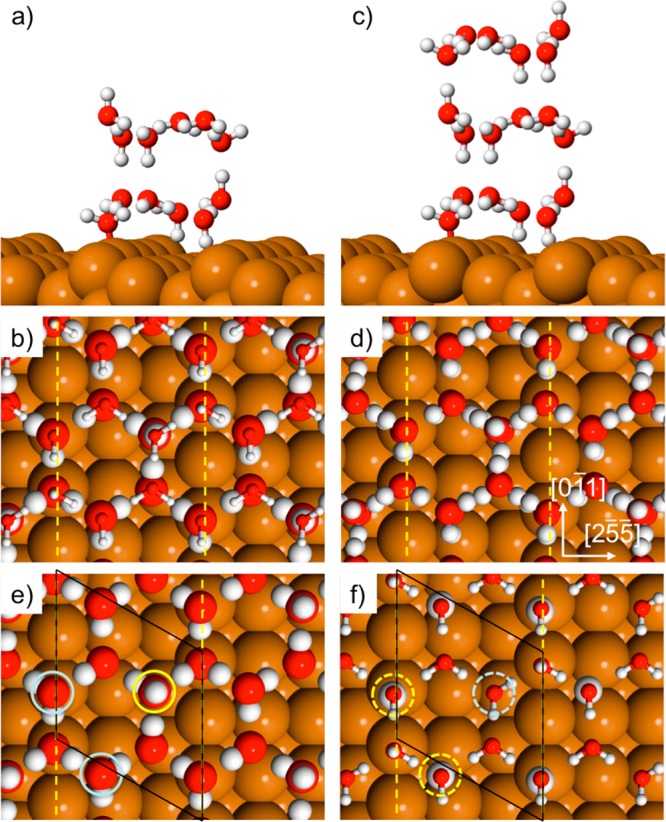
Calculated structures showing the best 2 and 3 layer structures found in a (3 0, −1 1) unit cell. Side and top view of (a–b) 2 ML water and (c–d) 3 ML water (adsorption energy −71.8 and −71.6 kJ/mol respectively). The top frames show a single unit cell of water, while the top layer in (b) is reduced in size. Frames (e,f) show the first and second layers of the 2 layer structure separately. The three first layer sites (e) that link the two layers are circled with the H-up donor in yellow and the acceptor sites in blue. Frame (f) shows the corresponding second layer donor/acceptor sites highlighted by dashed circles, with the H donors enlarged. Copper step sites are indicated by the yellow dashed lines.

Second layer growth has previously been imaged on several flat, close packed metal surfaces, where it shows characteristic behavior. Water forms complex first layer structures on Ni and Pt,^17,24 with water oriented H-down and no OH groups available to stabilize second layer water.²² Further water adsorption initially forms second layer islands,^16,17 with calculations finding a two layer “sandwich” structure is particularly stable. This structure consists of two flat hexagonal water layers arranged with the bottom layer aligned H-up and the second layer H-down, so that each water forms one H-bond to the other layer⁴⁷⁻⁴⁹ (cf. Figure S6f). Two layer clusters of this type have been found on hydrophobic surfaces, such as Au,⁴⁹ but the absence of free OH groups makes them unsuitable for further ice growth. Instead of completing the second water layer, both Ni and Pt dewet to form 3D ice clusters and monolayer water.^17,24 Similarly, on Ru(0001) water forms ordered second layer islands on regions of hexagonal first layer water,¹⁶ but again the water film dewets as the coverage is increased.²³ In all these systems, the driving force for dewetting is the reduction in contact area between ice and the solid, implying the free energy of the ice–solid interface is sufficiently great that bulk ice clusters and monolayer water form to reduce the solid–ice contact area. Evidently water at these solid–ice interfaces is unable to adapt its lateral arrangement and H-bonding sufficiently to stabilize an ice layer, but the structure of the buried interface is unknown.

In contrast to the plane surfaces, the corrugated Cu(511) surface forms a complete commensurate second layer ice film, which covers the surface with no evidence for dewetting. The ability to nucleate a continuous 2D ice film can be attributed to two key factors, formation of a hexagonal wetting layer with a close lattice match to bulk ice (Δ ≈ −1.7%) and the ability of this first layer to create a 3-fold arrangement of donor and acceptor sites, in next nearest neighbor positions, with the correct corrugation to bind and stabilize multilayer ice films. Calculations show that stable multilayer ice films form with water on the step acting as an acceptor and at least one of the other two sites acting as a donor to the second ice layer. Whereas calculations for flat surfaces predict double layer water forms a nonwetting hexagonal “sandwich” structure,¹⁷ this arrangement is unstable on Cu(511) (see Figure S6f). Water in the first layer rotates H-down beneath the step to improve bonding to the solid at the expense of a reduced H-bonding between the two water layers, preventing formation of a “hydrophobic” 2 layer structure. The requirement to provide both donor and acceptor sites with the correct corrugation ensures that flat hexagonal networks, formed on plane surfaces, do not provide good templates for ice growth.^13,50,51 Surface corrugation is therefore key in creating the buckled network of donor and acceptor sites that allows first layer water to form a stable interface between bulk ice and the solid surface on Cu(511). This picture is consistent with recent models for ice nucleation on feldspar, where nucleation occurs preferentially on the corrugated (100) face.⁶

Conclusions

We have shown that saturating a stepped Cu(511) surface with water causes the first layer to compress from a complex, H-down arrangement of pentamer and octomer rings into a simple buckled hexagonal network containing a mixture of H donor and acceptor sites. Second layer water adsorbs on top of this first layer to form a commensurate ice film with the same lateral water density as the first layer, allowing ice multilayers to grow freely. Structure calculations show that the ice multilayer is stabilized by relaxing the corrugation and H orientation of water in the first layer to create one H-donor and two H-acceptor sites at next nearest neighbor positions around the water hexagons, mimicking the arrangement in bulk ice Ih(0001). This process involves displacement of one acceptor species away from the surface and local reorientation of first layer water without breaking any hydrogen bonds. Fully H-bonded, two layer sandwich structures (which have no free H atoms to stabilize further water) are unstable on the corrugated surface, with some water molecules rotating “H-up” to create H-donor sites that stabilize continued multilayer growth. The DFT calculations shed light on the factors influencing the stability of the solid–ice interface layer and support model calculations²⁷ that suggest nanoscale surface corrugation can stabilize and direct ice growth. A good ice nucleating agent requires a close lateral match of first layer water to a bulk ice lattice plane and suitable corrugation to match the surface array of H donor and acceptor sites to the ice structure. These results suggest that the presence of nanoscale hydrophilic/hydrophobic corrugation at the surface of ice nucleating agents is one key to their efficiency.

Methods

Experiment

Experiments were conducted in 3 different chambers using different crystals, polished to within 0.1° of the (511) face (Surface Preparation Lab). The surface was cleaned by cycles of Ar⁺ ion sputtering and annealing to 800 K. LEED and TPD measurements were conducted in an ultrahigh vacuum (UHV) chamber with base pressure of 1 × 10^–8 Pa equipped with a dual-MCP amplified LEED system to minimize electron damage to water structures.²⁸ Water (D₂O, 99.9%) layers were dosed via a collimated, effusive molecular beam, allowing the surface coverage to be selected to ca. ± 1%. The water uptake was measured using the King and Wells technique, and TPD profiles were recorded as a function of the coverage. The relative coverage was calculated by integrating either the uptake profile or the TPD signal, with one layer being defined as the coverage just prior to the appearance of a multilayer desorption peak in TPD. The surface was annealed to 138 K to order water structures with the temperature measured by a K type thermocouple attached to the crystal, which was held at 100 K during LEED measurements. Further details are given in the Supporting Information.

Helium atom scattering (HAS) was recorded as described earlier,^28,52 using a He beam with a mean energy of 9.69 meV. Water was dosed from a leak valve, and the development of the different diffraction peaks followed as a function of water dose. Saturation coverage was established from a local maximum in He reflectivity as the surface layer completes. During extended 2D scans, the surface was held at 120 K with a background pressure of water vapor chosen to maintain a constant He reflectivity. STM measurements were conducted in a Createc STM with the sample held at 77 K during water adsorption and then annealed to 138 K to order the water.²⁸ STM images were recorded in constant current mode at 77 K with an electrochemically etched tungsten tip. Bias voltages are applied to the sample, so that positive voltages correspond to electrons tunneling into the surface (empty state images). STM images proved largely insensitive to the bias voltage but required the use of low tunnel currents (<40 pA) to prevent reorientation of water in the adlayer.

Theory

Calculations were performed using VASP^53,54 with the optB86b-vdW exchange-correlation functional,^55,56 in a (3 0, −1 1) or doubled, (3 0, 1 2) unit cell, using (9 × 9 × 1) or (4 × 7 × 1) k points respectively and a 400 eV cutoff. The slabs had a vacuum gap >10 Å above the upper water layer and were dipole corrected perpendicular to the slab. The optB86b-vdW functional includes van der Waals interactions, which are known to be important in stabilizing surface adsorption relative to 3D ice formation,^36,46 and has a similar performance to other vdW functionals for systems where physisorption is important.⁵⁷ Additional tests to determine the sensitivity of the relative binding energy of different structures to the functional chosen were performed using rev-vdW-DF2;⁵⁸ further details are given in the Supporting Information. Trial structures are converged so that the forces on the atoms are <0.01 eV/Å. The water adsorption energy (E_ad), or binding energy (E_b), quoted in the text are defined by

1

where E_slab^tot is the energy of the final slab, E_Cu is the energy of the metal slab alone and E_H2O the energy of an isolated water in vacuum. STM simulations were performed using the Tersoff Hamann approximation,^59,60 which approximates the tunnel current as the integral of the electronic density from the bias voltage to the Fermi energy. This model generally provides reasonable qualitative agreement with experimental STM images recorded for monolayer water,^20,28 but does not account for charging or the low conductivity of thicker ice films which prevent us imaging 3 layer islands in experiment. Experimental images recorded at low bias voltage in the band gap (to avoid disrupting the structure) show a reduced apparent height, particularly for ice multilayers, and must be interpreted on the basis of apparent height change with coverage.³⁹

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/jacs.8b08796.

• Additional characterization of the saturation monolayer and a complete list of the binding energies and structures calculated for the monolayer and multilayer ice films discussed in the text (PDF)

The authors declare no competing financial interest.