Evaluating tensile damage of brain tissue in intracerebral hemorrhage based on strain energy

Abstract

Intracerebral hemorrhage (ICH) may lead to physical and pathological damage and has been a focus of research for decades. Evaluating tensile damage caused by deformation in ICH is an important component of damage assessment for correct diagnosis and treatment. Traditional research on ICH paid little attention to quantified brain tissue damage resulting from mechanical factors, and only a few reported the mechanical properties of damaged brain tissue. The aim of the present study was to present an effective method that is able to evaluate the tissue damage degree in ICH, based on strain energy function. Two finite element analysis (FEA) models were analyzed: A three-dimensional (3D) model for tissue's tension experiment and a two-dimensional (2D) model for brain tissue's deformation in ICH. The polynomial fitting function of stress vs. stretch curve, which was derived from previous reports, was used in the FEA as the constitutive function of brain tissue. The present study demonstrated that white matter could be regarded as hyperelastic material when stretch was <1.343, and with stretch increasing, tissue injury exacerbated when stretch was >1.343. The strain energy loss was not linear in this process, and Neo-Hookean and Ogden model's results demonstrated a similar change in trend, but a difference in quantity. The results from 2D and 3D simulation, respectively, demonstrated the degree of damage according to the above dividing criteria and the possible distribution of tissue damage after ICH ictus. An analytical model from a biomechanical perspective for white matter injury in ICH may facilitate to improve clinical diagnosis and treatment.

Introduction

Extensive research on brain injury following the onset of intracerebral hemorrhage (ICH) has focused on mass effect, ischemia and release of clot components (1). However, these findings rarely involved how to evaluate tissue's direct damage caused by the deformation of tissue in ICH. Following a hemorrhagic stroke attack, the initial bleeding causes physical injury to the brain's physiological structure (2). As a result, the formation of cracks by physical disruption provides space for occurrence of hematoma, and the hematoma's mass compresses brain tissues, exerting a direct force on white matter in particular (3). With the expansion of the hematoma, the extent of physical disruption and deformation of surrounding tissues increases, thus the stretch caused by deformation induces tissue damage (4). In fact, earlier research had investigated soft tissue damage under mechanical loadings (5–9). For instance, by comparing morphological injury and electrophysiological impairment in an adult guinea pig, the tissue-level mechanical thresholds for axonal injury were determined in vivo (7). The stress-stretch relationship of the human brain, within 12 h of death, had been quantitatively studied, and the tissue deformation had been described as similar to filled elastomers (8). Furthermore, the application of computer-aided tools has been extended to evaluate tissue damage. For example, a study by Cheng and Hannaford (9) used finite element analysis (FEA) to predict tissue damage with in vivo uniaxial experimental data of liver and compared the effect of damage evaluation between a two-dimensional (2D) and three-dimensional (3D) model. Although increased interests focused on the injury mechanisms of soft tissue caused by external mechanical forces, there is currently no broadly accepted indicator system for evaluating soft tissue damage, and brain tissue is regarded as extremely soft tissue (10). To overcome this problem, the present study introduced a novel method to evaluate the tensile damage of white matter in ICH. Experimental tensile data of white matter from former literature (8) was used as the analysis object in the present study. The present work was based on the energy conservation principle, strain energy theory and hyperelastic theory in continuum mechanics.

Recently, research has used FEA as an effective tool for simulating brain tissue deformation of different scales; however, it is unable to sufficiently meet the needs of grading brain tissue injury in ICH (11,12). In addition, an accurate mechanical model is based on accurate experimental data and reasonable assumption. The mechanical test data of human brain is scarce, whether in vivo or in vitro, because of ethics and scarcity of materials. However, some researchers have obtained worthy experiment results. For example, a study by Jin et al (13) tested 240 brain tissue specimens under tension, compression and shear mode at varying strain rates, and these experimental results provided useful information to develop accurate constitutive equations for brain tissue. However, unfortunately the maximum strains were set below 0.5 by Jin et al (13), yet the majority of tissue strains surrounding hematoma in ICH are over 0.5, according to computed tomography (CT) or magnetic resonance imaging (MRI) images (4). A study by Franceschini et al (8) presented the whole damage evolution and fracture process in a prismatic specimen of white matter, and all these data met the requirements of the present study.

Using a suitable mechanical model to fit the experimental data, unknown material properties may be determined. To predigest the solving process and promote model practicability, brain tissue was treated as isotropic and homogenous in the majority of studies, and this setting is also applicable to the present study. In a common constitutive equation used to describe brain tissue deformation, strain always changes with location and time (14–16), which is called strain rate effect. However, the deformation of brain tissue in ICH is a one-way process before interventional therapy, and the deformation slowly continues, with hematoma increasing following the onset of ICH (3). It was reasonable to leave relaxation effect and strain rate effect out of account in the present work.

The objective of the present study was to identify an effective evaluating method for grading white matter tensile damage in ICH. On account of ignoring tissue damage in the deformation process, an overwhelming majority of previous research neglected detection of biological structure integrity following experimental operation. Therefore, these results were not applicable in present work. Furthermore, it is easier to understand that tissue structural damage may lead to change of mechanical properties. The mechanical properties of soft tissues are changing continually when deformation exceeds strain threshold (17) and, up until now, no suitable constitutive equation was able to describe this process. Research has demonstrated that, in stretching the optic nerve in vivo, the tissue-level strain thresholds for injury ranged from 0.09–0.47, with an average strain of 0.181 (7). Even if theories of fracture mechanics make significant developments, after more than 15 years, no suitable mathematical physics model has incorporated stretch with structure damage. Therefore, the present study established a grading evaluation criterion, which was obtained from comparing the quantitative change of strain energy between ideal hyperelastic deformation and actual deformation, and based on strain energy theory and strain energy loss. From a biomechanical perspective for white matter's tensile damage in ICH, this simple analytical model may facilitate the improvement of clinical diagnosis and treatment.

Materials and methods

Strain energy function

With strain energy loss in deformation as the studied object, the mechanical behavior of white mater under uniaxial tension (8) was the main experimental data source. As demonstrated in Fig. 1, white matter stretched under the uniaxial tension until structure failed, and the results of nominal stress vs. stretch were analyzed by mathematical and mechanical methods. Hyperelastic models and polynomial fitting models were used to fit the mechanical properties, and FEA was used to demonstrate the strain and stress distribution during stretching. Model solutions were obtained by using ABAQUS/Standard finite element v. 6.12 software (Dassault Systems Simulia Corp., Johnston, RI, USA).

Figure 1.

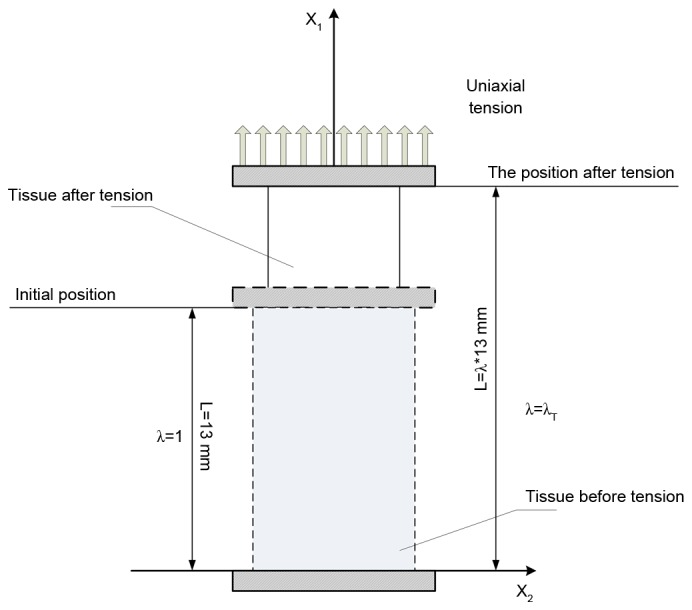
Schematic representation of uniaxial tensile experiment, the stretch is defined as the ratio of the initial length to the length after tension. λ, stretch; L, distance; X₁, vertical direction; X₂, horizontal direction.

The strain energy function may either be a direct function of the principal stretch ratios, W=W (λ₁, λ₂, λ₃), or a function of the strain invariants, W=W (I₁, I₂, I₃). Let the deformation gradient tensor as:

$$\underset{\_}{F}=\frac{d\underset{\_}{x}}{d\underset{\_}{X}}$$ (i)

X is the reference position of a material element and X is the current position of the same element. The tension deformation, as demonstrated in Fig. 1, may be written as:

$$x_1={\lambda }_1{X}_1,x_2={\lambda }_2{X}_2,x_3={\lambda }_3{X}_3$$ (ii)

Where λ_i are the principal stretch ratios of tension in the Rectangular Cartesian coordinate system:

$$\underset{\_}{F}=\left[\begin{array}{ccc}{\lambda }_1& 0& 0\\ 0& {\lambda }_2& 0\\ 0& 0& {\lambda }_3\end{array}\right]$$ (iii)

We assumed that tissue kept a fixed volume and initial form in tension deformation. Thus:

$${\lambda }_1{\lambda }_2{\lambda }_3=1\mathit{\text{and}}{\lambda }_1={\lambda }_T,{\lambda }_2={\lambda }_3={\lambda }_T–\frac{1}{2}$$ (iv)

Where λ_T is the principal stretch ratio in the stretching direction. Then:

$$\underset{\_}{F}=\left[\begin{array}{ccc}{\lambda }_T& 0& 0\\ 0& {\lambda }_T–\frac{1}{2}& 0\\ 0& 0& {\lambda }_T–\frac{1}{2}\end{array}\right]\mathit{\text{and}}{\underset{\_}{F}}^T=\left[\begin{array}{ccc}{\lambda }_T& 0& 0\\ 0& {\lambda }_T–\frac{1}{2}& 0\\ 0& 0& {\lambda }_T–\frac{1}{2}\end{array}\right]$$ (v)

From equation (ii), the right Cauchy-Green deformation tensor (18) maybe be determined as follows:

$$\underset{\_}{\mathrm{C}}={\underset{\_}{F}}^T\underset{\_}{F}=\left[\begin{array}{ccc}{\lambda }_T^2& 0& 0\\ 0& {\lambda }_T^{–1}& 0\\ 0& 0& {\lambda }_T^{–1}\end{array}\right]$$ (vi)

In general, an isotropic hyperelastic incompressible material is characterized by a strain-energy density function, W, which is a function of two principal strain invariants only: W=W (I₁, I₂), where I₁ and I₂ are defined as (19):

$$\begin{array}{cc}{\mathrm{I}}_1=tr\underset{\_}{C}={\lambda }_T^2+2{\lambda }_T^{–1},& I_2=\frac{1}{2}\left({\mathrm{I}}_1^2–tr{\underset{\_}{C}}^2\right)={\lambda }_T^{–2}+2{\lambda }_T\end{array}$$ (vii)

So that:

$$\mathrm{W}=\mathrm{W}(I_1,I_2)=\mathrm{W}({\lambda }_T^2+2{\lambda }_T^{–1},{\lambda }_T^{–2}+2{\lambda }_T)=\mathrm{W}({\lambda }_T)$$ (viii)

During uniaxial tension tests, the tension stress was generally evaluated as σ₁₁=T/A, where T is the tension force and A is the area of a cross-section of the specimen. Thus:

$$\int {\sigma }_{11}d{\lambda }_T=\mathrm{W}({\lambda }_T)$$ (ix)

Hyperelastic models

Neo-Hookean strain energy function

The Neo-Hookean model (20) is often used for the modeling of nonlinear elastic material. It is based on the statistical thermodynamics of cross-linked polymer chains and depends on the first invariant of the right Cauchy-Green deformation tensor. The strain energy function for an incompressible Neo-Hookean material under uniaxial mode is given:

$$\mathrm{W}({\lambda }_T)=C_1(I_1–3)$$ (x)

It yields the following uniaxial tension stress component σ₁₁ along the x₁-axis:

$${\sigma }_{11}={\mathrm{W}}^{\prime }({\lambda }_T)=2C_1(–\frac{1}{{\lambda }_T^2}+{\lambda }_T)$$ (xi)

Where C₁ is a material constant.

Ogden strain energy function

The Ogden model has been used previously to describe the nonlinear stress-strain behavior of complex materials, such as rubbers, biological tissue and brain tissues (20) The Ogden hyperelastic function is given by:

(xii).

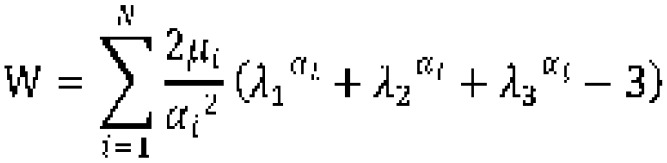
In uniaxial tension, the following equation applies:

$$\mathrm{W}({\lambda }_T)=\sum _{i=1}^N\frac{2{\mu }_i}{{\alpha }_i^2}\left({\lambda }_T^{{\alpha }_i}+2{\lambda }_T^{–\frac{1}{2}{\alpha }_i}–3\right)$$ (xiii)

It yields the following uniaxial tension stress component, σ₁₁, along the x₁-axis:

$${\sigma }_{11}={\mathrm{W}}^{\prime }({\lambda }_T)=\sum _{i=1}^N\frac{2{\mu }_i}{{\alpha }_i^2}\left({\lambda }_T^{{\alpha }_i–1}–{\lambda }_T^{\frac{–1}{2}{\alpha }_i–1}\right)$$ (xiv)

For N=1:

$${\sigma }_{11}={\mathrm{W}}^{\prime }({\lambda }_T)=\frac{2{\mu }_1}{{\alpha }_1}(–{\lambda }_T^{–1–\frac{{\alpha }_1}{2}}+{\lambda }_T^{–1+{\alpha }_1})$$ (xv)

For N=2:

$${\sigma }_{11}={\mathrm{W}}^{\prime }({\lambda }_T)=\frac{2{\mu }_1}{{\alpha }_1}(–{\lambda }_T^{–1–\frac{{\alpha }_1}{2}}+{\lambda }_T^{–1+{\alpha }_1})+\frac{2{\mu }_2}{{\alpha }_2}(–{\lambda }_T^{–1–\frac{{\alpha }_2}{2}}+{\lambda }_T^{–1+{\alpha }_2})$$ (xvi)

Where μ_i and α_i are material constants, and λ_i are the principal stretch ratios.

Mooney-Rivlin strain energy function

The strain energy function for an incompressible Mooney-Rivlin material (20) is:

$$\mathrm{W}={\mathrm{C}}_1({\mathrm{I}}_1–3)+{\mathrm{C}}_2({\mathrm{I}}_2–3)$$ (xvii)

Its strain energy depends on the first and second strain invariants. In uniaxial tension:

$$\mathrm{W}({\lambda }_T)={\mathrm{C}}_1({\lambda }_T^2+2{\lambda }_T^{–1}–3)+{\mathrm{C}}_2({\lambda }_T^{–2}+2{\lambda }_T–3)$$ (xviii)

So that:

$${\sigma }_{11}={\mathrm{W}}^{\prime }({\lambda }_{\mathrm{T}})=(2{\mathrm{C}}_1+\frac{2{\mathrm{C}}_2}{{\lambda }_T})({\lambda }_T^2–{\lambda }_T^{–1})$$ (xix)

Where the C₁ and C₂ are material constants.

Assumptions

The present study was based on the following assumptions: White matter was considered to be an incompressible material, and were demonstrated to be isotropic and homogenous before structures failing; under a small range of stretch (λ≤1.15) loading, the mechanical response of white matter, particularly under tension load, could be described by hyperelastic models; with the premise of assumption that no structural damage occurred in white matter during the whole stretch process, the hyperelastic model and material parameters mentioned above could be extended to use in a wider range (λ≤2.24); and, without consideration of energy loss, such as heat transfer, during the actual deformation process under tension loading, the transmission of energy was just restricted to energy storage, which was expressed as strain energy, and structural failure.

Damage evaluation

As previously mentioned, the present study assumed that brain tissue could be treated as a hyperelastic material in a small range of deformation under tension. These limited data could be fitted by using common hyperelastic constitutive models, and the constitutive relation could be generalized to present an ‘undamaged’ stress-stretch relationship in large deformation in tension. Then, W_UDG was defined as strain energy for the ‘undamaged’ stress-stretch curve and W_EPT as strain energy for the experimental curve. Therefore, it was evident that the difference between W_UDG and W_EPT, which could be defined as:

$${\mathrm{W}}_{\text{DMG}}={\mathrm{W}}_{\text{UDG}}–{\mathrm{W}}_{\text{EPT}}$$ (xx)

Quantified the degree of tissue damage in stretching

According to equation (ix), the W_UDG and W_EPT could be obtained by getting the definite integral of fitting functions. Considering white matter as a soft and vulnerable material, a traditional polynomial function, rather than common mechanical constitutive models, were used to describe the relationship between experimental tension stress values and the corresponding amount of stretch, and the parameters were given by nonlinear least-square fitting. The regression equation was as follows:

$${\sigma }_{11}=B_0+\sum _{i=1}^N{B}_i{\lambda }_T^i$$ (xxi)

Where σ₁₁ is tension stress, λ_T is the principal stretch ratio in the stretching direction and B_i is the coefficient in each term. The fitting procedure was performed by using the nonlinear fitted module in OriginPro 8.0 (OriginLab, Northampton, MA, USA) and the quality of fit for each model was assessed based on R². Table I demonstrated the coefficients of the regression equation, and inflexion points have been sought through high order derivation, as demonstrated in Fig. 2. The first inflexion point appeared when stretch reached 1.343, and it marked the beginning of tissue mechanical property change. In the present study, it was enough to ensure an ideal hyperelastic deformation if the stretch was not >1.15.

Table I.

Coefficients of the regression equation.

Parameters	Value	Standard Error
Intercept	162.54421	83.33519
B1	−813.54332	342.58013
B2	1629.70556	591.66707
B3	−1710.6673	556.7951
B4	1023.37927	308.54665
B5	−350.50895	100.75664
B6	63.9283	17.96696
B7	−4.81159	1.35075
R2	0.9954	–

B_i, coefficient in the regression equation.

Figure 2.

Stretch-stress curve for polynomial function, inflexion points and extreme point.

If a small stretch (λ≤1.15) of brain white matter could be regarded as ‘undamaged’ deformation, we could have the hyperelastic constitutive function based on strain energy function by fitting these experimental data, and if the above constitutive function could be used to describe an ‘undamaged’ deformation of brain white matter in the whole process of tension load, we could have the ‘undamaged’ constitutive equation, which presented the different stress-strain relationship with the experimental curve. It was clear that W_DMG was a relation of function dependent on stretch, and the increment in W_DMG expressed the intensity of structural failure.

Finite element analysis

The 3D model from the white matter stretch experiment with geometry and displacement by Franceschini et al (8) was applied in Fig. 1. To simplify simulation, a finite element model that only included tested tissue had been set up. The tensile process was divided into three stages according to protrude and concave of the polynomial fitted curve, as demonstrated in Fig. 2. The 2D model of brain tissue deformation with geometry and displacement for bleeding in ICH was demonstrated in Fig. 3. The model comprised 4313 8-node quadrilateral elements of type CPE8RP (ABAQUS v. 6.12 Standard,), and 13,373 nodes. All nodes on the outer edge in all directions constrained except for the gap edge between the left and right hemisphere. Elements were detached along the direction of the hematoma's common position on the cross section. The load was acted on the detached free edge, and the load simulated the pressure applying on the edge by the mass effect of hematoma in ICH.

Figure 3.

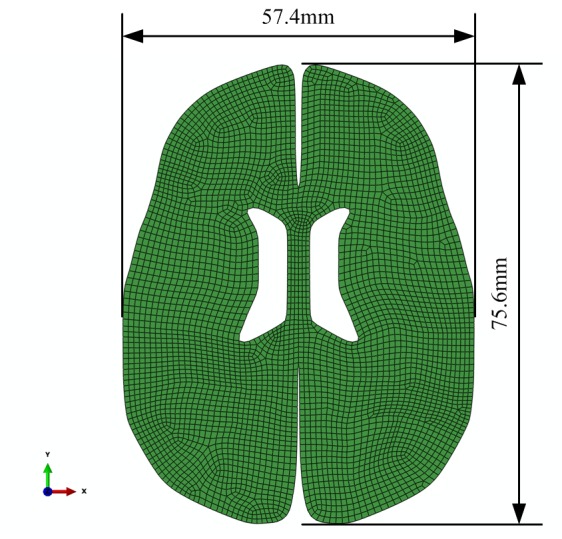
2D grid of the brain parenchyma.

Results

Model validation

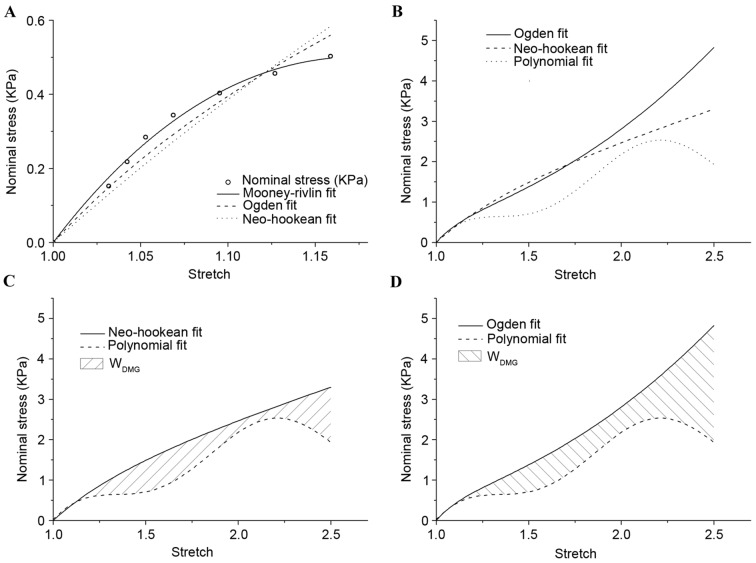
The fitting results for stretch no greater than 1.15 was plotted in Fig. 4, and all hyperelastic models demonstrated good agreement with experimental results (8). On the premise of λ≤1.15, the material constants for white matter were indicated in Table II. The Mooney-Rivlin model demonstrated an improved fitting effect compared with the other models. The Ogden and Neo-Hookean models were not stable for extending to a larger scale. When the stretch was >1.18, the changing curve of stress declined in the Mooney-Rivlin model. This result was not consistent with the stress-strain relationship in this simple tension experiment, and so the Mooney-Rivlin model was eliminated.

Figure 4.

Comparison of the experimental results with theoretical models. (A) Results on the premise of λ≤1.15. (B) Results on the premise of ideal ‘undamaged’ deformation. (C) Neo-Hookean fitting curve compared with polynomial fitting curve and the degree of tissue damage in tension. (D) Ogden fitting curve compared with polynomial fitting curve and the degree of tissue damage in tension. λ, stretch.

Table II.

List of material constants for white matter on the premise of the stretch at λ≤1.15.

	Model
Material constant	Neo-Hookean	Ogden	Mooney-Rivlin
C1	762.75	–	−2097.043
C2	–	–	3134.634
µ1	–	1799.094	–
α1	–	−7.0557	–

In Fig. 4B, the results of nominal stress vs. stretch for the Ogden and Neo-Hookean models were demonstrated, which were extrapolated to a larger scale by material constants on the premise of λ≤1.15 and polynomial fitting. The majority of the Ogden and Neo-Hookean fitting curves were located above the polynomial fitting curve. The area under the curves demonstrated corresponding strain energy, and the shaded area in Fig. 4C and D indicated W_DMG: The degree of tissue damage in comparison with the Ogden and Neo-Hookean fitting curves, respectively. ΔW_Neo-Hookean and ΔW_Ogden were used to represent the difference of strain energy between the hyperelastic model and the polynomial fitting model with increasing stretch. Fig. 5A demonstrated that there was no distinction in the trend of strain energy loss during the tensile process. By setting fix-stretch-increment=0.01, per unit increment of ΔW_Neo-Hookean and ΔW_Ogden had been calculated and compared (Fig. 5B). The change of per unit increment of strain energy loss in the two groups demonstrated a similar trend; however, the maximum value appeared at stretch=1.61 in ΔW_Neo-Hookean and at stretch=2.24 in ΔW_Ogden. Combining this result with the inflexion points on the polynomial fitting curve in the present study, the level of damage in stretch could be divided into four phases: Undamaged (λ≤1.343); slight damage (1.343≤λ≤1.863); serious damage (1.863≤λ≤2.241); and fracture (λ≥2.241).

Figure 5.

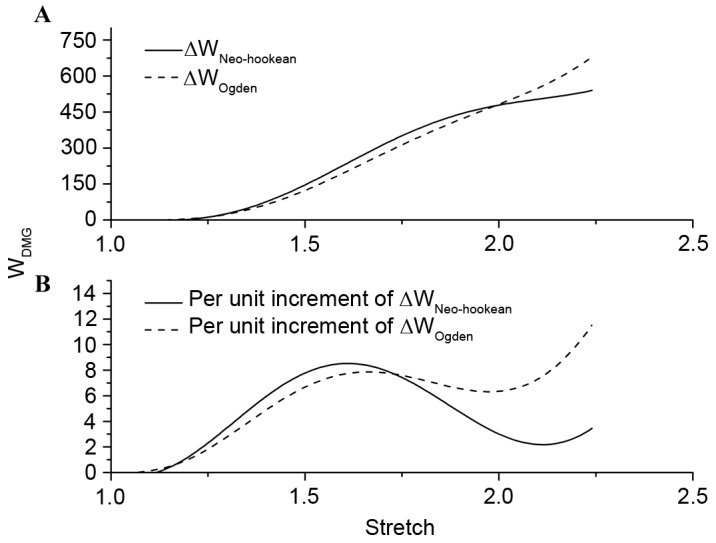
Difference of strain energy loss and per unit increment of strain energy loss between hyperelastic model and the polynomial fitting model with the increase of stretch. (A) Strain energy loss and (B) per unit increment of strain energy loss. W_DMG was defined as difference between strain energy for the ‘undamaged’ stress-stretch curve strain energy for the experimental curve, and ΔW is the loss strain energy between fitting curve and hyperelastic models.

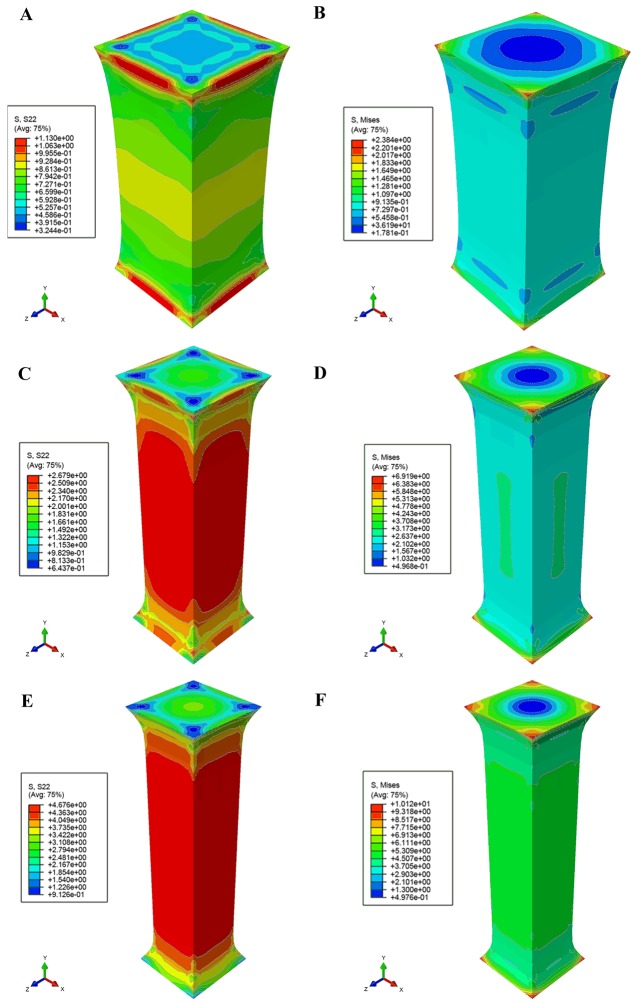
Taking the polynomial fitting model (equation xxi) as a constitutive function, Fig. 6 demonstrated Mises- and S22-stress distribution under the different stretch lengths based on the study by Franceschini et al (8). The simulation demonstrated a strong agreement with the experimental results that both sides of a specimen had been fixed on a stretching device so that the deformation of both ends was less than the mid part in the stretching direction. The concentration Mises stresses were located in the corner regions in contact with the stretching device, and tensile stress was concentrated in the mid part. The tensile load on the end of the white matter agreed with experimental data in checkpoints (λ=1.343, 1.863 and 2.241), as demonstrated in Fig. 6A, C and E. Results also indicated that the tissue broke in experiments described by Franceschini et al (8), when the S22 reached ~4.676 kPa.

Figure 6.

Finite element analysis of uniaxial tension experiment on white mater. (A) S22 stress distribution and (B) Mises stress distribution at λ=1.343. (C) S22 stress distribution and (D) Mises stress distribution at λ=1.863. (E) S22 stress distribution and (F) Mises stress distribution at λ=2.241. λ, stretch.

Stress distribution

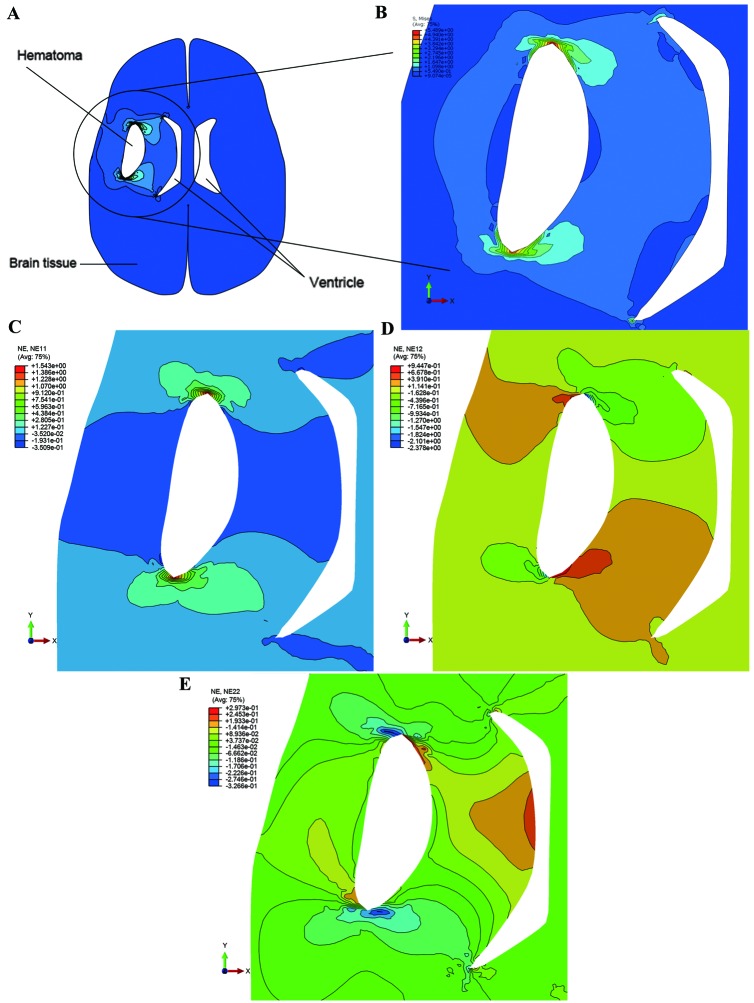
Fig. 7 demonstrated the Mises stress distributions of the loading caused by the mass effect of the hematoma. Stress increased around the crack as the pressure was applied on the crack edges, and maximum stress was located in both ends of the crack. As demonstrated in Fig. 6F, the maximum tolerance of Mises stress was set to 4.908 kPa (mean of Mises stress on the mid part). The area of ventricle close to the hematoma was evidently reduced when the loading was set to 5.96 kPa, caused by the mass effect of the hematoma. Apart from at both ends of the crack, the stress was concentrated at regions located in the ventricle side. Fig. 7C-E, respectively, demonstrated the strain distribution in the X-axis, Y-axis and X-Y-axis directions. The maximum value of strain derived from numerical simulation was 1.543 and the experimental expectation value was 1.241.

Figure 7.

Von Mises stress and strain distributions in the simulation of intracerebral hemorrhage. (A) Deformation of whole parenchyma after hematoma accumulation. (B) Distribution of the stress concentration. Deformation distributions in (C) NE11, (D) NE22 and (E) NE12 direction. NE11, horizontal direction; NE22, shear direction; NE12, vertical direction.

Discussion

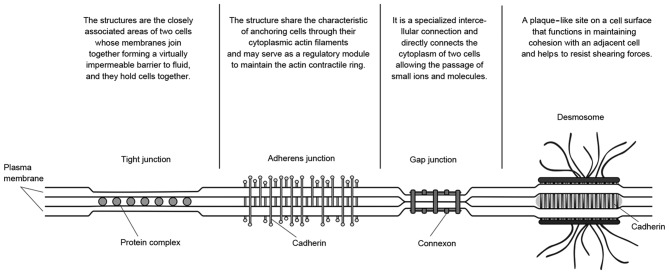
Spontaneous intracerebral hemorrhages commonly occur in the white matter, which is described as a particular location where axons gather and interact with each other by fibers (21). Due to hemorrhage, the effect of a tear on white matter is the direct physical injury; however, the potential damage, which is caused by tissue deformation and mass effect, cannot be ignored. Within a small deforming range, the deformation behavior of brain tissue is considered to obey nonlinear hyperelastic law, as does the majority of biological soft tissues (20). However, within a larger deforming range, the deformation has been indicated to be entirely different due to structural damage of the biological tissue itself (7), which may be predominantly attributed to the failure of cellular structure and cell junctions. As demonstrated in Fig. 8, common cell junctions may have a role in linking cells with other cells or the surrounding matrix, regardless of what physiological functions or connection strength they had. The degree of irreversible distortion determines whether the cell junctions have been damaged (22). In former literature, according to nonlinear mechanical law, the stretch-stress curves obtained in the present study may be divided into five parts: An initial stiff response; hardening behavior; locking behavior; hardening; and softening (8). However, before white matter suffers irreversible structural damage, it is a reasonable condition to treat white matter as a simple homogeneous material, although it will not be sufficient to describe mechanical properties of white matter under large deformation. It is reasonable to infer that each part corresponds to a certain degree of failure of cell or tissue structure and junctions. With the deformation intensified, the mechanical behavior of brain tissue may change constantly, and it is difficult to abstract mechanical parameters according to mechanical law, such as continuum mechanics or fracture mechanics (23). Therefore, in the present study, the method, which combines strain or stretch with strain energy loss, should be an effective way to gauge the damage degree of brain white matter.

Figure 8.

Sketch map of cell junctions.

During uniaxial stretching of white matter, the curve of nominal stretch vs. nominal stress demonstrated mechanical behavioral changes at different stages, and the entire process could be divided into three parts: 1) nondestructive deformation; 2) destructive deformation; and 3) fracture. The axonal microstructure in the optic nerve demonstrated an undulated appearance (22), which possesses the ability to withstand some degree of distortion for deformation, and individual axons in white matter demonstrate a similar appearance (2). While deforming, if the degree of deformation exceeds the limit, cell junctions and cytoskeletons will fracture, and cell structure will collapse (22). When structural damage reaches the critical level, severe tear ictus may occur (24). It was comparatively easy to match nondestructive deformation and fracture with a section of the stress-stretch curve; however, the degree of structure damage under destructive deformation is difficult to measure. The fitting curves for nominal stretch to nominal stress had been studied for the correlation between the degree of structure damage and the concavity and convexity of fitting function. In the present study, regarding deformation before the point (1.343, 0.648) as nondestructive deformation, and after the point (2.241, 2.685) as fracture, the inversion point (1.863, 1.738) was likely to partition destructive deformation into two sub-phases, which corresponds to certain structural failure. A study by Bain and Meaney (7) investigated tissue-level thresholds for axonal damage in central nervous system white matter injury, and their results, which agreed with the result in the present study, demonstrated that the 90% probability value strain of 0.34 defined the liberal threshold for morphological injury.

In this simple tension experiment, when the stretch was <1.15, the stress-strain relationship may be presented by Mooney-Rivlin, Ogden and Neo-Hookean models (20), which were commonly used for modeling nonlinear elastic material and brain tissue (11,16,25,26). The Mooney-Rivlin model was not stable for extending to a larger scale despite demonstrating an improved fitting effect compared with the other models. The present study indicated that there was not only a negligible difference of W_DMG between the Ogden and Neo-Hookean fittings, but also between ΔW_Neo-Hookean and ΔW_Ogden; however, per unit increment of ΔW demonstrated different trends in the late tension stage. The increment of ΔW_Ogden increased with increasing stretch, and the increment of ΔW_Neo-Hookean demonstrated a trend of fluctuations. The former implied that stretch increase aggravated structural failure, while the latter declined gradually after reaching its maximum. It may be inferred that structural failure of white matter is not an irregular linear process, but a process controlled by multiple structures, and the failure of different structures is not synchronized.

3D FEA results demonstrated that Franceschini et al (8) experimental data cannot expound the stress distribution. The maximal von Mises stress focused on both fixed surfaces, and it highlighted the influence of the fixation method on the results. S22 stress distribution demonstrated that the stresses were concentrated in the mid part rather than at both ends of the specimen. In the experiment by Franceschini et al (8), the fracture took place in the region near the ends where the large range of tension stress was distributed; this result was in conformity with previous FEA results. The polynomial fitting function could be reliably used as a constitutive function to model the mechanical behavior of white matter under tension. The present study indicated that deformation caused by hematoma compression is predominantly distributed around the hematoma, and made the ipsilateral ventricle smaller. After ICH ictus, the space occupied by hematoma, which is called mass effect, causes direct tearing injury and will produce deformation on the region of stress concentration, resulting in varying degrees of structural failure (3). The distribution of stress and strain demonstrate the potential damage distribution, but stress, which may be calculated with constitutive function and the variable of strain, depend on the material itself and cannot be directly measured, particularly in vivo. Therefore, it is reasonable to use strain as an evaluating standard for brain tissue damage in ICH.

Uniaxial tension experimental data (8) was analyzed and evaluation criterion of tissue damage based on strain was discussed in the present paper. However, the deformation of brain tissue is a complex process that simultaneously includes tension, compression and shear (10). The lack of similar experimental data under simple shear makes it difficult to obtain a revised evaluation criterion. Nevertheless, biological tissues are so complex and specific that it is difficult to ensure the result reproducibility of experiments, even if the test tissues are taken from the same sample (19). Additionally, the test tissues cannot be intact after suffering any mechanical load greater than the maximum tolerance. Fortunately, FEA software, such as ABAQUS and ANSYS, are able to evaluate mechanical parameters of material by analyzing a single type of strain-stress data if soft tissues are assumed to be hyperelastic material in a certain range of deformation, and the uniaxial tension test is a common way of obtaining parameters. Through these methods, the model has a limited application area, for instance, it cannot evaluate damage caused by compression and shear. In the stage of this research, damage evaluation under compression and shear will be investigated.

White matter is anisotropic and heterogeneous, and each independent sample demonstrates different mechanical parameters (13). The evaluation in the present study was only able to accurately evaluate the damage degree of a single specimen and would be unable to obtain an accurate and universal assessment standard unless we knew precisely the stress-stretch relationship of each evaluation object. In the present study, the strain rate dependency was ignored because the majority of medical images are acquired 4 h after ICH ictus. The deformation of brain tissue in ICH may be treated as a one-way process if the process of cerebral hemorrhage is simplified to the process of hematoma increasing continuously; however, in reality, cerebral hemorrhage is a complex biochemical and physical process.

With further simulation studies, animal experiments and tissue-level mechanical experiments, direct evidence for tissue damage may be obtained. Despite gaining understanding of the relationship between stress and strain, the keystone of future work may be to design a device that is able to realize the quantitative deformation of brain tissue, including tension, compression and shear in vitro. An ICH tensile damage evaluation method based on CT or MRI images may be developed by composing digital image processing technology with the results of the present study.

Funding

The present study was supported by the National Basic Research Program of China (973 program; grant no. 2014CB541600) and by the Visiting Scholar Foundation of Key Laboratory of Biorheological Science and Technology (Chongqing University) and the Ministry of Education (grant no. CQKLBST-2018-019).

Availability of data and materials

All data generated or analyzed during this study are included in this published article.

Authors' contributions

PR performed the modeling, the finite element analysis and was a major contributor in writing the manuscript. BCW, YZW and SLH performed the simulation analyses. TWG and XFL performed the simulations and contributed in the preparation of the manuscript. All authors read and approved the final manuscript.

Ethics approval and consent to participate

Not applicable.

Patient consent for publication

Not applicable.

Competing interests

The authors declare that they have no competing interests.