A Dynamical Systems Model of Intrauterine Fetal Growth

Abstract

The underlying mechanisms for how maternal perinatal obesity and intrauterine environment influence fetal development are not well understood and thus require further understanding. In this paper, energy balance concepts are used to develop a comprehensive dynamical systems model for fetal growth that illustrates how maternal factors (energy intake and physical activity) influence fetal weight and related components (fat mass, fat-free mass, and placental volume) over time. The model is estimated from intensive measurements of fetal weight and placental volume obtained as part of Healthy Mom Zone (HMZ), a novel intervention for managing gestational weight gain in obese/overweight women. The overall result of the modeling procedure is a parsimonious system of equations that reliably predicts fetal weight gain and birth weight based on a sensible number of assessments. This model can inform clinical care recommendations as well as how adaptive interventions, such as HMZ, can influence fetal growth and birth outcomes.

1. Introduction

High infant birth weight is associated with subsequent childhood and adult-onset obesity, type 2 diabetes, cardiovascular disease, and some forms of cancer [1–8]. High maternal body mass index (BMI) and excessive gestational weight gain (GWG) are independent predictors of higher infant fat mass and, in turn, large for gestational age birth weight [9]. High BMI and GWG are also associated with complications such as intrauterine growth restriction, cesarean delivery, and preterm birth [1, 10, 11]. Nearly 70% of pregnant women in the United States failed to adhere to the Institute of Medicine guidelines for appropriate GWG, with 50% or more women exceeding guidelines [12]. Given the increased risk for high infant birth weight among women who are obese or have excessive GWG, research is warranted to better understand the underlying mechanisms of fetal growth, and effcient interventions are needed to regulate maternal and fetal weight [13].

Our prior work has described a conceptual framework for managing GWG in over-weight/obese women [14] and for regulating infant birth weight [15]; this framework relies on methods from control systems engineering to develop decision policies that optimize the adaptation for participant response. The implementation of such a framework calls for developing advanced control systems which rely on dynamical models that are able to predict individualized responses to different intervention components and subsequently predict GWG, the intrauterine growth profile, and infant birth weight [15–17]. In particular, one important end use of a dynamical systems model of intrauterine fetal growth is as the internal model in a model-based controller that accomplishes an optimized, adaptive intervention [18–20].

Energy balance for modeling weight and body composition change has been examined extensively, including among pregnant women [16, 21]. Modeling intrauterine growth has received some prior examination [22]; however, further modeling efforts are needed to better understand how prenatal status ‘programs’ fetal growth [23, 24]. To address this gap, we use intensive longitudinal data from Healthy Mom Zone (HMZ) [14], an ongoing trial, which is an individually-tailored, adaptive intervention to manage weight gain in overweight and obese pregnant women. While the model developed in this paper extends from prior work [22, 25], it grounds a more complete theoretical understanding for how external maternal factors (e.g., daily energy intake and physical activity) influence fetal growth profiles. The following are number of particular advancements made in this work:

• A single-output energy balance model. Building from the model in [22], the proposed energy balance model in this work features a single, easy-to-measure output (total fetal weight). In addition to grounding a better theoretical understanding of external factors and pre-existing conditions directly influence intrauterine fetal weight growth, this reformulation highlights less expensive and invasive requirements for estimating individualized model parameters; measurements of total fetal weight can be far more reliable than measurements of body composition (more so in the first trimester [26]).

• Application of the Second Law of Thermodynamics. The fetal energy balance model in this work provides a succinct, well-established accounting for the impact of entropy on fetal growth. Despite that the idea of entropy of new tissue formation has originated in Christiansen et al. [25], the work in [25] features an obesity model and the formulation cannot be directly re-purposed for quantifying fetal growth dynamics. Part of the contribution in this work is to merge efforts from Christiansen et al. and Thomas et al.: to produce a more rigorous and complete reformulation of fetal growth.

• Use of HMZ study data. Utilizing data from the HMZ study [14], the developed fetal model presents a method for quantifying the impact of daily changes of physical activity on fetal growth. Moreover, using intensive, longitudinal participant data from HMZ, it is possible to estimate and validate the general first-principles fetal model structure developed in this work, as well as estimate a logistic profile of fetal fat mass accretion whose structure is supported by the literature.

• An improved placental volume model. As is discussed in Section 2.3, in this work, the curvature of the proposed placental volume model is more independently parameterized, which gives a more intuitive and easier model to estimate. This model also implicitly enforces the initial condition at conception; hence, for model estimation and simulation, the proposed model does not require a placental volume measurement for establishing an initial condition.

In this paper, we present parameter estimation and model validation results drawn from four representative HMZ participants. The final fetal energy balance model parameters are estimated by solving a nonlinear least squares optimization problem; the set of estimated model parameters is then used to generate simulations for model validation.

This paper is organized as follows: Section 2 presents the underlying modeling assumptions and describes the derivation of the proposed fetal energy balance model. Section 3 features the optimization problem that accomplishes model parameter estimation from ultrasound measurements, followed by a presentation of the metrics and criteria used for model validation. Section 4 summarizes conclusions and future work.

2. Fetal Energy Balance Model

We begin by outlining important assumptions and simplifications leading to the final proposed fetal energy balance model. Next, building on insights from prior researchers [22, 25], we establish a first-principles energy balance model of fetal growth. Following the first law of thermodynamics, this fetal energy balance model applies the conservation of energy principle. Further, the presented derivation explicitly accounts for the energy loss due to new fetal tissue formation, as dictated by the second law of thermodynamics from which it follows that the conversion of energy requires energy. Finally, explicitly defined logistic growth functions are established to estimate the rate of fetal fat mass deposition and the placental volume.

2.1. Model Development

2.1.1. Initial Assumptions

The following initial assumptions and simplifications lead to the proposed fetal model (equation (21)):

• 1)Fetal body mass is divided into two main components: fat and fat-free tissues.
• 2)Fetal energy expenditure due to diet-induced thermogenesis is negligible.
• 3)Fetal physical activity in the womb is negligible.
• 4)The rate of fetal fat-mass deposition is only regulated by the total fetal body mass [25].
• 5)The contribution of daily maternal diet to fetal nutrition substantially exceeds additional nutrient supply originating from maternal body components.
• 6)Fetal energy imbalances are always positive and follow from the diet of a healthy, well-nourished mother.
• 7)The proportion of fetal body fat that contributes to expenditure is equal to that of fetal fat-free tissues.

Following the derivation of the fetal model in Sections 2.1.2 and 2.1.3, a discussion of the rationale for assumptions 6) and 7) is provided.

Nomenclature
Constants
${\mathrm{\lambda }}_{F{M}_f}$	Energy stored per unit fetal fat mass	[kcal/kg]
${\mathrm{\lambda }}_{FF{M}_f}$	Energy stored per unit fetal fat-free mass	[kcal/kg]
Parameters
$e_{F{M}_f}$, $e_{FF{M}_f}$	Efficiencies of conversion of excess energy to new fat and fat-free tissues, respectively	[1]
α	Proportionality constant	[d/kcal/ml]
γ	Conversion coefficient	[ml−1]
μ	Daily energy expenditure per unit fetal body mass	[kcal/kg/d]
Variables
t	Gestational age	[days]
Cf(t)	Daily energy accumulation in the fetus	[kcal]
If(t)	Daily fetal energy intake resulting from maternal energy intake	[kcal/d]
$E_{e_f}\left(t\right)$	Total fetal energy expenditure	[kcal/d]
$E_{M_f}\left(t\right)$	Energy required to maintain the fetus life	[kcal/d]
$E_{c_f}$	Energy required for the conversion of excess energy into new fetal tissue	[kcal/d]
FMf(t)	Fetal fat mass	[kg]
FFMf(t)	Fetal fat-free mass	[kg]
Wf(t)	Total fetal weight	[kg]
fr(Wf)	Rate of fetal fat mass deposition	[1]
Wm(t)	Total maternal weight	[kg]
Ef(t)	Total energy to build the fetal tissue up to day t	[kcal]
$E_{F{M}_f}\left(t\right)$	Total energy to build the fetal fat tissue up to day t	[kcal]
$E_{FF{M}_f}\left(t\right)$	Total energy to build the fetal fat-free tissue up to day t	[kcal]
m(t)	Maternal energy intake	[kcal/d]
PA(t)	Maternal physical activity	[kcal/d]
P(t)	Placental volume	[ml]
g(t)	Glycemic impact of intake	[1]
Kf(t)	Fetal gain coefficient from intake	[kg-d/kcal/ml]
τf(Wf)	Time constant of fetal weight growth	[d]
ef(Wf)	Overall efficiency of energy conversion	[1]

2.1.2. Energy Balance Equation

The basis for determining fetal growth is a daily energy balance based on the First Law of Thermodynamics that takes into account the metabolizable energy intake I_f (provided by the mother) and fetal energy expenditure $E_{e_f}\left(t\right)$ to define a rate of accumulation of the total fetal energy C_f(t). Considering the fetus as the system of interest, we have

$$\begin{array}{ccccc}\begin{array}{c}\text{Rate}\text{of}\text{Energy}\\ \text{Accumulation}\end{array}& =& \begin{array}{c}\text{Energy}\\ \text{Intake}\text{Per}\text{Day}\end{array}& -& \begin{array}{c}\text{Energy}\\ \text{Expenditure}\text{Per}\text{Day}\end{array}\\ \frac{d{C}_f\left(t\right)}{dt}& =& I_f\left(t\right)& -& E_{ef}\left(t\right)\end{array}$$ (1)

with

$$E_{ef}\left(t\right)=E_{Mf}\left(t\right)+E_{cf}\left(t\right)$$ (2)

accounting for fetal energy expenditure towards maintaining and sustaining life ($E_{M_f}$) and the energy required for the conversion of excess energy into new tissue ($E_{c_f}$).

Considering a two-compartment energy balance model (i.e., total body mass divided into fat and fat-free mass components), the positive rate of change of the total combustible fetal energy content, dC_f/dt, can also be calculated by accounting for changes of fetal body components [22], giving

$$\frac{d{C}_f\left(t\right)}{dt}={\mathrm{\lambda }}_{F{M}_f}\frac{dF{M}_f\left(t\right)}{dt}+{\mathrm{\lambda }}_{FF{M}_f}\frac{dFF{M}_f\left(t\right)}{dt}$$ (3)

which, in turn, when combined with (1), yields

$${\mathrm{\lambda }}_{F{M}_f}\frac{dF{M}_f\left(t\right)}{dt}+{\mathrm{\lambda }}_{FF{M}_f}\frac{dFF{M}_f\left(t\right)}{dt}=I_f\left(t\right)-E_{ef}\left(t\right)$$ (4)

with FM_f(t) and FFM_f(t) denoting the total fetal fat and fat-free masses, respectively; ${\mathrm{\lambda }}_{F{M}_f}$ and ${\mathrm{\lambda }}_{FF{M}_f}$ are the energy densities of the fetal fat and fat-free components, respectively (i.e., energy content per unit fat/fat-free mass). As depicted in equation (4), both ${\mathrm{\lambda }}_{F{M}_f}$ and ${\mathrm{\lambda }}_{FF{M}_f}$ are assumed time-invariant.

Equation (4) presents the basic fetal energy balance result following directly from the first law of thermodynamics, as similarly highlighted in the Thomas et al. (2008) model [22]. However, equation (4) involves terms that need to be further defined, are difficult to measure experimentally, or expensive to track in an intervention setting. More specifically, in this work, profiles describing the evolution of the fetal body composition (FM and FFM), portion of maternal energy intake contributing to fetal nutrition, and the influence of maternal physical activity are all terms that are explored and expanded further from (4). Moreover, the expenditure term, $E_{e_f}\left(t\right)$, requires estimates for the efficiency of energy conversion into new fetal fat and fat-free tissues (energy loss due to entropy); these efficiencies are difficult and expensive to measure experimentally. Furthermore, given current imaging technologies that build from well-studied sonographic methods to estimate total fetal weight, it is advantageous to reformulate the basic fetal energy balance equation shown as (4) in terms of the total fetal body mass (also referred to as total fetal weight, W_f(t)). In the following section, the primary aim is to establish a parsimonious fetal energy balance model that proves to overcome these challenges.

2.1.3. Effciency of Energy Conversion & Energy Balance Reformulation

The goal of this section is to formulate equation (4) in terms of total fetal weight. To achieve this outcome, we built from concepts used to develop human obesity models by Christiansen et al. (2005) [25]. The time-varying rate of fetal fat mass deposition (with respect to total fetal weight) is defined as follows:

$$f_r\left(W_f\right)\stackrel{\text{def}}{=}\underset{\mathrm{\Delta }{W}_f\to 0}{\text{lim}}\frac{\mathrm{\Delta }F{M}_f}{\mathrm{\Delta }{W}_f}=\frac{dF{M}_f}{d{W}_f}$$ (5)

which leads to the following expressions for the rate of change of FM_f and FFM_f in terms of total fetal weight W_f,

$$\frac{dF{M}_f}{df}=\frac{dF{M}_f}{d{W}_f}\frac{d{W}_f}{dt}\triangleq f_r\left(W_f\right)\frac{d{W}_f}{dt}$$ (6a)

$$\frac{dFF{M}_f}{dt}\triangleq \frac{d}{dt}\left(W_f-F{M}_f\right)=\left[1-f_r\left(W_f\right)\right]\frac{d{W}_f}{dt}$$ (6b)

With an explicitly defined f_r(W_f), the components FM_f(t) and FFM_f(t) become explicit functions of the total fetal weight, W_f(t). Using equations (3) and (6), we now have

$$\frac{d{C}_f}{dt}=\left({\mathrm{\lambda }}_{F{M}_f}{f}_r\left(W_f\right)+{\mathrm{\lambda }}_{FF{M}_f}\left[1-f_r\left(W_f\right)\right]\right)\frac{d{W}_f}{dt}$$ (7)

Second, we also define the efficiencies of new fetal tissue formation arising from the second law of thermodynamics as follows [27]:

$$\text{efficiency}\text{of}\text{fat}\text{mass}\text{deposition}=e_{F{M}_f}\stackrel{\text{def}}{=}{\mathrm{\lambda }}_{F{M}_f}\frac{dF{M}_f}{d{E}_{F{M}_f}}$$ (8a)

$$\text{efficiency}\text{of}\text{fat-free}\text{mass}\text{deposition}=e_{FF{M}_f}\stackrel{\text{def}}{=}{\mathrm{\lambda }}_{F{M}_f}\frac{dFF{M}_f}{d{E}_{FF{M}_f}}$$ (8b)

where $d{E}_f\triangleq d{E}_{F{M}_f}+d{E}_{FF{M}_f}$ captures the total energy required to increase the total fetal body energy content by dC_f. The efficiencies in (8) provide a useful parametric representation for the energy loss due to new fetal fat and fat-free tissue formation, respectively. Thus, from equations (6) and (8) we have

$$\frac{d{E}_f}{dt}\triangleq \frac{d{E}_{F{M}_f}}{dt}+\frac{d{E}_{FF{M}_f}}{dt}=\frac{{\mathrm{\lambda }}_{F{M}_f}}{e_{F{M}_f}}\frac{dF{M}_f}{dt}+\frac{{\mathrm{\lambda }}_{FF{M}_f}}{e_{FF{M}_f}}\frac{dFF{M}_f}{dt}=\left(\frac{{\mathrm{\lambda }}_{F{M}_f}{f}_r\left(W_f\right)}{e_{F{M}_f}}+\frac{{\mathrm{\lambda }}_{FF{M}_f}\left[1-f_r\left(W_f\right)\right]}{e_{FF{M}_f}}\right)\frac{d{W}_f}{dt}$$ (9)

As first realized by [25], the dynamic rate of change of E_f can be calculated by establishing the available energy for new fetal tissue deposition; i.e., the difference between the fetal energy intake and the energy expenditure required for sustaining and maintaining life of existing fetal tissues, thus

$$\frac{d{E}_f}{dt}\triangleq I_f-E_{M_f}$$ (10)

Combining (9) and (10) gives

$$\frac{d{W}_f}{dt}=\frac{d{W}_f}{d{E}_f}\frac{d{E}_f}{df}=\frac{I_f-E_{M_f}}{{\mathrm{\lambda }}_{F{M}_f}{f}_r\left(W_f\right)/e_{F{M}_f}+{\mathrm{\lambda }}_{FF{M}_f}\left[1-f_r\left(W_f\right)\right]/e_{FF{M}_f}}$$ (11)

which, when substituted into (7), gives

$$\frac{d{C}_f}{dt}=\underset{e_f\left(W_f\right)}{\underbrace{\left(\frac{{\mathrm{\lambda }}_{F{M}_f}{f}_r\left(W_f\right)+{\mathrm{\lambda }}_{FF{M}_f}\left[1-f_r\left(W_f\right)\right]}{{\mathrm{\lambda }}_{F{M}_f}{f}_r\left(W_f\right)/e_{F{M}_f}+{\mathrm{\lambda }}_{FF{M}_f}\left[1-f_r\left(W_f\right)\right]/e_{FF{M}_f}}\right)}}\left(I_f-E_{M_f}\right)$$ (12)

Where now the ratio between dC_f/dt and (I_f − E_{M f}) represents the overall time-varying thermodynamic efficiency of energy conversion into new fetal tissue, 0 ≤ e_f(W_f) ≤ 1; this was first similarly established by [25], however, with a constant f_r assumed. Inserting equation (2) into equation (1) and contrasting with (12) provides an accounting method for the energy loss due to new tissue formation

$$E_{cf}\left(t\right)=\left(1-e_f\left(W_f\right)\right)\left(I_f\left(t\right)-E_{M_f}\left(t\right)\right)$$ (13)

with e_f(W_f) per equation (12).

To establish the I_f(t) term in (12), it is known that the fetal energy intake through the placenta (whose volume is denoted by P(t)) originates mainly from two nutritional sources: maternal diet, m(t), and maternal body components (e.g., muscles, fats, bones, etc.) [28], hence giving

$${\widehat{I}}_f\left(t\right)=\gamma \left(t\right)\left[f\left(t\right)m\left(t\right)+{\alpha }_W\left(t\right)W_m\left(t\right)\right]P\left(t\right)$$ (14)

where W_m(t) is daily total maternal weight; α_W(t) is a function that captures the daily fraction of maternal body mass directly contributing to fetal nutrition ([=] kcal/kg/d). g(t) denotes the daily glycemic impact of intake (ranges from 0 to 1); γ(t) is a conversion coefficient that is associated with maternal physical activity, as postulated in equation (22) (and discussed later in the paper). However, for the case of a healthy, non-fasting and well-nourished mother, it may be accepted to assume that the basic nutritional needs for fetal growth can be met by daily maternal diet alone [29, 30]. Hence, it is assumed that g(t)m(t) ≫ α_W(t)W_m(t) ∀t, giving (identical to [22])

$$I_f\left(t\right)=\gamma \left(t\right)m\left(t\right)g\left(t\right)P\left(t\right)$$ (15)

The fetal energy expenditure term in (12) ($E_{M_f}\left(t\right)$) can be considered, for simplicity, as a direct proportion of total fetal body mass [22]:

$$E_{M_f}\left(t\right)=\mu \left[F{M}_f\left(t\right)+FF{M}_f\left(t\right)\right]\triangleq \mu W_f\left(t\right)$$ (16)

where μ is the daily energy expenditure per unit fetal body mass. Hence, from (7) and (12) we have

$$\left({\mathrm{\lambda }}_{F{M}_f}{f}_r\left(W_f\right)/e_{F{M}_f}+{\mathrm{\lambda }}_{FF{M}_f}\left[1-f_r\left(W_f\right)\right]/e_{FF{M}_f}\right)\frac{d{W}_f\left(t\right)}{dt}=I_f\left(t\right)-E_{M_f}\left(t\right)$$ (17)

Applying equations (15) and (16) gives

$$\left({\mathrm{\lambda }}_{F{M}_f}{f}_r\left(W_f\right)/e_{F{M}_f}+{\mathrm{\lambda }}_{FF{M}_f}\left[1-f_r\left(W_f\right)\right]/e_{FF{M}_f}\right)\frac{d{W}_f\left(t\right)}{dt}=\gamma \left(t\right)m\left(t\right)g\left(t\right)P\left(t\right)-\mu W_f\left(t\right)$$ (18)

Furthermore, dividing equation (18) by μ and defining

$$K_f\left(t\right)=\frac{\gamma \left(t\right)g\left(t\right)}{\mu }$$ (19)

$${\tau }_f\left(W_f\right)=\frac{\mathrm{\lambda }F{M}_f{f}_r\left(W_f\right)/e_{F{M}_f}+{\mathrm{\lambda }}_{FF{M}_f}\left[1-f_r\left(W_f\right)\right]/e_{FF{M}_f}}{\mu }$$ (20)

yields a final fetal energy balance equation in terms of the total fetal weight:

$${\tau }_f\left(W_f\right)\frac{d{W}_f\left(t\right)}{dt}+W_f\left(t\right)=K_f\left(t\right)m\left(t\right)P\left(t\right)$$ (21)

Equation (21) features an intrauterine fetal weight growth model that conforms with the description of a first-order quasi Linear Parameter-Varying (quasi-LPV) system whose scheduling variable is the output, i.e., the total fetal weight, W_f(t). In equation (21), the growth parameter τ_f is the time constant [31] which characterizes the speed of response. The parameters γ(t) and g(t) appearing in equation (19) are discussed in the explanation of equations (22) and (30), respectively.

In addition to achieving the goal of reformulating equation (4) in terms of a single, measurable output variable (i.e., the total fetal weight), equation (21) features an intuitive, well-understood first-order dynamical systems model structure that is more amenable to system identification and control. A further outcome following from the development of (21) is that estimates for $e_{F{M}_f}$ and $e_{FF{M}_f}$ can be determined directly from ultrasound measurements.

Following the development of the model in equation (21) we make the following remarks:

• Given that the exact mechanism governing the influence of maternal physical activity on fetal weight is yet to become su ciently understood, we follow Thomas et al., 2008 [22] in assuming that maternal physical activity influences the placenta function, and thereby influences the fetus’ nutrition. This is further established in Clapp [32] from which it is known that the effect of maternal exercise on fetal growth depends on numerous factors such as type, frequency, intensity, and the time point in pregnancy when the exercise is performed. Hence, for simplicity, we assume that, over a baseline, maternal physical activity is proportional to placental function, which is captured via the γ(t) parameter in (21); that is

  $$\gamma \left(t\right)=\alpha PA\left(t\right)+\beta$$ (22)

  where PA(t) denotes the daily maternal physical activity, α is the proportionality constant, and β is the established baseline. Following the literature review presented by [22], we further assume that α ≤ 0 and β ≥ γ > 0 ∀ t ≥ 0.
• It follows from assumption 6) that dW_f/dt ≥ 0 during gestation; thus, from equation (21) we have

  $$K_f\left(t\right)=\frac{\gamma \left(t\right)g\left(t\right)}{\mu }\ge \frac{W_f\left(t\right)}{m\left(t\right)P\left(t\right)}\forall t\text{during}\text{gestation}$$ (23)

  providing one important criterion for model validation. Additionally, the inequality in (23) can serve as an approximate (yet useful) diagnostic tool indicating rate of fetal growth (as will be discussed later in Figure A5).
• Kennaugh and Hay (1987) [33] reported estimates where ${\mu }_{F{M}_f}$ and ${\mu }_{FF{M}_f}$ need not be averaged into a single proportion of energy expenditure (energy requirement); in which case, contrary to assumption 7), if ${\mu }_{F{M}_f}\ne {\mu }_{FF{M}_f}$, it can be shown that equation (21) becomes

  $${\tau }_f^{\prime }\left(W_f\right)\frac{d{W}_f\left(t\right)}{dt}+W_f\left(t\right)=K_f^{\prime }\left(t\right)m\left(t\right)P\left(t\right)+\left(\frac{{\mu }_{FFM}-{\mu }_{F{M}_f}}{{\mu }_{FF{M}_f}}\right){\displaystyle {\int }_0^{W_f\left(t\right)}{f}_r\left(W_f\right)d{W}_f}$$ (24)

  with

  $$K_f^{\prime }\left(f\right)=\frac{\gamma \left(t\right)g\left(t\right)}{{\mu }_{FF{M}_f}},{\tau }_f^{\prime }\left(W_f\right)=\frac{{\mathrm{\lambda }}_{F{M}_f}{f}_r\left(W_f\right)/e_{F{M}_f}+{\mathrm{\lambda }}_{FF{M}_f}\left[1-f_r\left(W_f\right)\right]/e_{FF{M}_f}}{{\mu }_{FF{M}_f}}$$

  where ${\mu }_{F{M}_f}$ and ${\mu }_{FF{M}_f}$ are the proportions of energy expenditure corresponding to maintaining and sustaining life of fetal fat and fat-free tissues, respectively. Nonetheless, given the desire for a parsimonious model, we continue to assume that ${\mu }_{F{M}_f}={\mu }_{FF{M}_f}=\mu$, where equation (21) applies.

• The model parameters γ(t), $e_{F{M}_f}$, and $e_{FF{M}_f}$ are assumed to vary on an individual level. According to the formulation of (21), these parameters may capture between- and/or within-group differences (e.g., genetic variations [34], exercising vs. non-exercising [22]).

2.2. Rate of fetal fat mass deposition

From Section 2.1, the importance of understanding the rate of fetal fat deposition, f_r(W_f), as a key variable to attaining a predictive fetal energy balance model is now clear. From data presented and analyzed in a fetal body composition study by Demerath et al. (2016) [35], good a priori knowledge is now available to establish the dependence of f_r on W_f(t). Literature also strongly suggests that the accretion of fetal fat starts accumulating after 26–30 weeks gestation [22, 36]; to this effect, the following piecewise modified logistic equation can be considered

$$F{M}_f\left(t\right)=F{M}_f\left(W_f\left(t\right)\right)=\{\begin{array}{ll}\frac{c_{f_r}}{1+e^{-a_{f_r}\left[W_f\left(t\right)-b_{f_r}\right]}}+C\hfill & t\ge t_0\hfill \\ 0\hfill & t<t_0\hfill \end{array}$$ (25)

with identifiable parameters $a_{f_r}$, $b_{f_r}$, $c_{f_r}$, and initial time, t₀, estimated as described in Section 3; C is a constant. When FM_f($W_{f_0}$) = 0 at t₀, we get

$$C=-\frac{c_{f_r}}{1+e^{-a_{f_r}\left(W_{f_0}-b_{f_r}\right)}}$$

where $W_{f_0}$ is the initial weight at the initial time t₀. From equations (5) and (25), f_r is now a well-defined function; namely,

$$f_r\left(W_f\right)=\{\begin{array}{ll}{a}_{f_r}{c}_{f_r}\frac{e^{-a_{f_r}\left(W_f\left(t\right)-b_{f_r}\right)}}{{\left[1+e^{-a_{f_r}\left(W_f\left(t\right)-b_{f_r}\right)}\right]}^2}\hfill & t\ge t_0\hfill \\ 0\hfill & t<t_0\hfill \end{array}$$ (26)

For simplicity, in this work we will assume that t₀ = 0 (or $W_{f_0}=0$). Finally, given a well-defined f_r (equal to (26) or otherwise), estimations of the fetal body components readily follow from equation (6); namely,

$$F{M}_f\left(t\right)={\displaystyle {\int }_0^{W_f\left(t\right)}{f}_r\left(W_f\right)d{W}_f}$$ (27)

$$FF{M}_f\left(t\right)=W_f\left(t\right)-{\displaystyle {\int }_0^{W_f\left(t\right)}{f}_r\left(W_f\right)d{W}_f}$$ (28)

2.3. Placental Volume Growth Model

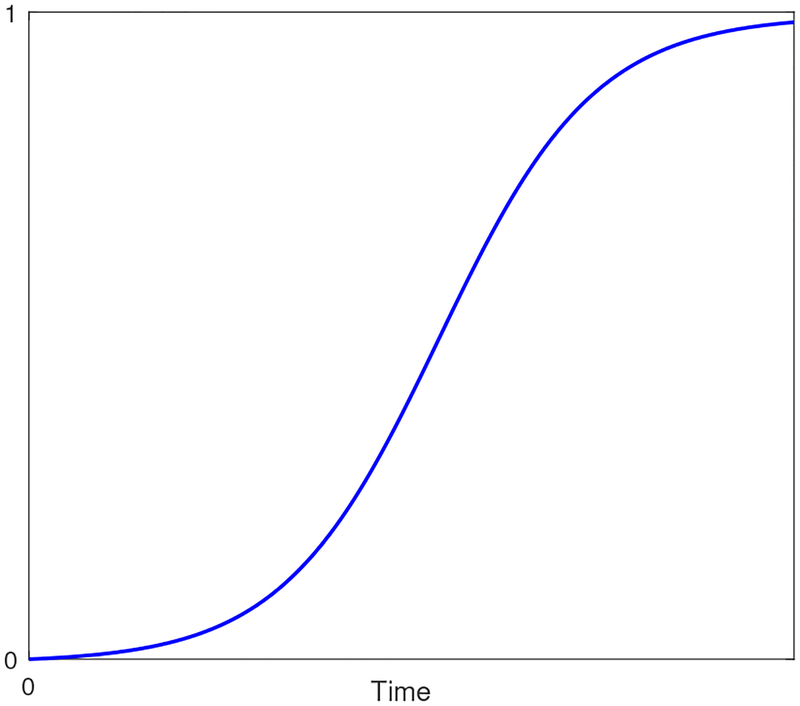
Following Thomas et al. (2008) [22, 37], we consider the placental volume P(t) as the most suitable variable to characterize placental growth. There is a substantial literature where placental development and growth profiles are presented and characterized throughout gestation for humans [38–40] and animals [41]. The placenta grows in three phases: first, a ‘lag’ phase in which cells begin to form; second, an exponential growth phase where cells continue to form and rapidly divide; and finally, due to space restrictions, a deceleration in the growth rate is expected in the final weeks towards birth. These three growth phases are adequately captured with a logistic function [22]. Figure 1 features a standard logistic growth profile where these three phases are depicted.

Figure 1:

Representative placental volume growth profile.

Similar to equation (25), the ‘modified’ logistic function is considered

$$P\left(t\right)=c_P\left[\frac{1}{1+e^{-a_P\left(t-b_P\right)}}-\frac{1}{1+e^{a_P{b}_P}}\right]\forall t\ge 0$$ (29)

with P(0) = 0 and $\underset{a_P{b}_P\to \infty }{\text{lim}}\underset{t\to \infty }{\text{lim}}P\left(t\right)=c_P\underset{a_P{b}_P\to \infty }{\text{lim}}\left(\frac{e^{a_P{b}_P}}{1+e^{a_P{b}_P}}\right)=c_P$, where a_P, b_P, and c_P (c_P is the ‘ultimate’ carrying capacity) are identifiable model parameters from the estimation procedure described in Section 3.2; it follows from Figure 1 that a_P, b_P, c_P ≥ 0. The algebraic model in equation (29) differs from the placental volume in [22] in that its curvature features are more independently parameterized: the pa rameter a_P assigns the rate of growth, b_P assigns the inflection point, and c_P assigns the ultimate carrying capacity or the scale of the profile (note c_P = 1 in Figure 1 for illustration). In [22], the proposed model does not apply when the initial condition is P(0) = 0, and hence, requires an additional estimated ultrasound measurement of EPV. Moreover, the parameters (including the initial condition) of the model in [22] play simultaneous role in determining its final curvature features, which makes it less intuitive.

It has been reported that the size and growth rates of the placenta are associated with physical activity [22, 32] and additional genetic factors [42]. In the presence of more intensive ultrasound measurements, the carrying capacity parameter c_P can be further investigated such that moderations of placenta size over time by physical activity or genetic differences are more understood; this also applies to the growth rate a_P and mid-point b_P parameters. In our parameter estimation, we assume constant parameters a_P , b_P, and c_P such that averaged, fixed-effects are captured.

3. Parameter Estimation and Model Validation

3.1. HMZ Estimation Data

The Healthy Mom Zone (HMZ) study [14] is an ongoing individual-tailored behavioral, adaptive intervention for managing weight in pregnant women with overweight and obesity. The target sample is 30 pregnant women who are randomized to either the intervention or control group from approximately 8 to 36 weeks gestation. Study measures including weight, physical activity, and energy intake. are obtained at baseline, throughout the course of the intervention (e.g., daily, weekly, or monthly), and at follow-up. The detailed intervention protocols that includes eligibility, recruitment, intervention description, dosages, and measurement schedule have been published elsewhere [14]. In addition, an ancillary project provides six ultrasound measures used to estimate fetal weight, placental volume, and fetal body composition. In this section, further discussion of each estimated measurement is presented; four representative completed participants (n = 4; three overweight, one obese; mean age=30.3 years, two intervention, two control) are considered.

3.1.1. Estimated Fetal Weight

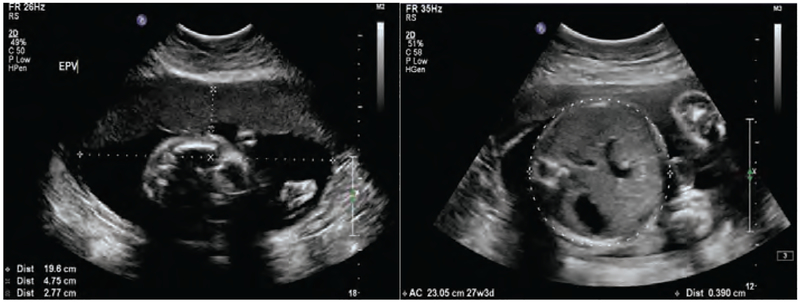
An estimated fetal weight (EFW) can be drawn from ultrasounds when specific biomarkers are measured as displayed in the example Figure 2. Using these biomarkers, one of the best known and well-established correlations that can be applied is the Hadlock et al. (1984–91) [43] estimation. For our model estimation, we use a set of six EFW measurements in addition to birth weight, as is described in more detail in Section 3.2. The first EFW is used to establish the upper and lower bounds for the initial condition (${\tilde{t}}_0$, ${\tilde{W}}_{f_0}$) used for solving equation (21). In this study, on average, the first ultrasound measurement was taken at 14 weeks gestation, followed by five additional measurements each every four weeks through 34 weeks gestation. Infant’s birth weight was measured immediately after delivery.

Figure 2:

Example of an ultrasound report for establishing estimated measurements of Estimated Fetal Weight (EFW), Estimated Placental Volume (EPV), and fetal body composition of an HMZ participant.

3.1.2. Estimated Placental Volume

As the case with EFW, up to six ultrasound measurements are used to obtain the estimated placental volume (EPV) measurements using the Azupura et al. (2010) approximation method, for which a number of simplifying assumptions have been made [37]. As detailed in Section 3.2.2, EPV measurements are incorporated in the estimation cost function with lower emphasis than EFW measurements. This is justified given the following:

• 1)Absence of EPV measurements at or near birth. The bias that can result from equally emphasizing EPV measurements with EFW in (32) given the missing value at birth is crucial since fitting to earlier measurements only will tend to produce an exponential growth profile that can be, misleadingly, well-captured with the modified logistic equation in (29).
• 2)The Azpurua et al. EPV estimation method using 2D ultrasound measurements (similar to Figure 2) provides a rather simplified approximation (assumes spherical topology) that is mainly targeted for establishing EPV in the first and second trimesters of pregnancy for patients with normal BMI index (in this paper, participants are either overweight or obese); this approximation can become exceedingly inaccurate at advanced gestational ages due to remaining technical difficulties associated with existing ultrasound technology [37].
• 3)The EPV approximation method in Azpurua et al. does not estimate standard errors; only 10^th, 50^th, and 90^th percentile trajectories are given.

3.1.3. Fetal Body Composition

Studying ultrasound reports similar to Figure 2 (namely, anterior abdominal wall thickness and abdominal circumference) also produced at least two acceptable estimates per participant for the fetal % body fat using the correlation presented by Bernstein and Catalano (1991) [26]. While the number of estimates can be as many as available ultrasounds, it is known that this estimate becomes more reliable at advanced gestational ages, and therefore we only consider a subset of the ultrasound measurements for the estimation of fetal % body fat.

3.1.4. Glycemic Index

Glycemic index (GI) was estimated using food items and portion sizes reported in a smart phone application. For each food, carbohydrate content (g) of the reported portion size was determined using the USDA Food and Nutrient Database for Dietary Studies (FNDDS) 2013–2014 data set. Next, a GI value for each food was determined by matching foods to the database generated by Flood et al. [44]. For foods without an exact match, the GI value of the closest matching item was used. Estimated GI of each day was then calculated as the average GI of all foods consumed in a day, weighted by their contribution to total carbohydrate intake for that day, i.e.

$${g\left(t\right)=\frac{{\displaystyle \sum _{i=1}^n\text{food}i\text{GI}\times \text{food}i\text{carbohydrate}\left[\text{g}\right]}}{{\displaystyle \sum _{i=1}^n\text{food}i\text{carbohydrate}\left[\text{g}\right]}}|}_{\text{day}t}$$ (30)

In equation (21), the glycemic index, g(t), is understood as a key variable for estimating fetal energy intake. One can generally presume a time-varying profile of g(t) on a daily scale; however, given that the collected g(t) time series shows to be stationary with a low variance, one can assume a constant $\overline{g}$ value drawn from the average of all available average daily estimates, $\overline{g}$. Table 1 lists the fractional average and standard deviation of estimated daily glycemic index values for the four participants presented in this paper.

Table 1:

Mean and standard deviation values of daily glycemic index estimations for four representative HMZ participants

Participant	$\overline{g}$	σg
A	0.5478	0.0461
B	0.5441	0.0653
C	0.5806	0.0644
D	0.5763	0.0835

3.1.5. Maternal Physical Activity

As noted in section 2.1.3, equation (22) characterizes the assumed simple, linear dependence of the fetal energy balance model in (21) on maternal physical activity. It is assumed that physical activity moderates the energy intake to the fetus by regulating the placental function (e.g., through blood flow [45]). In the HMZ study, intensive objective assessment of physical activity is carried out using wrist-worn activity tracker. Missing and implausible physical activity measurements are imputed with mean replacement. These data are also used to establish the estimated daily maternal energy intake in equation (31).

3.1.6. Maternal Energy Intake

The daily maternal energy intake variable, m(t), can be reliably estimated with the availability of daily maternal weights and estimated energy expenditure data; the latter are estimated by correlating with daily physical activity and estimated/measured resting metabolic rates. As presented in Guo et al. (2016) [17], back-calculated maternal energy intake from measured daily maternal weights and physical activity measures is considered; namely

$$m\left(t\right)=\frac{-W_m\left(t+2\right)+8W_m\left(t+1\right)-8W_m\left(t-1\right)+W_m\left(t-2\right)}{12T{K}_1}-\frac{K_2}{K_1}\left[PA\left(t\right)+RMR\left(t\right)\right]$$ (31)

where K₁ and K₂ are gains (coefficients) that map changes of daily energy intake and physical activity, respectively, into maternal weight gain/loss; T is the sampling time; PA(t) and RMR(t) are the maternal daily physical activity and resting metabolic rate, respectively. To reduce the significant variability in equation (31), it is necessary to smooth the weight measurement W_m(t). A 9-day moving average filter is considered for all participants, except for participant D where a 13-day moving average filter is considered.

3.2. Model Estimation Problem Formulation

In this section, we establish a problem formulation for the least squares objective from which, with the presence of su cient estimation and validation data, model parameters can be estimated and validated using nonlinear regression. Next, we describe in more detail how emphasis is split between different measured variables, and how the nonlinear optimization solver is initialized. Finally, in the results section, we present simulations of the estimated individual models and list the mean value and standard deviation associated with all model parameters.

3.2.1. Problem Formulation

The parameter estimation problem statement is formulated as a constrained optimization problem. The prediction error is minimized over estimation data using a non-linear least squares objective. For model estimation, using a total of N EFW measurements inferred from ultrasound reports (similar to the example sonographic images shown in Figure 2, including birth weight), M EPV measurements, and L estimated body composition data points, the approach considered is to solve

$$\begin{array}{ll}\underset{\theta }{\text{min}}\hfill & {\epsilon }^{T}Q\epsilon \hfill \\ \text{s}.\text{t}.\hfill & {\theta }_{lb}<\theta <{\theta }^{ub}\hfill \end{array}$$ (32)

where

$$\epsilon ={\left[\mathrm{\Delta }{W}_f\left(1\right)\cdots \mathrm{\Delta }{W}_f\left(N\right)\mathrm{\Delta }P\left(1\right)\cdots \mathrm{\Delta }P\left(M\right)\mathrm{\Delta }F{M}_f\left(1\right)\cdots \mathrm{\Delta }F{M}_f\left(L\right)\right]}^T$$

$$Q=\left[\begin{array}{ccc}{\mathrm{\lambda }}_1& & \\ & \ddots & \\ & & {\mathrm{\lambda }}_{N+M+L}\end{array}\right]$$

$$\theta ={\left[\alpha e_{F{M}_f}{e}_{FF{M}_f}{a}_P{b}_P{c}_P{a}_{f_r}{b}_{f_r}{c}_{f_r}{\tilde{W}}_{f_0}\right]}^T$$

$\mathrm{\Delta }{W}_f\left(t\right)=EFW\left(t\right)-W_f\left(t\right)$, $\mathrm{\Delta }P\left(t\right)=EPV\left(t\right)-P\left(t\right)$, and $\mathrm{\Delta }F{M}_f\left(t\right)={\widehat{FM}}_f\left(t\right)-F{M}_f\left(t\right)$ with EFW(t), EPV(t), and ${\widehat{FM}}_f\left(t\right)$ denoting the estimated ultrasound measurements of the fetal weight, placental volume, and fetal fat mass at day t, respectively; Q is a positive semi-definite weighting matrix used to establish the desired emphasis for model estimation. W_f(t) is obtained from the numerical solution of the following fetal model

$${\tau }_f\left(W_f\right)\frac{d{W}_f\left(t\right)}{dt}+W_f\left(t\right)=K_f\left(t\right)m\left(t\right)P\left(t\right),W_f\left({\tilde{t}}_0\right)={\tilde{W}}_{f_0}$$ (33a)

with

$${\tau }_f\left(W_f\right)=\frac{{\mathrm{\lambda }}_{F{M}_f}{f}_r\left(W_f\right)/e_{F{M}_f}+{\mathrm{\lambda }}_{FF{M}_f}\left[1-f_r\left(W_f\right)/e_{FF{M}_f}\right]}{\mu }$$ (33b)

$$K_f\left(t\right)=\frac{\gamma \left(t\right)\overline{g}}{\mu },\gamma \left(t\right)=\alpha PA\left(t\right)+\beta ,\alpha \le 0,\beta \ge \gamma >0\forall t\ge 0$$ (33c)

$$P\left(t\right)=c_P\left[\frac{1}{1+e^{-a_P\left(t-b_P\right)}}-\frac{1}{1+e^{a_P{b}_P}}\right]$$ (33d)

$$f_r\left(W_f\right)=a_{f_r}{c}_{f_r}\frac{e^{-a_{f_r}\left(W_f\left(t\right)-b_{f_r}\right)}}{{\left[1+e^{-a_{f_r}\left(W_f\left(t\right)-b_{f_r}\right)}\right]}^2}\forall t\ge 0$$ (33e)

with ${\tilde{t}}_0>0$ (initial time of simulation) and m(t) per equation (31). Lower and upper parameter bounds, θ_lb and θ^ub, are known a priori. The physical activity parameter α is constrained as shown in equation (33c). In this paper, for purposes of simplicity, the value of the β parameter is fixed at 0.000234 ml⁻¹, which is equal to the estimated nominal value of γ in [22]. Thermodynamic efficiencies $e_{F{M}_f}$ and $e_{FF{M}_f}$, by definition, range from 0 to 1. Also, given the strict growth of both P(t) and FM_f(t) profiles, the parameters a_P, b_P, c_P, $a_{f_r}$, $b_{f_r}$, and $c_{f_r}$ are bounded below at 0, and are unbounded above.

The optimization is initialized using nominal parameter values/ranges drawn from literature. For example, Christiansen et al. [25, 34] reports values for thermodynamic efficiencies drawn from animal studies; Thomas et al. [22] gives an estimate for the conversion parameter, γ(t); Demerath et al. [35] provides fat and fat-free mass profiles from preterm infants that are used for initializing $a_{f_r}$, $b_{f_r}$ and $c_{f_r}$ using standard regression; finally, also by similar means, EPV measurements calculated from our ultrasound data are used for initializing a_P, b_P, and c_P. In the following section, we report in additional detail on the final set of parameter values used for solver initialization.

3.2.2. Relative Weights & Initialization

In this section, the specific relative weights (λ_i in the diagonal Q matrix in equation (32)) are presented for each participant. In addition, the specific initialization points (initial guesses) are also established in this section. It must be noted that given the limited amount of estimation data and the non-convexity of the optimization problem, the non-linear least squares solver becomes increasingly sensitive to relative weights and proper initialization as multiple local minima are expected. To avoid undesired solutions, solver features such as multistart can be used [46].

Judicious selection of λ_i values is important for establishing an effective estimation cost function for each of the HMZ participants evaluated with this method. In the selection of λ_i values, output emphasis, scaling, number of measurements, and measurement standard errors are all taken into consideration. While each data point can have its specific assigned λ_i weight, we group measurements per model state (i.e., EFW, EPV, fetal FM) with one relative weight as λ_EFW : λ_EPV : ${\mathrm{\lambda }}_{F{M}_f}$. For participant A, the established ratios are 1 : 0.5 : 1, whereas for participants B, C, and D the ratios are 1 : 0.3 : 1.

Table 2 lists established initialization points for the studied HMZ participants. In the selection of these initializations, approximations from the literature, actual measurement values, and multiple iterations are all influencing factors. More specifically, initial guesses for $e_{F{M}_f}$ and $e_{FF{M}_f}$ were drawn from [25] followed by multiple iterations (multiple solutions); a_P was drawn from [22]; b_P, c_P, $a_{f_r}$, $b_{f_r}$, and $c_{f_r}$ were initialized from examining the actual measurements followed by multiple iterations; finally, the initialization of α was established after multiple iterations.

Table 2:

Initialization points for four representative HMZ participants

	α × 108	$e_{F{M}_f}$	$e_{FF{M}_f}$	aP	bP	cP	$a_{f_r}$	$b_{f_r}$	$c_{f_r}$
A	−0.5	0.77	0.11	0.03	175	1281	0.47	9.56	9.47
B	−0.5	0.77	0.11	0.03	175	864	0.47	9.56	12.30
C	−0.5	0.44	0.15	0.03	175	774	0.47	9.56	8.99
D	−0.5	0.77	0.11	0.03	175	760	0.47	9.56	10.98

3.2.3. Estimation Results

In this section, for each of the examined HMZ participants, qualitative and quantitative model fit to data are presented from simulations when actual measured inputs are applied to the model. In addition to the intrauterine fetal weight (primary model state), other model states (i.e., placental volume, body composition) and the evolution of intermediate constructs over time (e.g., e_f(t), τ_f(t), and K_f(t)) are also shown. Finally, estimated model parameters tabulated in Table 3 are discussed.

Table 3:

Estimated model parameter values for four representative HMZ participants (Mean and Standard Deviation (SD) are included)

	α × 108	$e_{F{M}_f}$	$e_{FF{M}_f}$	aP	bP	cP	$a_{f_r}$	$b_{f_r}$	$c_{f_r}$
A	−13.70	0.44	0.24	0.027	206.2	1519.1	0.655	7.86	11.33
B	−2.82	0.60	0.07	0.039	154.3	1026.8	0.441	9.71	12.30
C	−0.31	0.82	0.12	0.028	182.3	1031.0	0.267	12.10	6.84
D	−0.06	0.42	0.06	0.024	174.8	1101.7	0.577	8.22	11.27
Mean	−4.22	0.57	0.12	0.030	179.4	1169.7	0.485	9.47	10.44
SD	6.44	0.18	0.08	0.007	21.4	235.5	0.170	1.93	2.44

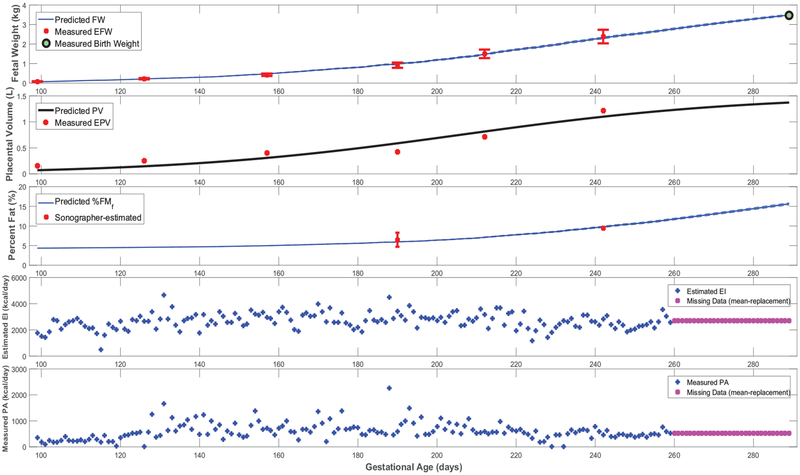
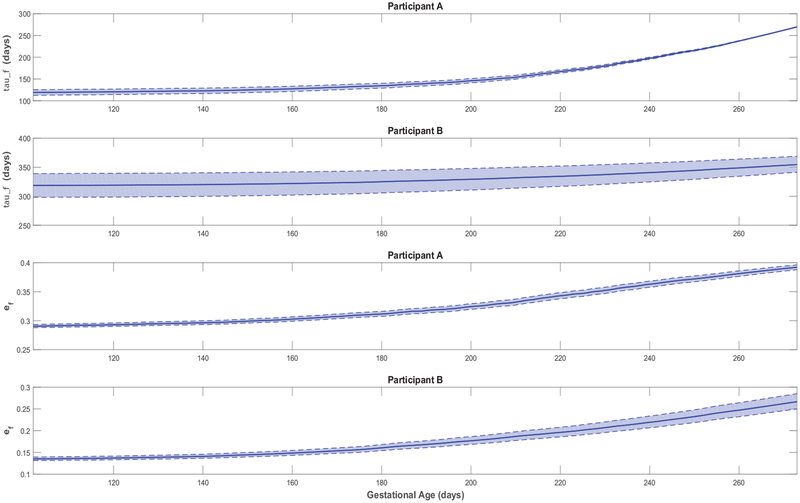
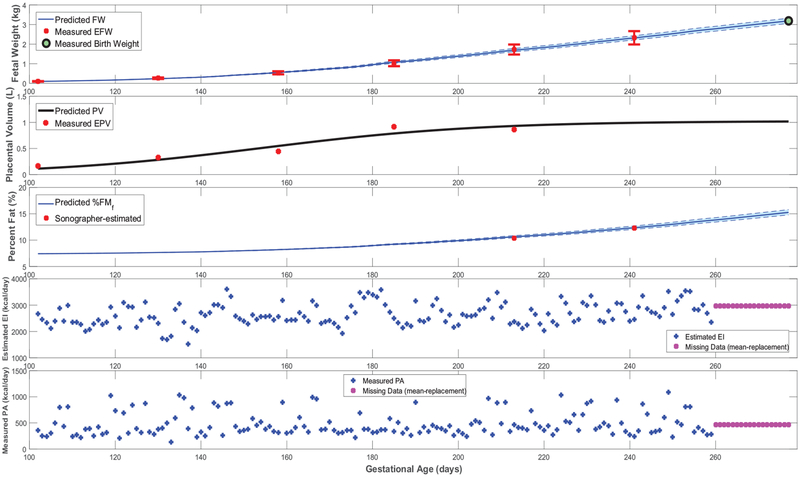
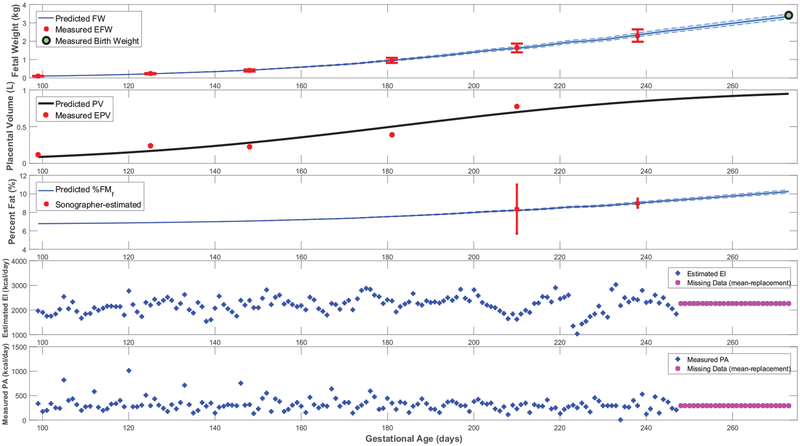
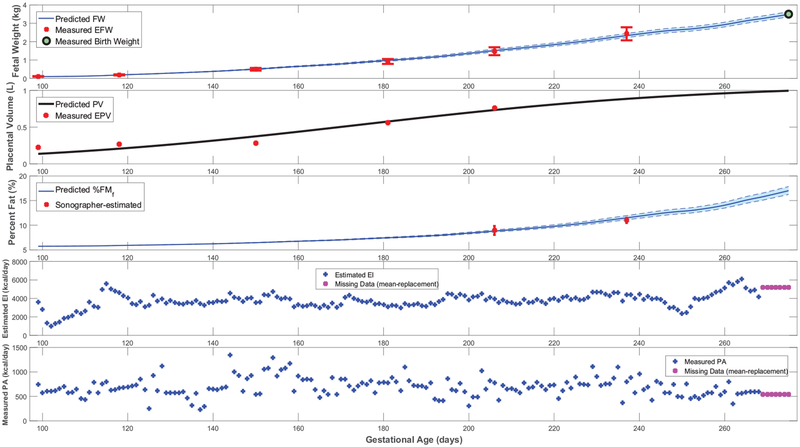
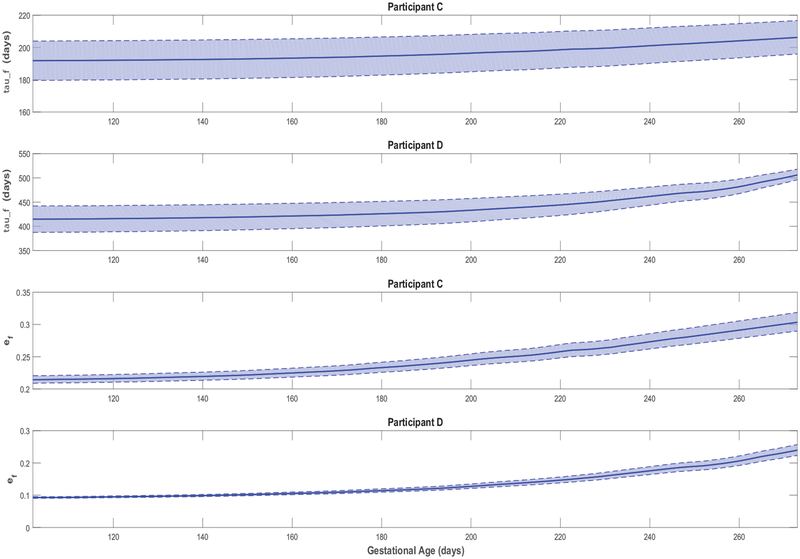
Figures 3–5 feature simulations of the estimated models for one intervention participant (participant A) and one control participant (participant B). Overall, the goodness of fit does not appear to differ across intervention and control participants. In Figures 3–5, the simulation start time is selected to match the day of the first ultrasound measurement; the simulation is carried out through the reported actual day of birth. In these simulations, measurements of the two model inputs, i.e., maternal energy in-take (back-calculated EI) and maternal PA (direct measurements), are displayed. In addition, the model states, i.e., fetal weight, placental volume, and body composition, are plotted and contrasted against estimated ultrasound measurements to qualitatively demonstrate the goodness of fit. Moreover, in Figure 6 and Figure A5 from Appendix A featuring the time-varying profiles of τ_f, e_f, and K_f; it can be seen that, across all individuals, both τ_f and e_f appear to exponentially increase over time as the fetus continues to grow. It is noted that [22] provides a significantly higher estimate for the overall efficiency (e_f = 0.799) than the estimated ranges from our data (approximately, in the 0.1–0.4 range). Finally, Table 3 summarizes the estimated model parameters with mean and standard deviation values for the examined participants.

Figure 3:

Time-domain response (fetal weight, placental volume, and fetal % body fat) with energy intake and physical activity for a representative HMZ intervention participant (participant A) (simulation starts at the day of first ultrasound measurement and ends at birth).

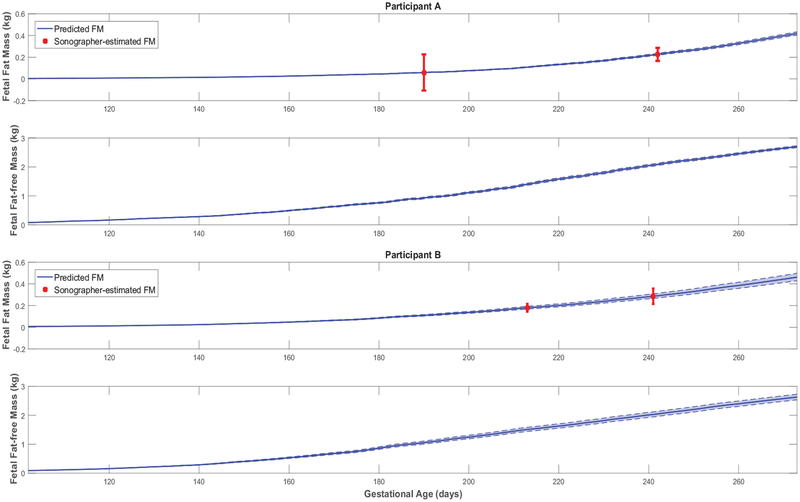
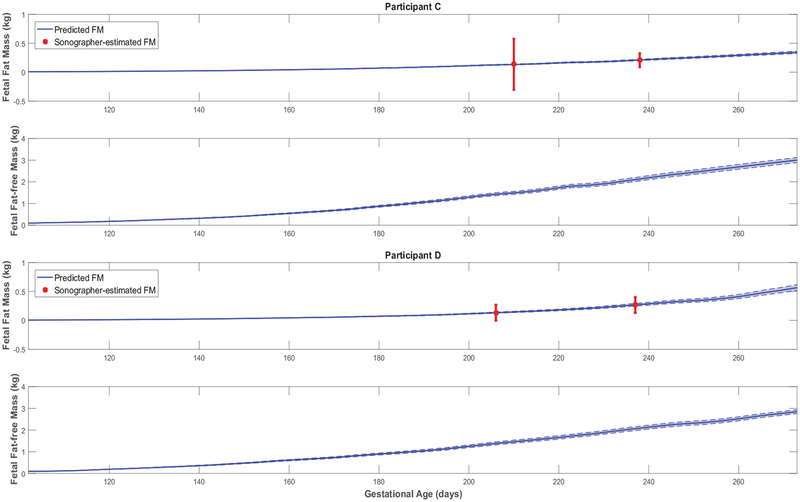
Figure 5:

Fetal fat mass and fat-free mass growth profiles over time for representative HMZ participants (participants A and B).

Figure 6:

Time-varying τ_f and e_f for representative HMZ participants (participants A and B).

3.3. Model Validation

Model validation is determined by goodness-of-fit metrics as well as contrasting diverse estimated model features such as structure, parameter ranges, and output profiles against a priori knowledge from the literature.

First, all simulated fetal weight and placental volume growth profiles in Figures 3, 4, A1, and A2 are plausible and consistent with expected growth profiles from literature (Hadlock et al. [43, 47, 48]; Arleo et al. [49]). Comparing model predictions against the experimentally observed data (ultrasounds), a summary of individualized model outputs fit against available data is presented in Table 4.

Figure 4:

Time-domain response (fetal weight, placental volume, and fetal % body fat) with energy intake and physical activity for a representative HMZ control participant (participant B) (simulation starts at the day of first ultrasound measurement and ends at birth).

Table 4:

Summary of the goodness-of-fit from various metrics for four representative HMZ participants

	NRMSEEFW	$R_{EFW}^2$	$R_{EPV}^2$	$R_{F{M}_f}^2$
Participant A	0.9619	0.9986	0.8953	1.0000
Participant B	0.9763	0.9994	0.9008	0.9925
Participant C	0.9608	0.9985	0.8969	0.9997
Participant D	0.9763	0.9994	0.9174	1.0000

The Normalized Root-Mean-Square Error (NRMSE) is defined as

$${\text{NRMSE}}_{\text{EFW}}=1-\frac{{\Vert EFW\left(t\right)-Wf\left(t\right)\Vert }_2}{{\Vert EFW\left(t\right)-\overline{EFW}\Vert }_2}$$ (34)

is considered as the primary metric for establishing the model goodness of fit against the HMZ data. W_f(t) is the simulated output, EFW(t) is the measured output, $\overline{EFW}$ is the mean of all measured EFW(t) values, and ${\Vert \cdot \Vert }_2$ denotes the l-norm. $R_{EFW}^2$, $R_{EPV}^2$, and $R_{F{M}_f}^2$ denote the coefficients of determination for fitting to estimated fetal weights, placental volumes, and fetal fat mass in utero, respectively. For a qualitative evaluation of model fit, the reader may refer to Figures 3–5.

Further giving validity to our model is that the estimated $e_{F{M}_f}$ values are consistently larger than $e_{FF{M}_f}$, in agreement with reported patterns only available from animal studies [25]. Moreover, the mean estimated value of the placental volume growth rate parameter a_P (with a narrow standard deviation of 0.003) matches the reported and validated value in [22, 50]: r = 0.03. Furthermore, from Figures 3, 4, A1, and A2, predicted % body fat at birth approximately ranges from 10 to 18%, which fall into the typical ranges reported in literature [26, 36, 51, 52]. In agreement with Demerath et al. (2016) [35], Figures 5 and A3 show that predicted FFM_f(t) profiles can be described as linear, while the FM_f(t) are curvilinear (linear-exponential).

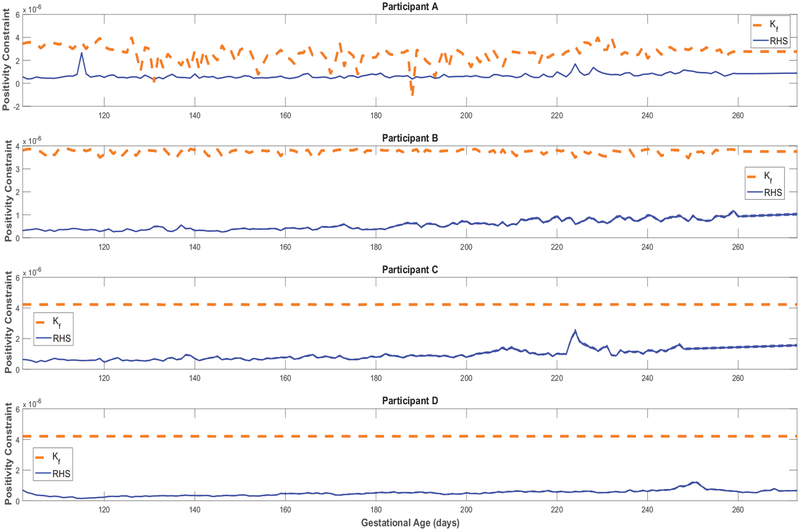
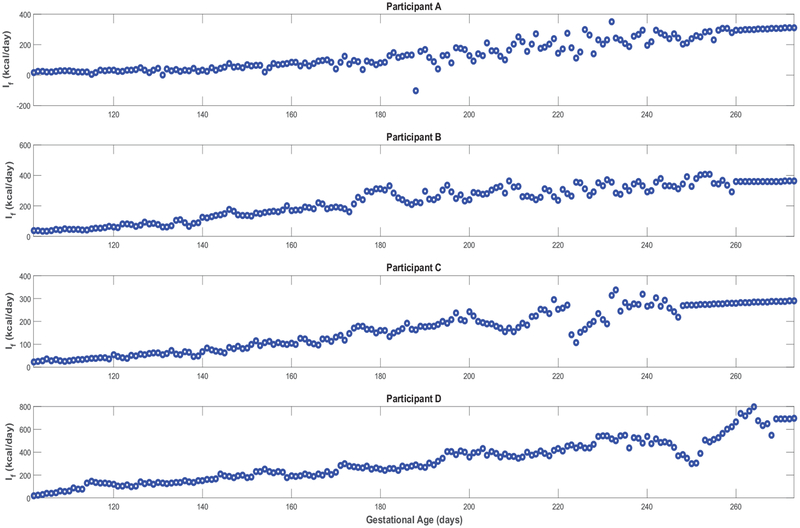
Finally, Figure A5 confirms that, except for only two brief instances in Participant A’s simulations, all estimated models satisfy the constraint in equation (23)) and hence validates the positive energy balance assumption throughout gestation. From Figure A6, one can observe the estimated rate of fetal energy intake I_f(t) (note the negative I_f(t) values in the two instances where Participant A’s positivity constraint is violated); comparing this to the maternal energy intake m(t) (‘Estimated EI’ in Figures 3, 4, A1, and A2) provides support for the assumption of a well-nourished mother.

4. Conclusions and Future Work

In conclusion, a dynamical systems model of intrauterine growth has been developed from first-principles, relying on the first and second laws of thermodynamics. This proposed model provides a rigorous yet more simple formulation than the fetal energy balance model of current literature (Thomas et al., 2008). In the parameter estimation of this model, a non-linear least squares, constrained multi-objective optimization problem was formulated and guided by a priori knowledge of ranges of model parameters. For the first time (to the authors’ knowledge), estimates (and an estimation method) for the thermodynamic efficiencies governing the formation of new tissues of human fetuses are established. This developed model has been estimated and validated against ultrasound measurements provided from the Healthy Mom Zone study; despite the explained challenges with the estimation measurements, predictions follow from this model show good agreement with the data.

The availability of more intensive estimation and validation datasets (i.e., datasets with more frequent measurements) in a future study should create opportunities for parameter refinement and increased model understanding. More intensive measurements will allow for further investigation of the contribution of maternal body components in fetal nutrition (see equation (14)). Moreover, additional ultrasound measurements (particularly closer to delivery) may allow estimation of a less biased fetal model described in equation (24). A better theoretical understanding of mechanisms behind the evolution of placental volume and the rate of fetal fat mass deposition is needed. This work considered a linear dependence of placental function on maternal physical activity; in future work, a more developed characterization of the influence of maternal physical activity may generate more resilient models: models with good predictions when input levels are far from those used in model estimation. Furthermore, a broader future goal is to use a combination of more experimental data and increased physiological understanding to reduce the modeling assumptions (outlined in Section 2.1) as much as possible.

Finally, the aims of this paper (achieved using a limited number of HMZ intervention and control participants) was to develop a more comprehensive energy balance model for fetal weight gain derived from first-principles modeling that can be validated through data. These aims were facilitated by the availability of intensive, longitudinal participant data from the HMZ intervention, which is ongoing. Model estimation and validation efforts for the remaining participants (N = 32) could enable making conclusions regarding participant differences and intervention versus control outcomes, which was not the scope of this paper. However, studying group differences (intervention vs. control) is a subject of current and future research.

Appendix A.

Simulations in support of Section 3.3 featuring additional HMZ participants (participants C and D), ancillary time-domain responses, and positive energy balance.

Figure A1:

Time-domain response (fetal weight, placental volume, and fetal % body fat) with energy intake and physical activity for a representative HMZ intervention participant (participant C) (simulation starts at the day of first ultrasound measurement and ends at birth).

Figure A2:

Time-domain response (fetal weight, placental volume, and fetal % body fat) with energy intake and physical activity for a representative HMZ control participant (participant D) (simulation starts at the day of first ultrasound measurement and ends at birth).

Figure A3:

Fetal fat mass and fat-free mass growth profiles over time for representative HMZ participants (participants C and D).

Figure A4:

Time-varying τ_f and e_f for representative HMZ participants (participants C and D).

Figure A5:

Time-varying gain and the establishment of positive fetal energy balance for representative HMZ participants (see equation (23)).

Figure A6:

Predicted time-domain profile of fetal energy intake I_f(t) for representative HMZ participants (see equation (15)).