Functional Alignment with Anatomical Networks is Associated with Cognitive Flexibility

Abstract

Cognitive flexibility describes the human ability to switch between modes of mental function to achieve goals. Mental switching is accompanied by transient changes in brain activity, which must occur atop an anatomical architecture that bridges disparate cortical and subcortical regions by underlying white matter tracts. However, an integrated perspective regarding how white matter networks might constrain brain dynamics during cognitive processes requiring flexibility has remained elusive. To address this challenge, we applied emerging tools from graph signal processing to examine whether BOLD signals measured at each point in time correspond to complex underlying anatomical networks in 28 individuals performing a perceptual task that probed cognitive flexibility. We found that the alignment between functional signals and the architecture of the underlying white matter network was associated with greater cognitive flexibility across subjects. By computing a concise measure using multi-modal neuroimaging data, we uncovered an integrated structure-function correlate of human behavior.

Cognitive flexibility is involved in virtually every complex behavior from mental arithmetic to processing visual stimuli. For example, when navigating complex environments, humans can flexibly switch between two foci of attention or between two processing modalities in order to effectively respond to sensory inputs. While a hallmark of human cognition, flexible switching is also associated with a measurable cost: moving from one task to another induces a natural extension in the time it takes a person to respond to stimuli [5]. In patients with neurological syndromes, this cost is even greater, to the point where it can hamper a patient’s ability to engage in the basic activities of daily living [6], impacting long-term cognitive outcomes [7]. In healthy individuals, cognitive flexibility varies considerably, and individual differences in this trait contribute to mental facets ranging from the development of reasoning ability [8] to quality of life into late age [9]. Clarifying the nature of cognitive flexibility in the human brain is critical to understand the human mind.

The physiological origins of cognitive flexibility are thought to lie in corticobasal ganglia-thalamo-cortical loops [10]: regions of the fronto-parietal and cingulo-opercular systems are activated by cognitive switching tasks [11, 12, 13, 14]. In switching paradigms, the anterior cingulate is thought to contribute negative feedback detection following switches [15], whereas the lateral prefrontal cortex maintains rules and inhibits incorrect responses [16] and the medial parietal lobes contribute to shifts in spatial attention, working memory, and categorization rules [17]. All of these regions anatomically connect to subcortical regions, which are postulated to mediate processes that both suppress prepotent motor responses and transition between behavioral outputs to meet task goals [18]. Interactions between cortical systems and motor outputs are thought to be anatomically mediated by subcortical circuits [11, 19, 20, 21, 13]. Yet, understanding exactly how this circuit supports task switching has remained challenging, particularly because it requires us to integrate regional activity, inter-regional anatomical connectivity, and observable measures of behavior. While regional activity and behavioral markers of cognitive flexibility are relatively straightforward to estimate, it is less straightforward to integrate these features with the white matter structure (the connectome [22]) that guides the propagation of functional signals [23, 24, 25].

Given the complex and diverse neurobiology involved in cognitive control, frameworks that include a concise correspondence between brain network structure, function, and cognitive measures have the potential to produce more comprehensive understanding of human cognition [26, 27]. Conceptually, underlying white matter network organization in the brain physically mediates communication among brain regions. However, analytic frameworks that explicitly use white matter structure to constrain cognitively relevant functional signals are lacking. Such approaches may allow investigators to adjudicate the relative contributions of well-described systems in the brain [28, 12] to specific cognitive variables by integrating neurophysiological dynamics and anatomy.

To address this challenge, we aimed to identify the multimodal integration of network anatomy and functional signals that supports cognitive switching. Here, we introduce an approach that allows us to examine the distinct contributions of functional signals in the context of anatomically linked regions in human brain networks. In a cohort of 28 healthy adult human subjects, we collected diffusion spectrum imaging (DSI) data as well as BOLD fMRI data acquired during the performance of a cognitive switching paradigm built on a set of shapes that could be perceived as composed of different features at the local versus global scales [29] (see Fig. 1). From the DSI data, we constructed anatomical brain networks in which 111 cortical, subcortical, and cerebellar regions [30, 31] were linked pairwise by the density of streamlines reconstructed by a tractography algorithm. Next, we used the eigenspectrum of these anatomical networks to measure the relative separation of framewise regional BOLD signals from the underlying white matter (see Fig. 2 and Methods). Specifically, each regional signal was decomposed into a portion that aligned tightly with the anatomical network (“aligned”) and a portion that did not align tightly with the network (“liberal”). Alignment and liberality measured different amounts of signal deviations from the underlying anatomical network.

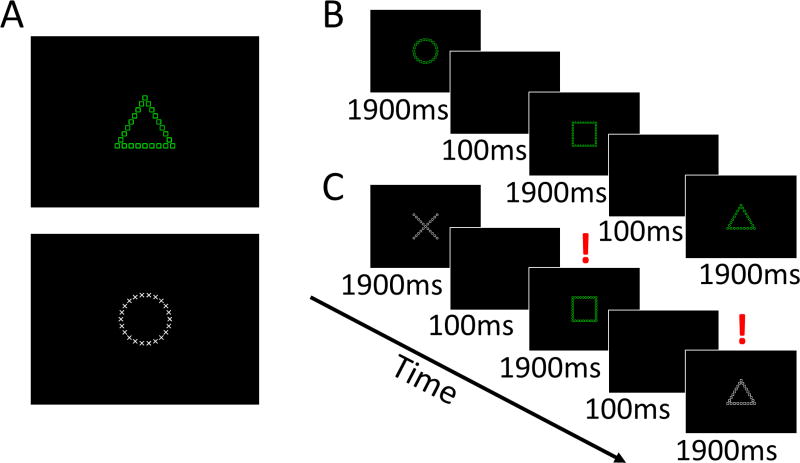
Figure 1. Cognitive task requiring perceptual switching.

(A) Example stimuli based on Navon local-global features. Subjects were trained to respond to the larger (or “global”) shape if the stimulus was green and to the smaller (or “local”) shapes if it was white. (B) An example of the non-switching condition for responses. Subjects viewed a sequence of images and were instructed to respond as quickly and accurately as possible. (C) An example of the switching condition between stimuli requiring global and local responses. Here, trials with a red exclamation point are switches from the previous stimulus.

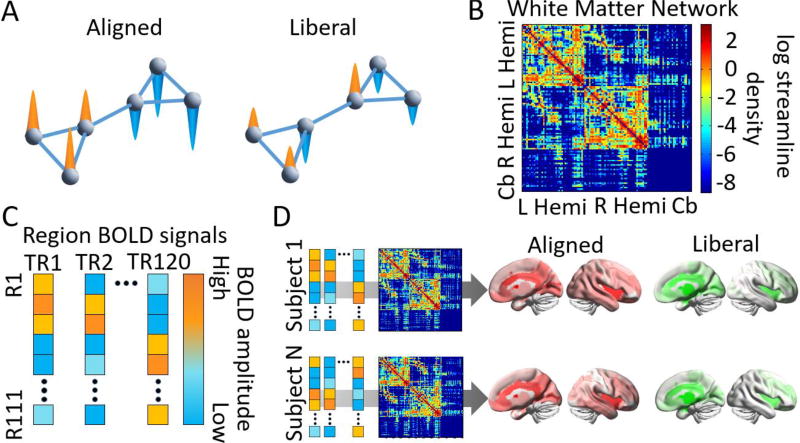
Figure 2. Multimodal approach to the study of cognitive switching using emerging graph signal processing tools.

(A) A notion of signal independence on a schematic modular network. Left: An aligned signal on top of a given graph is one in which the magnitude of functional signals, represented by the directionality of the colored cones, corresponds tightly to that expected by the network’s organization. In this toy example, one cluster of nodes contains similar positive signals, and the other cluster contains similar negative signals. Right: A liberal signal on top of a given graph is one in which signals diverge significantly from the underlying network. (B) For each of the 28 subjects, a white matter graph (a weighted adjacency matrix including white matter streamlines) is constructed from 111 anatomically-defined regions where connections are the streamline density between region pairs. (C) From BOLD fMRI data acquired during the performance of the Navon task, we extract regional mean time series which we treat as graph signals. (D) For each subject, graph signals are decomposed into aligned and liberal components using the underlying eigenspectrum of the white matter graph. Aligned and liberal signals are mapped to the nodes in the brain, and correlated with switch costs estimated from behavioral performance on the task. Cb = cerebellum. TR = repetition time. R = region. See Methods for details.

To define these measures, we used a generalization of the traditional Fourier Transform in time series analysis to the Graph Fourier Transform [32] which can characterize the manner in which signals are organized atop an underlying graph. In conventional frequency analysis using the Fourier Transform, low frequency components represent time series that vary slowly over time; high frequency components denote time series that vary rapidly over time. In graph frequency analysis using the Graph Fourier Transform, aligned components represent signals that vary smoothly across the graph; liberal components denote signals that vary highly across the graph at single moments in time. Since we used the GFT for BOLD measurements at each time point instead of across time points, this technique identifies where and to what extent BOLD signals across the brain are organized in a manner that is aligned with white matter networks. Conceptually, this technique allowed us to identify to what degree individual BOLD signals deviate weakly versus strongly from the underlying white matter anatomy. Just as a single brain region can display a time series with both low and high frequency components, so too can a single brain region display both aligned and liberal components.

We anticipated that functional alignment with anatomical networks is an individually variable feature that facilitates cognitive flexibility. Whereas prior literature has focused on region-specific mechanisms associated with this process, the current approach allowed us to examine the role of local neural processes across the brain’s distributed anatomical network. We hypothesized that moment-to-moment alignment in human brain networks facilitates switching performance, measured by switch costs, indicating interindividual variability in the degree of organization of information processing by anatomical topology. In the current study, our switching task presumably involved proactive control – sustained and anticipatory maintenance of goal-relevant information – and reactive control – transient, stimulus-driven goal reactivation [33]. In proactive switching, activation in the lateral prefrontal cortex is thought to be associated with maintaining task goals, whereas reactive control may be associated with a more transient activation of lateral prefrontal cortex and a broader network of cortico-basal ganglia mechanisms interacting with the pre-supplementary motor area, and anterior cingulate cortex [33]. Under this “dual mechanisms of control” framework, both processes may be semi-independent and engaged simultaneously, and normative human function may represent a balance between these modes of function [33]. However, the representation of these modes of function is incompletely understood in human brain networks, calling for a need to focus on the joint contributions of anatomical and functional network properties that support effective cognitive control [12, 34].

We postulated that we could identify anatomy-aligned functional signals in the brain, which potentially represent efficiently organized signals with respect to anatomy, in addition to liberal signals that do not correspond to the inherent organization of underlying white matter networks. In our approach, there existed four distinct possibilities: that either increasing or relaxing the alignment of the most aligned signals will be associated with better performance, or that increasing or relaxing the liberality of the most liberal signals will be associated with better performance. Among these possibilities, we anticipated that variation in liberality of the most liberal signals – those which deviate greatly from anatomical expectations – will be most strongly correlated to cognitive switching. This hypothesis built on the fact that the rules learned in our cognitive switching tasks are learned shortly before performing the task, and are unlikely to be represented in changes in long distance white matter pathways. Flexible functional deviations over white matter organization may thus be implicated during efficient switching. However, it was possible that either (1) increasing or (2) decreasing liberality would be associated with better performance. In the former case, particularly anatomy-divergent signal organization may have contributed to cognitive flexibility. In the latter case, modest alignment among liberal signals may have provided beneficial organization that efficiently supports cognitive flexibility. To discriminate between these possibilities, our method allowed us to examine whether structure and function operate synergistically or divergently to promote cognitive performance. We additionally examined the relationship between signal alignment and other related behavioral measures – inhibition and working memory – using a Stroop paradigm and working memory task (for brevity, references to Supplemental Tables for these two tasks are mentioned in the main text where relevant).

Results

BOLD signal alignment concentrations across the brain

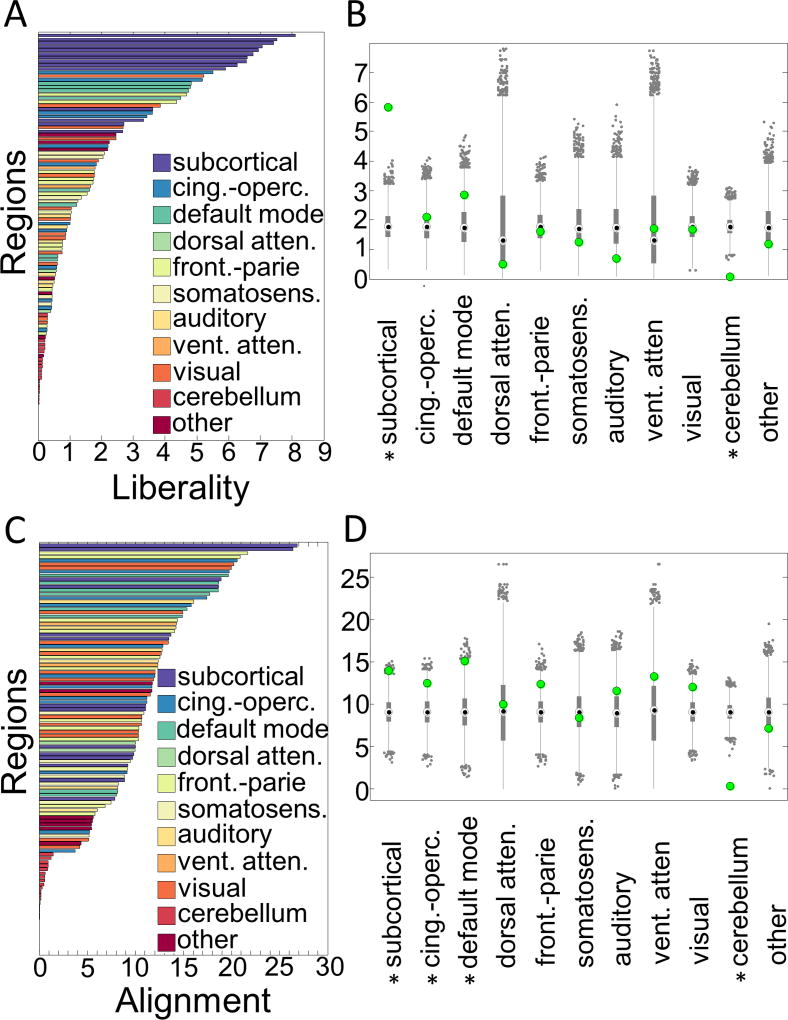
We observed that aligned signals are concentrated within default mode, fronto-parietal, cingulo-opercular, and subcortical systems across subjects, whereas the liberal signals were concentrated largely in the subcortical system (Fig. 3). The significance of these concentrations within systems was confirmed statistically using a non-parametric permutation test (α=0.05) in which we shuffled the values of alignment (or liberality) uniformly at random across brain regions before computing the mean alignment (or liberality) value within each system [4].

Figure 3. Non-parametric permutation test for signal concentration within cognitive systems.

In the 28 subjects, (A) liberal signal concentrations sorted from highest (top) to lowest concentration across all regions. (B) Liberal signals are most concentrated in subcortical regions. (C) Aligned signal concentrations sorted from highest (top) to lowest concentration across all regions in all 28 subjects. (D) Aligned signals are most concentrated in fronto-parietal, cingulo-opercular, default mode, and subcortical systems. The bars in panels (A) and (C) represent the mean signal liberality or alignment in the 111 regions color coded by their system assignment. The x-axes for the same panels represent the Graph Fourier Transformed signal values at each region, where increasing values represent more liberality in panel (A) and more alignment in panel (C). In panels (B) and (D), the gray bars represent the 25th and 75th percentiles of the values in the null permutations, the gray whiskers extend to the most extreme data points not considered outliers, and the gray dots represent outliers in the permutation distributions. The green dot represents the observed value for the system. An ∗ indicates a statistically significant signal concentration in the system relative to the null distribution in the permutation test (p<0.05). Cing.-operc = cingulo-opercular; atten = attention; front.-parie = fronto-parietal; somatosens = somatosensory; vent = ventral.

Interestingly, we observed that the insula, anterior cingulate, and subcortical systems shared both aligned and liberal signals, indicating that the content of BOLD signals in these areas are complex with respect to underlying anatomy. The values of both alignment and liberality were significantly greater than expected in these structures. Other regions across the brain expressed relatively lower amounts of both of these properties. By separating the signal components across regions, we were able to identify potentially behaviorally-sensitive portions of signals in complex brain network anatomy. To see results from an analysis of the spatial correspondence between aligned and liberal signals in the current data, please see Supplemental section “The concentration of aligned and liberal signals is observed in specific regions.”

Associations between BOLD signal alignment and cognitive switch costs

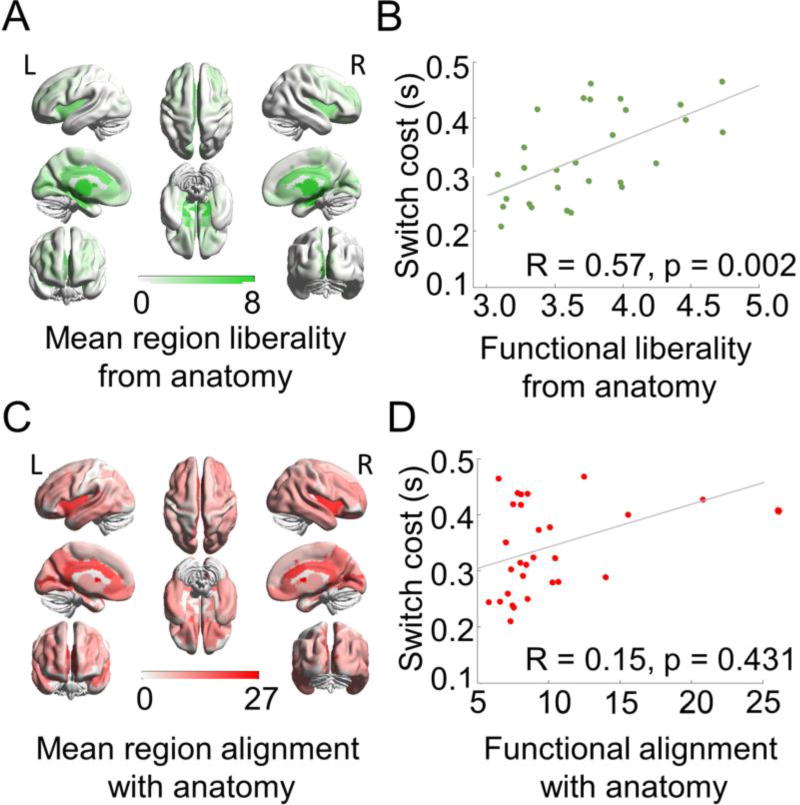
Next, we calculated the correlation between aligned and liberal BOLD signals across the brain and cognitive switch costs (response times during trials with a color-cued switch versus non-switching trials). We observed that variability in aligned signals was not associated with switch costs (R=0.15, p=0.43, accounting for 2% of the variance), while variability in liberal signals accounted for 32% of variance (R=0.57, p=0.002) see Fig. 4). Using aligned signals as covariates in a partial correlation analysis between liberality and switch costs revealed that the correlation remained significant (R=0.55, p=0.002). Among the liberal signals, lower values of liberality (that is, relative alignment) were also associated with lower switch costs both during fixation (R=0.62, p=0.0006) and during nonswitching (R=0.71, p=0.0001) perceptual blocks.

Figure 4. Lower independence is associated with lower switch costs.

In the 28 subjects, (A) liberal signals are concentrated especially in subcortical regions and cingulate cortices. (B) Reduced liberality (increased alignment) is associated with reduced switch costs across subjects. (C) Aligned signals are concentrated especially in subcortical, default mode, fronto-parietal, and cingulo-opercular systems. (D) Variability in aligned signals was not significantly associated with switch costs across subjects. In panels (A) and (C), the colorbars represent the Graph Fourier Transformed signal values at each region, where increasing values represent more liberality or alignment, respectively. In panels (B) and (D), the x-axes represent the mean liberality or alignment across regions of the brain, and the y-axes represent the mean switch cost during the Navon task. L = left hemisphere, R = right hemisphere.

These results demonstrate that relative BOLD signal alignment among liberal signals with anatomy was associated with greater cognitive flexibility, a finding that highlights the importance of simultaneously considering both functional and anatomical neuroimaging in the study of higher order cognitive processes. This indicates that behaviorally relevant signals can be dissociable in the graph domain even when the same regions partially contribute to both types of signals. Liberal signals were specifically related to cognitive switching as opposed to performance more generally during the Navon task. We found that the liberal signals in all blocks were correlated with response times during trials that occurred during switching blocks as well as switch costs. Liberal signals were not correlated with performance on the non-switching blocks, suggesting that these signals are specifically related to cognitive control demands introduced during the switching condition relative to the non-switching condition (see Supplementary tables 1–4).

The specificity of BOLD signal alignment in cognitive control

The fact that statistically significant relationships could be found between switching performance and the signals calculated in the Navon fixation, non-switching, and switching blocks suggests that liberal signal organization is a stable variable in the context of the Navon task (see also Supplemental section “Signal alignment stability in human brain networks”). Thus, testing whether liberal signals are specifically relevant during the switching task relative to other cognitive control processes such as inhibition and working memory is crucial. In supplementary analyses, covarying for Stroop performance did not reduce the correlations between liberality during the Navon task and switching behavior (see Supplementary Tables 17 and 18). Moreover, we find that BOLD liberality observed in the same subjects during fixation periods between Stroop inhibition task blocks does not relate to cognitive switching performance (see Supplementary Tables 21 and 22). Finally, no relationship between BOLD signal alignment and working memory performance was observed in an independent sample from the Human Connectome Project (see Supplementary Tables 27 through 30).

Discussion

Taken together, these findings indicate that the liberality-switching relationship was specific to the Navon task and not accounted for by cognitive inhibition or working memory, providing evidence of a sensitive and specific brain-behavior relationship. Overall, these findings may indicate that some brains are at a natural advantage to meet switching demands, and that switching-specific relations between signal and anatomy can be detected when task demands prioritize preparedness for cognitive switches. Given the persistence of the liberality signal across task blocks, the current study is compatible with the notion that these signals exist throughout the task, potentially representing proactive cognitive control. Future event-related studies could attempt to determine whether liberal versus aligned signals are associated with the proactive or reactive aspects of control in cognitive switching.

In some theoretical accounts of cognitive control, we might expect that performance is facilitated by associations between stimulus features that could have arisen from practice [35], and the neuroplastic changes that facilitate such learned associations could have effects at scales detectable with diffusion imaging [36, 37, 38, 39]. In that case, one assumption could be that greater reliance on these pathways (e.g., measured here as the highly aligned BOLD signal component) would be facilitative of better performance, potentially representing reliance on well-learned information when performing cognitive switches. However, the rules for the current Navon task were learned shortly before performance, perhaps limiting the utility of overlearned representations and emphasizing the neural processing represented by the liberal BOLD signals. Nevertheless, relative alignment of the liberal BOLD signals with white matter anatomy were associated with better performance, suggesting that even in the context of a recently learned task, increased functional reliance on major white matter network organization is advantageous for performance. While speculative, future studies could test whether a dissociation exists in overlearned versus newly learned tasks and whether the effect observed here generalizes to other recently learned switching tasks. This may help to enlighten us about the neuroanatomical expression of the interplay between learning at short versus long timescales and cognitive control.

These findings complement prior studies of executive function that have focused on node-level, edge-level, and module-level features of brain networks [3, 20]. Here, we examined brain function as a series of time-evolving states [4, 40] that were organized in relation to the underlying pattern of white matter tracts. The state-based focus of our approach also offers insights into the differential extent to which specific cognitive systems deviate from tract anatomy, underscoring anatomical contributions to the organization of brain dynamics across subjects. It also allowed us to examine complexity in BOLD signals that is not evident in functional connectivity computed over time [41]. Because functional connectivity is typically computed over many BOLD TRs, our approach characterizes the organization of the elements that constitute common functional connectivity measures.

Our results contextualize previous models of cortico-striatal cognitive switching mechanisms [18, 1] within a connectomic perspective. As a complement to prior findings implicating individual prefrontal, parietal, and striatal systems in cognitive switching, our results highlight the importance of anatomical network organization, and the central role of subcortical functional dynamics atop that structure. This observation is particularly interesting in the context of prior work showing that subcortical and anterior cingulate regions manage multiple inputs and outputs among cortical systems during task transitions [42, 13], potentially requiring more diverse signal organization relative to anatomical networks. In addition, a high convergence of weak liberal and aligned signals was observed in the cerebellum, complementing the high convergence of strong liberal and aligned signals in the cingulate and subcortical regions, which are thus responsible for most of the behavioral variance in our analysis (see Supplementary Tables 9 and 10). Notably, cerebellar architecture has a tenfold greater neural density than other regions in the brain [43] with distinctive neural dynamics; thus, our approach may not be sensitive to cerebellar signaling properties thought to contribute to higher cognitive function [44], which could form a focus for future research involving measurements of neural spike trains and cerebellar microcircuitry.

Our approach also adds a critical perspective on broader interests in the relationship between brain network anatomy and function. Prior reports have established relationships between anatomical networks and functional connectivity [45, 24, 46, 47, 48, 49]. The information content in BOLD correlations computed over long time series is relatively low [41]. Our current work applied an altogether distinct approach to this problem in linking anatomy, function, and cognition. The TR-wise analysis is closely akin to studies of BOLD signal amplitude in cognitive conditions, which has formed a primary backbone of cognitive neuroscience research since the invention of fMRI. Specifically, the alignment measure was based on the distribution of BOLD signal amplitudes across brain regions at single time points in different cognitive conditions, rather than correlations in BOLD signals across regions over time. This fact means that the alignment measure described a feature of neural organization that was expressed in each measurement in time in each individual, rather than a second-order functional connectivity statistic. We found that across cognitive conditions the alignment measure was highly stable, operating as a trait-like variable. This indicates that the function-anatomy relationship is consistent within persons but variable between persons, and thus useful in examining individual variability in cognition.

With respect to recent dynamic network analyses of executive function, our results contribute a crucial anatomically-grounded perspective. The current approach represents a framework in which to understand the dual features of anatomical organization and functional processes supporting cognitive flexibility in the human connectome. Here, high functional dependence in fronto-parietal, cingulo-opercular, default mode, and subcortical systems is not associated with intersubject switching variability. Critically, our results indicate that regions that participate in highly flexible systems [50] in temporal network analysis demonstrate high dependence on underlying anatomical networks across frames of BOLD data during fixation, low cognitive control conditions, and task conditions (see Supplement for further analysis and discussion). Previous studies identify dynamic network roles for fronto-parietal and cingulo-opercular regions in cognitive switching, and our results indicate that moment to moment signal configurations in highly flexible systems are strongly organized by structure across time (see Supplement for addition analysis and discussion). In the context of this highly organized cortical activity, the current results suggest that subcortical systems contain highly liberal signals. The extent to which subcortical systems exhibit relative alignment may form a flexible integrative role across the many computations supported by cortical systems. The relationship between anatomically-bound momentary signal organization and functional reconfigurations in temporal networks may more generally provide a fruitful area for future research.

Notably, our results do not explain the potential cognitive role of highly aligned signals. We hypothesized that signal organization in the most liberal signals would be related to flexibility, representing the brain’s dynamic freedom from anatomical constraints. It could also have been the case that relatively less alignment in the most aligned signals, representing modest dynamic freedom, was associated with greater flexibility. However, we did not observe this in the current data. It is possible that highly aligned signals are optimally configured in healthy brains. Important future directions could involve examining whether highly aligned signals are disrupted in clinical samples and associated with cognitive deficits.

It is possible that the role of aligned signals may be better explained in the context of other cognitive control processes [51]. One possible role for modestly aligned signals is to reduce noise when overcoming predisposed response tendencies for successful goal-directed behavioral switching. Specifically, subcortical structures maintain a high degree of signal alignment overall. Modest alignment of the most liberal signals in these same regions may allow for organized coordination across regions to facilitate switching. We speculate that anatomically aligned signals in fronto-parietal, cingulo-opercular, default mode, and subcortical systems organize the dynamic signals contributing to cortical mechanisms of cognitive control, attention, and resting and preparedness processes, respectively. It would be interesting to test whether highly aligned signals in association cortices and subcortical structures are associated with domain-general performance variability across modalities [52]. In cognitive switching specifically, the extent to which signal liberality relates to performance on tasks involving other sensory modalities, transitioning between internally and externally focused attention, and divergent thinking remains to be established. In addition, the relevance of liberal signals to cognitive flexibility may be further examined in populations with reduced performance such as aging [53], Gilles de la Tourette syndrome [54], and Parkinson’s disease [55].

Of note, the current study design establishes a correlative relationship between our neural measure of liberality and cognitive flexibility. Experiments that examine a causal relationship could provide important validation for our neural measure. Specifically, interventions involving medications that influence attention, behavioral training paradigms, and noninvasive brain stimulation could examine whether BOLD signal alignment is sensitive to interventions and if induced changes in liberal and aligned signals underlie changes in behavior. Some promising mechanistic approaches involve a combination of biologically plausible models combined with fMRI and diffusion tractography, such as in dynamic causal modeling [56]. In addition, many approaches to diffusion tractography and parcellation are now available, each presenting with strengths and limitations. Future studies that are especially focused on robust classification and prediction procedures could seek to further optimize network generation in these regards.

In conclusion, our results support the utility of network science in clarifying mechanisms of executive function specifically and cognition more generally [26, 27]. Recent literature firmly establishes that white matter organization is a critical, but incomplete determinant of functional signals in brain networks [45, 24, 46, 47, 48, 49]. Conceptually, the current approach acknowledges that without structure, functional signals lack a mediating organization. By examining functional signal alignment within underlying white matter networks, we identify an important definition of dynamic contributions to cognitive switching that powerfully discriminates between the contributions of subcortical and other systems in the brain. Similar applications to other large multimodal neuroimaging datasets could contribute to biomarker analyses in psychiatric disease and neurological disorders, many of which are associated with deficits in executive function [57, 58, 59].

Methods

In this study, subjects performed a Navon switching task and Stroop inhibition task during fMRI scanning. We additionally acquired diffusion spectrum imaging data for white matter tractography. Within the Desikan-Killiany anatomical atlas [60] combined with the Harvard-Oxford subcortical parcels [61], and Diedrichsen cerebellar atlas [31], we extracted preprocessed BOLD signals for each region for each time point. Then, we reconstructed diffusion tractography and extracted an anatomical network in the same parcellation for each subject. To create the measure of BOLD signal alignment with underlying anatomical networks, we used tools from graph signal processing. Specifically, we treated observed BOLD vectors across regions at each time measurement as a signal on each subject’s underlying anatomical graph. Then, we applied a GFT to identify the signals that were either highly aligned with the anatomical network, or liberal with respect to the anatomical network on the subject level. Across subjects, we calculate the correlation between the aligned (or liberal) signals and the behavioral variables of interest: in the Navon task, switch costs, which measure the time taken to perform a switch relative to a non-switch, and in the Stroop task, inhibition costs, which measure the time taken to respond to trials where cognitive inhibition is required relative to trials without inhibition demands.

Subjects

A total of 30 subjects were recruited. All subjects were screened for prior history of psychiatric or neurological illness. One subject was excluded due to near-chance performance on the task (accuracy = 52%). One additional subject was excluded due to technical problems on the day of scanning. The final sample included 28 individuals (mean age = 25.6, St.D. = 3.5, 70% Caucasian, 13 females). All subjects volunteered with informed consent in writing in accordance with the Institutional Review Board/Human Subjects Committee, University of Pennsylvania.

Behavioral task

All participants completed a local-global perception task based on classical Navon figures [29]. Local-global stimuli were comprised of four shapes – a circle, X, triangle, or square – that were used to build the global and local aspects of the stimuli. On all trials, the local feature did not match the global feature, ensuring that subjects could not use information about one scale to infer information about another. Stimuli were presented on a black background in a block design with three block types (See Fig. 2). In the first block type, subjects viewed white local-global stimuli. In the second block type, subjects viewed green local-global stimuli. In the third block type, stimuli switched between white and green across trials uniformly at random with the constraint that 70% of trials included a switch in each block. In all blocks, subjects were instructed to report only the local features of the stimuli if the stimulus was white and to report only the global feature of the stimuli if the stimulus was green. Blocks were administered in a random order. Subjects responded using their right hand with a four-button box. All subjects were trained on the task outside the scanner until proficient at reporting responses using a fixed mapping between the shape and button presses (i.e., index finger = “circle”, middle finger = “X”, ring finger = “triangle”, pinky finger = “square”). In the scanner, blocks were administered with 20 trials apiece separated by 20 s fixation periods with a white crosshair at the center of the screen. Each trial was presented for a fixed duration of 1900 ms separated by an interstimulus interval of 100 ms during which a black screen was presented.

Diffusion spectrum imaging acquisition and processing

Diffusion spectrum images (DSI) were acquired on a Siemens 3.0T Tim Trio for all subjects along with a T1-weighted anatomical scan at each scanning session. We followed a parallel strategy for data acquisition and construction of streamline adjacency matrices as in previous work [4, 62]. DSI scans sampled 257 directions using a Q5 half-shell acquisition scheme with a maximum b-value of 5,000 and an isotropic voxel size of 2.4 mm. We utilized an axial acquisition with the following parameters: repetition time (TR) = 5 s, echo time (TE)= 138 ms, 52 slices, field of view (FoV) (231, 231, 125 mm). We acquired a three-dimensional SPGR T1 volume (TE = minimal full; flip angle = 15 degrees; FOV = 24 cm) for anatomical reconstruction. All subjects volunteered with informed consent in writing in accordance with the Institutional Review Board/Human Subjects Committee, University of Pennsylvania.

DSI data were reconstructed in DSI Studio (www.dsi-studio.labsolver.org) using q-space diffeomorphic reconstruction (QSDR)[63]. QSDR first reconstructs diffusion-weighted images in native space and computes the quantitative anisotropy (QA) in each voxel. These QA values are used to warp the brain to a template QA volume in Montreal Neurological Institute (MNI) space using the statistical parametric mapping (SPM) nonlinear registration algorithm. Once in MNI space, spin density functions were again reconstructed with a mean diffusion distance of 1.25 mm using three fiber orientations per voxel. Fiber tracking was performed in DSI studio with an angular cutoff of 35, step size of 1.0 mm, minimum length of 10 mm, spin density function smoothing of 0.0, maximum length of 400 mm and a QA threshold determined by DWI signal in the colony-stimulating factor. Deterministic fiber tracking using a modified FACT algorithm was performed until 1,000,000 streamlines were reconstructed for each individual.

Anatomical scans were segmented using FreeSurfer[64] and parcellated using the connectome mapping toolkit [65]. A parcellation scheme including n=129 regions was registered to the B0 volume from each subject’s DSI data. The B0 to MNI voxel mapping produced via QSDR was used to map region labels from native space to MNI coordinates. To extend region labels through the grey-white matter interface, the atlas was dilated by 4 mm [66]. Dilation was accomplished by filling non-labelled voxels with the statistical mode of their neighbors’ labels. In the event of a tie, one of the modes was arbitrarily selected. Each streamline was labeled according to its terminal region pair.

Finally, we included a cerebellar parcellation [31]. We used FSL to nonlinearly register the individual’s T1 to MNI space. Then, we used the inverse warp parameters to warp the cerebellum atlas to the individual T1. We registered the subject’s DSI image to the T1. We used the inverse parameters from this registration to map the individualized cerebellar parcels into the subject’s DSI space. Finally, we merged the cerebellar label image with the dilated cortical and subcortical parcellation image.

From these data and parcellation, we constructed an anatomical connectivity matrix, A whose element A_ij represented the number of streamlines connecting different regions [24], divided by the sum of volumes for regions i and j [67]. Prior to data analysis, all cerebellum-to-cerebellum edges were removed from each individual’s matrix because cerebellar lobules are demonstrably not anatomically connected directly to one another [68].

Functional imaging acquisition and processing

fMRI images were acquired during the same scanning session as the DSI data on a 3.0T Siemens Tim Trio whole-body scanner with a whole-head elliptical coil by means of a single-shot gradient-echo T2* (TR = 1500 ms; TE = 30 ms; flip angle = 60°; FOV = 19.2 cm, resolution 3mm × 3mm × 3mm). Preprocessing was performed using FEAT v. 6.0 (fMRI Expert Analysis Tool) a component of the FSL software package [69]. To prepare the functional images for analyses, we completed the following steps: skull-stripping with BET to remove non-brain material, motion correction with MCFLIRT (FMRIB’s Linear Image Registration Tool; [69]), slice timing correction (interleaved), spatial smoothing with a 6-mm 3D Gaussian kernel, and high pass temporal filtering to reduce low frequency artifacts. We also performed EPI unwarping with fieldmaps in order to improve subject registration to standard space. Native image transformation to a standard template was completed using FSL’s affine registration tool, FLIRT [69]. Subject-specific functional images were co-registered to their corresponding high-resolution anatomical images via a Boundary Based Registration technique (BBR [70]) and were then registered to the standard MNI-152 structural template via a 12-parameter linear transformation. Finally, each participant’s individual anatomical image was segmented into grey matter, white matter, and CSF using the binary segmentation function of FAST v. 4.0 (FMRIB’s Automated Segmentation Tool [71]). The white matter and CSF masks for each participant were then transformed to native functional space and the average timeseries were extracted. Images were spatially smoothed using a kernel with a full-width at half-maximum of 6 mm. These values were used as confound regressors on our time series along with 18 translation and rotation parameters as estimated by MCFLIRT [72].

Functional decomposition into anatomical networks

To investigate our hypothesis that BOLD signal alignment with anatomy is related to cognitive flexibility, we applied an analysis from spectral graph theory [73]. Specifically, we used a Graph Fourier Transform (GFT; [32]) to represent the BOLD signals in the graph domain. This allowed us to take observed BOLD time series and examine the extent to which they were aligned to or liberal from the underlying graph representing the white matter connections between regions.

The approach differed from structure-function analyses of pairwise relationships between anatomical and functional network connections [45, 24, 46, 47, 48, 49]. The GFT provided a distinct perspective from connectivity analyses by allowing the spectrum of the entire anatomical matrix to inform estimates of how BOLD signals in each observation (not functional connections computed over time) align to white matter. Importantly, each element (region) in either the aligned or liberal BOLD signal vector represented the extent to which that region conformed to or deviated from the expected signal with respect to the entire white matter network’s topology, rather than with respect to single anatomical connections.

An important conceptual benefit of the GFT is that it could be used to study how the topology of an individual’s anatomical network informed the expected structure of the BOLD signal. We assessed the deviation of the BOLD signal from this expectation at each moment in time, as opposed to an average over all moments in time, which provides inherently limited information [41]. The approach thus took the functional measurements that are commonly used to construct functional graphs, and instead examined their expression atop anatomy in single individuals. Another important benefit of the GFT is that it allowed us to treat signal alignment and liberality as related phenomena that are not mutually exclusive from one another. Intuitively, this can be understood by analogy to Fourier analysis in the time domain, where a time series can be transformed into the frequency domain such that its high and low frequency content can be studied. Similarly, GFT can be used to transform a vector of BOLD magnitudes at a single TR into aligned and liberal portions with respect to the anatomical network. The aligned and liberal signals are directly analogous to low and high frequencies in traditional Fourier analysis, and as such are not mutually exclusive. Thus, the GFT allowed us to consider the amount of signal that was aligned and liberal with respect to the graph. Only if the signal was perfectly aligned or unaligned with the graph would we expect the transformed signals to exhibit nonzero quantities of both signal characteristics. This is analogous to expecting any natural signal in the time domain to represent frequency domain content that exceeds a single frequency.

Conceptually, there was no initial analytic constraint on where the aligned and liberal signals most prominently exist in the brain; indeed, it was possible that they may have overlapped in the same regions in the brain. This too can be understood by analogy to traditional time-frequency analysis using the Fourier transform. A priori, each moment in time in a Fourier transformation contributes to the transformed time-frequency representation of the data, including both high and low frequency activity. Analogously, regions across the brain expressed BOLD signals that contribute to both aligned and liberal signals that are separated by the GFT. This allowed us to detect which specific nodes are contributing most to aligned and liberal signals, and we could empirically determine to what extent the aligned and liberal signals overlapped in the brain. See Fig. 5 for a schematic illustrating the analogy between signal frequency in the time domain and signal alignment in the graph domain.

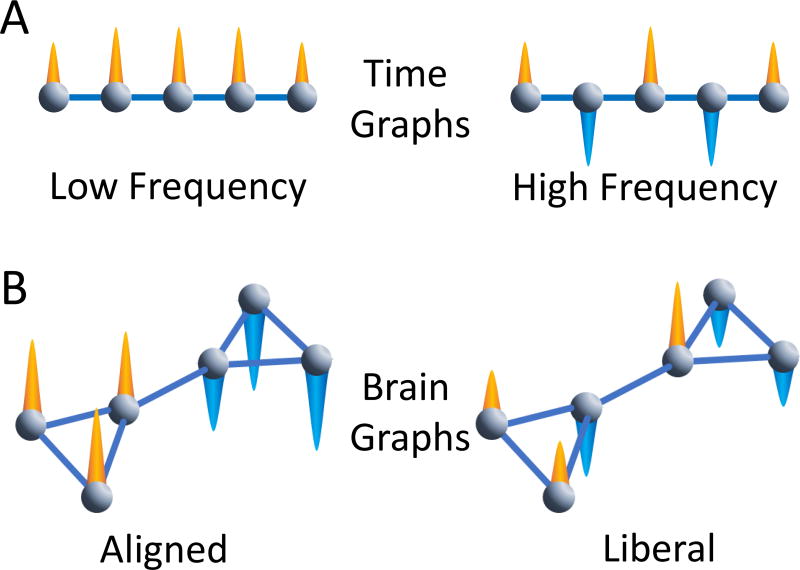
Figure 5. Signal frequency in the time domain versus alignment in the graph domain.

(A) A simple graph can represent a signal process in time. Imagine that the nodes in the graph are moments in time, and the edges between nodes represent links between adjacent moments in time. The image on the left then represents a low frequency signal process where the orange cones represent positive signals that do not vary significantly with respect to the time dimension. The image on the right represents a high frequency signal process where the orange cones represent positive signals and the blue cones represent negative signals. The signals flip from moment to moment, which is the basis of a high frequency signal. A traditional Fourier analysis on real signals can separate both high and low frequency activity observed in a single set of nodes (moments in time). (B) We can extend this notion directly to more complex graph structures such as those observed in human brain networks with the Graph Fourier Transform. As in the time graph in panel (A), we observe nodes, edges, and a signal at each node. Unlike the time graph, which constitutes a linear ordering of connected nodes, the more complex graph may have modules and other mesoscale features. On the left, we observe an aligned signal: the signals in nodes that highly connect to one another exhibit similar signals to one another. On the right, the signal is liberal with respect to the underlying graph: the signals in nodes that highly connect to one another do not exhibit similar signals to one another. In real signals, such as BOLD signals observed at a single moment in time, each node can contribute signals that may be to some extent aligned and to some extent liberal.

It is important to note that the ranges of aligned and liberal signals are extremes along a continuum of alignment selected to be robust to noise. We use the terms “aligned” and “liberal” to categorically refer to each extreme. Critically, it is the case that increasing alignment does not imply decreasing liberality, because these refer to two distinct ranges in the graph signal. This is because our selection of aligned and liberal signals is analogous to selecting the high and low frequency ranges of a signal in a traditional Fourier transformation. For example, if we used a traditional Fourier transformation on a full time series and selected only frequencies of 1–10 Hz and 90–100 Hz in the time-frequency domain, shifts from 1 to 10 Hz would represent “increasing frequency”, but would still be represented in the 1–10 Hz range. Similarly, shifts from 100 to 90 Hz would represent “decreasing frequency.” However, it is not necessarily the case that shifts in the 1 to 10 Hz range are associated with changes in the 90 to 100 Hz range and vice versa. Thus, it is sensible to speak about both ranges separately, and it is not necessarily the case that they correlate with one another. To determine if they are correlated with one another, the presence and variability at each end of the spectrum must be empirically investigated in a natural system.

It is crucial to clarify the biological and cognitive relevance of our measure. Biologically, our measure described the deviation of BOLD signal organization across the brain at each time measurement with respect to its underlying anatomy. This is interesting because we might assume that cognitive function must to some extent depend on underlying anatomy to organize signal processes, but on the other hand that some cognitive processes may benefit from deviating from this anatomy. In the current work, we anticipated that the most liberal signals would be sensitive to variability in switch costs because these are the signals that most highly deviate from underlying white matter network organization. Intuitively, these signals were those that may facilitate rapid cognitive switches based on a recently learned rule because the rules cannot be represented in the connecting white matter pathways reconstructed by our diffusion tractography. Our method identified the spatial distribution and intensity of the aligned and liberal signals so that we could test for the behaviorally relevant components of BOLD signal organization in subject specific white matter networks.

We now proceed to the technical definition of our alignment and liberality measures. We analyzed the signal defined on a connected, weighted, and symmetric graph, G=(V,A), where V={1,…,n} is a set of n vertices or nodes representing individual brain regions and A∈R^n×n is defined as above. Because the network A was symmetric, it had a complete set of orthonormal eigenvectors associated with it [74, 32]. For this reason, it had an eigenvector decomposition, A=V∧V^T, in which Λ was the set of eigenvalues, ordered so that λ₀≤λ₁≤…≤λ_n-1, and $\mathbf{V}={\left\{{\mathbf{v}}_k\right\}}_{k=0}^{n-1}$ was the set of associated eigenvectors. Following [32, 75], we used the eigenvector matrix to define the Graph Fourier Transform (GFT) of the graph signal x∈Rⁿ, defined as

$$\mathrm{\sim x}={\mathbf{V}}^T\mathbf{x}.$$ (1)

Given ∼x=[∼x₀,…∼x_n−1]^T, we could express our original signal as $\mathbf{x}=\sum _{k=0}^{n-1}{\mathrm{\sim x}}_k{\mathbf{v}}_k$, a sum of the eigenvector components v_k. The contribution of v_k to the signal x was the GFT component ∼x_k. Note that the smoothness of v_k on the network can be evaluated in the quadratic form ${\mathbf{v}}_k^T\mathbf{A}{\mathbf{v}}_k=\sum _{i,j\in V}{A}_{\mathit{\text{ij}}}{v}_k(i)v_k(j)$ and that ${\mathbf{v}}_k^T\mathbf{A}{\mathbf{v}}_k={\mathrm{\lambda }}_k$ is given by the eigenvector decomposition. The quantity $\sum _{i,j\in V}{A}_{\mathit{\text{ij}}}{v}_k(i)v_k(j)$ will be negative when the signal is varied (highly connected regions possess signals of different signs), and positive when the signal is smooth (highly connected regions possess signals of same signs); for these reasons, this quantity can be thought of as a measure of smoothness (alignment). Consequently, these GFT coefficients ∼x_k for small values of k indicated how much variables that are highly misaligned (liberality) with anatomy contribute to the observed brain signal x. GFT coefficients ∼x_k for large values of k described how much signals that were aligned with the anatomical network contributed to the observed brain signal x. The inverse (i) GFT of x with respect to A was defined as

$$\mathbf{x}=\mathrm{\sim V}x.$$ (2)

Given a graph signal x with GFT ∼x, we could isolate the liberal components corresponding to the lowest eigenvectors by applying a graph filter HL that only kept components with k<KL and sets other components to 0. The signal xL then contained the “liberal” components of x (those with a low alignment with network anatomy). Apart from the graph low-pass filter HL, we also considered a middle graph regime HM, which kept only components in the range of KL ≤k<n-KA, and an “aligned” graph regime HA, such that only network-aligned components with n-KA≤k were kept. Therefore, the liberal regime took the lowest KL components, the alignment regime took the highest KA components, and the middle regime captured the middle n-KL-KM components (here, we used the components with the 10 lowest alignment values to represent the liberal regime and the components with the 10 highest alignment values to represent the aligned regime; see Supplement for robustness of results to parameter selection). As such, since we used xM and xA to respectively denote the signals represented by the middle and highly aligned regimes, the original signal could be written as the sum x= xL+ xM+ xA. This formulation gave a decomposition of the original signals x into liberal, moderately aligned, and highly aligned components that respectively represented signals that had high, medium, and low signal deviation with respect to the anatomical connectivity between brain regions.

Prior work has consistently demonstrated that the aligned and liberal components aid in better estimation of unknown movie ratings in recommendation systems [76], better prediction of cancer using gene interaction networks [77, 78], and learning in neuroimaging data, where learning-related processes are demonstrably expressed in low and high components in fMRI data, and where the middle component xM is demonstrably less reliable and behaviorally uninformative [79]. In the supplement, we perform a similar analysis to [79] but with the current data to examine the stability of our low and high alignment measurements to parameter selection. The data indicates that the low and high alignment components in the current data are stable. Mathematically, this is expected in general in applications of the current approach because eigenvalues at the extreme low and high end are isolated from the middle values, which leads to robustness in the high and low ranges of the decomposition [80].

We note that this approach allowed signals on the anatomical network to contain both aligned and liberal components represented in the same region at a single TR. This feature occurred because the anatomical network of n nodes has n² entries (i.e., the connection information was encoded in the anatomical adjacency matrix for any node i to any node j). Rather than examining a single BOLD signal measurement as n independently observed values, the GFT represented the signal to be a composite of contributions to the signal across subject’s anatomical network topology. The decomposition occured across the entire set of signals (here, the vector of BOLD magnitudes across regions at a single TR), where there are only n entries. The GFT applied here leverages the fact that the n entries in a given vector are not isolated, but are signals on top of the complex anatomical network. In the current approach, instead of focusing on the single BOLD value observed at each region as a discrete entity, the decomposition was sensitive to the observation of pairwise differences among BOLD signals relative to that expected by the anatomical network. Some portion of each given region’s BOLD signal was estimated to be liberal with respect to the network, which was represented by xL, and some portion was estimated to be aligned with the network, which was represented by xA (See Fig.6). This mathematical separation established the notions of alignment and liberality of the BOLD signals in the anatomical network. All individual regions in the brain could have some degree of alignment and some degree of liberality given the complexity of BOLD signal patterns across the network, unless the observed BOLD signals in all regions were perfectly aligned or perfectly misaligned with the subject’s anatomical network. This highlights an important strength of the use of the Graph Fourier Transform to examine functional signal liberality in anatomical brain networks: in general, the signal can be understood as a network level composite of aligned and liberal signals, and the extent to which individual regions contribute to these properties can be examined as the variation in the weights of the region’s contribution to each of the aligned and liberal components.

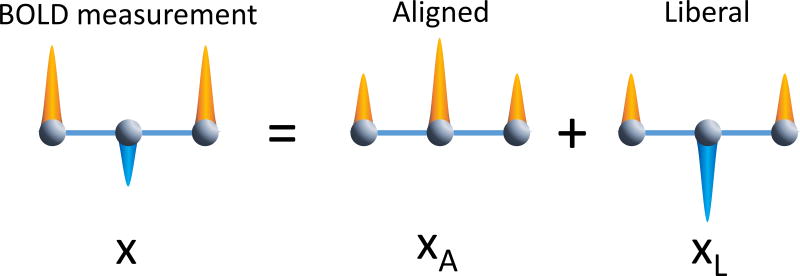
Figure 6. Signal decomposition into anatomy.

BOLD signals are decomposed into aligned and liberal signal components. Left of equation: a schematic BOLD signal on a simple anatomical network. Here, two signals are stronger in the high direction than the low direction. Right of equation: the signals across the network are decomposed into an aligned and liberal component. The original signals can be reconstructed from a basis set including a weighted part of the signal that is aligned with the anatomical network and another part that is liberal with respect to the anatomical network.

Relating signals to behavior

Following the signal decomposition into aligned and liberal signals, we associated the signal concentrations with median switch cost (median response time during switching trials versus no-switching trials) performance for all accurate trials. To do so, we computed a partial Pearson’s correlation between the observed signal value for each subject with their median switch cost using the average framewise displacement across BOLD measurements as a second-level control for the influences of motion. Specifically, to examine the relationship between alignment and switch costs across subjects, we computed the partial correlation for the mean of xA for each subject with subjects’ switch costs, controlling for average framewise displacement. Then, to examine the relationship between liberality and switch costs, across subjects, we computed the partial correlation for the mean of xL for each subject with subjects’ switch costs, controlling for average framewise displacement. We additionally repeated these analyses including age and sex and found similar slopes of the associations between the liberality values and switch costs (see Supplement).

System permutation test

To examine the spatial significance of system-level concentration of aligned and liberal signals, we performed a non-parametric permutation test for each signal class. Separately for each of xL and xA, we shuffled the observed mean signal concentration values across regions in 10,000 permutations for aligned and liberal signals and computed a null distribution of system mean signal concentrations for each system. Signals were judged to be significantly concentrated in a system if the mean signal concentration in the system was greater or less than 95% of the null permutations.

Data and code availability

Requests for data and code can be addressed to the Corresponding Author, Danielle S. Bassett.