Identification and functional characterization of HIV-associated neurocognitive disorders with large-scale Granger causality analysis on resting-state functional MRI

Abstract

Resting-state functional MRI (rs-fMRI), coupled with advanced multivariate time-series analysis methods such as Granger causality, is a promising tool for the development of novel functional connectivity biomarkers of neurologic and psychiatric disease. Recently large-scale Granger causality (lsGC) has been proposed as an alternative to conventional Granger causality (cGC) that extends the scope of robust Granger causal analyses to high-dimensional systems such as the human brain. In this study, lsGC and cGC were comparatively evaluated on their ability to capture neurologic damage associated with HIV-associated neurocognitive disorders (HAND). Functional brain network models were constructed from rs-fMRI data collected from a cohort of HIV⁺ and HIV⁻ subjects. Graph theoretic properties of the resulting networks were then used to train a support vector machine (SVM) model to predict clinically relevant parameters, such as HIV status and neuropsychometric (NP) scores. For the HIV^+/− classification task, lsGC, which yielded a peak area under the receiver operating characteristic curve (AUC) of 0.83, significantly outperformed cGC, which yielded a peak AUC of 0.61, at all parameter settings tested. For the NP score regression task, lsGC, with a minimum mean squared error (MSE) of 0.75, significantly outperformed cGC, with a minimum MSE of 0.84 (p < 0.001, one-tailed paired t-test). These results show that, at optimal parameter settings, lsGC is better able to capture functional brain connectivity correlates of HAND than cGC. However, given the substantial variation in the performance of the two methods at different parameter settings, particularly for the regression task, improved parameter selection criteria are necessary and constitute an area for future research.

1. INTRODUCTION

HIV-associated neurocognitive disorders (HAND) are responsible for an array of cognitive, motor, and behavioral symptoms in over 25% of individuals with HIV,¹ including those with optimal viral control using highly active antiretroviral therapy (HAART).² Currently, the standard for HAND diagnosis and disease monitoring is an extensive battery of neuropsychometric (NP) tests, which are susceptible to confounding factors such as socioeconomic status and learning effects.^3,4 In addition, NP tests are neither sensitive nor specific for HAND and cannot detect the presence of HAND before the onset of neurologic and psychiatric signs of damage. Resting-state functional MRI (rs-fmRI) has been shown to detect patterns of altered brain connectivity in a variety of disease states, including autism spectrum disorder,⁵ schizophrenia,⁶ and Alzheimer disease.^7,8 In many such studies, conventional Granger causality (cGC) is used as a method to quantify directed information transfer between different regions of the brain on the basis of rs-fMRI time-series. Though cGC has offered promising initial results, it suffers from the mathematical limitations of its underlying autoregressive model, which limit its application for the analysis of complex high-dimensional systems such as the brain. Large-scale Granger causality (lsGC), which extends the scope of cGC with the addition of an embedded dimension reduction step, was specifically designed to circumvent this so-called curse of dimensionality and has recently been shown to perform better than cGC in a machine learning classification task of HIV⁺ and HIV⁻ subjects in which functional brain networks were used as input features.⁹ In this study, a quantitative retrospective analysis was performed on a rs-fMRI dataset obtained from a larger cohort of HIV⁺ and HIV⁻ subjects with the objective of distinguishing HIV⁺ and HIV⁻ subjects and predicting overall scores of NP tests. This work continues our group’s application of big data analysis in biomedical imaging by means of advanced pattern recognition and machine learning methods.^9–13

2. DATA

2.1 Functional MRI Acquisition

The study participants were comprised of 20 healthy HIV⁻ subjects with no history of severe psychiatric or neurologic disease (9 females; mean age 42 years; range 21-60 years) and 14 HIV⁺ subjects (5 females; mean age 46 years; range 23-71 years) with symptoms of HAND. In the HIV⁺ cohort, 4 subjects underwent neuroimaging and neuropsychometric evaluation twice. All subjects provided written consent, in accordance with the study protocol approved by the Institutional Review Board of the University of Rochester. The scan was acquired using a 3.0 Tesla, Siemens Magnetom TrioTim scanner, using the following fMRI scan parameters: Echo time (TE) = 23 ms, repetition time (TR) = 1650 ms, flip angle (FA) = 84°, 96 × 96 acquisition matrix. A total of 250 temporal scan volumes with 25 slices at a slice distance of 5 mm were acquired from each subject. During the fMRI acquisition period, the subjects were instructed to lie still in the scanner with eyes closed. High-resolution structural T1-weighted magnetization-prepared rapid gradient echo (MPRAGE) scans were also collected and used for registration.

2.2 Neuropsychometric testing

Neuropscyhometric (NP) testing was performed on all subjects using a standard battery for six cognitive domains: executive function, specialized function, motor ability, learning, memory, and attention. Scores from individual domains were combined into an overall score, which was normalized as a z-score.

2.3 Preprocessing

Preprocessing steps were performed using C-PAC¹⁴ and its underlying dependencies in the FMRIB Software Library (FSL, version 5.0, http://fsl.fmrib.ox.ac.uk/).¹⁵ The first 10 brain volumes acquired for each subject were discarded to eliminate the effects of initial saturation of the blood oxygen level dependent (BOLD) fMRI signal. On the 240 remaining volumes, head motion correction, slice timing correction, brain extraction, and registration to the standard Montreal Neurological Institute (MNI152) atlas space^16,17 was performed. Removal of the whole brain time-series was done using a nuisance regressor. In addition, high-pass filtering was performed to remove signal drifts and the voxel time-series were normalized to unit standard deviation and zero mean.

3. METHODS

3.1 Large-scale Granger causality

Large-scale Granger causality⁹ is a multivariate and directional method that is built on the principle of Granger causality (GC),¹⁸ in which time-series A is said to Granger-cause time-series B if the inclusion of information from time-series A in a predictive autoregressive model of time-series B decreases the variance of the residuals between the predicted and actual time-series B. Unlike conventional GC (cGC), however, lsGC can be extended to high-dimensional systems due to the embedding of a dimension reduction step using principal components analysis.

3.2 Parameter selection for Granger causality analysis

To perform lsGC, two model parameters must be chosen: number of retained principal components c and autoregressive order ρ. Parameter selection was informed by the Akaike Information Criterion (AIC)¹⁹ and Bayesian Information Criterion (BIC)²⁰ as well as by a previous lsGC rs-fMRI study.¹⁰ The following set of lsGC parameters were chosen: ρ = {1, 2, 3, 4, 5}, c = {1, 2}. For cGC, ρ = {1, 2} was evaluated, as orders greater than 2 could not be performed due to the mathematical limitations of cGC (c is not relevant for cGC, as there is no dimension reduction step).

3.3 Network property computation

90 regions of interest (ROIs) were defined according to the Automated Anatomical Labeling (AAL)²¹ template and the mean time-series from each ROI was extracted. For each subject, a 90 × 90 weighted affinity matrix was generated using lsGC and cGC with each parameter setting. Negative entries as well as entries on the main diagonal of the matrix were set to 0. The matrix was then binarized by setting the top 30% of entries to 1 and the bottom 70% of the entries to 0. This matrix is thus an equivalent to a network graph, in which ROIs are represented as vertices and the edges between them are denoted by the nonzero entries of the matrix.

The following local properties were calculated for each node of each subject’s brain network. In-degree: The sum of all incoming edges for a particular vertex. Out-degree: The sum of all outgoing edges for a particular vertex. Clustering coefficient: The fraction of connected triples centered on a node that are also triangles (a connected triple is a set of three vertices for which one vertex has direct incoming or outgoing edges to the other two; a triangle is a set of three vertices that are all directly connected by either outgoing or incoming edges). Betweenness centrality: The fraction of all shortest paths in a network that pass through a particular vertex²² (the shortest path between vertex i and vertex j is the minimum number of edges that must be traversed to travel from i to j; if such a path does not exist for a given pair of vertices, as might happen when a network becomes disconnected, then the maximum finite path length for the entire network is assigned as the shortest path length for that pair of vertices).

The following global properties were also calculated for each subject’s network. Degree variance: the variance of the incoming or outgoing edges of all vertices in a network. Modularity: The extent to which a network be partitioned into Louvain community detection algorithm-defined modules,²³ which have high intramodular connectivity and low intermodular connectivity.²² Small-worldness: The ratio of the random network-normalized global clustering coefficient and the random network-normalized shortest path length.²⁴ Degree distribution-matched random networks were produced for each empirical brain network by iteratively rewiring each edge approximately 10 times. Motif frequency: the frequency of occurrence of 13 three-vertex motifs.²⁵ Generation of the random networks and calculation of the network parameters were performed using the Brain Connectivity Toolbox (brain-connectivity-toolbox.net)²⁶ in MATLAB (2015b, The MathWorks, Natick, MA).

3.4 Machine learning with support vector machines

Each brain network property was normalized across all subjects to have a mean of 0 and a standard deviation of 1. All network properties and demographic factors (age and gender) for each subject were then concatenated into a single feature vector and used as the input features for a support vector machine²⁷ (SVM) model. To train and test the model, a 10-fold iterative cross-validation scheme was employed, in which the data were split into training (90%) and testing sets (10%). An SVM model was generated using the training set and its performance was assessed on the testing set. The outputs were either the classification of each subject as HIV⁺ or HIV⁻ or the prediction of the normalized NP score for each subject. For the HIV^+/− classification task, performance on the testing set was assessed using accuracy of classification and the area under the receiver operating characteristic curve (AUC), in which an AUC of 1 indicates a perfect classifier while an AUC of 0.5 indicates a classifier that performs no better than random chance. For the NP score regression, performance was assessed using the mean squared error (MSE). This scheme was iterated 100 times and the mean and standard error of the resulting AUC, accuracy, or MSE distributions were computed.

4. RESULTS

Functional brain network properties were used as input features to classify HIV⁻ and HIV⁺ subjects with SVM, and an iterative 10-fold cross-validation scheme was employed to train and test the model. The resulting classification accuracies and AUCs were highly dependent on the specific variant of Granger causality (GC) employed. As can be seen in Fig. 2, the AUCs of lsGC at c = 1 and c = 2 are significantly above those of even the peak AUC of cGC. Additionally, the classification performance of lsGC at c = 2 is generally greater than that at c = 1.

Figure 2.

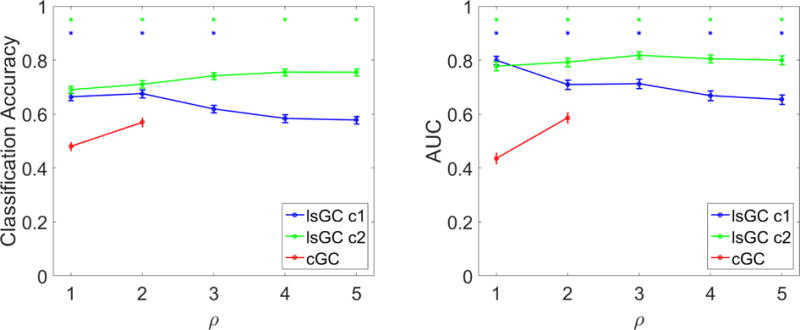
HIV status classification performance of SVM using graph properties derived from GC as input features, as assessed by classification accuracy (left) and AUC (right). Error bars represent standard error of the mean over 100 iterations of 10-fold cross validation. Blue and green asterisks (*) represent entries, where the performance of lsGC at c = 1 or c = 2, respectively, was significantly higher than that of the peak cGC performance at ρ = 2 (p < 0.001 using a one-tailed paired t-test). In terms of AUC, the performance of lsGC at either setting of c was significantly higher than that of cGC at all settings of ρ considered. The same is true with accuracy, with the exception of settings of ρ > 3, where lsGC at c = 1 no longer outperforms cGC. Our results suggest that lsGC outperforms cGC for classifying HIV status based on functional MRI analysis.

4.1 Neuropsychometric score regression

In addition to the HIV^+/− classification task depicted in Fig. 2, functional brain network properties were also used with SVM to predict the overall NP score for each subject. A cross-validation scheme similar to that employed in the classification task was used, with one major difference: HIV status of subjects was considered an additional feature for the regression task. The results of this analysis are shown in Fig. 3. For all orders considered, lsGC at c = 1 performs as well as or better than the other methods. Peak performance of cGC occurs at ρ = 2, where it performs better than lsGC at c = 2. LsGC at c = 2 appears extremely sensitive to the choice of ρ, as it initially decreases sharply, then increases gradually with ρ. It can be seen that at ρ = 1, lsGC generally outperforms cGC. As order is increased to 3, the performance of lsGC at c = 1 and c = 2 improves beyond the peak performance of cGC. At ρ > 3, however, lsGC at c = 2 starts to give progressively higher values of the MSE.

Figure 3.

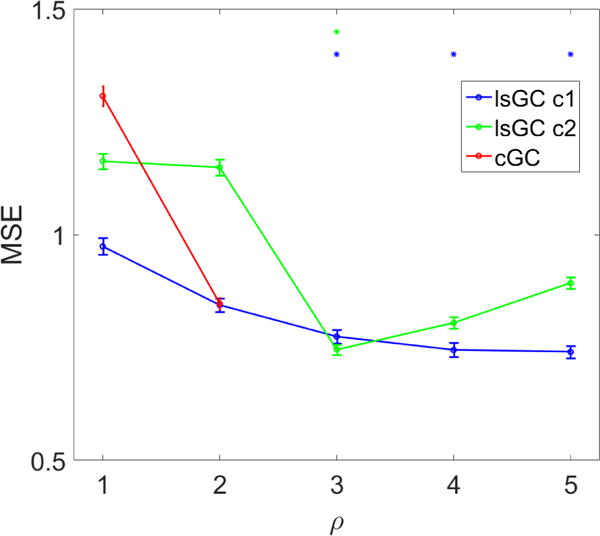
Overall NP score prediction with SVM. Error bars represent the standard error of the mean over 100 iterations of 10-fold cross-validation. Blue and green asterisks (*) represent entries where the MSE of lsGC at c = 1 or c = 2, respectively, was significantly lower than that of the lowest cGC MSE (p < 0.001 using a one-tailed paired t-test). Performance of all methods was highly sensitive to choice of parameters. At ρ ≥ 3, lsGC at c = 1 outperforms cGC with optimal parameters (ρ = 2). LsGC at c = 2, however, performs progressively worse at ρ ≥ 3. This figure shows that if the model parameters are chosen well, lsGC has the potential to yield superior performance to cGC. Further research into model selection criteria for lsGC is necessary.

5. NEW AND BREAKTHROUGH WORK

Here, large-scale Granger causality was used to generate functional brain networks that served as the basis for predicting clinically meaningful properties of human subjects, including HIV status and NP scores using a machine learning system trained with lsGC-derived network properties; these measures may capture additional levels of complexity not available with the raw connectivity matrices, which serve as the basis for traditional multi-voxel pattern analysis (MVPA) approaches. The high AUC and accuracy values obtained with this approach suggest that it is a viable method of extracting meaningful information from high-dimensional brain networks. Additionally, the application of functional brain network measures into a machine learning system to predict a real-valued variable in a regression task, i.e. NP score prediction, is novel. This contribution is significant, as it represents an extension of the scope of machine learning in rs-fMRI; such a regression system has the ability to detect nuanced patterns of neurologic damage in a continuum, which may more accurately reflect the underlying biological reality than binary disease vs. healthy classification.

6. CONCLUSION

A comparative analysis of cGC and lsGC for predicting HIV status and NP scores of human subjects on the basis of resting-state brain connectivity network properties is presented here. An iterative cross-validation procedure showed that lsGC (peak accuracy 0.76; peak AUC 0.83) significantly outperformed cGC (peak accuracy 0.59; peak AUC 0.61) in the HIV status classification task at nearly all parameter settings tested. In the NP score regression task, the performance of lsGC and cGC was highly dependent on parameter settings, though the peak performance of lsGC (MSE 0.75) was significantly higher than that of cGC (MSE 0.84). These results show that lsGC has the potential to augment resting-state functional connectivity analyses conventionally performed using cGC, though optimal parameter settings for lsGC, particularly for the prediction of NP scores, remains a topic for future research.

Figure 1.

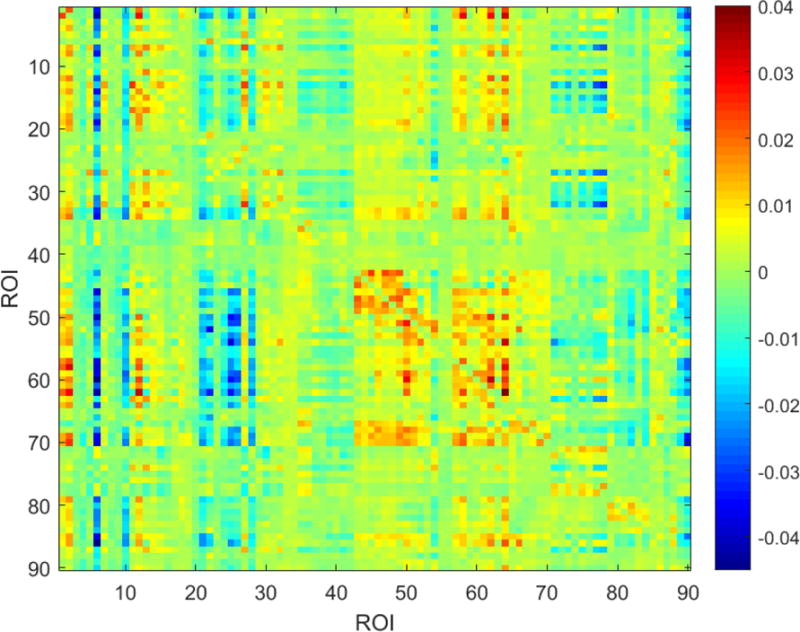
An example affinity matrix derived from large-scale Granger causality (lsGC). Each index in this matrix represents the directional strength of interaction between the corresponding ROIs, as inferred by lsGC.