SNR-Weighted Regularization of ADC Estimates from Double-Echo in Steady-State (DESS)

Abstract

Purpose

To improve the homogeneity and consistency of Apparent Diffusion Coefficient (ADC) estimates in cartilage from the Double-Echo in Steady-State (DESS) sequence by applying SNR-weighted regularization during post-processing.

Materials and Methods

An estimation method that linearizes ADC estimates from DESS is used in conjunction with a smoothness constraint to suppress noise-induced variation in ADC estimates. Simulations, phantom scans, and in vivo scans are used to demonstrate how the method reduces ADC variability. Conventional Diffusion Weighted Echo Planar Imaging (DW EPI) maps are acquired for comparison of mean and standard deviation of the ADC estimate.

Results

Simulations and phantom scans demonstrated that the SNR-weighted regularization can produce homogenous ADC maps at varying levels of SNR, while non-regularized maps only estimate ADC accurately at high SNR levels. The in vivo maps showed that the SNR-weighted regularization produced ADC maps with similar heterogeneity to maps produced with standard DW EPI, but without the distortion of such reference scans.

Conclusion

A linear approximation of a simplified model of the relationship between DESS signals allows for fast SNR-weighted regularization of ADC maps that reduces estimation error in relatively short T₂ tissue such as cartilage.

Introduction

Osteoarthritis (OA) is estimated to affect 27 million US adults [1] and to lead to annual medical care expenditures of $185 billion [2]. Furthermore, the number of US adults projected to have physician-diagnosed arthritis is expected to rise to nearly 67 million people, or 25% of the adult population by 2030 [3]. A limiting factor in the development of treatments for OA has been the inability to detect the disease until gross morphological changes have occurred, when its progress has become largely irreversible. Recently, quantitative MRI methods have been developed to help overcome this problem. These include measuring T_1ρ and T₂ for changes in the cartilage extracellular matrix and collagen network organization [4, 5]. Sodium concentration has also been measured for cartilage glycosaminoglycan content [6].

Another parameter relevant to osteoarthritis is the apparent diffusion coefficient (ADC). This has been shown to correlate with proteoglycan concentration in articular cartilage [7, 8]. The ability to use ADC measurements for early detection of osteoarthritis could potentially allow for more complete longitudinal studying of the disease progression. The ADC of cartilage has been measured in high-field MRI experiments as 1.6·10⁻³ mm²/s in vivo at field strengths of 1.5T-3T [9, 10, 11], with slightly lower values in vitro [12, 13]. It has also been shown to be almost twice as large at the articular surface compared to the bone-cartilage interface [14, 15]. Furthermore, elevated ADC has been measured in OA-affected cartilage by about 25% [16]. ADC is most commonly measured using 2D diffusion-weighted echo-planar imaging (DW EPI). However, DW EPI suffers from distortion due to off-resonance, limited spatial resolution, and SNR loss from the short T₂ of cartilage.

The Double-Echo in Steady-State (DESS) sequence [17, 18, 19] is an unbalanced 3D steady-state sequence that can be used to estimate the T₂ relaxation time [10, 20, 21, 22, 23] as well as the ADC without distortion [10, 11] in short scan times and with high SNR efficiency. The DESS sequence generates two echoes S₁ and S₂ in each repetition time TR, acquired before and after an unbalanced gradient. We will refer to this as a crusher gradient as it rephases magnetization, but in previous literature it has been referred to as a spoiler gradient [10, 11]. The relative echo amplitudes depend on the relaxation times T₁ and T₂ and the ADC of the tissue, as well as the imaging parameters used. This dependency can be quantified by using the analytic models of Wu and Buxton [24] or Freed [25], or by using Extended Phase Graph modeling [26, 27, 28], which enables numerical simulation of the signals. The second echo S₂ will have more diffusion contrast, and the sensitivity to diffusion will depend on the timing of the scan sequence, the flip angles used, and especially on the size of the crusher gradient. A larger crusher gradient will result in more diffusion-related signal loss in the second echo, similar to a conventional DWI scan.

By running the DESS sequence twice, with varying crusher gradient areas, four echoes with differing diffusion sensitivities can thus be acquired. We will label the first and second echoes, respectively, with S_1H and S_2H for the scan with high diffusion sensitivity and S_1L and S_2L for the scan with low diffusion sensitivity. By comparing the ratios of these measured signals to those predicted by theoretical models, estimates of the relaxation times and the ADC can be obtained. Various approaches of this kind have been developed, using different signal ratios depending on which parameters are to be estimated. In one approach [10], the ratios S_2H/S_1H, S_2L/S_1L, and S_1H/S_1L were used to provide simultaneous estimates of T₁, T₂, and ADC. Another approach [11] estimates ADC from the single ratio (S_2HS_1L)/(S_2LS_1H), which is largely independent of the relaxation times T₁ and T₂.

The DESS sequence has less sensitivity to ADC than to T₂, resulting in errors in ADC estimates when SNR is low. The second echo of the strongly-diffusion-weighted scan, S_2H, having experienced decay from both relaxation and diffusion, has the smallest amplitude of the four echoes and is therefore most sensitive to noise. Because most of the ADC sensitivity comes from the low-signal S_2H, ADC maps are often noisy. While prior work has investigated scan parameters for improved diffusion sensitivity [29], the sequence would still benefit from a postprocessing approach that suppresses noise-induced fluctuation in estimated ADC. Here, we investigate applying regularized fitting of the signals, with a penalty in ADC roughness. The method applies stronger regularization to regions with low SNR, by using a recent analytical expression for a combination of DESS signals [30]. We test the method in simulations, phantoms and in vivo scans.

Methods

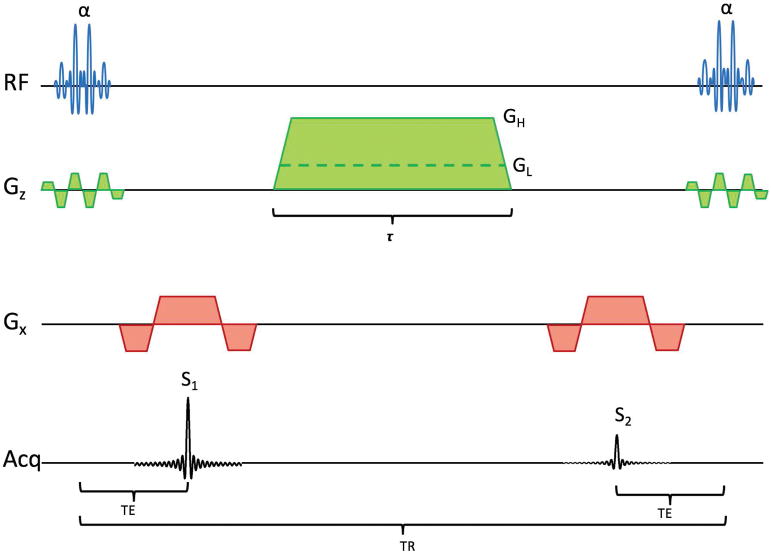
As described above, DESS produces signals S₁ before and S₂ after a crusher gradient. For estimating ADC, DESS is run twice, with a large and small crusher gradient, as shown in Fig. 1. This gives high (H) and low (L) diffusion sensitivity, producing four signals S_1H, S_2H, S_1L, and S_2L. It has been shown that the ratio

Figure 1.

Pulse diagram of the DESS sequence, showing both a large crusher giving high diffusion weighting (G_H) and a small crusher with low diffusion weighting (G_L). The RF pulses are spectrally selective, exciting only water.

$$\mathrm{f}(\text{ADC})=({\mathrm{S}}_{2\mathrm{H}}{\mathrm{S}}_{1\mathrm{L}})/({\mathrm{S}}_{1\mathrm{H}}{\mathrm{S}}_{2\mathrm{L}})$$ [1]

is sensitive to ADC while being insensitive to T₁ and T₂ under a wide range of scanning conditions [11].

A closed-form expression of the ratio S₂/S₁ can be obtained [30]:

$$\frac{S_2}{S_1}=B_2+B_4,$$ [2]

where

$$B_2=e^{-\frac{2(TR-TE)}{T2}\left(TR-\frac{\tau }{3}\right)\mathrm{\Delta }{k}^{2}D}{sin}^2\left(\frac{\alpha }{2}\right)\left(\frac{1+e^{-\frac{TR}{T1}-TR\mathrm{\Delta }{k}^{2}D}}{1-cos\alpha e^{-\frac{TR}{T1}-TR\mathrm{\Delta }{k}^{2}D}}\right)$$ [3]

and Δk =γGτ. We refer to [30] for an expression for B₄. For T₂ estimation, it is our experience that the B₂ term is sufficient. However, for the ADC estimates in this work, we include the B₄ term as well.

Eq. 2 allows a simple regularization that penalizes large differences in ADC between adjacent pixels and produces less noisy ADC maps:

$$\underset{\mathit{ADC}}{min}{\Vert \frac{S_{2H}{S}_{1L}}{S_{1H}{S}_{2L}}-f(\mathit{ADC})\Vert }_2^2+\lambda {\Vert D_{xy}(\mathit{ADC})\Vert }_2^2$$ [4]

where D_xy is a difference operator between neighboring pixels.

The expression in ref. [30] enables easy linearization of f with respect to a small update ΔADC using a first-order Taylor approximation at any given ADC value. This turns Eq. 4 into a quadratic equation for ΔADC that is easily solved for a given starting point, ADC₀, as follows:

$$\underset{\mathrm{\Delta }\mathit{ADC}}{min}{\Vert \frac{S_{2H}{S}_{1L}}{S_{1H}{S}_{2L}}-(f({\mathit{ADC}}_0)+f^{\prime }({\mathit{ADC}}_0)·\mathrm{\Delta }\mathit{ADC})\Vert }_2^2+\lambda {\Vert D_{xy}({\mathit{ADC}}_0+\mathrm{\Delta }\mathit{ADC})\Vert }_2^2$$ [5]

The regularization term can be SNR-weighted by multiplying the difference operator with the term W = (1 − S_1L/S_1L-max) at each pixel. For this calculation of W, the S_1L image is first lowpass filtered, in order to smooth out local signal variations. The S_1L-max value is then chosen as the maximum S_1L value after such filtering, and can be the maximum over a slice, over a 3D data set with multiple slices, or over a range of scans with multiple 3D data sets. This leads to the following:

$$\underset{\mathrm{\Delta }\mathit{ADC}}{min}{\Vert \frac{S_{2H}{S}_{1L}}{S_{1H}{S}_{2L}}-(f({\mathit{ADC}}_0)+f^{\prime }({\mathit{ADC}}_0)·\mathrm{\Delta }\mathit{ADC})\Vert }_2^2+\lambda {\Vert W·D_{xy}({\mathit{ADC}}_0+\mathrm{\Delta }\mathit{ADC})\Vert }_2^2$$ [6]

A region with high SNR will thus not be heavily regularized (having a small effective λ), while a region with lower SNR will experience more regularization. In an approach similar to the one in ref. [31], the minimizer of Eq. 4 can be obtained by repeatedly solving Eq. 6 and updating the ADC₀ as ADC₀ = ADC₀+ΔADC at each iteration. The iteration is terminated when the ΔADC becomes negligibly small, and thus the method converges to a local minimum around the initial solution. In this study, the initial parameters were set as T₁ = 1.2 s, T₂ = 40 ms, and ADC₀ = 1.6 μm²/ms, with no updates being made to T₁ and T₂ during the regularization process.

Simulations

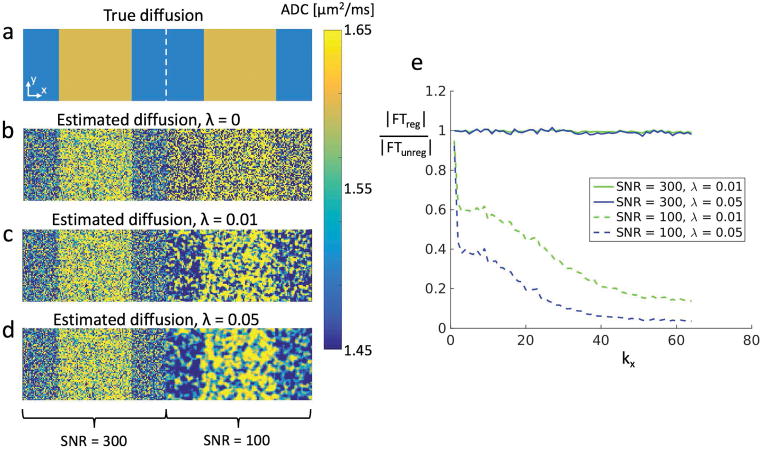
To simulate how the regularization affects the ADC estimation, Monte Carlo simulations were performed in Matlab (The MathWorks, Inc., Natick, MA). DESS signals were simulated over 256×64 pixels using Extended Phase Graphs (EPG) [27] with 6 dephasing states, with complex Gaussian noise added to the simulated steady-state signal measurements. The large number of dephasing states results in very accurate theoretical signal values. The scan parameters were TR=18ms, TE=4ms, flip angle=25°, large gradient moment=157mT/m·ms (corresponding to a dephasing of spins by 20 rotations per voxel), small gradient moment=0.001mT/m·ms (giving minimal spin dephasing), and gradient duration=3.4ms. The tissue parameters were T₁ = 1.2s, T₂ = 40ms, and ADC alternated between 1.6μm²/ms and 1.5μm²/ms, similar to reported values in cartilage [9, 32], as shown in Fig. 2a. The left half of the image was given three times the signal strength as the right half. This led to an SNR of 100 in the S_1L signal in the right half and 300 in the left half. Eq. 6 was then applied with λ=0, λ=0.01, and λ=0.05.

Figure 2.

(a) A 256×64 matrix with T₁=1.2s, T₂=40ms, ADC₁ = 1.5μm²/ms and ADC₂ = 1.6μm²/ms. The S_1L signal in the left half (128 pixels) has SNR=300 while in the right half this signal has SNR=100. (b) Without regularization, the underlying pattern is visible in the high-SNR half but very difficult to see in the low-SNR half (σ = 0.34/0.34 μm²/ms for ADC₁/ADC₂ giving an average of 0.34 μm²/ms). (c) Using Eq. 6 with λ=0.01, the structure of the ADC distribution starts becoming visible in the low-SNR half (σ = 0.15/0.14 μm²/ms for ADC₁/ADC₂ giving an average of 0.14 μm²/ms). Since the method reduces regularization in areas with high SNR, the left half of the image is almost unchanged. (d) Using Eq. 6 with λ=0.05 reveals the ADC distribution even more clearly, at the cost of smoothing of the sharp edges in the distribution (σ = 0.09/0.09 μm²/ms for ADC₁/ADC₂ giving an average of 0.09 μm²/ms). For b-d, the standard deviation of the high-SNR half was essentially the same (σ = 0.11/0.11 μm²/ms for ADC₁/ADC₂ giving an average of 0.11 μm²/ms). (e) The ratio of the magnitudes of the Fourier transforms with and without regularization (averaged over k_y). Higher spatial frequency components are suppressed in the low-SNR region but remain in the high-SNR region. This is more pronounced with a larger regularization factor.

Phantom scans

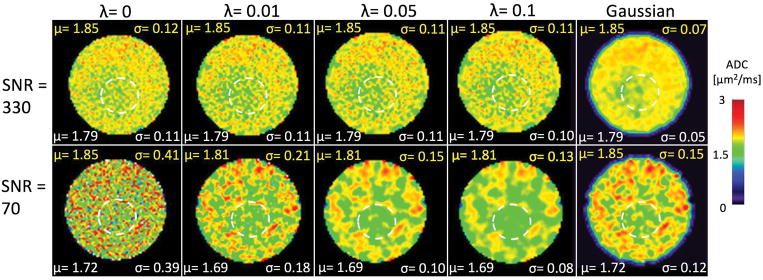
Next, the method was tested in phantom scans, again running two DESS scans with differing diffusion weighting, first with a wrist coil to provide high SNR, then with a single-channel knee coil for lower SNR. ADC was estimated with λ=0, 0.01, 0.05, and 0.1 for both coils. The scan parameters were TR=18ms, TE=5ms, flip angle=25°, large gradient moment=157mT/m·ms, small gradient moment=15.6 mT/m·ms (giving spin dephasing of 2 rotations per voxel), gradient duration=3.4ms, FOV=12cm×12cm, imaging matrix=256×256, slice thickness=3mm, 32 slices, readout bandwidth=±31.25kHz, with a resulting scan time of 2×2:28 min.

In vivo scans

For in vivo experiments, the participant signed an informed consent form approved by the Institutional Review Board.

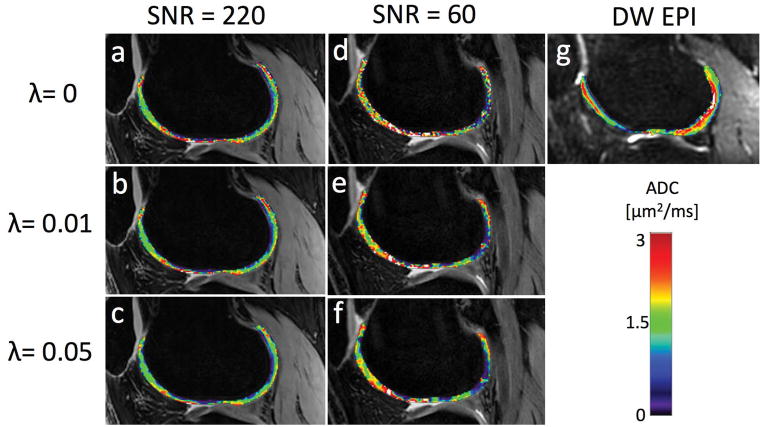
First, a pair of sagittal DESS knee scans in a healthy volunteer were acquired and processed with λ=0, 0.01, and 0.05. The scan parameters were TR=22ms, TE=5ms, flip angle=25°, large gradient moment=157mT/m·ms, small gradient moment=15.6mT/m·ms, gradient duration=3.4ms, FOV=16cm×16cm, imaging matrix=256×256, slice thickness=3mm, 40 slices, readout bandwidth=±31.25kHz, a water-only pulse, without parallel imaging, with a resulting scan time of 2×3:45 min. To obtain data at different SNR levels, the scan was done twice, once with a single-channel coil and once with a 16-channel coil that wrapped around the knee (Neocoil, Pewaukee, WI).

Then, to further examine how the regularization affects in vivo data at different SNR levels, noise was added to the higher-SNR in vivo scan (acquired with the 16-channel coil) to decrease its SNR. This was done multiple times to obtain multiple SNR levels between those acquired with the two coils. ADC maps in the cartilage were estimated at each SNR level and the standard deviation of each map was computed as a measure of the estimate variability.

For all scans, a DW EPI scan was collected for reference, with scan parameters TR=2.5s, TE=56ms, FOV=16cm×8cm, imaging matrix 120×60, 40 3mm slices, readout bandwidth=±125kHz and 8 averages. The scan used a reduced FOV in the phase-encode direction to reduce distortion. For the phantom scans, the reference scans had b-values of 0, 200, and 400 s/mm², while for the in vivo scans they had b-values of 0, 50, 100, 150, 200, and 400 s/mm². To maintain consistency in data analysis, the same S_1L-max value (from the higher-SNR scan) was used in Eq. 6 for both phantom data sets, and similarly the globally highest S_1L-max was used for all the in vivo data analysis. All scans were performed on a 3.0T GE Discovery MR750 scanner.

Results

Simulations

The simulation results are shown in Fig. 2. Fig. 2a shows the true ADC distribution, while Figs. 2b–d show the estimated ADC with λ=0 (no regularization), λ=0.01, and λ=0.05. The underlying ADC distribution is difficult to make out at lower SNR (right side) of Fig. 2b. In Fig. 2c, the true ADC pattern is starting to emerge for the low-SNR half. In Fig. 2d, the pattern is even clearer, at the cost of a smoothing of the edges in the underlying distribution. The regularization has very little effect on the higher-SNR half, since the method is designed to leave regions with the highest SNR essentially unaffected. This is further illustrated in Fig. 2e, which shows the ratio of the magnitude of the Fourier transform of the regularized map to the magnitude of the Fourier transform of the unregularized map. This is done for both SNR values and both regularization values, and averaged over k_y, in order to show the effect of the regularization on the frequency components of each region. The regularization process suppresses high spatial frequency components in the low-SNR region, but not in the high-SNR region. The standard deviation of the unregularized estimate in the left region (with SNR = 300) and in the right region (with SNR = 100) is 0.11 μm²/ms and 0.34 μm²/ms, respectively. This was found by computing the standard deviation for the areas with ADC = 1.5 μm²/ms and ADC = 1.6 μm²/ms separately and averaging the results. For the regularized estimate, the corresponding values for the left/right halves are 0.11/0.14 μm²/ms for λ=0.01 and 0.11/0.09 μm²/ms for λ=0.05.

Phantom scans

The phantom scan results are shown in Fig. 3. The measured SNR from the wrist and knee coil in the S_1L signal were 330 and 70, respectively. The high-SNR scan showed similar spatial patterns with and without regularization. The ADC map has a pattern of higher ADC near the edges. This is mostly due to B₁ inhomogeneity in the phantom, but is nonetheless useful for evaluating the ability of the ADC mapping technique to discern patterns unrelated to noise. For the case with low SNR, no particular pattern was discernible without regularization. When regularization was applied, the outer regions of the phantom showed higher ADC values than the center, and this became more prominent with higher regularization. The ADC estimates had average estimates of 1.81–1.85 μm²/ms, compared to the EPI DWI reference value of 1.96 μm²/ms. The reduction in ADC standard deviation in a uniform region of the low-SNR phantom scan is similar as for the low-SNR simulations, dropping by 54% going from λ=0 to λ=0.01 and a further 44% going from λ=0.01 to λ=0.05 (corresponding numbers for the simulations are 59% and 36%). The figure also shows a map obtained with simple Gaussian filtering. When the Gaussian approach reduces the map standard deviation comparably to the regularized approach, the high-SNR map is also clearly affected by the filtering and shows less detail than the regularized map.

Figure 3.

ADC maps of a phantom from scans with high and low SNR, with (λ = 0.01, 0.05, 0.1) and without (λ = 0) regularization, and with regular Gaussian filtering with a filter standard deviation of σ_f = 1. The regularized maps with high SNR retain most of the pattern that is seen without regularization, but this is not the case for the Gaussian filtered map. The mean μ and standard deviation σ for the different smoothing approaches and SNR values are shown in each figure panel, with units of μm²/ms. The yellow labels refer to values across the whole phantom, while the white labels refer to values measured across a relatively uniform ROI within the phantom (dashed white circle).

In vivo scans

The in vivo scans are shown in Fig. 4. The SNR levels for S_1H/S_2H/S_1L/S_2L in the femoral articular cartilage were measured as 200/45/220/75 with the 16-channel coil and as 55/15/60/25 with the single-channel coil. Similarly to the phantom, the higher-SNR maps are minimally affected by the regularization. The lower-SNR maps, however, are much smoother after regularization. The regularized maps indicate higher values in superficial cartilage than in deep cartilage, in agreement with ref. [33], which is difficult to discern from the non-smoothed maps (λ=0).

Figure 4.

(a) An unregularized DESS ADC map from a sagittal knee scan with high SNR. The mean ADC value was 1.40 μm²/ms with a 0.79 μm²/ms standard deviation. (b) The DESS ADC map from the same data but with a regularization factor of λ = 0.01. The map is not very affected by the regularization, with a mean of 1.34 μm²/ms and standard deviation of 0.73 μm²/ms. (c) The ADC map produced with λ = 0.05, with mean value of 1.29 μm²/ms and standard deviation of 0.66 μm²/ms. (d)–(f) The same maps but acquired with lower SNR. The mean/standard deviations are 1.67/1.05 μm²/ms, 1.56/0.90 μm²/ms, and 1.47/0.82 μm²/ms, respectively. Visually, the map is smoothed more than in the high-SNR case, especially between λ = 0 and λ = 0.01. (g) A reference DW EPI map, with mean 1.69 μm²/ms and standard deviation 0.77 μm²/ms.

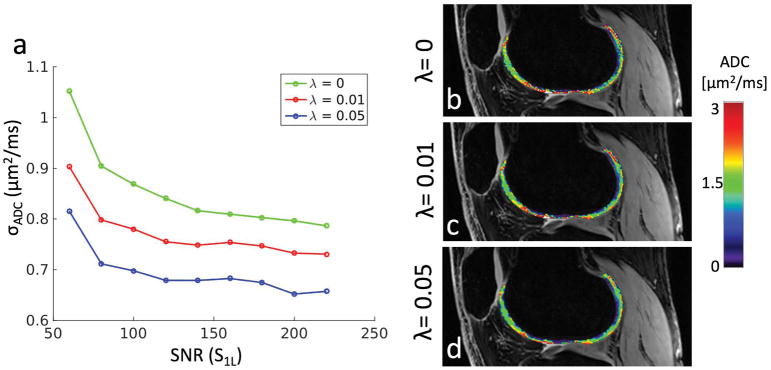
The in vivo results with synthesized SNR levels are shown in Fig. 5. The results show that the regularization always lowers the variability of the resulting ADC map. Moreover, the benefits of regularization are greatest at low SNR levels, in agreement with the acquired scan data. The data shows that increasing SNR beyond a certain level will yield progressively less improvement in ADC variability, but the regularization process continues to considerably improve the variability even at high SNR levels.

Figure 5.

(a) The standard deviation of the estimated ADC in cartilage as a function of the SNR of the S_1L signal. The leftmost and rightmost points are the actual scan results shown in Fig. 4, while the points in between are simulated by adding noise to the higher-SNR scan. (b)–(d) A sample set of points from the curves in panel (a), corresponding to the center points (SNR=140). These can be compared to panels (a)–(f) in Fig. 4.

Discussion

The DESS sequence provides the ability to simultaneously obtain both anatomical images and quantitative parameter maps of T₂ and ADC. This resolves potential issues with co-registering the anatomical reference to the parameter map. In this study, we have introduced a method to smooth the otherwise noisy ADC estimates with DESS, by introducing a roughness penalty in the estimation procedure. The regularization process is designed to treat variations in a region with high SNR as correct, while variations in low-SNR regions are more likely due to noise and are therefore smoothed. The difference in performance depending on SNR can be seen in Fig. 5a, where an aggressively regularized (λ = 0.05) in vivo ADC map with SNR = 60 has approximately the same variability as an unregularized map with SNR = 220.

An ADC map with noise suppression makes it easier to separate cartilage pathology from normal cartilage tissue, and to capture focal tissue changes in the early stages of OA. While a standard DW EPI acquisition will often produce smooth maps if its diffusion sensitivity (b-value) is high enough, the typical distortion and low resolution of such scans can cause problems, including difficulty with segmentation and distinguishing the interface between bone and cartilage.

Although Eq. 6 describes an iterative process, for the data sets in this study the iteration would converge after only one iteration. This implies that the first order Taylor approximation closely resembles the true signal ratio. Each iteration took about 200ms, but this will depend on the number of pixels to be fit. When the time necessary for reading, storing, and writing data is included, the whole process per data set took about 45 seconds.

The method presented applies SNR-weighted regularization, as demonstrated in Figs. 2–5. This is achieved by multiplying the ADC difference in the regularization with an SNR-weighting factor W at each pixel. Since W ≈ 1 for regions with low signal (low S_1L) and W ≈ 0 for regions with high S_1L, the ADC of each pixel is regularized inversely proportional to the SNR. This may not always be desired, as sometimes one might want to do some regularization even of areas with maximum S_1L. This can be easily achieved by normalizing by something larger than S_1L-max in the definition of W. Also, an alternative approach could be to use a sparsity constraint (i.e., make the second term in Eqs. 4–6 of the form ||D_xy(ADC||₁) instead of a smoothness constraint in the regularization. Some previous studies have demonstrated that such a constraint would give better conditioning of the problem, as well as better edge preservation than the smoothness prior [34, 35, 36].

Alternative methods of producing smooth ADC maps from DESS measurements might potentially include low-pass filtering or even doing SNR-based regularization on the source images before computing the ADC maps. However, the presented method has the benefit of regularizing the resolution of the desired maps themselves, which is not always straightforwardly related to the resolution of the source images in sequences such as DESS. When the desired objective is different from an ADC map, such as a T₂ map or one of the source images themselves, a similar methodology could be used to obtain SNR-weighted regularization.

In Figs. 3–4, some systemic differences between the ADC maps produced with high and low SNR can be observed, in addition to noise-related differences. These could be due to a number of factors, one being the fact that to generate the different SNR levels, the coils were switched, inevitably leading to slight misalignment between the scans, even though an effort was made to minimize this. Additionally, the diffusion-weighted S_2H signal is vulnerable to ghosting artifacts caused by blood vessel pulsation and patient motion, which can differ between scans. In Fig. 4, some differences are also apparent between the DESS ADC maps and the maps acquired with DW EPI. Sensitivity analysis demonstrates that this is unlikely to be due to erroneous assumptions in T₁, T₂, or flip angle (Supporting Information Figure S1). Other possible explanations include inaccuracies in the DW EPI maps, which can depend on the range of b-values used. In this study, the b-values were chosen to give similar diffusion sensitivity to the DESS scans. Additionally, the two sequences can experience different artifacts along different axes, such as distortion for DW EPI along the S/I axis and motion sensitivity for DESS along the A/P axis in this study.

This study has the limitation of only investigating subjects with healthy cartilage. Future studies could investigate the benefits of the presented method for both healthy controls as well as OA patients, and examining the repeatability of such results. Furthermore, such patient studies could compare the ADC differences in controls and patients with differences in T₂, to identify the similarities and differences in their patterns. Also, in this study the value of the regularization factor λ was chosen based on experience. Future work could investigate developing an analytic expression of the optimal λ given the imaging SNR, the desired map variability, and the scan parameters. Such an expression would remove the need to choose λ and instead compute it automatically based on measured SNR. However, such a derivation was beyond the scope of this work.

Conclusion

In conclusion, a simplified model of the relationship between DESS signals allows for fast, linearized, SNR-weighted regularization of ADC maps that reduces estimate variability in cartilage.

Supplementary Material

Supp figS1. Supporting Information Figure S1.

Simulations and scans to estimate the sensitivity of the ADC mapping method to errors in assumed T₁, T₂, and B₁₊. (a) Estimated ADC, based on the scan parameters of Fig. 4, and assuming T₁ = 1.2 s, T₂ = 40 ms, and flip angle 25°. The actual values of T₁ and flip angle are made to deviate by ±20%, while the assumed T₂ is accurate. The true ADC is set to 1.6 μm²/ms. The resulting ADC estimates deviate from the true value from about −25% to about +37.5%, with most values within a narrower range. (b) A similar simulation, where the assumed T₁ of 1.2 s is accurate but T₂ and flip angle are made to deviate by ±20%. The results are similar, but with less sensitivity to T₂. For both figure panels, the white circles represent the case where the assumed values are correct. (c) An in vivo ADC map, acquired with the same scan parameters as in Fig. 4, produced without a B₁⁺ map. (d) ADC map produced from the same data and with a B₁⁺ map. The two maps are very similar. (e) The B₁⁺ map used for panel d, acquired using a product Bloch-Siegert acquisition with TR = 12ms, TE = 6.3 ms, a 64×64 imaging matrix, 20 slices, each 6 mm thick, and a 10° flip angle. All figure panels use the color bar on the right, with panels a-d using the left (ADC) labels and panel e using the right (% of prescribed flip angle) labels.