Mapping Electrical Properties Heterogeneity of Tumor Using Boundary Informed Electrical Properties Tomography (BIEPT) at 7 Tesla

Abstract

Purposes

To develop and evaluate a Boundary Informed Electrical Properties Tomography (BIEPT) technique for high-resolution imaging of tumor electrical properties (EPs) heterogeneity.

Methods

Tumor EP distributions were inferred from a reference area external to the tumor, as well as internal EP spatial variations derived from a plurality of relative transmit B₁ measurements at 7 Tesla. Edge sparsity constraint was enforced to enhance numerical stability. Phantom experiments were performed to determine the imaging accuracy and sensitivity for structures of various EP values, as well as geometrical sizes down to 1.5 mm. Numerical simulation of a realistic rodent model was employed to quantify the algorithm performance in the presence of noise. Eleven athymic rats with human breast cancer xenograft were imaged in vivo, and representative pathological samples were acquired for comparison.

Results

Reconstructed EPs of the phantoms correspond well to the ground truth acquired from dielectric probe measurements, with the smallest structure reliably detectable being 3 mm. EPs heterogeneity inside a tumor is successfully retrieved in both simulated and experimental cases. In vivo tumor imaging results demonstrate similar local features and spatial patterns to anatomical MRI and pathological slides. The imaged conductivity of necrotic tissue is higher than that of viable tissues, consistent with expectation.

Conclusion

BIEPT enables robust detection of tumor EPs heterogeneity with high accuracy and sensitivity to small structures. The retrieved quantitative EPs reflect tumor pathological features, e.g. necrosis. These results provide strong rationale to further expand studies towards pathological conditions where EPs may yield valuable, non-invasive biomarkers.

INTRODUCTION

Electrical properties (EPs), comprised of electrical conductivity $\sigma$ and permittivity ${\epsilon }_r$, are intrinsic properties quantifying a tissue’s ability to conduct, dissipate, and deposit electrical energy. EPs of biological tissues are frequency-dependent, reflecting interactions of the applied electrical field with different constituents from tissue level to molecular level. EPs in the lower frequency band (<1 MHz) reflect tissue macroscopic structures, such as extracellular volume, cellularity, and cellular membrane integrity, while those in the microwave band (~1-100 GHz) correspond to the microscopic level such as overall ion concentration, water and macromolecule content, etc. In between is the radiofrequency (RF) band, in which EPs are influenced by mixed effects of the above factors (1).

Previous studies based on ex vivo dielectric probe measurements have reported deviation of tumor EPs from those of normal tissues across the electromagnetic spectrum, especially in the breast (2,3), setting the ground for EPs as potential biomarkers in cancer diagnosis and characterization. Several non-invasive imaging modalities have been proposed to retrieve tissue EPs across the spectrum, such as electrical impedance tomography (EIT) (4), magnetic resonance electrical impedance tomography (MREIT) (5), magneto-acoustic tomography with magnetic induction (MAT-MI) (6), and microwave imaging (7). Nevertheless, it remains a challenge to retrieve quantitative EP maps at high spatial resolution without injection of electric current, due to limited signal to noise ratio (SNR) of electromagnetic measurement in biological systems, as well as the ill-posed nature of image reconstruction problems derived from Maxwell’s Equations.

Alternatively, EPs can be derived by computational electrodynamics involving B₁ measurements obtained from MRI in high spatial resolution. This technique, dubbed magnetic resonance-based electrical properties tomography (MREPT or EPT), exploits the spatial variation of B₁ maps while alleviating the need for directly measuring E field (8–11). Compared with previous imaging modalities, MREPT substantially reduces the severity of ill-posedness and therefore represents a promising modality for non-invasive EPs imaging. The feasibility of MREPT was initially demonstrated using birdcage RF coils (12–14) and was more recently further developed using multi-channel RF coil arrays (15–21). Compared to a quadrature coil, a multi-channel coils array addresses the “transceiver phase assumption” that fails at high magnetic field (22). The plurality of unique B₁ measurements from the latter also provides abundant information that contributes to improvements in characterization of tissue transition zones.

Conductivity imaging of cancer based on MREPT has been attempted in the human brain, breast, and cervix (23–25), showing results consistent with the literature based on probe measurements. However, the reconstruction methods used in these studies are based on the Helmholtz equation that describes electromagnetic wave propagation in a homogeneous medium. Consequently, tumor heterogeneity cannot be appropriately identified; Instead it contributes to reconstruction artifacts in the resulting EP values and distributions, which can potentially jeopardize quantitative measurements (26). Moreover, permittivity values are intractable from these studies due to the assumptions made about B₁ in the reconstruction formalism.

A general approach to accurately image EPs heterogeneity at high spatial resolution, once developed, will provide additional information about the underlying tumor pathology. Potential correlations between this new contrast and tumor hallmarks can be exploited for improved sensitivity and specificity in cancer diagnosis, grading, and monitoring of treatment response. A preliminary framework has been reported by our group for in vivo imaging of rat cancer xenografts, which goes beyond the Helmholtz equation and takes into consideration the spatial variation of EPs in the reconstruction model (27). However, this approach requires collecting data during two consecutive MRI scanning sessions with physically flipped experimental setup executed with high precision, which is prone to operational error and consumes precious scan time. Its reconstruction was limited to a small region of interest (ROI) and not based on any calibration mechanism for quantitative EP calculation, hindering the ultimate resolution, SNR, and data interpretability across the 3D volume.

In this study, we introduce a boundary informed EPT (BIEPT) approach to quantitatively map tumor EPs with high spatial resolution, using a multi-transmit RF coil array at 7 Tesla. BIEPT demonstrates that EP distributions inside an ROI can be reliably retrieved using an external EP reference area and B₁ measurements from only one experimental setup. As such, we reduce the total scan time by a factor of two, and minimize opportunities for operational error which compromises imaging resolution and accuracy. The proposed technology was systematically validated using numerical simulations and phantom experiments. EP maps, as well as anatomical T1-weighted (T1w) and T2-weighted (T2w) images, were acquired in vivo from human breast cancer xenografts on eleven athymic nude rats. Ex vivo validation was performed using a dielectric probe. Representative whole-mount histopathological slides of tumor samples were obtained for comparison.

THEORY

In this section, starting from Maxwell’s Equations, we lay out the essential steps that eventually lead to a pixel-wise inverse problem linking MRI-measurable multi-channel relative B₁ to the spatial Wirtinger derivative ( $\frac{\partial }{\partial x}+i\frac{\partial }{\partial y}$) of EPs defined on a transverse plane. Then, we propose the central optimization problem that retrieves tumor internal EP distributions from their Wirtinger derivatives, with prior information of boundary EPs and use of an L₁-norm edge sparsity constraint.

Consider time-harmonic electromagnetic field at angular frequency $\omega$ in Cartesian coordinate system. By combining Ampère’s law and Faraday’s law to eliminate the electric field, we have

$${\mathit{\nabla }}^2\overrightarrow{B}=-{\omega }^2{\mu }_0{\epsilon }_c\overrightarrow{B}-\mathit{\nabla }{\epsilon }_c\times \frac{\mathit{\nabla }\times \overrightarrow{B}}{{\epsilon }_c}$$ [1]

assuming that magnetic susceptibility $\mu \approx {\mu }_0$ in biological tissues. The complex electrical properties ${\epsilon }_c$ is defined as ${\epsilon }_c≔{\epsilon }_r{\epsilon }_0-i\sigma /\omega$, where ${\epsilon }_r$ denotes relative permittivity to vacuum permittivity ${\epsilon }_0$, and $\sigma$ denotes conductivity. Equation 1 is a vector formula about $\overrightarrow{B}=\left(B_x,B_y,B_z\right)$ in phasor terms, which contains the following three equations corresponding to $x, y, z$ directions

$$\begin{gathered} {\mathit{\nabla }}^2{B}_x=-{\omega }^2{\mu }_0{\epsilon }_c{B}_x-\left(\frac{\partial B_y}{\partial x}-\frac{\partial B_x}{\partial y}\right)\frac{\partial ln{\epsilon }_c}{\partial y}+\left(\frac{\partial B_x}{\partial z}-\frac{\partial B_z}{\partial x}\right)\frac{\partial ln{\epsilon }_c}{\partial z} \\ {\mathit{\nabla }}^2{B}_y=-{\omega }^2{\mu }_0{\epsilon }_c{B}_y+\left(\frac{\partial B_y}{\partial x}-\frac{\partial B_x}{\partial y}\right)\frac{\partial ln{\epsilon }_c}{\partial x}-\left(\frac{\partial B_z}{\partial y}-\frac{\partial B_y}{\partial z}\right)\frac{\partial ln{\epsilon }_c}{\partial z} \\ {\mathit{\nabla }}^2{B}_z=-{\omega }^2{\mu }_0{\epsilon }_c{B}_z-\left(\frac{\partial B_x}{\partial z}-\frac{\partial B_z}{\partial x}\right)\frac{\partial ln{\epsilon }_c}{\partial x}+\left(\frac{\partial B_z}{\partial y}-\frac{\partial B_y}{\partial z}\right)\frac{\partial ln{\epsilon }_c}{\partial y} \end{gathered}$$ [2]

$\overrightarrow{B}$ is not directly measurable by MRI, but it is possible to measure its positively polarized component in the rotating frame $B_1^{+}=\left(B_x+i{B}_y\right)/2$ (28). B₁ and $B_1^{+}$ are used interchangeably in this manuscript for simplicity. Using linear combination of the first two equations in Equation 2, we have

$${\mathit{\nabla }}^2{B}_1^{+}=-{\omega }^2{\mu }_0{\epsilon }_c{B}_1^{+}+\frac{i}{2}\left(\frac{\partial B_y}{\partial x}-\frac{\partial B_x}{\partial y}\right)g_w+\left(\frac{\partial B_1^{+}}{\partial z}-\frac{1}{2}\frac{\partial B_z}{\partial x}-\frac{i}{2}\frac{\partial B_z}{\partial y}\right)g_z$$ [3]

where $g_w≔\frac{\partial ln{\epsilon }_c}{\partial x}+i\frac{\partial ln{\epsilon }_c}{\partial y},g_z≔\frac{\partial ln{\epsilon }_c}{\partial z}$. Utilizing Gauss’ Law for Magnetism, we have

$$\frac{i}{2}\left(\frac{\partial B_y}{\partial x}-\frac{\partial B_x}{\partial y}\right)=\left(\frac{\partial B_1^{+}}{\partial x}-i\frac{\partial B_1^{+}}{\partial y}-\frac{1}{2}\left(\frac{\partial B_x}{\partial x}+\frac{\partial B_y}{\partial y}\right)\right)=\frac{\partial B_1^{+}}{\partial x}-i\frac{\partial B_1^{+}}{\partial y}+\frac{1}{2}\frac{\partial B_z}{\partial z}$$ [4]

For an MRI coil comprised of long striplines, $\mathit{\nabla }{B}_z$ is negligible in the middle part of the coil elements compared to the transverse components (20). Taking this into consideration, the following equation can be derived based on $B_1^{+}$ field

$${\mathit{\nabla }}^2{B}_1^{+}\approx -{\omega }^2{\mu }_0{\epsilon }_c{B}_1^{+}+\left(\frac{\partial B_1^{+}}{\partial x}-i\frac{\partial B_1^{+}}{\partial y}\right)g_w+\frac{\partial B_1^{+}}{\partial z}{g}_z$$ [5]

This equation holds for any transmit field $B_{1p}^{+}$ from a single coil element indexed by $p$. However, the absolute phase of $B_{1p}^{+}$, i.e. absolute transmit phase, is intractable, since the phase of MRI signal has mixed contributions from transmit field, receive field, chemical shift, magnetic susceptibility, eddy current effects, etc. Taking the phase difference between two transmit channels $p$ and $r$, the common terms can be eliminated, resulting in a relative transmit phase distribution ${\phi }_{pr}^{+}$. The relationship between absolute and relative $B_1^{+}$ can be expressed as

$$B_{1p}^{+}=\left|B_{1p}^{+}\right|e^{i{\phi }_p^{+}}=\left|B_{1p}^{+}\right|e^{i({\phi }_{pr}^{+}+{\phi }_r^{+})}=B_{1pr}^{+}{e}^{i{\phi }_r^{+}}$$ [6]

$B_{1pr}^{+}$ is measurable, whereas ${\phi }_r^{+}$ is the unknown absolute transmit phase of the reference channel $r$. Combining Equation 6 with Equation 5, we have

$$\begin{gathered} e^{i{\phi }_r^{+}}{\mathit{\nabla }}^2{B}_{1pr}^{+}+2\mathit{\nabla }{e}^{i{\phi }_r^{+}}\cdot \mathit{\nabla }{B}_{1pr}^{+}+B_{1pr}^{+}{\mathit{\nabla }}^2{e}^{i{\phi }_r^{+}} \\ =-{\omega }^2{\mu }_0{\epsilon }_c{B}_{1pr}^{+}{e}^{i{\phi }_r^{+}} \\ +\left(e^{i{\phi }_r^{+}}\frac{\partial B_{1pr}^{+}}{\partial x}+B_{1pr}^{+}\frac{\partial e^{i{\phi }_r^{+}}}{\partial x}-i{e}^{i{\phi }_r^{+}}\frac{\partial B_{1pr}^{+}}{\partial y}-i{B}_{1pr}^{+}\frac{\partial e^{i{\phi }_r^{+}}}{\partial y}\right)g_w \\ +\left(e^{i{\phi }_r^{+}}\frac{\partial B_{1pr}^{+}}{\partial z}+B_{1pr}^{+}\frac{\partial e^{i{\phi }_r^{+}}}{\partial z}\right)g_z \end{gathered}$$ [7]

Cancelling out $e^{i{\phi }_r^{+}}$ from both sides of the equation

$$\begin{gathered} {\mathit{\nabla }}^2{B}_{1pr}^{+}+2i\mathit{\nabla }{B}_{1pr}^{+}\blacksquare \mathit{\nabla }{\phi }_r^{+}+B_{1pr}^{+}\left(i{\mathit{\nabla }}^2{\phi }_r^{+}-\mathit{\nabla }{\phi }_r^{+}{ }^2\right) \\ =-{\omega }^2{\mu }_0{\epsilon }_c{B}_{1pr}^{+}+\left(\frac{\partial B_{1pr}^{+}}{\partial x}-i\frac{\partial B_{1pr}^{+}}{\partial y}+i{B}_{1pr}^{+}\frac{\partial {\phi }_r^{+}}{\partial x}+B_{1pr}^{+}\frac{\partial {\phi }_r^{+}}{\partial y}\right)g_w \\ +\left(\frac{\partial B_{1pr}^{+}}{\partial z}+i{B}_{1pr}^{+}\frac{\partial {\phi }_r^{+}}{\partial z}\right)g_z \end{gathered}$$ [8]

For each spatial location, we have the following matrix form

$$\left[B_{1pr}^{+},\mathit{\nabla }{B}_{1pr}^{+}\right]\blacksquare \left[\begin{array}{c}{\omega }^2{\mu }_0{\epsilon }_c+i{\mathit{\nabla }}^2{\phi }_r^{+}-\mathit{\nabla }{\phi }_r^{+}{ }^2-i\left(\frac{\partial {\phi }_r^{+}}{\partial x}-i\frac{\partial {\phi }_r^{+}}{\partial y}\right)g_w-i\frac{\partial {\phi }_r^{+}}{\partial z}{g}_z\\ 2i\frac{\partial {\phi }_r^{+}}{\partial x}-g_w\\ 2i\frac{\partial {\phi }_r^{+}}{\partial y}+i{g}_w\\ 2i\frac{\partial {\phi }_r^{+}}{\partial z}-g_z\end{array}\right]=-{\mathit{\nabla }}^2{B}_{1pr}^{+}$$ [9]

Concatenating all $n$ transmit channels that share the same set of unknown ${\phi }_r^{+}$ and ${\epsilon }_c$-related variables, we have a linear system of equations $Ax=b$ for each image pixel containing 4 unknowns and $n$ equations, where

$$A=\left[\begin{array}{c}{B}_{1p1}^{+},\mathit{\nabla }{B}_{1p1}^{+}\\ B_{1p2}^{+},\mathit{\nabla }{B}_{1p2}^{+}\\ \begin{array}{c}⋮\\ B_{1pn}^{+},\mathit{\nabla }{B}_{1pn}^{+}\end{array}\end{array}\right],b=\left[\begin{array}{c}-{\mathit{\nabla }}^2{B}_{1p1}^{+}\\ -{\mathit{\nabla }}^2{B}_{1p2}^{+}\\ \begin{array}{c}⋮\\ -{\mathit{\nabla }}^2{B}_{1pn}^{+}\end{array}\end{array}\right]$$ [10]

This linear system of equations is solved in a sense of least-squares to obtain $x$, which is then used to calculate $g_w$ based on

$$\begin{gathered} -\mathit{real}\left(x\left(2\right)\right)-i\blacksquare \mathit{real}\left(x\left(3\right)\right)=-\mathit{real}\left(2i\frac{\partial {\phi }_r^{+}}{\partial x}-g_w\right)-i\blacksquare \mathit{real}\left(2i\frac{\partial {\phi }_r^{+}}{\partial y}+i{g}_w\right) \\ =\mathit{real}\left(g_w\right)+i\blacksquare \mathit{imag}\left(g_w\right) \\ =g_w \end{gathered}$$ [11]

Note that $g_w≔\left(\frac{\partial }{\partial x}+i\frac{\partial }{\partial y}\right)\ln {\epsilon }_c$ is the Wirtinger derivative (29) of $\ln {\epsilon }_c$ defined on the complex plane $\mathrm{ℂ}\equiv {\mathrm{ℝ}}^2=\left\{\left(x,y\right),x\in \mathrm{ℝ},y\in \mathrm{ℝ}\right\}$. In this study, we seek the numerical integral of the Wirtinger derivative defined on a simply connected two-dimensional domain with Dirichlet boundary condition as the integration constant. The central reconstruction problem inside such an ROI $\Omega$ is expressed as an equality-constrained convex optimization problem

$$\begin{gathered} {\mathit{minimize}}_{\theta }{\Vert \left(D_x+i{D}_y\right)\cdot \theta - g_w\Vert }^2+\lambda {\Vert \Delta \theta \Vert }_1 \\ \mathit{subject} \mathit{to}{\theta }_{\left(x_0,y_0\right)}={\theta }_0 \forall \left(x_0,y_0\right)\in {\Omega }_0 \end{gathered}$$ [12]

where $\theta$ is a vectorized form of $\ln {\epsilon }_c$ inside $\Omega$; $D_x$ and $D_y$ are the spatial derivative operators along $x$ and $y$ directions, respectively; $\Delta$ is the spatial Laplacian operator. $D_x$, $D_y$, $\Delta$ are implemented using finite difference method

$$\begin{gathered} \left(D_x+i{D}_y\right)\cdot \theta =\frac{\mathrm{\Theta }\left(x+d,y\right)-\mathrm{\Theta }\left(x-d,y\right)}{2d}+i\frac{\mathrm{\Theta }\left(x,y+d\right)-\mathrm{\Theta }\left(x,y-d\right)}{2d} \\ \Delta \theta =\frac{\mathrm{\Theta }\left(x+d,y\right)+\mathrm{\Theta }\left(x-d,y\right)+\mathrm{\Theta }\left(x,y+d\right)+\mathrm{\Theta }\left(x,y-d\right)-4\mathrm{\Theta }\left(x,y\right)}{d^2} \end{gathered}$$ [13]

where $d$ is discretization step size, $\mathrm{\Theta }$ is the 2D map corresponding to the $\theta$ vector. $\lambda$ is a regularization parameter heuristically determined per case by L-curve method corresponding to its maximum curvature (30,31); ${\Omega }_0$ is a subarea of $\Omega$ with known EPs ${\theta }_0$. Image sparsity is promoted by including the $\Delta {\theta }_1$ term that smooths homogeneous patches while preserving sharp edges.

For phantom experiments, the boundary condition is the EPs of the manually drawn boundary which falls into the background agar gel. Its EPs were measured using a dielectric probe as $\mathrm{\sigma }$ = 0.28 S/m, ${\mathrm{\epsilon }}_{\mathrm{r}}$ = 79 ${\mathrm{\epsilon }}_0$. For rat experiments, water-based ultrasound transmission gel was applied over the skin surface on top of the tumor to provide EP reference. The gel EPs were measured using the dielectric probe, which reported consistent results ( $\sigma$ = 0.28 S/m, ${\epsilon }_r$ = 77 ${\epsilon }_0$) during a 4-hour time window at room temperature (22 °C) and across a temperature range of 22-58 °C (Supporting Fig. S1). The gel also serves as a high-permittivity dielectric pad that boosts local SNR (32) and helps to alleviate susceptibility induced magnetic field alteration on the surface of tissue.

For ROI boundary pixels that fall into rat muscle tissue, the following relaxed boundary constraint is used to regularize reconstruction results

$${\Vert \theta -{\theta }_{\mathit{tissue}}\Vert }^2\le {\delta }_0$$ [14]

which allows unknown muscle pixels to fluctuate around the average muscle EP values ${\theta }_{\mathit{tissue}}$, calculated from $\sigma$ = 0.9 S/m and ${\epsilon }_r$ = 64 ${\epsilon }_0$, based on our previous study (27) and further confirmed by probe measurement results from the animal cohort in this study (n = 8, $\sigma$: 0.89 ± 0.06 S/m, ${\epsilon }_r$: 63.6 ${\mathrm{\epsilon }}_0$ ± 2.3 ${\mathrm{\epsilon }}_0$). ${\delta }_0$ is chosen empirically as $0.02$ times the boundary pixel number for all cases.

METHODS

Numerical Simulation

Radiofrequency electromagnetic simulation was performed in SEMCAD (Schmid & Partner Engineering AG, Zurich, Switzerland) based on the finite-difference-time-domain (FDTD) method. The 8-channel stripline coil array used in the experiment was numerically replicated in terms of geometrical structure and electrical circuitry. The coil was loaded with a realistic rat model (275 g female rat model, IT’IS Foundation, Zurich, Switzerland) in a similar positioning as in a real experiment. The EP values assigned to the normal composite tissues were extracted from a widely used database (33). A 20-millimeter-diameter sphere was placed on the left flank of the rat mimicking a tumor xenograft ( $\sigma$ = 1.0 S/m, ${\epsilon }_r$ = 65 ${\epsilon }_0$). Inside the tumor was a necrotic core with a diameter of 8 mm ( $\sigma$ = 1.3 S/m, ${\epsilon }_r$ = 76 ${\epsilon }_0$). The discretization grid with spatially variable density was generated by software based on the material and geometry of the model. Grid density was specified to be finer than 2 mm isotropic to ensure precision. The simulation was executed eight times with one channel transmitting at a time, and the input RF power was normalized to 1 Watt. The simulations were carried out on a Linux server equipped with dual high-performance GPUs (Tesla C2070, NVIDIA).

The simulated B₁ field at 298 MHz from each transmit RF channel was exported to MATLAB and re-gridded using cubic splines onto an isotropic 1 mm grid. Relative B₁ was calculated by combining the B₁ magnitude of each channel and the relative phase with respect to the reference channel. Complex white Gaussian noise was added to the relative B₁ maps to simulate various SNR levels. The standard deviation of the noise was determined by the average B₁ magnitude inside the simulated object and the desirable SNR value. 100 sets of noisy data were obtained for a Monte-Carlo test.

Phantom Preparation

Agar solution containing deionized water, agar, NaCl, and NiCl₂·6H₂O with mass ratio of 1000:9.0:1.12:0.5 was boiled, naturally cooled down to 45°C while remaining in liquid state, and poured into a 125-mm-high and 65-mm-wide cylindrical container. The EPs were measured as $\sigma$ = 0.30 S/m, ${\epsilon }_r$ = 79 ${\epsilon }_0$ using a dielectric probe described in a later section. Anomaly solutions with various EPs were prepared by doping deionized water with NaCl and polyvinylpyrrolidone (PVP). Glass capillary tubes and plastic straws with various diameters (from 1.5 mm to 11 mm) were filled with solutions of various EPs and inserted into the agar gel. The whole phantom was left to solidify in room temperature (22 °C) for 24 hours. Samples from all solutions were taken and their EPs measured using the dielectric probe.

MRI Methods

The experiments were conducted in a human whole-body 7 Tesla MRI system (Siemens, Erlangen, Germany) equipped with 16 × 1 kW RF amplifiers (Communication Power Corporation, Hauppauge, NY, USA). The amplifiers were driven by a phase/gain controller remotely operated by a software toolbox developed in-house based on MATLAB (34,35). The sample under test was positioned in the center of a dedicated 8-channel RF transceiver coil array, comprised of eight 100-mm-long and 12-mm-wide striplines azimuthally distributed on a 100-mm-diameter cylindrical surface (27). Each coil element was connected to a power source via a two-parameter tuning/matching capacitors network, which was adjusted before each experiment to minimized power reflection at the proton resonance frequency (297.2 MHz). Adjacent coil elements were de-coupled by a tunable capacitor so as to provide distinct B₁ distributions. The coil was then connected to the MRI system via a custom transmit/receive switch box.

A hybrid B₁ mapping method was used to retrieve the B₁ magnitude (36), which combines (i) a reference scan based on 3D actual flip-angle imaging (AFI) (37) with all channels transmitting together in large-flip-angle regime, and (ii) a series of multi-slice gradient echo (GRE) images in small-flip-angle regime pulsing through each channel sequentially. AFI parameters are FA = 60°, TR = 120/20 ms, TE = 3.23 ms, voxel size 1.0 × 1.0 × 2.0 mm³, spatial coverage 256 × 168 × 96 mm³, duration 12.4 min; GRE parameters are FA = 15°, TR = 126 ms, TE = 3.3 ms, in-plane resolution 1.0 × 1.0 mm², FOV 256 × 168 mm², 12 slices, 2 mm slice thickness, 8 averages, total duration 28.3 min. Relative B₁ phase was acquired using another set of GRE with the same parameters except FA = 60° and average number = 3, with duration of 10.6 min. Before the acquisition of the high-resolution B₁ data, scout low-resolution images of GRE and AFI were acquired for B₁ shimming and calibration purposes, with duration of ~10 min. The total B₁ mapping session is approximately 60 min.

T1w images in resolution of 0.5 × 0.5 × 1.0 mm³ were obtained by taking the ratio of images from a 3D magnetization prepared rapid acquisition gradient echo (3D-MPRAGE) sequence and a 3D small-flip angle gradient echo (GRE) sequence, so as to cancel out undesirable weightings such as transmit and receive B₁, T2*, and proton density (38). T2w images were based on a turbo spin echo (TSE) sequence in 0.25 × 0.25 × 0.5 mm³ resolution, with shimmed B₁ in the tumor to maximize excitation homogeneity.

In Vivo Experiments

All animal procedures and care were approved by the University of Minnesota Institutional Animal Care and Use Committee (IACUC) in accordance with federally approved guidelines.

Animal was initially anesthetized in an induction chamber with 5% isoflurane mixed with 70% medical air and 30% oxygen, then maintained during imaging via a nose cone (Kent Scientific) at 1-2% isoflurane. Animal heating was achieved by a heating pad during preparation and hot water surrounding the animal holder during MR imaging. The temperature of water flowing through tubing around the animal was controlled by a thermostat integrated with water bath circulator (NESLAB RTE 7, Thermo Scientific). The respiratory rate and body temperature were monitored by an MR-compatible small animal monitoring and gating system (SA Instruments) during the procedures. The animal was positioned to lie on its side with the implanted tumor facing upwards. The orientation and the central axial slices of the tumor were labeled using an extra-fine felt-tip marker. The skin area around the tumor was shaved, and ultrasound transmission gel (Aquasonic 100, Parker Lab. Inc.) was applied to form a layer of approximately 10 mm on top of the tumor. For terminal studies, the animal was euthanized by carbon dioxide inhalation after the scan.

Additional animal handling procedures may be found in the supporting information (Supporting Method S2).

Dielectric Probe Measurement

Measurement was performed using Keysight 85070E dielectric probe kit connected to an E4991A network analyzer. The probe, shaped like a planar disk, has a diameter of 18 mm. Measurement of samples smaller than 20 mm is not recommended by the manufacturer due to compromised accuracy. Prior to measurement, the system was calibrated with air, shorting block, and deionized water each time it was set up. Immediately after euthanasia of the animal, a central cut was performed to expose the maximum cross-section of the tumor, where the open-ended coaxial probe was positioned and held still for 5 seconds during one trial. Measurement was repeated 3~5 times for each sample. Since the measurements were completed in a short period right after sacrifice, we consider the rat body temperature (37 °C) as the measurement temperature.

Among the eleven animals involved in the study, six were both imaged and probed; Five were imaged but not probed, including three animals with tumor smaller than 20 mm, and two animals whose tumor contains substantial liquefaction that hinders a successful measurement. Two additional animals, in which tumor did not successfully grow, were used only for probe measurement of muscle tissue.

EPs Reconstruction

Noisy simulation data and experimental data were smoothed using a low-pass Gaussian filter with a kernel size of 5 × 5 × 3 pixels and standard deviation of 1.2 × 1.2 × 0.8 pixels. The spatial Laplacian and gradient of relative B₁ were taken using a Savitzky-Golay filter with a kernel size of 5 × 5 × 3. The pixel-wise inverse problem (Equ. 9) was solved in the least-squares sense in MATLAB using backslash operation.

For phantoms, target maps were generated from manual segmentation of pilot images followed by assignment to each patch the measured EP values obtained from the probe. During BIEPT reconstruction, EPs on the phantom boundary were given as prior information based on probe measurement of the agar background ( $\sigma$ = 0.30 S/m, ${\epsilon }_r$ = 79 ${\epsilon }_0$). For simulation and in vivo experiments, the “gel region” was contoured and assigned EP values based on probe measurement ( $\sigma$ = 0.28 S/m, ${\epsilon }_r$ = 77 ${\epsilon }_0$). Then a connected ROI was contoured that contains the whole tumor, part of the gel region and muscle tissue. For in vivo data, bone and tendon pixels were carefully excluded due to unreliable B₁ measurement caused by the weak MR signal.

The central optimization problem (Equ. 12) was generated for each 2-dimensional (2D) ROI and solved using CVX, a MATLAB compatible package for specifying and solving convex programs (39). It takes approximately 3 seconds to solve for each axial slice on a desktop with 3.4 GHz GPU and 32 GB RAM. Conductivity and relative permittivity were then computed from $\theta$ as

$$\begin{gathered} {\epsilon }_r=\mathit{real}(e^{\theta })/{\epsilon }_0 \\ \sigma =-\mathit{imag}\left(e^{\theta }\right)\cdot \omega \end{gathered}$$ [15]

Single slice EP results were interpolated using cubic splines to yield an in-plane resolution of 0.5 × 0.5 mm². The reconstructed EPs inside ROI are shown in color maps overlapped onto structural MRI.

A flowchart for the relative B₁ mapping and BIEPT reconstruction is shown in Figure 1.

FIG. 1.

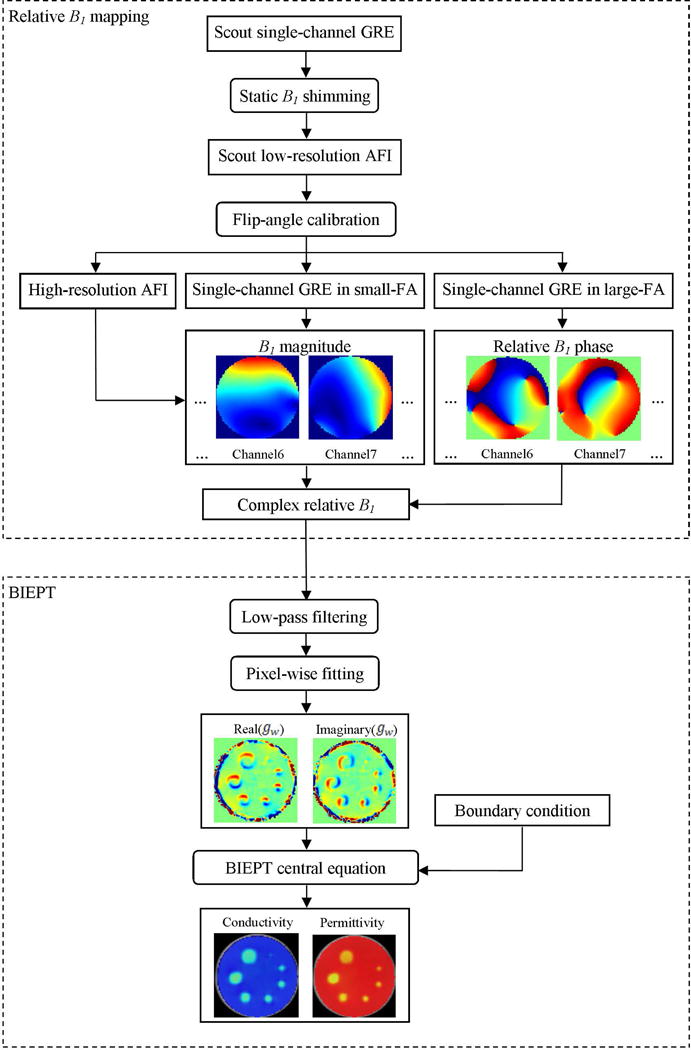
B₁ acquisition and BIEPT reconstruction flowchart. Single channel complex relative B₁ maps are acquired from an 8-channel RF coil array as input to the reconstruction algorithm. For BIEPT, pixel-wise fitting to Maxwell’s Equations is carried out first to retrieve the Wirtinger derivative of EPs. A region of interest (ROI) is assigned, in which boundary informed spatial integration is performed to retrieve the EP distributions.

RESULTS

Phantom Validation Results

Reconstruction results of the resolution phantom are shown in Figure 2. Compared to the target maps, the locations and shapes of the tube anomalies are faithfully reflected by the reconstructed EP images. The central profiles of the reconstructed tubes show successful preservation of the conductivity and permittivity contrasts in structures ≥ 3 mm. Stable plateaus can be observed for structures ≥ 7 mm. To separate the reconstruction error due to B₁ mapping from that due to BIEPT algorithm, this phantom was replicated in an electromagnetic simulation to acquire accurate B₁ for EP reconstruction. The reconstruction results using the same filters and regularization parameters are shown in Supporting Fig. S2. Similar smoothing effects on tube boundaries can be observed due to filtering in the algorithm, but imaging accuracy in the center of the large tubes is improved thanks to the use of accurate B₁.

FIG. 2.

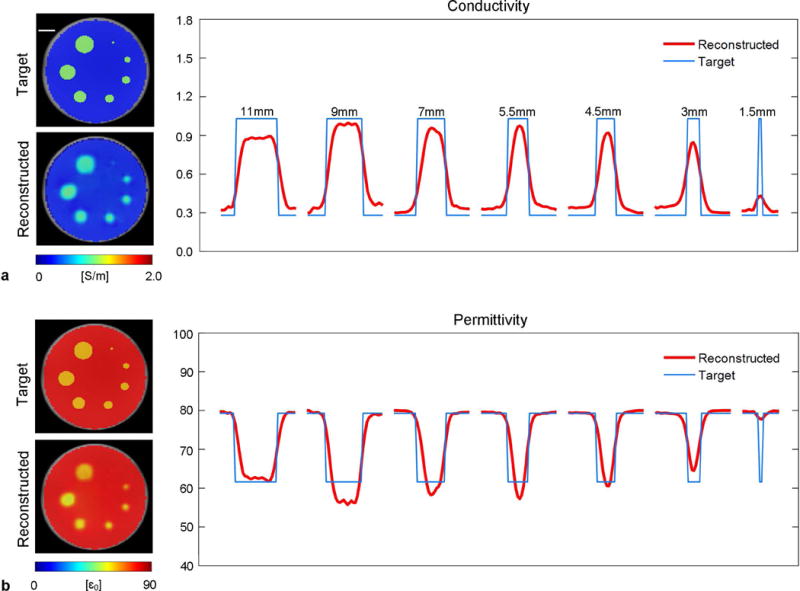
Reconstructed conductivity (a) and permittivity (b) from the resolution phantom containing 7 sample tubes of diameters from 1.5 mm to 11 mm filled with the same liquid solution ( $\sigma$ = 1.02 S/m, ${\epsilon }_r$ = 61.6 ${\epsilon }_0$). The targeted and reconstructed EP images are shown to the left of the plots. The central profile of each tube is plotted (red) against the targeted ones (blue). Scale bar: 10 mm.

Reconstructed EPs from the contrast phantom are shown and fitted to the target values in Figure 3. A good correlation between the reconstructed and target EP values is observed from the imaging results as well as linear fitting results, with ≤ 5% conductivity error and ≤ 12% permittivity error across the physiologically relevant EP ranges (0.3 S/m ≤ $\sigma$ ≤ 1.6 S/m, 50 ${\epsilon }_0$ ≤ ${\epsilon }_r$ ≤ 80 ${\epsilon }_0$). Conductivity imaging exhibits superior robustness to permittivity imaging, in the sense of image distortion and fitting accuracy. This phenomenon is consistent with previous studies (40,41,20) and will be discussed later.

FIG. 3.

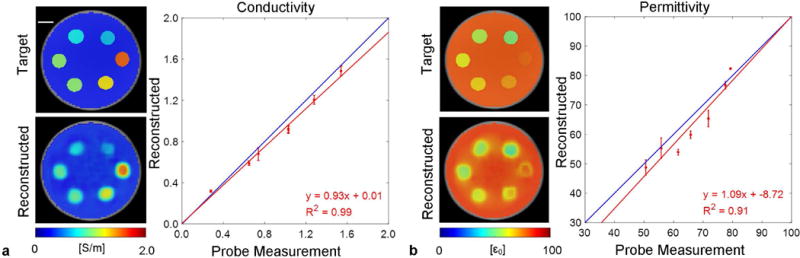
Reconstructed conductivity (a) and permittivity (b) from the contrast phantom containing 6 sample tubes of 9 mm diameter filled with different solutions spanning the EP ranges of interest. The targeted and reconstructed cross-section EP images are shown to the left of the plots. The reconstructed EPs inside each tube are shown as mean ± standard deviation, plotted and fitted against the dielectric probe measurement results. Scale bar: 10 mm.

Numerical Simulation Results

The simulation setup and single-channel absolute B₁ maps are shown in Figure 4a. Relative B₁ maps were measured and used to calculate EPs. Reconstruction results from two SNR levels, 150 and 50, are shown in Figure 4b. At both SNR levels, the simulated necrotic core with higher conductivity and permittivity can be clearly identified. The Monte-Carlo simulation of 100 trials demonstrates successful differentiation of EP differences among the three compartments on both noise levels, with less than 10% reconstruction error for both conductivity and permittivity. Nevertheless, contrast differences among the three compartments are smaller, due to the smoothing effects of the de-noise filter, as well as contrast leakage effects from the spatial integration process.

FIG. 4.

Numerical simulation of a realistic rat model. (a) Simulation setup and single channel B₁ distributions. (b) Comparison of the reconstructed EPs to the target maps using simulated relative B₁. Electrical conductivity and permittivity distributions are shown in color maps overlaid onto the grayscale sketch of the rat model. From left to right are the target maps and reconstruction results inside a manually drawn ROI with additive white Gaussian noise to adjust the SNR of the relative B₁ maps to 150 and 50, respectively. Scale bar: 10mm. (c) Three bar groups correspond to the tumor necrotic core, viable tumor, and muscle, respectively. In each group, from left to right shows the target EPs value and Monte Carlo simulation results from 100 trials at the corresponding SNR levels. The error bars show the standard error of the 100 mean values inside the corresponding region.

Effects of regularization parameter selection are shown in Figure 5 using simulated B₁ with SNR = 50. The $\lambda$ value corresponding to the maximum curvature of the L-curve gives a reasonable tradeoff between data fidelity and sparsity. The reconstruction results are insensitive to the exact value of $\lambda$ as long as it is in the “bending knee” region of the L-curve. Similarly, the results are robust against ${\delta }_0$ selection when it is close to the empirically chosen value marked in red.

FIG. 5.

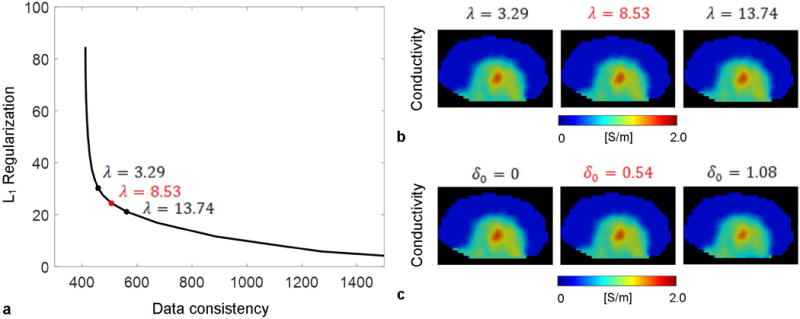
Selection of the regularization parameters in BIEPT. (a) L-curve for $\mathrm{\lambda }$ using simulated B₁ in rat with SNR=50. The chosen $\mathrm{\lambda }$ value is marked in red. Two additional $\mathrm{\lambda }$ values in the “bending knee” area of the curve are marked in black. (b) Reconstructed conductivity using the marked $\mathrm{\lambda }$ values in (a). (c) Reconstructed conductivity using the chosen ${\mathrm{\delta }}_0$ value in red and two other ${\mathrm{\delta }}_0$ values.

Animal Experiment Results

Bulk EP values obtained from BIEPT and the dielectric probe are shown in Figure 6. For each individual animal as well as grouped results, BIEPT reports average EP values close to those from the probe measurement. Probed conductivity is slightly higher than that obtained by BIEPT, potentially due to bleeding when cutting the tumor. The bulk EPs are found not to be significantly dependent on tumor size, which is consistent with previous finding in conductivity imaging of breast cancer patients (23). However, it can be observed that considerable EP variation resides in each imaging case, with standard deviation as large as 20% of the average values. These variations are less prominent in the values obtained from the physical probe measurements, which is expected since the latter report the bulk average of the entire tumor sample without spatial information, considering that the size of the physical probe is about the size of the tumor.

FIG. 6.

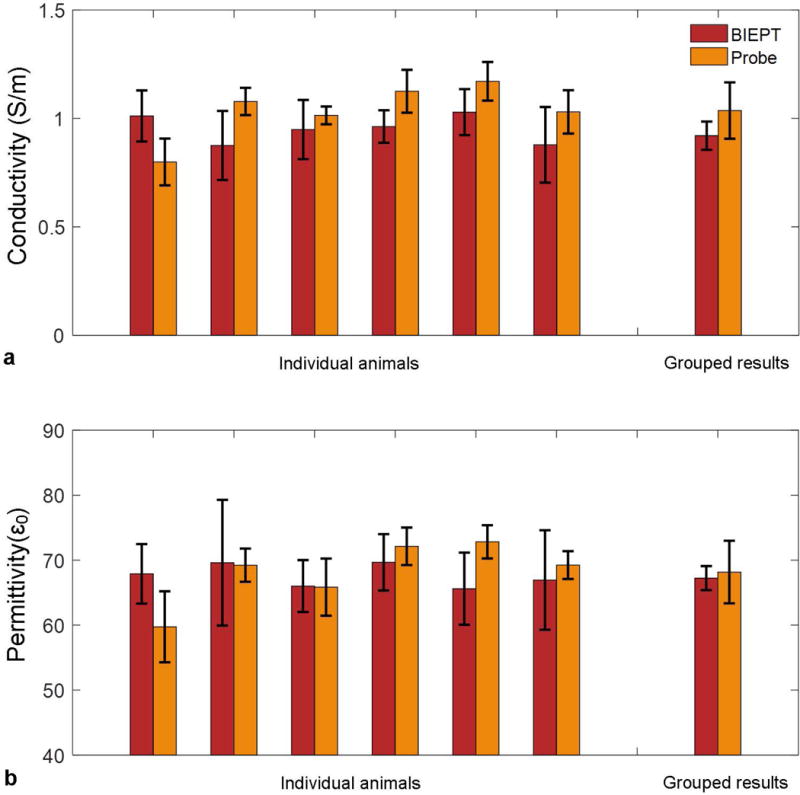
In vivo imaging and ex vivo probe measurement results from the animal experiments for conductivity (a) and permittivity (b). Individual imaging results are shown as mean ± standard deviation of tumor pixels in the central three axial slices. Individual probe measurement results are shown as mean ± standard deviation of four measurement trials on the central cut of tumor. Grouped imaging results are shown as mean ± standard deviation of 11 animals. Grouped probe measurement results are shown as mean ± standard deviation of 6 animals.

To demonstrate the capability of BIEPT to image tumor heterogeneity, we compare the reconstructed EP images with corresponding T1w, T2w images and whole-mount histopathology slides. Two representative cases are shown in Figures 7 and 8, respectively.

FIG. 7.

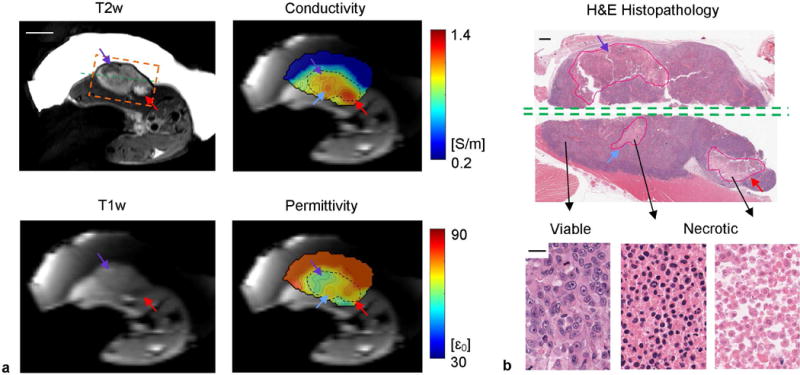
In vivo EP imaging of rat #1. (a) T1w, T2w, conductivity and permittivity maps. The black dashed contours on EP maps contour the tumor based on the T2w image. The orange dashed box shows the field of view of the histological slide in (b). The green dashed line shows the position where the tumor was cut through for probe measurement. Scale bar: 10 mm. (b) H&E histopathology of the same imaging slice in the orange dashed box as in (a). The necrotic cores were contoured by an experienced pathologist (E.R.). Examples of viable, necrotic, and highly necrotic tumor tissues are shown with distinct nuclear and cellular shape and density. Scale bars: 1 mm on whole-mount pathology and 20 $\text{μm}$ on zoomed pathology.

FIG. 8.

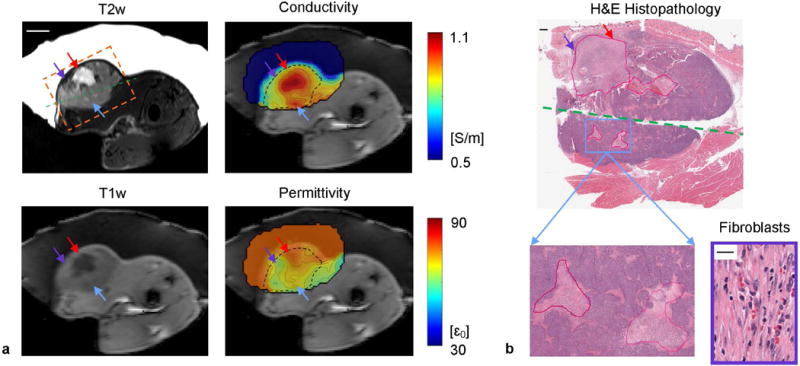
In vivo EP imaging of rat #2. Figure layout and annotations are same as in FIG. 6. The fibroblasts shown are taken from the necrotic core labeled by the purple arrow. Scale bars: 10 mm on MRI, 1 mm on whole-mount pathology and 20 $\text{μm}$ on zoomed pathology.

In the first case, the necrotic cores indicated by purple and red arrows show opposite signal change on T1w and T2w images compared to solid tumor (Fig. 7a). It is known that opposite T1w and T2w contrast variations can be observed within regions that are identified as necrotic in nature, due to two competing factors, paramagnetic ions and water content, with the former decreasing T1 and T2 and the latter increasing them (42). Yet both factors synergistically contribute to locally increased conductivity, as shown as distinguished tumor sub-regions on the conductivity map. On the other hand, water content contributes to permittivity elevation while ion concentration has minimal effect on the latter, leading to the contrast between these sub-regions on the reconstructed permittivity map. Hematoxylin and eosin (H&E) stain confirms the presence of three coagulative necrotic areas (Fig. 7b). Tumor necrosis is defined as irreversible cell and nuclear changes such as karyolysis, vacuolization of the nucleus and/or cytoplasm, and dissolution of the membrane integrity. As a result of these morphologic changes, necrotic areas will appear as “pink” areas on H&E stain within the tissue that are readily conspicuous at lower magnification. A central cut was made through the tumor along the green dashed line, allowing for dielectric probe measurement of the bulk tumor EPs, found as 1.01 ± 0.04 S/m and 65.8 ${\mathrm{\epsilon }}_0$ ± 4.4 ${\mathrm{\epsilon }}_0$, comparable to the BIEPT reported EP values of 0.95 ± 0.14 S/m and 66.0 ${\mathrm{\epsilon }}_0$ ± 4.0 ${\mathrm{\epsilon }}_0$.

In the second case, a large necrotic core appears in the second quartile of the tumor with two distinct areas showing clear contrast on T2w image (Fig. 8a, red and purple arrows). On T1w image, one area exhibits significant hypointensity (red arrow), while the other shows marginal hyperintensity (purple arrow). Nevertheless, both of these two areas show conductivity increase while discrepancy in permittivity is preserved. The H&E slide shows more than 80% necrosis with massive karyolysis and cell membrane loss in the left sub-region (Fig. 8b, purple arrow). Neutrophil and fibroblast infiltration is observed that removes water from tissue, in keeping with the underlying process of healing and scar formation, which may contribute to relatively low free water content. Figure 7a also shows successful detection of two 2-mm necrotic cores with elevated EPs, labeled by blue arrows, while their contrast on T1w and T2w images are less discernable. These two necrotic cores merge as a single hot spot on EP images due to the inherent smoothing properties of the reconstruction process. Probe measurement of the tumor reported 1.12 ± 0.10 S/m and 72.1 ${\mathrm{\epsilon }}_0$ ± 2.9 ${\mathrm{\epsilon }}_0$, comparable to the BIEPT measured EP values as 0.96 ± 0.08 S/m and 71.0 ${\mathrm{\epsilon }}_0$ ± 4.3 ${\mathrm{\epsilon }}_0$.

Despite the fact that each axial slice was reconstructed independently, consistent 3D EPs imaging results can be obtained thanks to the gel region that provides a reliable ground truth across all slices. Multi-slice EPs images are shown in the support information (Supporting Animation S4). A longitudinal study was also performed to monitor tumor growth in a 1.5-month time window, showing in high-resolution EP pattern evolution as the tumor grows (Fig. 9).

FIG. 9.

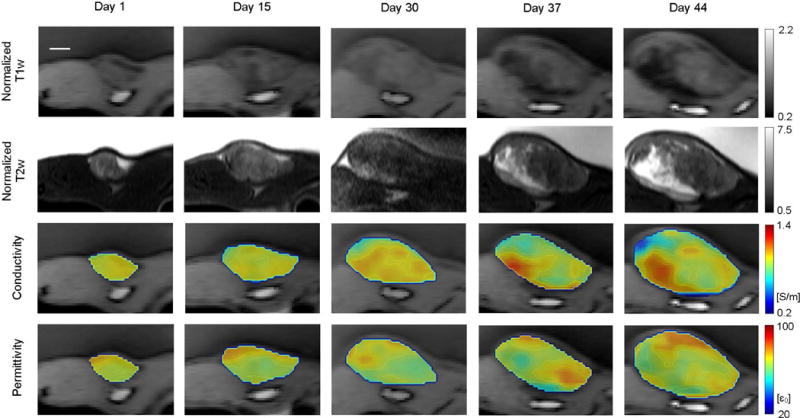
Longitudinal monitoring of a malignant human breast tumor in rat. MRI performed at five checkpoints as labeled on top of the images. From top to bottom: Normalized (to muscle) T1w images, normalized T2w images, quantitative conductivity and permittivity of tumor in color map overlaid on the T1w image. The animal was positioned similarly for all scans, and the axial slice with the largest tumor cross-section is shown in this figure. Images of the same contrast share the same colorbar. All images share the same scale bar shown on the top left, which is 5 mm.

DISCUSSION

In this study, we have proposed a Boundary Informed Electrical Properties Tomography (BIEPT) technique for high-resolution electrical conductivity and permittivity mapping from a boundary reference area and EPs’ Wirtinger derivative computed using a plurality of relative transmit B₁ measurements from a 7 Tesla MRI system, with enhanced numerical stability from edge sparsity regularization. This method does not require physical flipping of the imaging setup or image registration of multiple datasets, thus representing a more generalized methodology compared to gEPT in the context of multi-transmission. Simulation and phantom results demonstrated its high accuracy across physiologically relevant EP ranges and sensitivity to anomalies as small as 3 mm, under varied noisy conditions. In vivo tumor imaging experiments were performed on eleven rats with human breast cancer xenograft, referenced to externally applied ultrasound gel. We observed association of local conductivity elevation with tumor necrosis. We also noticed potential correlation of permittivity with additional tumor pathological characteristics such as healing and scar formation, yet the confidence level of permittivity is lower due to its susceptibility to image distortions and noise. Nevertheless, combination of the spatial distributions of both may give rise to a useful biomarker in clinical settings, such as tumor staging and treatment evaluation.

Previous human cancer studies based on either an invasive probe or non-invasive MREPT approaches have reported differences in mean EP values between benign and malignant tissues (3,43,24), tumors of low and high grades (25), as well as tumors in early and late stages (2). Despite the established correlation between EPs and those clinically meaningful tumor classifications, the underlying contrast mechanism and tumor biology remain unclear, partially due to the limited spatial resolution of the previous approaches and the practice of evaluating bulk EPs across large tumors (> 20 mm). To address this pivotal question, we developed BIEPT to retrieve high-resolution EP images from an animal tumor model in vivo. The observed association of EP changes with tumor necrosis may provide an explanation for the previously reported EP deviations in late-stage, high-grade, malignant tumors. Moreover, local feature identification and heterogeneity quantification of EPs derived from high-resolution image modality are potentially more sensitive biomarkers than bulk mean EPs in terms of tumor characterization (44,45).

Successful detection of both spontaneous and induced tumor necrosis is expected to have impacts on clinical practice. Spontaneous necrosis is often observed in highly invasive tumors with aggressive proliferation, due to multiple factors including deficiency of local blood perfusion that disrupts pH equilibrium, oxygen and nutrient supply, as well as removal of metabolic wastes (46). Necrotic tumors secrete stimulatory chemokines and cytokines which in turn facilitate tumor growth and infiltration (47,48). In practice, excessive necrosis is a feature of aggressive tumors with unfavorable prognosis in terms of early recurrence and mortality (49,50), and necrotic tumors are found to be more resistant to many types of chemotherapy as well as radiation therapy (51). Therefore, mapping the geometry and EPs of tumor necrosis can potentially provide valuable information to help guide clinical decisions and optimize individualized treatment plan. On the other hand, many successful cancer therapies, including chemo- and radiation-therapy approaches, induce intra-tumor necrosis when they are effective, and this typically takes place well before substantial changes in tumor volumetric numbers. Therefore, imaging tumor necrosis may provide not only early feedback on the effectiveness of the administered therapy but also partial response alerts. The proposed EPs based necrosis imaging technique is based on endogenous tissue contrast, representing a new avenue to be explored for monitoring early therapeutic response as well as a suboptimal therapy.

Based on our current findings of tumor necrosis, more investigations are warranted to explore the association of EP changes with other tumor signatures, such as angiogenesis and hypoxia, as well as tumor response to treatment. These biological effects typically happen on a much smaller spatial scale compared to necrosis, and they are expected to have more subtle impacts on EPs. Therefore, detection of these effects may have a better chance on dedicated animal scanners with higher gradient power for spatial encoding and higher magnetic field for improved SNR (52,53). In addition, animal tumor imaging in situ, i.e. in its original site, should be explored for improved modeling of tumor behavior, as well as patient studies to evaluate EPs as clinically meaningful biomarkers.

We include in this paper a single case of tumor growth monitoring over a 1.5-month time window. Despite the limited sample size, this case study demonstrates consistent spatial-temporal EP patterns in comparison to the anatomical T1w and T2w images. It provides an initial indication in favor of the reliability of the technology and as such may provide strong rationale to justify a larger sample number in longitudinal monitoring to eventually achieve biological significance.

In this study, BIEPT has been demonstrated to produce reconstruction results close to the ground truth in both simulation and phantom experiments. However, systematic reconstruction error can be spotted which mainly comes from two sources: B₁ mapping and BIEPT algorithm. There is small residual bias in the measured B₁, such as proton density and T1, which is amplified by its spatial differentiation and propagates to the reconstructed EPs. Therefore, improved imaging accuracy can be achieved in the simulation results using accurate B₁ (Supporting Fig. 2) compared to the experimental results using measured B₁ (Fig. 2). Supporting Fig. 2 also shows that BIEPT alone does not seem to significantly compromise the reconstruction accuracy in large structures ≥ 6 mm when using accurate B₁. Its effect is mainly smoothing out small structures, due to the low-pass filters and operational kernels involved that are unavoidable in a successful EP reconstruction. Previous studies have shown that, to the leading order, permittivity reconstruction is more sensitive to the accuracy of B₁ magnitude while conductivity reconstruction is more sensitive to the accuracy of B₁ phase (40,54,9,11). The potential sources of bias in our B₁ mapping method have more significant impacts on its magnitude than its phase, which partially accounts for the larger reconstruction error observed in permittivity than conductivity (Fig. 2). Using simulated B₁, conductivity and permittivity can be reconstructed at a similarly high-accuracy level (Supporting Fig. 2).

Current BIEPT presents other limitations that need to be addressed in future work. First of all, the current multi-channel B₁ mapping technique requires about one hour of acquisition time to produce 1.0 × 1.0 × 2.0 mm³ maps in 8 channels with satisfactory SNR. While providing high-quality B₁ maps in multi-channel arrays, the hybrid B₁ mapping method utilized in this work has not been specifically optimized for time efficiency; alternative B₁ mapping methods recently proposed, such as Bloch-Siegert method (55), DREAM (56), Large Dynamic Range B₁ mapping (57), could be implemented for comparison. Furthermore, a high count of receive channels positioned close to the imaged body could also be employed additionally to a transmit array to improve SNR, instead of a transceiver array which has inherently compromised receive performance compared with receive-only arrays. Another limitation in the current study stems from the fact that BIEPT is tested in a regularly shaped, simply-connected ROI, which serves our purpose well to image a tumor xenograft surrounded by the water-based gel. In cases where the ROI is irregularly shaped or has cavities, e.g. imaging near the bone or in the bowel, the robustness of BIEPT needs to be addressed. It is expected that prior knowledge about the average EPs of the imaging area and regularization methods will be helpful in those situations. BIEPT also requires an external reference area to infer the underlying EPs of a tumor, which would not be practical in most clinical settings. Nevertheless, EPs of normal body tissues have been well characterized, including some that have a relatively large area of reasonable homogeneity (e.g. muscle, liver, etc.), and may be used as a reference to BIEPT when a target tumor is contiguous to them. EP values of these normal tissues can be either extracted from the widely used literature by Gabriel et al. based on ex vivo measurements (33), or calculated in vivo using B₁ based on the Helmholtz equation.

As a technology to retrieve tissue EPs from the B₁ field instead of the full magnetic field $\overrightarrow{B}$ which cannot be directly measured by MRI, EPT intrinsically involves assumptions about the field distribution such as negligible $\mathit{\nabla }{B}_z$ to reduce the unknown variables in the central equation to a solvable level. This is especially important when the spatial variation of EPs is also considered in the EPT problem. Several studies have utilized the $\mathit{\nabla }{B}_z$ assumption and shown its validity in the central part of a quadrature volume coil (14,58,59) as well as a stripline coil element (20). However, this assumption posts limitation to the types of RF coil that can be used and the spatial imaging coverage. On the other hand, a series of numerical procedures need to be followed for a successful reconstruction of the EP contrast. These procedures include design the of low-pass filters, Laplacian and gradient kernels, spatial difference methods, regularization strategies, etc. The main goal of these procedures is to suppress measurement noise in B₁ and to achieve stability in the reconstruction results, at a price of imaging resolution and accuracy as well as algorithm complexity. There is a tradeoff among these metrics of imaging quality, which has been investigated from various aspects in previous work (53,60). In the future, technical innovations are called for, potential based on different imaging principles such as scattering field theory (59,61,62), to bypass a subset of the aforementioned field assumptions and approximations in order to further generalize the EPT technology and to bring its capability to the next level.

CONCLUSION

We conclude that tumor EPs heterogeneity can be inferred by the proposed boundary informed electrical properties tomography (BIEPT) technique based on unique transmit B₁ images measured from a multi-channel RF coil, using an external reference region and image edge sparsity constraint. Similar spatial patterns amongst tumor EP distributions, anatomical T1w and T2w images and pathology have been observed in animal experiments. Association of altered local EP values with tumor necrosis has been reported. Further investigations will be dedicated to improving and generalizing BIEPT for identification of EPs-related pathological features, as well as their evaluation as biomarkers in cancer patient care.