Scan-specific Robust Artificial-neural-networks for k-space Interpolation (RAKI) Reconstruction: Database-free Deep Learning for Fast Imaging

Abstract

Purpose

To develop an improved k-space reconstruction method using scan-specific deep learning that is trained on autocalibration signal (ACS) data.

Theory

Robust Artificial-neural-networks for k-space Interpolation (RAKI) reconstruction trains convolutional neural networks on ACS data. This enables non-linear estimation of missing k-space lines from acquired k-space data with improved noise resilience, as opposed to conventional linear k-space interpolation-based methods, such as GRAPPA, which are based on linear convolutional kernels.

Methods

The training algorithm is implemented using a mean square error loss function over the target points in the ACS region, using a gradient descent algorithm. The neural network contains three layers of convolutional operators, with two of these including non-linear activation functions. The noise performance and reconstruction quality of the RAKI method was compared with GRAPPA in phantom, as well as in neurological and cardiac in vivo datasets.

Results

Phantom imaging shows that the proposed RAKI method outperforms GRAPPA at high (≥4) acceleration rates, both visually and quantitatively. Quantitative cardiac imaging shows improved noise resilience at high acceleration rates (rate 4: 23% and rate 5: 48%) over GRAPPA. The same trend of improved noise resilience is also observed in high-resolution brain imaging at high acceleration rates.

Conclusion

The RAKI method offers a training database-free deep learning approach for MRI reconstruction, with the potential to improve many existing reconstruction approaches, and is compatible with conventional data acquisition protocols.

Introduction

Long scan times remain a limiting factor in MRI, often necessitating trade-offs with spatial and temporal resolution or coverage. In most applications, some form of accelerated imaging is required. Most clinical scans rely on parallel imaging for acceleration (1–3), where the local sensitivities of phased array coil elements are utilized for reconstruction to enable undersampled data acquisitions. The two most common parallel imaging approaches are sensitivity encoding, SENSE (2), and generalized autocalibrating partially parallel acquisition, GRAPPA (3). SENSE is a reconstruction approach which is formulated in the image domain as a linear inverse problem with a priori knowledge of the receiver sensitivities. In the GRAPPA algorithm, the reconstruction is an interpolation in k-space using shift-invariant convolutional kernels to estimate missing k-space lines from acquired lines, which constitutes a linear reconstruction method. For GRAPPA, these convolutional kernels are determined from a small amount of fully-sampled reference data, referred to as autocalibration signal (ACS). More recently, an alternative approach called iTerative Self-consistent Parallel Imaging Reconstruction, SPIRiT (4), which iteratively performs local interpolation and enforces data consistency has also been proposed, facilitating the use of regularization in the reconstruction process.

An alternative line of work relies on non-uniform sampling of k-space (5–10). Other than non-Cartesian acquisitions (5–8), randomly undersampled Cartesian acquisitions have recently gained attention with the advent of compressed sensing (9,10). While such undersampled acquisitions can be reconstructed using the linear conjugate gradient SENSE (8) or SPIRiT method, they are more traditionally processed with non-linear iterative algorithms that enforce some regularization based on the compressibility of images in a transform domain. Popular regularizations include l₁ norm of wavelet coefficients (10), total variation (9,11), low-rank schemes (12,13) and methods based on an adaptive generation of the sparsity transform domain (14–16). Regularized compressed sensing has been shown to have favorable noise properties in high-dimensional datasets (17), however linear parallel imaging has been shown to outperform it in lower-dimensional, especially 2D acquisitions (18). While the inherent denoising properties of CS-based techniques are desirable, the need for incoherent undersampled acquisitions, as well as its residual artifacts that are not readily accepted by clinical radiologists (18), have hindered its deployment. Thus, even though noise amplification remains a challenge for the linear reconstruction algorithms used in parallel imaging, these approaches continue to be the prominent technique for accelerated imaging in clinical MRI.

Recently, machine learning based techniques have gathered interest as a possible means to improve reconstruction quality with different undersampling patterns. So far, the focus of the MRI reconstruction community has been on generating more advanced regularizers by training on large amounts of datasets, along with both random and uniform undersampling patterns (19–23). Initial results indicate the promise of this approach in improving the reconstruction quality or providing a simple mapping from undersampled k-space to the desired image. Commonly, this training is performed in a manner that is not patient- or scan-specific, and thus requires large databases of MR images.

In this study, we develop a k-space reconstruction method that utilizes deep learning on a small amount of scan-specific ACS data. We focus on uniformly undersampled acquisitions, in order to improve the quality of parallel imaging reconstructions and for integration with existing data acquisition approaches. However, extensions to other sampling patterns such as random and non-Cartesian are possible within the described k-space method. Unlike most recent deep learning approaches, the proposed scheme does not require any training database of images. Instead the neural networks are trained for each specific scan, or set of scans, with a limited amount of ACS data, similar to GRAPPA. The proposed method, called Robust Artificial-neural-networks for k-space Interpolation-based (RAKI) reconstruction has an intuitive premise: Instead of generating linear convolutional kernels from the ACS data as in k-space interpolation-based reconstruction methods such as GRAPPA, we propose to learn non-linear convolutional neural networks from the ACS data. By using scan- and subject-specific deep learning, and learning all the necessary neural network parameters from the ACS data, any dependence on training databases or assumptions about image compressibility are avoided. After motivating our non-linear reconstruction approach, a brief review of convolutional neural networks is provided. We then introduce our reconstruction and training methods. Phantom experiments and in vivo imaging are performed, comparing the proposed reconstruction to the GRAPPA parallel imaging approach.

Theory

Non-linear Estimation of Missing k-space Lines

Reconstruction methods based on interpolation kernels in k-space aim to synthesize missing k-space lines as a linear combination of acquired lines across all coils (3,4,24,25). Specifically, for uniformly undersampled k-space data, GRAPPA uses linear convolutional kernels to estimate the missing data (3). Thus, for the j^th coil k-space data S_j, we have:

$$S_j(k_x,k_y-m\mathrm{\Delta }{k}_y)=\sum _{c=1}^{n_c}\sum _{b_x=-B_x}^{B_x}\sum _{b_y=-B_y}^{B_y}{g}_{j,m}(b_x,b_y,c)S_c(k_x-b_x\mathrm{\Delta }{k}_x,k_y-{\mathit{\text{Rb}}}_y\mathrm{\Delta }{k}_y)$$ [1]

where R is the acceleration rate; S_j (k_x, k_y − mΔk_y) are the unacquired k-space lines, with m = 1, …, R − 1; g_j,m(b_x, b_y, c) are the linear convolution kernels for estimating the data in the j^th coil specified by the location m as above; n_c is the number of coils; and B_x, B_y are specified by the kernel size. The convolutional kernels, g_j,m(b_x, b_y, c), need to be estimated prior to the reconstruction. This is typically done by acquiring an ACS region, either integrated into the undersampled acquisition as central k-space lines or as a separate acquisition (3). Subsequently, a sliding window approach is used in the ACS region to identify the fully-sampled acquisition locations specified by the kernel size and the corresponding missing entries. The former, taken across all coils, is used as rows of a calibration matrix, A; while the latter, for a specific coil, yields a single entry in the target vector, b (26). Thus for each coil j and missing location m = 1, …, R − 1, a set of linear equations are formed, from which the vectorized kernel weights g_j,m(b_x, b_y, c), denoted g_j,m, are estimated via least squares, as ${\mathbf{g}}_{j,m}=\text{arg }\underset{\mathbf{g}}{\text{min}}{\Vert \mathbf{b}-\mathbf{\text{Ag}}\Vert }_2$.

Since the encoding process in a multi-coil MRI acquisition is linear, the reconstruction for sub-sampled data is also expected to be linear. This is the premise of linear parallel imaging methods, which aim to estimate the underlying reconstruction process that exploits redundancies in the multi-coil acquisition, using a linear system with a few degrees of freedom. These degrees of freedom are captured in the small convolutional kernel sizes for GRAPPA or the smooth coil sensitivity maps for SENSE. In essence, linear functions with such limited degrees of freedoms form a subset of all linear functions. In linear parallel imaging, the underlying reconstruction is approximated with a function from this restricted subset. Our hypothesis is that the underlying reconstruction function, although linear in nature, can be better approximated from a restricted subset of non-linear functions with similarly few degrees of freedom. Examples of this phenomenon, i.e. using non-linear functions with few degrees of freedom to better approximate higher-dimensional linear functions, can be observed even in very low dimensions. For instance, assume a two-dimensional hyperplane, which is the range space of a two-dimensional linear mapping, is to be approximated. On average, using a one-dimensional non-linear mapping, parametrized by one independent variable, such as an Archimedean spiral, will be a better approximation compared to a one-dimensional linear mapping, which is a line through the origin, also parametrized by one independent variable. We hypothesize that similar approximations can be made in MRI reconstruction of multi-coil acquisitions. For instance, if the true underlying linear mapping is n-dimensional, an m-dimensional nonlinear mapping may outperform an m-dimensional linear mapping, where m << n. Thus, we seek to estimate missing k-space lines from acquired ones using such a non-linear mapping.

We confine the modeling of this non-linear process to few degrees of freedom using convolutional neural networks (CNNs). Thus, the degrees of freedom in the previous discussion refers to the CNN parameters. Note, similarly in the linear case for GRAPPA, the degrees of freedom refers to the coefficients of the linear convolutional kernels. We hypothesize that this restricted, yet non-linear, function space defined through CNNs enables to non-linearly learn redundancies among coils, without learning specific k-space characteristics, which may lead to overfitting. This is similar to the GRAPPA reconstruction, which successfully extracts such redundancies with a linear procedure, without adapting to k-space signal characteristics. The idea of using a larger class of nonlinear functions in modeling redundancies among coils for GRAPPA has also been explored previously (26), although a fixed nonlinear kernel mapping was used, instead of the deep learning strategies explored here. Thus, the modeling of the multi-coil system with a non-linear approximation with few degrees of freedom, instead of a linear approximation with similarly few degrees of freedom, is hypothesized to extract comparable coil information without overfitting, while offering improved noise resilience.

Another reason for using non-linear estimation relates to the presence of noise in the calibration data. For the GRAPPA formulation above, there is noise in both the target data, b, and the calibration matrix, A. When both sources of noise are present, it has been shown that linear convolutional kernels incur a bias when estimated via least squares, and this bias leads to non-linear effects on the estimation of missing k-space lines from acquired ones (26). In the presence of such data imperfections, which are in addition to the model mismatches related to the degrees of freedom described earlier, a non-linear approximation procedure may improve reconstruction quality and reduce noise amplification.

Convolutional Neural Networks for MRI Reconstruction in k-space

We propose to replace the linear estimation in GRAPPA that utilizes convolutional kernels with a non-linear estimation that utilizes CNNs (27). The proposed method, RAKI, is designed to calibrate the CNN from ACS data without necessitating use of any external training database for learning.

CNNs are a special type of artificial neural network, whose utility dates back to the late 1980s (28). They have recently gained interest due to the availability of efficient training implementations along with substantial gains in computing power (29), use of fast-converging nonlinear layers (30), and increased access to large training datasets (31). Thus, CNNs have been successfully applied to multiple fields, including image classification (29), face recognition (32), image super-resolution (33) and image denoising (34). CNNs are simple mathematical models that estimate a (potentially nonlinear) function f:X → Y, for two arbitrary sets X and Y. The fundamental idea is to combine multiple layers of simple modules, such as linear convolutions and certain point-wise nonlinear operators, in order to effectively represent complex functions of interest (27).

For the problem of nonlinearly estimating missing k-space data from acquired k-space data, a set of functions, f_j,m are desired such that

$$S_j(k_x,k_y-m\mathrm{\Delta }{k}_y)\approx f_{j,m}\left({\{S_c(k_x-b_x\mathrm{\Delta }{k}_x,k_y-{\mathit{\text{Rb}}}_y\mathrm{\Delta }{k}_y)\}}_{b_x\in [-B_x,B_x],b_y\in [-B_y,B_y],c\in [1,n_c]}\right)$$ [2]

where [a,b] denotes the set of integers from a to b inclusive. In RAKI, these functions f_j,m are approximated using CNNs, and their parameters are learned from the ACS data. CNN literature and the associated deep learning procedures are commonly based on mappings over the real field (27). Thus, prior to any processing, we map all the complex k-space data to real-valued numbers. For a complex-valued k-space dataset, s of size n_x×n_y×n_c, where n_c is the number of coils, we embed this into a real-valued space as a dataset of size n_x×n_y×2n_c, where the real part of s is concatenated with the imaginary part of s along the third (channel) dimension. Thus, effectively 2n_c input channels are processed. We note that other embeddings, which will increase dimensionality in the other dimensions, are possible, but were not explored due to the ease of implementation of the channel dimension.

Before a CNN can be trained, its structure, i.e. the number of layers and layer operations, needs to be determined. There is no optimization procedure for choosing the structure, and this is done in a heuristic manner (27). In this study, we use a three-layer structure, as depicted in Figure 1. Each layer, except the last, is a combination of linear convolutional kernels and a nonlinear operation called the rectified linear unit (ReLU), which has desirable convergence properties (30). The linear convolution in CNNs, denoted by *, e.g., z = w * s, and is defined as follows:

$$z(x,y,j)=\sum _{m=1}^{n_c}\sum _{p=1}^{b_x}\sum _{q=1}^{b_y}w(p,q,m,j)·s(x+p-1,y+q-1,m)\text{ for }j=1\cdots ,n_{\mathit{\text{out}}}$$ [3]

where s is an input data of size n_x×n_y×n_c, w is a kernel of size b_x×b_y×n_c×n_out, and z is the output data of size (n_x−b_x+1)×(n_y−b_y+1)×n_out. The ReLU is defined as

$$\mathit{\text{ReLU}}(x)=\text{max}(x,0).$$ [4]

The last layer performs the output estimation without any nonlinear operations. The details of the network is given next.

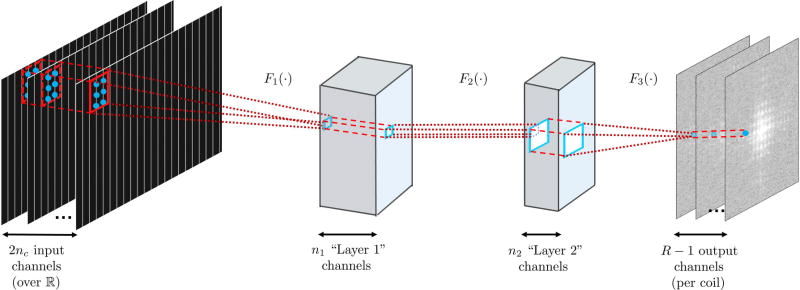
Figure 1.

The three layer network structure used in this study for the convolutional neural network. The first layer, F₁ (·), takes in the sub-sampled zero-filled k-space of size n_x×n_y×2n_c, as embedded into the real field. The convolutional filters in this layer, w₁ are of size b₁^x×b₁^y×2n_c×n₁. This is followed by a rectified linear unit (ReLU) operation. The second layer of our network, F₂ (·), takes in the output of the first layer and applies convolutional filters, denoted by w₂, are of size b₂^x×b₂^y×n₁×n₂. This layer also includes a ReLU operation. These two layers non-linearly combine the acquired k-space lines. The final layer of the network, F₃ (·), produces the desired reconstruction output by applying convolutional filters, w₃, of size b₃^x×b₃^y×n₂×n_out. In our implementation all missing lines per coil (over reals) is estimated simultaneously, therefore n_out = R − 1.

The first layer of our network takes in the sub-sampled zero-filled k-space of size n_x×n_y×2n_c, which has been embedded into the real field. The convolutional filters in this layer, denoted by w₁, are of size b₁^x×b₁^y×2n_c×n₁. The operation of this layer is given as

$$F_1(\mathbf{s})=\text{ReLU}({\mathbf{w}}_{\mathbf{1}}\ast \mathbf{s}).$$ [5]

The second layer of our network takes in the output of the first layer and applies convolutional filters, denoted by w₂, of size b₂^x×b₂^y×n₁×n₂. The operation of this layer is given as

$$F_2(\mathbf{s})=\text{ReLU}({\mathbf{w}}_{\mathbf{2}}\ast s).$$ [6]

Intuitively, the first two layers are non-linearly combining the acquired k-space lines, essentially integrating the ideas of creating “virtual” channels and coil compression with non-linear processing. The final layer of the network produces the desired reconstruction output by applying convolutional filters, w₃, of size b₃^x×b₃^y×n₂×n_out, yielding

$$F_3(\mathbf{s})={\mathbf{w}}_{\mathbf{3}}\ast \mathbf{s}.$$ [7]

Thus the overall mapping is given by

$$F(\mathbf{s})=F_3(F_2(F_1(\mathbf{s}))).$$ [8]

We note that a bias term is typically used in all layers in CNN applications. However, these were not included in our setup, as they change if the k-space is linearly scaled by a constant factor, for instance due to changes in the receiver gain, ultimately limiting robustness. In our implementations, all layers use kernel dilation (35) of size R in the k_y direction to only process the acquired k-space lines. We implement a CNN for each output channel, and perform the estimation of all the missing k-space lines, within the specified kernel size, leading to n_out = R − 1. Since there are 2n_c output channels over the real field, this process yields a set, ${\{F^j(·)\}}_{j=1}^{2n_c}$, of non-linear reconstruction functions, where each F^j(·) is an approximation of {f_j,m}_m in Equation [2] using CNNs.

Training Database-Free Learning of Scan-Specific Neural Networks

In order to learn a non-linear reconstruction function, F^j(·), the unknown network parameters, θ_j = {w₁, w₂, w₃} for that input channel need to be estimated. Note we omit the subscript j for the kernels for ease of notation. Let s denote the zero-filled acquired k-space lines, as the input to the network. The goal is to minimize a loss function between the reconstructed k-space lines using F^j(·), and the known ground truth for the target missing k-space lines in the ACS region, denoted by Y_j, which is formatted to match the output structure with the same number of n_out channels in the third dimension. The loss function we use is the mean squared error (MSE), matching the original GRAPPA (3) formulation:

$$L({\mathit{\theta }}_{\mathit{j}})={\Vert {\mathit{Y}}_{\mathit{j}}-F^j(\mathbf{s};{\mathit{\theta }}_{\mathit{j}})\Vert }_F^2,$$ [9]

where ‖·‖_F denotes the Frobenius norm. The main difference with GRAPPA is that instead of solving a linear least squares problem to calculate one set of convolutional kernels; we need to solve a non-linear least squares problem to calculate three sets of convolutional kernels. Unlike the linear least squares problem, a closed-form minimization of the objective function is not possible. Therefore, in RAKI, gradient descent with backpropagation (36) and momentum (37) is employed to minimize Equation [9]. In order to update the convolutional kernels, at iteration t, we have

$${\overline{\mathbf{w}}}_{\mathrm{i}}^{(t)}=\mathrm{\mu }{\overline{\mathbf{w}}}_{\mathrm{i}}^{(t-1)}+\eta \frac{\partial L}{\partial {\mathbf{w}}_{\mathbf{i}}^{(t-1)}},$$ [10]

$${\mathbf{w}}_{\mathbf{i}}^{(t)}={\mathbf{w}}_{\mathbf{i}}^{(t-1)}-{\overline{\mathbf{w}}}_i^{(t)},$$ [11]

where µ is the momentum rate, η is the learning rate, i ∈ {1,2,3}, and backpropagation is used to calculate the derivative $\partial L/\partial {\mathbf{w}}_{\mathbf{i}}^{(t-1)}$. The same approach is used to calculate all convolutional filters. We note that while stochastic gradient descent is popular in most deep learning applications due to the immense size of the training datasets (31), we can use simple gradient descent due to the limited size of the ACS region.

Methods

Reconstruction Algorithm: Implementation Details

The parameters used for the network are as follows: b₁^x= 5, b₁^y = 2, n₁ = 32, b₂^x= 1, b₂^y = 1, n₂ = 8, b₃^x= 3, b₃^y = 2, n_o = R − 1. Note that with this choice of parameters, at most 2R k_y lines are not estimated, which is the same as GRAPPA with a kernel size of [5,4] (3). Three convolutional kernels {w₁, w₂, w₃} are trained for each output channel. The input is the zero-filled sub-sampled k-space, on which all the necessary Fourier transform shifts in k-space have been performed using phase correction. Kernel dilation (35) is used at each layer in order to process only the acquired data. We note that there is no effective dilation in the second layer due to our choice of kernel size. The momentum rate is set to µ = 0.9. The learning rate is k-space scaling dependent. We scale the k-space such that the maximum absolute value across all input channels is set to 0.015, and use η = 100 for the first layer and η = 10 for the next two layers. A slower learning rate for the later layers is important for convergence, as has been reported in image processing applications (33,34). The n_out = R − 1 outputs per processed k-space location is placed back to the corresponding missing k-space locations, consistent with standard GRAPPA practice.

The gradient descent for learning and the reconstruction was implemented in Matlab (v9.0, MathWorks, Natick, MA), with the CNN convolution and backpropagation operations implemented using the MatConvNet toolbox (38). An implementation of the gradient descent, the CNN architecture and the reconstruction algorithm, will be provided online on http://people.ece.umn.edu/~akcakaya/RAKI.html.

Phantom Imaging

Phantom imaging was performed at a 3T Siemens Magnetom Prisma (Siemens Healthcare, Erlangen, Germany) system using a 32-channel receiver head coil-array. A head-shaped resolution phantom was imaged using a spoiled gradient recalled echo (GRE) sequence. The imaging parameters were: 2D multi-slice, FOV = 220×220 mm², in-plane resolution = 0.7×0.7 mm², matrix size = 320×320, slice thickness = 4 mm, TR/TE = 500 ms/15 ms, flip angle = 70°, 27 slices, bandwidth = 360 Hz/pixel.

The fully-sampled acquisition had an SNR of approximately 200. To test the noise robustness of RAKI, complex Gaussian noise was added to the raw k-space to bring the image domain SNR measured within an ROI in the phantom down to 20. This noisy k-space was retrospectively under-sampled using uniform undersampling of rates, R ∈ {1,2,3,4,5,6}. ACS data of size 40 was taken from the central k-space lines, and this was used for the training of the CNN in RAKI reconstruction, and for the determination of the convolutional kernels for GRAPPA reconstruction. GRAPPA reconstruction was implemented using a [5,4] kernel. For both GRAPPA and RAKI, no boundary extension was used. Thus, edges of k-space that do not fully lie in the edges of the convolutional windows were not evaluated. For both methods this meant the outermost 2(R−1) k_y lines were not calculated. The normalized mean square error (NMSE) of each reconstructed k-space was calculated with respect to the acquired k-space data. Additional experiments using higher SNR phantom data is provided in Supporting Figure S1.

In Vivo Imaging

The imaging protocols were approved by the local institutional review board, and written informed consent was obtained from all participants prior to each examination for this HIPAA-compliant study.

Cardiac imaging was performed at a 3T Siemens Magnetom Prisma (Siemens Healthcare, Erlangen, Germany) system using a 30-channel receiver body coil-array. SAPPHIRE myocardial T₁ mapping (39) was acquired in a mid-ventricular short-axis slice on four healthy volunteers (three men, 40 ± 17 years). A balanced steady-state free precession image acquisition was used with the following parameters: FOV = 300×300 mm², TR/TE = 2.6 ms/1.0 ms, flip angle = 35°, bandwidth = 1085 Hz/pixel. 11 images with different T₁ weights were acquired in a single breath-hold. One acquisition was performed with resolution = 1.7×1.7 mm², matrix size = 176×176, slice thickness = 8 mm, in-plane acceleration (iPAT) = 2, ACS lines = 32. Another high-resolution acquisition was performed with resolution = 1.1×1.1 mm², matrix size = 272×272, slice thickness = 6 mm, iPAT = 5. For this high-resolution acquisition, a separate calibration scan with resolution = 1.1×4.7 mm², corresponding to 64 ACS k_y lines, were performed in the same breath-hold with a 3 second delay to allow for T₁ recovery.

These datasets were used to test the robustness of RAKI across different contrasts. Specifically, the CNNs in RAKI and the convolutional kernels in GRAPPA were estimated using ACS data from only one T₁ weighted image. These CNNs and convolutional kernels were then used to reconstruct all 11 images with varying T₁ weights. Thus, this tested whether RAKI captured the coil information, as in GRAPPA, or performed over-fitting to specific image or k-space features. Three experiments were performed with these datasets: 1) The standard resolution acquisitions were reconstructed with RAKI and GRAPPA, where the CNN parameters and convolutional kernels were estimated using the integrated ACS region of the image with no T₁ preparation; 2) The standard resolution acquisitions were retrospectively undersampled to R = 4, and RAKI and GRAPPA reconstructions were performed on the same datasets and using the same ACS region of the image with no T₁ preparation; 3) The high resolution acquisitions were reconstructed with RAKI and GRAPPA, where the training and convolutional kernels were estimated using the ACS data from the additional low-resolution calibration scan. Non-linear reconstructions change the statistical distribution of the noise, and introduce dependencies between the reconstruction noise and reconstructed signal beyond additivity, hindering the definition of the equivalent of a g-factor (40,41). For these quantitative MRI datasets, the spatial variability of the T₁ times in the homogenous muscle tissue of the myocardium were used as a surrogate for noise performance (42) for both reconstruction methods.

Brain imaging was performed at a 7T Siemens Magnex Scientific (Siemens Healthcare, Erlangen, Germany) system using a 32-channel receiver head coil-array. Anatomical T₁-weighted imaging was acquired in a patient (man, 76 years) and in a healthy volunteer (man, 43 years) using a standard Siemens 3D-MPRAGE sequence with the following parameters: FOV = 230×230×154 mm³, resolution = 0.6×0.6×0.6 mm³, TR/TE = 3100 ms/3.5 ms, inversion time = 1500 ms, flip angle = 6°, bandwidth = 140 Hz/pixel, ACS lines = 40. The k-space data was inverse Fourier transformed along the slice direction, and a central slice, matrix size = 384×384, was processed for the rest of the study. A single slice of a 3D data set was chosen over 2D imaging to enable a 0.6mm isotropic acquisition, while overcoming inherent SNR limitations of the latter. The patient data was acquired with iPAT = 3, and was also retrospectively undersampled to R = 6. RAKI and GRAPPA reconstructions were performed on both these datasets. The healthy volunteer data was acquired with iPAT = 3,4,5,6. To further help the visualization of artifacts and avoid SNR losses, iPAT= 5 and 6 data were acquired with two averages. Thus, the only SNR penalty between iPAT = 3 and 6 acquisitions is due to differences in coil encoding. All datasets were reconstructed using RAKI and GRAPPA. These datasets were used to test RAKI at very high resolutions for robustness and potential blurring artifacts. Additional experiments on the effect of calibration region on the high-SNR high-resolution volunteer data is provided in Supporting Figure S2.

Additional brain imaging was performed at a 3T Siemens Magnetom Prisma (Siemens Healthcare, Erlangen, Germany) system using a 32-channel receiver head coil-array. T₁-weighted imaging was acquired in a healthy subject (man, 41 years) using a standard Siemens 3D-MPRAGE sequence with the following parameters: FOV = 224×224×179 mm³, resolution = 0.7×0.7×0.7 mm³, TR/TE = 2400 ms/2.2 ms, inversion time = 1000 ms, flip angle = 8°, bandwidth = 210 Hz/pixel, ACS lines = 40. Two separate acquisitions were performed with iPAT = 2 and 5. The k-space data was inverse Fourier transformed along the slice direction, and a central slice, matrix size = 320×320, was processed for the rest of the study. The R = 2 acquisition was retrospectively undersampled to R = 4 and 6. Reconstructions were performed using both RAKI and GRAPPA for R = 2, 4, 5, 6 to test the robustness of RAKI at very high resolutions for potential blurring artifacts.

Results

Phantom Imaging

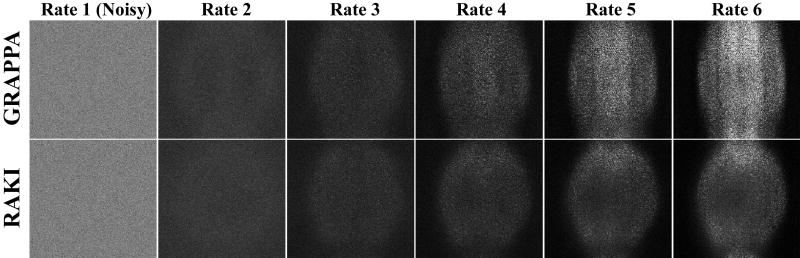
Figure 2 depicts the results from phantom imaging. GRAPPA and the proposed RAKI reconstructions from noisy data for various acceleration rates. While virtually no difference is observed at acceleration rates of 2 and 3, starting with rate 4, the noise performance of RAKI improves upon that of GRAPPA. RAKI reconstructions at acceleration rates 4 and 5 show visually improved noise properties over GRAPPA, which has high levels of noise amplification, especially in the center part of the phantom. The difference images depicted in Figure 3 are also in agreement with these observations, where the errors in GRAPPA reconstruction become apparent and structured from rate 4 onwards. The noise amplification behavior of the two reconstructions is further reflected with the quantitative NMSE performance. GRAPPA reconstruction exhibits NMSE 0.65, 0.51, 0.51, 0.66 and 0.89 from rates 2 to 6 respectively, whereas RAKI reconstruction has NMSE 0.65, 0.51, 0.46, 0.47 and 0.52 for the same rates. This corresponds to 0%, 0%, 11%, 28% and 41% decrease in NMSE respectively, using RAKI as compared to GRAPPA. Note the NMSE values reported here are not monotonically increasing, due to several reasons, including i) the averaging nature of NMSE in capturing the non-uniform noise characteristics, ii) noise-suppression outside the object in the reconstructions, iii) a noiseless reference in the NMSE calculation, iv) the tendency of k-space interpolation techniques to exhibit g-factors less than 1 in certain areas.

Figure 2.

Results of phantom experiments. Images reconstructed using GRAPPA (top row) and the proposed RAKI (bottom row) reconstructions from noisy data sets for various acceleration rates, as well as a fully-sampled noisy reference image. Starting with rate 4, the noise performance of RAKI improves upon that of GRAPPA. RAKI reconstructions at acceleration rates 4 and 5 show visually improved noise properties over GRAPPA, which has high levels of noise amplification.

Figure 3.

The difference images for the reconstructions in Figure 2, as compared to the original acquisition without additional noise, confirm the observations regarding the improved noise resilience of RAKI. NMSE quantification is also consistent with these observations: 0.65, 0.51, 0.51, 0.66 and 0.89 for GRAPPA versus 0.65, 0.51, 0.46, 0.47 and 0.52 for RAKI from rates 2 to 6.

In Vivo Imaging

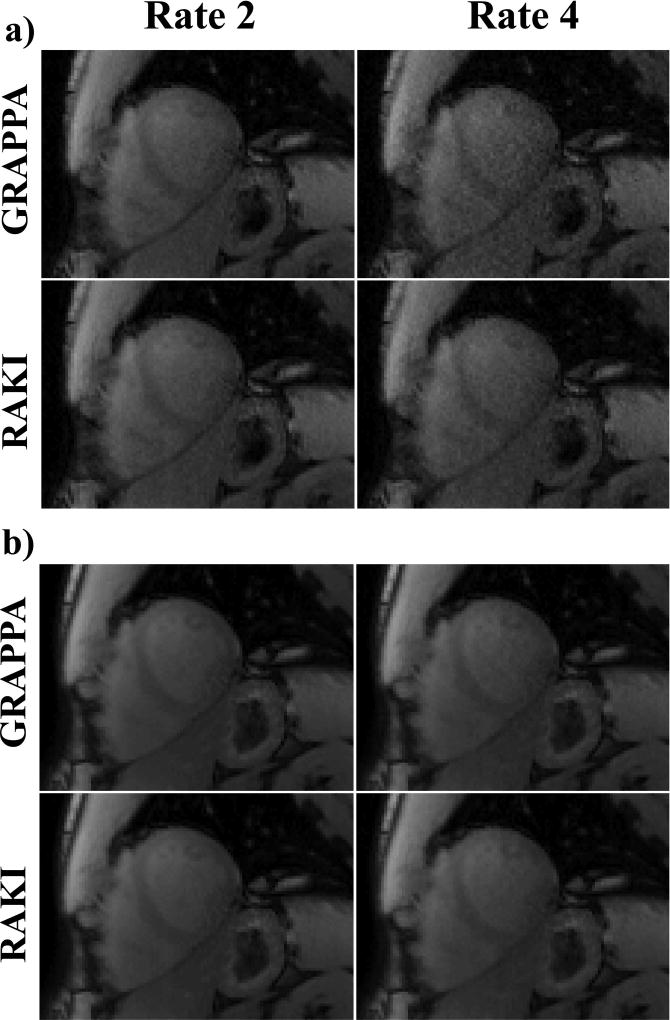
Figure 4 shows representative T₁-weighted images from SAPPHIRE T₁ mapping acquired at the conventional resolution of 1.7×1.7 mm². The images corresponding to the shortest inversion time, with a low SNR, are shown in Figure 2a for the acquisition acceleration rate of 2, as well as a retrospective acceleration rate of 4. There is visually no discernible difference between GRAPPA and RAKI at rate 2. However, at rate 4, the improved noise performance of RAKI over GRAPPA becomes visually apparent. Figure 2b shows T₁-weighted images acquired without any preparation, corresponding to the highest SNR images in the acquisition. At this higher SNR, the differences between RAKI and GRAPPA are visually minor even at the acceleration rate of 4, with a slight improvement in the left ventricle blood pool for the proposed approach. These observations are reflected in the quantitative T₁ measurements, with virtually no difference (<0.5%) in mean myocardial T₁ value among the two methods at either rate, and <1% difference in spatial variability at rate 2. However, RAKI showed an improvement of 10% in spatial variability over GRAPPA at rate 4. These trends are consistent across all subjects, where comparable quantification is observed with RAKI and GRAPPA reconstructions, with the exception of a 23% reduced noise variability with RAKI at rate 4 (average T₁ time ± average spatial variability: RAKI: 1562±197.0 ms vs. GRAPPA: 1542±258.8 ms). These experiments show the improved noise resilience of RAKI, as well as its robustness in reconstructing varying contrast weightings.

Figure 4.

Representative T₁-weighted images from SAPPHIRE T₁ mapping acquired at the conventional resolution of 1.7×1.7 mm². (a) Images with low acquisition SNR, corresponding to the shortest inversion time, at the acquisition acceleration rate of 2, and a retrospective acceleration rate of 4. At rate 4, the noise performance improvement of RAKI over GRAPPA becomes apparent. (b) Images with high acquisition SNR, where the differences between RAKI and GRAPPA are visually minor even at the acceleration rate of 4, with a slight improvement in the left ventricle blood pool for RAKI. A quantitative analysis of the resulting T₁ maps indicate that comparable quantification is observed for the two reconstructions, except for a 10% reduced noise variability with RAKI at rate 4.

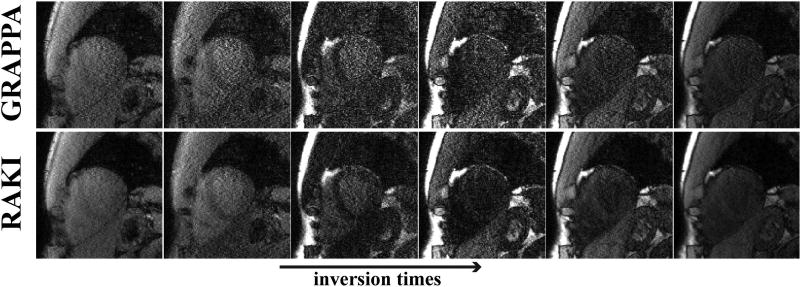
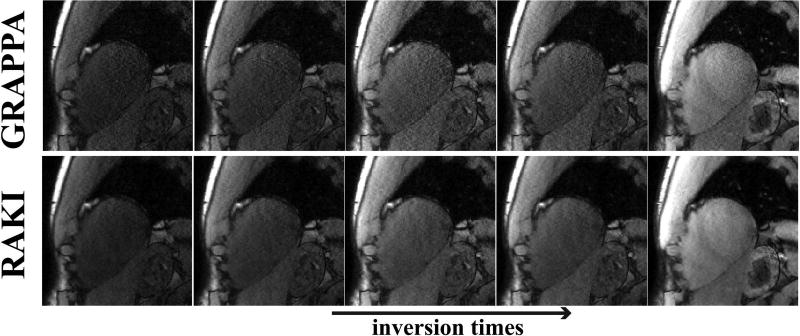
Figure 5 and 6 show all of the 11 T₁-weighted images acquired using the SAPPHIRE sequence at the improved spatial resolution of 1.1×1.1 mm², and acceleration rate 5. In this substantially lower SNR regime, due to the higher acceleration rate and improved resolution, the noise improvement of RAKI over GRAPPA is visually apparent for all images. A quantitative analysis of the resulting T₁ maps indicate that the spatial variability of the myocardial T₁ is 253.8 ms using the RAKI-reconstructed images versus 403.5 ms using the GRAPPA-reconstructed images, indicating a 37% improvement. The improvement is observable across all subjects, with an overall 48% improvement in spatial variability with RAKI. We note that in two cases, GRAPPA reconstruction do not provide image quality that allows for reasonable quantitative evaluation, as residual artifacts and excessive noise amplification, prevent reliable delineation of the myocardium against the blood-pools. For the remaining two cases, the improvements in spatial variability are 37% and 31% for RAKI.

Figure 5.

6 T₁-weighted images, corresponding to the shortest inversion times, acquired using the SAPPHIRE sequence at a high spatial resolution of 1.1×1.1 mm², and acceleration rate 5. At this high acceleration rate, the noise improvement of RAKI over GRAPPA is observable for all images. A quantitative analysis of the resulting T₁ maps indicate that the spatial variability of the myocardial T₁ is improved by 37% using RAKI versus GRAPPA.

Figure 6.

5 T₁-weighted images, corresponding to the longest inversion times, from the same dataset depicted in Figure 5. At this high acceleration rate, the noise improvement of RAKI is observable for all images. Quantitative analysis of T₁ map spatial variability shows 37% improvement using RAKI versus GRAPPA.

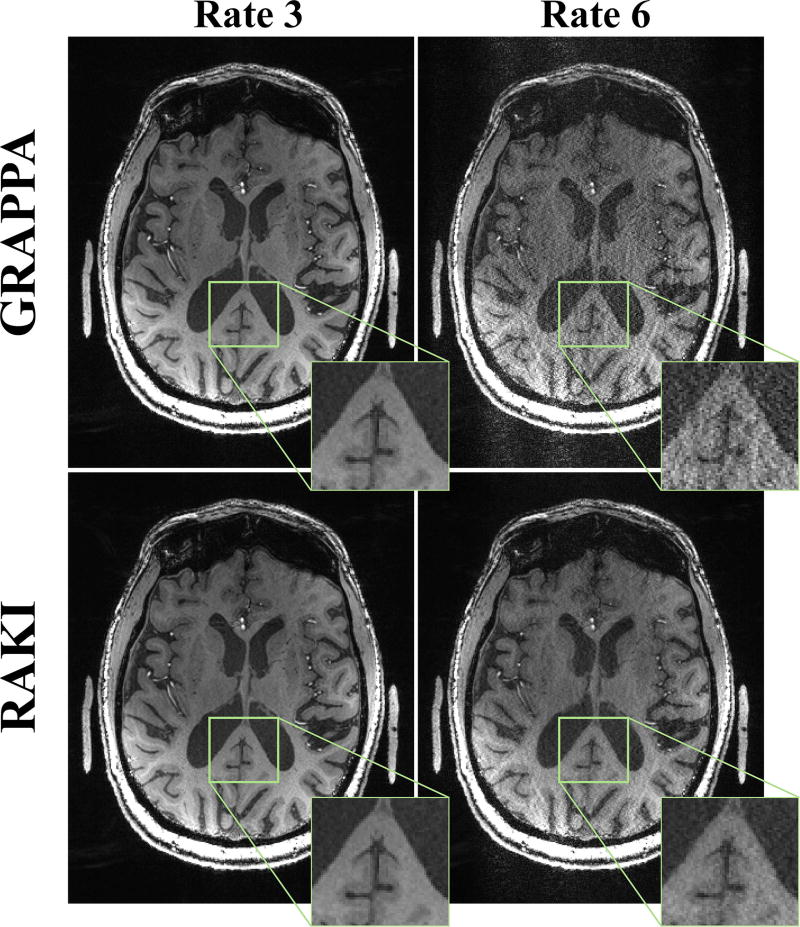
Figure 7 depicts a slice of the high-resolution 7T MPRAGE acquisition on the patient, both at the acquisition acceleration rate of 3, as well as at a retrospective acceleration rate of 6. At rate 3, RAKI and GRAPPA methods both successfully reconstruct the image with little residual artifacts. At rate 6, GRAPPA reconstruction suffers from pronounced noise amplification, whereas the proposed RAKI reconstruction exhibits better noise tolerance. However, some residual aliasing artifacts remain due to the high-level of in-plane acceleration. No blurring artifacts are observed with either method, even though the acquisition is performed at a very high resolution.

Figure 7.

A central slice of the high-resolution (0.6 mm isotropic) 7T MPRAGE acquisition, both at the acquisition acceleration rate of 3, as well as at a retrospective acceleration rate of 6. At rate 3, GRAPPA (top) and RAKI (bottom) methods both successfully reconstruct the image with little residual artifacts. At rate 6, GRAPPA reconstruction suffers heavily from noise amplification, whereas the proposed RAKI reconstruction exhibits improved noise tolerance without blurring artifacts.

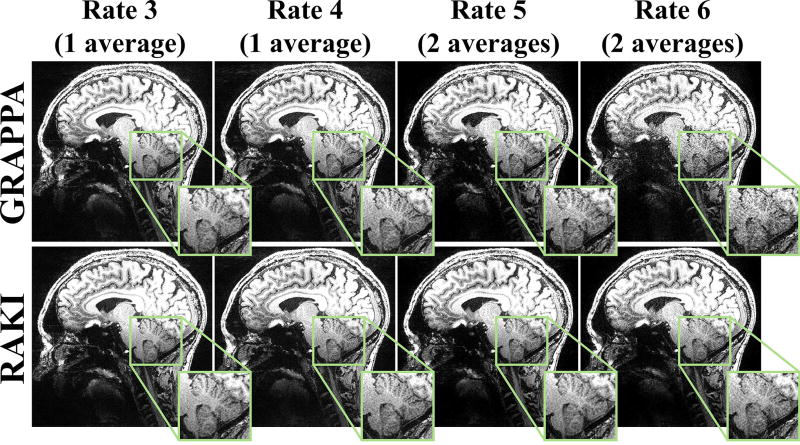
Figure 8 depicts a slice of high-SNR 0.6 mm isotropic 7T MPRAGE acquisition, at acceleration rates 3, 4, 5 and 6, where the latter two acceleration rates were acquired with two averages. At rates 3 and 4, both RAKI and GRAPPA successfully reconstructs the images with little artifacts. At R = 5, GRAPPA and RAKI starts exhibiting slight differences, with the latter showing better noise performance. The differences become more pronounced at R = 6, while the quality also degrades for both reconstructions. At the higher rates, RAKI has improved noise amplification with no apparent blurring.

Figure 8.

A central slice of the high-resolution (0.6 mm isotropic) MPRAGE acquisition at 7T, acquired at R = 3, 4, 5 and 6, where the first two rates were acquired with one average, and the latter two were acquired with two averages. Thus, the only SNR penalty between R = 3 and 6 is due to differences in coil encoding. The results show that at this high SNR, GRAPPA (top) and RAKI (bottom) reconstruct the images with little residual artifacts up to R = 4. At R = 5, slight differences between GRAPPA and RAKI can be observed, with the latter showing better noise performance. At R = 6, the difference is further pronounced. At the higher rates, RAKI has improved noise tolerance while exhibiting no blurring artifacts.

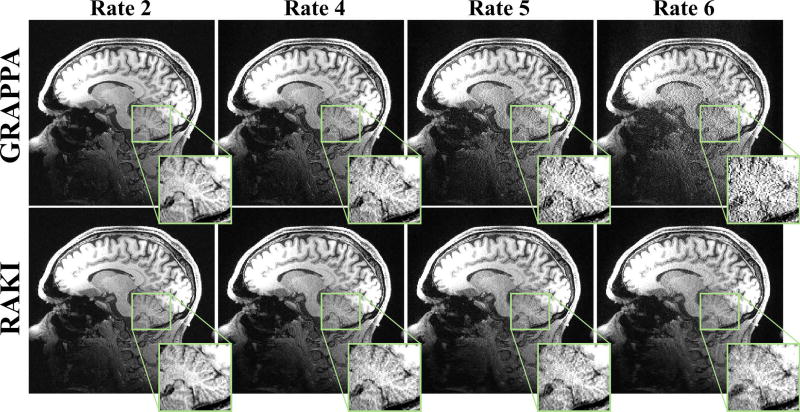
Figure 9 depicts a slice of the 0.7mm isotropic 3T MPRAGE acquisition, at the acquisition acceleration rates of 2 and 6, as well as at a retrospective acceleration rates of 4 and 6. At rate 2 and 4, RAKI and GRAPPA methods both successfully reconstruct the image with little residual artifacts. At rate 5, RAKI visually outperforms GRAPPA in terms of noise amplification, while incurring no visible reconstruction artifacts or blurring at this high-resolution. R = 6 reconstructions also show RAKI has visible noise advantages over GRAPPA, though at this high acceleration rate, both reconstructions have visible residual artifacts.

Figure 9.

A central slice of the high-resolution (0.7 mm isotropic) MPRAGE acquisition at 3T, acquired at R = 2 and 5, as well as retrospective R = 4 and 6. At rates 2 and 4, GRAPPA (top) and RAKI (bottom) methods both successfully reconstruct the image with little residual artifacts. At rates 5 and 6, noise amplification becomes visible for GRAPPA reconstruction. At these rates, RAKI has improved noise tolerance and exhibits no blurring artifacts.

Discussion

In this study, we developed a k-space method, called RAKI, enabling deep learning for reconstruction of undersampled data from ACS data, as an alternative to linear k-space interpolation techniques. This enables us to generate a non-linear function to estimate the missing k-space data from the acquired k-space lines without additional training on databases containing many subjects. In effect, our approach creates subject-specific neural networks for a non-linear reconstruction, which extends upon the subject-specific linear convolution kernels used successfully in many parallel imaging reconstruction techniques, including GRAPPA. Our results indicate that RAKI offers improved noise performance compared to GRAPPA in phantom and in vivo imaging.

The use of machine learning for MRI reconstruction has recently received increasing interest. These recent works aim to build on the immense success of deep learning in image processing applications, and have focused on training reconstruction algorithms on large amounts of datasets. Big data training has led to different regularization approaches for MR images, most often as regularizers without an explicit formula and based on CNNs (19,22,23,43), or as unsupervised learning of parameters for variational networks (21). In this work, we took an MRI-focused approach and considered the problem as a k-space estimation problem instead of an image domain regularization problem. This approach avoids dependency on large amounts of training data, and instead uses a small amount of ACS data, similar to existing parallel imaging reconstructions that are used in clinical practice. We also note that almost a decade ago, the use of neural networks was proposed for improving SENSE reconstruction in a scan-specific manner (44). However, this earlier work did not utilize CNNs, and was not further explored beyond the original conference publication. Furthermore, the work in (44) employs an image domain approach based on SENSE formulation. Due to the use of non-linear reconstructions, this is not necessarily equivalent to our k-space formulation, so its relative efficacy to our approach is hard to compare.

The non-linearity in our convolutional network architecture improves the noise performance of the reconstructions, as presented in our experiments. This non-linearity was introduced by the use of ReLU functions in all layers, except the last one. Other non-linear activation functions, such as sigmoid functions (27), have also been explored in neural network community, and can also be applied as part of our method. However, ReLU has several advantages. Since it has a gradient that is either 0 or 1 - unlike the sigmoid function, which can take arbitrarily small non-zero derivatives - its derivative can be back-propagated across multiple layers without convergence issues, enabling deeper network architectures. The nature of the ReLU function also enables sparsity in representations (45). With a random initialization of weights, half of the output values are zeroes, facilitating an inherent data sparsification.

The use of non-linear methods to improve GRAPPA reconstruction has been explored before (26,46), but without the use of concepts from neural networks. A fixed set of virtual channels for a higher-dimensional feature space (26) or transform-domain sparsity (46) has also been proposed before. RAKI differs from these techniques, by refraining from any explicit assumptions on k-space or transform domains. Instead neural networks were shown to effectively represent a non-linear function for estimating missing k-space data, successfully facilitating model-free reconstruction.

The advantage of our method over a linear reconstruction approach like GRAPPA becomes apparent at high acceleration rates or at low SNRs. In the other regimes, GRAPPA is known to perform very well, thus differences are not noticeable. At the high acceleration rate regime, both RAKI and GRAPPA approaches require larger ACS regions for better estimation of the reconstruction filters. Due to the multi-layer network architecture, RAKI has more unknowns. In most applications, where one is interested in these higher rates, e.g. diffusion, perfusion or quantitative MRI, it is not difficult to obtain one set of high-quality ACS data of sufficient size, which can be shared across multiple scans. The success of training a set of CNNs from one set of ACS data for varying contrast acquisitions was shown in our cardiac imaging experiments. Nonetheless, there may be applications where ACS region cannot be increased easily. In these cases, several modifications to our method are possible. One approach would be to reduce the number of layers. Another would be to reduce the output sizes for each layer. An alternative approach would be to perform a hybrid reconstruction, by first performing linear GRAPPA reconstruction in the central region to grow the ACS region and then use this larger area for training the neural network in RAKI reconstruction. All these approaches warrant further investigation in specific applications, but these were not pursued in this study.

Unfortunately there are no existing methods for optimally determining the network structure in deep learning applications (27). Therefore several parameters for the network architecture were determined heuristically. These include the number of layers, the kernel sizes for each layer, the output sizes for the first and second layer, as well as the activation functions. The kernel sizes were chosen to not increase the number of unestimated k_y boundary lines beyond a [5,4] GRAPPA kernel, while enabling contributions from neighboring locations in the first and last layers. The number of layers and output sizes of each layer were chosen to limit the number of unknowns in the CNN, in order not to increase the required ACS data for training. The output size for the last layer was also a design choice, and our networks were trained to output all missing lines per coil. Other alternatives are possible. For instance, a different network can be trained per coil per each missing k-space locations relative to the acquisition location. However, this increased the number of unknowns by roughly a factor of R − 1, and provided virtually no benefit in preliminary observations. An alternative approach would be to train the network to output all the missing lines for all coils. This would require deeper networks and bigger output sizes per layer. We did not explore this alternative since we wanted to avoid interactions across coils in the output layer, in order to provide a fair comparison to GRAPPA. However, alternative network architectures with such interactions may be beneficial and will be explored in future work.

Another design decision for the CNNs used in this work was the exclusion of bias terms for all three layers. In standard deep learning practice, both a set of convolutional filters and a set of biases are trained at each layer. For instance, in the first layer, this would correspond to convolutional filters w₁ of size b₁^x×b₁^y×2n_c×n₁, and a bias term b₁ of size 1×1×n₁, and the output of this layer would be calculated as ReLU(w₁ * x + b₁). However, due to their additive nature, inclusion of biases increases dependence on how the l₂ (or l_∞) norm of the k-space is scaled. This creates major limitations in processing data with multiple-varying contrast, as in quantitative MR parameter mapping, when training is done on one set of ACS data with a specific contrast weighting, which was the case in our experiments. Therefore biases were not used in our CNNs, although they may find utility in other settings.

The application of the CNN to missing lines is not significantly more time-consuming than the application of GRAPPA kernels. For the CNN architecture and GRAPPA kernels used in this manuscript, for acquired n_x·n_y/R k-space points, the complexity of the CNN approach per k-space point is (1280n_c² + 512n_c + 96(R−1)n_c) real additions and multiplications, and 40 logical comparisons. For GRAPPA this is approximately 20(R−1)n_c² complex additions and multiplications per acquired k-space point. Thus, in terms of the number of real multiplications, for n_c = 32, RAKI has a ~7-fold overhead at R = 4 and ~4-fold overhead at R = 6, compared with GRAPPA. However, the calibration of the GRAPPA kernel can be done with a simple linear least squares problem, whereas the CNN needs to be trained with a gradient descent. Our MATLAB implementation for the gradient descent has an approximate run-time of 5–6s for 250 iterations, which can likely be improved using optimized implementations or parallelization with graphics processing units (GPU).

There are limitations to the use of the current proposed approach. As with other parallel imaging approaches, the coil geometry in the acquisition has to be able to support the desired acceleration rates. Aliasing artifacts may persist if the rate is increased further (see Supporting Figure S1). As discussed earlier, the CNN architecture was heuristically selected. The performance of the approach may change based on different network parameters, similar to how the performance of linear methods is affected by kernel sizes. The optimization problem in the deep learning portion of the approach is based on minimizing a non-linear least squares objective function depicted in Equation [9]. Unlike the linear least squares problem in GRAPPA, this objective function is non-convex. Thus, there is a potential of converging to local minima. This is typically handled using momentum in gradient descent approaches, which has been shown to work well in practice (37). Nonetheless, the solution to Equation [9] is not exact, but approximate. A further limitation in our current implementation is the use of fixed learning rates in the gradient descent algorithm. While these rates were optimized heuristically for in-vivo datasets, they may not be optimal in all applications (see Supporting Figure S1 for phantom data). To overcome this limitation, further work on implementations and optimizers that can adaptively update the learning rate is warranted, and is one of our current topics of research.

Since our proposed method works with uniformly undersampled acquisitions, it has the potential to be applied to existing highly-accelerated and low-SNR datasets to improve reconstruction quality, such as those generated by Human Connectome projects (47). It could also easily be employed in most protocols, as it does not require modifications to data acquisition.

Our RAKI reconstruction naturally extends to other approaches that utilize k-space interpolation. Although we concentrated on GRAPPA and uniform undersampling for 2D acquisitions in this study due to their high utility, RAKI reconstruction is applicable to both 2D and 3D acquisitions with uniform undersampling (3,48,49), as well as to simultaneous multi-slice imaging (24,50). It is also applicable to random undersampling patterns as an alternative to SPIRiT convolution kernels (4), and can be combined with image regularization in this setting (10). It can also be extended to non-Cartesian acquisitions, as an alternative to linear convolutional approaches, such as radial (25) or spiral (4) acquisitions. These extensions are beyond the scope of the current study and will be explored in future work.

Conclusion

The proposed reconstruction uses a scan-specific deep learning approach with convolutional neural networks trained on limited ACS data to improve upon the reconstruction quality of linear k-space interpolation-based methods.

Supplementary Material

Supp info

Supporting Figure S1: Results from a higher SNR version of the experiment in the Phantom Imaging subsection. These highlight the effect of the heuristic choice of learning rate on the current implementation of the gradient-descent (g.d.) in the RAKI algorithm. RAKI reconstructions using in-vivo optimized (opt.) learning rates (bottom row) exhibits more artifacts than those using phantom optimized learning rates (middle row) during the training stage. All reconstructions perform similarly for R = 2,3,4, with RAKI using the in-vivo optimized learning rates showing higher noise amplification at R = 4. At R = 5, 6, all reconstructions suffer from residual aliasing and noise artifacts (arrows). Here, RAKI with phantom optimized learning rate has a similar degree of residual aliasing with GRAPPA (top row), and slightly lower noise amplification. RAKI with the in vivo optimized learning rate displays higher residual aliasing compared to the other two methods. These results indicate the use of fixed learning rates, as in the current implementation, is a limitation, and the use of alternative optimizers for RAKI is warranted during the learning stage.

Supporting Figure S2: RAKI reconstructions on a 0.6 mm isotropic 7T MPRAGE dataset, where the CNN was trained from the full ACS region (top row), and half the ACS region in the readout direction (middle and bottom rows). The reconstructions are almost identical, with minor differences in noise due to the number of points available in the training datasets, showing the training is robust to changes in the calibration region, if the SNR of the calibration region is not substantially altered.