A Bayesian hierarchical model for demand curve analysis

Abstract

Drug self-administration experiments are a frequently used approach to assessing the abuse liability and reinforcing property of a compound. It has been used to assess the abuse liabilities of various substances such as psychomotor stimulants and hallucinogens, food, nicotine, and alcohol. The demand curve generated from a self-administration study describes how demand of a drug or non-drug reinforcer varies as a function of price. With the approval of the 2009 Family Smoking Prevention and Tobacco Control Act, demand curve analysis provides crucial evidence to inform the US Food and Drug Administration’s policy on tobacco regulation, because it produces several important quantitative measurements to assess the reinforcing strength of nicotine. The conventional approach popularly used to analyze the demand curve data is individual-specific non-linear least square regression. The non-linear least square approach sets out to minimize the residual sum of squares for each subject in the dataset; however, this one-subject-at-a-time approach does not allow for the estimation of between- and within-subject variability in a unified model framework. In this paper, we review the existing approaches to analyze the demand curve data, non-linear least square regression, and the mixed effects regression and propose a new Bayesian hierarchical model. We conduct simulation analyses to compare the performance of these three approaches and illustrate the proposed approaches in a case study of nicotine self-administration in rats. We present simulation results and discuss the benefits of using the proposed approaches.

1. Introduction

Relative reinforcing efficacy (RRE) is a fundamental concept frequently used in substance abuse research.^1,2 It describes the reinforcing potency and abuse liability of a substance. A self-administration experiment is a valuable tool to assess RRE. Self-administration studies have been widely employed to study the reinforcing strength of various substances such as psychomotor stimulants and hallucinogens,^1,3 food,⁴ nicotine,^5,6 and alcohol.⁷ The demand curve data obtained from a self-administration experiment describe how demand of a drug or non-drug reinforcer varies as a function of price.⁸ According to the law of demand, the consumption of a commodity generally decreases when its price increases; as such, conceptually, the demand curve is always downward sloping.

The approval of the 2009 Family Smoking Prevention and Tobacco Control Act incentivizes research to determine the RRE of nicotine in order to inform the US Food and Drug Administration (FDA) about individual characteristics (such as gender, smoking history) in response to nicotine-reduction tobacco products, the feasibility of a nicotine-reduction policy, and its potential public health impact. Animal self-administration studies provide vital evidence to support the FDA’s future policy on tobacco product regulation because rodent models of nicotine self-administration (NSA) are the gold standard for assessing reinforcing properties of nicotine.⁶ In addition, human self-administration studies, such as cigarette purchase tasks, suffer from issues such as reporting errors, non-compliance, and loss of follow-up.

A number of models have been proposed to perform demand curve analysis;^9,10 the most recent and popularly used model is the exponential demand curve, which has the following form

$$\log Q=\log Q_0+K(e^{-\alpha P}-1)$$ (1)

In equation (1), Q is the quantity consumed, Q₀ is the amount consumed when the unit price P of a good approaches 0. For example, in animal and human research on drug addiction, Q₀ is the level of consumption of nicotine, cigarettes, or other abused drugs, when there is no cost or effort required to obtain those commodities. Other parameters in the demand curve described in equation (1) are K and α (a measure of demand curve elasticity). Elasticity describes the rate of decline in relative log consumption, i.e. how quickly consumption falls with increases in price. According to Hursh and Silberberg,⁹ α is the measure of reinforcing strength.

Another two clinically relevant quantities related to the demand curve are O_max and P_max. O_max is the maximum expense (price times consumption) a person is willing to spend for a commodity; P_max is the corresponding unit price. O_max is clinically important because of its correlation with clinical addiction indices in both alcohol and nicotine studies.¹¹ It can be calculated by the following equation

$$O_{max}=P_{max}Q=P_{max}{Q}_0{e}^{K(e^{-\alpha P_{max}}-1)}$$ (2)

P_max does not have a closed form solution and is obtained by solving the following equation

$$K\alpha P_{max}{e}^{-\alpha Pmax}=1$$ (3)

The conventional method popularly used to estimate exponential demand curve is the individual-specific nonlinear least squares regression model (NLIN),^9,7,11 which can be implemented through GraphPad Prism software. The NLIN method uses a three-step approach. First the parameter K in equation (1) is determined based the range of the data. K is calculated as the difference of maximum and minimum observed consumptions in the data in log_e unit and set as a constant across all animals in the data. Second, the individual values of α and Q₀ are determined by minimizing the residual sum of squares, one-subject-at-a-time. Finally, the overall α, Q₀, P_max and O_max estimates are calculated as the mean of individual α, Q₀, P_max, and O_max estimates obtained from each subject. The 95% confidence intervals for α, Q₀, P_max and O_max estimates are obtained by assuming the estimates are normally distributed.

There are several concerns in using the conventional approach for exponential demand curve analysis: (1) The estimation of P_max and O_max estimates rely heavily on graphical methods.^8,11 Although graphical methods could be straightforward, they have limitations in that the resolution of estimating P_max and O_max is restricted by the sample rate of price.¹¹ (2) The ad hoc estimation of K might have large impacts on the estimations of other parameters. (3) Current approaches do not obtain the standard errors for P_max and O_max in a model-based framework. These issues are addressed using alternative approaches considered in this study: mixed effects regression and a Bayesian hierarchical model.

A left-censored mixed effects regression method has been considered by Liao et al.¹² to model the exponential demand curve in settings with zero consumption. In order to obtain the standard deviation of P_max and O_max in the mixed effects model framework, we proposed to use the bias-corrected and accelerated bootstrap approach¹³ due to the skewness of P_max and O_max distribution. On the other hand, the Bayesian approach proposed in this study offers a straightforward approach to compute means, standard deviations, and 100(1–α) percent equal-tail credible intervals (equal-tail CIs) for P_max and O_max based on posterior distributions. This is particularly crucial because the distribution of P_max and O_max is often skewed. As a result of major developments of computational algorithms,¹⁴ the use of Bayesian approaches is rapidly increasing.¹⁵

In this paper, we discuss statistical inference and compare the performance of the three approaches: the NLIN, mixed effects approach via maximum likelihood (ML) estimation method, and the proposed Bayesian approach via the Markov chain Monte Carlo (MCMC) method, with a focus on small-to-moderate sample sizes.

In Section 2, we describe a motivating case study that estimated demand curves in rats self-administering nicotine during progressive unit-dose reduction.⁵ In Section 3, we describe the mixed effects regression and Bayesian hierarchical model. In Section 4, we present the implementation of the Bayesian hierarchical model using data from the case study. The simulation studies to compare the performance of the three approaches are presented in Section 5. Finally, a discussion of various approaches is presented in Section 6.

2. Material and study design

The data were collected from a study designed to model a nicotine-reduction policy in rats by arranging progressive decreases in the unit dose of nicotine to the point of extinction of self-administration in every subject. The study aimed to examine the gender difference in NSA in rats.⁵ Seven male and seven female Holtzman rats were trained to self-administer nicotine during daily 23-h sessions. The price of nicotine—defined as the number of responses required per unit dose¹⁶—was then increased weekly by reducing the unit dose of nicotine until responding fell to within the range of extinction levels. The amount of nicotine consumed (mg/kg/day) by each rat was recorded at each unit price. More details about the experimental procedures are described in Grebenstein et al.⁵ The data are represented in Table 1, and each value is the mean of three 23-h sessions. The blank cells in Table 1 indicate that the consumption of nicotine fell to within the range of extinction levels.

Table 1.

Observed price and consumption data in rats during progressive unit dose reduction in the nicotine self-administration case study.

	Price	50	100	150	300	429	750	1500	3000	6000	12000
Males	Nicotine consumption
1		2.022	1.611	1.246	0.8	0.4571	0.1692	0.032
2		1.482	1.08	0.82	0.613	0.1589	0.0588	0.0106
3		1.44	0.981	0.814	0.46	0.1449	0.052	0.014
4		2.22	1.461	1.04	0.643	0.4179	0.22	0.0346	0.0117
5		1.38	1.011	0.9	0.587	0.4809	0.22	0.088	0.029	0.00565	0.002175
6		1.68	1.32	1.046	0.6	0.476	0.2492	0.0834
7		1.656	0.771	0.72	0.46	0.2751	0.096	0.018
Females
1		3	1.44	1.026	0.683	0.168	0.0652
2		2.22	0.969	0.9	0.263	0.147	0.032
3		1.62	0.831	0.734	0.287	0.0959	0.0428	0.0094
4		3.36	1.899	1.126	0.683	0.567	0.3348	0.0586
5		1.998	1.17	1	0.55	0.4571	0.2188	0.0606	0.0193	0.0108
6		1.842	1.221	1.094	0.72	0.5159	0.2732	0.1314	0.0227	0.00885
7		2.322	1.35	0.926	0.67	0.4501	0.232	0.04	0.0157

3. Statistical methods

3.1. Mixed effects model

Let y_ij be the log consumption of nicotine for the ith rat at the jth price P_j. In the data under the study, the model can be written as follows

$$y_{ij}=[C_0+C_{M}I(Mal{e}_i)+u_i]+e^{\log K}\left\{e^{-[({\alpha }_0+{\alpha }_{M}I(Mal{e}_i)+b_i)P_j]}-1\right\}+{\epsilon }_{ij}$$ (4)

where C_M is the difference in the log consumption between male and female rats when the price P_j=0; α₀ represents the rate of decline; α_M captures the group difference of the rate of decline between male and female rats. The two random effects u_i and b_i represent the log consumption at price 0 and the rate of decline for each rat, respectively. These random effects follow a bivariate normal distribution with mean 0 and a covariance matrix structure ${\displaystyle \sum =}\left[\begin{array}{cc}{\mathit{\sigma }}_{\mathit{u}}^2& \mathit{\rho }{\mathit{\sigma }}_{\mathit{u}}{\mathit{\sigma }}_{\mathit{b}}\\ \mathit{\rho }{\mathit{\sigma }}_{\mathit{u}}{\mathit{\sigma }}_{\mathit{b}}& {\mathit{\sigma }}_{\mathit{b}}^2\end{array}\right]$, and ρ represents the correlation between the log consumption at price 0 and reinforcing value. The correlation of the log consumption of nicotine y_ij across different j for a given rat i is modeled through the random effects. Given the random effects u_i and b_i, the error terms ε_ij for a given rat i are independent and were assumed to follow a normal distribution with mean 0 and variance σ². In this model framework for male rats, the log consumption at price zero is C₀+ C_M, and the rate of decline in consumption is α₀+α_M.

Table 2 shows the analysis results using NLIN and mixed effects model. The results using the NLIN approach have been presented and described in Grebenstein et al.⁵ The results using two approaches yield consistent conclusion; however, the 95% CI estimates using the three-step NLIN approach assume that the parameter estimates follow normal distribution. This assumption can be violated when sample size is small or when the distributions of the estimators are skewed. In addition, the results in Table 2 also suggested that the ad hoc estimation of K has considerable impact on the estimations of other parameters using the NLIN approach.

Table 2.

Demand curve parameter estimates and their corresponding standard errors and 95% CI/equal-tail CI for rats during progressive unit dose reduction in the nicotine self-administration case study.

	Method
	Non-linear least square regression		Mixed effects regression		Bayesian hierarchical approach
Parameter	Estimate (95% CI)	SE	Estimate (95% CI)	SE	DF	Estimate (95% equal-tail CI)	SE
C0	2.69 (1.81, 3.56)	0.36	0.91 (0.66, 1.16)	0.12	12	0.92 (0.69, 1.16)	0.12
CM	0.67 (−0.25, 1.59)	0.41	−0.25 (−0.60, 0.10)	0.16	12	−0.28 (−0.59, 0.04)	0.16
α0	4.40 (2.63, 6.17)	0.72	10.54 (6.58, 14.50)	1.83	12	10.70 (7.19, 13.92)	1.71
αM	−0.03 (−2.00, 1.94)	0.89	− 1.93 (−7.33, 3.48)	2.48	12	−2.46 (−6.47, 1.83)	2.11
logK	2.50	NA	1.77 (1.73, 1.82)	0.02	12	1.77 (1.73, 1.82)	0.02

Note: The estimates and SEs are multiplied by 10⁴ in all methods.

In the mixed effects model, when the price is close to 0, indicating that there is no effort needed, female rats consume e^0.906 = 2.48 mg/kg of nicotine: this is statistically significant with 95% CI of (1.93, 3.18). Male rats initially consumed less nicotine in log scale than female rats; however, this is not statistically significant, because the parameter estimate for C_M is −0.25 with 95% CI of (−0.60, 0.10). The reinforcing strength for female rats (α₀) is 1.053 × 10⁻³ and is statistically significantly different from zero, with a 95% CI of (6.58 × 10⁻⁴, 1.45 × 10⁻³). Male rats have a lower rate of decline in nicotine consumption than female rats; however, this is not statistically significant because the parameter estimate α_M is −1.93 × 10⁻⁴, with a 95% CI of (−7.34 × 10⁻⁴, 3.48 × 10⁻⁴). The result suggests that there was no sex difference in the reinforcing efficacy of nicotine. The overall R² using the mixed effects model is 0.9865.

After obtaining the estimates of K, α₀, α_M, we calculated P_max by solving equation (3) and then calculated O_max using equation (2). We performed sampling with replacement to obtain bootstrap standard deviation for P_max and O_max and implemented a bias-corrected and accelerated approach¹³ to calculate the 95% CIs, as shown in Table 3. The bias-corrected and accelerated approach is a method of obtaining approximate CIs using the percentiles from the bootstrap histogram. The time required for bootstrap resampling depends on the number of bootstrap iterations and sample size. Using the data from the nicotine study in rats described in this paper, one iteration took around 4.4 s to complete using a single-core 2.8 GHz Intel Xeon X5560 Nehalem EP processor and 1000 iterations took around 73 min (4348 s).

Table 3.

P_max and O_max estimates and their corresponding standard deviations for the case study.

	Method
Parameter	Non-linear least square regression Estimate (95% CI)	Mixed effects regression Estimate (95% CI)	Bayesian hierarchical approach Estimate (95% equal-tail CI)
Pmax for Male rats	293.23 (151.08,435.38)	243.13 (220.00, 364.45)	255.18 (241.72, 422.31)
Pmax for Female rats	240.34 (116.28, 364.40)	198.70 (152.09, 292.60)	209.07 (148.02, 311.23)
Omax for Male rats	172.94 (126.36, 219.52)	153.73 (125.72, 267.47)	159.64 (116.74, 236.37)
Omax for Female rats	183.11 (l24.50, 241.73)	161.66 (117.80, 216.70)	167.29 (129.08, 225.16)

3.2. Bayesian hierarchical approach

We used the same notation as described in Section 3.1. Assuming that log consumption y_ij’s for each rat at different price P_j are independently distributed with mean η_ij and variance σ² = 1/τ. In the data we used in this study, the model can be written as

$${\eta }_{ij}=(C_0+C_{M}I({\mathrm{Male}}_i)+u_i)+e^{\log K}\left\{e^{-[{\alpha }_0+{\alpha }_{M}I({\mathrm{Male}}_i)+b_i)P_j]}-1\right\}$$

Let π(θ) be the prior joint distribution of C₀, C_M, u_i, logK, α₀, α_M, b_i, τ where θ=(C₀, C_M, u_i, logK, α₀, α_M, b_i, τ). The random effects follow a multivariate normal:

$$\left(\begin{array}{c}{\mathit{u}}_{\mathit{i}}\\ {\mathit{b}}_{\mathit{i}}\end{array}\right)~MVN\left[\left(\begin{array}{c}0\\ 0\end{array}\right),\sum \right],{\sum }^{-1}\sim \mathrm{Wishart}(\mathit{\Omega },p)$$

where Ω is a scale matrix, a prior guess for the covariance matrix and p is the degrees of freedom. The likelihood can be written as

$$L(Y|\theta )={\displaystyle \prod _{i=1}^N{\displaystyle \prod _{j=1}^M[f(y_{ij}|{\eta }_{ij},\tau )}}]$$

Thus, the posterior joint distribution of C₀, C_M, u_i, logK, α₀, α_M, b_i, τ given the observations is proportional to

$${\displaystyle \prod _{i=1}^N{\displaystyle \prod _{j=1}^M[f(y_{ij}}}|{\eta }_{ij},\tau )]\pi (C_0)\pi (C_M)\pi (u_i)\pi (b_i)\pi (\log K)\pi (a_0)\pi (a_M)\pi (\tau )$$

Posterior computation was done using MCMC methods¹⁴ and carried out using downloadable free software JAGS (http://mcmc-jags.sourceforge.net)¹⁷ and the rjags package in R (http://www.r-project.org/).¹⁸ The model code is available upon request. The burn-in consisted of 10,000 iterations; 50,000 subsequent iterations were used to compute the posterior summaries of the model parameter estimates. Convergence of MCMC was assessed using the Gelman and Rubin convergence statistic¹⁹ with three chains. The GR diagnostics for all parameter estimations are all close 1, which confirms that the chains have converged. The posterior credible intervals for C₀, C_M, α₀, α_M, and logK are obtained from the posterior distributions approximated by the posterior samples by using the MCMC chains.

4. Illustration

We assume that y_ij is normally distributed with mean η_ij and variance σ²=1/τ. Non-informative prior distributions were specified as τ ~ gamma(10⁻³, 10⁻³), C₀ ~ N(0, 10³), C_M ~ N(0, 10³), α₀ ~ N(0, 10³), α_M ~ N(0, 10³), and logK ~ N(0, 10³). The random effects for each rat $\left(\begin{array}{c}{u}_i\\ b_i\end{array}\right)$ were assumed to follow a bivariate normal distribution:

$$MVN\left(\left(\begin{array}{c}0\\ 0\end{array}\right),\sum \right),{\sum }^{-1}~\text{Wishart}\left(\left[\begin{array}{cc}0.1& 0.005\\ 0.005& 0.1\end{array}\right],3\right).$$

Based on the 5 × 10⁴ MCMC samples, Figure 1 presents the posterior distributions for C₀, C_M, α₀, α_M, logK, and τ. The posterior distribution of P_max can be obtained based on equation (3) using the 5 × 10⁴ MC samples for α₀ and logK. Likewise, O_max was calculated using equation (2) from the posterior samples of P_max, C₀, α₀, and logK. The values of P_max and O_max and their corresponding standard deviations for male and female rats are shown in Table 3 (right panel). The conclusions of analyzing the experimental data using Bayesian approach are consistent with the results from NLIN and the mixed effects regression.

Figure 1.

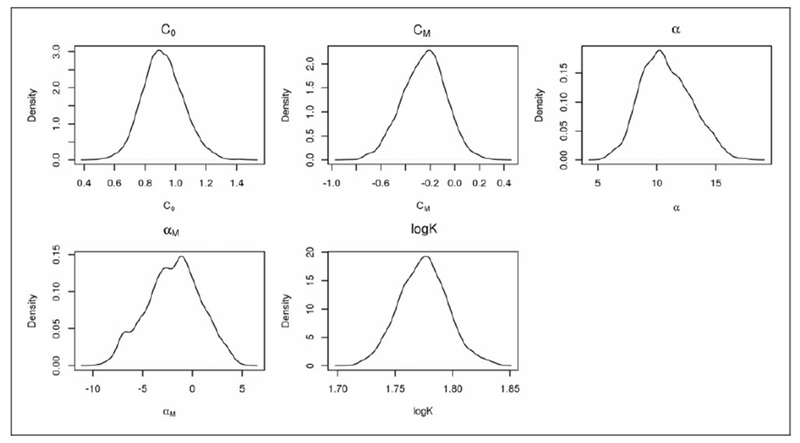
Posterior distributions for demand curve parameter estimates.

Figure 2 presents the posterior distributions for P_max and O_max for male and female rats, respectively. These distributions could not have been obtained by using a mixed effects regression approach. Figures 3 and 4 show the demand curve for each rat on log scale, with 95% equal-tail credible interval for log consumption of nicotine for each rat. These figures indicate that log nicotine consumption for all the rats in the data was well described using the Bayesian approach.

Figure 2.

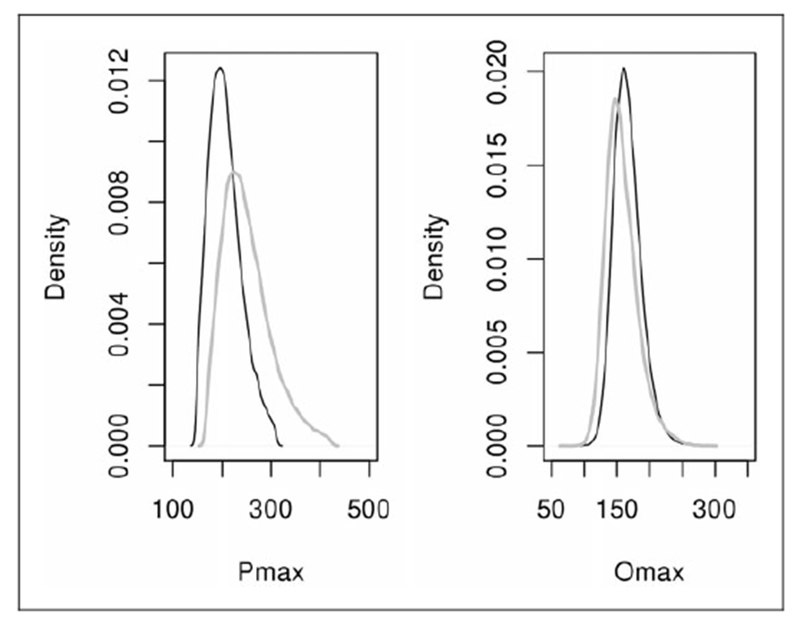
Posterior distributions of P_max and O_max for male (gray line) and female (black line) rats.

Figure 3.

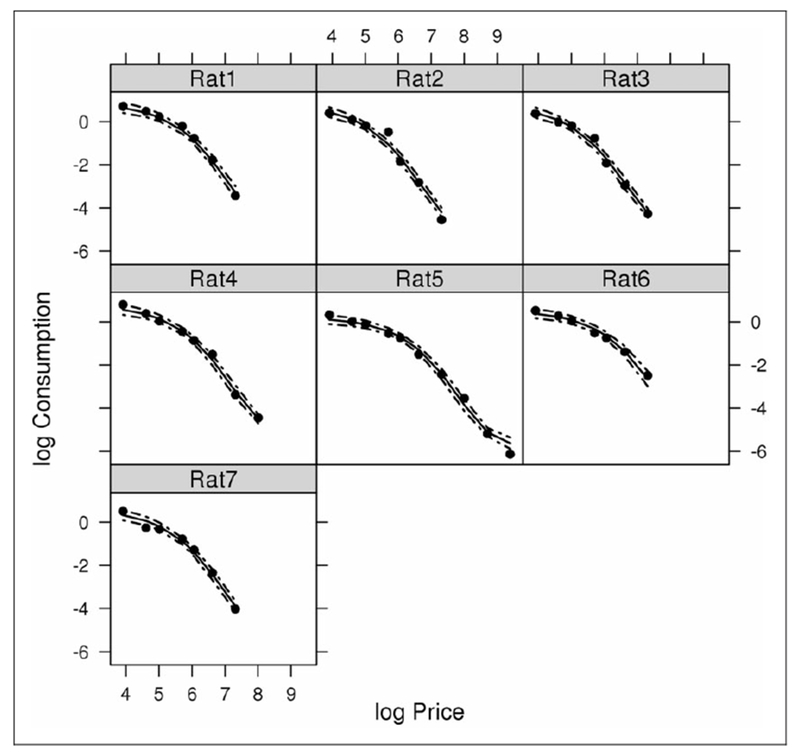
Demand curve for each male rat with 95% credible interval. Black dots represent observed value; solid lines are the predicted values from the Bayesian model with 95% credible intervals indicated by dotted line.

Figure 4.

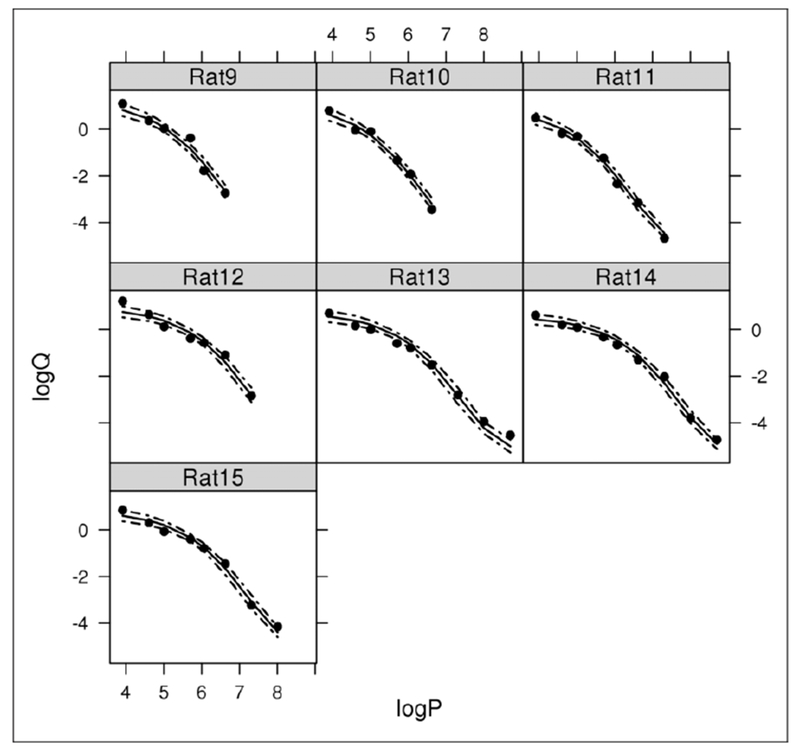
Demand curve for each female rat with 95% credible interval. Black dots represent observed value; solid lines are the predicted values from the Bayesian model with 95% credible intervals indicated by dotted line.

In addition, we calculated R² as the square of the correlation between the observed and predicted log consumption. The R² for three methods are 0.9747, 0. 0.9865, and 0.9866 for the NLIN, mixed effects model, and the Bayesian approach, respectively, as shown in Figure 5. These results are consistent with the conclusion in Grebenstein et al.⁵ The results further support Hursh’s claims that the demand curve offers a useful approach to model drug abuse policy in animals and humans.^8,16

Figure 5.

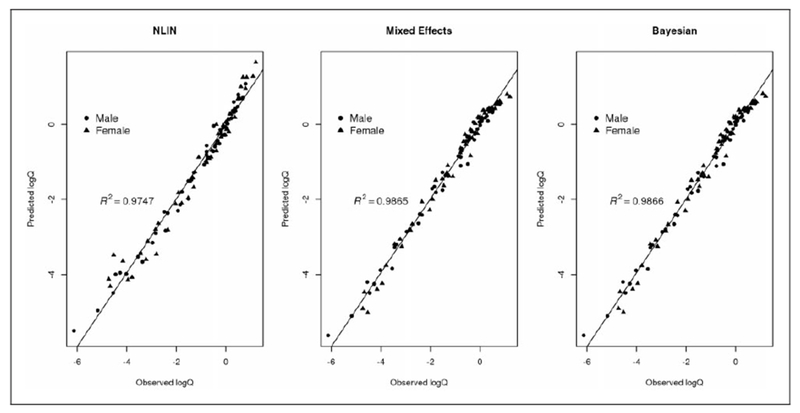
Predicted log nicotine consumed vs. observed values for NLIN, mixed effects model, and Bayesian approach.

To further validate the models, we applied leave-one-out cross-validation to assess the predicative performance of the models. We implemented two cross-validation approaches. In the first approach, we randomly set aside one observation and used the remaining observed values to fit models for each rat. Then, we calculated the mean absolute error (MAE) of the prediction for the holdout sample. We implemented 1000 cross-validation iterations. The MAEs (standard error) are 0.254 (0.0018), 0.209 (0.0014), and 0.203 (0.0013) for NLIN, mixed effects model, and the Bayesian approach, respectively. In the second approach, we hold out a randomly selected rat at a time and implemented 1000 cross-validation iterations. In the leave-a-rat-out-at-a-time approach, the MAEs are 0.551 (0.0054), 0.478 (0.0055), and 0.485 (0.0044) for NLIN, mixed effects model, and the Bayesian approach, respectively. According to the MAEs reported from both cross-validation approaches, the mixed effects model and Bayesian approach have comparable predicative performance, and both methods outperform the NLIN approach.

5. Simulation studies

We generated 1000 datasets with an even number of rats, half of which were males and the remaining half were females. Nicotine consumption measured at 10 various prices for all rats. The true values for C₀, C_M, α₀, α_M, logK were set at 1, −0.3, 10, −2, 1.8, respectively. Five sets of simulation studies were done by varying the sample sizes from 10 rats to 50 rats, at an increment of 10 rats each time. The random effects for each rat were generated from a bivariate normal distribution, and specifically the random effects were

$$\left[\begin{array}{c}{\mathit{u}}_{\mathit{i}}\\ {\mathit{b}}_{\mathit{i}}\end{array}\right]~N\left(\left[\begin{array}{c}0\\ 0\end{array}\right],\left[\begin{array}{cc}0.1& 0.005\\ 0.005& 0.1\end{array}\right]\right).$$

We analyzed the simulated datasets using three approaches: NLIN, mixed effects model with ML, and the Bayesian approach via the MCMC method.

The mean relative biases (MRBs) for the three approaches are shown in Table 4. The MRB is calculated as the mean difference between the true parameter and the estimated values divided by the value of the true parameter. Based on the simulation results, the NLIN approach demonstrates relatively large biases compared to the mixed effects and Bayesian hierarchical models. With increasing sample size, the biases for logK are larger using the NLIN approach. Consequently, due to the bias in estimating logK, the biases for α₀, α_M also grow large with increasing sample size. In addition, the biases for estimating the reinforcing strength of female rats (α₀) are the largest among all parameter estimations. On the other hand, the estimations for C₀, C_M are less affected by the bias in estimating logK in the NLIN approach; the MRBs for estimating C₀, C_M are smaller when the sample size increases. Compared to NLIN, both mixed effects and Bayesian hierarchical models demonstrate relatively small biases (less than 4%) in parameter estimations, and the results for the two approaches are similar.

Table 4.

Mean relative errors for demand curve parameters based on 1000 datasets.

Number of rats in each simulation	Parameter	Non-linear least square	Mixed Effects	Bayesian approach
N=10	α0	−0.27	0.0061	0.0106
	αM	0.06	0.0086	0.0140
	logK	0.12	0.0003	−0.0002
	C0	0.18	0.0006	0.0057
	CM	0.59	−0.0126	0.0000
N=20	α0	−0.35	−0.0017	0.0009
	αM	−0.05	−0.0240	−0.0195
	logK	0.14	0.0003	0.0000
	C0	0.11	−0.0034	−0.0021
	CM	0.57	−0.0280	−0.0303
N=30	α0	−0.40	0.0017	0.0029
	αM	−0.10	0.0109	0.0125
	logK	0.15	−0.0001	−0.0003
	C0	0.06	0.0087	0.0046
	CM	0.63	0.0385	0.0215
N=40	α0	−0.43	0.0020	0.0030
	αM	−0.16	−0.0006	0.0005
	logK	0.16	0.0002	0.0000
	C0	0.03	0.0039	0.0055
	CM	0.55	−0.0053	−0.0041
N=50	α0	−0.46	0.0005	0.0016
	αM	−0.21	0.0010	0.0015
	logK	0.17	0.0003	0.0002
	C0	−0.01	0.0035	0.0044

The empirical 95% coverage probabilities and the length of CIs or equal-tail CIs using the three approaches were calculated and are shown in Table 5. The empirical 95% coverage probability is the percent of the 95% CI or credible intervals (equal-tail CI) covering the true parameter based on 1000 Monte Carlo simulations. In the NLIN approach, logK is calculated based on the range of consumption; hence, the standard deviation and CIs cannot be obtained (shown as NA). As indicated by the simulation results, the NLIN approach demonstrates a relatively low 95% CI coverage rate compared to the other two alternative approaches. The 95% coverage rates are the lowest for α₀. Furthermore, the lengths of CIs obtained by the NLIN approach are longer than the other two alternative approaches. The simulation results shown in Table 5 suggest that the Bayesian hierarchical approach provides better 95% credible interval coverage rates for the estimation of C₀, C_M. On the other hand, for α₀, α_M estimation, the mixed effect model reports longer CI lengths and hence achieves better empirical 95% CI coverage probability.

Table 5.

Empirical coverage probability of 95% confidence/credible interval and interval lengths based on 1000 datasets.

Number of rats in each simulation	Parameter	nonlinear least square		Mixed effects		Bayesian approach
		Coverage probability	CI length	Coverage probability	CI length	Coverage probability	Equal-tail CI length
N=10	α0	0.18	3.05	0.97	2.95	0.94	2.55
	αM	0.89	3.75	0.97	3.78	0.95	3.27
	C0	0.74	0.76	0.88	0.57	0.93	0.66
	CM	0.86	1.07	0.88	0.78	0.94	0.92
	logK	NA	NA	0.98	0.07	0.95	0.06
N=20	α0	0.01	2.29	0.96	1.90	0.95	1.77
	αM	0.89	2.71	0.96	2.43	0.95	2.26
	C0	0.75	0.59	0.88	0.41	0.96	0.45
	CM	0.85	0.83	0.89	0.57	0.95	0.63
	logK	NA	NA	0.96	0.05	0.95	0.04
N=30	α0	0.00	1.93	0.96	1.51	0.95	1.44
	αM	0.84	2.20	0.96	1.93	0.95	1.83
	C0	0.77	0.51	0.87	0.34	0.94	0.37
	CM	0.81	0.73	0.88	0.47	0.94	0.52
	logK	NA	NA	0.95	0.04	0.94	0.04
N=40	α0	0.00	1.66	0.94	1.29	0.94	1.24
	αM	0.78	1.88	0.96	1.65	0.95	1.58
	C0	0.77	0.45	0.88	0.30	0.94	0.32
	CM	0.82	0.64	0.89	0.41	0.94	0.45
	logK	NA	NA	0.95	0.03	0.95	0.03
N=50	α0	0.00	1.47	0.95	1.14	0.94	1.10
	αM	0.72	1.64	0.96	1.45	0.95	1.41
	C0	0.73	0.41	0.87	0.27	0.95	0.29
	CM	0.82	0.58	0.90	0.38	0.95	0.40
	logK	NA	NA	0.95	0.03	0.96	0.03

To compare the robustness of the three methods when model is mis-specified, we simulated data with 100 rats under the model below¹⁰

$$\log Q_{ij}=\log l+b\log p_j-a{p}_j+{\epsilon }_{ij}$$

i = 1, 2, … 100 and j = 1, 2, … 10. In the above equation, Q_ij is the consumption for the ith rat at the jth price point. The predictive consumptions were obtained using the three models. The MAEs of predictive values are 22.128, 11.410, and 11.425 for NLIN, mixed effects model, and the Bayesian approach, respectively. The mixed effects model and Bayesian approach are much more robust than the NLIN approach when the model is mis-specified. In summary, our simulation analyses suggest that the Bayesian model and the mixed-effect model have comparable performance and both achieve better performance than NLIN approach.

6. Discussion

In this paper, we compared three existing approaches for analyzing demand curve data. In the analysis results from animal NSA data analysis, both mixed effects and Bayesian hierarchical approach are comparable. In the mixed effects regression framework, a general form of the exponential demand function can be expressed as:

$$y_{ij}=\left(C_0+{\displaystyle \sum _{k=1}^p{\beta }_k{X}_k}+u_i\right)+e^{\log K}\left[e^{-({\alpha }_0+{\displaystyle {\sum }_{k=1}^q{\gamma }_k}{Z}_k+b_i)P_j}-1\right]+{\epsilon }_{ij}$$

In this equation, C₀ is the original log consumption with price at zero; X_k and Z_k are the covariates that contribute to the differences of log consumption and rate of decline, respectively; β_k and γ_k are the corresponding coefficients. For the Bayesian approach, a general form for estimating the exponential demand curve can be expressed as

$${\eta }_{ij}=\left(C_0+{\displaystyle \sum _{k=1}^p{\beta }_k{X}_k}+u_i\right)+e^{\log K}\left[e^{-({\alpha }_0+{\displaystyle {\sum }_{k=1}^q{\gamma }_k}{Z}_k+b_i)P_j}-1\right].$$

The Bayesian approach provides direct statistical inference for two clinical relevant quantities: P_max and O_max through sampling from posterior distributions. Additional bias-corrected and accelerated bootstrap analysis is required to obtain 95% confidence for P_max and O_max through a mixed effects regression model. The predictive performance using cross-validation indicated that both Bayesian and mixed effects methods achieve smaller MAEs than the NLIN approach.

The computational time required for implementing NLIN, mixed effects, and Bayesian model using the data described in this paper are 0.21 s, 4362 s, and 3877 s in a single-core 2.8 GHz Intel Xeon X5560 Nehalem EP processor. Although the computational time for the mixed effect model and Bayesian approach are longer than the conventional NLIN approach, the simulation analyses (Tables 4 and 5) indicate that with small-to-moderate sample sizes, the popularly used NLIN approach demonstrates relatively large estimation biases and a low 95% CI coverage rate. The performances of mixed effects regression and Bayesian hierarchical approaches are comparable. The Bayesian approach provides posterior distributions for all estimated parameters. In addition, the advantages of using the Bayesian approach are more pronounced, when the sample size is small. With current advances in computing capacities and modern computational algorithms via MCMC, the Bayesian method can be easily implemented, and thus should be considered a good alternative when estimating the demand curve in public health research.