Pharmacokinetic/Pharmacodynamic Background and Methods and Scientific Evidence Base for Dosing of Second-line Tuberculosis Drugs

Abstract

A World Health Organization workshop systematically examined the evidence base for dosing second-line tuberculosis drugs, identifying knowledge gaps. To fill these in, pharmacokinetics/pharmacodynamics, Monte Carlo experiments, and artificial intelligence algorithms were used in hollow-fiber model studies and clinical data analyses.

What has been will be again, what has been done will be done again; there is nothing new under the sun. Is there anything of which one can say, “Look! This is something new”? It was here already, long ago; it was here before our time.

Kohelet (Ecclesiastes) 1:9

The World Health Organization (WHO) recommends treating multidrug-resistant (MDR) tuberculosis with a multidrug regimen that consists of drugs from 4 groups of drugs, shown in Table 1. The WHO also recommends short-course MDR tuberculosis treatment for select patients using, 7 drugs as induction and 4 as maintenance therapy, from the same groups in Table 1. In this short regimen, as well as with longer-course treatments for MDR tuberculosis, it is crucial to achieve optimal dosing. To facilitate better dosing of these second-line drugs, as well as first-line drugs, and to identify susceptibility break points for tuberculosis programs, the WHO convened a workshop in Versoix, Switzerland, in April 2017. The technical report resulting from the deliberations has been published by the WHO [1]. Some of the systematic analyses performed and presented at that meeting are published in the current special supplement. These analyses summarize the literature on what is currently known about dosing for these drugs. Where there was a poor evidence base, we performed pharmacokinetic/pharmacodynamic (PK/PD) experiments followed by Monte Carlo experiments (MCEs), and in some cases clinical validation of identified doses. These results are also published in the current supplement.

Table 1.

WHO Second-line Drugs, PK/PD Studies, and Systematic Analyses

Drug	Full PK/PD Experiments	Systematic Analysis
Group A: fluoroquinolones
Moxifloxacin	Current supplement (high dose)	No
Gatifloxacin	This supplement	No
Levofloxacin	This supplement	No
Group B: second-line injectable
Kanamycin	No	No
Amikacin	Past publications	This supplement
Capreomycin	No	No
Group C
Ethionamide (prothionamide)	Current supplement	No
Cycloserine (terizidone)	Current supplement	Current supplement
Linezolid	Past publications	Current supplement
Clofazimine	Past publications	No
Group D
D1
Ethambutol	Past publications	No
Isoniazid (high dose)	Current supplement	No
Pyrazinamide	Current supplement (high dose)	Past publications
D2
Bedaquiline	No	No
Delamanid	No	No
D3
Imipenem + cilastatin or meropenem + clavulanate	No	No
Para-aminosalicylic acid	No	No
Thioacetazone	No	No

Abbreviations: PK/PD, pharmacokinetic/pharmacodynamic; WHO, World Health Organization.

THE ANTIMICROBIAL PK/PD BASIS OF DOSING: HERE BEFORE OUR TIME

The treatment of many infectious diseases underwent a transformation with the introduction of PK/PD science [2, 3]. A series of brilliant articles that used in vitro and animal models of several gram-negative and gram-positive bacterial infections, starting with Harry Eagle in the 1950s [4] and systematized by Craig and colleagues in the 1980s and 1990s [3], 5–7], established the central aspects of this approach. They established that exposure-effect and dose fractionation study findings derived in preclinical models were invariant with findings in patients [2, 8]. An invariant function is one that remains unchanged when transformation is applied; in this case the exposure-effect relationship in preclinical models when translated to patients.

Why is this, in the case of the exposure-effect relationship? First, although antibiotics are not endogenous ligands, they satisfy postulates of receptor theory. Indeed, the concept of antibiotics as ligands was introduced by Paul Ehrlich 120 years ago [9], and was the forerunner to receptor theory, which arose later. Receptors or antibiotic target proteins in bacteria are saturable and finite. That is the basis of successful chemotherapy. Thus, as antibiotic concentration increases, microbial kill from the biochemical inhibition increases based on concentration-dependent binding to target protein, until saturation, at which point increasing antibiotic concentration does not kill any further or at a higher rate (maximum effect [E_max]). Thus, the inhibitory sigmoid E_max model is used for both antibiotics and receptor theory, as exemplified in the articles in this supplement. A prototypical exposure-response curve is shown in Figure 1, a side-by-side wither standard curve for ligand versus receptor curve.

Figure 1.

Receptor theory and antibiotic kill of pathogens. In standard receptor theory describing the occupancy of receptors by ligand, the log concentration plotted against percentage response is a sigmoid shape. The shape is the same for log-transformed bacterial burden versus drug concentration, except that instead of percentage response the actual bacterial burden measured is shown as the response. The E_max is the total microbial kill, at which point drug has occupied all the target proteins in bacteria: increasing the drug concentration (by increasing the dose) will not occupy any more target proteins to cause more biochemical inhibition or increase the microbial kill. Abbreviations: CFUs, colony-forming units; E_max, maximum effect; EC₅₀, half-maximal effective concentration.

Second, is the role of the minimum inhibitory concentration (MIC). The role of the MIC is perhaps best illustrated by a classic rat model of Pseudomonas infection study by Drusano et al [10], in which animals infected with isogenic wild-type strains or 2 or 4 times the wild-type MIC were treated with the same dose of lomefloxacin, and survivorship recorded. Rats infected with bacteria that had 2 times and 4 times the lomefloxacin MIC had a correspondingly poor survivorship as the MIC increased. Proportionate increase in dose improved survivorship to the same extent as in rats infected with the wild type. Thus, there was correspondingly poor outcome as the MIC increased. The drug concentration measures can be expressed as peak concentration or 24-hour area under the concentration-time curve (AUC_0–24). As a result of the inverse effect of MIC on outcome, these concentrations result in 3 PK/PD indices: the ratio of peak concentration to MIC (peak/MIC), AUC_0–24/MIC, or time that concentration persists above MIC. These are used as exposures in the inhibitory sigmoid E_max model, and compared with the bacterial burden to show the exposure-effect relationships.

Starting in 2002, PK/PD designs were also used in tuberculosis preclinical PK/PD studies in mouse and Guinea pig models and the hollow-fiber system model of tuberculosis (HFS-TB) [11–18]. These studies established the relationship between PK/PD exposure and microbial kill, based on the inhibitory sigmoid E_max model, as well as for acquired drug resistance (ADR), based on a new quadratic function model [12–24]. The PK/PD relationships were later demonstrated to be invariant in patients with tuberculosis [18, 25, 26]. However, not much PK/PD work had yet been done with the second-line antituberculosis drugs, except moxifloxacin, in WHO groups [1].

This supplement reports the use of the HFS-TB in identifying PK/PD relationships of single second-line drugs, as well as combination therapy, and the optimal duration of therapy. Where possible, clinical data from other studies were used to validate the HFS-TB plus MCE-based dose and MIC findings. The accuracy of HFS-TB in tandem with MCE output in forecasting optimal doses, MIC break points, the proportion of patients responding to therapy, or ADR, has been established as within 94% of the final value identified in clinical trials reported after publication of the HFS-TB work [18, 26, 27].

EXPERIMENTAL DESIGN IN HFS-TB PK/PD STUDIES: NOTHING NEW UNDER THE SUN

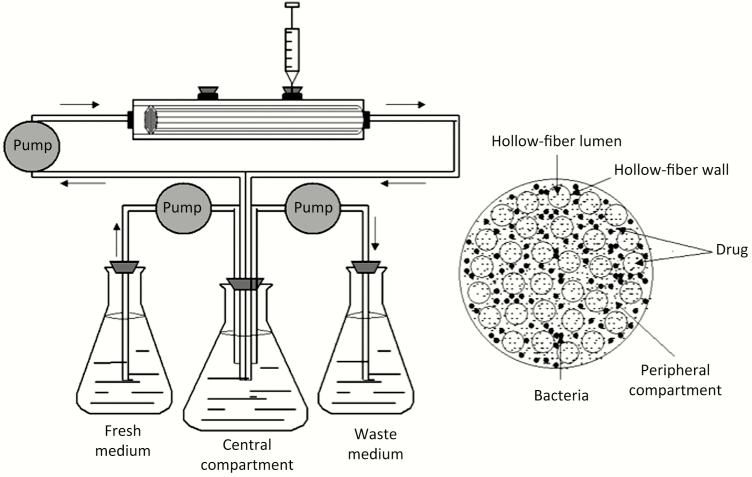
The HFS-TB models and design described in the current article are not new; they go back 16 years in the tuberculosis field and are based on general PK/PD work with other bacteria [3, 5–7]. The model consists of a peripheral compartment separated from central compartment by semipermeable or hollow fibers, as shown in the schematic in Figure 1. Mycobacterium tuberculosis are grown into log-phase growth for 4 days, or transformed to semidormant bacteria for 4 more days, after which 20 mL of 10⁶ colony-forming units/mL is inoculated into the peripheral compartment of several HFS-TB units. In some models of intracellular M. tuberculosis, human-derived monocytes are first infected with M. tuberculosis, and 20 mL of infected monocytes is inoculated. The bacteria are maintained in the peripheral compartment and cannot pass into the central compartment because the semi-permeable fibers have a low pore size with a cut-off of approximately 42 kD.

Antibiotics, which are small molecules, are administered via computerized syringe pump into the central compartment, circulate within the central compartment of the HFS-TB, and rapidly cross to the peripheral compartment where M. tuberculosis is housed under equilibrium. The antibiotic concentration declines at the same half-life as encountered in patients, and achieves peak concentrations as well as AUC_0–24 values encountered in patients. The dosing frequency is specified, as is the duration of therapy, by a computer program controlling the syringe pump. The concentration-time profiles achieved are validated by sampling the central compartment up to 12 times over a specified period and measuring the drug concentrations actually achieved, which are used to calculate AUC_0–24/MIC, peak/MIC, or the percentage of time that concentration persists above MIC. The peripheral compartment was sampled on days 0, 3, 5, 7, 10, 14, 21, and 28 to estimate the total M. tuberculosis burden, as well as the M. tuberculosis subpopulation resistant to 3 times the MIC. Advantages over animal models, such as rodents, include examination of the same concentration-time profiles as in humans (rodents have different concentration-time curves than human, often from rapid elimination), and repetitive sampling that allows examination of evolution of resistance within same unit over time, and hence better mathematical modeling of time to extinction of the M. tuberculosis population.

HFS tuberculosis output is analyzed using the inhibitory sigmoid E_max model, described above and shown in Figure 1. The PK/PD indices versus exposure, either the percentage of time that concentration persists above the MIC, the AUC_0–24/MIC, or the peak/MIC, are each examined versus bacterial burden, and the best PK/PD index is selected using Akaike information criteria [18, 27]. The inhibitory sigmoid E_max model is used to calculate the PK/PD exposure associated with 80% of maximal kill, depicted in Figure 2. The EC₈₀ is considered optimal because the inhibitory sigmoid E_max model maximal effect is on an asymptote and therefore the PK/PD exposure associated with 100% kill is at infinity. On the other hand, the relationship between the drug-resistant subpopulation and PK/PD exposure is not a sigmoid E_max curve, but instead a system of quadratic functions that change with time [21–25]. Each PK/PD index and exposure is also modeled against drug-resistant subpopulation in the quadratic function, and the index is linked to resistance, also chosen using Akaike information criteria. The EC₈₀ and the PK/PD exposure associated with suppression of ADR are invariant with patients, consistent with general PK/PD principles, and based on prior work in HFS-TB [18, 26–28].

Figure 2.

The hollow-fiber system model of tuberculosis schematic. The system consists of 3 components: a central compartment, peripheral compartment, and a computerized syringe pump (not shown). The central compartment comprises a central reservoir and circulation flow path, and the inner lumina of hollow fibers (semipermeable membranes). Fresh medium broth is added to the central compartment, and used medium is isovolumetrically removed to the waste medium container, to produce any elimination rates desired. The peripheral compartment is the abluminal part of the hollow fibers that is encased in a plastic cartridge. Extracellular bacteria, as well as intracellular bacteria, are added to peripheral compartment via syringes, which is also the way the system is sampled. The syringe pump is programmed to give any dose schedule and time to maximum concentration, and it delivers the drug directly into central compartment, where it circulates and is in rapid equilibrium with the peripheral compartment.

THE POPULATION PK BASIS OF EXPOSURE VARIABILITY

When a dose of any drug is administered to patients, between-patient PK variability leads to a wide distribution of peak concentration and AUC_0–24 values in the patients. The PK/PD consequence of between-patient PK variability is that even if patients were infected with pathogens that had identical MICs, they would achieve different values for AUC_0–24/MIC, peak/MIC, or percentage of time that concentration persists above MIC. However, the MICs in isolates vary from patient to patient and have their own distribution, compounding the variability in PK/PD exposure ratios. It was unclear for many years what role such PK and MIC variability played in determining outcomes in patients with tuberculosis. Starting with HFS-TB output in tandem with MCEs for trajectory of sputum bacterial decline 10 years ago, followed by prospective clinical studies and meta-analyses, several studies have since shown that PK and MIC variability are major determinants of ADR, sputum conversion, cure, relapse, and death [29–32]. Thus, in designing optimal doses for second-line drug doses, both PK and MIC variability need to be accounted for when transforming the invariant exposure-effect relationships from preclinical models to patients.

MCES INTEGRATE INVARIANT RELATIONSHIPS, PK AND MIC VARIABILITY

In 1985, Katz and D’Argenio [33] used MCEs to generate the randomness of PK parameters of aminoglycosides, based on PK parameter estimates and variability derived in 42 patients, to identify optimal doses. MCEs were first introduced by Metropolis and Ulam [31] in the 1940s in the Manhattan project, during the design of the first nuclear bomb. MCEs allow the generation of a distribution of PK parameters and exposures such as AUC_0–24, peak, and concentration-time profiles in up to 10000 random patients. Because serum or plasma concentrations are the most accessible data, the penetration into tuberculosis lung cavities and subarachnoid space is also taken into consideration in calculating the final concentrations in different tuberculosis anatomic sites [34–36]. Different doses are examined to generate AUC_0–24, peak concentrations, and T_MIC. The probability of target attainment (PTA) is the proportion of the 10000 virtual patients who achieve the PK/PD exposure target (EC₈₀ or the exposure suppressing resistance) at each MIC. The cumulative fraction of response (CFR), the proportion of patients who achieve the PK/PD exposure target, is calculated by summing results at each MIC (i):

$$\text{CRF = }{\displaystyle {\sum }_{i=1}^n{\text{PTA}}_i}\cdot F_i,$$

where i is the individal MIC and F is the proportion of isolates at each MIC. This is a conservative approach, in that it considers the effect of a single drug that will be used in combination therapy.

ARTIFICIAL INTELLIGENCE AND THE DECONVOLUTION OF EFFECT OF SINGLE DRUGS

The PK/PD approach of using HFS-TB and MCEs examines target attainment of a single drug at a time. A vexing problem in tuberculosis, and indeed in general pharmacology in which polypharmacy is used, was how to deconvolute the effect of component drugs in a combination regimen. Insights on how to deconvolute came from the realization that biological systems such as pharmacokinetics and patient responses have elements of randomness, do not satisfy the superposition principle, exhibit high-order nonlinear interactions, and are often even fractals [30, 37, 38].

According to the superposition principle, the net response is a sum of the responses to the multiple responses to the different stimuli (linear), which is always not true of patient response to multiple-drug therapy, hence concepts of synergy and antagonism. Response to drug A plus response to drug B plus response to drug C is not equal to the composite response to the combination ABC. Thus, a nonlinear science approach, such as machine learning (a branch of artificial intelligence [AI]), was required.

Several algorithms written by Breiman, Friedman, and colleagues between 1984 and 2002 [39–41] were chosen because they identify and classify predictors, rank predictors by order of importance, and were specifically designed to handle nonlinear higher-order interactions. Application in clinical studies identified the effects of the PK variability of component drugs in combinations, and their synergistic and antagonistic high-order interactions, and the effect of the MICs of component drugs [30, 37–43]. These approaches also identified optimal PK/PD thresholds, which were found to be virtually the same as those identified for preclinical PK/PD models of tuberculosis and MCEs. Truly, there is nothing new under the sun!

ESTABLISHMENT OF EVIDENCE BASE AND IDENTIFICATION OF PK/PD GAPS

For systematic analyses, PubMed and Web of Science were queried using the following search terms: (drug name OR alternative drug name) AND (tuberculosis OR TB OR Mtb) AND (pharmacokinetics OR concentration OR therapeutic drug monitoring OR TDM OR drug exposure OR drug monitoring OR pharmacology OR pharmacodynamics OR pharmacol* OR pharmacod*). We also examined the references of the identified articles to search for more articles. Two independent reviewers performed the search. Extraction and reporting was based on the Preferred Reporting Items for Systematic Reviews and Meta-analyses (PRISMA) guidelines. In case of differences, consensus was reached by discussion. Results were reported in tables, knowledge gaps were identified, and conclusions were drafted as short statements.

First, prospective, observational, or retrospective studies that reported PK variability in patients with tuberculosis, based on PK sampling at steady state, were included. Reviews, case reports, and studies in healthy volunteers were excluded. Assay parameters for drug concentrations measurements were judged on the basis of compliance with European Medicines Agency, US Food and Drug Administration, and/or Clinical and Laboratory Standards Institute guidelines for bioanalytical validation. Second, animal and HFS-TB PK/PD studies were selected if the studies reported on microbial kill or development of resistance. The studies were judged based on presentation of data on pharmacokinetics, MIC, and microbial outcomes (preferably including relapse in mice).

ORGANIZATION OF THE SPECIAL SUPPLEMENT: TINKER, TAILOR, SOLDIER, AUTHOR!

First, knowledge gaps in current dosing practices of second-line drugs were identified using systematic analyses and the framework of PK/PD science and PK variability. Second, HFS-TB PK/PD studies and MCEs based on the experimental designs described above were used to design new doses to fill in the identified gaps. Third, the AI approaches outlined above were used to analyze clinical studies that used the second-line drugs, to validate the HFS-TB and MCE findings. Fourth, because the question of duration of therapy is as important as dose size, a new approach was used that would take HFS-TB data and translate to duration of treatment. Results were then applied to a single HFS-TB-derived quinolone regimen. Results are presented following this order in the current supplement. The articles in the supplement were written by up to 40 authors as a result. The authors are practitioners in microbiology, MIC determination, pharmacologists, systematic analyses, AI, PK/PD analysis, HFS-TB models, and clinical care. They hail from across the world, including Bangladesh, Belgium, France, India, Indonesia, the Russian Federation, the Netherlands, Nepal, South Africa, Sweden, Tanzania, Switzerland, Thailand, the United Kingdom, the United States of America, Vietnam, and Zimbabwe, making this a global effort. Many others contributed but declined to be authors.

The order of articles in the supplement will follow the WHO second-line drug groups, shown in Table 1. Thus, the first set of articles are on group A antibiotics: gatifloxacin and levofloxacin [44–46]. Next, because a major focus of discussion at the WHO PK/PD session was the role of group B or injectable agents in Table 1, and their high rates of toxicity, a systematic analysis addressing amikacin efficacy versus toxicity was performed [47–50]. Group C agents have had no formal PK/PD studies, so the next grouping includes articles on cycloserine, ethionamide, and both old and new oxazolidinones [51, 52]. With regard to group D drugs, would high-dose moxifloxacin plus high-dose group D drugs such as isoniazid and pyrazinamide be able to shorten therapy? Murine tuberculosis studies predicted success of shorter-duration quinolone and high-dose therapy, but several phase III clinical trials were performed and demonstrated high failure rates for such regimens [45, 53–57].

Of the 2 penultimate articles, the first provides the derivation of an approach that could be used to predict optimal clinical therapy duration, starting in the HFS-TB, while the second applied the approach to high-dose group D drugs plus moxifloxacin HFS-TB findings to determine whether therapy duration could be shortened to <6 months [58, 59]. The final article is an editorial on the supplement, which summarizes how the results could be used to advance dosing in the clinical setting [60]. The conclusions made in the articles in this supplement are not formal recommendations on treatment, but they provide a useful background for future policy revisions

Notes

Financial support. This work was supported by the National Institute of Allergy and Infectious Diseases, National Institutes for Health (grant R56 AI111985).

Supplement sponsorship. This supplement is sponsored by the Baylor Institute of Immunology Research of the Baylor Research Institute.

Potential conflicts of interest. All authors: No reported conflicts of interest. All authors have submitted the ICMJE Form for Disclosure of Potential Conflicts of Interest. Conflicts that the editors consider relevant to the content of the manuscript have been disclosed.