Structural origin of slow diffusion in protein folding

Abstract

Experimental, theoretical and computational studies of small proteins suggest that inter-residue contacts not present in the folded structure play little or no role in the self-assembly mechanism. Non-native contacts can, however, influence folding kinetics by introducing additional local minima that slow diffusion over the global free-energy barrier between folded and unfolded states. Here we combine single-molecule fluorescence with all-atom molecular dynamics simulations to discover the structural origin for the slow diffusion that markedly decreases the folding rate for a designed α-helical protein. Our experimental determination of transition path times and analysis of the simulations point to non-native salt bridges between helices as the source, providing a quantitative glimpse of how specific intra-molecular interactions influence protein folding rates by altering dynamics and not activation free energies.

Summary

One 125 character sentence: Single-molecule experiments and all-atom MD simulations show how molecular interactions slow diffusion in protein folding.

One of the real surprises in studies of protein folding is that the rates for this complex self-assembly process can be adequately described by Kramers’ theory for diffusion of a single Brownian particle over a barrier on a one-dimensional free energy surface (1–6). The transition path, which corresponds to the barrier-crossing process, is the rare event in an equilibrium trajectory when the transition between folded and unfolded states actually takes place, and contains all of the mechanistic information on how a protein folds and unfolds (Fig. 1). Thanks to recent advances in both experimental methods and computer simulations, we are beginning to gain a deeper understanding of transition paths and folding mechanisms. The average time to cross the barrier, the transition path time, can now be experimentally determined from a photon-by-photon analysis of single molecule fluorescence experiments (7, 8). The transition path time is an important property because, unlike rate coefficients (Eq. 1) (1), which depend exponentially on the free energy barrier height, it is insensitive to the barrier height and gives direct information on the Kramers diffusion coefficient (Eq. 2) (7–11), i.e.

$$\frac{1}{k_f}=t_f=\frac{2\pi }{\beta D^{*}\sqrt{{\kappa }^{*}{\kappa }_{\text{U}}}}\text{exp}\left(\beta \text{Δ}{G}^{*}\right),$$ (1)

$$t_{TP}=\frac{1}{\beta D^{*}{\kappa }^{*}}\text{ln}\left(2e^{\gamma }\beta \text{Δ}{G}^{*}\right),$$ (2)

where D* is the diffusion coefficient for motion along the reaction coordinate at the barrier top and appears in the pre-factor of both equations. ΔG* corresponds to the barrier height, and κ_U and κ* correspond to the stiffness (curvatures) of the unfolded well and barrier top.

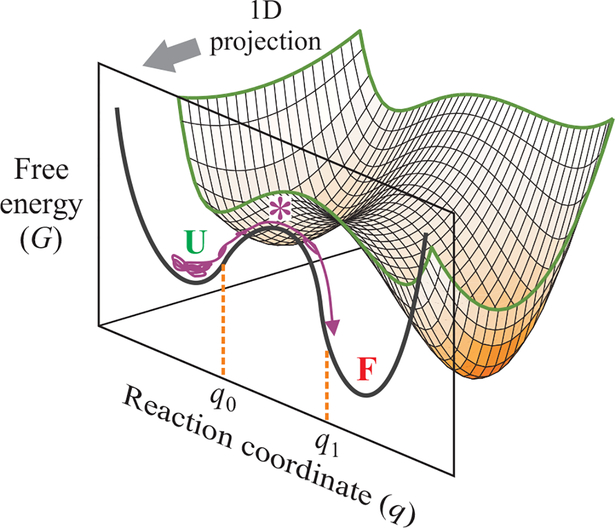
Fig. 1. One-dimensional free energy surface description of kinetics and dynamics of protein folding.

Protein folding dynamics are most often described by diffusion on a free energy surface obtained from a one-dimensional (1D) projection of a multidimensional free energy landscape. The folding transition path of a single molecule in an equilibrium trajectory is one that crosses q₀ on the reaction coordinate and reaches q₁ on the other side of the free energy barrier without recrossing q₀. The transition path appears as a jump in the experimental property being monitored in a single molecule trajectory. The folding rate coefficient, k_f, is the inverse of the average waiting (residence) time spent exploring the configurations of the unfolded well from which numerous unsuccessful attempts are made at crossing the free energy barrier.

The experimentally measured times can now be compared with those obtained from long trajectories containing many folding/unfolding transitions in all-atom molecular dynamics (MD) simulations of the folding process (12). These simulations also provide a wealth of atomistic detail on many aspects of the apparent mechanism of self-assembly, providing a structural basis for interpreting the experimental results (13–16). Analysis of the transition paths in simulations shows that for small proteins, non-native contacts appear to play little or no role in the mechanism (17) of folding. Such contacts, however, can influence the rates of folding in several ways. In addition to increasing the free energy barrier height, they can decrease folding rates by slowing diffusion over the barrier by introducing additional local minima and barriers in the underlying energy landscape, often called “roughness.” This latter effect reduces the Kramers diffusion coefficient (D*), which is a measure of the dynamics and appears in the pre-factor for both the rates and the transition path times (Eqs. 1 and 2). Consequently, D* is a key parameter in the theory of protein folding kinetics. It determines transition path times and sets the intrinsic time scale for folding rates. D* and the curvatures of the free energy surface also provide an estimate of the maximum rate at which a protein can fold, the so-called protein folding “speed limit” (18, 19), analogous to the von Smoluchowski diffusion limited rate for a bimolecular chemical reaction.

In spite of the importance of understanding the determinants of D*, there is as yet no information from experiments or simulations on the effect of specific types of inter-residue interactions on D*. The designed protein, α₃D (20, 21), a three-helix bundle, provides us with an opportunity to investigate this question because of its readily measurable, long transition path time at neutral pH (Fig. 2) (8). Analysis of previous simulations at neutral pH for α₃D showed that many non-native contacts form during the transition paths (13, 17), suggesting them as the structural origin for a lower D* that produces the long transition path time (Fig. 2). Non-native contacts are theoretically predicted to be more important for the kinetics and dynamics of designed proteins compared to naturally evolved protein. (22). Previous kinetic studies of α₃D showed that the folding rates are markedly increased when the carboxylates are neutralized at low pH (23) in urea solution at room temperature, suggesting that non-native salt bridges may play an important role. To test this hypothesis, we report here transition path time measurements from single molecule FRET experiments, along with a comparison of inter-residue interactions during transition paths from long equilibrium molecular dynamics trajectories in the presence and absence of the salt bridges.

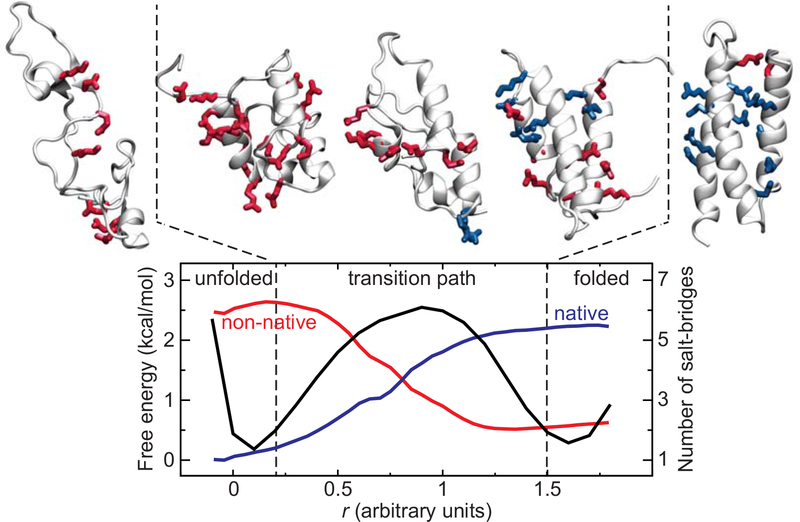
Fig. 2. α₃D folding transition path at neutral pH from MD simulation (13).

Exemplar structures from the unfolded state, the folded state, and the transition path are shown. The side chains of charged residues are represented in sticks and colored in red if they are involved in a non-native salt bridge, or in blue if the salt bridge is native. All other side chains are omitted for the sake of clarity. The transition path is defined as the region of the free energy surface (black) enclosed between the two dashed lines that separates the unfolded from the folded basin. The average number of native (blue) and non-native (red) salt bridges is also reported as a function of an optimized reaction coordinate. Salt bridges are determined using the stable-state picture (24) with cutoff distances of 4.5 and 8.0 Å between the Cγ of Asp or the Cδ of Glu and the Nζ of Lys or the Cζ of Arg. Salt bridges are considered native if they are within the longest cutoff distance in the experimentally determined structure 20. Note that due to the large number of highly flexible charged side chains present, ~2 non-native salt bridges can be transiently formed, on average, even in the folded state.

Experimental rates and transition path times

The FRET efficiency histograms in Fig. 3 show a marked increase in the folding rate for α₃D as the pH is lowered (23), in spite of a small change in the stability (Table S2 and Fig. 3). At neutral pH there are two clear peaks, one for the folded population at a high FRET efficiency and one for the unfolded population at a lower FRET efficiency. As the pH is lowered, the folded and unfolded peaks of the FRET efficiency histograms merge into a single peak at the average value for folded and unfolded molecules because there is a continuous increase in the number of transitions between the states that occur within the bin time of 1 ms (25). This phenomenon is similar to what is observed in nuclear magnetic resonance experiments where there are two peaks when structures exchange slowly compared to the difference in frequencies and a single peak when exchange is fast (25).

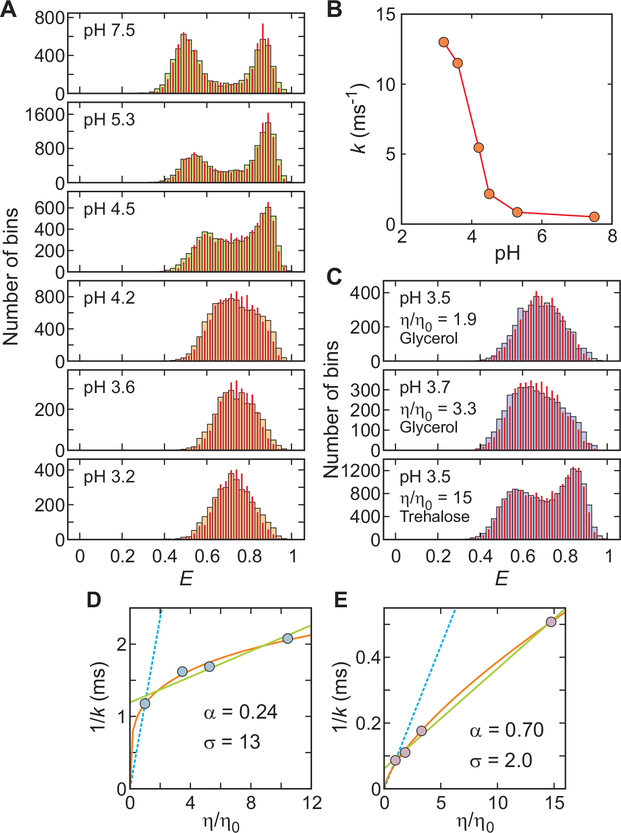
Fig. 3. pH and viscosity dependence of α₃D folding kinetics close to the chemical denaturant midpoint.

(A) FRET efficiency histograms as a function of pH. The concentrations of urea are 5 M at pH 7.5 and 6 M at all other pHs (Table S2). The FRET efficiency histograms were constructed from 1 ms bins in the trajectories with the mean photon count rate > 50 ms⁻¹. The near identity of the measured histograms (wide bars) and the histograms constructed from re-colored photon trajectories (red narrow bars), using the parameters obtained from the maximum likelihood method with the two-state model, indicate that this model is adequate (10, 26). (B) pH dependence of relaxation rate, k. (C) FRET efficiency histograms at different relative solvent viscosities. (D) Viscosity dependence of the inverse of the relaxation rate at pH 7.6 (Table S1) and (E) at pH 3.6 under conditions where the stability is only slightly altered (Table S3). The data was fitted to the power-law function A(η/η₀)^α (orange) or a linear equation A(σ + η/ η₀) (green) (27), where A is an amplitude and σ is the internal viscosity, which reflects the internal friction. The blue dashed lines show the dependence expected when the folding times are proportional to the first power of the solvent viscosity.

Using the maximum likelihood method of Gopich and Szabo (26), photon trajectories from which the histograms were constructed yield a relaxation rate (k = k_f + k_u, where k_f and k_u are folding and unfolding rate coefficients) that increases by 14-fold between pH 5.3 and 3.6 (Fig. 3B, Table S2). The sharp increase near pH 4, the pK_a of glutamic acid and aspartic acid residues, immediately suggests that protonation of the carboxyl groups, and therefore loss of salt bridges, is responsible for the rate increase, while the small change in the stability (Table S2) suggests that rate change does not come from a change in the free energy barrier height but from a change in D* in the pre-exponential factor of Kramers’ equation (Eq. 1).

We therefore studied the viscosity dependence of the folding relaxation rate at pH 3.6. Compared to neutral pH, where both the rate and transition path time exhibit a very weak viscosity dependence (8), much larger changes in rate were observed at pH 3.6. A relative viscosity change of 10-fold produces a 4.5-fold increase in the inverse relaxation rate without a significant change in the stability, suggesting that the friction associated with the local barrier crossings does not come from the solvent but is dominated by internal friction (Fig. 3D, E; Tables S1 and S3). (27, 28)

Even though the stability is unchanged upon lowering the pH, the rates could be increased by simply lowering the free energy barrier. To more convincingly determine whether the effect of lowering pH on the rate results primarily from an increase in D* rather than from a decrease in the free energy barrier height requires transition path time measurements, since the transition path time is insensitive to the barrier height (Eq. 2). If the change of the free energy surface is small, the transition path time would show the same pH and viscosity dependence as the inverse relaxation rate. The average transition path time for α₃D in the absence of viscogen at pH 7.6 and room temperature was previously measured to be 12 ± 2 μs in GdmCl solution (8), and is 13 ± 2 μs in the current measurements in urea solution at pH 5.3 (Fig. 4). (The relaxation rates and stability are similar at both conditions.) Assuming that all of the 14-fold increase in relaxation rate at pH 3.6 compared to pH 5.3 comes from a larger D*, the data in Tables S1 and S2 indicate that the transition path time is predicted to be only ~ 1 μs at pH 3.6. We therefore collected photon trajectories at the highest possible illumination intensity (an average of 600 – 900 photons/ms) that allowed observation of photon trajectories containing transitions before photo-bleaching of one of the dyes occurred. As before, the Gopich/Szabo maximum likelihood method, with a kinetic model consisting of folded, unfolded, and an additional virtual intermediate state to simulate the transition path, was used for determining the average transition path times (7, 8).

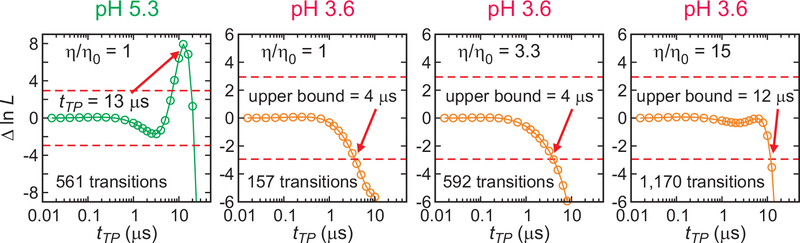
Fig. 4. Analysis of single-molecule photon trajectories.

The difference of the log likelihood, Δln L = ln L(t_TP) – ln L(0), is plotted as a function of the lifetime of the virtual intermediate state (= t_TP), for folding and unfolding transitions. L(0) is the likelihood for a model with instantaneous folding and unfolding transitions. Therefore, Δln L quantifies how much better or worse a model with a finite transition path time describes the data than a model with an instantaneous transition (Fig. S4). The transition path time is determined from the maximum of the likelihood function above the upper 95% confidence limit (Δln L = +3, red dashed line), which is 13.3 (± 1.8) μs at pH 5.3. The error is the standard deviation obtained from the curvature at the maximum of the likelihood function. The upper bound of transition path time is determined by the time when the likelihood curve crosses the 95% confidence limit (Δln L = −3, red dashed line) (30).

Figure 4 shows that, unlike the experiments at pH 5.3 where the transition path time was readily measurable from a peak in the difference log likelihood plot at 13 μs, only an upper bound of ~ 4 μs could be obtained at pH 3.6. To lengthen the transition path time and possibly make it experimentally resolvable, viscogens (glycerol or trehalose) were added to produce viscosities relative to the absence of viscogen of 3.3 and 15 (the highest viscosity at which solutions could be prepared at low pH in the presence of the high concentrations of urea necessary to attain 50% unfolding). At the higher viscosities, where there is less bimolecular quenching of the dye triplet states that result in photochemistry, it was necessary to include the interfering effect of fluorophore blinking in the analysis by adding non-fluorescent states to the kinetic scheme for determining the upper bound of the transition path time (29, 30). If the viscosity dependence is the same as found for the rate dependence at low pH (Fig. 3, Table S3), the predicted transition path times at these relative viscosities are ~ 2 μs and ~ 6 μs, below the current time resolution of these experiments, as judged by the analyses of simulated trajectories (Fig. S7). In keeping with this expectation, again no peak is observed and only upper bounds of 4 μs and 12 μs could be determined, even though the key parameters that determine the ability to observe a peak in the log likelihood plot are very similar to those at pH 5.3 -the photon detection rate, the number of observed transitions, and the difference in average FRET efficiencies between the folded and unfolded molecules.

Additional information was obtained by simulating trajectories with an assumed transition path time using the experimental parameters (Fig. S8) (30). The simulations, together with the present experimental results, lead to our best estimate for the average transition path time of ~ 1 μs. Consequently, we conclude that most, if not all, of the 14-fold increase in the relaxation rate upon protonating the carboxyl groups can be accounted for by increasing D* in the pre-exponential factor of Kramers’ equation (Eq. 1).

Simulations of rates and transition path times

MD simulations were used to provide an atomic-level structural interpretation of the experimental observations. We performed equilibrium reversible-folding simulations of α₃D in water at both neutral pH (aspartate and glutamate ionized) and low pH (aspartate and glutamate protonated). Two independent simulations were performed for each condition. During both the neutral- and low-pH simulations, α₃D reversibly folded several times to a structure less than 3 Å Cα RMSD from the experimentally determined structure (Fig. 5A, D). The calculated melting temperatures (~350 K at low pH and ~370 K at neutral pH) are consistent with the experimentally determined melting temperatures of 346 K at pH 2.2 and higher than 363 K at neutral pH (21). Folding times were calculated using a dual cutoff at values of 0.20 and 1.50 of an optimized reaction coordinate (Fig. 5B) (13). The calculated folding times at 370 K (10 ± 3 μs at low pH and 20 ± 4 μs at neutral pH) can be compared to the experimental values of 6 μs (21) and ~10 μs (obtained by extrapolation of the denaturant dependence at 295 K (23) assuming no temperature dependence; if the folding time increases with temperature, as observed at low pH and commonly observed in single-domain proteins, the folding time would be longer and the agreement between simulation and experiment would be even better). This result indicates that, despite being less stable, α₃D folds considerably faster at low pH than at neutral pH.

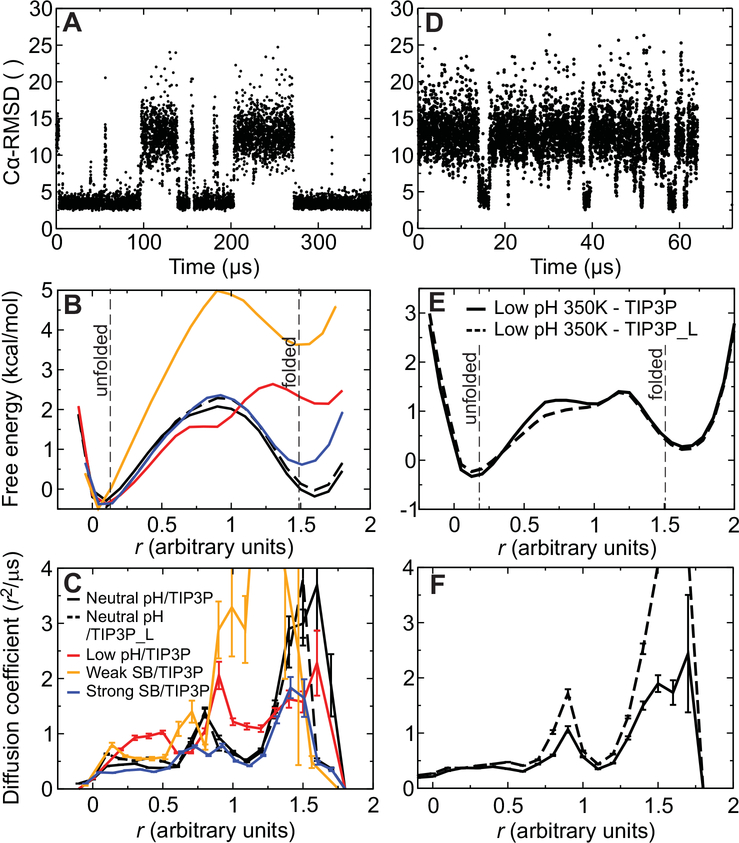
Fig. 5. Trajectories, free energy surfaces, and diffusion coefficients from MD simulations of reversible folding of α₃D.

(A) Time series of the Cα RMSD from the experimental native structure for a 360-μs simulation of α₃D performed at 370 K and neutral pH. (B) One-dimensional projection of the folding free energy surface along an optimized reaction coordinate (30). The cutoffs used for determining rates and transition path times in the analysis to define the folded and unfolded states are indicated by two vertical lines. The different simulations are distinguished using the color scheme described in panel C. (C) Diffusion coefficients along the optimized reaction coordinate for neutral-pH (black) and low-pH (red) simulations performed at 370 K. Results are also reported for simulations performed with weak (orange) or strong (blue) salt bridges and for a 370-K, neutral-pH simulation performed at low viscosity (black dashed line). (D) Time series of the Cα RMSD for a 65-μs simulation of α₃D performed at 370 K and low pH. (E) One-dimensional projection of the folding free energy surface for low-pH simulations performed at 350 K and either normal viscosity (black solid line) or low viscosity (black dashed line). (F) Diffusion coefficients (350 K) along the optimized reaction coordinate. The different simulations are distinguished using the same scheme employed in panel E.

This difference in folding rate cannot be readily explained by assuming a lower activation free energy, as the estimated folding free energy barrier appears to be slightly higher in the low-pH simulations than in the neutral-pH simulations (Fig. 5B), a result that does not depend on the data used to optimize the reaction coordinate (Fig. S12). The diffusion coefficient calculated in the region within 0.5 kcal mol⁻¹ of the top of the barrier, however, is approximately a factor of two larger at low pH with respect to neutral pH (1.33 ± 0.02 r² μs⁻¹ at low pH and 0.76 ± 0.02 r² μs⁻¹ at neutral pH; Fig. 5C). Accordingly, the calculated transition path time is shorter at low pH (0.24 ± 0.05 μs) than at neutral pH (0.43 ± 0.07 μs), by about a factor of two. These results suggest that all of the decrease in both the folding time and transition path time at low pH is caused by a decrease in Kramers D*, and not changes in curvatures of the 1D free energy surface (Eqns. 1 and 2), consistent with the interpretation of the experimental results.

To investigate the influence of viscosity on the folding rates in the different pH conditions, we performed low- and neutral-pH simulations near the melting temperature using either a normal TIP3P water model or TIP3P_L, a water model with one third of the total mass of TIP3P (30) that is characterized by a ~1.7 times lower viscosity (31). The use of TIP3P_L alters the dynamics, but not the thermodynamics, of the system. Indeed, we observed that essentially the same folding free energy surface was obtained in normal- and low-viscosity simulations (Fig. 5B, E).

In the simulations, as the viscosity was lowered by a factor of ~1.7, the folding time at low pH strongly decreased, while at neutral pH it remained essentially unchanged (Fig. 6A). A similar trend is observed for the average transition path time, which is very strongly viscosity dependent at low pH but not at neutral pH. Similarly to what was observed when we lowered the pH, the increase in both the folding rate and the transition path time with the decrease in viscosity at low pH is at least partially reflected in the diffusion coefficient in the barrier top region, which increases from 0.55 ± 0.02 r²μs⁻¹ at normal viscosity to 0.72 ± 0.02 r²μs⁻¹ at low viscosity (Fig. 5F). These findings are again consistent with the experimental results, which show that the transition path time at neutral pH is weakly dependent on solvent viscosity and that the folding times are less dependent on solvent viscosity at neutral pH than they are at low pH (Fig. 3D, E) (8). The smaller effects of pH observed in the simulations results from the high simulation temperature, where the apparent internal friction is much less (8) and therefore a smaller change in D*.

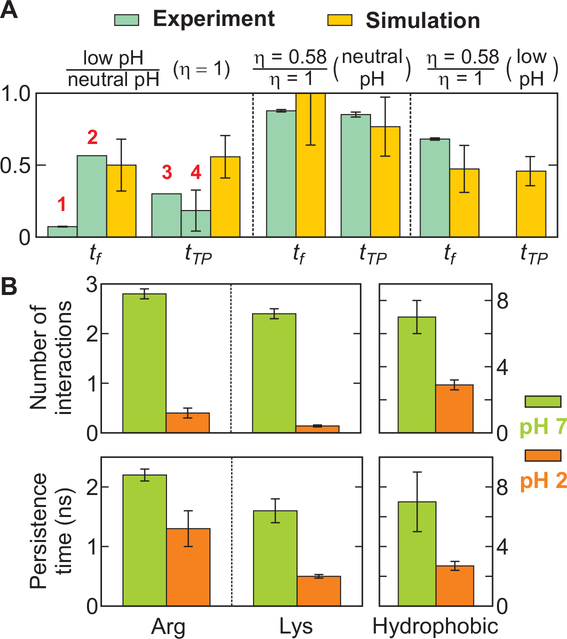
Fig. 6. Comparison of the effect of pH and viscosity on folding and transition path times from experiments and simulations and the average number and persistence time of non-native interactions during the transition path.

(A) The ratio of the folding and transition path times in simulation (yellow bars) were calculated from the values in Table S6. The experimental values (light blue bars) were calculated as follows. 1: The ratio of the relaxation times at pH 3.6 (low) and pH 5.3 (neutral) at 295 K; 2: The ratio of the folding time of 6 μs at pH 2 and 346 K(21) and the folding time of 10 μs at pH 7.5 obtained from the GdmCl dependence (23); 3: The transition path time at pH 3.6 (low) is an upper bound; 4: The transition path time at pH 3.6 was assumed to be 1 μs at 295 K, and it was extrapolated to 370 K using the viscosity dependence of t_TP ∝ η^0.7 obtained from the viscosity dependence of the kinetics (Fig. 3E). The transition path time at pH 7.5 and 370 K was calculated by extrapolation using the super-Arrhenius temperature dependence (D ∝ exp[-ε²/ (kT)²]) with the roughness (ε²) of 2.3 kT (T = 295 K) and t_TP = 12.3 μs at 295 K (8). The experimental viscosity dependence was calculated using the power law dependence (η^α) with the powers (α) of 0.24 (t_f, neutral pH, Fig. 3D), 0.30 (t_TP, neutral pH) (8), and 0.70 (t_f, low pH, Fig. 3E). See Table S6 for absolute times and additional details of the simulations. (B) Lowering pH significantly reduces the average number and persistence time of non-native salt bridges between positively charged side chains (Arg, Lys) and negatively charged side chains (Glu, Asp) and the non-native hydrophobic interactions during the transition path.

Figure 6A summarizes the comparison of the experiments and simulations. The temperatures and solvent conditions are different between the experiment and simulation because the objectives used in single molecule measurements cannot withstand the high temperatures of the simulations and folding is much too slow in denaturant at room temperature to obtain a sufficient number of transitions in the molecular dynamics simulations to draw any meaningful conclusions. Despite the differences in temperatures and solvent conditions, the overall trends in the experiments and simulations for both the rates and the transition path times are very similar under conditions in which there are nearly equal populations of folded and unfolded molecules.

Analysis of transition paths from simulations

Analysis of the formation of secondary structure and hydrophobic contacts shows that the folding transition path involves an initial collapse to a molten globule-like structure containing native and non-native contacts, followed by a gradual reorganization of the structure (17) (Fig. 2). Salt bridges and hydrophobic contacts appear to be the two most common and persistent types of side-chain interactions. We compared the average number and the average persistence time of these non-native contacts during the transition paths at the two different pH levels (Fig. 6B and Table S7). The persistence time is expected to be determined primarily by the height of the local barriers and, together with the number of contacts that form and break, reflect the overall roughness of the landscape due to non-native interactions.

In the neutral-pH simulations, four to five non-native salt bridges are formed, on average, at any given time during the transition paths between the positively charged lysine and arginine residues and the negatively charged carboxyl groups of the aspartates and glutamates. These salt bridges have an average persistence time of a few nanoseconds and occasionally may last for up to a few tens of nanoseconds. These interactions almost completely disappear at low pH—their population is reduced by an order of magnitude and their persistence time is two to three times shorter—because the addition of protons neutralizes the carboxylates and eliminates the Coulombic electrostatic attraction with the positively charged lysines and arginines (i.e., the salt bridges).

To analyze the relative importance of the total charge of the molecule, we performed simulations in which salt bridge interactions were either weakened or strengthened by slightly changing the nonbonded force field parameters while leaving the total charge of the system unchanged. When salt bridges are weakened, the native state is destabilized (ΔΔG ~3.5 kcal mol⁻¹, Fig. 5B), as was observed in the low-pH simulations. More importantly, diffusion along the optimized reaction coordinate is greatly increased (Fig. 5) and the transition path time decreases (Table S6). On the other hand, when the strength of salt bridges is increased, there is very little change in protein stability, but diffusion along the reaction coordinate becomes slower (Fig. 5), and the folding time and transition path time increase (Table S6). Taken together, these results support the idea that salt bridges directly influence the free energy landscape roughness, whereas the total charge of the molecule plays a minor role, if any.

Another interaction that in simulation is relatively persistent and disappears at low pH occurs between Asp and Glu side chains and the protein backbone. To elucidate the relative contribution of this interaction to the roughness of the free energy landscape, we performed simulations in which we selectively weakened this interaction. In these simulations, the stability of the folded state is unchanged, but the folding free energy barrier increases slightly and diffusion on the free energy surface is slightly faster (Fig. S13). These results suggest that these non-native backbone–side chain interactions contribute to the stability of the transition state for folding, but also slightly increase the energy landscape roughness. This effect appears to be minor compared to that of salt bridge interactions.

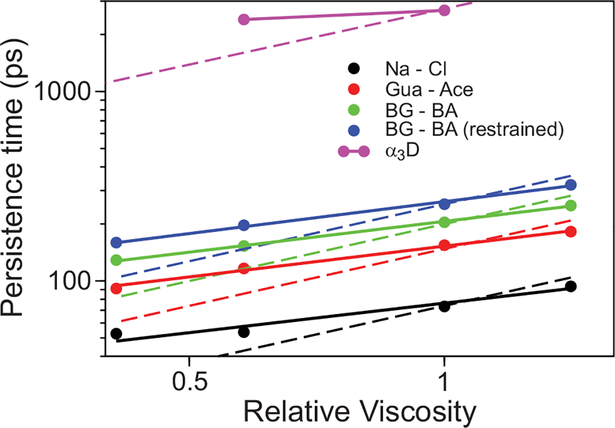
Having established that salt bridges provide an important contribution to the energy landscape roughness, we investigated the underlying reasons for the weak viscosity dependence of the folding rate of α₃D at neutral pH. To that end, we performed simulations of the viscosity dependence of the persistence times of ion-pair formation for systems of increasing complexity, ranging from the pairing of sodium chloride, to the pairing of Arg and Glu side chains, to the formation of Asp/Glu and Arg salt bridges in α₃D. In all of these systems, we observed a weak viscosity dependence that strongly deviates from the simple power dependence with an exponent of 1.0 expected from Kramers’ theory (Fig. 7). Ion pair formation for the Arg and Glu side chain analogs involves a first step, in which the ions diffuse through the solvent until they come into close proximity, followed by a reorganization step, in which the ions reorient themselves to achieve an optimal interaction (Fig. S14). We find that the kinetics of the last step are affected very weakly by changes in solvent viscosity (Fig. S14).

Fig. 7. Viscosity dependence of persistence times for a number of ion pairs.

The persistence time is reported on a logarithmic plot as a function of viscosity relative to TIP3P for the Na…Cl ion pair (black), the guanidinum…acetate ion pair (red), the butyl-guanidinum…butyric acid ion pair (green, representing the side chains of Arg and Glu), a butyl-guanidinum…butyric acid ion pair where the terminal carbon atoms have been restrained at a distance of 10 Å (blue), and the Arg…Glu/Asp salt bridges in the α₃D transition path (purple). A power-law fit with exponents ranging between 0.51 and 0.56 is reported in solid lines, while the exponent of 1.0 predicted by hydrodynamic Kramers’ theory is shown as a dashed line.

Discussion

By combining single molecule experiments with extensive all-atom molecular dynamics simulations, we have gained quantitative insight into how a specific type of inter-residue interaction influences the kinetics and dynamics in protein folding. The experiments show that the slower folding and longer transition path times for α₃D at neutral pH compared to low pH (Figs. 3 and 4), where the carboxyl groups are neutral, are due to a smaller D*, which appears in the pre-exponential factor for the folding time and the pre-logarithmic factor for the transition path time (Eqs. 1 and 2). In the molecular dynamics simulations, similar differences are also observed (Fig. 6A) and explained by changes in D* (Fig. 5C and 5F), so we can use them to gain insight at an atomistic level into what interactions are responsible. While salt bridge interactions are almost completely eliminated at low pH in the experiments, this does not demonstrate that they are solely responsible for the larger landscape roughness at neutral pH as reflected in the smaller D*. Indeed, at low pH the net charge of the protein increases from approximately −1 to +11, leading to a slightly more expanded transition path ensemble featuring a smaller number of non-native hydrophobic interactions compared to neutral pH (Fig. 6B and Table S7). To disentangle the importance of these two contributions to the landscape roughness, we took advantage of the ability of simulations to selectively alter the strength of specific interactions while leaving the rest of the system unperturbed. Decreasing the strength of the salt-bridges at neutral pH markedly increases D* and shortens the transition path time, while increasing the strength has the opposite effect (Table S6). These results support the idea that salt bridges directly influence the landscape roughness, whereas the total charge of the molecule plays a minor role, if any.

Understanding the dependence of the folding and transition path times on solvent viscosity in detail is a more subtle and difficult problem. At low pH, in both experiments (Figs. 3d and 3e) and simulations (Fig. 5) the folding time is more sensitive to solvent viscosity than at neutral pH, but the dependence is less than the first power expected from Kramers’ theory if all of the friction (ζ* = k_BT/D*) comes from the solvent and is linear in the solvent viscosity (Stokes law). Fractional power has been observed for isolated α-helices and other α-helical proteins (32–37). Jas et al. (32) suggested that the fractional power dependence for α-helices arises from a breakdown in Kramers’ theory due to barrier-top crossing times for the dihedral angle rotations that are faster than the solvent relaxation. In fact their exponent of 0.6 for the folding relaxation rate is remarkably close to the value of 0.7 observed for the all-α helical α₃D at low pH (Fig. 3E). This interpretation has also been suggested on theoretical grounds by Portman et al.(38) and supported by simulations of Best, Papoian and their coworkers. (39–41). The more challenging result to explain, however, is the much smaller fractional exponent of 0.2–0.3 for the folding (Fig. 3D) and transition path times (8) at neutral pH. One possibility is that it is caused by internal friction due to collisions between atoms of the non-native salt bridges. However, in the simulations the non-native salt bridges are almost completely exposed to the solvent molecules, so internal friction can provide only a partial explanation. The simulations suggest a more plausible additional non-Markovian effect. As shown in Fig. 7, the persistence time of ion pairs show reduced viscosity dependence (~η^0.5), a finding consistent with previous studies on the ion-pair association process of sodium chloride, where it has been shown that the reorganization step (in this case involving only the solvent shell) cannot be modeled accurately by Kramers’ theory (42, 43). The weak viscosity dependence observed for α₃D in the presence of non-native salt bridges may be the result of a combination of these two non-Markovian effects.