Abstract
Shear wave elasticity imaging (SWEI) characterizes the mechanical properties of human tissues to differentiate healthy from diseased tissue. Commercial scanners tend to reconstruct shear wave speeds for a region of interest using time-of-flight methods reporting a single shear wave speed (or elastic modulus) to the end user under the assumptions that tissue is elastic and shear wave speeds are not dependent on the frequency content of the shear waves. Human tissues, however, are known to be viscoelastic, resulting in dispersion and attenuation. Shear wave spectroscopy and spectral methods have been previously presented in the literature to quantify shear wave dispersion and attenuation, commonly making an assumption that the acoustic radiation force excitation acts as a cylindrical source with a known geometric shear wave amplitude decay. This work quantifies the bias in shear dispersion and attenuation estimates associated with making this cylindrical wave assumption when applied to shear wave sources with finite depth extents, as commonly occurs with realistic focal geometries, in elastic and viscoelastic media. Bias is quantified using analytically-derived shear wave data and shear wave data generated using finite element method models. Shear wave dispersion and attenuation bias (up to 15% for dispersion and 41% for attenuation) is greater for more tightly-focused acoustic radiation force sources with smaller depths of field relative to their lateral extent (height-to-width ratios < 16). Dispersion and attenuation errors associated with assuming a cylindrical geometric shear wave decay in SWEI can be appreciable and should be considered when analyzing the viscoelastic properties of tissues with acoustic radiation force source distributions with limited depths-of-field.
Keywords: Shear Wave Imaging, Shear Attenuation, Viscoelastic Materials, Dispersion
Introduction
Shear wave elasticity imaging (SWEI) noninvasively evaluates the mechanical properties of human tissues. Most shear wave speed reconstruction algorithms used on commercial scanners estimate quantitative values based on a group shear wave speed assuming that tissue is elastic; however, human tissues are known to be viscoelastic (VE), meaning that the shear wave speed is dependent on the wave’s frequency content. VE materials can be described by two frequency-dependent behaviors: shear dispersion and shear attenuation (Sridhar et al., 2007).
Several methods have been developed to measure shear wave dispersion using SWEI; however, quantifying shear attenuation is more difficult because the amplitude of the wave decays due to both shear attenuation and the effects of geometrical spreading. When shear wave dispersion is estimated alone, the change in speed with frequency is compared across materials by either assuming a material model, such as a Voigt model (Deffieux et al., 2009), or a dispersion model, such as a linear dispersion model that estimates a speed at a particular frequency and quasi-linear dispersion slope centered about that frequency (Nightingale et al., 2015). Other methods of shear attenuation estimation overcome the challenges of geometrical spreading by assuming a linear attenuation model and utilizing a shift in the frequency spectra to estimate attenuation (Bernard et al., 2016).
There are also several model-free approaches that estimate both dispersion and attenuation directly from the propagating shear wave data. In recent work by Nenadic et al., the authors developed Attenuation Measuring Ultrasound Shear Elastography (AMUSE), which uses 2-D Fourier Transform (FT) methods to quantify shear dispersion and attenuation (Nenadic et al., 2017). Methods by Budelli et al. and Kazemirad et al. use phase spectroscopy and an amplitude-based approach to measure shear attenuation and combine these estimates to report a complex shear modulus (G = G' + iG") (Budelli et al., 2016; Kazemirad et al., 2016); however, in vivo measurements of shear attenuation using these methods had large variances (>50 Np/m) (Budelli et al., 2016).
The model-free 2-D FT and amplitude-based methods for quantifying shear dispersion and attenuation are based on derivations that assume an infinitely tall, cylindrically-symmetric acoustic radiation force impulse (ARFI) source geometry that can be difficult to achieve experimentally with typical diagnostic arrays that have finite depth-of-fields (DOF). These methods also assume that at sufficient distances from the source, the shear wave will propagate as a cylindrical wave. Deviation from infinitely tall sources and cylindrical wave propagation introduces bias into the corresponding estimates of VE tissue properties. In this work, we investigate the impact of the acoustic radiation force source geometry on model-free VE material estimates by implementing amplitude-based shear attenuation estimation and phase spectroscopy on analytic and finite element simulation data. We evaluate several factors that could affect the robustness of these methods, including the applicability of cylindrical wave assumptions for a specific lateral reconstruction range and the minimum shear wave frequency for which the VE parameter estimates are valid. Additionally, we evaluate the effect of a finite depth of field of the ARFI excitation, and determine the axial range of the excitation that can reasonably be used for these estimates.
Methods
Background
The model-free methods for estimating viscoelastic material properties begin with the solution for shear wave propagation resulting from a harmonic infinite line source in an elastic solid as described by Graff:
| (1) |
where uz is the z component of displacement as a function of radial distance from the source r and time t, is a Hankel function, k is the wave number, and ω is the temporal frequency (Graff, 1991). This equation can be extended to describe shear wave propagation in viscoelastic media by introducing a complex wave number κ:
| (2) |
where the real component of the complex wave number is represented by k(ω) and the imaginary component is represented by α(ω), the shear attenuation (Chen et al., 2009; Deffieux et al., 2009). For sufficiently large distances from the source (kr >> 1), the asymptotic form of this solution is a cylindrical wave:
| (3) |
where α is the shear attenuation. The shear wave decays in amplitude due to both shear attenuation and geometric spreading. Where this asymptotic form is appropriate, the decay in amplitude due to geometrical spreading can be compensated for by multiplying (3) by with the remaining amplitude loss with distance arising solely from shear attenuation. The temporal FT can be used to assess discrete frequencies to estimate attenuation and dispersion. The natural log of the magnitude of the scaled frequency data is proportional to α(ω) by:
| (4) |
The phase of the scaled frequency data is proportional to k(ω) by:
| (5) |
where C is a constant. The real component of the complex wave number, k(ω), can be converted to a phase velocity c(ω) by:
| (6) |
The same equation (3) applies to particle velocity, differing by a multiplication factor of iω.
Analytic Methods to Generate Shear Wave Data
The derivation by Graff that leads to (1) and (3) does not account for the finite lateral-elevation size or temporal duration of an ARFI excitation. Rouze et al. described a method for creating analytic displacement and velocity data along a radial trajectory including terms for the excitation shape and duration while still assuming no dependence in the depth dimension (Rouze et al., 2016). The displacements are computed in the Fourier domain and the simplified analytic form assuming a cylindrically-symmetric source can be described by:
| (7) |
where is the temporal Fourier domain displacement signal, and μ(ω) is the complex shear modulus, is the Fourier transform of the temporal duration of the ARFI excitation, K0 is a modified Bessel function. Assuming an axisymmetric Gaussian excitation source, , S0 is a shape function describing the excitation in a lateral-elevation plane:
| (8) |
where A is the amplitude of the excitation, and σ modulates the full-width at half maximum (FWHM) of the excitation source. The inverse Fourier transform of the analytic displacements (7) can be used to evaluate shear wave reconstruction methods. The parameters modeling our typical imaging sequences are listed in Table 1, where the beamwidth was determined by σ, which was chosen such that the Gaussian would have a full width at half maximum (FWHM) of 1.4 mm, a value similar to experimentally-relevant excitations (Palmeri et al., 2017).
Table 1:
Parameters used to create analytic displacement data.
| Parameter | Value |
|---|---|
| fs | 10 kHz |
| σ | 0.84 mm |
| FWHM | 1.4 mm |
| Push duration | 364 μs |
| Sequence length | 30 ms |
| Radial position spacing | 0.3 mm |
Propagating shear waves were modeled using this analytic method in two linear elastic and three standard linear viscoelastic materials, representing a range of liver fibrosis disease states (Table 2). The displacement data were differentiated in time to create particle velocity data. The velocity data were then temporally-windowed using a Tukey window to reduce ringing in the frequency domain. Dispersion and attenuation curves were estimated, as described below, for a frequency range of 0–400 Hz. True dispersion and attenuation curves were calculated based on the material models to quantify bias in the estimated parameters (Rouze et al., 2015).
Table 2:
Material parameters of linear elastic and three parameter standard linear viscoelastic models of human liver of various disease states (Palmeri et al., 2017).
| Material | μ1 (kPa) | μ2 (kPa) | η (Pa-s) | Modeled Liver Type |
|---|---|---|---|---|
| M1 | 1 | 0 | 0 | Healthy |
| M2 | 4 | 0 | 0 | Fibrotic |
| M3 | 2 | 8 | 1.20 | Mild Fibrosis |
| M4 | 4 | 11 | 2 | Intermediate Fibrosis |
| M5 | 4 | 16 | 4 | Advanced Fibrosis |
Finite Element Methods to Generate Shear Wave Data
The analytic methods described above assume an infinite source in the z-dimension. Since experimentally-generated ARFI excitations have a finite axial extent, VE estimation methods commonly assume that shear waves follow cylindrical propagation within the depth-of-field (DOF) of the excitation as given by:
| (9) |
where λ is the wavelength of the ultrasonic pressure waves, F/# = z/D, z is the focal depth, and D is the aperture size. Previously-validated finite element (FE) models were used to simulate the dynamic response of an ARFI excitation in all dimensions for excitations with varying depths of field (Palmeri et al., 2005, 2017). In the first stage of this study, the lateral-elevation spatial distribution of acoustic radiation force remained fixed as a Gaussian, and the axial extent was systematically modified by changing the height of a Tukey distribution:
| (10) |
where is a rect function that sets the pulse duration to start at t = 0 and end at t = Ton, Wz is a Tukey window delineating the axial extent of the excitation, L is the axial length of the Tukey window, a is the rolloff factor (0.25), and z0 is the center of the Tukey window (60 mm). Although this is not an experimentally-realizable excitation, it is not as feasible to isolate changes due to purely a change in the height of the DOF by relying on the diffraction pattern of a particular transducer, since changing the focal configuration will simultaneously lead to changes in the beam pattern in all three dimensions.
The beamwidth of an ARFI excitation is typically approximated by λz/D, making the height-to-width ratio of the beamwidth to the DOF, 8F/#. The height, or approximate DOF, was varied by changing the axial length of the Tukey window, L (Table 3), using a fixed beamwidth (FWHM 1.4 mm) to create height-to-width ratios (HWR) of 8, 12, 16, and 20 (approximating F/1, F/1.5, F/2, and F/2.5 focal configurations), as well as one configuration that extends to nearly the edges of the mesh to mimic a cylindrical wave (HWR≈80). In addition, to capture the behavior of focused ARFI excitation sources, two transducers with similar beamwidths, but different focal configurations were simulated, including a HIFU piston (F/1, beamwidth 1.4 mm), a Verasonics C5-2v curvilinear array single focus excitation(F/2, beamwidth 1.3 mm) and a Verasonics C5-2v curvilinear array supersonic, multi-focal excitation (Bercoff et al., 2004). The multi-focal excitation used three rapid push excitations, placed in depth to have at least 50% overlap of the DOF as calculated by (9). Both arrays were modeled using Field II (Jensen and Svendsen, 1992) using the parameters in Table 4. These models simulated the diffraction pattern of a particular imaging case and the applied point loads were calculated from
| (11) |
where is the force per unit volume, α is the absorption coefficient, is the intensity of the acoustic beam, and c is the speed of sound in the medium.
Table 3:
Parameters of the excitation and imaging used to create FEM excitations, that are Gaussian in the x – y plane and a Tukey distribution in z.
| Parameter | Value |
|---|---|
| σx, σy | 0.84 mm |
| L | 1.12, 1.68, 2.24, 2.80, 11.50 cm |
| a | 0.25 |
| z0 | 60 mm |
| Push duration | 180 μs |
Table 4:
Transducer parameters for the simulated excitations from a HIFU piston and C5-2v curvilinear array.
| Transducer | Parameter | Value |
|---|---|---|
| HIFU Piston | f0 | 1.1 MHz |
| F/# | 1 | |
| Focal Depth | 63 mm | |
| Excitation Duration | 180 μs | |
| Fractional Bandwidth | 60% | |
| Verasonics C5-2v Curvilinear Array (Single Focus) | f0 | 2.36 MHz |
| Fractional Bandwidth | 70% | |
| Element Size | 0.412×15.75 mm2 | |
| Focal Depth | 60 mm | |
| Excitation Duration | 180 μs | |
| F/# | 2 | |
| Elevation Focus | 60 mm | |
| Verasonics C5-2v Curvilinear Array (Multi-Focal) | f0 | 2.36 MHz |
| Fractional Bandwidth | 70% | |
| Element Size | 0.412 *15.75 mm2 | |
| Focal Depths | 50, 60, 70 mm | |
| Total Excitation Duration | 590 μs | |
| F/# | 2 | |
| Elevation Focus | 60 mm |
Shear wave propagation was modeled using these FE methods in one linear elastic (M2) and one standard linear model viscoelastic material (M4) (Table 2). The three-dimensional, dynamic tissue responses to these excitations were solved through the balance of linear momentum using LS-DYNA3D (Livermore Software Technology Corp., Livermore, CA) with an explicit, time-domain method. The FE mesh had dimensions of 40 × 40 × 120 mm3 with 0.33, 0.33, 0.25 mm nodal spacing, respectively. Each material model was made nearly incompressible with either a specified Poisson’s ratio (ν = 0.499) in the linear elastic material or a bulk modulus was set (K = 249.8MPa) in the viscoelastic material model. Although there is not a simple relationship to define Poisson’s ratio in the viscoelastic model, if we use the elastic relationship of bulk modulus and instantaneous shear modulus (G0 = μ1 + μ2), the Poisson’s ratio is estimated to be 0.49996. Previous work shows the convergence and validation of these simulations as well as the conversion between the three parameter standard linear model and the more generalized viscoelastic material used by LS-DYNA, specified by G0, G∞, and β (Palmeri et al., 2017). The model used linear elements and perfect matching layers on the outer x-z and y-z faces to simulate a semi-infinite volume without reflection artifacts at the edges of the mesh. The top and bottom boundaries of the mesh were fixed to prevent bulk motion of the model from the excitation. The symmetric nature of an ARFI excitation about the axial-lateral plane allowed the simplification of the model to quarter symmetry to reduce memory and computational run-time. Simulations were performed for a total time of 30 ms with intermediate results saved at intervals of 100 μs. The z-displacements through time were extracted for the elevation plane y = 0. The displacement data were differentiated in time to create particle velocity data. The velocity data were then temporally-windowed using a Tukey window to reduce ringing in the frequency domain. Dispersion and attenuation curves were estimated for each plane in depth, as described in the next section.
Attenuation and Dispersion Estimation Methods
Dispersion and attenuation estimates were made using a single depth plane of particle-velocity-through-time profiles from each analytic or FE-generated data set. The particle velocity data were separated into their individual frequency components by a temporal Fourier transform. The frequency data were multiplied by a factor of , where r is the radial distance from the source, to correct for amplitude decay due to geometric spreading. The scaled frequency data were divided into their magnitude and phase components. The natural log of the frequency magnitude was linearly fit over a radial extent of 4 to 8 mm to calculate α(ω) at each frequency. The minimum radial position (4 mm) was chosen to insure that kr >> 1 for the frequencies in the shear wave signal bandwidth, and 8 mm was chosen as the maximum radial position to limit the analysis to a range that would experimentally provide relatively large signal amplitude. The starting radial position, frequency, and phase speed are interdependent parameters that must be optimized for each excitation and material properties to avoid introducing significant bias from a violation of the farfield assumption (kr >> 1). Using a larger lateral range will decrease the noise on lower frequency estimates, but may introduce bias into higher frequency estimates which are more quickly attenuated. A small lateral range also opens the opportunity to make multiple phase velocity and attenuation estimates in heterogeneous tissue. For each frequency, a line was fit to the phase of the frequency data as a function of radial distance (4–8 mm) to estimate the wave number k(ω) using (5) (Deffieux et al., 2009; Budelli et al., 2016). The phase velocity c(ω) was then calculated from (6).
Results
Analytic Shear Wave Data
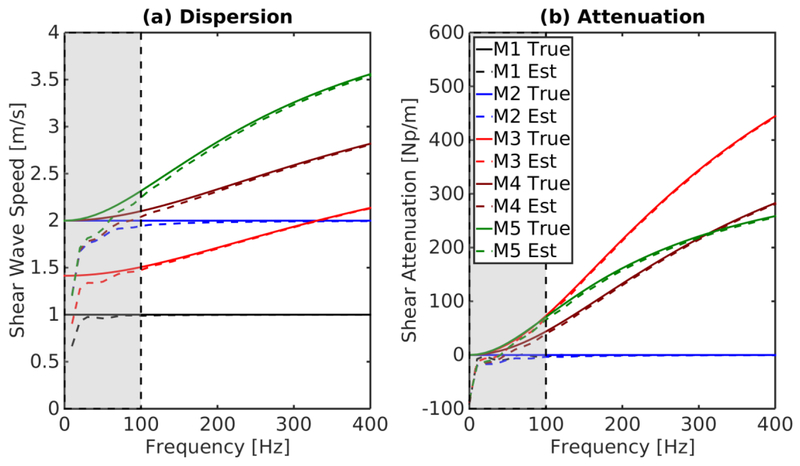
The analytic generated shear wave data that have infinite depth extent most closely match the assumptions of the amplitude-based shear wave attenuation and phase spectroscopy derivations. These data converge to a similar solution to the derivation outside the lateral-elevation extent of the finite source. The estimated dispersion and shear attenuation curves for the five materials are shown in Figure 1 with dashed lines. Solid lines indicate the true dispersion and attenuation curves. While the analytic derivations used angular frequency ω in rad/s, all results will show frequencies in Hertz . Values of kr are shown for each material in Table 5 for 100 Hz. All values of kr are greater than one, and in all materials at 100 Hz the dispersion bias was < 3% and the bias in attenuation estimates was < 10%, so a minimum frequency of 100 Hz and an experimentally feasible frequency range will be used for the remainder of the analyses in this work.
Figure 1:
Estimates of (a) dispersion and (b) attenuation in five materials that are representative of different stages of liver fibrosis. The true dispersion and attenuation curves are shown using solid lines, and the corresponding estimates shown in dashed lines. These estimates were made from shear wave data created using an analytic model that accounts for a finite excitation size and duration and assumes the excitation has no depth dependence. These data show excellent agreement between the estimated and true values from 100–400 Hz. Note that there is minimal bias for frequencies above 100 Hz, but low frequencies (kr < 1) indicated by the gray shaded regions are more susceptible to bias.
Table 5:
Values of kr for r = 4 mm at 100 Hz.
| M1 | M2 | M3 | M4 | M5 | |
|---|---|---|---|---|---|
| kr | 2.51 | 1.26 | 1.67 | 1.20 | 1.09 |
The root-mean-square error (RMSE) of the estimates in Figure 1 from the true values of dispersion and attenuation are listed in Table 6 over a range of 100–400 Hz.
Table 6:
RMSE of dispersion and attenuation estimates from analytic shear wave data (100–400 Hz).
| M1 | M2 | M3 | M4 | M5 | |
|---|---|---|---|---|---|
| Dispersion (m/s) | <0.01 | 0.02 | 0.01 | 0.03 | 0.04 |
| Attenuation (Np/m) | 0.7 | 1.6 | 2.2 | 2.9 | 3.7 |
FEM Shear Wave Simulations
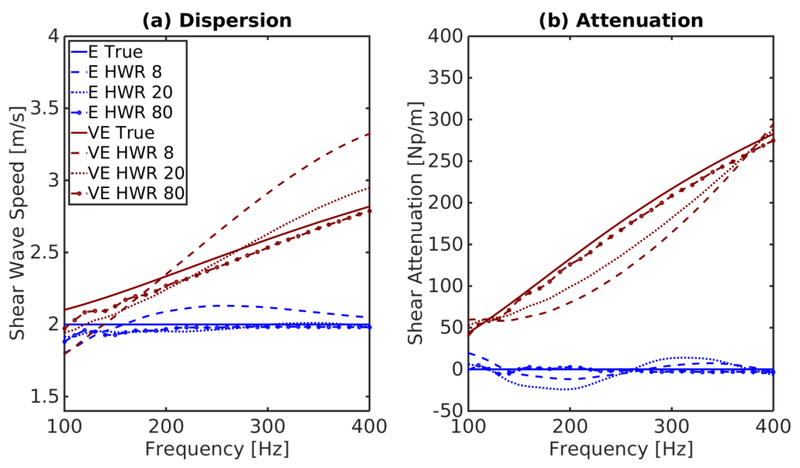
The height of ARFI excitations was modulated in a controlled way using the length of a Tukey window to mimic a DOF, while maintaining a constant lateral-elevation spatial distribution. A single depth plane at the center of each excitation (z = 60 mm) was evaluated, estimating dispersion and shear attenuation curves over the range of 100–400 Hz. The resulting estimates are shown in Figure 2 for the tallest excitation (HWR 80), as well as the excitations with HWR of 8 and 20 in an elastic material (M2) and a representative viscoelastic material (M4). The HWR of 12 and 16 excitations were intermediate points of the HWR 8 and 20, and were omitted for clear visualization of the trends.
Figure 2:
Estimates of (a) dispersion and (b) attenuation in an elastic (M2) and a viscoelastic (M4) material. These estimates were made from a single plane at the center of the Tukey window excitation (60 mm) in the HWR 8, 20, and 80 sources. As expected the HWR 80 source closely follows the expected values as it is the closest approximation to a cylindrical source; however, the excitation with the smallest extent in z (HWR 8) shows significant deviation from the known values for both dispersion and attenuation estimates.
The RMSE from the known values of dispersion and attenuation are listed in Table 7 for each finite height excitation. The overall RMSE in the dispersion and attenuation generally decrease with increasing HWR, with the exception of the attenuation estimates from the shortest excitation (HWR 8). The RMSE from the excitation that approximates a cylindrical source (HWR 80) approaches the RMSE seen from the analytic data.
Table 7:
RMSE of dispersion and attenuation estimates in Tukey-windowed excitations.
| HWR | 8 | 12 | 16 | 20 | 80 | |
|---|---|---|---|---|---|---|
| Elastic (M2) | Dispersion (m/s) | 0.1 | 0.06 | 0.04 | 0.04 | 0.04 |
| Attenuation (Np/m) | 8.1 | 23.3 | 20.4 | 13.6 | 2.8 | |
| Viscoelastic (M4) | Dispersion (m/s) | 0.3 | 0.2 | 0.1 | 0.1 | 0.07 |
| Attenuation (Np/m) | 41.8 | 42.8 | 35.7 | 27.6 | 8.2 |
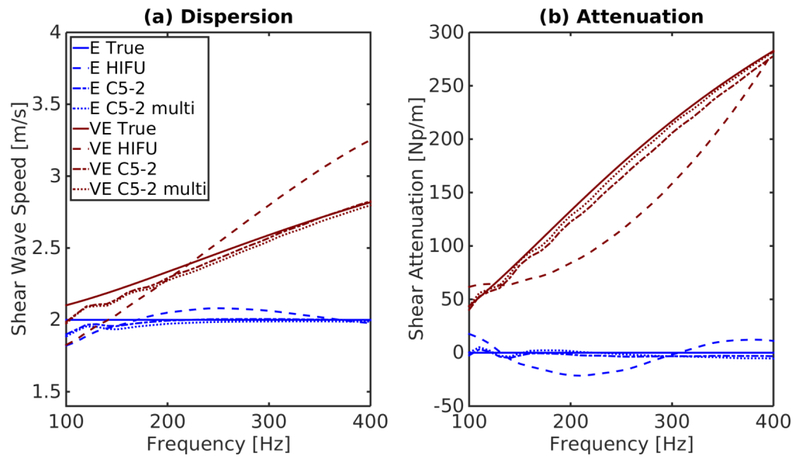
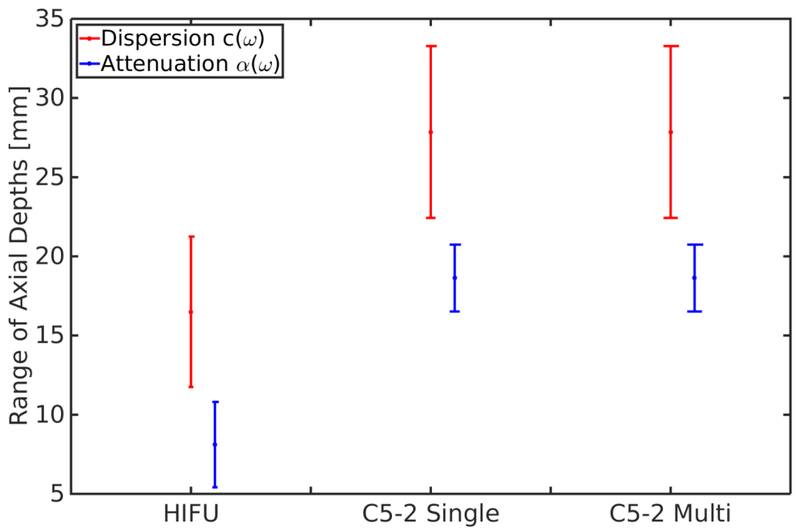
To determine how experimental transducer-based excitations would perform in the same materials, dispersion and shear attenuation were estimated from three Field II-simulated excitations: a HIFU piston, a single focus C5-2v excitation, and a multi-focal C5-2v excitation using a single plane at their respective focal depths of 63, 60, and 60 mm. These results are shown in Figure 3. Table 8 lists the RMSE of the dispersion and attenuation estimates calculated from the HIFU piston and C5-2v excitations. The C5-2v curvilinear array single focus excitation has a larger F/# than the HIFU piston, and thus a longer DOF. As expected, the RMSE from the C5-2v single focus excitation are smaller than those from the HIFU piston. The multi-focal excitation should extend the DOF as compared to the single focus C5-2v excitation. There is a negligible difference between most of the estimates made with the single focus and the multi-focal excitations. The improvement in RMSE from the single focus to the multi-focal excitation is greatest for the attenuation estimates in the viscoelastic material (M4).
Figure 3:
Estimates of (a) dispersion and (b) attenuation in an elastic (M2) and a viscoelastic (M4) material. These estimates were made from a single plane at the focal depth of the experimentally realistic, Field II simulated excitations. The HIFU piston has an F/1 focal configuration (HWR 8) and has similar results to the HWR 8 Tukey windowed excitation (Figure 2). The single focus excitation from the C5-2v transducer has an F/2 configuration (HWR 16), and outperforms the Tukey windowed excitation of the same HWR. The multi-focal C5-2v excitation has negligible differences in estimates from the single focus excitation, except in estimating attenuation in the VE material (M4), where it has a slight decrease in bias across the estimates from 100–400 Hz.
Table 8:
RMSE of dispersion and attenuation estimates in Field II-simulated transducer excitations for materials M2 and M4 (Table 2).
| HIFU Piston | C5-2 Single Focus |
C5-2 Multi-Focal | ||
|---|---|---|---|---|
| Elastic (M2) | Dispersion (m/s) | 0.07 | 0.03 | 0.04 |
| Attenuation (Np/m) | 13.3 | 3.0 | 3.3 | |
| Viscoelastic (M4) | Dispersion (m/s) | 0.2 | 0.04 | 0.06 |
| Attenuation (Np/m) | 43.5 | 9.9 | 4.1 |
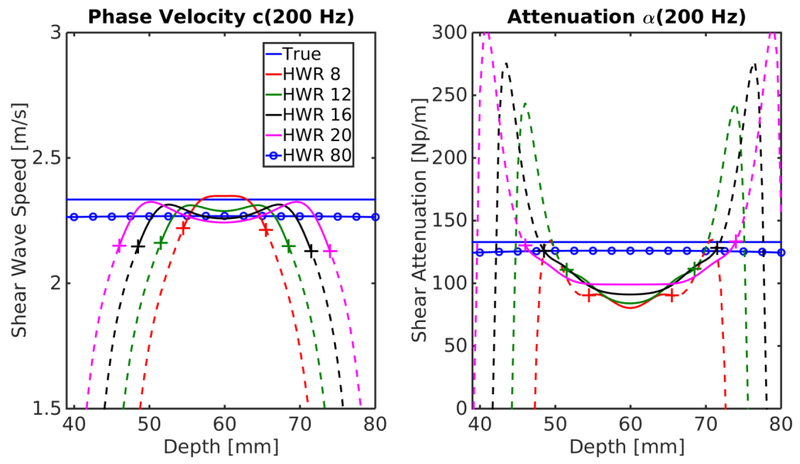
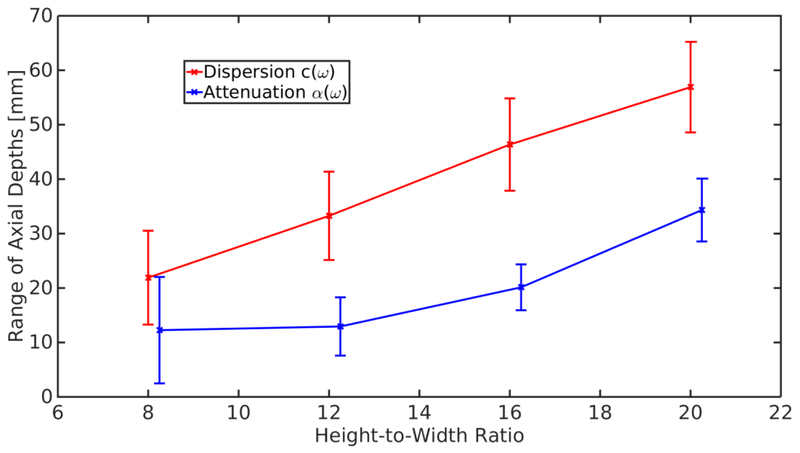
The dispersion and shear attenuation curves in Figures 1-3 were estimated from velocity data at a single depth. In experimental data, often multiple depths are averaged together to reduce noise from displacement estimation. Figure 4 shows dispersion and shear attenuation estimates in a viscoelastic material (M4) at 200 Hz as a function of axial depth for the Tukey window excitations with HWR 8, 12, 16, and 20. It has been shown that 200 Hz is a relevant frequency in shear wave imaging (Nightingale et al., 2015); however, similar trends were seen for other frequencies within the bandwidth of the shear wave. The range of depths that varied < ± 5% from the estimate at the center of the excitation are shown in Figure 5, where the errorbars represent the variation seen over the frequency range of 100–400 Hz. We conclude that this is the axial range that could reasonably be used to average shear wave signals through depth in order to improve SNR.
Figure 4:
Estimates of (a) phase velocity and (b) attenuation at 200 Hz as a function of relative depth in a viscoelastic (M4) material (Table 2). The DOF, given by the length of the Tukey window as listed in Table 3, is indicated by the solid line, bounded by + markers. Estimates outside the DOF are indicated by a dashed line. As expected, the estimates of dispersion and attenuation are consistent near the center of the excitation. As the DOF increases the region of consistency also increases, with HWR 8 having the smallest and HWR 20 having the largest DOF. Note that within the DOF the dispersion estimates are more consistent with depth than estimates of attenuation, although both estimates have increasing bias outside the DOF. The offset seen between the HWR 80 and the true values (0.07 m/s and 6.9 Np/m) show the limit of the methods based on the value of kr at this frequency (kr = 2.15). To further reduce this bias at 200 Hz, a larger r would need to be used in this material.
Figure 5:
The range of depths that varied < ± 5% from the dispersion or attenuation estimate at the center of the excitation for HWR 8, 12, 16, and 20 in the VE material M4 (Table 2). Errorbars represent the variation seen over the frequency range of 100-400 Hz. As the height of the excitation increases the range of depths that give a consistent estimate also increases, although the range of depths for attenuation is always smaller than the range of depths for dispersion. The range of depths were symmetric about 60 mm due to the excitation symmetry above and below the center of the excitation as seen at 200 Hz in Figure 4. Note that these estimates do not take into account bias in an estimate, only the consistency of the measurement made.
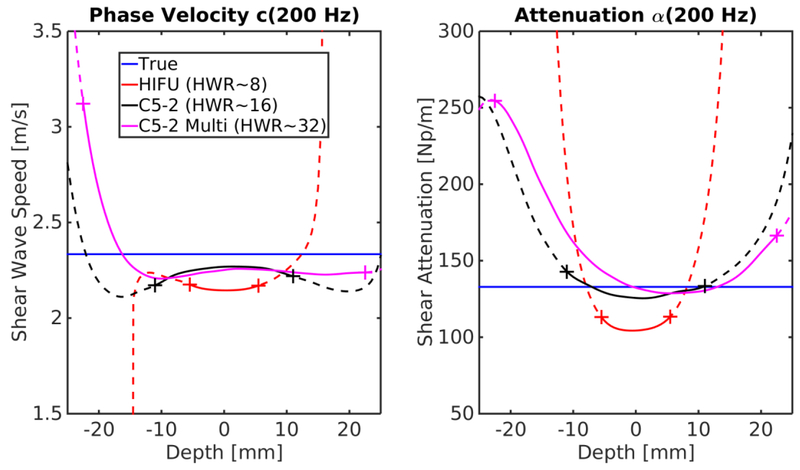
Figure 6 shows dispersion and shear attenuation estimates in a viscoelastic material at 200 Hz as a function of depth for the HIFU piston, the single focus C52-v, and multi-focal C5-2v curvilinear array excitations. Each excitation has been shifted so its focus occurs at 0 mm to allow the relative DOF to be more easily visualized. The range of depths that varied < ± 5% from the estimate at the focal depth of the excitation are shown in Figure 7, where the errorbars represent the variation seen over the frequency range of 100–400 Hz. This demonstrates the axial range that could reasonably be used to average shear wave signals through depth in order to improve SNR.
Figure 6:
Estimates of (a) phase velocity and (b) attenuation at 200 Hz as a function of depth in an viscoelastic material (M4 as listed in Table 2). Each excitation has been shifted so the focal depth occurs at 0 mm. The DOF, as calculated from (9), is 11 mm, 21 mm, and 42 mm for the HIFU piston, single focus C5-2v, and multi-focal C5-2v curvilinear array excitations respectively, and is indicated by the solid line, bounded by + markers. Estimates outside the DOF are indicated by a dashed line. The estimates of dispersion and attenuation are consistent over the approximate DOF for the HIFU piston and single focus C5-2v excitation. However, using a multi-focal excitation does not extend consistent estimates across an expanded DOF. Note the bias present throughout the DOF for each excitation that appears as an offset between the estimates and the true values. At the focal depth (0 mm), the offset from true is the same offset appearing in Figure 3 at 200 Hz.
Figure 7:
The range of depths that varied < ± 5% from the dispersion or attenuation estimate at the center of the excitation for the HIFU piston, single focus, and multi-focal C5-2v curvilinear array excitations in the VE material M4 (Table 2). Errorbars represent the variation seen over the frequency range of 100-400 Hz. As the DOF of the excitation increases from F/1 in the HIFU piston to F/2 in the single focus C5-2v excitation the range of depths that give a consistent estimate also increases, although the range of depths for attenuation is always smaller than the range of depths for dispersion. However, the range of depths using a multi-focal excitation did not significantly change relative to its single focus counterpart. The range of depths were asymmetric about the focal depth due to axial asymmetries in the excitation. In general the range of depths tended to skew shallow to the focal depth as seen at 200 Hz in Figure 6. Note that these estimates do not take into account bias in an estimate, only the consistency of the measurement made.
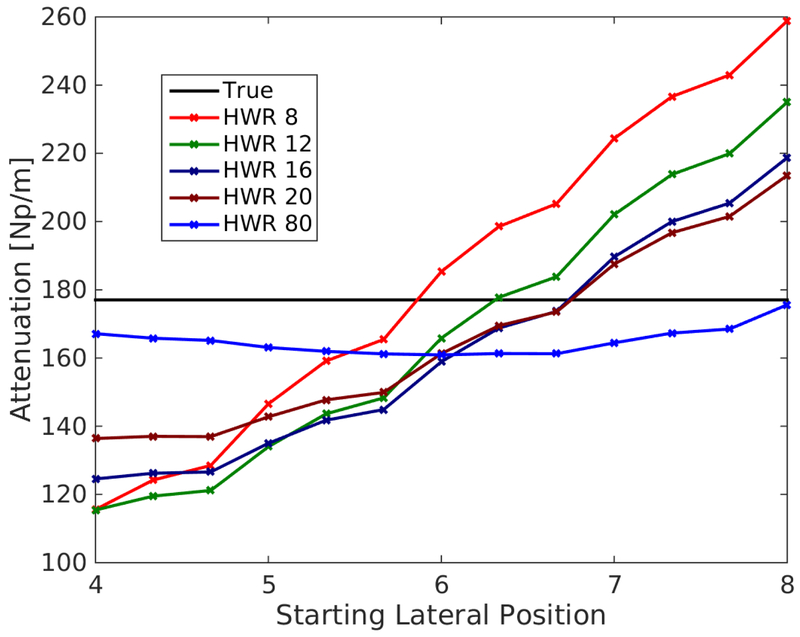
Figure 8 shows shear attenuation estimates in a viscoelastic material at 250 Hz as a function of starting lateral position for the Tukey window excitations with HWR 8, 12, 16, 20, and 80. For all starting lateral positions, a constant 4 mm reconstruction range was used. For a true cylindrical wave, the lateral reconstruction range should not have an effect on attenuation estimates; however, for excitations with finite height the lateral range used can change the bias in attenuation reconstructions.
Figure 8:
Attenuation estimates at 250 Hz relative to the true value in the VE material M4 (Table 2) as a function of starting lateral position for excitations of different HWR. Notice that there is a trend of underestimation for starting lateral reconstruction location closer to the excitation that transitions to overestimation of attenuation as that starting position gets farther away, with that transition of under-to-over estimation varying as a function of HWR.
Discussion
Commercial implementations of SWEI report group shear wave speeds, rather than phase speeds, for several reasons. Dispersion estimation methods are limited in vivo by relatively poor shear wave signal-to-noise ratio (SNR) and quantifying shear wave attenuation has been challenged by the fact that shear wave displacement amplitudes depend on both shear attenuation and the decay due to geometrical spreading. In this work, we investigated some of the factors that challenge viscoelastic reconstructions by evaluating the effects of acoustic radiation force source geometry while assuming cylindrical shear wave propagation. It is known that the cylindrical propagation assumption can be overly simplistic, but it is sometimes a necessity when the overhead of more accurate but complex numerical models representing focused excitation geometries and different material properties are not practical. For this reason, we have demonstrated how well these viscoelastic reconstruction methods work with “tall” axisymmetric excitations that best match the cylindrical assumptions, versus “short” axisymmetric excitations that deviate from the cylindrical assumption by one degree of freedom in the height of the excitation. Finally, we use more experimentally realistic excitation spatial distributions in single and multiple foci configurations modeling typical SWEI systems to evaluate how well they satisfy these cylindrical assumptions and the bias that is introduced in attenuation estimates when this assumption is violated.
The results from Figure 1 show that for data using the assumptions of an infinite source in the z-dimension, the amplitude and phase-based model-free methods reconstruct accurate material properties (Budelli et al., 2016; Kazemirad et al., 2016). The overall RMSE in the dispersion and attenuation estimates are negligible in comparison to the standard deviations seen in typical experimental results (±0.1 m/s and ±40 Np/m, respectively) (Budelli et al., 2016). These results also give a baseline bias for the dispersion (< 0.07 m/s) and attenuation error (<6.5 Np/m) for the frequency range of 100-400 Hz in the range of materials used, under the assumption of the asymptotic form given kr >> 1. This kr value decreases for a constant r (4 mm in our analyses) as the stiffness increases, so increasing bias with increasing speed for a particular frequency is expected as seen at low frequencies (< 100 Hz) in Figure 1. Although the values of kr calculated for these materials at 100 Hz were all greater than one, we can still observe some bias in dispersion and attenuation estimates around 100 Hz in the stiffest materials. This shows the trade-off between reconstruction accuracy and frequency range. For a fixed radial reconstruction range, the unbiased frequency range will be shifted toward higher frequencies in stiffer media. For a fixed frequency range, the starting position of the reconstruction range will need to shift further from the source in stiffer materials to meet the cylindrical wave assumptions. However, this relationship between starting lateral position and frequency range is an oversimplification of the challenges, since stiffer media will displace less for the same excitation, and thus have lower SNR, so there may not be enough signal at sufficient distance from the source to accurately estimate values of dispersion and attenuation in stiffer media.
The dispersion and attenuation estimates from analytic shear wave data provide accurate reconstructions for a range of materials assuming a source with infinite extent. Dispersion and attenuation are also accurately reconstructed from the FEM modeled shear waves with HWR 80 with small deviations from ground truth (Figure 2 and Table 7), bridging the results from the analytic shear wave data to that generated using FEM models. This allows us to isolate one aspect of the excitation (in this case the height) to demonstrate the effects of the height of the excitation on the ability to accurately calculate dispersion and attenuation. Figure 2 shows that bias increases in shear attenuation estimates for ARFI excitations with a smaller HWR. This observation is supported by RMSE in Table 7 and is consistent with the assumption in phase spectroscopy and amplitude-based attenuation methods that the excitation is infinite in the axial direction; therefore, a plane at the center of the excitation would most closely follow this behavior when the excitation has a large HWR. When the HWR is smaller, the correction overcompensates for the decay due to geometric spreading, which artificially appears as a decrease in shear attenuation in the VE material (Figures 2 and 3).
Underestimation of attenuation for small HWR excitations may be counter-intuitive because the amplitude decay due to geometric spreading increases as a source moves from being cylindrical to spherical in shape (i.e., to 1/r). As the excitation height decreases and amplitude decay due to geometric spreading approaches 1/r, attenuation would be overestimated using assumptions of cylindrical wave propagation. Figures 2 and 3 show attenuation is underestimated for the lateral range used (4 - 8 mm). This demonstrates even the excitations with the shortest HWR or DOF still appear to have a finite height and there is a complex interference pattern as the shear waves propagate away from the source. Figure 8 shows that as the lateral range is moved further from the excitation source, the bias transitions from underestimating to overestimating attenuation. This indicates that at large distances from a source with a small DOF, spherical correction of geometric decay may be appropriate; however, most of the signal in these simulations has decayed with 1 cm of propagation, so any reconstructions beyond this range will be limited by SNR. Additionally, the decrease in RMSE in attenuation estimates of the Tukey HWR 8 excitation compared to the HWR 12, is most likely due to the proximity of the plane at the center of the excitation to the axial gradients in displacement at the top and bottom edges of the excitation, and the complex wave dynamics result in less bias in estimating the attenuation of the elastic material (M2).
Experimental SWS reconstructions in tissue-mimicking phantoms have an accepted variability of 5 to 10% of the true speed. The overall bias seen in the dispersion and attenuation estimates in the elastic material were relatively small compared to these typical variations; however, the bias in dispersion and attenuation estimates were higher in the viscoelastic material, particularly in excitations with a small DOF, highlighting the importance of excitation geometry. This inconsistency across materials shows that simulation of an excitation geometry in VE materials is important to highlight material-dependent bias (Figures 2 and 3).
The excitation simulated from the HIFU piston has an F/1 focus and the results are similar to the Tukey window length that approximates this focal configuration (HWR 8). The single focus excitation from the C5-2v transducer has an F/2 configuration (HWR 16), but outperforms the Tukey windowed excitation of the same HWR with smaller RMSE. The multi-focal C5-2v excitation has negligible differences in estimates from the single focus excitation, except in estimating attenuation in the VE material (M4), where it has a decrease in bias across the estimates from 100–400 Hz. This is most likely because the single focus excitation is the same as the second of the three rapid excitations in the multi-focal excitation. The elevation focus of the C5-2v curvilinear array is at 60 mm, and it may be that there is an increase in bias in estimating VE parameters at depths shallow or deep to the elevation focus.
In experimental data, VE reconstruction methods are often SNR limited, so commonly multiple depths are averaged together to reduce noise from displacement estimation. The extent of the DOF affects the region over which averaging should be applied for reconstructing a shear dispersion or attenuation curve. As can be seen in Figures 4 and 6, the estimates are relatively consistent over the height of the excitation (DOF). As the HWR increases, a greater range of depths can be used for dispersion and shear attenuation estimates without introducing significant additional bias. Figure 4 also shows the increase in attenuation estimates near and just beyond the top and bottom of each excitation. This demonstrates the increase in geometric spreading near the ends of each excitation, resulting in an overestimation of shear attenuation.
A longer DOF also provides the opportunity to make multiple measurements of dispersion and attenuation to better characterize any heterogeneities with depth. Figures 5 and 7 show this trend as well, where increasing the height of the excitation leads to a longer range of depths that report a consistent measurement. It is interesting that the range of depths for attenuation roughly align with either the length of the Tukey window used, or the DOF of the single focus excitations, but the dispersion estimates extend beyond this range. The methods for estimating dispersion only assume a linear change in phase as a function of radial propagation, so they appear to be more robust in making accurate estimates of dispersion in areas of edge effects. The attenuation methods assume a decay due to geometric spreading and an exponential decay due to shear attenuation, which is less accurate outside the depth of field.
Averaging multiple depths does not reduce bias in the estimate introduced due to the excitation geometry. The bias present throughout the DOF for each excitation appears as an offset between the estimates and the true values. For example, the offset between the true values and the estimates from the HIFU piston excitation (Figure 6), is also consistent over the DOF. Using a multi-focal excitation does not create consistent estimates across an extended DOF, as is predicted by the + markers at the top of the shallowest and the bottom of the deepest excitations (Figure 3). The range of depths is nearly the same as the single focus excitation. This bias away from the center of the excitation is consistent with results presented by Budelli et al. (Budelli et al., 2016).
The dispersion and shear attenuation estimates are symmetric with depth for the Tukey excitations (Figure 4) because the excitation is symmetric about its center at 60 mm, but the excitations from the HIFU piston and C5-2v curvilinear array have depth distributions based on the diffraction of the focal configurations and are not axially symmetric about their foci, causing the resulting dispersion and shear attenuation curves to be asymmetric in depth about the focus as well. Based on the work by Rouze et al., we might expect bias in the dispersion and attenuation estimates due to the asymmetry introduced by independent lateral and elevation focusing (Rouze et al., 2015). In this study, the C5-2v focal configuration is F/2 laterally and F/3 in elevation. This small asymmetry does not appear to introduce bias in either attenuation or dispersion estimates over the DOF using a single focus excitation; however, this may contribute to the bias present in dispersion and attenuation estimates shallow to the elevation focus using the multi-focal excitation.
The errors due to the ARFI source geometry have potential implications beyond the methods explored in this work. Other model-free methods, such as the 2-D FT methods, are based on the same derivations assuming an infinitely tall source. Further investigation is needed to determine the error that these methods are susceptible to from finite height DOF. A limitation of this study is that the lateral-elevation spatial extent of the Tukey window excitations was held constant while the axial extent was modified. In an experiment, creating a longer DOF by increasing the F/# would also result in a wider beamwidth; however, the frequency content (f) of the shear wave is related to the beamwidth (which approximates λ) by c = fλ. The fixed lateral-elevation spatial extent used herein keeps the relative frequency content the same, and isolates changes in dispersion and attenuation estimates due to the spatial extent in the z dimension. Experimentally, one common approach to extend the DOF without changing the beamwidth is to use a multi-focal zone excitation (Bercoff et al., 2004); however, the in the geometry studied, using a multi-focal excitation led to only modest improvements in attenuation estimates and negligible differences in dispersion estimates. Other aspects of experimental acquisitions that may contribute to variability in dispersion and attenuation estimates, such as the effects of ultrasonic tracking, tissue motion, and speckle bias are not considered in this manuscript.
Conclusions
Methods to estimate viscoelastic properties from shear wave spectroscopy and amplitude decay-based attenuation work well in data generated from excitations that meet the assumption of a large DOF to approximate an infinite source in depth. More experimentally realistic, smaller DOFs result in underestimation of shear attenuation due to an overestimation of the decay due to geometric spreading. Although estimates of dispersion were less affected by the finite height of the excitation geometry than attenuation estimates, a HIFU piston with an F/1 focal geometry was associated with bias in both estimates of dispersion (up to 15%) and attenuation (up to 41%). When using a curvilinear array, small differences in lateral (F/2) and elevation (F/3) focusing did not have a strong impact on the ability to estimate dispersion and attenuation. A single focal depth with an F/2 focal configuration using a curvilinear array appears to provide relatively consistent estimates of dispersion and attenuation for the range of material properties evaluated herein. Although experimentally an extended DOF can be created with a multi-focal zone excitation, for the geometry studied herein, using a multi-focal excitation led to only modest improvements in attenuation estimates and negligible differences in dispersion estimates.
Acknowledgments
The authors would like to thank Ned Danieley for computer system administration and NIH funding source R01-EB002132 and R01-EB022106.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Bercoff JJ, Tanter M, Fink M. Supersonic Shear Imaging: A New Technique for Soft Tissue Elasticity Mapping. IEEE Trans Ultrason Ferroelectr Freq Control 2004, 51(4):396–409. [DOI] [PubMed] [Google Scholar]
- Bernard S, Kazemirad S, Cloutier G. A frequency shift method to measure shear wave attenuation in soft tissues. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 2016, PP(99):1–1. [DOI] [PubMed] [Google Scholar]
- Budelli E, Brum J, Bernal M, Deffieux T, Tanter M, Lema P, Negreira C, Gennisson J-L. A diffraction correction for storage and loss moduli imaging using radiation force based elastography. Physics in Medicine and Biology 2016, 62(1):91. [DOI] [PubMed] [Google Scholar]
- Chen S, Urban MW, Pislaru C, Kinnick R, Zheng Y, Yao A, Greenleaf JF Shearwave dispersion ultrasound vibrometry (SDUV) for measuring tissue elasticity and viscosity. IEEE Trans Ultrason Ferroelectr Freq Control 2009, 56(1):55–62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Deffieux T, Montaldo G, Tanter M, Fink M. Shear wave spectroscopy for in vivo quantification of human soft tissues visco-elasticity. IEEE Trans Med Imaging 2009, 28(3):313–322. [DOI] [PubMed] [Google Scholar]
- Graff KF Wave Motion in Elastic Solids, Dover, Mineola, NY, chap. 5 1991. [Google Scholar]
- Jensen JA, Svendsen NB Calculation of Pressure Fields from Arbitrarily Shaped, Apodized, and Excited Ultrasound Transducers. IEEE Trans. Ultrason., Ferroelec., Freq. Contr. 1992, 39(2):262–267. [DOI] [PubMed] [Google Scholar]
- Kazemirad S, Bernard S, Hybois S, Tang A, Cloutier G. Ultrasound shear wave viscoelastography: Model-independent quantification of the complex shear modulus. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 2016, 63(9): 1399–1408. [DOI] [PubMed] [Google Scholar]
- Nenadic IZ, Qiang B, Urban MW, Zhao H, Sanchez W, Greenleaf JF, Chen S. Attenuation measuring ultrasound shearwave elastography and in vivo application in post-transplant liver patients. Physics in Medicine and Biology 2017, 62(2):484. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nightingale K, Rouze N, Rosenzweig S, Wang M, Abdelmalek M, Guy C, Palmeri M. Derivation and analysis of viscoelastic properties in human liver: impact of frequency on fibrosis and steatosis staging. Ultrasonics, Ferroelectrics, and Frequency Control, IEEE Transactions on 2015, 62(1): 165–175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmeri M, Sharma A, Bouchard R, Nightingale R, Nightingale K. A finiteelement method model of soft tissue response to impulsive acoustic radiation force. IEEE Trans. Ultrason. Ferroelectr. Freq. Control 2005, 52(10): 1699–1712. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Palmeri ML, Qiang B, Chen S, Urban MW. Guidelines for finite-element modeling of acoustic radiation force-induced shear wave propagation in tissue-mimicking media. IEEE Transactions on Ultrasonics, Ferroelectrics, and Frequency Control 2017, 64(1):78–92. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouze N, Deng Y, Palmeri M, Nightingale K. Measurement of the stiffness and viscosity of viscoelastic materials using group shear wave speeds. In: Ultrasonics Symposium (IUS), 2015 IEEE International. 2016. [Google Scholar]
- Rouze NC, Palmeri ML, Nightingale KR An analytic, fourier domain description of shear wave propagation in a viscoelastic medium using asymmetric gaussian sources. The Journal of the Acoustical Society of America 2015, 138(2): 1012–1022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sridhar M, Liu J, Insana MF. Viscoelasticity imaging using ultrasound: parameters and error analysis. Physics in medicine and biology 2007, 52(9):2425–43. [DOI] [PMC free article] [PubMed] [Google Scholar]