Abstract
A coupled photosynthesis-stomatal conductance model with single layer sunlit and shaded leaf canopy scaling is developed for the Pleim-Xiu land surface model (LSM) option in the meteorology and air quality modeling system - WRF/CMAQ (Weather Research and Forecast model and Community Multiscale Air Quality model). The photosynthesis-based model for the PX LSM (PX PSN) is implemented and evaluated in a diagnostic box model that has evapotranspiration and ozone deposition components taken directly from WRF/CMAQ. We evaluate PX PSN for latent heat (LH) estimation at four FLUXNET sites with different vegetation types and landscape characteristics and at one FLUXNET site with ozone flux measurements against the simple Jarvis approach used in the current PX LSM. Overall, the PX PSN simulates LH as well as the PX Jarvis approach. The PX PSN, however, shows distinct advantages over the PX Jarvis approach on grassland that likely results from its treatment of C3 and C4 plants for CO2 assimilation estimation. Simulations using Moderate Resolution Imaging Spectroradiometer (MODIS) LAI rather than LAI observations assess how the model would perform with the grid averaged data available in the Eulerian grid model (WRF/CMAQ). While MODIS LAI generally follows the seasonality of the observed LAI, it cannot capture the extreme highs and lows of the site measurements. MODIS LAI estimates degrade model performance at all sites but one site having old and tall trees. Ozone deposition velocity and ozone flux along with LH are simulated especially well by PX PSN as compared to significant PX Jarvis overestimation.
1. Introduction
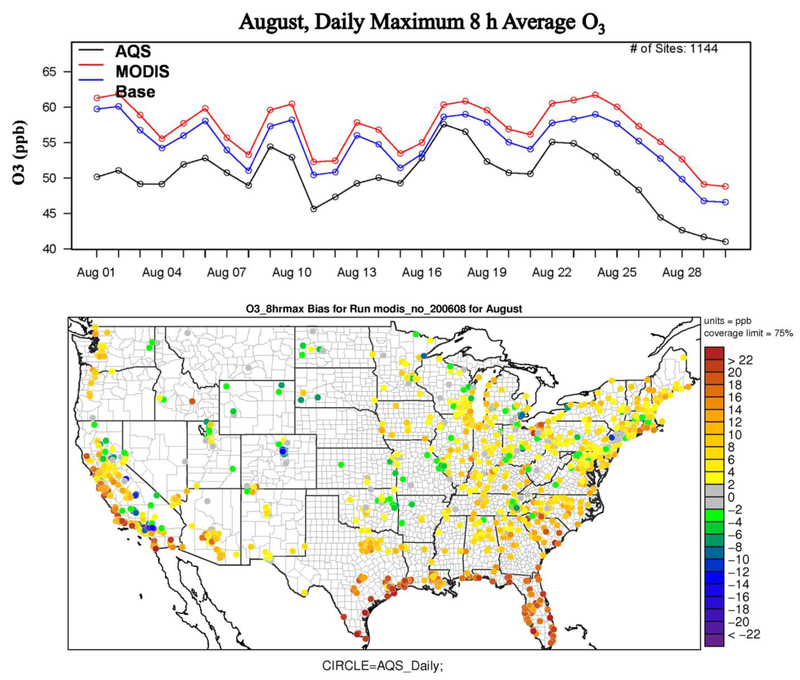
The combined meteorology and air quality (AQ) modeling system, composed of the Weather Research and Forecast (WRF) model [Skamarock et al., 2008] and Community Multiscale Air Quality (CMAQ) model [Byun and Schere, 2006] is an important tool that increases our understanding of the chemical and physical processes contributing to air quality impairment, and facilitates the development of policies to mitigate harmful effects of air pollution on human health and the environment around the world [Cohan et al., 2007; Wang et al., 2010; Compton et al., 2011; Hogrefe et al., 2014; Xing et al., 2015], In spite of significant improvements in model performance over the past decade, improvements are still needed [Foley et al., 2010; Appel et al. 2011], For example, WRF/CMAQ tends to overestimate ozone (O3) in the southeastern and Gulf of Mexico regions of the United States (U.S.), while O3 estimates in the northern U.S. agree well with observations. The recent study by Ran et al. [2016] shows that the model’s tendency to overestimate O3 in these regions persists (figure 1). Many components from this complex modeling system including emissions, transport, photochemistry, and land surface exchange may contribute to these errors. This research focuses on advancing land surface model (LSM) meteorological (heat, moisture, and momentum) and chemical (dry deposition and bi-directional exchange) surface flux processes in the retrospective WRF/CMAQ system by reducing uncertainty associated with the simulation of vegetation processes.
Figure 1.
Evaluation of August 2006 daily maximum 8-hour average O3 (ppb) simulated from an improved WRF/CMAQ with/without (base) MODIS vegetation and albedo input against the Environmental Protection Agency Air Quality System (AQS) sites. The top plot displays mean of daily maximum 8-hour average O3 from the base model (blue line), the model with MODIS input (red line), and all AQS sites (black line). The bottom plot displays the mean bias for daily maximum 8-hour average O3 simulated from WRF/CMAQ without MODIS input. The base model’s vegetation is computed from vegetation parameters prescribed in land use category lookup tables using equations 2 and 3 in Ran et al. [2015].
Plants open their stomata to obtain atmospheric carbon dioxide for photosynthesis while at the same time they lose water because of the diffusion of water molecules from leaf chloroplasts to the atmosphere. LSMs model stomatal conductance to estimate evapotranspiration (ET) which includes leaf transpiration and evaporation from soil pores, plant litters, open water bodies, and leaf cuticle surfaces [Bonan, 2008], The Pleim-Xiu (PX) [Pleim and Xiu; 1995; Xiu and Pleim, 2001] is routinely used in retrospective WRF meteorology simulations for air quality [Eder et al., 2009; Kelly et al., 2014; Hogrefe et al., 2014] because it is specifically designed for CMAQ which has a dry deposition model using the same stomatal and aerodynamic resistances computed in the PX LSM WRF and has the same planetary boundary layer (PBL) model, the Asymmetric Convective Model version 2 (ACM2) [Pleim, 2007a and 2007b], that can be consistently configured in WRF. Unlike climate LSMs [e.g. Oleson et al., 2013; Clark et al., 2011] with complex hydrology and dynamic vegetation coupled with climate to model processes over decadal to century future periods, PX LSM has relatively simple canopy treatments with a big-leaf empirical function stomatal conductance following the approach described in the Interactions Soil Biosphere Atmosphere (ISBA) LSM by Noilhan and Planton [1989] as well as simple soil hydrology and snow processes. Surface characteristics including vegetation parameters and surface albedo are specified in LSM land use look-up tables and plant phenological dynamics are modeled using simple time and deep soil temperature dependent functions. With increasing needs to conduct year-long retrospective WRF/CMAQ simulations, the LSM using simple canopy treatment with table prescribed surface representations clearly show limitations in capturing seasonal landscape changes (e.g. phenology and albedo) and disturbances (e.g. fires, storm damages) [Ran et al.,2016], In addition, lacking a biochemically-based photosynthesis-conductance scheme could limit not only the model’s dynamic responses to environmental conditions such as temperature, air pollutants (e.g. O3) and CO2 concentration but also their applications in assessing the coupling effects of air quality and vegetation productivity in changing climate.
There are ongoing efforts to improve the surface representation in WRF/CMAQ. For instance, the high resolution 30-m National Land Cover Database (NLCD) as well as MODIS 500-m land cover data [Pleim and Ran, 2011, Ran et al., 2010, Ran et al., 2012] are used in WRF/CMAQ simulations with the PX LSM. Gridded 2011 NLCD/MODIS land cover data at the 9-arc second resolution for most of North America are available in the WRF Preprocessing System (WPS) for WRF/CMAQ with the PX LSM to use the 40-class NLCD/MODIS land cover data routinely. In addition, there are recent improvements to the vegetation, soil, and PBL processes in the WRF/CMAQ with the PX LSM and ACM2 [Pleim et al., 2015]. Ran et al. [2015 and 2016] incorporated MODIS vegetation and albedo products in the WRF/CMAQ modeling system with the PX LSM. They conclude that realistic vegetation characteristics and phenology from MODIS products help improve the 2 m mixing ratio (Q) simulation during the growing season. With the climate change from the relentless rise of CO2 levels in the atmosphere, the simple vegetation treatment following the empirical function Jarvis stomatal conductance approach [Jarvis, 1976] without the CO2 effect by the PX LSM [Noilhan and Planton, 1989; Pleim and Xiu, 1995] is limited over extended simulations for regulatory and scientific research related to climate-air quality co-benefit studies. Therefore, incorporating the impacts of CO2 in WRF/CMAQ through using a photosynthesis-based stomatal conductance approach in the PX LSM will be an important advance in the modeling capabilities with changing CO2 levels in space and time which can be captured by the Environmental Protection Agency (EPA) CO2 emission inventory. This research furthers the study presented by Ran et al. [2016] by enhancing the vegetation model using a photosynthesis-based stomatal physiology process model which is commonly used in Earth system models [Bonan et al., 2011; Clark et al., 2011; Kowalczyk et al., 2013; Oleson et al., 2013].
The objective of the study is to develop, implement and evaluate a coupled leaf photosynthesis and stomatal conductance approach in the PX LSM for meteorology and air quality modeling with MODIS vegetation input. This paper focuses on the development and evaluation of a coupled photosynthesis and stomatal conductance approach in a diagnostic box model with the PX LSM and CMAQ dry deposition model components that are directly from the updated WRF/CMAQ system presented by Ran et al. [2016]. The questions which the papers addresses are: (i) how does the PX LSM with a coupled leaf photosynthesis and stomatal conductance approach influence the performance of latent heat and ozone deposition and flux, (ii) can the photosynthesis approach in PX LSM better represent diurnal variations in latent heat, and ozone deposition and flux than the current approach, and (iii) how does the PX LSM with a coupled leaf photosynthesis and stomatal conductance approach combined with MODIS leaf area index (LAI) influence latent heat fluxes?
A sunlit and shaded big leaf photosynthesis-based stomatal conductance approach developed and implemented in the diagnostic PX LSM box model is described in section 2 based on the 2006 flux measurements from the FLUXNET Harvard Forest US-Ha1 site. The photosynthesis-based approach is further evaluated and analyzed against the measurements from four selected FLUXNET sites (Missouri Ozark/US-MOz, Mead Irrigated Rotation/US-Ne2, Fermi Prairie/US-IB2, and Wind River Field Station/US-Wrc) which have different vegetation types and against ozone and surface flux measurements by EPA at the Duke Forest Open Field site in North Carolina. MODIS vegetation input to the diagnostic box model is also evaluated to demonstrate the advantages and limitations in using MODIS input to the advanced PX LSM. MODIS LAI is evaluated against observed LAI which are available at the four selected FLUXNET measurement sites. Conclusions and future work are presented in the last section.
2. Photosynthesis-based Stomatal Conductance Approach
Vegetation plays an important role not only in the surface energy budget but also water and carbon cycles [Jarvis and McNaughton, 1986; Katul et al., 2012]. In addition, vegetation can act as both a source and a sink of atmospheric gas-phase chemical species including CO2 O3, NH3, NO2, SO2, and a wide array of volatile organic compounds (VOCs) [Pleim and Ran, 2011], Plants open their stomata to optimize the intake of atmospheric CO2 for photosynthesis, while minimizing the diffusion of water molecules through leaf stomata to the atmosphere. A key function of LSMs is to estimate latent heat flux (λE), which is the product of latent heat of evaporation (λ) times evaporative water flux (E, also called evapotranspiration - ET). ET estimates include leaf transpiration and water evaporation from soil, litter and vegetation surfaces and open water bodies [Bonan, 2008]. During the growing season, transpiration is often dominant in controlling ET from vegetated lands [Budyko, 1974]. Stomata control the amount of water transpired by vegetation so that stomatal conductance and its scaling from leaf to canopy are key processes in estimating ET. Following approaches developed for global climate models (GCMs) [Dai et al., 2004; Cox et al., 1998; Bonan et al., 2011; Clark et al., 2011; Kowalczyk et al., 2013; Oleson et al., 2013] and ecosystem productivity models [Campbell and Norman, 1998; Medlyn et al., 2005; Song et al., 2009; Evers et al., 2010; Baker et al., 2010], we implemented a coupled photosynthesis-based stomatal conductance model with sunlit and shaded leaves in the PX LSM for coupling ET estimation with CO2 assimilation.
2.1. Stomatal Conductance
The current PX LSM models canopy stomatal conductance (Gst) of gasses following the empirical multiplicative Jarvis approach [Jarvis, 1976] which assumes independent environmental functions. The PX LSM treats the whole canopy as a single leaf (big-leaf model). The canopy fluxes from the big leaf are then calculated by summing the fluxes of individual leaves [Jarvis, 1995], Following the Jarvis approach presented in the ISBA LSM [Noilhan and Planton, 1989], with modifications for PX LSM [Pleim and Xiu, 1995], the canopy level conductance, Gst, is computed as:
| (1) |
where Rstmin is the minimum stomatal resistances for each land cover type specified in the LSM land cover lookup table. The functions F1–4, which are defined by Xiu and Pleim [2001], represent the fractional degree (0 to 1) of stomatal closure caused by the environmental factors: photosynthetically active radiation (PAR), root-depth soil moisture (w2), relative humidity at the leaf surface (RHs), and air temperature in the canopy (Tic) The influence of ambient CO2 concentration on stomatal opening is not included in the current PX LSM with the assumption that the CO2 concentration is constant for the relatively short periods typically used for mesoscale meteorology simulations. The advantage of this simple empirical approach is that it can be easily implemented for large scale simulations with a small set of vegetation parameters such as LAI and Rstmin and that it generally produces reasonable results for retrospective simulations with initial or real-time assimilated soil conditions [Noilhan and Mahfouf, 1996; Chen and Dudhia, 2001; Xiu and Pleim, 2001]. The weakness of such simplistic models is that they depend on the limited number of multiplicative functions, which are related to environment variables that are often not actually independent. The multiplicative big leaf model does not depend on measurable physiological or physical parameters and must be calibrated using stand-level and canopy level eddy flux measurements. Although the big leaf model is simple and widely used in many disciplines, it is often criticized for ignoring canopy gradients and differences between plant and soil components within the canopy [Jarvis, 1995; dePury and Farquhar, 1997; Wang and Leaning, 1998].
The stomatal conductance (gst) at the leaf scale in the photosynthesis-based PX LSM is modeled after the widely-used Ball-Woodrow-Berry (BWB) approach [Ball et al., 1987], which connects gst directly to net CO2 assimilation rate (Anet) based on plant physiological processes. gst is modeled in the PX LSM following the semi-empirical BWB model described by Collatz et al. [1991], applied in a GCM by Sellers et al. [1996], and implemented in the Community Land Model version 4 (CLM4.5) [Bonan et al., 2011; Oleson et al. 2013] within the Community Earth System Model as:
| (2) |
where g0 is set to 0.01 mol m−2 s−1 for C3 plants and 0.04 mol m−2 s−1 for C4 plants, mg is a plant type parameter which is 9 for C3 plants and 4 for C4 plants, cs is the CO2 partial pressure at the leaf surface, es is the vapor pressure at the leaf surface, ei is the saturation vapor pressure inside the leaf stomata at the vegetation surface temperature (Ts), and Pa is the atmospheric pressure. Soil moisture stress is considered similarly to the PX Jarvis LSM, where the empirical function F2 (eq. 3) is used to scale canopy stomatal, and net CO2 assimilation rate following the approach used by the Joint UK Land Environment Simulator (JULES) LSM model [Clark et al., 2011]. The function F2 with a relatively smooth S shape very similar to the JULES soil stress factor is computed as:
| (3) |
with
where wfc is the volumetric water content at field capacity and wwlt is the wilting point.
2.2. Leaf-scale Photosynthesis
The new PX LSM formulation defines the net CO2 assimilation rate, Anet, of C3 and C4 plants at the leaf scale as a function of the photosynthetic assimilation rate described by Farquhar et al. [1980]. GCMs [Collatz et al., 1991, and 1992, Sellers et al., 1996, Cox et al., 1999, Clark et al., 2011, Bonan et al. 2011, Oleson et al., 2013] and land surface exchange studies [Medlyn et al., 2005; Song et al., 2009; Evers et al., 2010; Baker et al., 2010] commonly employ this approach when modeling plant evaporation and productivity. Anet (mol CO2 m−2 s−1) is calculated based on colimitation among three potential assimilation rates (Ac, Aj, and Ae), limited by Rubisco (nitrogen related), light (photon related), and transport of photosynthetic products for C3 plants and phosphoenolpyruvate (PEP) carboxylase limitation for C4 plants. The Rubisco-limited assimilation rate (Ac mol CO2 m−2 s−1) is a function of the maximum rate of carboxylation of Rubisco (Vcmax mol CO2 m−2 s−1) and is formulated following JULES [Clark et al., 2011] as:
| (4) |
with
| (5) |
| (6) |
Where ci(Pa) is the CO2 partial pressure inside the leaf stomata, cc (Pa) is the CO2 compensation point in the absence of non-photorespiratory respiration, Oa (Pa) is the partial pressure of atmospheric oxygen, and Kc (Pa) and Ko (Pa) are the Michaelis-Menten constants for CO2 and O2. Cc, Kc, and Ko are computed based on parameters and equations used in JULES [Cox et al., 1998; Clark et al., 2011], Vcmax at any leaf surface temperature is estimated based on the maximum rate of carboxylation of the enzyme Rubisco at 25°C (VCmax25 mol CO2 m−2 s−1), limited by the assumed optimal temperature range defined by parameters Tup (°C) and Tlow (°C) for specific plant function type (PFT). The average Vcmax25 value is assumed to be related to leaf nitrogen concentration and is computed based on the top of the canopy Vcmax25 (Vcmax25_0) integrated for sunlit and shaded leaves based on the equations described by Bonan et al. [2011] as:
| (7) |
| (8) |
where Kn is the foliage nitrogen decay coefficient, Kdir is the direct beam attenuation coefficient within the canopy (described by equation 19), and LAIsun and LAIshd are the LAI values for sunlit and shaded leaves (described by equations 17 and 18). As one of the most important parameters in the photosynthesis approach, Vcmax25 shows a range of values among and within PFTs [Kattge et al., 2009] mainly due to different nitrogen use efficiencies. The value used is often tightly related to the foliage nitrogen decay coefficient (Kn) which also varies among models [Bonan et al., 2011], The PX LSM photosynthesis model follows the Vcmax25 values after nitrogen constraints and assigns Kn = 0.17 based on the values analyzed by Bonan et al. [2011]. Bonan et al. [2011] uses Kn = 0.11 in their evaluation study; but the value is set to 0.3 in CLM4.5 for multi-layer model considerations [Oleson et al., 2013].
The light-limited assimilation rate (Aj mol CO2 m−2 s−1) is a function of the rate of electron transport (J mol electron m−2 s−1) and is computed as:
| (9) |
with
| (10) |
| (11) |
| (12) |
where J is solved using the quadratic equation 10, ε is the quantum yield (mol CO2 mol−1 photon) and £j (mol CO2 mol−1 photon) is the computed electron transport quantum use efficiency following the studies by Medlyn et al. [2005] and applied in Song et al. [2009]. Jmax is the maximum electron transport rate (mol electron m−2 s−1) and is estimated to be 1.97 times VCMAX following Bonan et al. [2011], Iapar (mol photon m−2 s−1) is the absorbed photosynthetically active radiation (APAR) by the leaf. Although a number of alternative functions are used to model Jmax and Vcmax dependence on temperature across the literature, Medlyn et al. [2002] categorizes them into two basic types: the Arrhenius (such as the JULES approach) and the peaked function (such as the CLM4.5 approach). They also show that the peaked function represents the temperature-dependent Jmax better for almost all species-based experiments in their review. For mesoscale simulations over relative short-time scales, compared with climate simulations, the photosynthesis-based PX LSM uses the Arrhenius function approach which requires fewer PFT-specific temperature constraint parameters.
The photosynthesis rate (Ae) limited by the transport of photosynthetic products for C3 plants and PEP carboxylase limitation for C4 plants is computed following JULES [Clark et al., 2011] as:
| (13) |
The final CO2 assimilation rate (A) is computed by solving the colimitation equations described by Bonan et al. [2011] shown in equations 14 and 15, and the net CO2 assimilation rate is computed by subtracting leaf dark respiration from A as:
| (14) |
| (15) |
| (16) |
where Ai is the smoothed minimum of Ac and Aj. Ai and A are the smallest roots of the quadratic equations. fdr is the dark respiration coefficient which is set to 0.015 for C3 plants and 0.025 for C4 plants following JULES.
2.3. Leaf to Canopy Scaling
Up-scaling the coupled CO2 assimilation rate and stomatal conductance from the leaf to canopy is complicated by spatial heterogeneity within plant canopies in both the vertical and horizontal dimensions. LAI [Chen et al, 2006], leaf inclination angles and leaf clumping [Pisek et al. 2013], crown gappiness [Song et al. 2009], leaf nitrogen and photosynthetic capacity [Leuning et al., 1995; Baldocchi and Meyers, 1998] vary within the canopy, collectively affecting canopy transpiration, CO2 assimilation, and other flux processes. In addition, the non-linearity of key physiological and physical processes such as leaf photosynthesis and transpiration with many abiotic regulating variables (e.g. solar and terrestrial radiation, temperature, humidity, wind speed, and soil moisture) further complicates the difficulty in upscaling those processes [Jarvis, 1995; Campbell and Norman, 1998]. Leaf stomatal conductance in a canopy can be quite different at different locations due to both current and past varying abiotic and biotic conditions (e.g. age, height) [Jarvis and McNaughton, 1986; Jarvis, 1995]. Because of this complication, modeling and validating parameterized processes that govern land-surface fluxes across different time and space scales remains challenging [Moorcroft, 2006]. Scaling methods from the leaf to canopy vary with different complexity from the simplest big leaf models [Monteith, 1981; Jarvis, 1995; Pleim and Xiu, 1995, Chen and Dudhia, 2001] to multi-layer models [Kobayashi et al., 2012]. A weakness of the simple big leaf model is that it treats sunlit and shaded leaves within the canopy equally. This equal treatment of the canopy leaves often results in overestimation of flux rates (e.g. CO2) [dePury and Farquhar, 1997; Wang and Leuning, 1998]. The sunlit and shaded leaves have distinct differences in leaf surface temperature, which results in different surface vapor pressure. Thus, stomata will behave differently under varying micro-meteorological conditions within the canopy. dePury and Farquhar [1997] and Wang and Leuning [1998] demonstrated that a single-layer sunlit/shaded big leaf model is simpler, but has equivalent predictive capabilities for CO2 assimilation rate and latent heat as a multi-layer model. Zhang et al. (2001) also showed that the sunlit/shaded big leaf approach also compares well to multi-layer models for representing the stomatal pathway in dry deposition models. For the mesoscale modeling purpose, the photosynthesis-based PX LSM model also adopts the two-big leaf approach for canopy scaling. The sunlit and shaded leaf areas are computed using the equations described by Campbell and Norman [1998] and applied in many studies [e.g., Song et al., 2009] as:
| (17) |
| (18) |
Campbell [1986] suggested a simple equation to compute the direct beam attenuation coefficient (Kdir) as:
| (19) |
Where θsun is the sun zenith angle, x is the canopy leaf orientation parameter with 0 for vertical leaves and 1 for spherical leaf orientation (randomly oriented). Following the work by Goudriaan [1977] and applied in many studies [e.g. Song et al., 2009], the transmittance of beam radiation for non-horizontal scattering leaves with leaf absorptivity (αleaf) can be computed as:
| (20) |
The extinction coefficient for diffuse light (Kdif) within the canopy can be estimated by first computing the transmittance for diffuse radiation for the entire upper hemisphere (τdif) as:
| (21) |
| (22) |
The computed direct and diffuse extinction coefficients, the mean radiation intensity on the sunlit and shaded leaves from visible (or PAR) and near infrared (NIR) bands are estimated based on the direct and diffuse PAR and NIR radiation estimations at the top canopy using the methods described by Song et al. [2009], The net radiation (Rnet) for the sunlit and shaded leaves is computed individually as:
| (23) |
with
| (24) |
where APAR and ANIR are the absorbed PAR and NIR at the leaf (sunlit or shaded) (W m−2), LWfloor, LWair, and LWcanopy are the long wave radiations (W m−2) from the floor, air, and canopy computed following the methods of Song et al. [2009], and fLW is the scaling factor of the longwave radiation to the canopy. The leaf temperature is computed following the method described by Evers et al. [2010] using the Penman-Monteith equation with Rnet computed for each leaf.
The canopy stomatal conductance (Gst) and net CO2 assimilation rate (Acnet) for the whole canopy with the soil moisture constraint are then computed as:
| (25) |
| (26) |
where gst_sun gst_shd (m s−1), Anet_sun, and Anet_shd (mol m−2 s−1) are computed leaf-scale stomatal conductance and net CO2 assimilation rate for the sunlit and shaded leaves. The transpiration from the sunlit or shaded canopy leaf (TRc_sun or TRc_shd), with the soil moisture constraint on the stomatal conductance is computed following the PX LSM approach [Pleim and Xiu, 1995] as:
| (27) |
where ρair is the air density (kg m−3), qs (Ts_sun) is the saturated mixing ratio for water vapor at the sunlit leaf temperature Ts_sun, qa is the ambient water vapor mixing ratio above the canopy, Rbw is the boundary resistance for water (m s−1), Ra is the air dynamic resistance (m s−1), and gstw_sun is the sunlit leaf stomatal conductance for water (m s−1) computed from gst (eq. 2) for CO2. The transpiration for the shaded leaf is computed using the same equation, but with parameters for the shaded leaf. The transpiration (TRc) for the whole canopy is then computed as:
| (28) |
The evapotranspiration (ETc) for the canopy is then computed as:
| (29) |
where Ess and Evs are the evaporation from the bare soil surface and vegetation surface and they are estimated based on the current PX LSM approach [Pleim and Xiu, 1995; Ran et al., 2016], Both the photosynthesis-based model and current PX approach use the same estimated Ess and Evs in ET computation. Thus, the comparison of LH between the two approaches purely reflects the differences in modeled plant transpiration.
2.4. Box Model Implementation
The coupled photosynthesis and stomatal conductance (PX-PSN) approach is implemented in a diagnostic box model with the ET and ozone deposition velocity routines from WRF/CMAQ with PX LSM described by Ran et al. [2016]. This box model is designed to use as many observational data as possible from the FLUXNET L2 standardized data [Baldocchi, 2008] for evaluating modeled LH and ozone fluxes from the photosynthesis-based approach (PX PSN) and the current Jarvis approach (PX Jarvis) in comparison with observations. Since the box model is diagnostic and there is no energy budget calculation, observed sensible heat is used to compute aerodynamic surface temperature, which is used as the leaf temperature in the PX Jarvis approach. Observed friction velocity (u*) is used to compute the boundary layer resistance and aerodynamic resistance based on the Monin-Obukov similarity theory (MOST) [Monin and Obukhov, 1954; Oleson et al., 2013; Pleim and Ran, 2011]. The computed aerodynamic surface temperature is not used in the PX PSN, which estimates the sunlit and shaded leaf surface temperatures using the net radiation for sunlit and shaded leaves. Thus, the PX Jarvis approach may have some advantage in these box model experiments by using more observed data in estimating stomatal conductance and ET than are used by the PX PSN approach. The observed air temperature, wind speed, LH, PAR, soil moisture, ambient CO2 concentration, relative humidity, vapor pressure deficit, air pressure, precipitation, and LAI (if available) are input to the box model. To solve the equations for each sunlit and shaded leaf, an iterative numerical scheme, similar to CLM4.5 [Oleson et al., 2013], is used to estimate the leaf surface CO2 partial pressure (cs Pa), gst, Anet, and ci until ci converges. At the same time, the leaf temperature is also numerically iterated outside the ci iteration using the Penman-Monteith equation with Rnet for each leaf. ET from the canopy is obtained by adding computed transpiration from the canopy (eq. 29) to the evaporation estimated from the soil and the leaf surface.
2.5. Photosynthesis-based Model
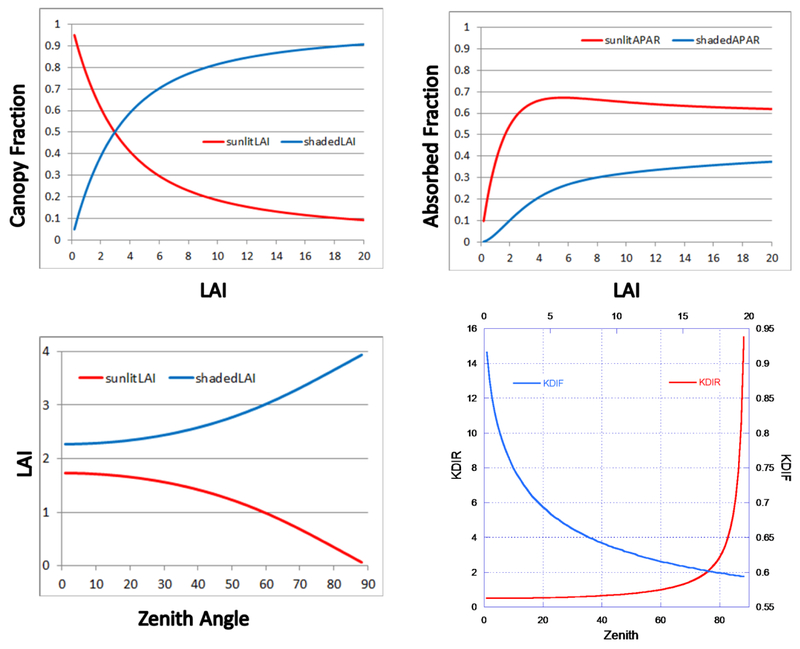
The key parameters for canopy scaling and canopy radiative transfer are evaluated in figure 2 based on the Harvard Forest US-Ha1 site data on 13 June 2006 at 12pm. The sunlit leaf is dominant at the lower LAI while the shaded leaf increases with the increase of LAI (top left in figure 2) for the assumed spherical leaf distribution of the broadleaf forest site. The sunlit leaf absorbs the majority of the incident PAR (top right in figure 2) at the top of the canopy; the absorbed fraction peaks for LAI around 4 with a slightly decreasing trend following the increase of LAI due to the increase of shaded leaf LAI. The changes of the sunlit/shaded LAI and absorbed PAR fractions are very similar to the parameters displayed by Bonan et al. [2011]. With an assumed LAI at 4, most of the leaves are shaded and the sunlit leaf fraction is greatest at 0 zenith angle (bottom left in figure 2). The shaded leaf LAI increases and the sunlit leaf LAI decreases with increasing zenith angle. The direct beam extinction coefficient (red line in the low right plot) increases with the zenith angle exponentially (particularly after 80°) and is greater than 1 for zenith angles greater than 60°, which is consistent with Campbell and Norman [1998]. Since Kdir is multiplied by the incident direct beam PAR in estimating the total PAR on the sunlit leaves [Campbell and Norman; 1998], high Kdir values give much higher estimated PAR on the sunlit leaves than the incident PAR at the top of the canopy during hours with high zenith angle (morning or evening) when the sunlit leaf is a small fraction of the canopy. This condition sometimes causes the sunlit leaf temperature to be unrealistically high when u* is exceptionally low in the early morning (very stable conditions with high boundary layer and aerodynamic resistances). The very small sunlit leaf fraction when sun is just rising and the much higher sunlit PAR due to high Kdir sometimes result in unstable numerical iteration without convergence. Thus, Kdir is limited to 3 in the model. The diffuse beam extinction coefficient is a function of LAI (blue line in the bottom right plot) and it decreases exponentially with the increase of LAI.
Figure 2.
Canopy scaling and radiative transfer parameter plots. The top row plots are the leaf canopy fraction (top left), and the ratio of absorbed PAR to incident PAR (top right) for the sunlit and shaded leaves. The bottom row plots show are the sunlit and shaded LAI (bottom left) with changing zenith angle, and the direct and diffuse extinction coefficients (bottom right) as a function of zenith angle and LAI. Parameters are computed based on US-Ha1 data on 13 June 2006 at 12pm with longitude = W 72.1715, latitude = N 42.5378, LAI = 4 (m2 m−2), zenith angle = 20°, x = 1 (spherical leaf), αleaf = 0.8 for PAR (leaf absorptivity), and αleaf = 0.2 for NIR, forest floor reflectance = 0.10.
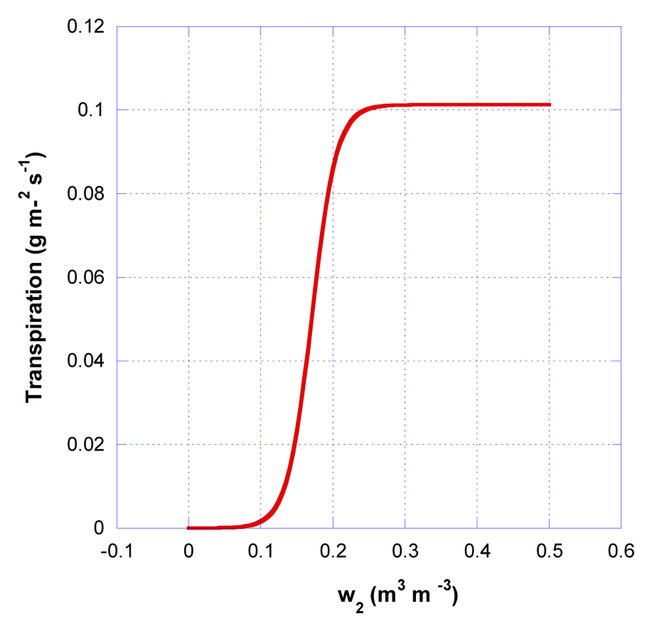
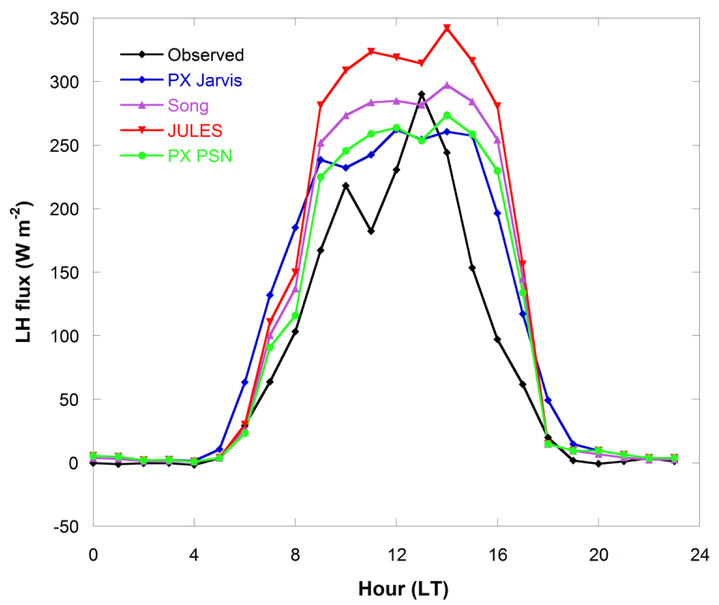
Figure 3 illustrates the influence of deep soil moisture on the canopy transpiration, stomatal conductance, and net assimilation rate (eq. 25, 26, 28). The S shape function indicates that transpiration, stomatal conductance, and net CO2 assimilation reach their potential values where the soil moisture is greater than field capacity, and is severely limited below the wilting point. Since the assimilation rate computation in the PX PSN follows the components from JULES and methods used by Song et al. [2009], figure 4 compares median diurnal LH estimates from the PX PSN with the approaches used by JULES [Clark et al., 2011] and Song et al. [2009] (implemented in the box model) against the results from the PX Jarvis and the US-Ha1 site measurements [Urbanski et al., 2007] for July 2006. Although all models perform well in comparison with the observations (black line), the JULES approach tends to overestimate LH around peak photosynthesis hours because the model does not have constraints on the absorbed PAR in estimating the rate of electron transport. Latent heat estimated using the Song approach is slightly larger than PX PSN estimations because some constants used in the three assimilation rate computations are slightly different from the JULES approach. The PX PSN, which uses the JULES approach to compute Ac, Ae and the Song’s approach to compute Aj with all constants from JULES, results in better LH estimation during the peak transpiration hours. The PX Jarvis does well except in the morning hours and late evening with relatively high LH estimation. All models tend to overestimate LH during the morning and late afternoon with the photosynthesis approaches performing better in the morning. LH from the PX PSN is closest to the observations in the morning, while all photosynthesis approaches perform the best around hour 18 (6 pm). The much improved LH estimation around hour 18 has important implications for meteorology and air quality modeling as WRF/CMAQ tends to overestimate LH and pollutant concentrations during the evening transition when the modeled PBL tends to stabilize too quickly. Lesser LH estimation may help increase sensible heat flux, preventing premature stabilization at the surface, and thus reducing pollutant concentrations.
Figure 3.
Transpiration as a function of deep soil moisture (eq. 3) and changing deep soil moisture (w2). Computations are based on US-Ha1 data on 2 July 2006 at 12pm. The box model uses the loam soil properties (wfc = 0.24 m3 m−3, wsat = 0.451 m3 m−3, wwlt=0.155 m3 m−3) from the PX LSM for the site.
Figure 4.
Diurnal median comparisons of the estimated latent heat (LH) from the photosynthesis approaches used by JULES [Clark et al., 2011], Song et al. [2009], and photosynthesis-based PX LSM (PX PSN) to compute three potential assimilation rates (Ac, Aj, and Ae), with LH from the PX LSM Jarvis approach [Pleim and Xiu, 1995] and observations at the FLUXNET Harvard Forest US-Ha1 site [Urbanski et al., 2007]. The broadleaf C3 plant simulations use July 2006 US-Ha1 standardized L2 data, with canopy height = 25 m, x = 1 (spherical leaf), αleaf = 0.8 for PAR (leaf absorptivity), αleaf = 0.2 for NIR, forest floor reflectance = 0.10, VCMAX25_0 = 30×10−6 mol m−2 s−1, kn = 0.17, Tlow = 0.0 °C, Tup = 36 °C, leaf scattering coefficient 0.15, quantum yield ε = 0.08 (mol CO2 mol−1 photon), and Jarvis Rstmin = 200 s m−1.
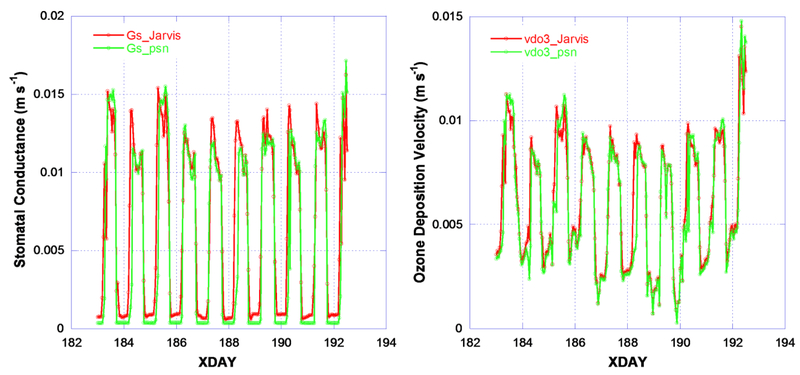
Figure 5 illustrates the response of ozone deposition velocity estimates to canopy stomatal conductance estimates from the PX Jarvis and PSN approaches over the 2 to 11 July 2006 period (chosen as an example of summer conditions for a short period without any missing data). The PX Jarvis approach tends to have higher stomatal conductance during this period, which results in slightly higher ozone deposition velocity. The ozone deposition involves several pathways including deposition to wet/dry cuticle surfaces, to soil surface, and via stomata including effects of mesophyll resistance [Pleim and Ran, 2011]. Thus, ozone deposition velocity is not simply linearly related to stomatal conductance as demonstrated by the comparison plots in figure 5.
Figure 5.
Stomatal conductance (m s−1, left) and ozone deposition velocity (m s−1, right) computed from the PX Jarvis and photosynthesis-based approach from 2 to 11 July 2006 with the modeling parameters described in the figure 4 caption.
3. Model Evaluation and Analysis
The PX PSN model is evaluated and analyzed for LH estimation at four selected FLUXNET sites with different vegetation types and landscape characteristics. The evaluation is conducted over the period with FLUXNET LAI measurements for each site and LAI is linearly interpolated for the days in between LAI observations. Additional model simulations are made using the 2006 gap-filled MODIS vegetation data processed for each land cover type within a WRF/CMAQ 12 km grid cell to show the model performance and limitations when using the averaged MODIS vegetation for each PFT within a grid cell for typical mesoscale applications. The gap-filled MODIS LAI data are processed from 2006 MODIS Collection 5 LAI and FPAR data (MOD15A2GFS) at 1 km resolution and every 8 days [Gao et al., 2008; Myneni et al., 2011] from the North American Carbon Program as used in the previous studies by Ran et al. [2015 and 2016]. The model is further evaluated based on the 2013 ozone flux measurements at the Duke Forest Open Field - US-Dk1, made by U.S. EPA [Almand-Hunter et al., 2015], to assess the impact of the photosynthesis-based approach on LH, ozone deposition velocity, and ozone flux. Site descriptions, key parameters adopted from CLM4.5 [Oleson et al., 2013], JULES [Clarks et al., 2011], and PX LSM [Xiu and Pleim, 2001; Pleim et al., 2013] based on site PFT, and simulation year for the four FLUXNET sites and one EPA ozone measurement site are presented in table 1. There are two soil moisture measurements at two different depths available in the FLUXNET Level 2 (L2) standardized file. At some sites the soil moisture measurements are at the same depth as the soil temperature measurements, while at other sites they are at different depths. Some sites, such as Harvard forest, report no soil moisture measurements at all. Depending on the season, the model responds to the two soil moisture measurements differently, as plants tend to use shallow water with more nutrients when there is no water stress, but tap into deeper soil water when the upper layers are dry during the hot summer. Interpolated soil water between the two measurements generally requires that it be weighted by root distribution before model performance improvement is noted. Therefore, the model uses the soil moisture measurement which fits model performance best for the simulation periods at each site.
Table 1.
Site and key parameters for selected four FLUXNET sites and EPA flux ozone site.
| Site Name | Info. | Key Parameters |
|---|---|---|
| FLUXNET Measurmerits: | ||
| 2006 Missouri Ozark/US-Moz | Deciduous Broadleaf C3, location(−92.2, 38.7441), Elevation 219 m, Missouri, Gu et al. [2006] | Canopy height = 24 m, OBS LAI, x=1 (spherical leaf), αleaf PAR = 0.8, αleaf NIR = 0.2, forest floor reflectance = 0.10, VCMAX25_0 = 30×10–6 mol m-2 s-1, kn = 0.17, Tlow = 0 C, Tup = 36 C, leaf scattering coefficient 0.15, quantum yield ε = 0.08 (mol CO2 mol-1 photon), and Jarvis Rstmin = 200 s m-1 (same as Harvard Forest US-Ha1 site), silt loam with wsat = 0.485, wfc= 0.255, wwlt = 0.178 |
| 2008 Wind River Field Station/US-Wrc | Evergreen Needleleaf C3, location(−121.9519, 45.8205), Elevation 371 m, Wahsington, Paw U et al. [2004] | Canopy height = 56 m, LAI = 8.6, x = 1 (spherical leaf), αleaf PAR = 0.8, αleaf NIR = 0.2, forest floor reflectance = 0.10, VCMAX25_0 = 55×10-6 mol m-2 s-1, kn = 0.17, Tlow = −10 C, Tup = 26 C, leaf scattering coefficient 0.17, quantum yield ε = 0.08 (mol CO2 mol-1 photon), and Jarvis Rstmin = 175 s m-1, silt loam with wsat = 0.485, wfc = 0.255, wwit = 0.178 |
| 2006 Fermi Prairie/US-1B2 | Grasslands C4, location(−88.241, 41.8406), elevation 226 m, Illinois, Allison et al. [2005] | Canopy height = 1 m, OBS LAI, x = 0.85, αleaf PAR = 0.8, αleaf NIR = 0.2, forest floor reflectance = 0.10, VCMAX25_0 = 25×10-6 mol m-2 s-1, kn = 0.17, Tlow = 13 C, Tup = 45 C, leaf scattering coefficient 0.17, quantum yield ε = 0.06 (mol CO2 mol-1 photon), and Jarvis Rstmin = 100 s m-1, silty clay loam with wsat = 0.477, wfc = 0.322, wwit = 0.218 |
| 2006 Mead Irrigated Rotation/US-Ne2 | Soybean C3, location(−96.4701, 41.1649), elevation 362 m, Nebraska, Verma et al. [2005] | Canopy height varies with OBS LAI, x = 0.81, αleaf PAR = 0.8, αleaf NIR = 0.2, forest floor reflectance = 0.10, VCMAX25_0 = 90×10-6 mol m-2 s-1, kn = 0.17, Tlow = 0 C, Tup = 36 C, leaf scattering coefficient 0.15, quantum yield ε = 0.08 (mol CO2 mol-1 photon), and Jarvis Rstmin = 70 s m-1, silty clay loam with wsat = 0.477, wfc = 0.322, wwlt = 0.218 |
| U.S. EPA Measurments: | ||
| 2013 Duke Forest Open Field/US-Dk1 | Grasslands C3, location(–79.0934, 35.9712), elevation 168 m, North Carolina, Almand-Hunter et al. [2015] | Canopy height = 1 m, LAI = 3, x = 0.85, αleaf PAR = 0.8, αleaf NIR = 0.2, forest floor reflectance = 0.10, VCMAX25_0 = 26×10-6 mol m-2 s-1, kn = 0.17, Tlow =0 C, Tup = 36 C, leaf scattering coefficient 0.15, quantum yield ε = 0.12 (mol CO2 mol-1 photon), and Jarvis Rstmin = 100 s m-1, loam with wsat = 0.451, wfc = 0.24, wwlt = 0.155 |
Estimated fluxes are evaluated using diurnal median comparisons between the two approaches against observations. In addition, the two approaches are evaluated using scatter plots of daily values of estimated fluxes (e.g. latent heat and O3 flux) against observations with computed normalized mean bias (NMB) and normalized mean error (NME) from daily flux estimations. The NMB and NME metrics for model estimations are calculated as [e.g. Yu et al., 2006]:
| (30) |
| (31) |
where Mi and Oi are the estimated and observed daily total fluxes for day i. The two relative metrics in percent are useful to evaluate errors of modeling results against observations for fluxes which can have quite different magnitude and variability across the different sites.
3.1. FLUXNET Site Simulations
Missouri Ozark/US-Moz site
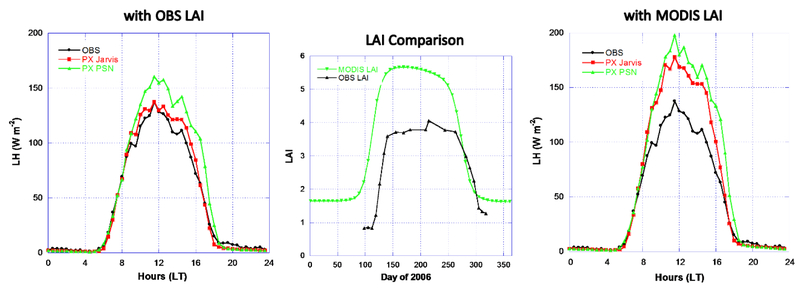
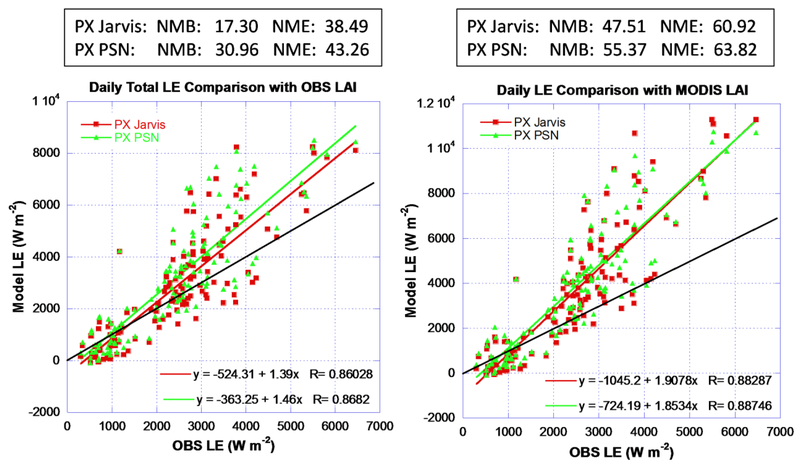
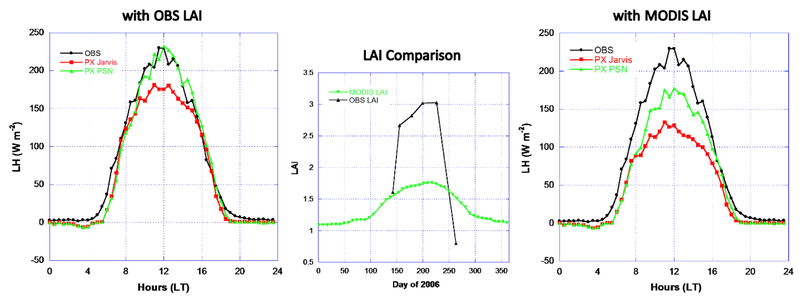
Figure 6 compares the simulated LH from the PX PSN approach at the Missouri Ozark/US-Moz FLUXNET site [Gu et al., 2006] to the LH simulated from the PX Jarvis approach and the LH observations. The measured LAI is much lower than the MODIS LAI for this deciduous broadleaf land cover type in the CMAQ 12km grid cell in which the site is located. However, the peak green of MODIS LAI (phenology) parallels the measured LAI (middle plot in figure 6). Using the observed LAI, the PX PSN and Jarvis approaches perform reasonably well in general (left plot in figure 6) for simulations from 9 July (day 190) - 14 November (day 318) 2006. The PX PSN, however, tends to overestimate LH for most of the hours after 9am until the evening. Using the MODIS LAI, both models overestimate LH (right plot in figure 6) due to higher LAI from MODIS. Scatter plots of estimated daily total LH estimations against the observations (figure 7) show that the PX Jarvis approach performs slightly better than the PX PSN approach. Ideally the fitted regression line in the scatter plot should have a slope = 1, a y-intercept = 0, and R = 1. While the R value is quite high indicating good correlation with the observations, the slope > 1 shows a general tendency to overestimate LH by both approaches.
Figure 6.
Missouri Ozark/US-Moz site LH diurnal median comparisons. LH is simulated with the photosynthesis-based and Jarvis approaches using the observed LAI (left plot) and the MODIS LAI (right plot) from 9 July (190) - 14 November (318) 2006. The observed LAI from the site 2006 biological data and processed 2006 MODIS LAI for the deciduous broadleaf land cover type at the 12 km CMAQ grid cell are displayed in the middle plot. Soil moisture measurements at 100 cm deep are used.
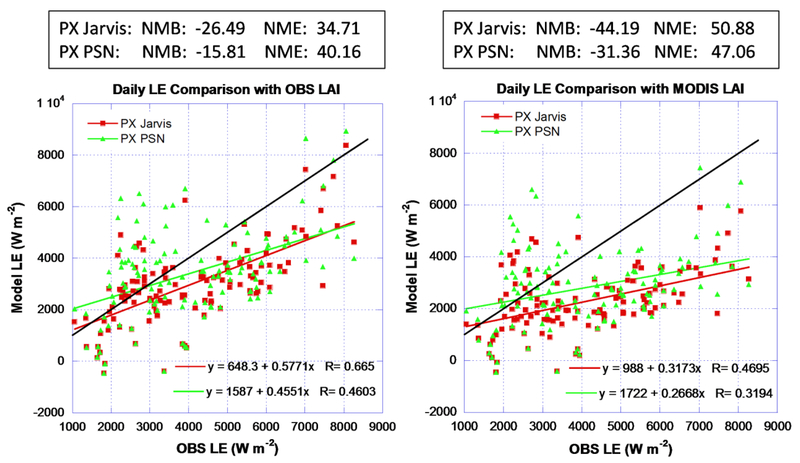
Figure 7.
Missouri Ozark/US-Moz site scatter plot comparisons of daily total LH estimations. The black line is the 1:1 reference line.
In contrast to the pattern at the Harvard Forest US-Ha1 site with the same PFT (deciduous broadleaf), here the PX PSN tends to overestimate LH from mid-morning to evening at the US-Moz site over the much longer simulation period (July to November versus one month for the US-Ha1 site). Though both sites have the same vegetation PFT, the species are different. Red oak, red maple, mature hemlock, and white pine are dominant at the Harvard Forest US-Ha1 site [Urbanski et al., 2007], while the Missouri Ozark/US-Moz site is in an oak-hickory forest which is uniquely located in an important transitional zone between hardwood and grassland in the central States. Thus, the model, which classifies both sites in the same PFT and therefore the same Vcmax, plant absorptivity, and other parameters, is unable to differentiate varying physiology from different trees within the same PFT at the two sites. In addition, soil moisture plays a key role in controlling the performance for the Moz site. There are only two soil moisture measurements, at 10 cm and 100 cm, available in the standardized L2 dataset. The soil moisture at 100 cm is almost above the field capacity for most of the year while the soil moisture at 10 cm varies rapidly. For the first half year with almost constant deep soil moisture above the field capacity, both approaches overestimate LH significantly. During the growing season after early July, the deep soil moisture shows more variation allowing the model to be more responsive to soil moisture conditions. Thus, the simulation is conducted and analyzed over the period after early July for this site. Through testing with soil moisture data at different depths for some of the selected sites, both models seem to perform best when using the soil moisture measured at root zone depth which is generally from 25 cm to 60 cm deep depending on the region and vegetation type (such as much deeper rooted trees in western drylands). Thus, it is crucial to choose the right soil moisture and temperature measurement for the diagnostic simulation because the measurement depths are usually different in the standardized L2 files for each FLUXNET site. Although both models use the same soil moisture limiting function F2, the PX PSN tends to overestimate LH when soil moisture is not limiting, while the Jarvis approach generally performs better. It is possible that the aerodynamic surface temperature, which is calculated from observed sensible heat and used by the PX Jarvis computation, helps minimize the error in LH estimation for the tall canopy.
Wind River Field Station/US-Wrc site
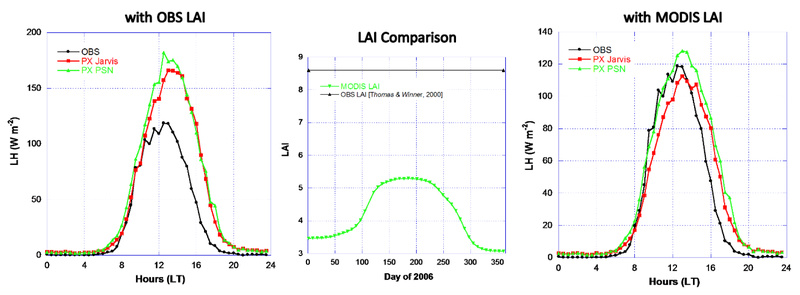
Simulation of LH at the Wind River Field Station/US-Wrc site is particularly challenging using the two stomatal conductance approaches [Jarvis, 1976; Farquhar, 1980; Ball et al., 1987; Collatz et al., 1991] in the box model. The old growth forest site is dominated by tall Douglas-fir (more than 60 m tall) more than 500 years old and tall western hemlock (more than 50 m tall). Using the observed LAI 8.6 (m2 m−2) at the site [Thomas and Winner, 2000], both approaches significantly overestimate LH by more than 50 W m−2 (left plot in figure 8) for simulations from 7 January (day 7) - 28 November (day 333) 2008. Using 2006 MODIS LAI for the evergreen needleleaf land cover type reduces the over estimation of LH significantly (right plot in figure 8) because the MODIS LAI (maximum around 5.3 m 2 m−2) is much less than the observed LAI at the site. The MODIS LAI and FPAR algorithms tend to be saturated at high LAI (Yang et al. 2006). The PX PSN has higher estimation of LH than the PX Jarvis approach in general for this site. With MODIS LAI, the PX PSN slightly overestimates LH while the PX Jarvis approach slightly underestimates around the peak radiation hour. From the late afternoon, both the approaches overestimate LH. The scatter plot evaluation is not conducted for this site due to the poor performance from the both approaches over the long simulation period. The 2008 FLUXNET measurement data is used for the modeling because the 2006 measurements have too many gaps and most of the soil moisture data are missing. Since FLUXNET does not have the biological data with measured LAI for this site, the observed LAI [Thomas and Winner, 2000] over late 1990s and available 2006 MODIS LAI for WRF/CMAQ are used for the simulation with the assumption that LAI does not change too much for this PFT old growth site. The MODIS LAI does show seasonal variation of LAI which peaks in late spring for the vegetation in this area with wet cool winters and hot dry summers. As the site is located in the subtle divide between the Wind River and Trout River in the north-south oriented Cascade Mountains, the soil moisture is limited during the hot summer [Paw U et al., 2004, Shaw et al., 2004].
Figure 8.
Wind River Field Station/US-Wrc site LH diurnal medium comparisons. LH is simulated with the photosynthesis-based and Jarvis approaches using the observed LAI (left plot) and the MODIS LAI (right plot) from 7 January (7) - 28 November (333) 2008. The observed LAI of the C3 vegetation from the study by Thomas and Winner [2000] and processed 2006 MODIS LAI for the evergreen needleleaf land cover type at the 12 km CMAQ grid cell are displayed in the middle plot. Soil moisture measurements at 40 cm deep are used.
Similar to other sites, the model seems to be very sensitive to the soil moisture data used for LH estimation at the Wind River site. Soil moisture measurements are available at eight different depths between 0 to 2 m for this site. The measurement at 40 cm which shows most reasonable variations during the hot summer is selected for modeling. However, the soil moisture is mostly above the field capacity during the rest of the year which results in LH overestimation for the first of the half year (similar to the situation at the US-Moz site). With most plant roots within 0.5 m, deep roots extending to 1 – 2 m deep, and fine roots in the top 0 – 0.3 m deep [Shaw et al, 2004], it seems that the soil moisture measurements used for the modeling are too deep for the cool seasons but about right for the dry seasons. This indicates that the optimal soil moisture depth for modeling plant transpiration not only varies with different sites and vegetation composition but also with different seasons depending on the soil moisture demand by vegetation. This may be particularly important for the US-Wrc site which has diverse vegetation species composition and canopy structures [Thomas and Winner, 2000]. Furthermore, the more than 500 year old tall Douglas-fir and western hemlock that are dominant at the site present ecological modeling complexity regarding age, height, biomass, and under/over story structures. Many studies [McDowell et al., 2002; Phillips et al., 2002; Wharton et al., 2009; Pangle et al., 2015] have investigated the relationship between the canopy flux of water and tree height since Ryan and Yoder [1997] first proposed the hydraulic limitation hypothesis. With the increased path from soil to the canopy stoma for tall trees, it is assumed that leaf-specific hydraulic conductance may decrease resulting in reduced stomatal conductance. McDowell et al. [2002] and Phillips et al. [2002] tested the hypothesis at the US-Wrc site with young and old Douglas-fir trees and their results do not support the hypothesis as there is no observed decrease of stomatal conductance and photosynthesis for the old-growth trees compared to the younger shorter trees from their summer observations. They suggest that old tall Douglas-fir trees may evolve to compensate for the hydraulic limitation by having more efficient sap conductance. The study by Pangle et al. [2015] shows that the hydraulic limitation hypothesis is supported by all species they measured including western hemlock except Douglas-fir in the Pacific Northwest. Also, since FLUXNET measurements are based on the eddy covariance method to directly measure the flux density above the canopy, the direct measurement method comes with the assumption that the terrain is flat and with uniform vegetation and that the atmosphere is in steady state. Thus, eddy covariance derived fluxes include significant uncertainties due to non-ideal conditions in natural, heterogeneous landscapes, which is particularly true for this site with measurement height at 85 m above the ground over the tops of the clumped conifer canopy with diverse understory species. Accuracy of turbulent fluxes from this method is around 5-15% for the sensible heat and 10-20% for latent heat [Mauder et al., 2006; Foken et al., 2008] with systematic errors from sensor configurations and turbulence data processing around 5–10% and random errors from natural variation in vegetation and atmospheric turbulence around 5% [Baldocchi, 2008], Since only the flux from the small eddies is measured at almost all FLUXNET network sites, some portion of the flux from larger eddies and advection is missing [Finnigan et al., 2003]. Larger eddies may play an important role because of the 85 m measurement height at the site and drainage flows from surrounding hills [Shaw et al., 2004]. Finally, turbulent flux computation in LSMs uses empirically determined non-dimensional profile functions in accordance with MOST even though MOST is defined under ideal environments. The validity of MOST is limited to flat terrain with homogeneous landscape and land cover and to a steady and horizontally homogeneous flow by averaging from 10 minutes to around an hour [Monin and Obukhov, 1954]. Even under ideal environments, MOST has around 10–20% errors [Foken, 2006]. In non-ideal conditions, MOST-based model calculations will be less accurate and result in more uncertainties in estimating aerodynamic resistance [Wangand Dickinson, 2012]. Given the uncertainty associated with flux measurement and computation for both model estimates and observations across the sites, caution should be used when interpreting model performance differences.
Fermi Prairie/US-IB2 site
The performance of simulated LH from 22 May (day 142) - 20 September (day 263) 2006 for the C4 tall grass prairie at the Fermi Prairie/US-IB2 site is evaluated and shown in figure 9. Soil moisture measurements at 25 cm deep (not in the standardized L2 data) are used for the modeling. Using the observed LAI, the PX PSN performs well while the PX Jarvis underestimates LH by around 50 (W m−2) around peak radiation hours. Both approaches tend to underestimate LH in early morning and evening hours. The PX PSN treats C3 and C4 plants differently when modeling CO2 assimilation, which then seems to give it an advantage when modeling LH for C4 species in high light, dry, and hot environments. The peak MODIS LAI (around 1.75 m 2 m−2) is much lower than the observed LAI (around 3 m 2 m−2, middle plot in figure 9). But, the MODIS LAI peaks coincide with the observed LAI peak in late July and early August. In general, the MODIS LAI cannot capture the peak and low LAI values compared to site observations (exception at the US-Moz site) due to averaging at the WRF/CMAQ 12 km modeling resolution [Ran et al., 2015]. With MODIS LAI, both the approaches underestimate LH, with the PX PSN by around 50 (W m−2) and the PX Jarvis by around 100 (W m−2) around noon (right plot in figure 9). Both approaches have high uncertainties in the daily total LH estimations as indicated by the relatively low R value (figure 10). The PX PSN has lower NMB and higher NME for daily total LH estimations than the Jarvis approach for simulations with observed LAI. For MODIS LAI simulations, the PX PSN performs better with lower NMB and NME. Since this tall grassland site has rather uniform landscape with homogeneous vegetation and flat terrain [Allison et al., 2005], it meets the assumptions of the eddy covariance FLUXNET measurement and the turbulent flux computation by MOST relatively well in comparison with the previous two FLUXNET sites located in landscape transitional zones. Thus, both measurements and flux computations are likely to be less error prone, and the demonstrated strength of the PX PSN approach is likely to be robust.
Figure 9.
Fermi Prairie/US-IB2 site LH diurnal median comparisons. LH is simulated with the photosynthesis-based and Jarvis approaches using the observed LAI (left plot) and the MODIS LAI (right plot) from 22 May (142) - 20 September (263) 2006. The observed LAI of the C4 grassland from the site 2006 biological data and processed 2006 MODIS LAI for the grassland land cover type at the 12 km CMAQ grid cell are displayed in the middle plot. Soil moisture measurements at 25 cm deep are used.
Figure 10.
Fermi Prairie/US-IB2 site scatter plot comparisons of daily total LH estimations. The black line is the 1:1 reference line.
Mead Irrigated Rotation/US-Ne2 site
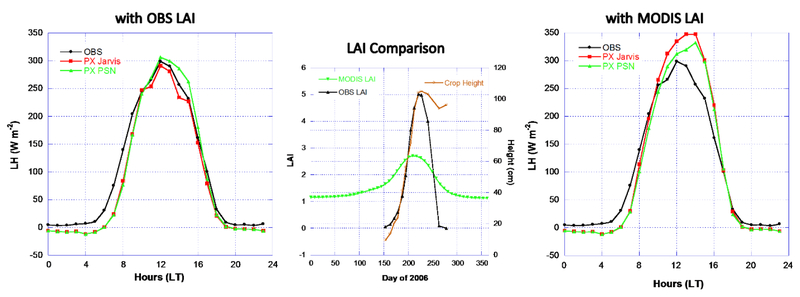
The box model is further evaluated for soybean crop at the Mead Irrigated Rotation/US-Ne2 site [Verma et al., 2005] from 12 June (day 163) - 5 October (day 278) 2006. Soil moisture is set to field capacity due to irrigation. Distinct from the other sites with constant plant height, the measured, seasonally varying crop height along with LAI from the site biological dataset are used in the simulation. While both models perform well with the observed LAI and crop height (left plot in figure 11), in the early morning the two models tend to underestimate LH. The PX PSN tends to overestimate LH in the early afternoon, while the PX Jarvis slightly underestimates. The PX Jarvis LSM was originally developed based on soybean measurements in Kentucky [Pleim et al. 2001; Pleim and Xiu, 2003], thus it is not surprising that it performs well at this site for soybeans. The fact that the PX PSN performs as well as the PX Jarvis for this crop validates its potential applicability for modeling agricultural crop land category in PX LSM. The peak LAI for soybeans can reach 5 (m 2 m−2) with canopy height around 1 m, but the peak MODIS LAI is only around 2.75 (m 2 m−2). The height of the plant follows the LAI until the leaves senesce (greenness or LAI declining to zero) just before harvesting. The soybeans were planted on 1 May (day 121) and harvested on 5 October (day 278) for 2006. According to the measurements, it took almost a month after planting for the plants to have measurable LAI. Similar to other sites, the MODIS LAI peaks coincident with the observations, but cannot capture the high and low of the observed LAI at the site. With MODIS LAI, both models overestimate LH because the peak soybean LAI period is short and on average, MODIS LAI is higher than the observations over the modeling period. Using the MODIS LAI, the estimated LH median from the PX PSN is close to observations around noon while the Jarvis approach overestimates LH by around 50 (W m−2) and both models tend to underestimate LH in the early morning hours. The two approaches perform well in daily total LH estimations with lower NMB and NME from the Jarvis approach (left plot in figure 12) in simulations with the observed LAI. Neither approach, however, performs well with the MODIS LAI which results in much higher errors and scatter (much lower R values), in spite of smaller bias (right plot in figure 12). Thus, accurate LAI as well as crop height is crucial for simulations over crop lands. Because crop lands are treated as one land cover category in the current WRF/CMAQ system, the mesoscale model cannot distinguish LAI and crop height associated with planting, fertilizing, irrigating, and harvesting of different crops. Although MODIS LAI tends to be low for the peak growing season at this soybean site, it does provide some information on plant LAI changes which are related to natural (e.g. temperature and precipitation) and human influences in comparison with the table-prescribed landscape in the current system.
Figure 11.
Mead Irrigated Rotation/US-Ne2 site LH diurnal median comparisons. LH is simulated with the photosynthesis-based and Jarvis approaches using the observed LAI (left plot) and the MODIS LAI (right plot) from 12 June (163) - 5 October (278) 2006. The observed LAI of C3 soybean from the site 2006 biological data and processed 2006 MODIS LAI for the cropland land cover type at the 12 km CMAQ grid cell are displayed in the middle plot. Soil moisture is set to field capacity.
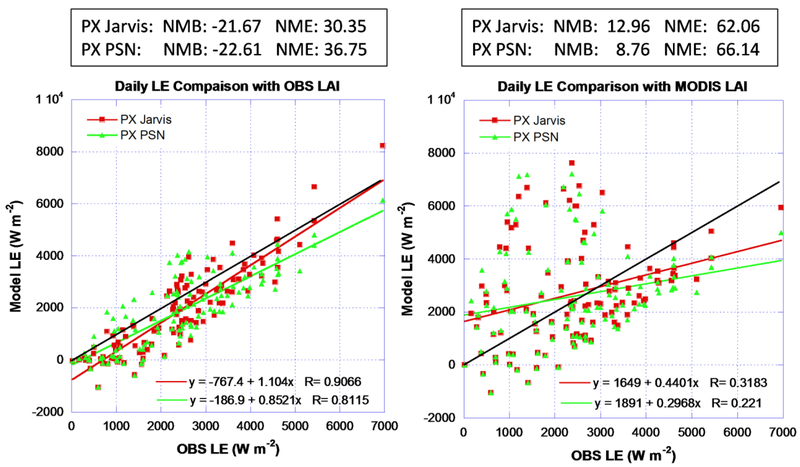
Figure 12.
Mead Irrigated Rotation/US-Ne2 site scatter plot comparisons of daily total LH estimations. The black line is the 1:1 reference line.
3.2. Ozone Site Simulations
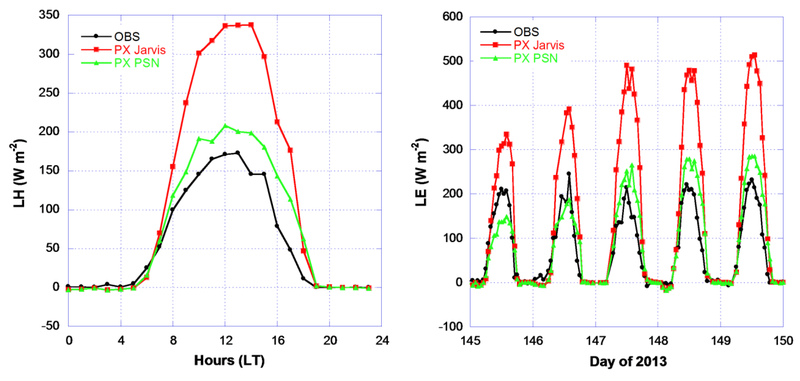
Simulated LH, stomatal conductance, and ozone deposition and flux from the PX Jarvis and PSN approaches over 40 days from 17 May to 18 June and 18 to 28 September 2013 are evaluated against the flux measurements conducted by U.S. EPA at the Duke Forest Open Field/US-Dk1 site [Almand-Hunter et al., 2015]. Soil temperature and volumetric water content used are the average measurements over 0 - 5 cm depth used in site measurement data processing. Figure 13 shows the diurnal median statistics (left plot) for the simulations and selected 5-day hourly estimations (right plot) of LH using the two models against the observations. The PX Jarvis significantly overestimates LH by a factor of around 2 (~ 170 W m−2) while the PSN overestimates LH by about 50 W m−2. The hourly estimation plot for the selected 5 days shows a similar pattern with significant overestimation from PX Jarvis while the PX PSN underestimates LH for the first two days (days 145 and 146) and overestimates LH for the last three days. The stomatal conductance estimated from the PX Jarvis is much greater than that from the PX PSN (by about a factor of 2, left plot in figure 14). Similarly, ozone deposition velocity and computed ozone flux based on ozone concentration measurements are also higher from the PX Jarvis but by a smaller margin because of influences of other ozone deposition pathways. The peak ozone deposition velocity from the PX PSN is lower than the observation peak but the peak timing follows the observations well in the early morning (middle plot in figure 14). In contrast to LH which is often highest around noon with roughly symmetric trends for morning and afternoon hours, ozone deposition velocity normally peaks in the early morning (around 8 am for the site), similar to stomatal conductance, with gradual decline throughout the daylight hours. Stomatal conductance usually decreases as relative humidity declines with increasing temperature. While low relative humidity reduces stomatal conductance, it also drives the fluxes from stomata to the ambient atmosphere due to increasing moisture gradient. Thus, the two influences often cancel out for LH resulting in the symmetric shape of the LH diurnal profile. Diurnal ozone flux also peaks around noon with a similar symmetric shape as LH because as deposition velocity declines in the afternoon the ozone concentration usually increases.
Figure 13.
Duke Forest Open Field/US-Dk1 site LH diurnal median (left plot) and selected hourly (right plot) comparisons. Simulations are conducted based on LAI = 3 (m2 m−2) and other parameters listed in table 4.1 for the periods of 17 May (day 137) to 18 June (day 169) and 18 to 28 September (day 261 to 271) 2013 with measurements. Hourly display is for 25 to 30 May 2013 (day 145 to 150).
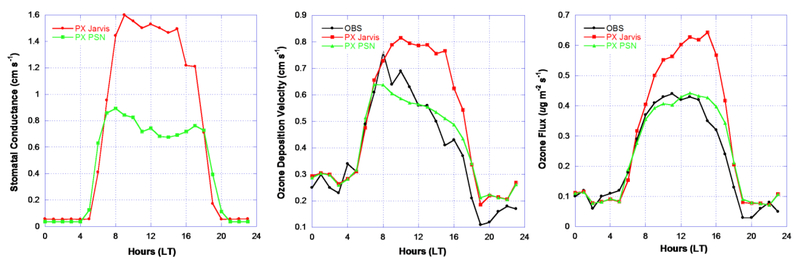
Figure 14.
Duke Forest Open Field/US-Dk1 site diurnal median comparisons for estimated stomatal conductance (cm s−1, left plot), ozone deposition velocity (cm s−1, middle plot), and ozone flux (μg m−2 s−1, right plot).
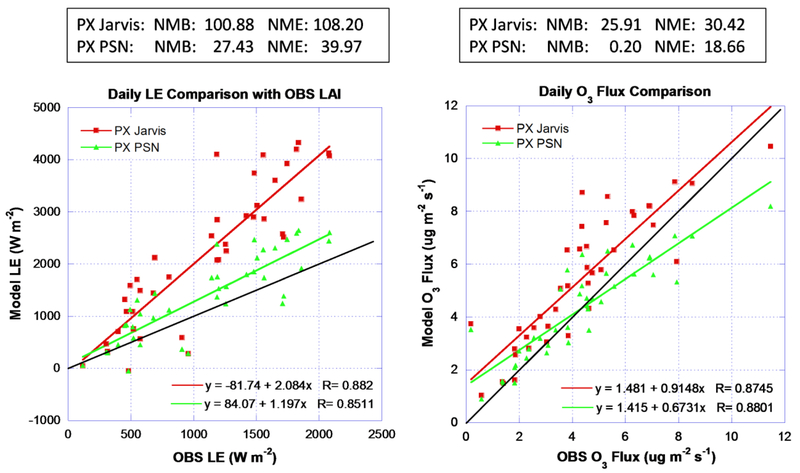
The middle and right plots in figure 14 show that the estimated ozone diurnal distribution and ozone flux from the PX PSN match the observations much better than the estimations from the PX Jarvis. However, estimated ozone deposition velocity and flux are high in both models from the afternoon to late evening with the PX PSN over-estimating to a much lesser degree. The daily total LH and O3 flux estimations both show better agreement with the observation from the PX PSN with much lower NMB and NME (figure 15). While the scatter plots show good correlations for both LH and O3 fluxes (R values > 0.85), a factor of 2 over prediction by PX Jarvis for LH is reflected in the slope of the regression line (slope > 2). The over prediction of O3 flux is by the PX Jarvis is evident from the scatter plot with all but 4 points above the 1-to-1 line. The low slope of the regression line and high y-intercept for PX PSN indicates a tendency to over predict at the low end and under predict at the high end.
Figure 15.
Duke Forest Open Field/US-Dk1 site scatter plot comparisons of daily total LH and ozone flux estimations. The black line is the 1:1 reference line.
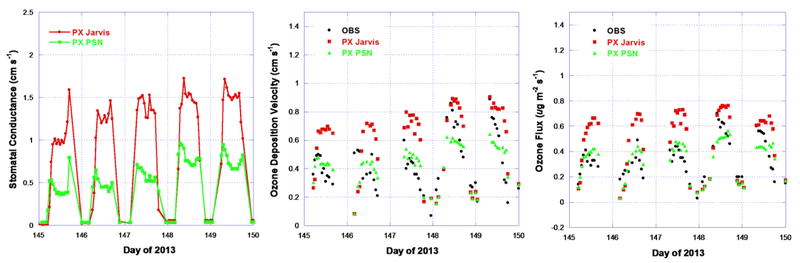
The PX Jarvis has much higher estimation of stomatal conductance than the PX PSN for the displayed 5 day period from 25 to 30 May 2013 (left plot in figure 16). However, the PX PSN estimates ozone deposition velocity and flux better for the first three days while the PX Jarvis does better for the last two days (middle and right plots in figure 16). The ozone scatter plots in figure 16 exclude data points which fail quality control criteria, such as points with turbulence not fully developed or with significantly changing conditions. The big difference between the two models at this site seems to be much larger than the differences demonstrated by the four FLUXNET site LH evaluations discussed above. The use of measured sensible heat flux by the PX Jarvis for computing the aerodynamic surface temperature to be used in stomatal conductance computation as the leaf surface temperature may be degrading the model performance at this site. This approach seems to benefit the PX Jarvis at the Missouri Ozark/US-Moz and Wind River Field Station/US-Wrc sites which have tall tree canopies that serves as a barrier between the ground and the atmosphere. Since the surface energy budget is dominated by the canopy at these forest sites, the aerodynamic surface temperature is a good surrogate for leaf temperature. At the Duke site, the computed aerodynamic surface temperature is much higher than the ambient temperature around the noon hours (e.g. around 6 C°) because the surface energy is more influenced by the ground rather since the grasses which have much less mass and volume than forest. Thus, the aerodynamic surface temperature is not as good of a surrogate for the leaf temperature. The higher leaf temperature results in a higher mixing ratio gradient between the leaf stomata and the ambient atmosphere which drives greater LH flux. In the full PX LSM with WRF/CMAQ, the difference between the two approaches are likely to be much smaller because there is full energy budget with sophistical radiation models and dynamic feedbacks which will be equally applied to both approaches at a time scale of less than 40 seconds.
Figure 16.
Duke Forest Open Field/US-Dk2 site hourly comparisons for estimated stomatal conductance (cm s−1, left plot), ozone deposition velocity (cm s−1, middle plot), and ozone flux (μg m−2 s−1, right plot) over the period of 25 to 30 May 2013 (day 145 to 150) with invalid ozone data points excluded.
4. Conclusions and Future Work
A coupled photosynthesis and stomatal conductance approach with simple parameterization is developed, implemented, and evaluated in a diagnostic box model with ET and ozone deposition components from WRF/CMAQ with the PX LSM. The performance of the diagnostic model is influenced by many factors including parametrizations based on broad PFTs, site-related input data, and measurement errors in addition to physical process formulations. Results from the box model comparisons should be interpreted with caution because off-line simulations cannot completely represent the performance in the full scale model with real-time feedbacks [Samuelsson et al., 2003; On and Henderson-Sellers, 1998]. The purpose for this study is not to develop a site-specific model which matches measurements; but rather to develop applicable algorithms to be applied to the multi-scale (urban, region to global) WRF/CMAQ simulations for realistic treatments of grid cell average surface fluxes of heat, moisture, and trace chemical species. The performance of the developed model over varieties of vegetation and landscape types at the selected sites demonstrates that the model is applicable in large scale modeling domains for the most prevalent vegetated land surface environments across the globe (i.e. deciduous and coniferous forest, grassland, and cropland).
The photosynthesis-based stomatal conductance model with two-leaf scaling is constrained by many additional model parameters, particularly related to photosynthesis such as the maximum rate of carboxylation of Rubisco - Vcmax, the foliage nitrogen decay coefficient – Kn, maximum electron transport rate - Jmax, and quantum yield – ε. This gives the model advantages in distinguishing plants with different photosynthesis mechanism (C3 and C4) and efficiency among PFTs (such evergreen or deciduous from boreal, temperate, or tropic regions, different crops). However, those parameter values vary among and within PFTs across literature and different models. It is important to choose the values which represent plant types for the modeling approach including scaling implemented in the full Eulerian grid model. The model performs differently even at the sites with same PFT (such as US-Ha1 and US-Moz sites with broadleaf deciduous trees) using the same photosynthesis-related parameters due to different vegetation composition. In addition, LAI and soil moisture and texture influence the performance of the both approaches.
The evaluation using observed LAI and MODIS LAI processed for the WRF/CMAQ 12 km grid domain shows that accurate LAI is important for matching site measurements. With the MODIS LAI input, both approaches perform worse, relative to observed LAI, except at the Wind River Field Station US-Wrc site where lower LAI from averaged MODIS LAI at WRF/CMAQ grid cells help reduce LH and match the observations well. Although the MODIS LAI is generally different from the observed LAI, the change of MODIS LAI over the growing season does peak with the observed LAI. Thus, MODIS LAI captures the seasonality (or phenology) of vegetation, that is consistent with the results from Ran et al. [2015 and 2016]. Note that, in the full Eulerian grid model LSM performance is improved through real-time soil moisture and temperature nudging in the WRF PX LSM [Pleim and Xiu, 2003; Pleim and Gilliam, 2009] which continually adjusts soil moisture and temperature to reduce errors in LH flux thereby reducing air temperature and humidity errors. This scheme compensates for model errors due to inaccurate parameters as well as over-simplified canopy and soil algorithms. Thus, even though the box model simulations use whatever soil moisture measurements that are available, the overestimation of LH which is observed at most sites is likely to be corrected in WRF simulations with the PX LSM soil nudging scheme and dynamic feedbacks.
The photosynthesis-based approach is evaluated at the Harvard Forest (US-Ha1) FLUXNET site for July 2006 and the model performs well in comparison with the current PX Jarvis approach and two other CO2 assimilation methods compared to observations. The advanced approach can simulate LH as well as the PX Jarvis approach in general for four selected FLUXNET sites (US-Moz, US-Wrc, US-IB2, and US-Ne2) though the performance varies at different sites. For the US-Moz and US-Wrc sites with tall forest canopy, the PX Jarvis approach shows some advantage during the peak noon hours. The photosynthesis-based approach shows clear improvement in modeling short vegetation (e.g. grassland and soybean), particularly for the C4 grassland at the Fermi Prairie US-IB2 site by distinguishing C3 and C4 plants in modeling the CO2 assimilation rate. Both the approaches significantly overestimate LH at the Wind River Field Station US-Wrc site with observed LAI because of the complex landscape dominated by old growth tall Douglas-fir and western hemlock. The hydraulic limitation, which is one of many factors which may contribute to the overestimation, seems to apply to western hemlock but not to Douglas-fir [McDowell et al., 2002; Phillips et al., 2002; Pangle et al., 2015] at this site. As the developed photosynthesis-bases model is a single layer two-leaf model for meso-scale modeling, it shows limitation in modeling sites with complex canopy structures including different species at different heights. For the complex canopy, a multi-layer model [Baldocchi and Meyers, 1998; Meyers et al., 1998] likely performs better. The advanced model performs much better than the Jarvis approach at the Duke Forest Open Field US-Dk1 grassland site in simulating LH and ozone flux. The photosynthesis model shows the ability to simulate the diurnal shape of ozone deposition velocity which usually peaks in the early morning. The Jarvis approach is known to have difficulty in simulating the diurnal shape [.Finkelstein et al., 2000; Pleim et al., 2001] and this deficiency is clearly demonstrated at the site. The simulated ozone flux from the advanced approach matches the observations much better than that from the Jarvis approach which overestimates ozone flux by around 50%.
The current PX WRF/CMAQ uses 20-class NLCD land cover types [Anderson et al., 1976] for the U.S. and 20-class MODIS International Geosphere-Biosphere Programme (IGBP) types [Belward, 1996] for areas outside the U.S [Ran and Hanna, 2016]. There is an ongoing effort at EPA to develop new land cover classes with detailed PFTs for vegetation from boreal, temperate, tropical, and dryland regions and with major crop categories including irrigation information. The new land cover types with more specific PFTs are more suitable for the photosynthesis-based PX LSM than the current land cover types used in the system. With realistic vegetation and albedo from MODIS products being ingested into WRF/CMAQ [Ran et al., 2016], the system has more accurate vegetation and surface representation which helps improve not only spatial and temporal characteristics of vegetation and land surface but also improves the meteorology performance. The next step is to implement the evaluated photosynthesis-based stomatal conductance model into WRF/CMAQ PX LSM with MODIS input and new land cover types. Thus, the system with improved land surface representation and vegetation processes can be used in research and applications in coupling air quality, climate, and vegetation productivity directly with CO2 concentration which changes temporally and spatially. In addition, the effects of air pollutants such as O3 on ecosystem productivity can also be easily implemented in this advanced approach [Sitch et al., 2007; Lombardozzi et al., 2012] for EPA’s secondary standard assessments under the “CAA” to protect the environment.
Acknowledgments
The authors would like to acknowledge the help of Ian T. Baker from Colorado State University at Fort Collins and Gordon B. Bonan from University Corporation for Atmospheric Research at Boulder, Colorado, USA on the photosynthesis approach used in climate land surface modeling through the email communications. The review from Ellen Cooter at EPA is also greatly appreciated.
Footnotes
Disclaimer
While this work has been reviewed and cleared for publication by the U.S. EPA, the views expressed here are those of the authors and do not necessarily represent the official views or policies of the Agency.
References
- Allison VJ, Miller RM, Jastrow JD, Matamala R, and Zak DR (2005), Changes in soil microbial community structure in a tallgrass prairie chronosequence, Soil Sci. Soc. Am. J, 69 (5), 1412–1421. [Google Scholar]
- Almand-Hunter BB, Walker JT, Masson NP, Hafford L, and Hannigan MP (2015), Development and validation of inexpensive, automated, dynamic flux chambers, Atmospheric Measurement Techniques, 8, 267–280. [Google Scholar]
- Anderson JR, Hardy EE, Roach JT, and Witmer RE (1976), A land use and land cover classification system for use with remote sensor data, U.S. Geological Survey Professional Paper 964:28. [Google Scholar]
- Appel KW, Foley KM, Bash JO, Pinder PW, Dennis RL, Allen DJ, and Pickering KA (2011), Multi-resolution assessment of the Community Multiscale Air Quality (CMAQ) model v4.7 wet deposition estimates for 2002–2006, Geosci. Model Dev, 4, 357–371. [Google Scholar]
- Baker IT, Denning AS, Hanan N, Prihodko L, Vidale PL, Davis K, and Bakwin P (2010), North American gross primary productivity: regional characterization and interannual variability, Tellus, 62B, 533–549. [Google Scholar]
- Baldocchi D (2008), TURNER REVIEW No. 15, ‘Breathing’ of the terrestrial biosphere: lessons learned from a global network of carbon dioxide flux measurement systems, Australian Journal of Botany, 56:(1), 1–26. [Google Scholar]
- Baldocchi DD and Meyers T (1998), On using eco-physiological, micrometeorological and biogeochemical theory to evaluate carbon dioxide, water vapor and trace gas fluxes over vegetation: a perspective, Agricultural and Forest Meteorology, 90(1–2), 1–25. [Google Scholar]
- Ball MC, Woodrow IE, and Berry JA (1987), A model predicting stomatal conductance and its contribution to the control of photosynthesis under different environmental conditions, In Progress in Photosynthesis Research (ed Biggins J), Martinus Nijhoff Publishers, Dordrecht, Netherlands: 221–224. [Google Scholar]
- Belward AS, ed. (1996), The IGBP-DIS global 1 km land cover data set (DISCover)-proposal and implementation plans: IGBP-DIS Working Paper No. 13, Toulouse, France: 13:61. [Google Scholar]
- Bonan GB (2008), Ecological climatology: concepts and applications, Cambridge University Press, New York. [Google Scholar]
- Bonan GB, Lawrence PJ, Oleson KW, Levis S, Jung M, Reichstein M, Lawrence DM, and Swenson SC (2011), Improving canopy processes in the Community Land Model version 4 (CLM4) using global flux fields empirically inferred from FLUXNET data, Journal of Geophysical Research: Biogeosciences (2005–2012), 116(G2). [Google Scholar]
- Budyko M, 1974. Climate and life, Academic, New York. [Google Scholar]
- Byun DW and Schere KL (2006), Review of the governing equations, computational algorithms, and other components of the Models-3 Community Multiscale Air Quality (CMAQ) modeling system, Appl. Mech. Rev, 59, 51–77. [Google Scholar]
- Campbell GS (1986), Extinction coefficients for radiation in plant canopies calculated using an ellipsoidal inclination angle distribution, Agricultural and forest meteorology, 36(4), 317–321. [Google Scholar]
- Campbell GS, and Norman JM (1998), An introduction to environmental biophysics Springer Science & Business Media. [Google Scholar]
- Chen F, and Dudhia J (2001), Coupling an advanced land-surface/hydrology model with the Penn State/NCAR MM5 modeling system. Part I: Model implementation and sensitivity, Mon. Wea. Rev, 129, 569–585. [Google Scholar]
- Chen JM, Govind A, Sonnentag O, Zhang Y, Barr A, and Amiro B (2006), Leaf area index measurements at Fluxnet-Canada forest sites, Agricultural and Forest Meteorology, 140(1), 257–268. [Google Scholar]
- Clark DB, Mercado LM, Sitch S, Jones CD, Gedney N, Pryor M, Rooney GG, Essery RLH, Blythl E, Boucher O, Harding RJ, Huntingford C, and Cox PM (2011), The joint UK land environment simulator (JULES), model description–Part 2: carbon fluxes and vegetation dynamics, Geoscientific Model Development, 4(3), 701–722. [Google Scholar]
- Cohan DS, Boylan JW, Marmur A, and Khan MN (2007), An Integrated Framework for Multipollutant Air Quality Management and Its Application in Georgia, Environ. Manage, 40, 545–554. [DOI] [PubMed] [Google Scholar]
- Cohen WB, Maiersperger TK, Turner DP, Ritts WD, Pflugmacher D, Kennedy RE, Kirschbaum S.W.Running, Costa N, and Gower ST, 2006. MODIS land cover and LAI collection 4 product quality across nine sites in the western hemisphere. IEEE Transactions on Geoscience and Remote Sensing 44:1843–1857. [Google Scholar]
- Collatz GJ, Ball JT, Grivet C, and Berry JA (1991), Physiological and environmental regulation of stomatal conductance, photosynthesis and transpiration: a model that includes a laminar boundary layer, Agricultural and Forest Meteorology, 54(2), 107–136. [Google Scholar]
- Collatz GJ, Ribas-Carbo M, and Berry JA (1992), Coupled photosynthesis-stomatal conductance model for leaves of C4 plants, Aust. J. Plant Physiol, 19, 519–538. [Google Scholar]
- Compton JE, Harrison JA, Dennis RL, Greaver TL, Hill BH, Jordan SJ, Walker H, and Campbell HV (2011), Ecosystem services altered by human changes in the nitrogen cycle: a new perspective for US decision making, Ecology Letters, 14, 804–815. [DOI] [PubMed] [Google Scholar]
- Cox PM, Huntingford C, and Harding RJ (1998), A canopy conductance and photosynthesis model for use in a GCM land surface scheme, Journal of Hydrology 212 (1998), 79–94. [Google Scholar]
- Dai Y, Dickinson RE, and Wang YP (2004), A two-big-leaf model for canopy temperature, photosynthesis, and stomatal conductance, J. Clim, 17, 2281–2299. [Google Scholar]
- de Pury DGG and Farquhar GD (1997), Simple scaling of photosynthesis from leaves to canopies without the errors of big-leaf models, Plant Cell Environ, 20, 537–557. [Google Scholar]
- Eder B, Kang D, Mathur R, Pleim J, Yu S, Otte T, and Pouliot G (2009), A performance evaluation of the National Air Quality Forecast Capability for the summer of 2007, Atmospheric Environment, 43(14), 2312–2320. [Google Scholar]
- Evers JB, Vos J, Yin X, Romero P, Van Der Putten PEL, and Struik PC (2010), Simulation of wheat growth and development based on organ-level photosynthesis and assimilate allocation, Journal of Experimental Botany, 61(8), 2203–2216. [DOI] [PubMed] [Google Scholar]
- Farquhar GD, von Caemmerer S, and Berry JA (1980), A biochemical model of photosynthetic CO2 assimilation in leaves of C3 species, Planta, 149, 78–90. [DOI] [PubMed] [Google Scholar]
- Finkelstein PL, Ellestad TG, Clarke JF, Meyers TP, Schwede DB, Hebert EO, and Neal JA (2000), Ozone and sulfur dioxide dry deposition to forests: Observations and model evaluation, Journal of Geophysical Research: Atmospheres (1984–2012), 105(D12), 15365–15377. [Google Scholar]
- Finnigan JJ, Clement R, Malhi Y, Leuning R, and Cleugh HA (2003), A reevaluation of long-term flux measurement techniques part I: averaging and coordinate rotation, Boundary-Layer Meteorology, 107, 1–48. [Google Scholar]
- Foley KM, Roselle SJ, Appel KW, Bhave PV, Pleim JE, Otte TL, Mathur R et al. (2010), Incremental testing of the Community Multiscale Air Quality (CMAQ) modeling system version 4.7, Geoscientific Model Development, 3(1), 205–226. [Google Scholar]
- Foken T (2006), 50 years of the Monin-Obukhov similarity theory, Bound.-Layer Meteorol. 119, 431–447. [Google Scholar]
- Foken T (2008), The energy balance closure problem: An overview, Ecol. Appl, 18(6), 1351–1367. [DOI] [PubMed] [Google Scholar]
- Gao F, Morisette J, Wolfe R, Ederer G, Pedelty J, Masuoka E, Myneni R, Tan B, and Nightingale J (2008), An Algorithm to Produce Temporally and Spatially Continuous MODIS-LAI Time Series, IEEE Geoscience and Remote Sensing Letters, 5(1), 60–64. [Google Scholar]
- Goudriaan J (1977), Crop micrometeorology: a simulation study, Pudoc, Center for Agricultural Publishing and Documentation. [Google Scholar]
- Gu L, Meyers T, Pallardy SG, Hanson PJ, Yang B, Heuer M, Hosman KP, Riggs JS, Sluss D, and Wullschleger SD (2006), Direct and indirect effects of atmospheric conditions and soil moisture on surface energy partitioning revealed by a prolonged drought at a temperate forest site, Journal of Geophysical Research: Atmospheres (1984–2012), 111, D16. [Google Scholar]
- Hogrefe C, Pouliot G, Wong D, Torian A, Roselle S, Pleim J, and Mathur R (2014), Annual application and evaluation of the online coupled WRF–CMAQ system over North America under AQMEII phase 2, Atmospheric Environment. [Google Scholar]
- Jarvis PG (1976), The interpretation of the variations in leaf water potential and stomatal conductance found in canopies in the field, Philosophical Transactions of the Royal Society of London, Series B, 273, 593–610. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jarvis PG, and McNaughton KG (1986), Stomatal control of transpiration: Scaling up from lead to region, Adv. in Ecol. Res. 15:1–49. [Google Scholar]
- Jarvis PG (1995), Scaling Processes and Problems. Plant Cell and Environment, 18(10): 1079–1089. [Google Scholar]
- Kattge J, Knorr W, Raddatz T, and Wirth C (2009), Quantifying photosynthetic capacity and its relationship to leaf nitrogen content for globalscale terrestrial biosphere models, Global Change Biol, 15:976–991. [Google Scholar]
- Katul GG, Manzoni S, Palmroth S, Oren R (2010), A stomatal optimization theory to describe the effects of atmospheric CO2 on leaf photosynthesis and transpiration, Ann. Bot. 105(3):431–442. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly JT, Baker KR, Nowak JB, Murphy JG, Markovic MZ, VandenBoer TC, Ellis RA, …and Misenis C(2014), Fine-scale simulation of ammonium and nitrate over the South Coast Air Basin and San Joaquin Valley of California during CalNex-2010, Journal of Geophysical Research: Atmospheres, 119(6), 3600–3614. [Google Scholar]
- Kobayashi H, Baldocchi DD, Ryu Y, Chen Q, Ma S, Osuna JL, and Ustin SL (2012), Modeling energy and carbon fluxes in a heterogeneous oak woodland: A three-dimensional approach, Agricultural and Forest Meteorology, 152 (2012), 83–100. [Google Scholar]
- Kowalczyk EA, Stevens L, Law RM, Dix M, Wang YP, Harman IN, … and Ziehn T(2013), The land surface model component of ACCESS: description and impact on the simulated surface climatology, Australian Meteorological and Oceanographic Journal, 63(1), 65–82. [Google Scholar]
- Leuning R, Kelliher FM, Depury DGG, and Schulze ED (1995), Leaf Nitrogen, Photosynthesis, Conductance and Transpiration - Scaling from Leaves to Canopies, Plant Cell and Environment, 18(10), 1183–1200. [Google Scholar]
- Lombardozzi D, Levis S, Bonan G, and Sparks JP (2012), Predicting photosynthesis and transpiration responses to ozone: decoupling modeled photosynthesis and stomatal conductance, Biogeosciences, 9, 3113–3130, doi:10.5194/bg-9-3113-2012. [Google Scholar]
- Mauder M, Liebethal C, Göckede M, Leps J-P, Beyrich F, and Foken T (2006), Processing and quality control of flux data during LITFASS-2003, Boundary-Layer eteorology, 121, 67–88. [Google Scholar]
- McDowell NG, Phillips N, Lunch C, Bond BJ, and Ryan MG (2002), An investigation of hydraulic limitation and compensation in large, old Douglas-fir trees, Tree Physiology 22 (11), 763–774. [DOI] [PubMed] [Google Scholar]
- Medlyn BE, Dreyer E, Ellsworth D, Forstreuter M, Harley PC, Kirschbaum MUF, Le Roux X, Montpied P, Strassemeyer J, Walcroft A, Wang K, and Loustau D (2002), Temperature response of parameters of a biochemically based model of photosynthesis. II. A review of experimental data. Plant, Cell & Environment, 25(9), 1167–1179. [Google Scholar]
- Medlyn BE, Robinson AP, Clement R, and McMurtrie RE (2005), On the validation of models of forest CO2 exchange using eddy covariance data: some perils and pitfalls, Tree Physiology, 25(7), 839–857. [DOI] [PubMed] [Google Scholar]
- Meyers TP, Finkelstein PL, Clarke J, Ellestad TG, and Sims PF (1998), A multilayer model for inferring dry deposition using standard meteorological measurements, J. Geophys. Res, 103, 22645–22661. [Google Scholar]
- Monin AS and Obukhov A (1954), Basic laws of turbulent mixing in the surface layer of the atmosphere, Contrib. Geophys. Inst. Acad. Sci., USSR, 151, 163–187. [Google Scholar]
- Monteith JL (1981), Evaporation and Surface-Temperature, Quarterly Journal of the Royal Meteorological Society, 107 (451), 1–27. [Google Scholar]
- Moorcroft PR (2006), How close are we to a predictive science of the biosphere? Trends in Ecology & Evolution, 21(7), 400–407. [DOI] [PubMed] [Google Scholar]
- Myneni R, Knyazikhin Y, and Shabanov N (2011), Leaf Area Index and Fraction of Absorbed PAR Products from Terra and Aqua MODIS Sensors: Analysis, Validation, and Refinement. Land Remote Sensing and Global Environmental Change, Remote Sensing and Digital Image Processing, 11, 603–633. [Google Scholar]
- Noilhan J and Planton S (1989), A simple parameterization of land surface processes for meteorological models, Mon. Wea. Rev, 117, 536–549. [Google Scholar]
- Noilhan J and Mahfouf JF (1996), The ISBA land surface parameterisation scheme, Global and Planetary Change, 13(1), 145–159. [Google Scholar]
- Oleson KW, Lawrence DM, Bonan GB, Drewniak B, Huang M, Koven CD, Levis S, Li F, Riley WJ, Subin ZM, Swenson SC, Thornton PE, Bozbiyik A, Fisher R, Kluzek E, Lamarque JF, Lawrence PJ, Leung LR, Lipscomb W, Muszala S, Ricciuto DM, Sacks W, Sun Y, Tang J, and Yang ZL (2013), Technical Description of version 4.5 of the Community Land Model (CLM). Near Technical Note NCAR/TN- 503+STR, National Center for Atmospheric Research, Boulder, CO, 422 pp, DOI: 10.5065/D6RR1W7M. [Google Scholar]
- Pangle RE, Kavanagh K, and Duursma R(2015), Decline in canopy gas exchange with increasing tree height, atmospheric evaporative demand, and seasonal drought in co-occurring inland Pacific Northwest conifer species, Canadian Journal of Forest Research ja. [Google Scholar]
- Paw U KT, Falk M, Suchanek TH, Ustin SL, … and Matista AA (2004), Carbon dioxide exchange between an old growth forest and the atmosphere. Ecosystems, 7, 513–524. [Google Scholar]
- Phillips N, Bond BJ, McDowell NG, and Ryan MG (2002), Canopy and hydraulic conductance in young, mature and old Douglas-fir trees, Tree Physiology, 22(2–3), 205–211. [DOI] [PubMed] [Google Scholar]
- Pisek J, Sonnentag O, Richardson AD, and Mõttus M (2013), Is the spherical leaf inclination angle distribution a valid assumption for temperate and boreal broadleaf tree species?, Agricultural and Forest Meteorology, 169, 186–194. [Google Scholar]
- Pleim JE (2007a), A combined local and nonlocal closure model for the atmospheric boundary layer. Part I: model description and testing, J. Appl. Meteor. Clim, 46, 1383–1395. [Google Scholar]
- Pleim JE (2007b), A combined local and nonlocal closure model for the atmospheric boundary layer. Part II: application and evaluation in a mesoscale meteorological model, J. Appl. Meteor. Clim, 46, 1396–1409. [Google Scholar]
- Pleim JE and Gilliam R (2009), An indirect data assimilation scheme for deep soil temperature in the Pleim-Xiu land surface model, J. Appl. Meteor. Clim, 48, 1362–1376. [Google Scholar]
- Pleim JE and Ran L (2011), Surface Flux Modeling for Air Quality Applications, Atmosphere, 2(3), 271–302. [Google Scholar]
- Pleim JE and Xiu A (1995), Development and testing of a surface flux and planetary boundary layer model for application in mesoscale models, J. Appl. MeteoroF, 34, 16–32. [Google Scholar]
- Pleim JE and Xiu A (2003), Development of a Land Surface Model. Part II: Data Assimilation, J. Appl. Meteor, 42, 1811–1822. [Google Scholar]
- Pleim JE, Xiu A, Finkelstein PL, and Otte TL (2001), A coupled land-surface and dry deposition model and comparison to field measurements of surface heat, moisture, and ozone fluxes. Water, Air and Soil Pollution: Focus, 1(5–6), 243–252. [Google Scholar]
- Pleim J, Gilliam AAR, Appel W, and Ran L, 2015: Recent Advances in Modeling of the Atmospheric Boundary Layer and Land Surface in the Coupled WRF-CMAQ Model, 34th International Technical Meeting on Air Pollution Modelling and its Application, 4–8 May, 2015, Montpellier, France. [Google Scholar]
- Qu WQ, and Henderson-Sellers A (1998), Comparing the scatter in PILPS off-line experiments with that in AMIP I coupled experiments, Global and Planetary Change, 19, 209–223. [Google Scholar]
- Ran L, and Hanna A (2016), Spatial Allocator Version 4.2, the Community Modeling and System analysis at the University of North Carolina, Chapel Hill, NC, 02/May/2016. Available at: https://www.cmascenter.Org/sa-tools/documentation/4.2/Raster_Users_Guide_4_2.pdf, last access: June 2016. [Google Scholar]
- Ran L, Pleim J, Gilliam AR, Benjey W, Hanna A (2012), Application and Evaluation of 2006 NLCD and MODIS in the WRF/CMAQ System Part I: Meteorology Simulations, the 2012 CMAS Conference, Chapel Hill, NC: Oct. 15 – 17, 2012 (oral presentation). [Google Scholar]
- Ran L, Pleim J, Gilliam AR (2010), Impact of High Resolution Land-Use Data in Meteorology and Air Quality Modeling Systems, In Air Pollution Modeling and Its Application XX. Springer, the Netherlands: 3–7. [Google Scholar]
- Ran L, Gilliam R, Binkowski FS, Xiu A, Pleim J, and Band L (2015), Sensitivity of the Weather Research and Forecast/Community Multiscale Air Quality modeling system to MODIS LAI, FPAR, and albedo, J. Geophys. Res. Atmos, 120, 8491–8511, doi: 10.1002/2015JD023424. [Google Scholar]
- Ran L, Pleim J, Gilliam R, Binkowski FS, Hogrefe C, and Band L (2016), Improved Meteorology from an Updated WRF/CMAQ Modeling System with MODIS Vegetation and Albedo, submitted to J. Geophys. Res. Atmosphere. [Google Scholar]
- Ryan MG, and Yoder BJ (1997), Hydraulic limits to tree height and tree growth, BioScience, 47, 235–242, doi: 10.2307/1313077. [Google Scholar]
- Samuelsson P, Bringfelt B, Graham LP (2003), The role of aerodynamic roughness for runoff and snow evaporation in land-surface schemes - comparison of uncoupled and coupled simulations, Global and Planetary Change, 38, 93–99. [Google Scholar]
- Sellers PJ, Randall DA, Collatz GJ, Berry JA, Field CB, Dazlich DA, Zhang C, Collelo GD, and Bounoua L (1996), A revised land surface parameterization (SiB2) for atmospheric GCMs. Part I: Model formulation, J. Clim, 9, 676–705. [Google Scholar]
- Shaw DC, Franklin JF, Bible K, Klopatek J, Freeman E, Greene S, and Parker GG (2004), Ecological setting of the Wind River old-growth forest, Ecosystems, 7(5), 427–439. [Google Scholar]
- Sitch S, Cox PM, Collins WJ, and Huntingford C (2007), Indirect radiative forcing of climate change through ozone effects on the land-carbon sink, Nature, 448, 791–794. [DOI] [PubMed] [Google Scholar]
- Skamarock WC, Klemp JB, Dudhia J, Gill DO, Barker DM, Wang W, and Powers JG (2008), A description of the advanced research WRF version 3. NCAR Tech Note, NCAR/TN 475+STR: 125 pp. [Google Scholar]
- Song C, Katul G, Oren R, Band LE, Tague CL, Stoy PC, and McCarthy HR (2009), Energy, water, and carbon fluxes in a loblolly pine stand: Results from uniform and gappy canopy models with comparisons to eddy flux data, Journal of Geophysical Research: Biogeosciences (2005–2012) 114(G4). [Google Scholar]
- Thomas SC, and Winner WE (2000), Leaf area index of an old-growth Douglas-fir forest estimated from direct structural measurements in the canopy, Canadian Journal of Forest Research, 30(12), 1922–1930. [Google Scholar]
- Urbanski S, Barford C, Wofsy S, Kucharik C, Pyle E, Budney J, McKain K, Fitzjarrald D, Czikowsky M, and Munger JW (2007), Factors controlling CO2 exchange on timescales from hourly to decadal at Harvard Forest, J. Geophys. Res, 112(G2), G02020, doi: 10.1029/2006JG000293. [Google Scholar]
- Verma SB, Dobermann A, Cassman KG, Walters DT, Knops JM, Arkebauer TJ, … and Waiter-Shea EA (2005). Annual carbon dioxide exchange in irrigated and rainfed maize-based agroecosystems, Agricultural and Forest Meteorology, 131(1), 77–96. [Google Scholar]
- Wang K, and R. E. Dickinson (2012), A review of global terrestrial evapotranspiration: Observation, modeling, climatology, and climatic variability, Reviews of Geophysics 50(2). [Google Scholar]
- Wang SX, Zhao M, Xing J, Wu Y, Zhou Y, Lei Y, He KB, Fu LX, and Hao JM (2010), Quantifying the air pollutants emission reduction during the 2008 Olympic Games in Beijing, Environ. Sci. Technol, 44, 2490–2496. [DOI] [PubMed] [Google Scholar]
- Wang YP, and Leuning R (1998), A two - leaf model for canopy conductance, photosynthesis and partitioning of available energy. I: Model description and comparison with a multi-layered model, Agric., For. Meteorol, 91, 89–111, doi:10.1016/S0168-1923(98)00061-6. [Google Scholar]
- Wharton S, Schroeder M, Bible K, and Falk M (2009), Stand-level gas-exchange responses to seasonal drought in very young versus old Douglas-fir forests of the Pacific Northwest, USA, Tree physiology, 29(8), 959–974. [DOI] [PubMed] [Google Scholar]
- Xing J, Mathur R, Pleim J, Hogrefe C, Gan C-M, Wong DC, Wei C, Gilliam R, and Pouliot G (2015), Observations and modeling of air quality trends over 1990–2010 across the Northern Hemisphere: China, the United States and Europe, Atmos. Chem. Phys, 15, 2723–2747, doi: 10.5194/acp-15-2723-2015. [Google Scholar]
- Xiu A and Pleim JE (2001), Development of a Land Surface Model. Part I: Application in a Mesoscale Meteorological Model, J. Appl. Meteor., 40, 192–209. [Google Scholar]
- Yang W, Shabanov NV, Huang D, Wang W, Dickinson RE, Nemani RR, Knyazikhin Y, and Myneni RB (2006), Analysis of leaf area index products from combination of MODIS Terra and Aqua data, Remote Sensing of Environment, 104(3), 297–312. [Google Scholar]
- Yu S, Eder B, Dennis R, Chu SH, and Schwartz SE (2006), New unbiased symmetric metrics for evaluation of air quality models, Atmospheric Science Letters, 7(1), 26–34. [Google Scholar]
- Zhang L, Moran MD, Brook JR (2001), A comparison of models to estimate in-canopy photosynthetically active radiation and their influence on canopy stomatal resistance, Atmos. Environ, 35, 4463–4470. [Google Scholar]