Abstract
The rapid increase in the number of new laboratory methods has led to the necessity of reliable verification methods. Validation of a new measurement method for application to medical practice requires comparison with gold standard techniques. The Bland-Altman analysis is a frequently applied technique in studies that investigate the agreement between two methods of the same medical measurement. In this review, potential areas of usage of Bland-Altman analysis is elaborated from a clinical viewpoint, and possible pitfalls in study designs are discussed in statistical perspective.
Keywords: Bland-Altman analysis, Limits of agreement, Correlation analysis, Biostatistics
1. Introduction
The Bland-Altman analysis was proposed by Martin Bland and Douglas Altman over thirty years ago with an article published in Lancet.1 In this article, their main argument was about the incorrect use of correlation coefficients in comparison of a new measurement technique with an established gold standard. This article is accepted as the sixth most-cited paper in statistics literature and was about the differences between measurements obtained by two different measurement systems.2 In the following years, their method has become the most appropriate way of determining the limits of agreement (LOA) between measurements.
Medical laboratories and clinicians often need to assess the agreement between two measurement methods. Validation of a clinical measurement method is a compelling and lengthy process, which necessitates acceptable LOA between two techniques. When the comparing methods are continuous variables (e.g. leucocyte count, antibody titer, body temperature), the Bland-Altman analysis is an appropriate way to perform this comparison and presents quantified measures to decide whether the new method is acceptable or not. This review focuses on the current approach to the Bland-Altman method and its applications in clinical practice.
2. Concept of correlation analysis
For many years, correlation analysis has been used to assess the relationship between one variable and another. Correlation analysis is classified as a part of a larger class of statistical techniques known as regression. Regression analysis uses the principles of correlation, but it does more than just to describe the strength of a relationship between two variables.3 The main result of correlation analysis is the correlation coefficient (r), which ranges from −1.0 to +1.0. The closer the coefficient is to the ends of this range, the greater the strength of the linear relationship is.4 Correlation coefficients can be handled as linear measures for the relationship between variables without providing their agreement.
A fictitious data set is provided in Table 1. In this dataset, potassium measurements from venous blood gas analysis and biochemistry panel are presented for each patient. It is easy to make an approximate estimate of these values, and conclude that they are very close to each other. Also using a Spearman correlation analysis, correlation coefficient (Spearman's rho) can be found as 0.885 (p < 0.001), which indicates a very strong relationship between the variables.5
Table 1.
Dataset for potassium levels in venous blood gases and blood electrolyte work-up.
| Potassium level (mEq/L) (Obtained from venous blood gas analysis) | Potassium level (mEq/L) (Obtained from blood electrolyte levels) | Mean potassium level (mEq/L) | Difference between potassium levels (mEq/L) | |
|---|---|---|---|---|
| Patient Nr. 1 | 4.5 | 4.7 | 4.6 | 0.2 |
| Patient Nr. 2 | 3.8 | 4.2 | 4.0 | 0.4 |
| Patient Nr. 3 | 5.1 | 5.1 | 5.1 | 0.0 |
| Patient Nr. 4 | 4.9 | 5.3 | 5.1 | 0.4 |
| Patient Nr. 5 | 3.9 | 4.0 | 3.95 | 0.1 |
| Patient Nr. 6 | 4.0 | 3.8 | 3.9 | −0.2 |
| Patient Nr. 7 | 4.1 | 4.0 | 4.05 | −0.1 |
| Patient Nr. 8 | 4.3 | 4.0 | 4.15 | −0.3 |
| Patient Nr. 9 | 5.3 | 5.3 | 5.3 | 0.0 |
| Patient Nr. 10 | 5.2 | 5.1 | 5.15 | −0.1 |
| Patient Nr. 11 | 3.9 | 4.0 | 3.95 | 0.1 |
| Patient Nr. 12 | 4.1 | 4.4 | 4.25 | 0.3 |
| Patient Nr. 13 | 4.0 | 4.2 | 4.1 | 0.2 |
| Patient Nr. 14 | 5.3 | 5.1 | 5.2 | −0.2 |
| Patient Nr. 15 | 5.5 | 5.3 | 5.4 | −0.2 |
| Patient Nr. 16 | 4.4 | 4.2 | 4.3 | −0.2 |
| Patient Nr. 17 | 4.9 | 5.0 | 4.95 | 0.1 |
| Patient Nr. 18 | 3.7 | 3.9 | 3.8 | 0.2 |
| Patient Nr. 19 | 3.9 | 3.7 | 3.8 | −0.2 |
| Patient Nr. 20 | 4.8 | 4.7 | 4.75 | −0.1 |
| Patient Nr. 21 | 5.5 | 5.2 | 5.35 | −0.3 |
| Patient Nr. 22 | 3.7 | 3.8 | 3.75 | 0.1 |
| Patient Nr. 23 | 3.7 | 3.9 | 3.80 | 0.2 |
| Patient Nr. 24 | 4.8 | 4.2 | 4.5 | −0.6 |
| Patient Nr. 25 | 5.1 | 5.6 | 5.35 | 0.5 |
Does this mean that we can use a given variable instead of the other? Can we replace a laboratory method with the new one, regarding this strong relationship? This argument is not always correct. Unfortunately, correlation analysis provides a link between variables which just happen to occur together, without having an association in between. In this setting, Spearman's rho indicates only the power of this relationship, and this small p-value suggests just strong evidence against the null hypothesis. Consequently, the null hypothesis is rejected and there is probably a relationship. However, results of the correlation analysis do not answer following questions: [a] Is this occurrence an incidental finding or have they a meaningful clinical association? [b] What is the probability of error in each measurement of potassium? A high correlation does not explicitly imply that there is good agreement between the two methods.4 Moreover, data which seem to be in a poor agreement can produce quite high correlations.
3. Analysis of the differences between variables
Bland and Altman quantified the difference between measurements using a graphical method. They draw a scatterplot in which the X-axis represented the average [(K1 + K2)/2], and the Y-axis represented the difference (K1 – K2) of two measurements. After the graph is drawn, the mean bias (mean of the K1 – K2) and its confidence limits (limits of agreement) should be quantified. Using statistical software, a one-sample T-test can be performed to calculate the mean bias and its SD. To represent mean bias and limits of agreement, we need only mean of the difference of measurement methods and its standard deviation obtained from one-sample T-test. Secondly, the data points can be restricted using +2 standard deviation (SD) to demonstrate a 95% confidence interval (CI; precisely defined: mean ± 1.96 standard deviations) of distributed data. An ideal agreement is zero difference between measurements. Thus average difference and its limits can also be found near zero in this setting.
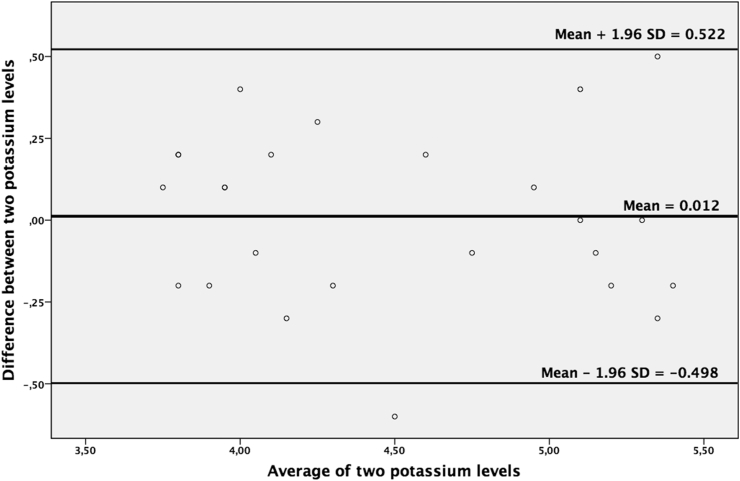
For our dataset, the mean difference (mean bias) was found as 0.012 with an SD of 0.260. A scatterplot should be drawn to understand dispersion of variables using X-axis (average) and Y-axis (difference). The LOA can be drawn manually if the statistical software does not automatically demonstrate them. In our data set, the upper limit can be calculated using mean + 1.96 x SD (0.012 + 1.96 x 0.260 = 0.522) and the lower limit can be calculated using mean – 1.96 x SD (0.012–1.96 x 0.260 = –0.498). The appropriate statement used in the manuscript can be following: The Bland-Altman plot showed the mean bias ±SD between first and second potassium levels as 0.012 ± 0.260 mEq/L, and the limits of agreement were −0.498 and 0.522 (Fig. 1).
Fig. 1.
Agreement between two potassium measurements (Bland-Altman plot).
The scatterplot can be evaluated according to the scatter dispersion. In a good agreement, the scattering of points is diminished, and points lie relatively close to the line which represents mean bias. As a quantifiable measure, mean bias and limits of the agreement give information about the utility of the new measurement method. Regarding our data set, those two methods can be used interchangeably as the limits vary from nearly one mEq/L of potassium.
4. Clinical implication and potential areas of usage
Only a clinician, who uses the test results in a clinical setting can decide whether the mean bias and LOA are acceptable or not. For instance, a mean bias of 0.2 mEq/L is obviously acceptable for potassium levels. However, 3 mEq/L is too broad and can lead to lethal complications if the actual potassium value is higher in biochemistry panel.
Bland-Altman analysis was previously used in many method comparisons in the literature. It may be used to compare two new measurement methods or one measurement method against a reference standard. These measurement variables should be continuous (not categorical) such as hemoglobin level (g/dl), anti-HCV antibody titer or the size of a tumor (cm). The Bland-Altman method is a popular approach, and there are reports including but not limited to compare two hemodynamic measurements,6 end-tidal carbon dioxide measurement methods,7,8 different electrolyte level measurement methods,9 self-assessed general well-being scores,10 performance of different computed tomography technologies in evaluating pulmonary nodules.11
5. Pitfalls in Bland-Altman analysis
One of the critical problems in the Bland-Altman analysis is the need to meet the assumption of normal distribution. The continuous measurement variables need not to be normally distributed, but their differences should. If the assumption of normal distribution is not met, data may be logarithmically transformed.4 The data may be tested against the normal distribution using classical methods such as the Shapiro-Wilk test or Kolmogorov-Smirnov test. Visual evaluation of the histogram plot may not be adequate.
Another problem arises from the sample size. Studies comparing methods of measurements should be adequately sized to conclude that the effects are universally valid. If the sample size is not adequate, it is possible to find a low mean bias and reduced limits of agreement by comparing two methods.12 Such methods cannot be recommended for general use without verification of the results of other studies. To calculate sample size, maximum allowed difference derived from other studies should be provided.
Some authors argue that also regression analysis can be performed to compare two methods of measurements. The Bland-Altman analysis may bring proportional bias, which is present when the difference in values resulting from two methods increases or decreases in proportion to the average values.13 Although it is an uncertain area of expertise, Ludbrook indicated that two methods could be used for different purposes: According to him, regression analysis can be used if the concern of the investigator is to calibrate one measurement against another or to detect bias between two methods of measurement. However, if the goal is to determine whether a method may be safely substituted for another, particularly in clinical practice, the Bland-Altman method may be used.13
An other problem in the Bland-Altman analysis is repeated measure designs. The Bland-Altman analysis is not an appropriate method to compare repeated measurements. However, it can be performed by adding a random effects model to the analysis.14,15 In addition, some statistical softwares allow to perform analysis for repeated designs using Bland-Altman method. Besides, a meta-analysis of studies conducted with the Bland-Altman analysis is still under debate, recently a framework for the meta-analysis of Bland-Altman studies based on limits of agreement approach is published.16
6. Conclusion
Correlation analysis may lead to incorrect or debated results in comparison of two measurement methods. The Bland-Altman analysis is a simple and accurate way to quantify agreement between two variables and may help clinicians to compare a new measurement method against another one or a reference standard.
Conflict of interest
The author declares no conflicts of interest.
Source of funding
None declared.
Author contributions
NOD designed and wrote the manuscript, he also takes responsibility for the paper as a whole.
Footnotes
Peer review under responsibility of The Emergency Medicine Association of Turkey.
References
- 1.Bland J.M., Altman D.G. Statistical methods for assessing agreement between two methods of clinical measurement. Lancet. 1986;1:307–310. [PubMed] [Google Scholar]
- 2.Ryan T.P., Woodall W.H. The most-cited statistical papers. J Appl Stat. 2005;32:461–474. [Google Scholar]
- 3.Greenfield M.L., Kuhn J.E., Wojtys E.M. A statistics primer. Correlation and regression analysis. Am J Sports Med. 1998;26:338–343. doi: 10.1177/03635465980260022901. [DOI] [PubMed] [Google Scholar]
- 4.Giavarina D. Understanding Bland Altman analysis. Biochem Med. 2015;25:141–151. doi: 10.11613/BM.2015.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Akoglu H. User's guide to correlation coefficients. Turk J Emerg Med. 2018;18:91–93. doi: 10.1016/j.tjem.2018.08.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Brazdzionyte J., Macas A. Bland-Altman analysis as an alternative approach for statistical evaluation of agreement between two methods for measuring hemodynamics during acute myocardial infarction. Medicina (Kaunas) 2007;43:208–214. [PubMed] [Google Scholar]
- 7.Pekdemir M., Cinar O., Yilmaz S., Yaka E., Yuksel M. Disparity between mainstream and sidestream end-tidal carbon dioxide values and arterial carbon dioxide levels. Respir Care. 2013;58:1152–1156. doi: 10.4187/respcare.02227. [DOI] [PubMed] [Google Scholar]
- 8.Doğan N.Ö., Şener A., Günaydın G.P. The accuracy of mainstream end-tidal carbon dioxide levels to predict the severity of chronic obstructive pulmonary disease exacerbations presented to the ED. Am J Emerg Med. 2014;32:408–411. doi: 10.1016/j.ajem.2014.01.001. [DOI] [PubMed] [Google Scholar]
- 9.Altunok İ., Aksel G., Eroğlu S.E. Correlation between sodium, potassium, hemoglobin, hematocrit, and glucose values as measured by a laboratory autoanalyzer and a blood gas analyzer. Am J Emerg Med. 2018 Aug 18 doi: 10.1016/j.ajem.2018.08.045. [In Press] [DOI] [PubMed] [Google Scholar]
- 10.Hofman C.S., Melis R.J., Donders A.R. Adapted Bland-Altman method was used to compare measurement methods with unequal observations per case. J Clin Epidemiol. 2015;68:939–943. doi: 10.1016/j.jclinepi.2015.02.015. [DOI] [PubMed] [Google Scholar]
- 11.Paks M., Leong P., Einsiedel P., Irving L.B., Steinfort D.P., Pascoe D.M. Ultralow dose CT for follow-up of solid pulmonary nodules: a pilot single-center study using Bland-Altman analysis. Medicine (Baltim) 2018;97(34):e12019. doi: 10.1097/MD.0000000000012019. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bunce C. Correlation, agreement, and Bland-Altman analysis: statistical analysis of method comparison studies. Am J Ophthalmol. 2009;148:4–6. doi: 10.1016/j.ajo.2008.09.032. [DOI] [PubMed] [Google Scholar]
- 13.Ludbrook J. Confidence in Altman-Bland plots: a critical review of the method of differences. Clin Exp Pharmacol Physiol. 2010;37:143–149. doi: 10.1111/j.1440-1681.2009.05288.x. [DOI] [PubMed] [Google Scholar]
- 14.Myles P.S., Cui J. Using the Bland-Altman method to measure agreement with repeated measures. Br J Anaesth. 2007;99:309–311. doi: 10.1093/bja/aem214. [DOI] [PubMed] [Google Scholar]
- 15.Woodman R.J. Bland-Altman beyond the basics: creating confidence with badly behaved data. Clin Exp Pharmacol Physiol. 2010;37:141–142. doi: 10.1111/j.1440-1681.2009.05320.x. [DOI] [PubMed] [Google Scholar]
- 16.Tipton E., Shuster J. A framework for the meta-analysis of Bland-Altman studies based on a limits of agreement approach. Stat Med. 2017;36:3621–3635. doi: 10.1002/sim.7352. [DOI] [PMC free article] [PubMed] [Google Scholar]