Assessing patterns for compressive fluorescence lifetime imaging

Abstract

A novel hyperspectral single pixel system was used to compare different compressive basis patterns for intensity imaging, lifetime imaging, and FRET quantification. Six popular basis patterns were compared experimentally in a phantom containing two fluorescent dyes. The basis patterns that performed best for lifetime quantification were used to measure FRET occurrence in well-plate samples with varying acceptor–donor ratios. The ABS-WP approach using Haar patterns and the compressive sensing approach with Hadamard Ranked patterns displayed the best overall performances at a 50% compression ratio.

Fluorescence lifetime imaging has been widely used to investigate biosamples at the macroscopic and microscopic levels [1–5]. Fluorescence lifetime is an intrinsic property of fluorophores that depends on its molecular environment and not on its concentration [6]. Its imaging is particularly useful to quantify Förster Resonance Energy Transfer (FRET), which is widely employed as a nanoproximity assay for biomedical applications [7–9]. Recently, macroscopic hyperspectral single-pixel imaging has been proposed as one avenue to spatially image FRET occurrence in vitro as well as in vivo in preclinical models [10]. Single-pixel imaging exploits spatially compressed optical signals to recover 2D images from a few 1D measurements [11]. Mathematically, it consists of inverting the linear equation to solve for the sample plane s

$$m=\Delta tPs,$$ (1)

where m represents the measured data, P the illumination patterns, and Δt the integration time for each pattern. The imaging performance depends on the choice of compression patterns as well as the strategy for selecting a subset for measurements [12]. Multiple basis patterns such as Hadamard [13], Fourier [14], speckle [15], and wavelet [16] have been proposed. Intensity imaging using Hadamard and Fourier patterns have been compared in Ref. [14]. In this Letter, our contribution is: (1) to compare patterns (e.g., wavelets) that have not been considered so far, and (2) to assess fluorescence lifetime and FRET quantification. Herein, we experimentally investigate six different approaches and assess their ability for 2D imaging as well as to quantify monolifetime and NIR FRET interactions, which represents a challenging biexponential application.

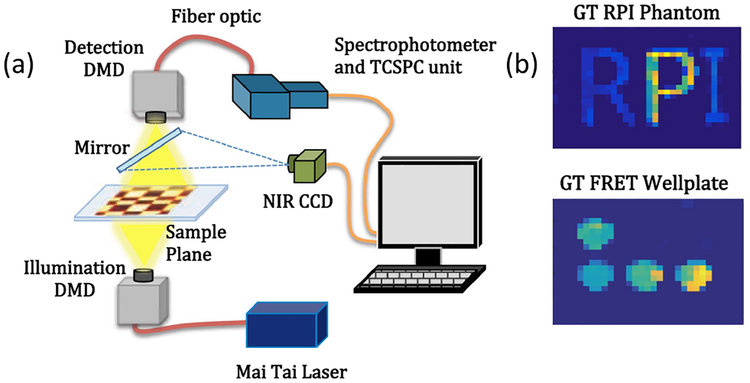
The hyperspectral single-pixel system employed in this study is described in Ref. [10] and depicted in Fig. 1(a). In brief, the system operates in transmission with two digital micromirror devices (DMD, D4110, Digital Light Innovations, Texas). The illumination DMD, where compressive basis patterns are implemented, is coupled to a Ti:Sapphire pulsed laser (Mai Tai HP, Spectra Physics, California) that can be tuned from 690 to 1020 nm. Light emitted by the sample is collected through the wide-field detection DMD, which is coupled to a 16-channel detection PMT spectrophotometer (MW-FLIM, Becker and Hickl GmbH, Germany) via a fiber bundle. Note that this double-DMD architecture is not required for 2D single-pixel imaging but implemented to also be able to perform optical tomography [17]. A time-correlated single-photon counting unit (TCSPC) records the fluorescence decays over the 16 spectral channels in parallel. The system is controlled through LabView. All patterns are generated using MatLab, considering 32 × 32 images that are converted to eight-bit integers and resized to 672 × 672 to match the DMD physical resolution. The patterns are divided into positive and negative parts for further processing after data collection. Herein, we used only 512 patterns out of the 32 × 32 = 1024 patterns, resulting in a 50% compression ratio. The list of basis patterns to be compared is: (a) Hadamard Normal, (b) Hadamard Sign, (c) Hadamard Ranked, (d) Speckle, (e) Fourier, and (f) Haar. The Hadamard patterns are generated using a natural sequence through the Hadamard Matlab function [18–20]. We consider three different Hadamard pattern orders: Normal uses the default sequence provided by the function (see Visualization 1) and Sign are the normal patterns arranged by positive and negative parts (see Visualization 2). The patterns are further arranged from low to high spatial frequency to yield Ranked Hadamard patterns (see Visualization 3). Speckle patterns are obtained from uniformly distributed random multiplicative noise using the imnoise Matlab function [15,21] with a mean of 0 and variance of 10 (see Visualization 4). Fourier patterns are accomplished by cosine function generation. The x∕y frequencies change from 1 to 8 with eight phase shifts (see Visualization 5). Haar patterns are taken from a Haar wavelet basis that contains 16 scaling functions [16] (see Visualization 6). To investigate the performances of these various basis patterns in the case of monolifetime, we prepared fluorescence phantoms with RPI letters: R and I contained AF750 (ThermoFisher Scientific, A33085) fluorescent dye at 4.16 μM concentration prepared with PBS 1X; letter P contained HITCI (Sigma Aldrich, 252034) dye at 40 μM concentration prepared with 100% ethanol. The volumes of the RPI letters are 149, 124, and 81 μL, respectively. Using a piecewise homogeneous phantom allows estimation of the noise of the reconstructed image.

Fig. 1.

(a) Hyperspectral single pixel imaging platform [10] and (b) RPI phantom and FRET wellplate.

Seven identical phantoms were prepared: one per basis patterns and one for measuring lifetime ground-truth values with a gated-ICCD system [22,23]. To minimize evaporation effects, we filled each phantom with the same stock solutions of the dyes before measuring each basis patterns. Moreover, because lifetime is considered independent of concentration, minimal evaporation changes should not compromise its quantification. The system illumination and detection schemes were calibrated with the six different pattern sets. The calibration process involved matching the field-of-view of the illumination and detection DMDs. In addition, the patterns were projected on the image plane and recorded using an external NIR CCD to be later used during the image reconstruction step [Fig. 1(a)]. Each pattern accounted for 0.5 s exposure time, and the excitation wavelength was 740 nm. A 780 nm (Semrock FF01–780/12–25) filter with spectral range 774–786 nm was added to the detection optics, and the PMT detection range was defined from 715 to 778 nm with central wavelength at 742 nm. The field of view (FOV) was 35 mm × 35 mm, and the optical power density was ~5.49 mW∕cm². Using constant parameters for each basis patterns, we acquired a data cube composed of one time point spread function (TPSF) per pattern and per detection channel. The TCSPC unit produced each TPSF over 256 time channels. We first evaluated the 32 × 32 intensity images recovered by the different approaches for different compression ratios. For all basis patterns, we considered increasing compression ratios (~50%, 60%, 70%, 80%, and 90%) by decreasing the number of patterns. While most approaches select patterns prior to acquisition [14], adaptive strategies select patterns during acquisition [16,24]. For Hadamard, Fourier, and Speckle basis, patterns were chosen a priori, and a linear solver reconstructed the images from the raw data. We used the so-called TVAL3 algorithm [25], which promotes piecewise constant solutions. For Haar wavelet patterns, we implemented an adaptive basis scan by wavelet prediction (ABS-WP) using the SPIRIT toolbox [26]. The Haar patterns were selected among the Haar basis during acquisition, and the image was simply recovered through fast inverse wavelet transforms of the raw data. The images reconstructed for a 50% compression ratio are shown in Fig. 2(a), and the image reconstruction quality for increasing compression ratios is plotted in Fig. 2(b).

Fig. 2.

(a) 32 × 32 pixels ground-truth (GT) and reconstructed intensity images at 512 patterns and (b) SSIM in relation to ground-truth.

Intensity images are computed by integrating the hyperspectral time-resolved data cube over the detection channel located between ~760 and 765 nm and over the 256 time channels. Before every experiment, a ground-truth image was measured using the NIR CCD camera described in Fig. 1. The 616 × 619 CCD image is resized to 32 × 32 to match the size of the single-pixel reconstructed intensity images. Both the ground-truth and the recovered intensity image are normalized to their maximum value. We used the structural similarity index (SSIM) metric to measure the similarity between the ground-truth and the recovered images

$$\text{SSIM}=\frac{\left(2{\mu }_x{\mu }_y+c_1\right)\left(2{\sigma }_{xy}+c_2\right)}{\left({\mu }_x^2+{\mu }_y^2+c_1\right)\left({\sigma }_x^2+{\sigma }_y^2+c_2\right)},$$ (2)

where μ_x and μ_y are the local means, σ_x and σ_y are the standard deviations, σ_xy is the cross-covariance, and the c₁ and c₂ terms are regularization constants for luminance and contrast [27]. Variable x constitutes the output 32 × 32 reconstructed image, and y is the ground-truth 32 × 32 CCD image. In this case SSIM was calculated globally. Overall, the best intensity images are recovered by the ABS-WP approach, no matter the compression ratio. Ranked Hadamard patterns provided similar results to the ABS-WP approach, up to a compression rate of 70%. Normal Hadamard reconstruction shows large artifacts, which are related to the measurement of high-frequency patterns leading to low signals that are highly affected by noise. The SSIM values for Sign Hadamard and Fourier patterns are similar for compression ratios below 70%. Finally, speckle patterns yielded lower SSIM values than the other basis patterns, except for the normal order Hadamard that led to the worst image quality. Second, we exploited the time domain data to quantify lifetimes. Each TPSF from the 12th spectral channel of the recovered data cube was fitted to a monoexponential decay convolved with the instrument response function (IRF), i.e.,

$$m(x,y,t)=\text{ IRF}(t)*\text{exp}\left(\frac{-t}{\tau (x,y)}\right),$$ (3)

where m(x, y, t) is the TPSF recovered at pixel (x, y), and τ is the fluorescence lifetime. The IRF was measured after each basis measurement with a wide-field illumination pattern. Each pixel of the TPSF is denoised with a one-dimensional low-pass filter and normalized. The fluorescence decay was then tail-fitted using a Matlab built-in optimization interior-point algorithm. Initial values of 1 (ns) with ±0.05 (ns) boundaries were provided for letter P and 0.5 (ns) with ±0.05 (ns) for letters R and I, where the letters are segmented from the ground-truth images shown in Fig. 2(a). To deliver accurate fits with low residuals, initialization values were provided to the optimization algorithm per each letter. The obtained lifetime maps are displayed in Fig. 3(a). To quantitatively compare the performance of each compressive basis patterns, we also computed, in each letter, the mean lifetime and standard deviation values as summarized in Fig. 3(b).

Fig. 3.

(a) Lifetime maps. (b) Mean lifetime and standard deviation within letters R (red), P (blue), and I (black); the horizontal lines indicate ICCD ground-truth values.

To compute the descriptive statistics, the lifetime values on each letter were ordered and 60% of them used, that is 60 pixels for R, 52 pixels for P and 25 pixels for I. By imaging the additional RPI phantom on a gated ICCD system, mean values of 0.50 ± 0.017 (ns) were obtained for letters R and I containing AF750 dye and 0.92 ± 0.018 (ns) for letter P containing HITCI dye. The lifetime range for each letter is evaluated, and a closer relation of the mean value and standard deviation to ground-truth are therefore desired. In terms of mean values for letter P containing HITCI dye, the closest mean relation is accomplished by ABS-Haar, which also displays the smallest standard deviation range after the Hadamard Sign. The standard deviations of the other basis patterns partially contain the ground-truth range for this letter. On the other hand, ABS-Haar and Ranked Hadamard better approximate the ground-truth mean for letters R and I, which contain the same dye AF750 and therefore should ideally yield the same lifetime mean. For these letters ABS-Haar, Fourier, and Hadamard Ranked display the smallest standard deviation ranges. Even though normal Hadamard encloses the ground-truth values, its range for letter P also encloses values present in the lifetime range of letter R and vice-versa. Overall, the ABS-Haar and Hadamard Ranked basis patterns showed the most accurate lifetime estimations for all letters (i.e., closer means to ground truth and smaller standard deviation for both fluorophores). To further compare these basis patterns, we conducted an experimental study focusing on one of the most challenging lifetime-based applications, NIR FRET. As the ranked and sign Hadamard, ABS Haar, and Fourier were the best at quantifying lifetime on the RPI phantom, the quantification of FRET was restricted to these basis patterns. The FRET sample contained AF700 Mouse IgG1 (ThermoFisher Scientific, MG129) donor dye and AF750 goat antimouse IgG (ThermoFisher Scientific, A-21037) acceptor dye with respective concentrations of 50 and 100 μg/mL. A PBS 1X solution was used to prepare the desired concentrations. Six wells were filled with 250 μl of different acceptor–donor combinations. The wells described in Fig. 1(b) for well 1 contain AF700 only, well 2 and well 3 PBS only, and wells 4 to 6 contain ratios of AF750 to AF700 of 1∶1, 2∶1, and 3∶1, respectively. The PBS and AF700 only wells were used as experimental control; therefore, FRET interaction is only expected in wells 4 to 6. Four well-plate samples were prepared from stock solutions. Samples were excited at 695 nm and exposed for 1.5 s per pattern. A 715 nm long pass filter (Semrock, FF01–715/LP-25) was added to the detection optics. The third channel, which was used for reconstructions (~720 to 730 nm), would detect minor acceptor bleed-through. All the experimental parameters were kept constant for all patterns. Hadamard Ranked, Hadamard Sign, and Fourier were reconstructed through TVAL3 and Haar patterns through the ABS-WP approach. A biexponential fit yielded the amplitudes and lifetimes of the FRETing and non-FRETing populations. At each pixel, we assume:

$$m(t)=\text{ IRF}(t)*\left[a_F\text{exp}\left(\frac{-t}{{\tau }_F}\right)+a_{NF}\text{exp}\left(\frac{-t}{{\tau }_{NF}}\right)\right],$$ (4)

where a_F, a_NF are the amplitudes of the FRETing and non-FRETing donor and τ_F, τ_NF their respective lifetimes. Amplitudes are normalized such that a_F +a_NF =1. Initial values of 1 ± 0.05 (ns) and 0.35 ± 0.05 (ns) for long and short lifetime were provided. Figure 4(a) shows the FRET donor fraction (a_F) percentage maps for wells 1–4 for the different basis patterns. For increasing acceptor to donor ratios, the FRET interaction should increase linearly [22]. Although well 1 contains a 0∶1 ratio and no FRET interaction is expected, relative amplitudes of ~15% and ~85% are estimated. The correction of this inherent type of bias, which has already been reported in Refs. [10,22,28], falls outside the scope of this study. Figure 4(c) displays the mean values of each well and their standard deviation range. ICCD ground-truth values for the FRET samples are also included. A linear trend within ground-truth values is observed for the four sets of patterns, with ABS-Haar displaying the least accurate 0∶1 ratio estimation and linearity. Fourier patterns on the other hand result in a smoother FRET Donor Fraction (FD%) map (though without recovering the lower FRET donor fraction spatial distribution in its entirety). It is important to mention that FRET quantification experiments are limited by the variability of FRET interactions from sample to sample; however, similar ground-truth linear trends have been previously reported [10,22,28]. In summary, all basis patterns investigated herein were successfully implemented in a single pixel paradigm for lifetime imaging. In all cases, spatially resolved TPSFs could be reconstructed. Though, when spatial accuracy and lifetime quantification were assessed, the ABS-WP approach and ranked Hadamard strategy outperformed the other compressive basis patterns. The ABSWP approach and ranked Hadamard strategy provided very similar performances for a compression rate at 50%, both for intensity and lifetime-based quantification. Ranked Hadamard performed better for FRET quantification. Considering that the excitation wavelength, exposure time, power density, detection range, and FOV were kept constant, comparing raw TPSFs for the highest photon counts between the ABS-WP approach and ranked Hadamard reveals that ABS-WP based on Haar patterns lead to more noisy TPSFs with a lower number of photon counts, as displayed in Fig. 4(b). This is most likely the reason why ranked Hadamard performs better in the case of biexponential fitting with short components (NIR FRET). However, it is important to note that the ABS-WP approach performed better at higher compression ratios for intensity reconstructions. Because employing higher compression ratios is critical to enable the implementation in single-pixel methodologies for bed side applications, this finding elicits the need for further refinements and investigation on the performances of the ABS-WP approach at very high compression ratios. The ABS-WP approach implemented herein used the Haar wavelets, but further evaluation of ABSWP wavelets like biorthogonal CDF [29] should be carried out and compared to the ranked Hadamard methodology. Additionally, in this study, the ABS-WP approach was implemented a posteriori (the whole Haar basis patterns were acquired and then pattern prediction was performed postacquisition). Further study should focus on seamless experimental implementation of on-the-fly prediction and compare its computational burden to the fixed pattern basis as obtained with ranked Hadamard. It is expected that the implementation of the ABS-WP approach will then lead to robust and very fast imaging protocols for lifetime imaging, especially in the case of monolifetime applications. Overall, after selection of the appropriate illumination basis patterns and the reconstruction approach, compression ratios higher than 50% should be explored to improve both resolution and acquisition times.

Fig. 4.

(a) FD% maps per basis patterns. (b) Highest raw data TPSFs. (c) FD% mean and standard deviation to ground-truth.