CREATING MEASURES OF THEORETICALLY RELEVANT NEIGHBORHOOD ATTRIBUTES AT MULTIPLE SPATIAL SCALES

Abstract

Accurately measuring attributes in neighborhood environments allows researchers to study the influence of neighborhoods on individual-level outcomes. Researchers working to improve the measurement of neighborhood attributes generally advocate doing so in one of two ways: improving the theoretical relevance of measures and correctly defining the appropriate spatial scale. The data required by the first, “ecometric” neighborhood assessments on a sample of neighborhoods, are generally incompatible with the methods of the second, which tend to rely on population data. In this article, the authors describe how ecometric measures of theoretically relevant attributes observed on a sample of city blocks can be combined with a geostatistical method known as kriging to develop city block–level estimates across a city that can be configured to multiple neighborhood definitions. Using a cross-validation study with data from a 2002 systematic social observation of physical disorder on 1,663 city blocks in Chicago, the authors show that this method creates valid results. They then demonstrate, using neighborhood measures aggregated to three different spatial scales, that residents’ perceptions of both fear and neighborhood disorder vary substantially across different spatial scales.

1. INTRODUCTION

Studies investigating how neighborhood characteristics affect individuals have grown in number as well as in the diversity of outcomes being investigated (Entwisle 2007). Researchers have considered outcomes as diverse as high school dropouts (Harding 2003), crime (Sampson, Raudenbush, and Earls 1997), childhood cognitive development (Sampson, Sharkey, and Raudenbush 2008), and a number of health outcomes and behaviors (Leventhal and Brooks-Gunn 2000; Robert 1999; Sampson, Morenoff, and Gannon-Rowley 2002). With their burgeoning interest to study the relationship between neighborhood environment and individual outcomes, social scientists identify two areas in which this research should be focused: improving the theoretical relevance of neighborhood attributes measured and identifying the appropriate spatial scale at which neighborhood attributes might influence outcomes. Identifying a method that can simultaneously account for both of these areas would be a welcome addition to the toolkit of social scientists exploring neighborhood influences on individuals.

Improvements to the theoretical nuance of neighborhood-level measures have been aided most effectively by the “ecometric” framework, which uses multiple items to capture latent environmental characteristics at the neighborhood level while adjusting for measurement error (Mujahid et al. 2007; Raudenbush and Sampson 1999; Sampson and Raudenbush 1999). These methods have pushed neighborhood measures beyond the limited number of demographic and economic measures primarily available from the census and begun using “nonroutine” data sources (Cummins et al. 2005), such as systematic social observations (SSOs) designed to systematically measure neighborhood attributes. The cost of deploying and coding SSO data compels researchers to sample units for observation. Ensuring sufficient statistical power at each level of observation within the ecometric framework requires neighborhoods to be defined prior to entering the field. Except where a researcher can develop a complete count of measures for all units of observation (e.g., from administrative data), neighborhood definitions are inflexible to alternative definitions because they are defined a priori, usually using census boundaries.

At the same time, emerging research has also identified a potential shortcoming of relying on administrative boundaries such as census tracts to define neighborhood boundaries as the ecometric framework does (Grannis 1998). Studies from this emerging research have shown, using data available at very small spatial scales (e.g., city blocks), that analytical results depend on the spatial scale and neighborhood definition that is used (Hipp 2007; Lee et al. 2008). Yet because the information available at small levels of aggregation is typically only very basic information, such as the age or racial composition of a block, it has been difficult to determine how associations with more theoretically relevant neighborhood attributes might vary at different spatial scales. Thus, researchers have both improved the theoretical nuance and focused greater attention on accurately defining the spatial scale of neighborhood measures, but the methods used by each have, to date, made the advances in one incompatible to incorporate with the advances in the other.

Combining the strengths of these two contributions to neighborhood measurement would enable researchers to simultaneously advance efforts both to improve the theoretical relevance of neighborhood measures and to allow flexibility in defining the spatial scale and boundaries of neighborhoods. We propose such a framework in this article and present a statistical technique adapted from environmental sciences known as kriging that will enable social scientists to develop theoretically relevant measures of neighborhood attributes at multiple spatial scales. Kriging is a spatial interpolation method designed to estimate values at nonobserved locations using the spatial autocorrelation structure of values obtained from a smaller sample of observed locations and can be used to model the continuous spatial variation of attributes over space. We demonstrate how this technique can be combined with the ecometric measurement method to provide spatially smooth, city block–level estimates of theoretically relevant measures of neighborhood environments.

We first take information about the level of physical disorder present in a sample of 1,663 city blocks from the city of Chicago and use kriging to estimate the level of physical disorder on unsampled blocks. We then cross-validate city block–level estimates of physical disorder obtained using kriging with the known values from sampled blocks to demonstrate its effectiveness. Finally, on the basis of the city block–level estimates of physical disorder on the over 24,000 blocks in the city of Chicago, we aggregate city block–level measures of physical disorder to three different spatial scales and show that the relationship between physical disorder and residents’ perceptions of their neighborhood (a resident’s fear of walking alone at night, perceived physical disorder, and perceived social disorder) vary substantially across those three scales. We conclude by discussing the implications and limitations of this method for measuring neighborhood environments.

2. THEORY AND MEASUREMENT OF NEIGHBORHOOD ENVIRONMENTS

2.1. Emergence of Neighborhood Effects Research

A long tradition of sociological research has conceived of the city as a living laboratory and used neighborhoods as a unique vantage point from which to study the role of structural influences on the lives of individuals (DuBois [1899] 1996; Gieryn 2006; Park and Burgess [1925] 1984; Suttles 1972). Interest in exploring the relationship between neighborhoods and the individual life chances of residents was renewed by debates about the rise of the “urban underclass.” Many of the explanations of poverty given up to the debate regarding the urban underclass focused on individual pathologies and cultural deficiencies—a “culture of poverty” (Lewis 1959)—to explain the persistence of urban poverty. Wilson (1980, 1987) and Massey and Denton (1993) countered this dominant trend and reshaped the debate by highlighting how structural factors that concentrated the poor into geographically and socially isolated neighborhoods limited the ability of residents to improve their life chances. Although they disagreed about which structural factors were most important, their debate recast the frame in which the causes and consequences of urban poverty were viewed. In pointing to the structural causes of urban poverty and demonstrating how residential contexts constrain individual agency, they helped reinvigorate the debate about the influence of contextual factors on individual outcomes.

Building on this long tradition and especially Wilson’s (1987, 1996) hypothesis of material deprivation, a great deal of research followed as investigators expanded the number and diversity of outcomes they studied for evidence of neighborhood contextual effects. With the aid of advances in geographic information system software and the development of multilevel statistical modeling techniques that allow proper statistical inferences, studies have increasingly been designed to examine factors that influence individual outcomes at both the individual and neighborhood levels (Morenoff et al. 2007; Sampson et al. 1997; Sastry et al. 2006). Building on work that had investigated neighborhood factors that predict crime, this research has expanded dramatically to include, among others, educational, psychological, and health-related outcomes (for reviews, see Entwisle 2007; Leventhal and Brooks-Gunn 2000; Sampson et al. 2002).

2.2. Measurement of Neighborhood Environments

Although the scope of neighborhood research is expanding to include more outcomes of interest, the measures used to characterize neighborhoods have remained limited. Researchers have relied almost exclusively on data from the census to measure neighborhood residential environments and, even among those variables available in the census, have predominantly relied on a single characteristic, economic disadvantage, to explore neighborhood effects (Entwisle 2007). Relying on census data to characterize neighborhood conditions has also meant that researchers have typically relied on census boundaries (e.g., census tracts) to define neighborhoods. Although researchers have developed specific hypotheses about neighborhood characteristics that negatively (e.g., disorder, crime) or positively (e.g., walkable environments, access to retail) affect residents, the lack of data specifically measuring those characteristics limits their ability to test the specific hypotheses.

2.2.1. SSO of Neighborhood Environments

To overcome the limitations of existing data, researchers have started to develop innovative methods for measuring aspects of the residential environment. These have included using geocoded data from secondary sources (e.g., municipal business registries and commercial business listings) to measure local conditions (Bader et al. 2010; Laraia et al. 2004; Moore and Diez Roux 2006; Rundle et al. 2009), fielding supplemental surveys querying independent samples of respondents about neighborhood conditions (Auchincloss et al. 2007; Sampson et al. 1997), and using trained observers to obtain systematic observations of physical and social conditions of the neighborhood environment (Pikora et al. 2003; Reiss 1971; Sampson et al. 1997). The “nonroutine” (Cummins et al. 2005) data obtained from these methods allow researchers to test hypotheses about relationships between specific attributes of the neighborhood environment and individual-level outcomes that cannot be investigated using the more routine measures available from the census.

Among the methods used to collect nonroutine sources of data, SSO is particularly useful for measuring physical characteristics of the residential environment because it allows researchers to define important elements of neighborhood environments, such as physical signs of disorder, building upkeep, and the condition of sidewalks and paths. In this method, trained observers rate the conditions of the physical environment using an SSO instrument that is designed by investigators (Reiss 1971). Researchers can use the ratings obtained from conducting the SSOs on a sample of locations (e.g., streets or city blocks) within neighborhoods (e.g., census tracts) to compare the condition of neighborhood environments across all neighborhoods in a way that is analogous to using a sample of individuals to compare survey responses across groups in a population (Reiss 1971; Sampson and Raudenbush 1999). SSO is advantageous for collecting data on neighborhood environments because it can be implemented relatively inexpensively (especially in comparison with fielding a separate survey to gauge respondents’ perceptions of neighborhoods), and because the instruments are designed by the investigators, there is a great deal of latitude to determine which measures to obtain on the basis of theoretically driven research hypotheses, which is an advantage over secondary sources of data from companies or governments that are collected for purposes other than research (Caughy, O’Campo, and Patterson 2001; Pikora et al. 2003).

2.2.2. Ecometric Measurement Methods

The richness of SSO data and their flexibility to measure aspects of the environment that researchers find important are their primary strength. Unfortunately, collecting SSO data is a resource-intensive process that, although more feasible than fielding a second survey to an independent sample of respondents, limits the number of observations that can be observed. It would be very costly, for example, to conduct an SSO of every block in a large city. Therefore, the geographic scope of SSO data is necessarily limited. In response, the “ecometric” measurement framework was developed to create neighborhood-level measures from a sample of smaller geographic entities (e.g., city blocks; Mujahid et al. 2007; Raudenbush and Sampson 1999).

Developed from item response theory and psychometric measurement methods, ecometric measurement models are used to estimate scales that measure theoretically relevant latent constructs in the residential environment. The theory underlying these methods is that some characteristics of the neighborhood (e.g., physical disorder) are complex in nature and are likely to be measured better by multiple items that indicate the presence of the underlying theoretical construct than any single item. This is because any individual item that is measured is prone to measurement error. Thus, the construct we are interested in measuring (e.g., physical disorder) can be thought of as latent, in that we cannot measure it directly but can measure it only through the multiple manifest indicators that are actually observed. Furthermore, some of the items indicate a greater presence of the latent variable than others (e.g., although litter and drug paraphernalia both indicate disorder, the latter is likely to indicate a more severe level of disorder than the former). Ecometric measurement models are designed to aggregate these measures from multiple items at multiple locations within a neighborhood to a neighborhood-level measure that can successfully discriminate between neighborhoods. In doing so, the resulting ecometric scale adjusts for both measurement error in the reporting of individual items and random variation across the multiple locations sampled within neighborhoods, and items in the scale are weighted by the severity of the items that are observed within neighborhoods (Raudenbush and Sampson 1999; Sampson and Raudenbush 1999). Because the measures are created at the neighborhood level and adjust for measurement error in aggregation to the neighborhood unit of analysis, this also means that the measurement properties of the scale, such as the reliability and intraclass correlation, are appropriately assessed at the neighborhood level (Mujahid et al. 2007).

2.3. Moving Beyond Administrative Neighborhood Boundaries

Although some researchers have focused on the problems associated with using only basic neighborhood demographic and economic data in analyses, others have highlighted the potential problems inherent in the dominant practice of using census administrative boundaries to define neighborhoods. Census tract boundaries, by far the most common geographic definition of neighborhood boundaries, can vary greatly in size in a way that can change the meaning of “neighborhood” significantly for people living in different areas (Lee et al. 2008). Although efforts are made to respect local ecological boundaries and define socially and economically homogeneous areas, census tracts are, ultimately, administrative units used to facilitate collection and tabulation of data (U.S. Census Bureau 1994). The definitions of neighborhood boundaries to which data are aggregated have been shown to have effects on the statistical conclusions drawn about social processes (Hipp 2007), a problem known in the geographical literature as the “modifiable areal unit problem” (Fotheringham and Wong 1991).¹ In response, investigators have proposed theoretically derived neighborhood boundaries including, for example, neighborhoods defined by the local street network (Grannis 1998) or the walking distance of a typical adult (e.g., 400 meters) around a resident’s home (Pikora et al. 2002). Others have considered neighborhood definitions on the basis of what individual respondents report as their neighborhoods (Coulton et al. 2001; Talen 2000). All of these different definitions of neighborhood boundaries, based on the social processes under investigation rather than administrative convenience, potentially improve the measurement of the neighborhood spaces at which researchers believe residents are exposed over the traditional administrative boundaries of census tracts.

2.3.1. Spatial Inflexibility of the Ecometric Framework

These concerns expose the greatest problem of the ecometric measurement framework: despite the promise the ecometric framework offers to improve neighborhood research through the development of theoretically nuanced measures, the resulting measures are inflexible to definitions of neighborhood boundaries other than those on which researchers initially sampled. Because the ecometric framework relies on sufficient within-neighborhood samples to be able to decompose variance into measurement error (within-neighborhood variance) and “true” neighborhood variation (between-neighborhood variation), it is difficult to use neighborhood boundaries other than those used by researchers to develop the sampling frame. As researchers continue to explore the effects of spatial scale and neighborhood definitions on individuals’ outcomes and behaviors, this inflexibility presents two problems for some topics of inquiry.

The first problem is that ecometric models assume that the best way to represent the neighborhood environment affecting individual outcomes is by using discrete ecological units. Although the ecometric approach can account for the clustering of observations within these discrete ecological units, the measurement within these entities is assumed to capture a spatially constant process within the neighborhood boundaries (Chaix et al. 2005). The ecometric framework assumes that any variation that exists across different sampled units (e.g., city blocks) within ecological neighborhoods (e.g., census tracts) is random measurement error. Chaix et al. (2005) found that the strength of the relationship between neighborhood deprivation and substance abuse related disorders increased at smaller spatial scales and that the strongest relationship existed at a scale smaller than administrative boundaries.

The assumption that all variation that exists within neighborhoods is due to measurement error is compounded by the fact that the ecometric measures require neighborhoods to be drawn before observations are made to develop appropriate within-neighborhood sample sizes. Although relevant for some outcomes of study, particularly those for which well-developed theory exists that matches the social process being studied to the proper ecological unit (Sampson 2008), the expanded use of the ecological framework presents two challenges to deployment in current social scientific studies. First, it assumes that variation at a scale smaller than the neighborhood definition can be attributed to measurement error. Second, many social scientific and health studies include multiple outcomes (e.g., the L.A. Family and Neighborhood Study, the Health and Retirement Study, the National Longitudinal Study of Adolescent Health). Risks at different spatial scales might matter for different outcomes within the same study, suggesting that permitting more flexible definitions of neighborhood boundaries might be warranted. In addition, even within the same study, the relationship between neighborhood attributes and individual outcomes might vary for different subpopulations (e.g., elderly or mobility-impaired residents might be influenced by more local conditions than younger or able-bodied residents).

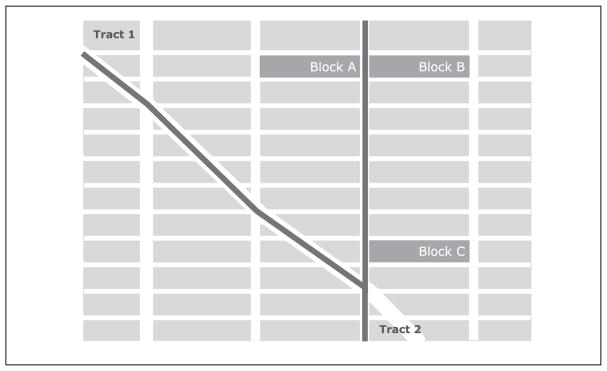
The diagram depicted in Figure 1 can help illustrate this problem. In this schematic diagram, census blocks are represented by gray blocks created from the network of streets, represented using white lines, with each block belonging to a tract that is demarcated by black lines. In the figure, there are three highlighted blocks: Block A falls in tract 1 and is adjacent to block B, which falls in tract 2 because the street separating the two blocks is the border between tracts 1 and 2. Block C is some distance away from blocks A and B but still falls inside tract 2. If we are measuring some characteristic of the environment using ecometric models, say physical disorder, the assumptions above mean that the values obtained for the adjacent blocks (A and B) are, statistically speaking, independent of each other, whereas the measures of physical disorder for the distant blocks that fall in the same tract (B and C) are exactly the same. However, it is likely that adjacent blocks are more similar to each other than distant blocks, and measures of the residential environment should be able to capture the reality of this physical proximity. Although large ecological boundaries (e.g., large streets, rivers, highways) might create socially meaningful boundaries, most blocks in a city do not sit on such boundaries. If we are measuring residents’ exposure to some environmental characteristic such as physical disorder, then these assumptions mean that the exposure to physical disorder of residents living on block A are, statistically speaking, independent of the exposure on block B, whereas respondents living on block B and block C are assumed to have the exact same exposure.

Figure 1.

Diagram of a hypothetical neighborhood with streets and tract boundaries drawn.

Recent methods developed by Savitz and Raudenbush (2009) have relaxed the assumption that neighboring tracts are statistically independent and shown that using the spatial dependence between ecological units (e.g., tracts 1 and 2 in Figure 1) can be used to improve ecological measures of neighborhood attributes. This means that the level of exposure for residents of block A is assumed to be correlated with the exposure experienced by residents of block B. Yet even within Savitz and Raudenbush’s spatial dependency framework, any differences between blocks B and C are assumed to be measurement error within tract 2, not the difference in levels of disorder that exists because of changes in the physical environment that occur over the distance that separates block B from block C.²

The second and related problem is that defining neighborhood boundaries a priori assumes that all relationships between individual outcomes and behaviors will be influenced by neighborhood contexts at the same spatial scale or using the same neighborhood definition. Most observational studies in the social sciences are fielded to examine multiple outcomes. As the number and diversity of outcomes being investigated for neighborhood contextual effects increases and surveys are fielded that measure multiple outcomes, the lack of flexibility in neighborhood definitions is becoming a more pressing problem for neighborhood research. It is unlikely that all outcomes being studied are influenced by neighborhood context at the same spatial scale or that the same spatial scale is appropriate for all residents. The appropriate area of influence may vary by outcome, requiring flexibility in the definition of neighborhood boundaries. Therefore, having a single definition for neighborhood units of analysis that is defined before entering the field increases the chances that the spatial extent of neighborhood context is misspecified for at least some subset of the outcomes in a survey. Furthermore, not only might misspecification occur for different outcomes, but it is also entirely possible that the appropriate neighborhood definition might differ across subgroups. For instance, smaller neighborhood contexts might matter more for groups with limited mobility—young children, the elderly, disabled residents—than groups with less restricted mobility.

We should hasten to add that these are not problems associated only with ecometric models but are problems of all models that use ecological units to define neighborhoods, including those that use census boundaries and census data (Hipp 2007; Lee et al. 2008). In fact, by parsing the variance in measurements between the level of observation (e.g., street or face-block) and the neighborhood-level ecological unit, ecometric measures are less susceptible to the problem of small-scale variability than studies that naively aggregate observations to larger ecological units; however, in that they assume that neighborhoods are internally homogeneous and spatially independent units, these methods are limited in their ability to capture the true extent of small-scale variability in residential contexts.

2.3.2. Measuring Theoretically Relevant Characteristics at Multiple Spatial Scales

Researchers who have highlighted the problems of using administrative boundaries to represent neighborhoods have investigated alternative, theoretically derived neighborhood definitions using data that are available at the city-block level. Sociologists focusing on the importance of neighborhood definitions have typically focused on racial composition of neighborhoods and do so because racial composition measures are available at the census-block level. The availability of racial composition data at the census-block level permits larger scale neighborhood definitions that can be reconfigured by researchers almost at will. For example, Grannis (1998) examined the potential misspecification of neighborhood boundaries and argued that neighborhoods bounded by small, walkable streets are a superior level of aggregation than larger census tracts and examined this proposition by studying levels of racial residential segregation. Similarly, Reardon et al. (2008) studied how estimates of being racially isolated vary substantially depending on the spatial scale of neighborhoods that are used.

Some researchers have moved beyond using just census data and have obtained other administrative or commercial data available at small levels of aggregation. For example, a large body of research has emerged examining the influence of neighborhood commercial environments on individual health outcomes and behaviors (Moore et al. 2008; Rundle et al. 2009). Using data obtained from city governments or business data vendors, researchers have used geographic information system software to geocode street addresses of food stores (e.g., grocery stores, fruit and vegetable markets, fast food restaurants), recreation facilities (e.g., parks, running and biking trails), and other local amenities to examine how the presence or density of these features affect outcomes such as obesity, fruit and vegetable intake, and physical activity. Many of these studies have used buffers of varying sizes surrounding respondents’ homes on the basis of either Euclidean or street network–based measurements to examine how the built environment affects health outcomes (Rundle et al. 2009).

By using different neighborhood definitions on the basis of their theoretical relevance to the outcome under investigation, these studies have helped neighborhood researchers understand the importance of neighborhood definitions, but the measures these studies use generally have only very basic information. Because researchers have only very basic data, it is difficult to develop theoretically motivated measures of neighborhood environments. For instance, although researchers can detect clustering by racial composition or know the types of stores surrounding a respondents’ house, they cannot measure more nuanced attributes, such as the level of physical disorder, that the ecometric framework permits. Thus, although these measures allow researchers to flexibly define neighborhoods, they lack the flexibility to develop the theoretically motivated measures of neighborhood environments that ecometric methods permit.

Among the most advanced of these studies is that conducted by Chaix et al. (2005). Using data from a complete population of residents in Sweden that included health outcome data and the residential location of each individual, they estimated the influence of neighborhood characteristics by creating “neighborhoods” measured as the most geographically proximate individuals. They found that the influence of neighborhood characteristics varied by spatial scale and found the largest effect at the smallest scale. This is among the most sophisticated studies to examine spatial patterns of health outcomes and offers a substantial contribution; however, our approach differs in important ways that we believe will help the field progress in different ways. First, we examine neighborhood characteristics observed independently of the residents who constitute the study (in our case from ecometric measures developed from SSOs). Second, their data are relatively unique to Sweden, and similar sources (i.e., a census with geocoded addresses and health care utilization records) remain unavailable to most researchers interested in spatial influences. Our approach permits analysts to develop measures similarly adaptive to spatial scales on the basis of only a sample of locations rather than a census.

Therefore, a more flexible method with which to construct neighborhood measures would allow the nuance of the ecometric framework while permitting flexibility in the construction of neighborhood boundaries at different spatial scales. In this article, we propose a method to create theoretically relevant measures that are flexible to different neighborhood definitions by combining existing ecometric methods with the geostatistical method known as kriging that is used to create spatially smoothed estimates of an attribute measured at a sample of locations. In the following sections, we describe kriging and how its properties can be beneficial for social scientific research. Then we describe how it can be combined with an ecometric model measuring physical disorder at the city-block level to allow for the flexible construction of neighborhood boundaries and cross-validate this method. Finally, we provide an empirical example demonstrating the benefits of kriging by showing how estimates of the association between physical disorder and residents’ perceptions of fear vary substantially at three different spatial scales.

3. USING KRIGING TO MEASURE NEIGHBORHOOD ENVIRONMENTS

Kriging is a geostatistical method that uses information from a sample of locations across a study region to interpolate information at unsampled locations. It is based on a two-step process. In the first step, we determine the extent to which sampled data covary across space. If there is no spatial autocorrelation, kriging will offer no benefits; however, if there is spatial autocorrelation, we can determine the spatial covariance structure that the sampled data follow. In the second step, we use the spatial covariance structure determined in the first step to calculate a weight to the value from each sampled location. We can then obtain the interpolated value at any unsampled location by summing across the products of each sampled value with its corresponding weight. This can be depicted schematically as follows:

$$(\text{Interpolated}\text{Value})=\sum [(\text{Value}\text{Measured}\text{at}\text{Sampled}{\text{Location}}_i)\times (\text{Weight}\text{for}{\text{Location}}_i)].$$

For every unsampled point we are estimating, we recalculate the weights applied to the sampled locations to reflect the unique distance vector from the unsampled location to each of the sampled locations. As we show later, the weight applied to each sampled location is directly proportional to the proximity of that sampled location to the point being estimated and inversely proportional to the proximity of that sampled location to other sampled locations. Using this method, any point in the study region can be estimated on the basis of the weights applied to the sampled values, and if many points across the study region are estimated, we can create a smoothed surface of attribute values across the entire study region.

Our objective in the current analysis is to obtain estimates of physical disorder on the more than 24,000 blocks in the city of Chicago; however, we have measures of physical disorder only for a sample of 1,663 blocks. Thus, we use the information about physical disorder we have from the sampled blocks to derive estimates for each of the unsampled blocks. Kriging was developed to handle a similar problem in natural resource exploration (Matheron 1963) and has been used to investigate problems in epidemiology (Auchincloss et al. 2007; Jerrett et al. 2005) and real estate prices (Basu and Thibodeau 1998; Dubin 1992).³ In the sections that follow, we describe the properties of kriging that make it an attractive application for measuring neighborhood environments and provide a brief overview of the method.

3.1. Properties of the Kriging Method

Kriging has several properties that make it particularly useful for measuring neighborhood environments. The first property that makes kriging attractive for interpolating values at unknown locations is that the spatial covariance structure used to interpolate those values is derived from the data themselves. This means that one uses the empirical data from the sampled locations to estimate the spatial correlation or spatial covariance structure. This data-derived method of uncovering how points are spatially autocorrelated stands in contrast to other spatial interpolation methods that weight observations by an assumed decay function, such as inverse distance, inverse distance squared, or Gaussian decays. In fact, as we have mentioned, and as we describe in more detail below, the first step to implement kriging is to evaluate the covariance of sampled locations as a function of the distance separating those observations. For processes for which a known or strongly theorized spatial decay function exists, the data can be evaluated against this function as a validity check; however, for the vast number of other outcomes for which a known or theorized spatial decay function does not exist, the function can be derived empirically.

The second attractive property is that it is an exact interpolator, meaning that the estimated value of a sampled point is exactly equal to the observed value at that point. Again, this stands in contrast to methods such as inverse distance weighting, in which the value at a sampled point is undefined (because one cannot divide by a separation distance of zero). Beyond the theoretical value of having a single function that can describe the entire study surface, having an exact interpolator has the added practical benefit that it is not necessary to add an additional step of substituting measured values at the end of the interpolation process.

The third beneficial property of kriging is that it provides both an estimate of the value at any location in the study region as well as an estimate of the error surrounding the estimated value. These errors provide a considerable advantage over other methods of spatial interpolation because analysts can determine the confidence with which they predict a value at any given point in the study region. With this information, researchers can target areas where they can collect more data if the survey is still in the field or, by knowing which locations have more measurement error, interpret results from those particular locations with more caution.

3.2. How Kriging Works

To describe how kriging can be usefully applied to research on neighborhood environments, we provide a brief introduction to the concepts and calculations used in this method. This introduction is not intended to be comprehensive but is instead intended to provide enough of the background to understand its particular application to the measurement of neighborhood environments.⁴ As we have mentioned, kriging can be understood as a two-step process. The first step determines if and how the sampled data covary across space. Determining this spatial covariance is necessary to first determine if kriging is a useful methodological tool for a particular problem and, second, uncover the functional form of the spatial covariance structure among the sampled locations. The second step, interpolating the values, is accomplished through weighting the measured observations at each of the sampled locations to generate estimates of the attribute at the nonsampled locations.

3.2.1. Determining If and How the Sampled Data Covary across Space

To examine if and how the data covary across space, we use an instrument called a variogram. A variogram visually depicts the amount of variation between the values measured at two sampled points as a function of their separation distance. Formally, for any point, x, separated from another point by distance h, the variogram function can be estimated as

$$\mathrm{\gamma }(h)=\frac{1}{2}E[{(Z_{x+h}-Z_x)}^2],$$ (1)

where γ(h) is the value of the variogram for any two points separated by a distance h, E[·] is the expectation operator, Z_x is the measurement of the attribute at point x, and Z_{x + h} is the value of the measurement separated from the point x by the distance, h. To assess the spatial dependence in the sampled data, we calculate this variogram value for all $\frac{n\times (n-1)}{2}$ pairs of sampled locations and then plot the value by the distance that separates the two points. The resulting $\frac{n\times (n-1)}{2}$ pairs of points are plotted in a “variogram cloud”; however, with so many data points, it is difficult to assess whether and how the values at sampled locations covary over space. Therefore, to determine the functional form of the variogram, we average the variogram values within bins defined as equal intervals of separation distance, also known as the “lag distance.” The averaged values within bins are then plotted at the midpoint of the separation distance to provide an “empirical” or “sample” variogram function.⁵ After creating this empirical variogram, a functional form of the variogram, γ(h), that fits the form of the empirical variogram can be determined.

3.2.2. Interpolating Values

As we mentioned previously, the values of the physical attribute are estimated at any location by calculating a weight to each of the sampled locations. The weights are based on the spatial structure and are determined through the creation of the variogram in the previous step and are described in more detail below. The particular value at any location is simply the summed products of the measured value at the sample locations and the sampled locations’ corresponding weight. This can be expressed as

$$z_0^{\ast }={\mathbf{\lambda }}^{\mathrm{T}}\mathbf{z},$$ (2)

where $z_0^{\ast }$ is the estimated value at a particular location of the attribute being estimated; λ is a vector of weights at each of N sampled locations, λ = {λ₁, λ₂, …, λ_N}; and z is a vector of measured values of the attribute for each sampled location, z = {z₁, z₂, …, z_N}.

3.2.3. Calculating the Weights

The weights used to calculate the interpolated value are based on the function estimated from the variogram determined in the first step. More precisely, the weights are based on the spatial covariance, σ(h), which, for a stationary process, can be calculated as

$$\mathrm{\sigma }(h)=\mathrm{\sigma }-\mathrm{\gamma }(h),$$ (3)

where σ(h) is the covariance at a separation distance of zero and γ(h) is the variogram function calculated from equation (1). A stationary process is one in which the covariance between two points varies only as a function of the separation distance between two points. This implies that the attribute has a spatially constant variance around a constant, if unknown, mean.

Using this covariance function, the vector of weights is calculated for every location at which a value of the attribute is being interpolated. It can be shown that the interpolated value from equation (2), $z_0^{\ast }$, is the best linear unbiased estimate on the basis of the spatial covariance using the following system of equations:

$$\begin{array}{c}\left[\begin{array}{cccc}{\mathrm{\sigma }}_{11}& \cdots & {\mathrm{\sigma }}_{1N}& 1\\ ⋮& \ddots & ⋮& ⋮\\ {\mathrm{\sigma }}_{N1}& \cdots & {\mathrm{\sigma }}_{NN}& 1\\ 1& \cdots & 1& 0\end{array}\right]\\ \mathbf{A}\end{array}\begin{array}{c}\left[\begin{array}{c}{\mathrm{\lambda }}_i\\ ⋮\\ {\mathrm{\lambda }}_N\\ -\mathrm{\nu }\end{array}\right]\\ \mathbf{X}\end{array}=\begin{array}{c}\left[\begin{array}{c}{\mathrm{\sigma }}_{01}\\ ⋮\\ {\mathrm{\sigma }}_{0N}\\ 1\end{array}\right]\\ \mathbf{B}\end{array}.$$ (4)

The values, σ_ij, in the cells of matrix A are determined by the spatial covariance function, σ(h), for the distance h (equation 3), that separates sampled point i from sampled point j, while the values of the cells in matrix B, σ_0i, equal the value of the covariance function for the separation distance between the point being estimated and the sampled point, i. Because the values of λ_i and ν (the weight assigned to sample location i and a Lagrange multiplier to constrain the sum of the λ_i values to 1, respectively) are the only unknowns in the system, one can solve for the vector X to obtain the weights and constraint. The first N elements of the vector X constitute the vector of weights, λ, introduced in equation (2) and can now be used to calculate the interpolated value.

From the system of equations above, one further beneficial property unique to kriging bears mentioning now that the process of estimation has been described. To solve for the matrix X, we multiply the inverse of matrix A by matrix B (i.e., X = A⁻¹B). Remembering that the value of the covariance function, σ(h), is larger as separation distance decreases, one will notice that the kriging weights, λ, are based on two pieces of information. First, the weights are directly proportional to the proximity of a sampled location, i, to the location of the point at which the value is being interpolated. This can be seen because the values of σ(h) in the elements of matrix B are larger the closer they are to the sampled location, i, and the matrix B is proportional to the value of element i in vector X. Second, taking the inverse of matrix A indicates that the weights are inversely proportional to the proximity of sampled locations with each other because the value of the element ij in matrix A is larger the closer the two sampled locations are to each other, and the value of matrix A is inversely proportional to the value of X. This means that kriging not only accounts for the spatial proximity of the point being estimated to the sampled points but also weights spatially clustered sample locations less heavily so that the interpolated value is not inflated by assuming that each sampled point provides independent information to be used in the interpolation. In other words, the weight assigned to each sampled location is penalized not only for its distance from the point being estimated but also for providing less unique spatial information if it is close to other sampled points that provide information.

3.2.4. Assumptions

This type of estimation is formally known as “ordinary kriging” and is used for the estimation of stationary random functions. As mentioned previously, stationarity implies that there is a constant mean throughout the study region (i.e., first-order stationarity), assuming that the measured values of the attribute at the sampled locations are independently and identically distributed. Ordinary kriging also assumes that the variance of the attribute is constant throughout the entire study region (i.e., second-order stationarity). On the basis of these assumptions, the variance of the estimates (i.e., the estimation error) can be estimated as

$${\mathrm{\sigma }}_{\text{OK}}^{2\ast }={\mathrm{\sigma }}_{00}-{\mathbf{\lambda }}^T{\mathbf{\sigma }}_{\mathbf{0}}+\mathrm{\nu },$$ (5)

where σ₀₀ is the value of the covariance function at a separation distance of zero. Methods have been developed that relax assumptions about a constant mean, constant variance, and normality, though they are beyond the scope of this article (for more information, see Chiles and Delfiner 1999; Isaaks and Srivastava 1989).

4. KRIGING NEIGHBORHOOD PHYSICAL DISORDER

Now that we have described the properties of kriging that make it beneficial to estimating a spatially smooth surface of an attribute, we turn our attention to demonstrating how it can be combined with the ecometric measurement framework. To do so, we develop city block–level measures of physical disorder derived from an ecometric measurement model and on the basis of data collected through SSO in Chicago.

4.1. Measuring Physical Disorder

The physical disorder data for the present study come from the SSO component of the Chicago Community Adult Health Study (CCAHS). The CCAHS is a multistage area probability sample of 3,105 adults living in Chicago between May 2001 and March 2003. The sample was stratified into 343 neighborhood clusters (NCs) defined in the Project on Human Development in Chicago Neighborhoods (PHDCN) as one or more geographically contiguous census tracts that were joined on the basis of the demographic characteristics of the population, local knowledge of the city’s neighborhoods, and major ecological boundaries (Sampson et al. 1997).

The SSO was developed on the basis of the instrument used by the PHDCN (Raudenbush and Sampson 1999; Sampson and Raudenbush 1999); however, unlike the PHDCN SSO, the CCAHS SSO was conducted in all 343 NCs in the city of Chicago by trained research staff members walking around sampled blocks (the PHDCN SSO used video cameras mounted inside of vehicles). In total, 1,663 blocks were observed, containing 13,251 face-blocks. A face-block is a single side of a street that forms the boundary of a block; a typical block is bounded by four sides and, because each side of the street is a face-block, has eight face-blocks. There was an oversample of blocks from 80 “focal” neighborhoods on the basis of the NCs that were observed in the PHDCN SSO.

The 1,663 blocks that were systematically observed become the sampled blocks in the kriging model. Therefore, we require measurements of physical disorder at those locations to estimate values on the other city blocks in the city of Chicago. We take advantage of the benefits of the ecometric measurement methods described previously—the ability to combine, empirically weight, and estimate measurement error on multiple items—by creating ecometric scales of physical disorder at the city-block level. The value of the physical disorder scale and geographic coordinates can then be used to create the spatially continuous kriged measures that were described in the previous section.

The physical disorder scale is virtually identical to that used by Raudenbush and Sampson (1999) in their introduction of the ecometric framework. The scale is composed of nine items measuring the presence of markers signaling physical disorder in the environment: (1) garbage, litter, or broken glass; (2) cigarette or cigar butts or discarded cigarette packages; (3) empty beer or liquor bottles; (4) gang graffiti; (5) other graffiti; (6) evidence of graffiti painted over; (7) abandoned cars; (8) discarded condoms; and (9) needles, syringes, or drug-related paraphernalia. Raters marked whether each of these nine items was present on each face-block in a block. Then, a three-level item response model was constructed to measure the level of physical disorder on the block on the basis of these nine items:

$${\mathrm{\eta }}_{\mathit{ijk}}={\mathrm{\pi }}_{000}+\sum _q^8{\mathrm{\pi }}_{q00}{X}_{\mathit{ijk}}+\sum _t^5{\mathrm{\pi }}_{00t}{T}_{tk}+r_{0jk}+u_{00k},$$ (6)

where η_ijk is the log odds of an item i being present on face-block j on block k, and π_q00 is the item severity of item i that is measured by the dichotomous indicator X_ijk for eight of the nine items (garbage and litter were used as the reference item). All items were centered on their grand means, making π₀₀₀ the conditional mean level of disorder on the average block. The face-block and block random components, r_0jk and u_00k respectively, are normally distributed around means of zero and variances τ and Ω, respectively. Because some indicators of disorder are likely to vary by the time of day, the models also include a series of dichotomous indicators, T_tk, that measure the independent influence, π_00t, of the time of day the block was observed.

The level of physical disorder on an individual block, z_k, can be obtained by adding the fitted value of the model to the block-level random component of the multilevel item response model in equation (6):

$$z_k={\mathrm{\eta }}_{\mathit{ijk}}^{\ast }+u_{00k}.$$ (7)

A histogram of the physical disorder variable (not shown) revealed that the variable was approximately normally distributed. We use the geographic coordinates at the block centroid as our location of measurement for each city block j. Because the locations of the sampled blocks are known, the vector of values of physical disorder at sampled locations, z = {z₁, z₂, …, z_K}, can now be used to calculate the variogram and estimate the values at unsampled locations in the city.

Using block centroids does introduce some level of imprecision into measurement; however, we feel that it is justified for two reasons. First, blocks are an appropriate basic human ecological level from which to build measurements in an urban setting. Second, developing estimates at any smaller level (e.g., streets) quickly increases the number of calculations, and given that blocks are created by the street grid, it does not significantly improve the spatial precision of measurement.

4.2. Validation of Kriging Physical Disorder

To validate the kriged values of physical disorder, we randomly divide the blocks from the SSO data into thirds and use the values of physical disorder on the first two thirds (n = 1,108) to predict the value of physical disorder on the remaining third of blocks (n = 555) so that we can then compare the predicted values with the measured values on the reserved third of blocks. Using the coordinates at the centroids of each of the blocks (as we describe above), in the first subset as the sampled locations, we calculate the variogram and kriged estimates of physical disorder at the location of each of the block centroids for the reserved third of SSO blocks. We then compare the estimates calculated by kriging to the measured values at the reserved locations to determine how well kriging estimates the value of physical disorder at unsampled locations.

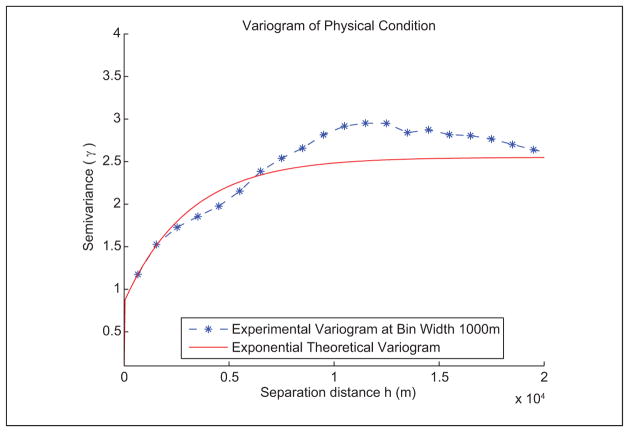
A plot of the variogram can be viewed in Figure 2. This figure shows the empirical variogram at a lag distance of 1,000 meters for the points in the larger subset of sampled blocks as well as the theoretical variogram. The value of the variogram is plotted for all pairs of block coordinates on the vertical axis against the separation distance between the pairs of coordinates in the horizontal axis. The empirical variogram is created by taking the mean value of the plotted points falling within successive 1,000-meter bins plotted at the midpoint of the bin. This summarizes the empirical distribution of the spatial correlation in the raw data. On the basis of this empirical diagram, it appeared that an exponential functional form was best suited to model physical disorder over space.

Figure 2.

Variogram of physical disorder with experimental variogram at bin width 1,000 meters and exponential theoretical variogram (see equation 8).

We determined that an exponential functional form best fit the data on the basis of the evidence from the empirical variogram that the spatial variance increased over separation distance until leveling off at the sill. Three common functions follow this pattern: exponential, spherical, and Gaussian. We eliminated a Gaussian model because it assumes that spatial variation is smooth enough to be differentiable near the origin, an assumption we could not make given occasional discontinuities at close separation distances. Neither the spherical nor exponential model assumes that the underlying spatial process is smooth enough to be differentiable, and thus either might be appropriate for our purpose. We chose an exponential function because it assumes that the spatial variation gradually tapers as separation distances approach the sill, whereas a spherical model assumes a sharper transition at the sill. Because there is no theoretical evidence for a sharp transition at a particular bandwidth, we used an exponential model.

The spherical functional form is described with the following equation:

$$\mathrm{\gamma }(h)=b+c\left(1-exp\left\{-\frac{h}{a}\right\}\right)\text{where}b=\{\begin{array}{ll}{b}_{\mathrm{s}},\hfill & h>0\hfill \\ b_{\mathrm{m}},\hfill & h=0\hfill \end{array}.$$ (8)

Using this functional form, the value of a is one third of the practical range, meaning that the distance at which the spatial covariance so closely resembles zero that no spatial variation can be said to practically exist beyond that point. The value of c, called the “sill,” is the asymptotic limit as the separation distance, h, moves toward infinity minus b, called the “nugget effect.”

The nugget effect, named because in geological applications it would often be possible to discover nuggets of ore without a larger deposit, reflects the sum of two components. The first is the small-scale variability in the data, b_s, that is at a spatial scale that is too small to be captured by the sample taken. This would reflect, for instance, the variability between two streets on the same block. The second component of the nugget effect is the measurement error in the instrument, b_m. Because the instrument (the ecometric scale based on the items rated in the SSO) imperfectly measures the latent construct of physical disorder, we must also account for the error surrounding the estimate even at measurement locations.⁶ As an approximation of the measurement error, we used the overall block-level scale reliability of the ecometric scale, which was 0.928 in the CCAHS sample.⁷ Therefore, we considered 92.8 percent of the nugget effect to be due to very small scale variation and the remaining 7.2 percent to be attributable to measurement error. We estimate the values of the variables in the theoretical variogram to be a = 3,100, b_s = 0.79, b_m = 0.06, and c = 1.70.⁸

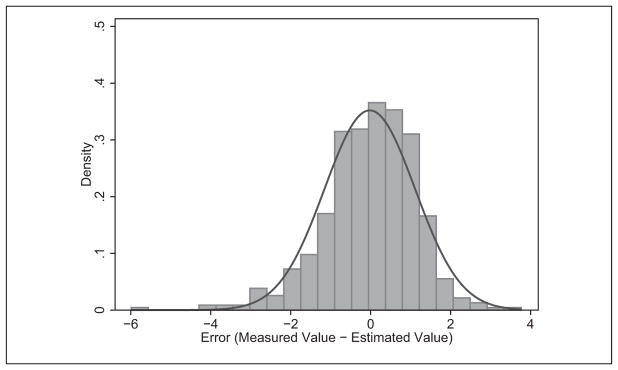
Using the variogram function estimated in the previous step, we calculated the covariance function using equation (3). On the basis of this covariance function, we estimated the values at the location of each of the 555 reserved blocks using the subset of 1,108 blocks as our sampled locations. To assess how closely the kriged estimates reproduced the values at the 555 reserve locations, we subtracted the estimated value of physical disorder from the measured value of physical disorder to obtain the errors. A histogram of these errors is shown in Figure 3 along with a plot of the normal distribution. The errors approximate a normal distribution around a mean of −0.02. In addition to the estimate, we obtained the variance of each estimate on the basis of equation (5). Using this value, we calculated the 95 percent confidence interval for each location and found that 525 of the 555 measured values (94.6 percent) fell within the 95 percent confidence intervals. At 43 percent of the 555 validation locations, the error between predicted and measured values was less than 0.5 standard deviations of the observed values at those 555 locations, while 75 percent were within 1 standard deviation. These statistics indicate that kriging performs well at estimating the value of block-level physical disorder.

Figure 3.

Histogram of error between interpolated and measured value of physical disorder on reserved sample of blocks.

Several concerns might arise from these validation estimates. First, one might expect that points more proximate to other points to be either more accurately or precisely estimated, especially because blocks in particular neighborhoods were oversampled. To examine this possibility, we calculated the mean distance to the five sampled points nearest to a point being validated. We then binned validation points into deciles on the basis of this measure and calculated the mean error and variance for validation points falling within each bin. Figure 4 plots the results at the midpoint of each bin. The results demonstrate that neither the mean nor variance change substantially as a point becomes more distant from neighboring points.

Figure 4.

Mean and variance of errors obtained by subtracting estimated values from observed values on 555 reserved blocks by deciles of the average distance to the five nearest points.

A second concern that arises from combining city block–level ecometric estimates with kriging interpolation is that the estimates tend to smooth over a substantial amount of variance. We compared the variance of the kriged estimates on the reserved 555 blocks with the variance of the measured values at those same locations. We found that the variance of the kriged estimates was 1.45, whereas the variance of the measured values was 2.69, an approximately 46 percent reduction in the variance. For comparison, we estimated the NC values of disorder based only on the 1,108 sampled locations. Assigning the reserved blocks the value estimated for the NC results in the same variance loss. The variance of the reserved blocks was also 1.45 but was based on only 534 blocks, because six NCs contained no blocks in the sample of 1,108 locations.

In subsequent analyses that use interpolated values, the reduction in variance could artificially increase the confidence with which we make conclusions about results using the interpolated values. To solve this problem, we would be able to develop simulations, or “conditional realizations,” of city block–level estimates that account for the underlying spatial covariance structure between the blocks being estimated (Lantuéjoul 2002). These simulations will then be used as imputations in a multiple imputation framework to reduce the influence of measurement uncertainty from the interpolated measures.

5. SPATIAL SCALE OF EFFECTS OF PHYSICAL DISORDER ON PERCEPTIONS OF FEAR AND DISORDER

Thus far, we have described the method of kriging and how it can be used with the ecometric measurement framework to provide valid city block–level measures of physical disorder within an urban environment. Now, we turn our attention to demonstrating how this combination of kriging and the ecometric framework can be used to study the how relationships between the neighborhood physical disorder and individual-level perceptions of neighborhood safety vary at different, and relatively small, spatial scales.

5.1. Relationship between Observed Physical Disorder and Fear, Perceived Physical Disorder, and Perceived Social Disorder

Physical disorder has been connected to multiple individual- and neighborhood-level outcomes (Chang, Hillier, and Mehta 2009; Ross and Mirowsky 2001; Sampson et al. 1997), and one path through which disorder is thought to influence individual-level outcomes is by invoking fear in residents (Ross and Jang 2000). As physical signs of disorder in a neighborhood increase, residential environments seem more disorganized and become less hospitable for residents who might then fear being out and about in their neighborhoods (Ross and Mirowsky 2001; Sampson et al. 1997). This process can reduce the size of social networks, limit the capacity of neighborhood residents to confront neighborhood problems, and reduce structural investment in neighborhoods (Bursik and Grasmick, 1993; Ellen 2000; Sampson and Raudenbush 2004; Taub, Taylor, and Dunham 1984). However, perhaps just as important, the presence of observed physical disorder in the neighborhood does not necessarily perfectly correlate with residents’ perceptions of either physical or social disorder that might cause such behavioral responses (Ross and Mirowsky 2001; Sampson and Raudenbush 2004).

It is possible, however, that a resident’s perception of fear of—or intermediate perceptions of disorder in—his or her environment could be heightened based not on the physical disorder present in the entire ecological neighborhood but on the areas more proximate to that resident’s house. Hipp (2007) postulated such a hypothesis and demonstrated that perceptions of social disorder, physical disorder, and crime depended on the level of aggregation used in the analysis. Using block-level measures aggregated from nearby respondents acquired from a special tabulation of the American Housing Survey, he found that patterns of associations varied depending on whether he used the block as the unit of analysis or the census tract. Although the present study differs from Hipp’s,⁹ our analysis builds on his conclusion that neighborhood researchers must be careful to specify appropriate geographic scales of analysis in their research. In addition, we measure similar attributes to those he investigated in his study: measures of fear, perceived physical disorder, and perceived social disorder.

5.2. Analyzing the Relationship between Physical Disorder and Fear and Perceptions of Disorder at Multiple Spatial Scales

Despite its innovation, one shortcoming Hipp (2007:676) identified is the fact that he was limited to block- and tract-level analysis, and he claimed that “a more ideal approach would flexibly aggregate the structural characteristics to varying geographic sized areas, rather than just the block and the tract.”¹⁰ In this analysis, we demonstrate how the combination of kriging and ecometric measurement models can address this limitation and be used to examine the relationship between physical disorder and perceptions of fear and disorder at three geographic scales. The primary interest is to examine whether the small-scale variation in neighborhood conditions surrounding respondents’ homes more accurately captures the influence of physical disorder on the levels of fear and disorder respondents report. Therefore, we do not attempt to provide a complete explanatory model of associations with neighborhood fear or an exhaustive inventory of proposed neighborhood definitions; rather, we use perception of fear for neighborhoods defined as radial buffers surrounding respondents’ blocks as an example of why the spatial scale at which contextual characteristics are measured is important. We leave the examination of a more complete explanatory model of influences on neighborhood fear, as well as the influence of physical disorder on fear at alternative neighborhood definitions, to future work.

The outcome measure of fear in this analysis is the answer to the question “How safe is it to walk around alone in your neighborhood after dark?” Respondents were given four response categories from which to choose: (1) completely safe, (2) fairly safe, (3) somewhat safe, or (4) extremely dangerous. Perceptions of physical and social disorder use the same psychometric scales Sampson and Raudenbush (2004) used in their study of neighborhood perceptions. The perceived physical disorder scale includes three Likert-type scales with four levels each (all coded such that 1 = “none” and 4 = “a lot”) that measure the amounts of (1) broken glass or trash, (2) graffiti, and (3) vacant or deserted houses or storefronts.¹¹ The perceived social disorder scale also includes three Likert-type measures asking for the frequency of social behaviors on a four-point scale (1 = “never” to 4 = “very often”): (1) drinking in public places, (2) selling or using drugs, and (3) unsupervised children hanging out.¹²

We measure the spatial context as the area that is covered by drawing a circular buffer around the centroid of the block on which respondents live with 250-meter, 500-meter, and 1-kilometer radii. To do so, we use the measured level of physical disorder on the 1,663 blocks sampled in the SSO and then estimate the level of physical disorder on every city block in the city of Chicago using kriging. We then average the kriged estimates of physical disorder within the respective radii surrounding each city block.

We also control for socioeconomic and demographic characteristics of the neighborhood environment that might affect perceptions of fear. We include the racial and ethnic composition of the neighborhood environment. We use the block-level measures of racial and ethnic composition from Census Summary File 1 to aggregate the proportion non-Hispanic African American and the proportion Hispanic for each of the three radii. We also include a measure of neighborhood disadvantage that is a scale composed of variables from Census Summary File 3 that includes the percentage of residents with incomes less than $10,000, the percentage with incomes greater than or equal to $50,000 (reverse coded), the percentage unemployed, the percentage in poverty, and the percentage receiving public assistance (Cronbach’s α = .94).¹³

Finally, we control for individual-level characteristics of respondents as well. These include self-reported race/ethnicity (a four-category measure with non-Hispanic black as the reference), age (a six-category measure with the youngest age group as the reference), gender (with male as the reference), educational attainment (a three-category measure with less than a high school diploma as the reference), and family income (a five-category measure with the highest income category as the reference). Details for how these measures were constructed are available on request.

We use an ordinal logistic regression to model fear (to account for the four-category outcome variable) on the basis of neighborhood characteristics measured at the three different spatial scales: 250 meters, 500 meters, and 1 kilometer. For the models at each scale, we create 10 conditional realizations, or imputations, of the physical disorder on the basis of the spatial covariance structure and measurements at observed locations. Using principles of multiple imputation, we estimate parameters and standard errors on the basis of these 10 conditional realizations and other measured characteristics of the neighborhood environment at each of the three different spatial scales. Given the multistage clustered sampling design of the CCAHS, we use complex survey weights to adjust estimates to the Chicago population and use robust estimates of standard errors that account for respondent clustering on blocks (up to five respondents live on the same block). We then follow the same procedure except using ordinary least squares for both perception measures while accounting for the clustered structure of the data. We estimated analytical models using the “mi” and “svy” suites in Stata version 11.2 (StataCorp LP, College Station, TX).

5.3. Spatial Variation in the Neighborhood Contextual Effects of on Fear and Perceptions of Disorder

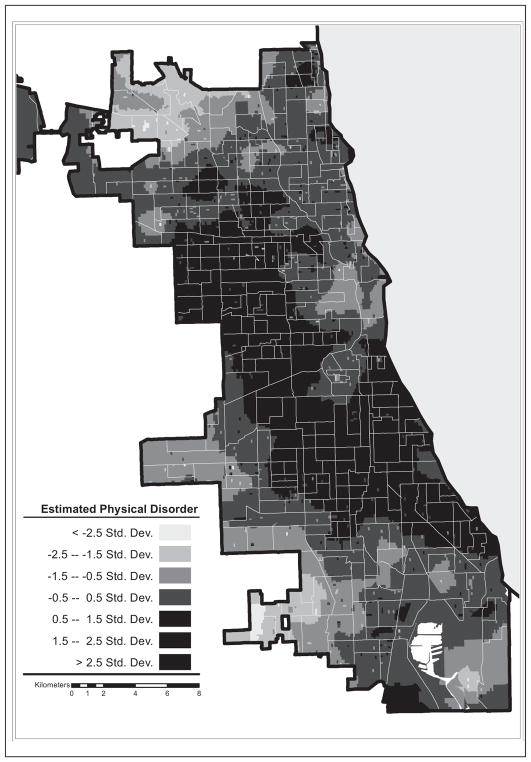
Figure 5 shows a map of the kriged estimates of physical disorder in the city of Chicago. Additionally, the map overlays the boundaries of the NCs on which respondents were sampled and that would, using the standard ecometric framework, be used as neighborhood boundaries for developing measures of disorder. Viewing the values of disorder within NCs, we can see that physical disorder varies at a spatial scale smaller than the NC boundaries, and it becomes obvious what can be missed by aggregating up to larger neighborhood boundaries. Although there are some NCs with relatively homogeneous levels of physical disorder, there are other instances where the level of physical disorder varies drastically within NC boundaries. Thus, examining the attributes of neighborhood environments using a spatially smooth surface can enhance the detail with which attributes of neighborhood context can be estimated. Kriged measures retain 78 percent of the variance of ecometric measures at the NC level when five or more blocks were sampled, while kriged estimates retain 63 percent of the variance in neighborhoods where four or fewer blocks were sampled.

Figure 5.

Map of kriged estimates of physical disorder at the city-block level with neighborhood cluster boundaries, with levels of disorder reported by standard deviation of estimates.

It is not enough, however, to simply demonstrate, as Figure 5 does, that the spatial variation varies at a relatively small spatial scale. It is also important to investigate whether these small-scale variations matter when exploring the effect of neighborhood context on individual-level outcomes. Table 1 reports the results of an ordered logistic regression of perceived fear on individual- and neighborhood-level characteristics at three different scales to investigate whether patterns vary across spatial scales. The coefficients for the effect of physical disorder on a resident’s level of fear can be found in the last row of the table. These coefficients show that the effect size of physical disorder decreases as the spatial scale of the analysis increases. When we measure the residential context at 250 meters, a one-unit increase in the physical disorder scale increases the odds of a respondent reporting a higher category of fear by 1.10 (i.e., exp{0.092}). This effect is statistically significant from the null hypothesis (p < .05). When we measure the residential context at the 500-meter scale, the odds of reporting a higher level of disorder are 1.04 times higher, an effect that is statistically indistinguishable from a null effect. In the 1-kilometer context, the influence of physical disorder is essentially zero.

Table 1.

Ordinal Logistic Regression Estimates and Standard Errors of Fear of Walking on Neighborhood Level Variables at Three Scales

Predictor	250 m	500 m	1 km
Individual predictors
Non-Latino/a white	0.739*** (0.143)	0.746*** (0.146)	0.704*** (0.145)
Latino/a	0.081 (0.161)	0.095 (0.164)	0.063 (0.165)
Non-Latino/a other	0.312 (0.256)	0.296 (0.256)	0.204 (0.248)
Female	0.210** (0.074)	0.219** (0.074)	0.214** (0.074)
30–39 years	−0.328** (0.101)	−0.300** (0.101)	−0.293** (0.101)
40–49 years	−0.295** (0.108)	−0.293** (0.108)	−0.301** (0.107)
50–59 years	−0.265* (0.119)	−0.265* (0.118)	−0.300* (0.117)
60–69 years	−0.293 (0.152)	−0.298 (0.153)	−0.355* (0.153)
≥ 70 years	−0.315 (0.174)	−0.312 (0.176)	−0.348* (0.172)
First-generation immigrant	0.384** (0.124)	0.393** (0.126)	0.430*** (0.128)
Second-generation immigrant	0.465*** (0.133)	0.471*** (0.133)	0.473*** (0.134)
High school diploma or General Educational Development certificate	−0.175 (0.102)	−0.190 (0.102)	−0.201* (0.102)
Bachelor’s degree or higher	−0.225 (0.132)	−0.263* (0.131)	−0.270* (0.130)
<$5,000	−0.112 (0.163)	−0.091 (0.164)	−0.061 (0.165)
$5,000–$14,999	−0.073 (0.130)	−0.046 (0.130)	0.017 (0.128)
$15,000–$39,999	0.060 (0.098)	0.070 (0.098)	0.108 (0.097)
Missing	0.131 (0.108)	0.143 (0.108)	0.165 (0.108)
Neighborhood contextual predictors
Proportion non-Latino black	2.355*** (0.228)	2.492*** (0.240)	2.464*** (0.246)
Proportion Latino	2.450*** (0.239)	2.544*** (0.252)	2.626*** (0.270)
Disadvantage scale	0.454*** (0.073)	0.466*** (0.072)	0.508*** (0.073)
Population density	0.365*** (0.079)	0.509*** (0.084)	0.452*** (0.091)
Kriged physical disorder	0.092* (0.046)	0.038 (0.051)	−0.003 (0.059)
Cut 1 intercept	2.444**	3.906***	3.466***
Cut 2 intercept	5.643***	7.109***	6.643***
Cut 3 intercept	8.037***	9.507***	9.033***

^*p <.05.

^**p <.01.

^***p <.001.

The results reveal important substantive differences in the outcome, perceived safety of walking, that could influence behavior. To provide context on the size of this effect, if we rank all of the blocks on which resident live and compare the neighborhood with the 25th highest level of disorder to the one with the 75th highest, the odds of increasing a level of fear on the ordinal scale will be 1.17 times higher on the second block compared with the first. Thus, going from a moderately orderly to a moderately disorderly neighborhood is similar to, though slightly lower than, the gender difference in perceived disorder (women’s odds of increasing a level are 1.23 times those of men).

Table 2 reports the coefficients and standard errors of the ordinary least squares regression predicting respondents’ perceptions of disorder by individual- and neighborhood-level predictors at the same three geographic scales. The estimates of the parameter predicting physical disorder at the three different scales using the kriged ecometric measure demonstrate a similar pattern to that for fear. At 250 meters, each unit increase in the observed disorder score predicts an increase of 0.042 units of perceived disorder, and the difference in perceived physical disorder associated with a change across the interquartile range (i.e., 0.073) reflects approximately 14 percent of a standard deviation. The influence diminishes by about 20 percent when the neighborhood is measured at 500 meters and diminishes by half at 1 kilometer. The results for perceived social disorder, reported in Table 3, reflect similar patterns and magnitudes. Thus, for all three of these outcomes—fear of walking, perceived physical disorder, and perceived social disorder—we see diminishing influences of observed physical disorder when measured at larger spatial scales, suggesting that physical disorder in one’s immediate environment might be the most salient for shaping residents’ perceptions.

Table 2.

Ordinary Least Squares Regression Estimates and Standard Errors of Perceived Physical Disorder on Neighborhood-Level Variables at Three Scales

Predictor	250 m	500 m	1 km
Individual predictors
Non-Latino/a white	0.233*** (0.036)	0.225*** (0.036)	0.220*** (0.035)
Latino/a	0.073 (0.040)	0.069 (0.040)	0.063 (0.040)
Non-Latino/a other	0.130 (0.069)	0.120 (0.070)	0.098 (0.069)
Female	−0.009 (0.017)	−0.009 (0.017)	−0.011 (0.017)
30–39 Years	−0.078*** (0.024)	−0.070** (0.024)	−0.065** (0.024)
40–49 years	−0.125*** (0.025)	−0.122*** (0.025)	−0.122*** (0.025)
50–59 years	−0.142*** (0.029)	−0.141*** (0.029)	−0.148*** (0.029)
60–69 years	−0.200*** (0.034)	−0.203*** (0.034)	−0.214*** (0.034)
≥ 70 years	−0.243*** (0.034)	−0.242*** (0.034)	−0.249*** (0.035)
First-generation immigrant	−0.205*** (0.029)	−0.205*** (0.029)	−0.196*** (0.030)
Second-generation immigrant	−0.024 (0.031)	−0.026 (0.031)	−0.025 (0.031)
High school diploma or General Educational Development certificate	0.029 (0.021)	0.026 (0.022)	0.022 (0.022)
Bachelor’s degree or higher	0.038 (0.027)	0.030 (0.028)	0.024 (0.028)
<$5,000	0.019 (0.041)	0.024 (0.041)	0.036 (0.041)
$5,000–$14,999	−0.025 (0.028)	−0.016 (0.028)	0.002 (0.028)
$15,000–$39,999	0.019 (0.023)	0.025 (0.023)	0.035 (0.023)
Missing	−0.068** (0.024)	−0.064** (0.024)	−0.058* (0.024)
Neighborhood contextual predictors
Proportion non-Latino black	0.373*** (0.052)	0.371*** (0.055)	0.368*** (0.058)
Proportion Latino	0.565*** (0.053)	0.573*** (0.056)	0.601*** (0.061)
Disadvantage scale	0.177*** (0.016)	0.176*** (0.018)	0.181*** (0.018)
Population density	0.038* (0.019)	0.058** (0.021)	0.053* (0.022)
Kriged physical disorder	0.042*** (0.010)	0.033** (0.012)	0.022 (0.015)
Intercept	1.969*** (0.186)	1.771*** (0.211)	1.791*** (0.225)

^*p <.05.

^**p <.01.

^***p <.001.

Table 3.

Ordinary Least Squares Regression Estimates and Standard Errors of Perceived Social Disorder on Neighborhood-Level Variables at Three Scales

Predictor	250 m	500 m	1 km
Individual predictors
Non-Latino/a white	0.158*** (0.044)	0.143** (0.044)	0.104* (0.044)
Latino/a	0.080 (0.052)	0.075 (0.052)	0.043 (0.051)
Non-Latino/a other	0.030 (0.078)	0.014 (0.077)	−0.036 (0.076)
Female	−0.095*** (0.022)	−0.093*** (0.022)	−0.096*** (0.022)
30–39 years	−0.097*** (0.029)	−0.088** (0.029)	−0.082** (0.030)
40–49 years	−0.128*** (0.031)	−0.126*** (0.031)	−0.127*** (0.031)
50–59 years	−0.225*** (0.037)	−0.226*** (0.037)	−0.234*** (0.037)
60–69 years	−0.340*** (0.041)	−0.342*** (0.041)	−0.357*** (0.042)
≥ 70 years	−0.457*** (0.044)	−0.457*** (0.045)	−0.464*** (0.045)
First-generation immigrant	−0.224*** (0.037)	−0.224*** (0.037)	−0.217*** (0.038)
Second-generation immigrant	−0.039 (0.039)	−0.040 (0.039)	−0.044 (0.039)
High school diploma or General Educational Development certificate	−0.028 (0.028)	−0.032 (0.028)	−0.036 (0.029)
Bachelor’s degree or higher	−0.060 (0.036)	−0.070 (0.036)	−0.075* (0.037)
<$5,000	−0.002 (0.048)	0.006 (0.048)	0.021 (0.048)
$5,000–$14,999	0.012 (0.035)	0.024 (0.035)	0.045 (0.035)
$15,000–$39,999	0.058* (0.028)	0.065* (0.028)	0.079** (0.028)
Missing	−0.018 (0.033)	−0.012 (0.033)	−0.003 (0.034)
Neighborhood contextual predictors
Proportion non-Latino black	0.589*** (0.068)	0.580*** (0.072)	0.530*** (0.078)
Proportion Latino	0.658*** (0.071)	0.659*** (0.075)	0.684*** (0.083)
Disadvantage scale	0.185*** (0.020)	0.193*** (0.022)	0.203*** (0.024)
Population density	0.104*** (0.024)	0.130*** (0.027)	0.118*** (0.030)
Kriged physical disorder	0.043** (0.014)	0.028 (0.015)	0.014 (0.021)
Intercept	1.315*** (0.236)	1.066*** (0.260)	1.184*** (0.300)

^*p <.05.

^**p <.01.

^***p <.001.

6. DISCUSSION

6.1. Theoretically Relevant Measures for Spatially Flexible Neighborhoods

As researchers’ interest in the role of neighborhood environments has grown, so too has the need for methods to measure neighborhood environments that capture theoretically relevant attributes of neighborhood context. At the same time, researchers have also highlighted the importance of defining appropriate boundaries that might vary according to the outcome or subgroup under investigation. As we have presented in this article, kriging offers a solution that permits theoretically relevant measures of contextual attributes while preserving geographic flexibility to define multiple, alternative definitions of neighborhood boundaries. The properties of kriging—its data-derived spatial covariance structure, exact interpolation, estimation of error, and spatially balanced weights structure—make it readily adaptable to social scientific applications.

The findings of our analysis demonstrate the validity of using kriging as a method of creating measures of neighborhood attributes and the contribution that kriging can make to investigating neighborhood associations at multiple scales. The cross-validation exercise showed that city block–level estimates of physical disorder were unbiased and that errors were randomly distributed within the confidence intervals expected under the assumptions of kriging. Aggregating city block–level estimates to neighborhood boundaries at three different scales revealed the potential importance of considering spatial scale when investigating neighborhood effects. The relationship between a resident’s perceptions of fear and disorder and observed physical disorder varied substantially at three different scales.

6.2. Limitations

Despite the promise of kriging as a method to allow researchers to develop a theoretically nuanced and geographically flexible measurement strategy, there are some important limitations to this measurement approach. One limitation of the analysis presented here is that it relies on a relatively basic spatial estimation strategy. We assumed a constant mean and variance of physical disorder throughout the city of Chicago. This is unlikely the case. Let us take for example the likely possibility that physical disorder is higher on major thoroughfares simply because they are used more and, thus, are more likely to have some of the indicators of disorder. To introduce the method without unneeded complexity, we do not account for this possibility in the present analysis, a decision that is likely to increase the imprecision of our measures; however, the models could be easily adapted to account for such a possibility. Additionally, we used relatively naive measures of separation distance, the Euclidean distance between two points, to determine the spatial covariance structure. Future applications should consider potentially more theoretically relevant distances such as street network distances or travel time to determine the spatial covariance. We believe that these adjustments would improve the accuracy of spatially interpolated estimates, and thus our analysis of physical disorder’s influence on perceived safety provides a conservative test of the associations.

Another possibility is that the models do not reflect “true” changes in the influence of physical disorder measured at different scales but instead reflect increasing multicollinearity of the independent variables at increasing spatial scales. We examined the variance inflation factors (VIFs), and they do rise at larger spatial scales; however, none of the VIFs for the disorder measure reach very problematic levels (the VIFs for physical disorder are 2.364, 2.823, and 3.750 at 250 meters, 500 meters, and 1 kilometer, respectively).

6.3. Implications

Despite these limitations, we believe that kriging offers an addition to neighborhood researchers’ toolkit of neighborhood measurement methods that permits the development of theoretically derived and geographically flexible measures of neighborhood attributes. Recent developments in spatial statistical approaches provide analysts with more sophisticated tools for analyzing patterns of outcomes across space. With these tools, social scientists can test spatially informed theories of social and economic behavior; however, without measures of environments similarly informed by spatial patterns, these tools will not reach their maximum utility. Given that developing theoretically derived measures often relies on measurements taken at a sample of locations, the methods we describe here permit analysts to create spatially informed risk exposures to test theories of social interaction in space. Although we use data recorded from SSO, it would also be possible to similarly develop spatially interpolated ecometric measures from samples consisting of survey responses, georeferenced data from commercial or administrative entities, or, increasingly, samples of georeferenced web data accessible through application programming interfaces.

Using this method has implications for how neighborhood environments should be sampled to develop the most accurate neighborhood measures. First, sampling strategies should be inclusive of the larger residential environment. For example, in the present study, only residential blocks where households were sampled were observed as part of the SSO. This means that no nonresidential blocks were included in the measurement, including commercial or industrial blocks. Attributes such as physical disorder are likely to be very different on these types of nonresidential blocks and likely to affect individual outcomes. Thus, it is important to develop sampling strategies designed to sample the entirety of the neighborhood environment, not exclusively the residential portions. A second and related implication is that study regions should be sampled on the basis of a spatial rather than demographic frame. Because the most precise kriged estimates are those based on a relatively dense, but regular, spatial pattern, reducing the error in measures should take this into account.

One potential solution would be to observe blocks that are sampled on the basis of a relatively coarse, but regular, spatial grid and supplement that sample with blocks on which respondents live. This means that there are not entire swaths of the city that remain unobserved but that locations surrounding residences are more carefully measured (for empirical justification of this strategy, see Laslett 1994). Because kriging accounts for the clustering of sampled locations, interpolated estimates will not be biased by the additional sampling surrounding a respondent’s house. At the same time, the estimates surrounding a respondent are more likely to be precise, whereas those where few respondents live (where it is less important to have precise measurement) will have less precise estimates.

Finally, although this work provides new possibilities for analysis of theoretically relevant neighborhood characteristics, the method is only a tool to help researchers develop neighborhood measures at different scales. Its successful application relies on social scientific theories that explicitly postulate the role of space in social processes. In the absence of theories describing how and at what scale space matters, empirical analyses will mislead researchers because searches for significant influences at different scales will render findings of studies uninterpretable. Theories must seek explanations at both more proximate and more global spatial scales, because it is possible that larger spatial contexts might be more important for some outcomes. Social scientists must devote greater attention to the processes and mechanisms that lead one’s spatial context to influence particular outcomes through, for example, greater cooperation between quantitative and qualitative researchers. In this vein, we note that the estimates of structural characteristics (e.g., racial and class composition) do not change much across spatial scale, suggesting that the context created by these forces might be pervasive across spatial scales. This would provide researchers more confidence that associations between these structural characteristics and their outcomes of interest do not depend on the spatial scale of neighborhood measurement. The persistent influence of racial and class composition could, however, be an artifact of measurement error and future research should identify which one of these two explanations provides a more plausible explanation.

7. CONCLUSIONS

As researchers continue to expand their interest in the number and diversity of individual-level outcomes, methods for measuring theoretically relevant characteristics of neighborhoods at multiple spatial scales are critical. This need is particularly important for social science research, in which multiple outcomes are measured in the same survey and each is potentially influenced by neighborhood context but possibly at different spatial scales or definitions of neighborhoods. Conceptualizing changes in neighborhood environments as occurring from block to block by using the combination the ecometric framework and kriging provides researchers with the ability to develop theoretically nuanced measures at different spatial scales or definitions of neighborhood boundaries. As we demonstrate by examining the effect of physical disorder on perceptions of fear and disorder, the spatial scale at which neighborhood context is measured matters for the conclusions we draw. Although adapting these methods will require developing new sampling strategies for measuring neighborhood environments, the methods described in this article will present researchers with new possibilities to hypothesize and test how neighborhood attributes affect individuals at different spatial scales and definitions of neighborhoods.

Biographies

Michael D. M. Bader is assistant professor of Sociology and the Center on Health, Risk, and Society at American University in Washington, D.C. His research focuses on the causes and consequences of neighborhood racial, ethnic, and economic change. He is currently examining methods that use digital tools to characterize neighborhood conditions.

Jennifer A. Ailshire is assistant professor in the Davis School of Gerontology and Andrus Gerontology Center at the University of Southern California. Her research focuses on the importance of the neighborhood environment and social relationships in determining health over the life course. She is currently exploring how neighborhood social and physical conditions promote or impair health and functioning among the growing U.S. population of community-dwelling older adults.