Incorporating regulatory guideline values in analysis of epidemiology data

Abstract

Fundamental to regulatory guidelines is to identify chemicals that are implicated with adverse human health effects and inform public health risk assessors about “acceptable ranges” of such environmental exposures (e.g., from consumer products and pesticides). The process is made more difficult when accounting for complex human exposures to multiple environmental chemicals. Herein we propose a new class of nonlinear statistical models for human data that incorporate and evaluate regulatory guideline values into analyses of health effects of exposure to chemical mixtures using so-called ‘desirability functions’ (DFs). The DFs are incorporated into nonlinear regression models to allow for the simultaneous estimation of points of departure for risk assessment of combinations of individual substances that are parts of chemical mixtures detected in humans. These are, in contrast to published so-called biomonitoring equivalent (BE) values and human biomonitoring (HBM) values that link regulatory guideline values from in vivo studies of single chemicals to internal concentrations monitored in humans. We illustrate the strategy through the analysis of prenatal concentrations of mixtures of 11 chemicals with suspected endocrine disrupting properties and two health effects: birth weight and language delay at 2.5 years. The strategy allows for the creation of a Mixture Desirability Function i.e., MDF, which is a uni-dimensional construct of the set of single chemical DFs; thus, it focuses the resulting inference to a single dimension for a more powerful one degree-of-freedom test of significance. Based on the application of this new method we conclude that the guideline values need to be lower than those for single chemicals when the chemicals are observed in combination to achieve a similar level of protection as was aimed for the individual chemicals. The proposed modeling may thus suggest data-driven uncertainty factors for single chemical risk assessment that takes environmental mixtures into account.

1. Introduction

Human biomonitoring data of mixtures of environmental toxicants, particularly during pregnancy, provide important evidence of exposure to chemicals with purported adverse health outcomes (e.g., endocrine disrupting chemicals; EDCs). However, simply identifying critical mixtures and chemicals that are “bad actors”, through epidemiology data, does not adequately inform public health risk assessors about “acceptable ranges” of environmental exposures – which is fundamental to (non cancer) regulatory guidelines and mitigation strategies.

Guideline values, such as the tolerable or acceptable daily intake (TDI/ADI) or reference (RfD) values are important tools for risk assessment of chemicals in the environment, including e.g., contaminants and pesticide residues. These values are generally derived from single chemical experimental toxicity studies and describe a “safe” exposure level of a single chemical to which a person can be exposed each day for a long time (usually lifetime) without suffering harmful effects. It is determined by applying assessment factors (to account for the uncertainty in the data) to point of departures (PODs) such as the highest dose in human or animal studies which has been demonstrated not to cause toxicity (NOAEL) and the lower confidence interval of a Benchmark dose (BMDL) (EPA, 2007). When animal based PODs are used, assessment factors are generally applied to account for (1) differences between the experimental setup and the actual human exposure, e.g. route-to-route extrapolation, subchronic-to-chronic extrapolation, (2) interspecies differences, (3) intra-species differences/ variability within the human population, i.e. differences between the typical/average human and sensitive humans, and (4) uncertainty in the data, e.g., poor quality data and missing toxicity studies.

Progress in analytical chemistry and toxicokinetic modeling has created possibilities of monitoring toxicants in biological media (i.e., blood, urine, hair, nails, body tissues, fluids and exhaled breath, or the amount of metabolites in tissues and fluids). A first official reference to guidance values for human biomonitoring (HBM) values was made in 1974, and a first set of three so called Biological Limit Values (BLV) (lead, toluene and trichloroethylene), was introduced for occupational settings with the MAK list in 1981 (Bolt and Thier, 2006). The first American Biological Exposure Indices (BEI) report was published by ACGIH in 1984 (ACGIH, 1984).

For environmental exposure to the general public, two main no-menclatures have been concurrently developed but both refer to the guidance values translated to equivalent human concentration levels in blood, urine, or other biological matrices using complex pharmacokinetic modeling. Scientists in the United States have derived so-called biomonitoring equivalent (BE) values (Hays et al., 2007; Aylward et al., 2013). BE values are concentrations of a chemical or its metabolites in a biological medium that is consistent with an existing health-based exposure guideline (Krishnan et al., 2010). Concurrently, the German Human Biomonitoring Commission defined two HBM-values: the HBM-I value is defined as the concentration of a single substance in humans below which no adverse health effect should be expected (i.e., identifying an “acceptable exposure range”); the HBM-II value is defined as the concentration of a substance in human biological material at which (and above) adverse effects are possible, indicating an acute need for reduction of exposure (Angerer et al., 2011; Apel et al., 2016). The evaluation of HBM values is a part of the recently funded HBM4EU, a joint project of 28 countries, the European Environment Agency and the European Commission (https://www.hbm4eu.eu/the-project/).

We note the equivalence of HBM-I and BE values. Both values are generally based on single chemical experimental data from animal studies (i.e., dose response experiments). However, they do not account for exposure to mixtures of similarly acting environmental chemicals. This is a major shortcoming since all available data demonstrate that humans are not exposed to single compounds, but to complex mixtures of numerous molecules (e.g., Crinnion, 2010).

Herein, we propose methods to incorporate this regulatory concept of PODs in human data, somewhat analogous to (unadjusted) BE values and HBM values, into the analysis of mixture related health effects using epidemiological data. Specifically, we propose to estimate guideline values directly in human data with uncertainty factor adjustments made post hoc. To our knowledge such estimates of guideline values from human studies in mixtures has not been previously considered.

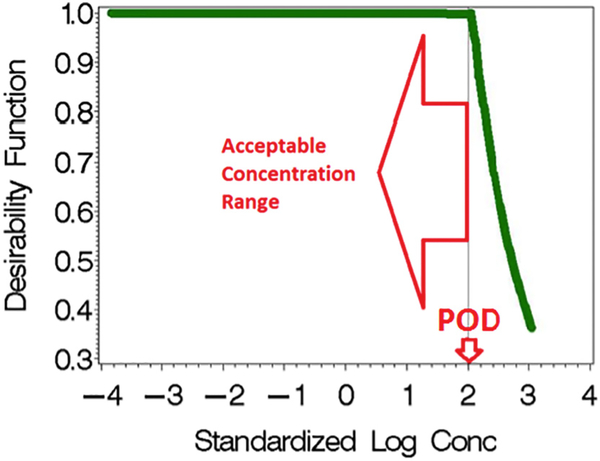
We incorporate the concept of “acceptable concentration ranges” of exposure below identified regulatory guideline values (i.e., HBM and BE values are uncertainty adjusted PODs; for convenience, subsequently referred to as HBM values) in regression models using desirability functions (DF) (Fig. 1). DFs are widely used in industry for optimizing processes with multiple responses, where the quality of a product or process with one or more characteristic outside of some “desired” limits are unacceptable (Harrington Jr., 1965; Derringer, 1994; Derringer and Suich, 1980; Shih et al., 2003; Coffey et al., 2007; Costa et al., 2011). However, DFs have not been applied to mixtures of environmental exposures in a regulatory context.

Fig. 1.

Linking Desirability Functions (“low is better” shape) to regulatory guidance values.

Our objective is to demonstrate simultaneous estimation of “points of departure” values in a new class of models, i.e., “Acceptable Concentration Range” (ACR) models, using maternal concentrations of EDCs from biomonitoring in a pregnancy cohort linked to health effects in the children, i.e., birth weight and language delay at 2.5 years of age. This is a first step in the development of a new class of statistical models that incorporates regulatory guidance concepts into regression models of epidemiology data.

2. Methods

2.1. Pregnancy cohort study

The Swedish Environmental Longitudinal, Mother and child, Asthma and allergy (SELMA) is a pregnancy cohort study designed to investigate prenatal exposure to environmental chemicals and health outcomes related to growth, developmental and chronic diseases in children. SELMA recruited pregnant women in the county of Värmland, Sweden, between September 2007 and March 2010. Women who could read Swedish and were not planning to move out of the county were recruited at their first antenatal care visit; 8394 pregnant women were identified, 6658 were eligible and 2582 (39%) agreed to participate. The women were enrolled at median week 10 of pregnancy (range week 3–27, where 96% were recruited before week 13 of pregnancy). Detailed recruitment selection criteria and sample collection procedures have been published previously (Bornehag et al., 2012). The Ethics Committee in Uppsala, Sweden approved the SELMA protocol and all participants signed informed consents prior to the start of data collection.

2.2. Outcome variables

Language development is routinely assessed in Sweden when children are 30 months of age. This validated assessment consists of a nurse evaluation and a parental questionnaire on language use. If warranted, the nurse discusses possible referral (to a speech therapist, audiologist, psychologist or pediatrician) with the parent (Mattsson et al., 2001). The questionnaire asks about the number of words the child uses; responses are categorized as < 25, 25–50 and > 50 words. Our primary study outcome is a parental report of the use of 50 words or fewer (yes or no), which we denote here as Language Delay (LD). Data on LD are available from 1113 children. However, with complete case analyses using covariates, the sample size reduced to 840.

Data on birth weight (and gestational age at birth), from the Swedish birth register, are available for 1938 children. However, with complete case analyses using covariates, the sample size reduced to 1323.

2.3. Selection of covariates for analyses

Models for LD were adjusted for child sex and gestational age at birth, maternal education, early pregnancy weight, smoking status, and urinary creatinine to adjust for urinary dilution. Birth weight models also included parity, maternal age and fish intake in the family.

2.4. Exposures

Exposure data from the first trimester of pregnancy (at enrollment) are available for 41 compounds in urine (metabolites) and serum from over 2300 mothers in the SELMA study, with concentrations above levels of quantification (LOQ) in at least 50% of the samples. Of these 41 compounds, we identified 11 with established HBM values, derived by the HBM Commission of the German Environmental Agency (Commission, 2014) or BE values from the Centers for Disease Control and Prevention (Aylward et al., 2013) (Table 1). These HBM values are defined as the concentration or range of concentrations of a chemical or its metabolites in a biological matrix that is consistent with an existing non-cancer health–based exposure guidance value such as a RfD or TDI (Hays et al., 2008a, 2008b; LaKind et al., 2008).

Table 1:

Published HBM and BE values (μg/L) with estimated single analyte and mixture estimates using desirability functions (DF: based on B = 100 bootstrap samples for single chemicals and B= 1000 for the mixture analyses) for reduced birth weight (N = 1323) and language delay (N = 840). The p-values are associated with the test for significance of the final DF or MDF (i.e., the bootstrap average) in generalized linear models (GLM). The interval given in the single analyte analyses is the 5th and 95th percentiles from the bootstrap distribution of the δm values. Generally, the more desirable the concentration/mixture the higher the birth weight (positive regression coefficient) and a decrease in the risk of language delay (negative regression coefficient).

(μg/L)	Observed Concentration Statistics			Published HBMa or BEb values	Analysis of birth weight			Analysis of language delay
Analyte	Median	95th	Max		δm estimates and 90% CI from single chemical analyses	p value for single analyte DF in GLMs	δm estimates in Mixture analysis (p = 0.001)	δm estimates and 90% CI from single chemical analyses	p value for single analyte DF in GLMs	δm estimates in mixture analysis (p = 0.008)
MEP (urinary)	62	527	4419	18,000b	241 (89, 421)	0.818	247 (57, 954)	211 (45, 1399)	0.522	124 (10, 1010)
MBP (urinary)	71	232	2720	200/2,700b	161 (48, 980)	0.639	177 (74, 379)	150 (69, 542)	0.175e	169 (25, 825)
MBzP (urinary)	17	101	3545	3,800b	45 (10, 204)	0.336	30 (7, 131)	57 (22, 339)	0.139e	26 (1, 212)
DEHPc (urinary)	37	150	2166	300a	130 (33, 546)	0.581	147 (58, 373)	143 (100, 244)	0.221	186 (77, 1312)
DINP (urinary)	24	207	4872	1500b	163 (97, 844)	0.065e	158 (27, 498)	218 (68, 1693)	0.140e	130 (25, 2067)
BPA (urinary)	1.5	6.4	111	200a/2,000b	5.4 (2, 35)	0.514e	4.9 (2. 12)	3.0 (1.3, 5.5)	0.577e	3.1 (0.2, 28)
Triclosan (urinary)	0.8	325	3357	3,000a/6,400b	13 (0.1, 50)	0.819	15 (0.4, 190)	29 (4, 1361)	0.512	33 (2, 1084)
PFOA (plasma)	1.6	4.0	21	2a	2.3 (1.5, 3.7)	< 0.001	1.9 (1.3, 6.2)	4.5 (2.8, 14)	0.370	4.1 (2.2, 6.9)
PFOS (plasma)	5.3	12	32	5a	8.6 (4.8, 14.9)	0.037	8.7 (4.5, 17.3)	18 (9, 39)	0.296e	13 (8, 22)
PCBsd (serum)	0.25	0.57	1.27	1.75a	0.54 (0.37, 1.1)	0.022	0.56 (0.46, 0.83)	0.74 (0.34, 1.6)	0.564e	0.65 (0.4, 1.3)
DDT + DD (serum)	0.18	0.70	19.9	38.7f	0.40 (0.30, 0.60)	0.002	0.64 (0.47, 1.1)	0.83 (0.35, 3.2)	0.061e	0.83 (0.4, 2.7)

^aGerman HBM Commission (Commission, 2014).

^bAylward et al., 2013, EHP.

^cSum of DEHP metabolites: 5 oxo- and 5 OH-MEHP in urine.

^dSum of PCB138, PCB153, PCB180 in serum; the published HBM is listed as 3.5μg/L for twice the value of the sum.

^ep values associated with negative β1 coefficients; otherwise, the β₁ coefficient is positive.

^fBE for DDT +DDE is 5 μg/g serum lipid. Adjusting to μg/L using average total lipid in pregnant women from NHANES (2005–06; 773 mg lipid/dL serum) =(5) (773)/100 = 38.65 μg/L.

First morning void urine samples were obtained from 2325 pregnant women (out of the 2582 participating women) at their first visit to the antenatal care center, i.e., at enrollment to the study (Bornehag et al., 2012). Urine samples were collected in supplied glass containers at home and transferred into polypropylene tubes, without any other assisting equipment, for easy transportation. Samples were stored at −20 °C before being processed at the laboratory at Occupational and Environmental Medicine (OEM), Lund University, Sweden, according to methods/procedures previously described in (Bornehag et al., 2015). Metabolites from phthalates and alkyl phenols were analyzed according to the method presented by Gyllenhammar et al. (2017). Aliquots of 0.2 mL of urine were treated with glucoronidase and labeled internal standards (IS) of all analyzed compounds were added and the samples were analyzed using liquid chromatography triple quadrupole linear ion trap mass spectrometer (LC/MS/MS). The LOD was determined from chemical blank samples. Quality control (QC) samples and chemical blank samples were analyzed within each sampling batch (96 samples including standards, QCs and lab blanks). The creatinine concentrations were analyzed according to an enzymatic method described by Mazzachi et al. (2000). Urinary phthalates including 10 metabolites were analyzed including; Mono‑ethyl phthalate (MEP), metabolite of DEP; Mono‑n‑butyl phthalate (MnBP), metabolite of DBP; Mono‑benzyl phthalate (MBzP), metbolite of BBzP; Mono‑(2‑ethylhexyl) phthalate (MEHP), Mono‑(2‑ethyl‑5‑hydroxylhexyl) phthalate (MEHHP), Mono‑(2‑ethyl‑5‑oxohexyl) phthalate (MEOHP), Mono‑(2‑ethyl‑5‑car-boxypentyl) phthalate (MECPP), metabolites of DEHP; Mono‑hydroxy‑iso‑nonyl phthalate (MHiNP), Mono‑, oxo‑iso-nonyl phthalate (MOiNP), Mono‑carboxy‑iso‑octyl phthalate (MCiOP), metabolites of DiNP; and urinary alkyl phenols including 2 compounds; Bisphenol A (BPA) and Triclosan (TCS).

Serum collected at enrollment was analyzed for perfluorinated alkyl acids (PFAAs) and cotinine using LC/MS/MS at OEM according to Lindh et al. (2012). Briefly, aliquots of 0.1 mL serum were added with IS for all analyzed compounds and the proteins were precipitated by acetonitrile and vigorously shaking for 30 min. The samples were then centrifuged and the supernatant analyzed. The analyses of PFOA and PFOS are part of the Round Robin inter-comparison program (Professor Dr. Med. Hans Drexler, Institute and Out-patient Clinic for Occupational-, Social- and Environmental Medicine, University of Erlangen-Nuremberg, Germany) with results within the tolerance limits. Analyses were made of 8 compounds including perfluoroheptanoic acid (PFHpA), perfluorooctanoic acid (PFOA), perfluorononanoic acid (PFNA), perfluorodecanoic acid (PFDA), perfluoroundecanoic acid (PFUnDA), perfluorododecanoic acid (PFDoDA), perfluorohexane sulfonate (PFHxS) and perfluorooctane sulfonate (PFOS). If cotinine levels were below 0.2 ng/mL, subjects were categorized as non-smoker; if cotinine levels were > 15 ng/mL, subjects were considered as active smokers; and while in between, subjects were considered as passive smokers (Jefferis et al., 2010).

Finally, PCB and DDT/DDE were also analyzed in serum. In the sample preparation, ¹³C-labeled internal standards of each compound were added to samples. Dichloromethane-hexane was used for extraction. Extracts were cleaned with multilayer silica columns. The eluate was concentrated for GC–MS/MS analysis (Agilent 7010 GC–MS/MS system, Wilmington, DE, USA) (Koponen et al., 2013). In each batch of samples (total n = 76) two blanks, control serum sample (NIST SRM 1958) and an in-house low concentration control samples (1 to 9 dilution of SRM 1958 with new born calf serum) were included. Coefficients of variation (CV) were below 5% for SRM 1958 and diluted SRM 1958, with the exception of p,p′-DDT in the diluted samples (RSD % = 12%).

The BE value for DDT + DDE is 5 μg/g serum lipid (Aylward et al., 2013). Lipid concentrations are not available in SELMA women. The average total lipid (TL) concentration in pregnant women (N = 186) from the 2005–06 cycle of NHANES (NCHS and CDC, 2005) was calculated using TL = (2.27 ∗ Total Cholesterol) + Triglycerides + 62.3. With average Total Cholesterol = 229 mg/dL and average Triglycerides = 190 mg/dL, the average TL = 773 mg/dL. The adjusted BE is (5) (773)/100 μg/L = 38.65 μg/L serum.

2.5. Statistical considerations

Desirability Functions translate any variable of interest to a “desirability scale” between 0 (completely undesirable) and 1 (most desirable) (Fig. 1). We propose DFs where each chemical concentration X_m is mapped to a desirability (unit) scale using a chemical-specific DF. A desirability value for chemical m, d_m, takes value d_m = 1 when that exposure is in the “acceptable range” (i.e., similar to the concept of exposure below the HBM values). Less desirable values, those above the acceptable range, receive values 0 < d_m < 1 with d_m = 0 being completely undesirable. Following the DF literature (e.g., (Harrington Jr., 1965)), exposure-specific DFs are combined using the geometric mean, which, in this setting, gives the mixture DF (MDF), denoted by D, that characterizes overall desirability. For a mixture, D = 1 if all components of a mixture are within their respective acceptable range, while 0 < D < 1 if at least one component of the mixture is outside the acceptable range. As noted by Coffey et al. (2007), the geometric mean is used in the DF literature to create the MDF because the product in the geometric mean is more sensitive than the sum in the arithmetic mean to values below 1.

Various models for DFs have been used in the literature; e.g., smooth functions (Shih et al., 2003; Gennings et al., 2010); and connected line segments (Harrington Jr., 1965; Coffey et al., 2007). Coffey et al. (2007) noted the choice of the functional form of the DFs did not have an appreciable impact on the results of their analysis.

We use non-smooth “join-point” DFs with join-points δ_m, m = 1, …, M, that parameterize the boundary of the acceptable range and slope parameters γ_m, m = 1, M, that characterize potency for exposures above the acceptable ranges. Specifically, we use the “low is better” type of DF functions (e.g., (Coffey et al., 2007)) corresponding to HBM values where d_m = 1 for X_m < δ_m with decreasing desirability for X_m > δ_m (Fig. 1):

$$d_m^{low}=\left\{\begin{array}{cc}1& X_m<{\delta }_m^{low}\\ exp\left[-{\gamma }_m^{low}\left(X_m-{\delta }_m^{low}\right)\right],& X_m\ge {\delta }_m^{low}\end{array}\right\}$$

This non-smooth “join-point” function is of interest as the join point supports the concept of regulatory guidance values that define “acceptable concentration ranges”, i.e., below δ_m (These are the proposed unadjusted HBM values without an uncertainty factor adjustment). The γ_m parameter determines the steepness of the function above the join point; i.e., the higher the value the faster the function approaches zero, the asymptote of the function. These slope parameters are associated with the potency of the compound. For convenience in interpretation, we transform all concentrations (X_m) to centered and scaled log-concentrations (i.e., the difference in log transformed concentrations and the sample mean, divided by the sample standard deviation (SD) so that a unit change in concentration is 1 SD for each chemical). Finally, we note these are empirical models and are not purported to have biological interpretations.

2.5.1. Estimation

For a single analyte the unknown parameters of the DF are estimated in a generalized nonlinear model (Seber and Wild, 1989); i.e.,

$$g\left({\mu }_i\right)=\left\{\begin{array}{cc}{\beta }_0+{\beta }_1(1)+Z_i^T\theta & X_i<{\delta }^{low}\\ {\beta }_0+{\beta }_1\left(\exp \left[-{\gamma }^{low}\left(X_i-{\delta }^{low}\right)\right]\right)+Z_i^T\theta & X_i\ge {\delta }^{low}\end{array}\right\}$$ (1)

where X_i is the centered and scaled concentration of the analyte and Z_i is a vector of covariates for the i^th subject with a link function g(.) relating the mean to the regression model (e.g., a logit link for binary data such as language delay). For the identity link (i.e., g(μ) = μ), the criterion for estimation is to minimize sum of squared errors (SSE); for the logit link, the criterion is to maximize the binomial likelihood. In either case, nonlinear iterative algorithms are used to determine parameter estimates where the “current” vector of parameter estimates is changed a step at a time using a linear approximation, a Taylor series approximation, or modification of these (Seber and Wild, 1989). In the piecewise ACR model, these step changes may result in parameter estimates of the join point that fall outside the observed data range.

When the join point is estimated outside the data range, the model is over-parameterized and the covariance matrix is not positive definite. For this reason we construct percentile-based asymmetric confidence bands on the join points (δ_m’s) using B = 100 bootstrap samples (i.e., 100 random samples with replacement each of size N). However, join point estimates that exceed the data range are somewhat arbitrary as they do not change the objective function for estimation (i.e., SSE or log likelihood function); e.g., a join point 1 unit above max(X) has the same objective function as a join point 10,000 units above max(x). Thus, interpretation of the upper limit of the percentile-based confidence interval should be made relative to the observed data range. Finally, for comparison to the exponential model in Eq. (1), we have considered a piecewise model using a logistic nonlinear function in the supplement (Table S3).

For a mixture of M analytes, the analyte-specific join points (δ_m’s) and potency parameters (γ_m’s) are jointly estimated from the generalized nonlinear model using the mixture desirability function (MDF):

$$g\left({\mu }_i\right)={\beta }_0+{\beta }_1{\left(d_1\times d_2\times \dots \times d_M\right)}^{\frac{1}{M}}+Z_i^T\gamma ={\beta }_0+{\beta }_{1}MDF+Z_i^T\gamma$$ (2)

This is a novel estimation of a metric in environmental epidemiology where only concentrations above estimated guidance values contribute to the estimated mixture effect. A simplified case of the “low is better” DF is where the potency weights are fixed at γ = 1 and only the join points are estimated, which may be useful when the problem is ill-conditioned and or to get good starting values for the join point(s).

To accommodate complex correlation patterns among the environmental chemicals, we include an ensemble step. That is, similar to weighted quantile sum (WQS) regression (Carrico et al., 2015), we estimate the unknown parameters across a large number (generally, B = 1000) of bootstrap samples; i.e., samples of the observations taken with replacement for the specified total sample size. The average estimates for the join-point and potency parameters across the bootstrap samples comprise the final estimates for the analysis with bootstrap confidence intervals for the join points. Tests of significance of β₁ in Eqs. (1) and (2) are conducted using a generalized linear model (GLM), adjusted for covariates.

2.6. Demonstration of the HBM models using simulation studies

We simulated data using a threshold response surface model to relate X and Y, thereby simulating from a model with an acceptable concentration. Following Schwartz et al. (1995), consider the generalized linear threshold model,

$$g(\mu )=\left\{\begin{array}{cc}{\beta }_0,& x^T\theta \le \delta \\ {\beta }_0+x^T\theta -\delta ,& x^T\theta >\delta \end{array}\right\}$$

where 𝜃 is an M-vector containing regression parameters that define the threshold contour (i.e., where x^T𝜃 = δ and g(μ) = β₀). We used this model in a simulation study of DEHP and PFOA as estimated from SELMA data. In brief, we used observed standardized concentrations of DEHP and PFOA from the SELMA study. We hypothesized an association with birth weight using the threshold response surface model with an identity link (g(μ) = μ), where higher concentrations are associated with a lower mean. These data were used to demonstrate the proposed strategy in the next section.

3. Results

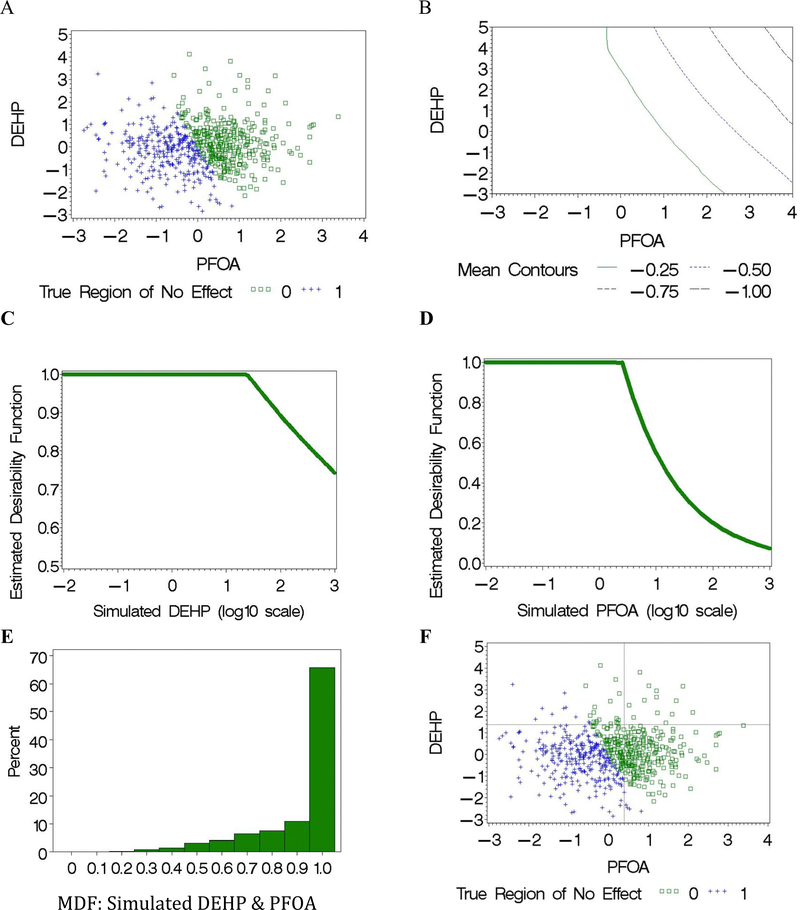
To set the concept of incorporating guideline values into the analysis of human data, we begin by simulating data for two environmental chemicals based on birth weight in the SELMA cohort. We use prenatal DEHP metabolite levels in urine and PFOA levels in prenatal serum, using standardized concentrations (Fig. 2A), where the simulated region of no effect can be seen for these two compounds. We assume an underlying response surface of standardized birth weight with contours of constant response below the mean of concern (i.e., contours of constant response are depicted in Fig. 2B indicating lower birth weight as the concentrations of either chemical increases), where the ‘true region of no effect’ is identified by observations marked as blue in Fig. 2A. We simultaneously estimated the delta values in the DFs for (simulated) DEHP and PFOA in the MDF embedded in the regression model (Eq. (2)) as depicted in Fig. 2C and D. The model allows for different potencies for the chemicals where the slope above the “HBM value” decreases in “desirability” for PFOA at a faster rate than for DEHP. The resulting histogram for the MDF indicates that roughly 65% of the subjects had concentrations in the acceptable region and 35% had concentrations of at least one of the two chemicals above the join point (Fig. 2E). Estimation of the MDF results in the construction of an “acceptable region” as a square in the lower left quadrant (generalized to a hyper-cube in higher dimensions) based on the corresponding single DFs (Fig. 2F). Thus, the subjects denoted by blue plus signs in the lower left quadrant are correctly identified as in an acceptable region where the green squares denote subjects incorrectly identified in this quadrant; i.e., the risk of the health effect is underestimated for the subjects denoted by green in the estimated acceptable region. On the other hand, the subjects denoted by green points in the other three quadrants are correctly identified as in a region of concern.

Fig. 2.

Simulated dose-response data for DEHP and PFOA (standardized log concentrations; μg/L) with (A) simulated concentrations; and (B) contours of standardized simulated response. The estimated DFs from the simulated data for (C) DEHP and (D) PFOA are used to estimate the MDF with histogram given in (D). (F) The estimated join points for DEHP and PFOA define the acceptable region (i.e., lower left quadrant).

3.1. Analysis of prenatal exposures in SELMA

Of the 41 compounds/metabolites measured in urine and serum during 1st trimester in the SELMA cohort, we identified published HBM values for 11 chemicals/classes (Table 1) including phthalate metabolites, phenols, PFOS and PFOA, sum of three PCBs and DDT/DDE. The published HBM values for these compounds/metabolites are generally higher than high exposures determined by the 95th percentile measured in SELMA, i.e., has an adequate margin of safety. The notable exceptions are for the PFOS and PFOA where the HBM values (2 and 5 ng/mL blood plasma, respectively) are below the 95th percentile in the SELMA pregnant women, indicating that adverse health effects cannot be excluded (Table 1).

We evaluated the potential association between prenatal exposure data from the SELMA pregnancy cohort and health outcomes (birth weight and language delay at 30 months of age) adjusted for covariates. Data on birth weight and covariates were available for 1323 children. For language delay data were available for 840 children. We estimated single analyte HBM values both separately following Eq. (1) and simultaneously in a mixture model following Eq. (2).

3.1.1. Analysis of birth weight

The single analyte estimates of PODs (i.e., the join points in Eq. (1)) were below the published values for 9 of 11 analytes, PFOA and PFOS were slightly higher (Table 1). This means that the measured exposures for 9 of the 11 chemicals were considered “safe” according to the current published HBM values since their concentrations were below the corresponding published HBM value. Nevertheless, there is an observation in the human data that concentrations below the published values are associated with changes in birth weight (i.e., less desirable prenatal concentrations are associated with lower birth weight). Further, the upper bootstrap 90% confidence limit on the single chemical PODs were within the observed concentration ranges and below the published guidelines with the exception of DEHP, PFOA and PFOS; thus, even accounting for uncertainty in the estimates, the upper limits are generally below published values. However, only four of the beta coefficients associated with the DF for the single chemical analyses were significant (PFOA, PFOS, PCBs and DDT/DDE). So even though there is an indication of an association with lower birth weight, seven single chemical analyses did not reach statistical significance. When estimated simultaneously, 10 of the 11 POD estimates from the MDF were within the bootstrap 90% confidence interval on the single chemical POD values; all 11 of the 90% confidence intervals from the MDF overlapped those of the single analyte analyses. As expected, single chemical evaluations are conducted in the presence of other chemicals and may therefore be somewhat similar to the mixture model.

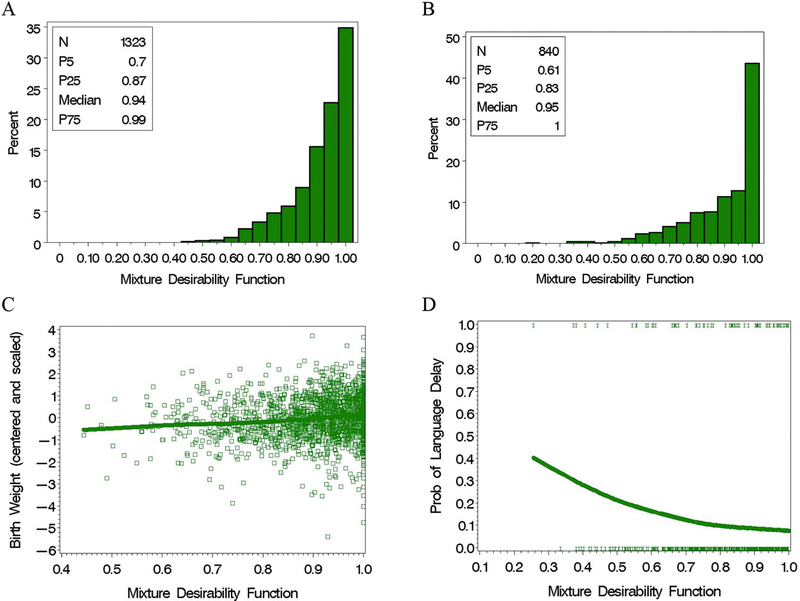
Using the mixture model, roughly 35% of the SELMA women had all 11 of these prenatal concentrations in the acceptable range (i.e., D = 1) as indicated by the MDF (Fig. 3A). Among the remaining 65% of the subjects with D < 1 (i.e., less desirable concentrations of one or more components in the mixture), there was a significant association between higher desirability (as measured by MDF) and increased birth weight (Table 2, p < 0.001; Fig. 3C). The beta coefficient 0f 0.97 associated with MDF (Table 2) indicates that, for example, a 0.1 increase in the MDF (e.g., from 0.8 to 0.9) is associated with a 0.097 increase in standardized birth weight, i.e., a 9.7% of the SD of birth weight increase. Thus, the MDF decreased by 0.1 units (corresponding to higher, less desirable concentrations) is associated with a 9.7% SD decrease in birth weight.

Fig. 3.

Histograms for the MDF associated with (A) reduced birth weight (N =1323), and (B) risk of language delay (N = 840); and LOESS plots of (C) birth weight, and (D) risk of language delay; adjusted for covariates.

Table 2:

Model parameter estimates relating MDF and birth weight (centered and scaled) using mixtures of 11 EDCs (MEP, MBP, MBzP, DEHP, DINP, BPA, triclosan, PFOA, PFOS, PCBs, and DDT&DDE; N = 1323) with 1000 bootstrap samples.

Variable	Regression coefficient estimate	Standard error	p value
MDF	0.97	0.23	<0.001
Sex (centered)	0.11	0.02	< 0.001
Creatinine (centered and scaled)	−0.01	0.02	0.790
Maternal education (centered)	0.02	0.02	0.469
Maternal weight (centered and scaled)	0.20	0.02	< 0.001
Maternal smoking (centered)	−0.01	0.03	0.692
Gestational week at birth (centered)	0.30	0.01	< 0.001
Parity (centered and scaled)	0.18	0.03	< 0.001
Maternal age (centered and scaled)	0.01	0.03	0.833
Fish intake (centered and scaled)	−0.02	0.02	0.368

For comparison, when the published BE values, or when not available, HBM values, were set as join points in a MDF (i.e., where the join points were fixed by published values in Table 1 and the slope parameters were estimated, compared to above where both the join points and slope parameters were estimated), 43% of the SELMA women were estimated to have prenatal concentrations completely in the acceptable range. The significant association with birth weight (Table S1) was dominated by PFOA and to a lesser degree, PFOS. Thus, the estimated PODs indicated there is additional signal in more analytes than just the two perfluorinated compounds.

3.1.2. Analysis of language delay

The upper limits of the 90% asymmetric confidence intervals were within the observed data range for 9 of 11 of the analytes, with PFOS and the PCBs the exception. We omit the PCBs from comparison of the upper limit (1.6) to the published value (1.75) since the estimates above the data range are not supported by a change in the objective function. The single analyte estimates of the join points were below the published values for 9 of 11 analytes (Table 1) with PFOA and PFOS above the published values. However, none of the beta coefficients associated with the DF for the single chemical analyses were significant. When estimated simultaneously, all 11 analytes had estimated POD values within the 90% confidence intervals of the single analyte models and all 11 of the 90% confidence intervals for the single chemicals and the MDF overlapped. As expected the single chemical and mixture estimates are similar; even single chemical analyses are implicitly adjusted for other compounds. Using the mixture model, roughly 45% of the SELMA women had all 11 of these prenatal concentrations in the acceptable range (i.e., D = 1) as indicated by the MDF (Fig. 3B). Among the remaining 55% of the subjects with D < 1 (i.e., less desirable concentrations of one or more components in the mixture), there was a significant association between higher desirability (as measured by MDF) and decreased risk of language delay (Table 3, p = 0.013; Fig. 3D).

Table 3:

Model parameter estimates relating MDF and language delay using mixtures of 11 EDCs (MEP, MBP, MBzP, DEHP, DINP, BPA, triclosan, PFOA, PFOS, PCBs, and DDT&DDE; N = 840) with 1000 bootstrap samples.

Variable	Regression coefficient estimate	Standard error	p value
MDF	−2.2	0.87	0.013
Sex (centered)	0.53	0.13	< 0.001
Creatinine (centered and scaled)	−0.22	0.14	0.121
Maternal education (centered)	−0.25	0.13	0.049
Maternal weight (centered and scaled)	0.12	0.12	0.285
Maternal smoking (centered)	−0.12	0.20	0.548
Gestational week at birth (centered)	−0.06	0.06	0.327

In contrast, when the published HBM values were set as join points in a MDF, 99% of the SELMA women were estimated to have prenatal concentrations completely in the acceptable range and there was no significant association with language delay (Table S2; p = 0.172). Thus, the HBM model parameterized to include the risk assessment concept of acceptable range of concentrations provides an indication that the published HBM values are too high to provide adequate protection for neurodevelopmental effects as measured by language delay from prenatal exposures to mixtures in the SELMA pregnancy cohort.

3.2. Comparison between the piecewise exponential model and the piecewise logistic model

We compared the estimates of the join points using the piecewise exponential ACR model in Eq. (1) to the estimates using a piecewise logistic ACR model (Supplementary Results, Table S3); i.e.,

$$g(\mu ;\gamma >0)=\{\begin{array}{cc}{\beta }_0+{\beta }_1(1)+Z_i^T\theta ,& X<\delta \\ {\beta }_0+{\beta }_1\left(\frac{2}{1+\exp \{\gamma (X-\delta )\}}\right)+Z_i^T\theta ,& X\ge \delta \end{array}\}$$

Comparisons were made using the metric of absolute difference in estimates relative to the average (ADA): i.e.,$\frac{\left|{\delta }_1-{\delta }_2\right|}{\left({\delta }_1+{\delta }_2\right)/2}$ where δ₁ is the estimate from the piecewise exponential ACR model and δ₂ is the estimate from the piecewise logistic ACR model. The join point estimates are closer in the analysis of birth weight compared to the binary outcome of language delay, using the average ADA. In the analysis of birth weight, in single chemical models the average ADA was 9% (SD = 0.03); in the MDF, the average ADA was 3% (SD = 0.02). In the analysis of LD, in single chemical models the average ADA was 22% (SD = 0.17); in the MDF, the average ADA was 25% (SD = 0.14). This comparison of two functional forms for the DF in Eq. (1) is the beginning of a more extensive characterization of the ACR model proposed herein.

4. Discussion

We have proposed a new class of regression models for human based epidemiology data where the concept of regulatory guidelines is embedded within the model using desirability functions. The resulting models are nonlinear models with both a potency parameter and join point (i.e., POD, an unadjusted HBM value) parameter estimated per analyte. We further propose a bootstrap step where the final POD estimates are given by the average across the bootstrap sample estimates; bootstrap confidence intervals are produced for each single chemical POD parameter and within the mixture. These are new models; we illustrate their use using chemical mixtures from the SELMA pregnancy cohort related to risk of low birth weight and language delay. Our objective is to introduce the concept of embedding regulatory guideline parameters in regression models of human data. We leave as future research further lines of inquiry regarding more complete characterization of the models.

The estimate of δ_m is an empirical estimate of a POD for the m^th compound (e.g., (Apel et al., 2016)). The impact of mapping concentrations of environmental chemicals to a DF is that all concentrations below the estimated POD are collapsed to a single value (i.e., d_m = 1), similar to a background control group. This incorporates the regulatory concept that these concentrations are all “acceptable” while higher concentrations are less desirable. Importantly, we do not interpret the analyses as a biological indication of no effect below the join point as in a threshold model; instead, it is a regulatory concept imposed on the data. The advantage of the mapping is that the geometric mean of the individual d values is available for construction of an index for evaluating the mixture effect.

We have presented percentile-based asymmetric confidence intervals on the join points (δ_m) based on bootstrap sampling. When the join point is estimated above the observed data (i.e., δ_m > max(X_m)), the model is over-parameterized with no change in the objective function for an estimate of, say, 1 unit or 10,000 units above max(X_m). Thus, the interpretation of the upper limit of the confidence interval should be in comparison to the maximum observed concentration. The upper 95th percentile of the join point estimates was within the observed data range in all cases (Table 1) except for PFOS and the PCBs in the analysis of LD. We can claim the concentrations of PFOS exceeds the BE value since even the average bootstrap estimate exceeds the guideline; however, the upper confidence limit on the PCBs cannot be compared to the BE value as it is (arbitrarily) estimated above the observed data range.

It is important to note the distinction between HBM values derived from in vivo studies with pharmacokinetic models linking the PODs from animals to humans, and those estimated POD values from epidemiology data, as proposed herein. Even when estimating single joinpoints in Eq. (1) using human data, the true exposure is to multiple chemicals not specified in the model. It is reasonable to expect that the estimated PODs would be lower than those from experimental animal studies that truly represent a single exposure. In fact, these estimated values of the join points might provide additional information for selecting uncertainty factors (UFs) for published HBM values in order to address the lack of information related to combined exposure. Comparing the published values in Table 1 with estimated values (Single chemical analyses and Mixture analysis), the “mixtures UF” for the phthalates (except for DEHP) and phenols could be in the order of 10 to 100 (e.g., the published BE value for MEP is 18,000 μg/L compared to the estimated join points for single chemical and mixture models ranging between 150 and 325 μg/L, ratios between 55 and 120). For PFOS and PFOA, however, the published HBM values are quite similar to the PODs estimated in the analysis of birth weight and language delay, and hence the mixture UF would be close to 1. Interestingly, the HBM values for PFOA and PFOS are based on human epidemiological studies (translation of commission report into English: (HBM, 2016)), whereas, HBM-values for the other chemicals are based on single chemical experimental dose-response studies performed with laboratory animals.

The proposed ACR models estimate PODs using important health effects as an outcome variable (here, birth weight for growth and language delay for neurodevelopment). A continuing line of inquiry is how to select estimated PODs across multiple health effects. There is a growing literature that humans are at risk for comorbid conditions, so that estimated PODs may be similar (e.g., within an order of magnitude) across a set of analyses. For example, neurodevelopment may impact impulsive behavior, which may lead to over-eating and to obesity (Nazar et al., 2016). The analysis of impulsive behavior may provide useful HBM values also to measures of obesity.

As the number of analytes increases in the analysis of MDF, we anticipate potential ill-conditioning concerns from complex correlation patterns in exposure variables. Good starting values from single analyte analyses may be found by conditioning on join points to estimate weight parameters, and using/comparing multiple nonlinear iterative algorithms. We also set d = 1 for components when the single analyte estimate of the join point exceeds the observed data and remove the corresponding DF parameters from the mixture model.

4.1. Limitations

As with all analyses, the proposed class of models has limitations. As depicted by the two-dimensional description of the acceptable region (Fig. 2), there are errors in identifying subjects as falling into, or out of, the acceptable region due to the shape of the region being a square (or hyper-cube in multiple dimensions). If we allowed the region to be a different shape, the error rates would be lower, but the complexity of the estimation would increase due to the interactions among the components. Second, we use the average estimate of the POD values across B bootstrap samples. Perhaps another summary statistic could be used, e.g., the 75th percentile. We are currently conducting simulation studies to evaluate these decisions. We have considered 11 jointly detected chemicals in the current analyses. We leave as future work the effect of considering a dozen or more components simultaneously on the quality of the estimated parameters. The SELMA cohort has dozens of other chemicals measured in the same samples, which were not included in this analysis. Herein, we limited our focus to those chemicals where BE or HBM values have been published, which permitted a comparison of empirical estimates from our model to the published values. Finally, these data have not been previously published with more complete discussion around their interpretation (e.g., the potential for reverse causation, the use of using exposure estimates in a single sample with compounds with short half lives, the potential from confounding from the other chemicals).

4.2. Summary and conclusions

We introduce a new class of models, called ACR models, that include the regulatory concept for non-cancer endpoints where there is an acceptable region of exposure to environmental chemicals. The proposed nonlinear models are parameterized to estimate the point of departure in terms of biomonitoring data for each chemical from a mixture of chemicals. We illustrate the strategy using prenatal concentrations from 11 environmental chemicals and two health outcomes: birth weight and language delay. We determine that the published HBM values are in most cases orders of magnitude higher than those estimated using human data.

The new proposed method complements current risk assessment methods by estimating guideline values using human epidemiology biomonitoring data where multiple chemical concentrations are measured simultaneously and represents human relevant exposures, i.e., complex mixtures. This is in contrast to using surrogate experimental models of single chemicals to estimate points of departure in risk assessment. However, causation is proven in experimental assays and is more difficult to claim in human studies. Integration of information from both models provides further insight into health effects related to environmental exposures. When applying this new class of models, the results suggest that chemical-by-chemical approaches underestimate risk by a factor that range from 1 to 100 for different chemicals.