RemBrain: Exploring Dynamic Biospatial Networks with Mosaic Matrices and Mirror Glyphs

Abstract

We introduce a web-based visual comparison approach for the systematic exploration of dynamic activation networks across biological datasets. Understanding the dynamics of such networks in the context of demographic factors like age is a fundamental problem in computational systems biology and neuroscience. We design visual encodings for the dynamic and community characteristics of these temporal networks. Our multi-scale approach blends nested mosaic matrices that capture temporal characteristics of the data, spatial views of the network data, Kiviat diagrams and mirror glyphs that detail the temporal behavior and community assignment of specific nodes. A top design specifically targeted at pairwise visual comparison further supports the comparative analysis of multiple dataset activations. We demonstrate the effectiveness of this approach through a case study on mouse brain network data. Domain expert feedback indicates this approach can help identify trends and anomalies in the data.

INTRODUCTION

Recent neuroscience research indicates that cognitive operations are performed not by individual brain regions working in isolation, but by networks consisting of several discrete brain regions which act in synchrony.¹ These networks share “functional connectivity,” meaning that activity in these regions is tightly coupled—in the sense of a statistical association or dependency among two or more anatomically distinct time-series events. Functional connectivity between brain regions can change rapidly over time,^2,3 giving these networks a highly dynamic characteristic. Abnormalities in functional connectivity have been linked with various degenerative and developmental affections. Evidence suggests, for example, that Alzheimer’s disease spreads from one brain region to a non-adjacent region within a specific network, which is “activated when a person is recalling recent autobiographical events.”¹ However, even for simple networks, the subtle dynamics of these networks are not fully understood. Therefore, techniques that are able to extract the dynamics of functional connectivity from brain imaging data have high potential value to the neuroscience community.

At the same time, advances in imaging technology allow, at increasing pace, the comparative investigation of functional connectivity dynamics at multiple scales, both at the temporal level (time series, trials) and at the space level (neurons, neurons grouped in pixels, regions of interest). In computational neuroscience and computational systems biology, each imaging snapshot captures one activation pattern in the temporal behavior of a biological system. The connectivity is then extracted from these images, in the form of networks with large numbers of nodes (over 20,000). Next, computational models are employed to calculate the functional network dynamics. In order to study the mechanisms of disease or aging, the process of imaging and modeling is performed repeatedly over multiple subjects, specimens or conditions, leading to a rich tapestry of spatio-temporal imaging and computing data that need to be analyzed. Visual analysis of such complex neuroimaging data can help domain experts understand temporal features along with their spatial references.

In this work, we present the design and implementation of RemBrain, a novel visualization tool for the comparative analysis and exploration of dynamic brain activation networks. RemBrain (named after the intrepid Pixar rodent Remy) is a multi-scale web-based application that supports the tracking of temporal network behaviors. Responding to the novel data characteristics above, RemBrain integrates interactive, multi-scale 2D visualizations of imaging data; displays network connectivity data for each activation snapshot; captures the temporal behavior of a subregion of nodes using novel encodings; and supports pairwise visual comparison of multiple activations. This work, a follow-up to the award-winning Swordplots⁴ (published in JIST), enables the exploration and comparison of different activations at multiple levels in dynamic biological networks. The main contributions of the paper are:

• A description of the domain data and problems in comparative neuroscience dynamic network analysis.

• A novel multi-scale visual representation, which enables the exploration of networks at multiple levels: overview, regional, detail. Aggregate Slices (overview), Mosaic Matrices (regional), and Mirror Glyphs (detail) track community dynamics over time.

• A flexible workflow for comparative visual analysis, which supports the pairwise comparison of activations.

• An application to dynamic neurobiology mouse brain data, developed in collaboration with domain experts.

• A demonstration through a case study and a summary of the feedback provided by domain experts.

BACKGROUND AND RELATED WORK

Domain Background

In a typical project that seeks to analyze dynamic biological networks, data is collected through time-series imaging of the biological system as the system is stimulated in some way. Bright spots in the imaging data indicate neurons (or cell components) that are activated at that time step (Figure 1(a)). Correlation networks can be automatically constructed from these bright spots; over the time series, the correlation networks change dynamically (Fig. 1(b)).

Figure 1.

Data processing. (a) Neuroscientists collect time series of biological imaging data (in this instance, mouse brain slices). Bright spots in each image indicate activated (firing) neurons. (b) We use the Pearson correlation method to construct, from these images, an equivalent time series of correlation networks (top, abstraction). The correlation networks (bottom, image overlay) correspond to three time steps; blue dots encode the active nodes and green edges encode the links between correlated pairs. (c) We apply CommDy to these networks to infer dynamic communities (top, abstraction). Four communities (blue, green, orange, red) are overlaid on mouse brain images, for three time steps, in the bottom image.

Algorithms—many originally developed for dynamic social network analysis^5,6—can then be applied to the network data to infer groups of neurons that act as a community over time (Fig. 1(c)). In the context of brain network analysis, a “community” is analogous to a neural assembly,⁷ which we define as a group of neurons that are functionally connected and have similar temporal behaviors.

Brain Connectivity Visualization

Many techniques exist for visualizing brain connectivity at either macroscopic (region level)^8–12 or microscopic (neuron) scale.^13–17 In this work, we design a neural encoding inspired by the Swordplots of Ma et al.⁴ However, to the best of our knowledge, no other visualizations exist for multi-scale biological connectivity data.

Our data further blends spatial and non-spatial features. Marai¹⁸ identified two prevalent paradigms for integrating spatial and non-spatial features: overlays and multiple linked views. In neuroscience studies, an overlay approach^8,19,20 is commonly used when the non-spatial feature represents only functional connections. However, as the non-spatial data becomes more complex (activation levels, connectivity, clusters, dynamic characteristics, and other statistics), the linked-view paradigm^15–17,21 becomes the default choice. Nowke et al.¹⁴ use a hybrid approach that consists of both overlays and linked views. We follow a similar hybrid approach to support the exploration of dynamic biospatial networks.

Dynamic Network Visualization

In static network visualization, the most common visual representations are node-link diagrams²² and matrix-based visualizations.²³ Several projects^24–26 use a hybrid approach that combines both representations.

Dynamic networks and graphs are usually visualized using either animation or a timeline-based representation.²⁷ Several projects^28–31 use animation to represent networks with temporal components. To display dynamical changes of networks into a single static view, Greilich et al.³² placed a sequence of graphs onto a timeline. Several other projects^33–35 use timeline-based representations to visualize the evolution of communities in dynamic networks. Rufiange and McGuffin³⁶ presented a hybrid approach for visualizing dynamic networks. In addition to mapping the time to the 2D space, Bach et al.³⁷ developed a Matrix Cube representation based on the space–time cube metaphor. The Matrix Cube shows the network structure using the 2D matrix and maps time to a third dimension. However, their technique is only scalable to networks that consist of a few nodes across short periods.

While, as shown above, a large number of visualization techniques exist for static brain connectivity, as well as for dynamic non-spatial networks, to the best of our knowledge this novel domain is the first to require visualizing and integrating both types of data.

Multi-scale and Comparative Visualization

In the visual analysis of neuroscience data, VisNEST¹⁴ and NeuroLines¹⁶ integrate data at macroscopic level with microscopic level. We similarly adopt a multiple views approach for different levels using both focus+context and details on demand. Visual comparison of brain spatial–non-spatial data is a relatively new research problem in neuroscience. Only a few tools^38,39 can be found. Maries et al.³⁸ introduced a comparative framework for mining brain geriatric data. Lindemann et al.³⁹ presented a comparative visualization system that explicitly encodes changes of brain tumor segmentation volumes in shape and size before and after treatment. Outside the application domain, Gleicher et al.⁴⁰ proposed a general taxonomy that groups visual designs for comparison into three categories: juxtaposition (side by side), superposition (overlay) and explicit. Because of the complexity of our data, in our approach we use side-by-side linked views.

DATA AND TASK ANALYSIS

Data Analysis and Processing

The input data consists of flavoprotein autofluorescence imaging data collected, in this case, from mice brain specimens captured in the TIFF format. A pixel contains roughly 100 neurons, and the image acquired at a specific time step has dimensions of 172 × 130, leading to a file size of 24 KB. One activation cycle lasts about 100 time steps. Fig. 1(a) shows an example of a time-series data collected from mouse brain slices. The raw imaging data has two critical features: the pixel (node) signal value—pixel intensity (gray) value, which indicates the activation level, and the pixel (node) spatial location in the brain slice. This imaging data is processed in three steps: (1) infer a network model, (2) perform dynamic community analysis, and (3) compute community metrics.

Network Model Creation

To create a network model, we associate each pixel in the image with one network node. To capture internode interaction, we compute all pairwise correlations for the 172 × 130 nodes over a given window using the Pearson product-moment correlation coefficient (PCC)⁴¹—a measurement of the strength of the linear relationship between signals of two nodes. This process leads to a weighted correlation network, represented by a list of weighted edges that connect pairs of nodes. Weighted edges w(X,Y) represent the linear correlation coefficient between any pair of two nodes (X and Y) over a time window t (Eq. (1)).

$$\begin{gathered} \omega (X,Y)=\mathit{corr}(X,Y)=\frac{1}{t-1}\sum _{i=1}^t\left(\frac{X_i-X_{\text{mean}}}{S_X}\right) \\ \times \left(\frac{Y_i-Y_{\text{mean}}}{S_Y}\right),\mathit{corr}(X,Y)\in [-1,1],\text{where} \\ {X}_{\text{mean}}=\frac{1}{t}\sum _{i=1}^t{X}_i\text{and}{S}_x=\sqrt{\frac{1}{t-1}\sum _{i=1}^t{(X_i-X_{\text{mean}})}^2}. \end{gathered}$$ (1)

By repeating the computation of correlation while shifting the window one time step for each iteration over the entire timeline T, we obtain a time series of weighted and thresholded correlation networks. Fig. 1(b) bottom shows an example correlation network at three time steps; blue dots represent active nodes and green edges represent links between pairs of correlated nodes. Summarized characteristics of each node, e.g., the node degree, can yield insight into mechanisms underlying system growth.⁴²

To determine the appropriate time window and correlation coefficient thresholds for applying dynamic network analysis to brain imaging data, we tested the system with an analysis window size of 25, 50, 100 and 200 frames. The 50-frame window successfully yielded high temporal resolution while not introducing spurious correlations, and consequently was chosen for analysis.

Dynamic Community Analysis

In network analysis, a cluster or community is formed by a group of nodes that have either more or stronger connections with each other. Nodes belonging to different communities have few and weaker connections. Community analysis can be applied to a variety of fields from social networks to biological networks.⁴³

Because networks change their topological structure dynamically, a dynamic community identification method is needed. For example, a node may belong to a specific community most of the time (Home community), but also join temporarily a different community (Temporary community), as shown in Figure 2. In brain network analysis, neurons that belong to the same community likely have similar functionality. Neurons visiting or joining another community may indicate a change in their functionality.

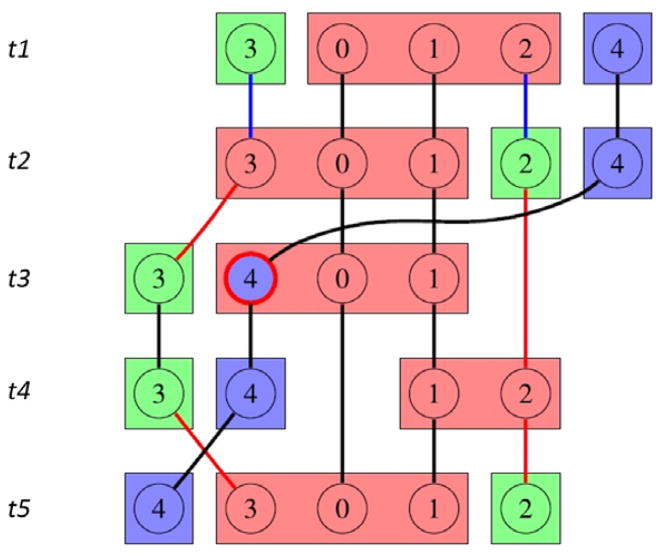
Figure 2.

Illustration of CommDy on an example data set that includes five members, shown here over five time steps t1–t5.¹³ Colors encode communities (circles for the Home community, and squares for the Visiting community, if different). Members 0 and 1 stay permanently in the pink community. Members 2 and 3 alternate their Home memberships from the pink/green community to green/pink twice (at t2 and t5). Member 4 temporarily visits the pink community at t3, but maintains a Home membership to the blue community.

We use the Dynamic Community Interface (CommDy) method^5,44–46 to analyze how the interactions and structures of communities change over time in the dynamic brain networks. CommDy produces two identification codes: a Home community that identifies the community the node belongs to by default, and a Temporary community that identifies the community the node currently visits. The visiting behavior means the node leaves its own community temporarily but will return back very soon. Fig. 1(c) top shows an example network of five nodes across three time steps. In this illustration, the color of the inner circle represents the Home community identification code of the node, and the square surrounding the circle represents the Temporary community.

Fig. 1(c) bottom shows the dynamic community analysis results of the example networks in Fig. 1(b) bottom. Because imaging noise can introduce small spurious communities of 2–3 nodes, domain experts keep for analysis only the ten largest communities identified by the CommDy algorithm (where size is averaged over the entire timeline).

Note that spatial relationships between nodes are not considered when detecting communities, to avoid the potential introduction of biased assumptions about the relationship between structural and functional connectivity.

Metrics Computation

Finally, the dynamic community characteristics are used to generate metrics that summarize the behavior of active nodes. CommDy quantitatively describes the characteristics of the inferred networks, at both node and structural level, based on network analysis theory.⁴⁷ We use 10 relevant metrics to describe the interactions between nodes. These metrics include the average time spent by a node in a community, the number of jumps across communities executed by a node, the fraction of node peers who were its peers in the previous time step and so on. All these characteristics are normalized to a value within the range of 0–1. Table A.1 summarizes the full list and definition of the node metrics. Based on the results produced from the current datasets, the number of active nodes varies with different activations of different subjects from approximately 5000 to nearly 10,000.

Task Analysis

Based on several interviews with a domain expert, we identified the following tasks for the comparative analysis of brain activations, and in particular for understanding how aging impacts the auditory cortex (AC) of mice:

• Task 1: Explore the community spatial distributions at multi-scale. Brain imaging data contain thousands of nodes. Neuroscientists need to get an overview of the entire dataset, but also to observe a subregion or even an individual node in detail.

• Task 2: Track temporal changes at multiple levels. Be able to observe the evolution of communities over a user-defined time window, compare the temporal behaviors of nodes in the same subregion, or track the behavior of a particular node across the entire time period.

• Task 3: Explore relationships between functional connections and spatial structures. An interesting and expected finding would be that specific nodes located in different regions of the brain have similar temporal behaviors.

• Task 4: Compare the differences in temporal and spatial behaviors between young and aged animals at multiple levels.

These tasks map to three groups in the visual data analysis taxonomy:⁴⁸ Explore: Task 1, Task 2, Task 3 and Compare: Task 4.

Visual Design

The spatio-temporal datasets and comparison tasks captured above are particularly complex. Furthermore, they feature a mix of spatial and non-spatial data, and the experts lack familiarity with complex visual encodings. Because of these combined reasons, we follow a coordinated multi-view top-level design, which has been shown to assist in visual scaffolding.¹⁸ In this design, a set of multiple views at different scales provides guidance to the domain expert when exploring the data. In addition to the exploration tasks, pairwise comparison is supported by side-by-side views (Task 4).

Figure 3 shows the interface of RemBrain, which consists of four main visual components: (1) an overview spatial panel (Fig. 3(a) and (b)) that nests subregion temporal information through a mosaic-matrix encoding; (2) an individual behavior panel (Fig. 3(e) and (f)) that includes a novel Mirror glyph to display in detail the dynamic attributes for a particular node, and a Kiviat diagram for the summarized characteristics of the corresponding node; and (3) a timeline representation (Fig. 3(c) and (d)) that controls the spatial panel and the mosaic-matrix view. These multi-scale views are linked through interaction. Two sets of each panel are placed side by side for visual comparison.

Figure 3.

RemBrain implements a visual approach for the analysis of spatio-temporal brain network data. Two aggregate panels (a) and (b) encode the spatial distribution of neuron communities in mouse brains, overlaid with the medical imaging data. mosaic-matrix views (top left of panels) encode temporal changes in a selected subregion. Two timeline views (c) and (d) show the number of active nodes over time; (c) shows that the activation has 8387 active nodes at time step 50, and (d) shows the activation has 6890 active nodes at time step 48. Two mirror glyphs and Kiviat diagrams (e) and (f) allow tracking dynamic changes over time at a single node level. A control panel (g) enables filtering of node communities; colors are mapped to community IDs.

The side-by-side comparison design, in conjunction with the multi-scale views, supports Task 4. The slice-based panel displays the community distribution in space and thus explicitly supports Task 3. The individual behavior view enables exploration at the level of individual nodes (Task 2). The mosaic matrix enables exploration at the level of subregions (Task 2, Task 1). The three views work together to support Task 1 through Task 3. Below we describe in detail each visual component. The web-based visualization tool is implemented in JavaScript using the D3 data visualization library.

Aggregate Slice Panel

The slice-based view shows the community distribution map overlaid upon the brain slice image. In this distribution map, nodes are color-coded by their Home community ID. To enable multi-scale temporal analysis (Task 2), instead of displaying the community information at a single time point, we aggregate over a user-selected time period and color the active nodes by their most common community during that time period. We assign to each of the 10 largest communities a unique color (Fig. 3(g)) from a qualitative colormap from ColorBrewer2.org. Nodes colored in gray are either inactive or belong to a community not in the top ten. A control panel filters which communities are shown. The view is automatically updated according to the selection in the timeline widget (Fig. 3(c) and (d)).

Individual Panel: Mirror glyphs and Kiviats

The aggregate slice-based view shows the spatial distribution of communities. However, it is also important to display the temporal distribution of communities, along with other temporal attributes. To this end, the individual behavior panel combines in a novel design time-dependent numerical and categorical data. This detail view allows users to explore in detail the dynamic behavior of individual nodes through a timeline-based representation. The panel (Fig. 3(e) and (f)) integrates a mirror glyph for analyzing the temporal node data and a Kiviat diagram for visualizing multiple summarized characteristics.

Mirror Glyph

The mirror glyph supports tracking the characteristics of a particular node over time. These dynamic characteristics include raw signal values, node degrees, and two community identification codes over time, the Home community and the Temporary community (Table A.1). A preliminary illustration of dynamic community analysis results is shown in Fig. 2, in which circles are individual nodes labeled with their identification numbers, and rectangles correspond to communities. Communities are identified through matching colors. However, this visual encoding does not scale well to a large number of nodes. Additionally, it is hard to track an individual’s community behavior over a long time period, and there is no reference to the spatial location of the nodes. Because a timeline-based representation was an intuitive and simple way to track temporal changes, we design a mirror glyph to visualize an individual node’s temporal behavior (Task 2).

Each mirror glyph (Figure 4) has three components: middle black trunk, upper bar chart, and a mirror-like lower bar chart. The height of the upper and lower bar charts represents the node degree over time, because domain experts indicated the degree evolution over time was the important quality in this context, next to the Home and Temporary IDs. The upper chart color encodes the Temporary community while the lower chart color encodes the Home community. The color of bars in the charts indicates the community ID of the node over time. Mouse interaction further shows the type of community represented by a bar. While the upper and lower charts are often almost symmetric (hence the “mirror” aspect), they can also be asymmetric. Frequent horizontal color changes in this composite glyph indicate node instability. Similarly, a vertical asymmetry between the upper and lower charts indicates high instability.

Figure 4.

Mirror glyph showing a node that belongs predominantly and consistently to the green community, as its signal increases over time, without much visiting or switching. The only temporary visiting event happens at t1, when the node briefly visits the blue community. Two switching events happen at times t2 and t3, when the node joins the orange community, followed by the blue, just as the node signal is about to peak (middle trunk). The node degree (chart height and content) is almost symmetric: the Temporary community (upper chart) almost mirrors the Home community (lower chart).

The line plot in the middle black trunk of the mirror glyph encodes the variation in raw signal intensity over the activation period, from 0 to 100, which is the maximum number of time steps in our datasets. The trunk’s gray segment highlights the user-selected time period. The vertical axis indicates the maximum node degree during the entire timeline. Fig. 4 illustrates how this composite glyph can capture dynamic node behaviors. The end mirror glyph result captures a high temporal resolution of the node behavior. The spatial location of the corresponding node is highlighted in the aggregate slice-base view.

We converged toward this streamlined mirror glyph design through parallel prototyping with multiple iterations; some prototypes were completed on paper, and some in software. Driven by the experts’ preference for clarity over compactness, the glyph design converged toward this dual layout, as opposed to stacked graphs or a non-flipped layout. To this end, we note that the data itself was extremely complex and that detecting brief community visits was relevant to the tasks. Similarly, the raw signal intensity and its evolution over time in relation to the community distribution and degree were task-relevant. In this case, the trunk design favored the signal charts that the experts were familiar with.

Kiviat Diagram

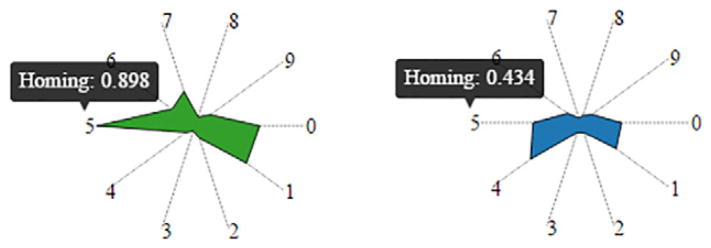
To encapsulate the 10 summarized attributes (e.g., observed, time span, switching, etc.) shown in Table A.1, either parallel coordinates or star plots are natural choices. However, in the parallel prototyping stage, PCPs were overruled due to low visual literacy among the domain experts and to their less compact appearance. The experts’ specific goals, in this case, were detecting significant differences and similarities in the data, to be later analyzed quantitatively (as opposed to precise visual comparison). In fact, one of our two experts remarked on the imprecise nature of measurements computed at the single node scale. Because the experts further favored legibility over precise comparison, we converged toward a star-based Kiviat diagram encoding (Figure 5), as opposed to a line-based star plot, or simple dots on axes. Nevertheless, the Kiviat representations can be optionally superimposed (with transparency) to better support comparison. Each axis of the Kiviat diagram represents one of the ten node metrics. The most common community of a node is encoded in the color of the Kiviat diagram.

Figure 5.

Kiviat diagrams for two nodes that reside most time in the green, respectively blue community. The Kiviat shapes indicate that the green node has longer activation duration, stays in particular communities for longer periods, and is more consistent with its Home community. Conversely, the blue node switches its Home communities and visits other communities more often. Note the details on demand and index indirection dictated by real-estate constraints.

Mosaic-Matrix View

The aggregate slice-based view shows the community spatial distribution at an overview level with high spatial resolution, but low temporal resolution. On the other hand, the individual panel shows the community temporal distribution per node with high temporal resolution but low spatial resolution. While each of these representations has strengths, our task analysis indicates that visual exploration at a level with both reasonable temporal and spatial resolution was important. To support this type of analysis, we design a mosaic-matrix encoding. The encoding captures temporal and regional changes and integrates them into the community spatial distribution map.

Because nodes are densely located in brain slices, using 1D timeline-based representations was not feasible. Instead, we adopt a compact two dimensional layout to encode time-dependent behavior. The layout is composed of a set of cells that define a mosaic matrix. The set corresponds to a node region, and each cell encodes the temporal behavior of an individual node in that region (Figure 6). Each cell, in its turn, is a 2D dense pixel layout that wraps time into 2D. The sub-cells encode with color the set of communities that node belongs to during the selected time period. Figure 7 shows two mosaic matrices for a subregion of 9 nodes across 33 time steps (top), respectively 64 nodes across 12 time steps (bottom). Fig. 6 further demonstrates the nesting of community temporal information across 64 time steps into the brain slice of an aged mouse. The selected area highlighted in the black circle is a region of 9 nodes. Each of the nine nodes within the selected region is represented in the mosaic matrix as a cell. The 64 (8 × 8) sub-cells encode temporal behavior, with time increasing from left to right and top to bottom.

Figure 6.

Integration of temporal community characteristics into the brain slice of an aged mouse, across 64 time steps.

Figure 7.

Two mosaic-matrix views representing two regions (at different zoom levels) across different time periods: (a) a region of 9 nodes across 33 time steps; (b) a region of 64 nodes across 12 time steps. In (a), the node in the top-left corner of the mosaic matrix is initially part of the green community, then moves to the orange community, and finally joins the pink and blue communities in the last two time steps. In (b), the mosaic captures instability (frequent changes) in the region selected.

However, the integrated temporal features may not be easily observed when displaying the entire brain slice. Additionally, zooming into a small region loses the relevant spatial references. Therefore, we enabled a detailed region view without losing the context of the slice. The resulting mosaic-matrix view is composed of several sets of cells.

Fig. 7(a) displays the temporal behavior across 33 time steps, while Fig. 7(b) displays 12 time steps. In Fig. 7(a), the node in the top-left corner of the mosaic matrix is initially part of the green community, then moves to the orange community, and finally joins the pink and blue communities in the last two time steps. Unlike the traditional timeline-based (one dimension) visualization for time-series data, the mosaic-matrix view allows us to effectively nest the temporal features into the spatial structures.

Users can both interactively translate a selection lens in the slice-based view and drag the zoom size slider in the control panel (Fig. 3(g)) to adjust the region size (number of nodes) selected. The mosaic matrix can flexibly capture from one node to 100 nodes, as well as from one to 100 time steps, the length of the entire timeline in this study. Because in this study more than half of the brain slice was inactive at all times, we overlay the mosaic-matrix view on the top half of the slice, to efficiently use space. In cases where the image activation data may become obscured by the mosaic-matrix view, the mosaic-matrix window can be moved by dragging the upper gray bar.

Timeline Widget

The timeline widget enables navigation over time in the slice-based view and mosaic-matrix view. Using the widget, a user can click and drag to select the time window. To further help identify the time window during which each slice is most active, the timeline widget also encodes as a plot the total number of active nodes over time (Fig. 3(c) and (d)). Two dashed lines mark peak activity—the time step with the largest number of active nodes.

Synchronization and Comparison Support

To support the pairwise comparison of activations (Task 4), we adopt a coordinated side-by-side dual layout (Fig. 3(a)–(f)). This layout integrates multiple views at different levels: two slice-based views, two timeline views, two mosaic-matrix views, and two individual behavior panels. In our experience, because of the data complexity and a large number of differences in the datasets that are typically compared, the use of juxtaposed views effectively reduced visual clutter when compared to superposition. Moreover, the domain experts valued raw data and strongly objected to the superposition of brain slices (via registration) from different specimens. Although the individual behavior panel does lend itself to superposition, and we do support Kiviat overlays, the designers and the domain experts converged to a side-by-side layout for all views, in order to maintain consistency. As in other studies that involve domain scientists and require visual scaffolding,^18,38 we found that design clarity and consistency principles take precedence over expressiveness.

Because domain experts perform the comparison in both the spatial and temporal domain, we implement two default options for synchronization: a timeline synchronization (timeline widget) and a region synchronization (aggregate slice view). However, when comparing different specimens, the activations and spatial structures may not be completely aligned. Because of this constraint, we provide an asynchronization option as well, which allows the domain experts to manually align temporal or spatial features.

RESULTS AND DISCUSSIONS

We evaluated RemBrain through a combination of multiple demonstrations and case studies (real data, real tasks, real users) with our collaborators: an established neuroscientist researcher (DL) who specializes in computational biology, neuroimaging and neurobiology, and a senior researcher in sensory-motor performance (RK), who has a broad background in studying the adaptation of motor systems and imaging data from physiological systems. Both experts have been working together on dynamic brain network analysis for several years. Throughout the evaluation process, we used a “think-aloud” technique,⁴⁹ which asks users to verbalize their thoughts as they interact with the system, and we collected feedback at the end.

Here we report a case study performed separately by the two scientists, in separate sessions. In this study, the domain experts seek to understand the impact of aging on the AC in mouse brains. To this end, they had collected imaging data from a young mouse and an old mouse. Brain slices from each specimen were artificially stimulated, and the resulting activation levels were imaged as a time series. The case study and verbiage reported below have been simplified for a lay audience.

Case Study: Aging analysis in mouse brains

The domain experts wished to investigate how aging relates to auditory processing changes, through the comparison of network activity in the AC from young and aged mice, at multiple scales (Task 1 through 4). Each expert started by loading the dataset of the first activation of young mouse No.40 (5.5 months) and the dataset of the first activation of aged mouse No.38 (22 months) in the two side-by-side views.

Overview spatial, multi-scale in time exploration

The analysis started at the high overview level of the entire AC. The community distribution differences were immediately noticed in the slice-based panels (Figure 8(a) and (b)): over the same time window, the young mouse AC features an additional community, shown in green. The young mouse AC (Fig. 8(a)), in particular, featured a ring-type structure of community distributions. That structure was stable even as the experts translated and scaled their time window selection in the widget (Task T2, T4). In contrast, the community distributions in the aged mouse AC (Fig. 8(b)) were less structured. In fact, the neuroscientist expert noted that no contiguous region in this brain image was associated with one single community. The second expert noted that in the timeline views the activations from the two specimens decayed at different rates after reaching their peak. The timeline also captured a higher total number of active nodes for the younger specimen, which was expected. The domain experts concluded that the connectivity between neurons diminishes with age, which “probably correlates with a particular receptor [decay].”

Figure 8.

Case Study: Aging Analysis. The slice-based views (a) and (b) capture a difference in the community spatial distributions between young and aged mice. The mosaic-matrix views in (a) and (b) present both the spatial and temporal features of communities in two similar regions of young and aged mice. The timeline views (c) and (d) show a higher total number of active nodes for the younger specimen. While the (a) (d) views compare the two specimens at a high and regional level, the individual behavior views (e) and (f) allow for comparison at the individual node level, both spatially and temporally.

Regional Spatial, Multi-scale Time Exploration

The multi-scale analysis moved next smoothly to the regional scale captured by the mosaic-matrix views (Task T1, T3, T4). For this analysis, the experts disabled synchronization, and manually selected two regions (marked by red boxes) in roughly the same area of each AC. The difference in the dynamic community behavior between the two regions was striking. The cleaner and predominantly blue mosaic-matrix view in Fig. 8(a) captured a homogeneous dynamic behavior in the young mouse AC region. Most nodes in this brain region spend their time in only one community, blue. In contrast, the mosaic matrix for the aged brain in Fig. 8(b) indicates significant instability, which revealed the heterogeneity of the aged mouse AC. Only a few nodes stayed in a single community during the user-selected time. Furthermore, the aged AC network was significantly more fragmented over time, especially as the experts enlarged the time window size. The experts moved their attention repeatedly between the regional scale and the overview scale.

Individual Spatial, Multi-scale in Time Exploration

In the final analysis stage, the dynamic behavior at the scale of a single node was taken into consideration, in addition to the previously examined spatial scales (Task T1, T4). In several iterations, the experts selected specific cells in the mosaic matrix, one at a time, and examined them through the individual panel (Fig. 8(e) and (f)). The nodes examined in this figure are located in the bottom left corner of the mosaic-matrix views. Surprisingly, both young and old nodes exhibited symmetric behavior with respect to their Home and Temporary distribution. However, the node degree over time was almost double for the young neuron, when compared to the old. Furthermore, the mirror glyph encoding quickly showed, for example, that sample nodes in the young mouse brain featured few major changes in dynamic communities over the entire time window. In Fig. 8(e), the selected node switches only twice closed to the start of the window, from green to blue and from blue to purple. In contrast, the aged mouse node shown in Fig. 8(f) switches much more frequently at the start of the activation.

The difference noted above was reinforced by the Kiviat diagrams, where the two Kiviat shapes were notably similar in many respects. In the example shown, both nodes score along the normalized average time span of communities (axis 1), but only the aged neuron has a non-zero normalized switching cost (axis 2). Furthermore, the aged mouse also had a shorter activation time (axis-0), and fewer connections than the young mouse. At this point, the neuroscientist expressed interest in seeing the raw signal data. To this end, the experts examined the raw signal plots in the behavior mirror glyphs, and discovered that the old mouse rising time is generally slower and that the curve during the rising time is less smooth for the old mouse.

Case Findings

This multi-scale analysis indicated that aging is associated with a series of changes in node metrics, such as community size and switching cost, and also with temporal changes in individual behavior, such as dynamic community distribution. These changes are consistent at multiple spatial and temporal scales. Together, the domain experts hypothesized that those aging-related changes at multiple scales might be related to changes in intracortical connectivity (Task T4). Using the insight from the multi-scale visual exploration, they are designing methodology to capture and quantitatively report these correlations.

Domain Expert Feedback

The domain expert feedback included comments such as “very cool, interesting tool,” “fantastic,” and “useful to generate hypotheses.” Since everything in biology is “so tied to spatial location,” the experts found that the integration of the spatial layout and non-spatial network attributes was far more useful than analyses based only on the non-spatial data. In addition, the mosaic matrix provided the ability to explore temporal relationships between nodes with close proximity in the same region, and thus preserved a useful spatial context. While originally unfamiliar to the experts, the mirror glyphs and Kiviats were later praised for their potential to drive hypotheses at the neuron level, once crisper node data become available through the next imaging project. Overall, the experts found that RemBrain augmented their ability to analyze the heterogeneous and multifaceted datasets common in dynamic bionetwork analysis.

Compared to prior analyses of the data, which were done directly with data files and relied on the experts’ mental model of the node location within an image, our visual approach succeeded in communicating the spatial findings to others. Also, the experts noted that interactively exploring the imaging data to identify an interesting time step was far more efficient than manually searching an image from a repository.

DISCUSSIONS

Meeting the Original Goals

The case study and expert feedback demonstrate the effectiveness of this multi-scale visualization approach to the comparative exploration of dynamic activation networks across multiple brain imaging datasets at multiple levels. Experts were able to find new, interesting patterns in datasets they had explored using different tools before. They both are eager to adopt the tool for research purposes, both in an exploratory setting and in an explanatory setting (for publication purposes).

The overall design was successful at supporting comparative analysis in a variety of dataset combinations. We note that few guidelines exist in visual comparison design. In most instances in our design we favored juxtaposed (side-by-side) layouts, to attain better clarity and consistency, and to circumvent alignment issues. One exception is the star panel, where the lack of a physical structure supports superposition. Overall, we found that a hybrid approach best supported the tasks revealed by the domain analysis.

The experts considered the inclusion of the spatial context a most valuable feature, and reported the approach was far more useful than analyses based only on the non-spatial data. The chosen visual encodings showed complementary strengths in supporting multi-scale spatio-temporal analyses. When coupled with a coordinated multi-view approach, these encodings enabled visual analysis across the entire pipeline for dynamic bionetwork data analysis: raw data, network results (node degree), dynamic community analysis based on the results of dynamic networks, and summarized node metrics based on the dynamic community analysis. The experts were able to navigate smoothly between multiple scales in both space and time.

Novelty

The mirror glyphs and the embedding of temporal features in a spatial context through the mosaic-matrix views are novel contributions. The composite mirror glyphs, in particular, are not restricted to the presentation of dynamic node behavior in neuroscience. These glyphs can also be applied to general temporal data with multiple variables that include both numerical (height) and categorical data (color). Such datasets exist in other domains where symmetric/asymmetric time-dependent behavior is of interest, for instance in the analysis of spectrograph data in astronomy,⁵⁰ in the analysis of financial data, or in the analysis of Electronic Health Records. The mosaic-matrix nesting approach may find application in other spatially dense temporal datasets.

The combination of visual encodings in a tool to handle multivariate data in dynamic bionetwork analysis and the side-by-side multi-scale design that supports pairwise comparison for spatio-temporal data are also novel. The approach has direct application to the analysis of other spatially dependent dynamic biological networks, for instance in computational systems biology.

Design Lessons and Issues

One of the most important lessons from this work relates to limitations arising from increasing model scales and complexity. As scientific models move from static to dynamic, and single model analysis shifts to the comparison of multiple models with spatial and non-spatial features, even known integration paradigms break down with scale: one cannot keep track effectively of tens of coordinated views. Overlays may similarly fail, and in some instances may not be applicable (in our case, due to domain restrictions related to alignment and the importance of raw data). In the approach illustrated here, we have successfully nested the time-driven behavior into spatial structures and used overlaying and details on demand where possible, to overcome space limitations. Still, the resulting interface is information-dense; on a large tiled display, there was still too little space to attach legible Kiviat labels directly to axes. As the range of data acquisition instruments keeps expanding, these issues will only become more stringent in the visualization field.

The second important lessons arising from this experience relate to the necessity of visual scaffolding¹⁸ when dealing with domain experts who are not familiar with sophisticated visual encodings. In our design experience, the application of HCI principles such as clarity and consistency, and the careful consideration of the overall application gestalt were particularly important. For instance, the final design includes dual views for all representations, even though we do support superpositions where possible. We furthermore found success by building upon domain-specific encodings, such as the slice-based views and the timeline widgets. Using those familiar encodings within a linked-view framework served as a visual scaffold, allowing the domain experts to harness and expand their previous analysis experience.

Limitations

In terms of limitations, one of our two domain experts noted that interpreting individual node behavior could be too daring given the current imaging done on the datasets. Nevertheless, he did see the future utility of the behavior glyphs in the context of their next imaging project, which will capture node identity more crisply. Another limitation is that RemBrain can currently be used only as a post hoc analysis tool, due to the data preprocessing load. The dynamic correlation networks computation for each activation costs roughly ten hours. Depending on the size of such networks, the computation cost of dynamic communities identification and network metrics analysis is between one and two hours. This limitation is due primarily to the network metric computation load. Last but not least, matching precisely communities between different experiments (beyond the size proxy for the ten largest communities) is an open research issue, not just in this work, but in dynamic community analysis in general. This limitation is mainly because dynamic analysis methods currently do not consider the spatial relationship of nodes in different experiments. In this case, the domain experts are well aware of and willing to accept this current limitation.

CONCLUSION

In conclusion, we have presented a web-based visual comparison approach for the systematic exploration of dynamic activation networks across biological datasets. As part of this work, we have proposed visual encodings for the dynamic and community characteristics of these temporal networks. Our approach blends multi-scale, nested overviews of the biological data and their temporal behavior, mirror glyph descriptors of network metrics for describing node behaviors, and widgets which detail the temporal behavior and community assignment of specific nodes. A case study on mouse brain network data and the domain expert feedback indicate our approach is effective in the comparative visual analysis of dynamic excitable bionetworks. Last but not least, we have characterized the novel and complex data arriving from the application domain and summarized the lessons learned from visualizing these data, which are spatio-temporal and multi-scale. We believe these lessons transfer across application domains. Future work may apply this multi-scale visual approach to imaging data that has higher spatial resolution, e.g., calcium imaging, or extend these techniques to other biological or geospatial networks.

APPENDIX

Table A.1.

Data descriptors for dynamic bionetwork analysis.

Static/Dynamic	Node Attribute	Attribute Descriptors
Static	Spatial Location	Coordinates in the grayscale image of a brain slice
Dynamic	Signal Value	Pixel (node) intensity value: 0–255 (8 bit)
Dynamic	Node Degree	Number of connections a node has
Dynamic	Home Community	The community a node belongs to
Dynamic	Temporary Community	The community a node currently visits
Static	Observed	Number of time steps a node is active or observed (normalized by the entire time steps)
Static	Time Span	Average span of the communities (the last time step minus the first time step of the communitys existence) with which an individual is affiliated (as a member or absent)
Static	Switching	Number of community switches made by an individual (normalized by the entire time steps)
Static	Absence	Number of absences of an individual from a community (normalized by the entire time steps)
Static	Visiting	Number of visits made by an individual to another community (normalized by the entire time steps)
Static	Homing	Fraction of individual’s current peers, at each time step, who were peers in the previous time step
Static	Avg Group Size	Average size of group of which an individual is a member
Static	Avg Community Size	Average size of community of which an individual is affiliated (as a member or absent)
Static	Avg Community Stay	Average number of consecutive time steps an individual stays as a member of the same community (normalized by the entire time steps)
Static	Max Community Stay	Maximum number of consecutive time steps an individual stays as a member of the same community (normalized by the entire time steps)