Signatures of Hybridization and Speciation in Genomic Patterns of Ancestry

Abstract

Genomes sampled from hybrid zones between nascent species provide important clues into the speciation process. With advances in genome sequencing and single nucleotide polymorphism (SNP) genotyping, it is now feasible to measure variation in gene flow with high genomic resolution. This progress motivates the development of conceptual and analytical frameworks for hybrid zones that complement well-established cline approaches. We extend the perspective that genomic distributions of ancestry are sensitive indicators of hybridization history. We use simulations to examine the behavior of the number of ancestry junctions – a simple summary of genomic patterns – in hybrid zones under increasingly realistic scenarios. Neutral simulations revealed that ancestry junction number is shaped by population structure, migration rate, and population size. Modeling multiple genetic architectures of hybrid dysfunction, with an emphasis on epistatic hybrid incompatibilities, showed that selection reduces junction number near loci that confer reproductive barriers. The magnitude of this signature was affected by the form of selection, dominance and genomic location (autosome vs. sex chromosome) of incompatible loci. Our results suggest that researchers can identify loci involved in reproductive isolation by scanning hybrid genomes for local reductions in junction number. We outline necessary directions for future theory and method development to realize this goal.

Introduction

During speciation, reproductive barriers evolve that impede gene flow between species and support the cohesion of lineages. Nascent species often come into secondary contact and hybridize in nature (Arnold 1997; Rieseberg 1997; Mallet 2005), offering special opportunities to understand the reproductive isolation that maintains species integrity. Patterns of genetic and phenotypic variation in hybrid zones document hybridization history and reveal reproductive barriers, including mating preferences and hybrid dysfunction (Barton and Hewitt 1989; Jiggins and Mallet 2000; Burke and Arnold 2001; Gompert et al. 2017).

Hybrid zone studies often consider how the frequencies of traits or alleles that are diagnostic of species change over space (Haldane 1948; Endler 1977), using the shape of these geographic clines to draw inferences about the balance between gene flow and selection against hybrids (Szymura and Barton 1986; Barton and Hewitt 1989; Mallet et al. 1990; Barton and Gale 1993; Porter et al. 1997). An alternative framework (“genomic clines”) compares allele and genotype frequencies in individual genomic regions to genome-wide admixture proportions, with deviations detecting loci potentially targeted by selection (Lexer et al. 2007; Gompert and Buerkle 2009, 2011; Fitzpatrick 2013). Geographic and genomic clines in hybrid zones reveal marked inter-locus heterogeneity in gene flow across a range of species pairs (Payseur 2010; Gompert et al. 2017), suggesting that species boundaries are semipermeable (Key 1968; Bazykin 1969; Barton and Hewitt 1981; Harrison 1986, 1990; Wu 2001; Harrison and Larson 2014).

Advances in genome sequencing, single nucleotide polymorphism (SNP) genotyping, and statistical methods for detecting hybridization have the potential to substantially increase the genomic resolution of inference in hybrid zones (Sousa and Hey 2013; Seehausen et al. 2014; Payseur and Rieseberg 2016). In particular, it is now possible to characterize changes in genetic variation on a fine physical scale along hybrid chromosomes. This capacity highlights the need for new conceptual and analytical frameworks specifically designed for application to genomic data in hybrid zones. One promising perspective focuses on ancestry. Genomic distributions of ancestry are proving to be sensitive indicators of recent demographic history in human populations (Gravel 2012; Ralph and Coop 2013; Browning and Browning 2015; Baharian et al. 2016). This progress has been catalyzed by the development of methods that probabilistically reconstruct changes in ancestry across the genome (McKeigue et al. 2000; Sankararaman et al. 2008; Price et al. 2009; Browning and Browning 2011, 2013; Wegmann et al. 2011; Corbett-Detig and Nielsen 2017).

In hybrid zones, meiotic recombination between heterogenic chromosomes - those inherited from different species - creates switch-points in genomic ancestry called junctions (Fisher 1954; Baird 1995). As a result, hybrid genomes are mosaics with junctions delineating genomic ancestry tracts. Once junctions appear, they are inherited like point mutations (Fisher 1954). Because junctions only form in heterogenic regions of the genome, they provide unambiguous evidence of hybridization (Baird 2006).

Previous results from mathematical theory and simulations suggest that genomic ancestry patterns in hybrid zones contain useful information about speciation. The lengths of ancestry tracts are directly connected to the number of generations of hybridization. This observation raises the prospect of using a “recombination clock” to characterize the timescale of hybridization (Baird 1995; Pool and Nielsen 2009; Sedghifar et al. 2015), an approach that has been successfully applied in sunflowers (Ungerer et al. 1998; Buerkle and Rieseberg 2008) and cichlids (Meier et al. 2017). Reproductive isolation conferred by heterozygote disadvantage is predicted to maintain longer ancestry tracts under some conditions (Barton 1983; Baird 1995; Sedghifar et al. 2016). The interaction between gene flow and recombination in hybrid zones is expected to produce geographic gradients in ancestry tracts (Sedghifar et al. 2015).

In this article, we use simulations to understand the behavior of ancestry junctions in hybrid zones in increasingly realistic scenarios. We consider the dynamics of junctions in a stepping-stone model of migration, a mainstay of cline theory that approximates the structure of many hybrid zones. We model a genetic basis of reproductive isolation that is supported by empirical studies. In particular, we describe how epistatic selection against hybrid incompatibilities, including those involving the sex chromosomes, shapes chromosomal patterns of ancestry. Our results motivate incorporation of ancestry junctions into the analysis of real hybrid zones to identify the loci responsible for reproductive barriers and to improve inferences of hybridization history.

Methods

We sought to determine how several biological factors shape genomic patterns of ancestry in a hybrid zone. Those factors include complex demographic history with population structure and genetic drift, natural selection against several types of hybrid incompatibilities, and multiple modes of inheritance (including sex linkage). Analytical models combining these factors would be either too complex or would require overly simplistic and restrictive assumptions. Therefore, we chose to use individual-based, forward simulations.

Simulation Overview

To model ancestry junctions in hybrid zones, we developed a simulator (“HapHazard”; source code in C++ is freely available through GitHub at www.github.com/payseurlab/HapHazard). This program simulates genomes with multiple chromosomes and types of inheritance in sexually reproducing diploids. Chromosomes are composed of junctions, which denote the genetic positions at the ends of ancestry tracts (Fisher 1954). New junctions are added when recombination occurs between tracts from different ancestries. This approach enables efficient simulation of genomes at high resolution. Generations are discrete and follow three fundamental steps: migration, selection, and reproduction with recombination.

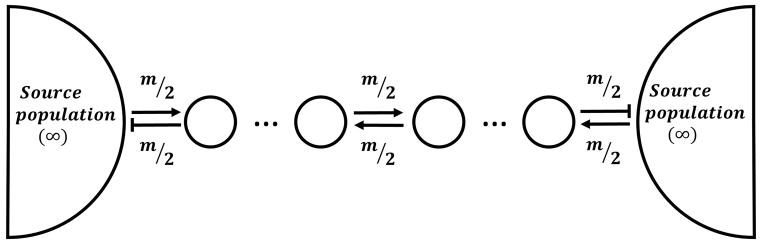
Our simulations of hybrid zones utilized different stepping stone models. The stepping stone cline model (SSC) (Feldman and Christiansen 1974), like the finite stepping stone model (FSS) (Felsenstein 1975; Slatkin and Maruyama 1975), incorporates migration between multiple adjacent sub-populations (demes) arranged linearly in a chain. In addition, it includes migration from infinitely large source populations at each end of the stepping stone. We focused on this model (Figure 1) because it was developed to characterize hybrid zones (Feldman and Christiansen 1974).

Figure 1.

Stepping-stone model. A cline comprises a chain of demes that are linked by migration (at rate m). The stepping stone is flanked at each end by infinitely large source populations containing pure individuals from their respective ancestries.

The first step in each generation of the simulations was migration between demes. Individuals randomly chosen from their parent demes migrated to an adjacent deme once per generation. Migrants from source populations had pure genomes with singular ancestries and no junctions. Individuals that migrated to the source populations were removed, leaving the source populations unaffected.

During the reproduction step, we simulated diploid mating between pairs of females and males with XX and XY sex chromosomes, respectively. The mating process followed these steps: (1) a female (male) was chosen randomly from the same deme; (2) the reproductive fitness of the chosen female (male) was computed based on genomic ancestries at specific loci (see below); (3) if the fitness was larger than a uniform random number, the female (male) was kept in a mating pair; if not, the female (male) was put back in the pool of potential mates; (4) once chosen, each mating pair produced one offspring; (5) the procedure was repeated until the constant population size of the deme was reached. All mating pairs were chosen from the same deme. To calculate ancestry-based reproductive fitness we used the model:

$$w=\mu +\sum a_i(g_i)+\sum b_{ij}(g_{ij})$$

where μ = 1, the expected reproductive fitness without selection. To model selection, we included the additive effects of alleles, a_i, as indicated by the ancestries at selected loci, g_i, and the epistatic effects between loci b_ij(g_ij). We assumed that alleles were fixed in each source population. This flexible model allowed us to simulate several modes of selection that are suspected to play important roles in hybrid zone dynamics, including underdominant selection and selection against epistatic hybrid incompatibilities.

Following mating and selection, gametes were created by recombination and random assortment of each chromosome. Individual genomes contained one pair of sex chromosomes and one pair of autosomes. On autosomes in both sexes and XX-pairs in females, the number of recombination events was randomly drawn from a Poisson distribution with mean equal to the chromosome’s genetic length (1 Morgan (M)). We assumed no recombination between the X and Y chromosomes. Crossover positions along chromosomes were randomly drawn from a uniform distribution. Resulting ancestry tracts of genetic length less than 10⁻⁸ M were discarded; all others were retained. Results reported below were based on 1000 simulation replicates for each parameter combination.

Demography

The parameter values we chose (Table 1) were intended to capture characteristics of natural hybrid zones. The demographic model had four parameters: deme number, deme size, migration rate, and number of generations. Because the number of individuals was the primary determinant of computational speed, we restricted deme size and deme number. All simulations of the SSC and FSS models had 10 demes to elucidate the effects of population structure and distance across a cline. We used six parameter combinations to explore the effects of migration and drift on the temporal and spatial dynamics of ancestry. Deme size (N) was set to 50 or 500 individuals and held constant across demes in an experiment. Migration rate (m) was set to 0.5, 0.1, or 0.01. Simulations were run for at least 2000 generations, during which time migration-recombination-drift equilibrium was approached in most of the cases reported below. When modeling the SSC, we attempted to simulate a stepped cline at first contact between two species. Thus, only two ancestries were included, and each deme was initially fixed for the ancestry of the nearest source population. For comparison with the SSC, we conducted simulations of single hybrid populations without migration from sources (admixed Wright-Fisher model, AWF) and single hybrid populations with migration from sources (hybrid swarm model, HS).

Table 1.

Parameters and conditions for hybrid zone simulations.

Parameter	Simulated Values/Conditions
Number of individuals across all demes (N)	500, 5000
Number of individuals within a single deme (d)	50, 500
Number of demes (D)	1, 10
Initial proportion of ancestry A in demes i through j (pi … pj)	Stepped cline [1,…,1,0,…,0]
Migration rate between adjacent demes (m)	0.01, 0.1, 0.5
Genetic compartments of paired BDMI loci	Autosome-Autosome X Chromosome-Autosome
Selection coefficient (s)	0.1, 0.5
Dominance of BDMI loci	Dominant-Dominant Recessive-Recessive Dominant-Recessive Additive Network (see Figure 2)
Linkage between BDMI loci	Unlinked (different chromosomes), 30 cM, 10 cM, 1 cM
Number of individuals sampled per deme	10
Generation number at which samples were taken (t)	250, 500, 750, 1000, 1250, 1500, 1750, 2000

Natural Selection

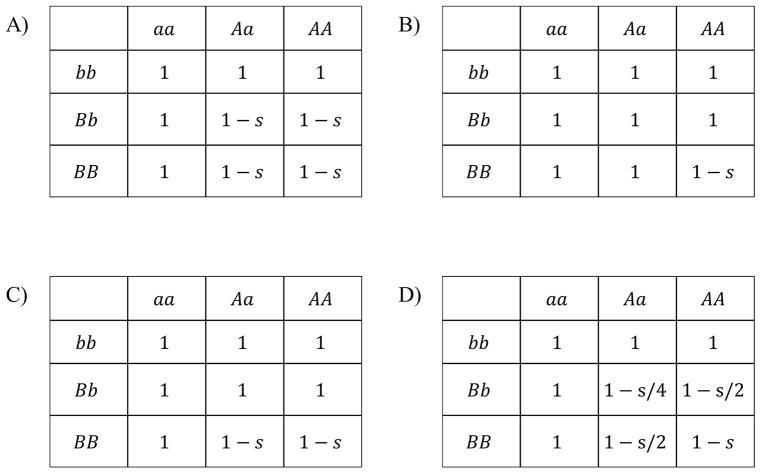
In simulations with selection, we included four additional parameters to define the genetic architecture and strength of selection. Recognizing the importance of Bateson-Dobzhansky-Muller incompatibilities (BDMIs) (Bateson 1909; Dobzhansky 1937; Muller 1942) in hybrid inviability and hybrid sterility (Coyne and Orr 2004), most of our experiments simulated epistatic selection against two-locus BDMIs. The shape of the BDMI fitness landscape was determined by both the strength of selection and the dominance of the incompatible alleles (Figure 2). We modeled four different combinations of dominance in BDMI simulations: dominant-dominant (DD), dominant-recessive (DR), recessive-recessive (RR), and additive-network dominance (AN) (Figure 2). For linked BDMIs, we considered pairs of loci separated by 30 cM, 10 cM, or 1 cM. For unlinked BDMIs, we considered autosomal:autosomal locus pairs and X-linked:autosomal locus pairs.

Figure 2.

BDMI classes. Genotypic fitnesses are shown for Dominant-Dominant BDMIs (A), Recessive-Recessive BDMIs (B), Dominant-Recessive BDMIs (C), and Additive-Network BDMIs (D). s is the fitness cost to the genotype.

Sampling

For analyses, we took random samples of 10 individuals from each deme. To study the dynamics of genomic ancestry through time, we sampled every 25 generations for the first 100 generations, and every 250 generations thereafter. The simulator produced ancestry tract data, genomic ancestry markers spaced every 1 cM, and ancestry frequencies for each marker in each deme (ancestry clines). We used this output and custom R scripts to compute summary statistics described below. For simplification, we assumed that ancestries were distinct between the parent species and that hybrid ancestries were determined without error.

Junction Density

A variety of measures could be used to summarize genomic ancestry. Here, we focus on ancestry junctions for two reasons. First, the formation of junctions requires recombination in hybrid individuals, suggesting that the density of junctions should be sensitive to demographic and selective processes occurring in hybrid zones. Second, the inference of junctions does not require knowledge of haplotype phase, which will often be challenging to reconstruct from genomic data in hybrid zones.

To summarize the density of ancestry junctions at chromosomal and genomic scales, we computed the reciprocal of mean ancestry tract length in each individual. For each simulation, the average of this statistic across the 10 sampled individuals in each deme was computed. We report means and 95% confidence intervals of this measure of junction density across 1000 simulations.

To summarize junction density on sub-chromosomal scales, we computed the mean number of junctions in non-overlapping 1 cM windows (a total of 100 on a 1 M chromosome) across the 10 sampled individuals in each deme for each simulation. We plotted several mean junction densities (over 1000 simulations) against genomic position to qualitatively compare junction densities between simulation experiments. We also tested whether BDMI loci could be distinguished from neutral loci by comparing junction densities in 1 cM windows between neutral and selection experiments using Wilcoxon ranked sum tests.

To further connect junction patterns with hybridization, we computed two additional measures of admixture: hybrid index and heterogenicity. Hybrid index was calculated as the proportion of one ancestry found across the 200 markers (100 on each of the two simulated chromosomes) in an individual. Following Fisher’s (1954) study of ancestry junctions, we treated heterogenicity as observed heterozygosity in ancestry. Heterogenicity was computed as the proportion of markers that harbored different ancestries in an individual (excluding the X chromosome in males). For both measures, we computed means across the 10 sampled individuals in each simulation replicate, and subsequently computed means and 95% confidence intervals of these statistics across simulations. Simulation input files and data produced in this study are archived at Dryad (doi:10.5061/dryad.668g444).

Results

Dynamics of Junction Density Over Time

We first studied the accumulation of ancestry junctions over time in neutrally admixing populations with different demographic histories to understand the background from which signatures of selection against hybrid incompatibilities emerge. Junction formation depends on the level of heterogenicity in a hybrid population, and heterogenicity changes over time. In the simplest case we examined, an admixed Wright-Fisher (AWF) population, heterogenicity should decay exponentially just as heterozygosity does in a Wright-Fisher population (Chapman and Thompson 2002; Buerkle and Rieseberg 2008). In the most complex case we modeled, the stepping stone cline (SSC) population, heterogenicity should accumulate until migration and drift reach equilibrium (Feldman and Christiansen 1974; Slatkin and Maruyama 1975; Felsenstein 1975). Thus, we expected junction density to increase until heterogenicity was lost from the population or until migration-drift equilibrium was achieved. We studied three main demographic factors that influence levels of heterogenicity: (1) migration with source populations, (2) migration between hybrid demes (population structure), and (3) deme size.

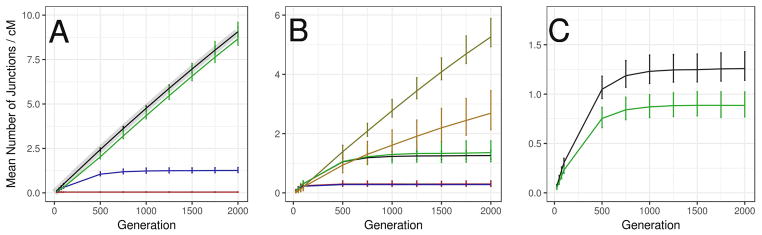
The temporal changes in average junction density for several neutral demographic models are displayed in Figure 3. Junctions accumulated rapidly until heterogenicity decayed or until junction formation and loss were balanced (Figure 3A). Junction density was highest in the AWF model (at 2000 generations, mean junctions/cM = 9.07; 95% confidence interval = 8.79–9.33) and closely matched expectations from analytical theory (Chapman and Thompson 2002). In contrast, the hybrid swarm (HS) model had the lowest average junction density at this time point (0.046 (0.029–0.062)). The only difference between these two demographic models was the exchange of migrants with source populations. In AWF populations, haplotypes could drift to higher frequencies while accumulating junctions, whereas unbroken tracts could migrate into HS populations, replacing junction-rich haplotypes. A similar pattern was observed when comparing the SSC with source migration (1.26 (1.12–1.42)) and the FSS without source migration (8.66 (8.31–9.60)).

Figure 3.

Junction density over time. Lines indicate means over 1000 simulations of junction density in a 1 cM window in samples taken from a central deme. Error bars indicate 95% confidence intervals. (A) The effect of population structure and source migration in populations with N=5000. Black: An admixed Wright-Fisher population. Gray: Analytical expectations for a Wright-Fisher population computed using formulas in Chapman and Thompson (2002). Red: a hybrid swarm with source migration but no population structure. Blue: a stepping stone cline with d=500, m=0.1. Green: a stepping stone cline with d=500, m=0.1, but no source migration. (B) The six stepping stone cline demographic histories used throughout this study. Black: d=500, m=0.1, Green: d=50, m=0.1, Blue: d=500, m=0.5, Red: d=50, m=0.5. Yellow: d=500, m=0.01, Orange: d=50, m=0.01. (C) Comparison among the autosome (black) and X chromosome (green) in a stepping stone cline with d=500, m=0.1.

We examined the role of population structure by comparing junction densities between simulations of subdivided metapopulations (SSC and FSS) and panmictic populations (AWF and HS) (N=5000 individuals). Population structure exerted several subtle but important effects on junction density in a stepping stone model. First, if a hybrid zone exchanged migrants with its source populations, population structure buffered against the replacement of admixed haplotypes by impeding the flux of source haplotypes. This effect allowed junction density to increase relative to panmixia, as demonstrated by our comparison between the HS (0.046 (0.029–0.062)) and SSC (1.26 (1.12–1.42)) models (with N=5000, m=0.1). Second, within each deme, population structure magnified the effects of drift on heterogenicity and junction frequencies, causing an increase in the variance of junction density among simulations.

Next, because most of our simulations modeled hybrid zones as stepping stone clines, we focused on how differences in migration rate and deme size among the six primary demographic histories affected junction density over time. Hybrid zones with high migration rates approached equilibrium faster, and showed reduced mean junction density (Figure 3B) and reduced variance in junction density (see 95% confidence intervals in Figure 3B) among simulations. SSC simulations reached equilibrium between 100 and 250 generations when the migration rate was highest (m=0.5), and between 750 and 1000 generations when the migration rate was intermediate (m=0.1). With low migration (m=0.01), SSC simulations did not achieve equilibrium within our experimental time frame of 2000 generations. Because comparing equilibrium vs. non-equilibrium conditions can complicate interpretations, we further investigated the behavior of the SSC with low migration (m=0.01) by reducing chromosome size to 10 cM and running simulations for up to 7000 generations. Between generations 6500 and 7000 the per-generation gain of junctions per cM was very small (<0.01 on average), indicating the cline was approaching equilibrium. Additionally, the junction density patterns described below were all visible by 1000 generations. Given these dynamics and limitations on computational resources, we proceeded (with caution) to compare SSC models with low vs. high migration at 1500 generations. At this time point, sets of simulations with different migration rates generated distinct average junction densities, with non-overlapping 95% confidence intervals (Figure 3B). The other factor that differed among the primary SSC models was deme size. Smaller demes (n=50) exhibited lower mean junction density and wider confidence intervals (Figure 3B), presumably because more junctions were lost by drift. These effects were substantial when the migration rate was low (m=0.01).

We compared the temporal dynamics of junction density on the autosome and the X chromosome (Figure 3C). In all neutral scenarios, the ratio of X-chromosomal to autosomal junction density fell between 0.61 and 0.72, reflecting the reduced effective population size of the X chromosome (¾ of autosomal effective population size in these simulated populations with a 1:1 breeding sex ratio), as well as its reduced rate of recombination (2/3 of the autosomal recombination rate). Junction density on the X chromosome exhibited larger confidence intervals compared to the autosome.

Dynamics of Junction Density Across Space

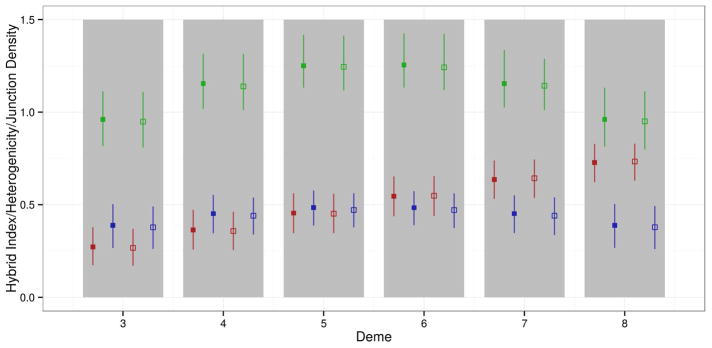
To further define expectations for genomic ancestry in a hybrid zone, we charted changes in junction density across geographic space. First, we studied the hybrid index and heterogenicity in six neutral SSC models and compared these summaries to junction density. Under neutrality with equal and symmetric migration between demes, a linear gradient in the hybrid index across the cline was observed at equilibrium (Figure 4). The average gradient in hybrid index and heterogenicity across the cline was the same for all six neutral SSC models. However, migration rate and deme size affected the amount of variation in ancestry frequency among the demes and across simulations. Increasing migration rates and deme size reduced this variation considerably. Junction density was highest in central demes and lowest in peripheral demes for all six neutral models (Figure 4). Effects of migration rate and deme size we observed previously were also seen across all demes in the SSC. Levels of heterogenicity followed the same pattern as junction density, with the highest values (close to 0.5) in central demes (Figure 4). Overall, these results demonstrated a tight coupling between junction density, heterogenicity, and the degree of admixture (measured by the hybrid index).

Figure 4.

Measures of admixture from an autosome across a cline (d=500, m=0.1) in demes 3–8 (gray bars) at neutral equilibrium (solid boxes) and with selection on a pair of linked BDMI loci (open boxes, DD-BDMI, s=0.5, 30 cM apart). Red = hybrid index. Blue = heterogenicity. Green = number of junctions per cM. Vertical lines indicate 95% confidence intervals.

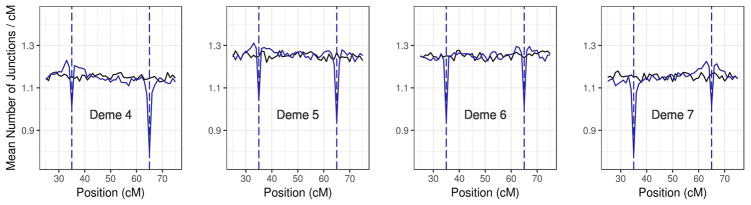
Next, we examined the difference between SSC models with and without strong selection on BDMIs (Figures 4 and 5). When strongly selected BDMIs (DD type, s=0.5) were present, the hybrid index gradient became slightly steeper while both heterogenicity and junction density were slightly reduced for chromosomes containing BDMIs relative to the neutral model (Figure 4). These effects were barely noticeable on the chromosomal scale. In contrast, junction densities analyzed in 1 cM windows showed clear signatures of selection against BDMIs (Figure 5). The mean junction density across simulations was reduced around each BDMI locus. In addition, there was an asymmetry in signal strength at interacting loci on opposite sides of the hybrid zone center. In deme 5, the percent differences in junction density in BDMI regions relative to comparable neutral scenarios were −16.5% (BDMI locus 1 at 35 cM) and −25.7% (BDMI locus 2 at 65 cM) respectively, whereas in deme 6 these differences were reversed (−24.6% at 35 cM; −18.5% at 65 cM). Presumably BDMIs showed stronger signatures in non-native demes because opportunities for deleterious interactions increased. Furthermore, the strength of the selection signal (measured as the percent difference relative to the neutral model) increased as deleterious ancestry blocks introgressed farther beyond the central deme. These results demonstrated that the center of a hybrid zone offers the greatest potential to detect signatures of selection against BDMIs.

Figure 5.

Genomic junction density across a cline. A comparison of mean junction density across 1000 simulations on an autosome measured in the four central demes in a ten-deme SSC model (d=500, m=0.1). Black = junction density of the neutral model. Blue = junction density with DD BDMIs (s=0.5) located at 35 and 65 cM.

Effects of Natural Selection on Junction Density

Our next goal was to determine how natural selection in a hybrid zone shapes patterns of junction density more generally. Based on observed patterns of junction accumulation in neutral simulations, we focused on analyzing junction density at generation 1500. Results from our simulations (see above) suggested that the clearest signatures of selection against hybrid incompatibilities would be found in central demes. Therefore, we next used samples from the two central demes in the SSC to examine in detail the effects of selection on junction density. In these samples, we calculated the average number of junctions across sampled chromosomes in 1 cM windows in each simulation, and we compared averages over simulations between experiments.

Important genetic determinants of clines in hybrid zones include: the form of selection (is gene flow deleterious or advantageous?), the number of selected loci, interactions between alleles within and among selected loci (dominance and epistasis), the recombination landscape, and the inheritance of selected loci (autosomal or sex-linked). Our simulations revealed that these genetic parameters also shape genomic patterns of ancestry.

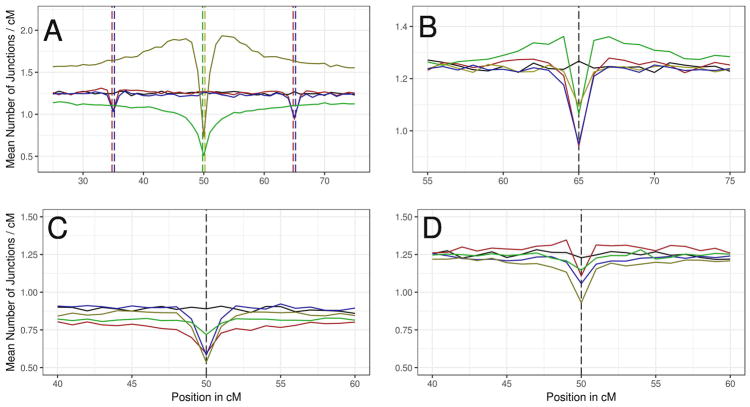
Selection Targeting Single Loci

Most single-locus selection models yielded junction density deficits at selected loci relative to comparable neutral models (Figure 6A). Selection signals were also visible in chromosomal regions outside targeted loci, in ways that differed between forms of selection. Underdominant selection induced a deep trough in junction density (59.9% reduction) at the selected locus as well as a deficit across the entire chromosome. Adaptive introgression yielded a deep valley at the locus under selection (42.2% reduction) that sharply decayed with increased recombinational distance, with junction density rising above that expected from neutrality along the remainder of the chromosome. The reductions in junction density near targets of underdominant selection and near targets of positive selection in a hybrid zone resemble the decrease in nucleotide diversity predicted by models of selection at linked sites in non-hybrid populations (e.g. Kaplan et al. 1989).

Figure 6.

The effect of genetic architecture of reproductive isolation on junction density. Mean junction densities across 1000 simulations in 1 cM windows are plotted against their genetic positions on an autosome. In all graphs, the solid black line represents the junction density in the neutral demographic model (d=500, m=0.1). Vertical dashed lines indicate the positions of loci under selection. Colors match their corresponding mean junction densities and black dotted lines are used when loci are at the same location for all experiments plotted. (A) Comparison of single-locus selection to epistatic (BDMI) selection. Yellow = single-locus positive selection with s=0.1 (additive); green = single-locus underdominant selection with s=0.1; red = epistatic selection against DD BDMI with s=0.5; blue = epistatic selection against DD BDMI with s=0.1. (B) Comparison of different modes of dominance among BDMIs with s=0.5. Red = DD, yellow = RR, green = DR, and blue = AN. (C and D) Comparison between signatures on the X chromosome (C) and the Autosome (D) for unlinked X-autosome BDMI pairs (with each locus shown in its non-native deme). Yellow line = DD BDMI; green line = RR BDMI; red line = dominant X-linked allele and recessive autosomal allele; blue line = recessive X-linked allele and dominant autosomal allele.

Selection Targeting Bateson-Dobzhansky-Muller Incompatibilities

Because hybrid incompatibilities play an important role in the genetics of hybrid inviability and hybrid sterility (Coyne and Orr 2004), we considered in detail the effects of epistatic selection against BDMIs on genomic ancestry patterns.

STRENGTH OF SELECTION AND DOMINANCE OF INCOMPATIBILITIES

Distortions in junction density induced by selection against BDMIs were milder and more localized than those caused by selection targeting single loci (Figure 6A). Junction troughs were visible at both partner loci, with the locus harboring the non-native allele (based on the side of the hybrid zone of the sampled deme) showing the greater deficit. Changing the strength of incompatibility selection had a limited effect on the reduction in junction density (s=0.5: 25.7%; s=0.1: 24.2%).

Incompatibility dominance, which also altered the genotype-fitness landscape (Figure 2), was a stronger determinant of junction density than selection strength, at least over the range of simulated parameter values (Figure 6B). Focusing on the locus harboring the non-native allele and assigning s=0.5, dominant-dominant (DD) BDMIs exhibited the strongest reductions in junction density (25.7%), presumably because the largest proportion of possible two-locus genotypes (4/9) experienced fitness decreases. Additive-network (AN) DMIs yielded the next-strongest reductions in junction density (25.0%). AN BDMIs affected the same genotypes as DD BDMIs, but the double and single heterozygotes experienced milder fitness declines. Selection against dominant-recessive (DR) BDMIs yielded 18.3% and 16.1% decreases in junction density at the non-native dominant and recessive locus, respectively. Because the incompatibility allele at one locus was recessive, these BDMIs only affected two of the nine possible genotypes, reducing the overall magnitude of selection, and amplifying the asymmetries in signal intensity between the two loci. Finally, recessive-recessive (RR) BDMIs showed weaker reductions in junction density (12.2%), presumably because only one genotype suffered a fitness cost.

CHROMOSOMAL INHERITANCE OF INCOMPATIBILITIES

Motivated by the disproportionate contribution to hybrid sterility and hybrid inviability of BDMIs involving the sex chromosomes (Coyne and Orr 2004; Presgraves 2008), we explored the effects of selection against BDMIs with one X-linked locus and one autosomal partner locus (Figure 6C and 6D). In the following description, we focus on incompatible alleles in their non-native demes. DD BDMIs showed the strongest deficits in junction density at both X-linked (39.7%) and autosomal (24.3%) loci, whereas RR BDMIs displayed the weakest effects (X-linked: 19.2%; autosomal: 6.74%). Signals of selection against DR BDMIs depended on chromosomal location. Junction density around a dominant X-linked allele was reduced by 33.3%, while junction density near its autosomal recessive counterpart was reduced by only 9.87%. Local junction densities around a recessive X-linked allele and its incompatible autosomal dominant allele were reduced by 34.5% and 13.9%, respectively.

These results show that X-linkage enhances the ancestry effects of selection against BDMIs. Junction deficits associated with dominant X-linked alleles were larger than those associated with dominant autosomal BDMIs. Additionally, recessive X-linked alleles were associated with junction deficits similar to those near autosomal dominant BDMIs.

RECOMBINATION AMONG INCOMPATIBLE LOCI

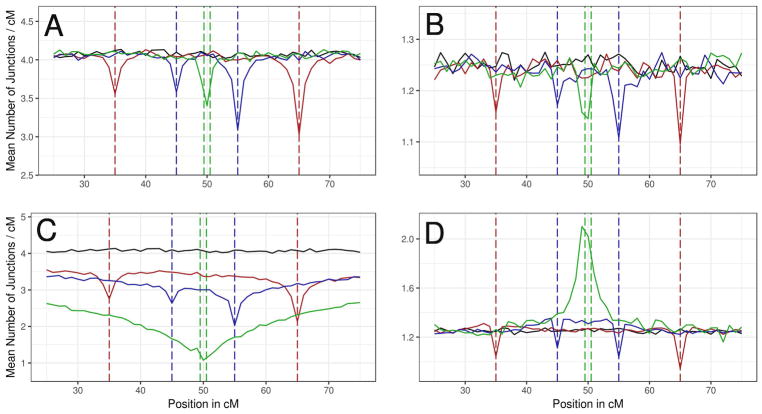
The degree of linkage among the loci that confer reproductive isolation is a critical determinant of barriers to gene flow in hybrid zones (Barton 1983; Barton and Gale 1993; Payseur 2010). We analyzed the contribution of linkage to genomic ancestry patterns by measuring junction densities near BDMIs separated by differing genetic distances along the same chromosome. We discovered that linkage exerts important effects on signatures of selection against BDMIs that vary in combination with other factors, including dominance and migration rate.

We expected to find deficits of junction density between linked RR BDMI loci since the only genotype that suffered a fitness reduction (one heterospecific, double homozygote) had to arise from combining two gametes with recombinant chromosomes. Although no such deficits in junction density between loci were observed, junction densities were locally reduced at RR BDMI loci, and these reductions tended to increase with genetic distance between loci (Figure 7A and 7B). While enhancing the opportunity for recombination between RR BDMI loci raised the frequency of the unfit genotype and the magnitude of local deficits in junction density, it appeared that junctions were not selected against directly but instead were affected by the marginal fitness of linked alleles.

Figure 7.

Combined effects of linkage, dominance, and migration rate on BDMI ancestry junction signatures. Mean junction densities from 1000 simulations in 1 cM windows are plotted against their genetic positions on an autosome. In all graphs, the solid black line represents junction density in a neutral demographic model with a deme size of 500 at 1500 generations. Colored lines represent simulations with linked BDMIs spaced at different intervals: Red = 30 cM; blue = 10 cM; green = 1 cM. Vertical dashed lines indicate the positions of loci under selection with corresponding colors: red = BDMI loci spaced at 30 cM; blue = 10 cM; green = 1 cM; black = neutral model with d=500; all at 1500 generations. (A) RR BDMI, m=0.01. (B) RR BDMI, m=0.1. (C) DD BDMI m=0.01. (D) DD BDMI, m=0.1.

Signatures of selection against DD BDMIs showed the opposite pattern, with more severe reductions in junction density as BDMI loci moved closer (Figure 7C). Tightly linked DD BDMI loci (spaced at 1 cM) displayed a substantial local decrease in junction density with effects extending across the entire chromosome (Figure 7C), resembling the signature of underdominant selection at a single locus. This pattern probably arose from selection against heterogenicity; with tight linkage, the double heterogenic genotype was most frequent.

For both RR BDMIs and DD BDMIs, changing the migration rate drastically altered local patterns of junction density. Increasing migration weakened the reduction in junction density at RR BDMI loci (compare Figure 7B and 7A). For instance, percent decreases in junction density for the BDMI locus at 65 cM at migration rates of 0.01, 0.1, and 0.5, were 25.8%, 13.5%, and 11.6% respectively. This effect was probably explained by the replacement of recombinant haplotypes that gave rise to unfit RR BDMI genotypes by (fit) non-recombinant haplotypes from source populations. Migration affected selection signatures for DD BDMIs differently (compare Figure 7D and 7C). Remarkably, tightly linked DD BDMI loci were associated with a substantial increase in junction density with higher migration. For instance, the DD BDMI loci separated by 1 cM yielded a single peak representing a 67.2% rise in junction density. This result probably reflected the increased frequency of the double heterogenic genotype with higher migration; the easiest route to escaping deleterious effects of DD BDMIs was to generate recombinants.

DETECTING SELECTION AGAINST INCOMPATIBILITIES FROM ANCESTRY PATTERNS

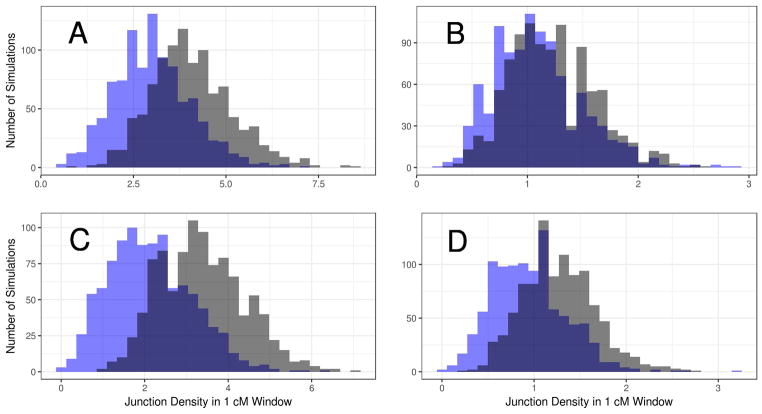
Our results raised the prospect that BDMI loci could be located in the genome through their effects on junction density in hybrid zones. To investigate this possibility in a preliminary manner, we statistically compared junction density distributions in 1 cM windows from simulations with and without BDMIs. Mean junction density (taken across simulations) deficits generated by DD, DR, and AN BDMIs were significant reductions compared to neutrality (Wilcoxon rank sum test; p<0.05) under all demographic scenarios. Junction densities around RR BDMI loci were also significantly different from those observed in neutral simulations, with one exception (RR BDMI with a migration rate of 0.5 in its non-native deme). Nevertheless, distributions of junction density taken across simulations showed substantial variance and overlap between windows with and without BDMIs (Figure 8). Together, these patterns should motivate a detailed examination of the power to detect the signatures of selection we report in individual genomic scans.

Figure 8.

Comparison of junction density in genomic windows with and without BDMIs. Each panel shows two distributions taken across 1000 simulations: junction density in a 1 cM window containing a BMDI locus (with its incompatible counterpart located 30 cM away; s=0.5; blue) and junction density in a 1 cM window at a different location from the same chromosome (no BDMI locus; gray). (A) RR BDMI, m=0.01; (B) RR BDMI, m=0.1; (C) DD BDMI, m=0.01; (D) DD BDMI, m=0.1.

Discussion

Geographic clines (Szymura and Barton 1986; Barton and Hewitt 1989; Mallet et al. 1990; Barton and Gale 1993; Porter et al. 1997) and genomic clines (Szymura and Barton 1986; Gompert and Buerkle 2009, 2011; Fitzpatrick 2013) enable inferences about speciation from genomic data in hybrid zones. We extended the idea that analyzing ancestry switching across genomes is a useful and complementary strategy (Barton 1983; Baird 1995, 2006; Ungerer et al. 1998; Buerkle and Rieseberg 2008; Sedghifar et al. 2015, 2016).

Our results confirm that the density of ancestry junctions – a simple summary of genomic patterns – is shaped by demographic history, including population structure, migration rate, and population size. Under a neutral model, the density of junctions is expected to reach migration-recombination-drift equilibrium after a few thousand generations in scenarios that approximate the conditions of some hybrid zones. The ways demographic factors shape junction patterns can be largely understood through their effects on heterogenicity.

Our simulations demonstrate that selection against BDMIs leaves localized reductions in junction density. Although understanding the causes of this pattern will require further theoretical investigation, we propose the following verbal model. We simulated a pairwise BDMI with an asymmetrical fitness array, following expectations under the Bateson-Dobzhansky-Muller model (Muller 1942; Wu and Beckenbach 1983). With this array, the compatible (ancestral) allele at each locus enjoyed a marginal fitness advantage. When selection against hybrids was strong, each compatible allele could rise in frequency and could even fix, removing the BDMI from the hybrid zone (Lindtke and Buerkle 2015). The resulting reduction in heterogenicity would decrease the rate at which new junctions were formed. If the rise in frequency of this allele was rapid, there also would be less time for junctions to accumulate close to the selected locus than near a neutral locus. The implication is that localized reductions in junction density could be used to detect selection against BDMIs even for a period of time after the incompatible alleles have disappeared. This model fits several patterns seen in our simulations. It explains why junction density decreased for unlinked BDMIs, where the junctions themselves could not affect fitness. Furthermore, if the marginal fitness of each compatible allele is the key determinant of local junction number, junctions should be decreased near BDMI loci on the same chromosome, but not between them. This framework further predicts that the strongest reductions in junction density should be located near dominant-dominant BDMIs because compatible alleles at these loci experience stronger (positive) selection.

There are other signs that the genetic architecture of reproductive isolation molds signatures of selection in hybrid ancestry patterns. Dominance exerts a key role that depends on the genomic locations of incompatible alleles (linked vs. unlinked; X chromosome vs. autosome). Junction patterns for epistatic selection against BDMIs are distinct from those for single-locus underdominant selection and single-locus positive selection. Selection against BDMIs involving X-linked loci leaves stronger signatures than selection against BDMIs between autosomes.

Future theoretical work focused on ancestry junctions in hybrid genomes could follow several paths. Our simulations limited the number of BDMIs to one pair per chromosome. Although this assumption may be appropriate for recently diverged species, larger numbers of BDMIs could generate different patterns. For example, a stretch of the genome containing a high density of BDMIs could experience stronger selection relative to recombination rate (Barton 1983; Barton and Bengtsson 1986; Lindtke and Buerkle 2015), thereby leaving ancestry signatures more pronounced than those we report. Future models could consider information about ancestry junctions beyond their genomic densities. Ancestry identity on either side of a junction (Sedghifar et al. 2016) and the frequency spectrum of junctions across a collection of individuals are both promising characteristics. Since junctions are inherited like point mutations (Baird 2006), we might expect a positive correlation between the age of a junction and its frequency. Based on results from Sedghifar et al. (2015, 2016), modeling the consequences of selection for geographic junction patterns is likely to be another fertile direction. Furthermore, the extent to which BDMIs can block gene flow between species remains a topic worthy of attention (Gavrilets 1997; Bank et al. 2012; Lindtke and Buerkle 2015).

Our findings raise the prospect that loci responsible for reproductive barriers between species could be identified by scanning genomes sampled from hybrid zones for local deficits in ancestry junctions (Sedghifar et al. 2016). Reaching this goal will require several additional steps. Ancestry junctions are unobserved and need to be inferred. Along these lines, we anticipate challenges for two classes of hybrid zones. Recently diverged species may not have accumulated enough informative variants to accurately reconstruct ancestry along the genomes of their hybrids. Individuals from hybrid zones that formed long ago and were maintained in the absence of new gene flow from parental source populations might have a junction density that is too high to be detected with existing variants. Probabilistic methods that reconstruct ancestry across the genome in admixed populations offer potential solutions (Wegmann et al. 2011; Corbett-Detig and Nielsen 2017), but their performance in hybrid zones should be evaluated. It is worth emphasizing that alternative frameworks for analyzing hybrid zone data (including geographic clines and genomic clines) usually assume that species ancestry can be reconstructed from variant genotypes. Focusing instead on ancestry inference itself will enable error inherent in this process to be incorporated directly into analyses.

Drawing the conclusion that observed reductions in junction density along chromosomes reflect selection against BDMIs (or selection against underdominant loci) will necessitate accounting for demographic history. One approach would be to use genome-wide patterns to reconstruct major aspects of demographic history in a hybrid zone (e.g. population size and migration rate), and then simulate under the best-fit neutral model to determine statistical thresholds for selection in genome scans. A more challenging issue will be incorporating variation in recombination rate across the genome, which directly contributes to inter-locus heterogeneity in ancestry. Hybrids from species with recombination hotspots are expected to accumulate junctions less quickly than those with uniform recombination rates (Janzen et al. 2018). Furthermore, crossover interference, gene conversion, and chromosomal inversions have the potential to affect the variance in junction density. We recommend that researchers conduct simulations across a range of possible recombination rates to develop empirical predictions.

Using junctions to summarize genomic ancestry patterns has advantages and disadvantages compared to other ancestry measures. Counting junctions does not require knowledge of haplotype phase in hybrid individuals. Error inherent in the statistical reconstruction of phase could be exacerbated in hybrid populations, which often violate assumptions of phasing algorithms (e.g. demographic equilibrium). On the other hand, differences in evolutionary history between the two haplotypes an organism carries could be masked by diploid junction patterns. For example, a diploid genomic region containing many junctions could reflect a fast rate of switching along one or both chromosomes. In practice, we encourage researchers to consider junctions alongside other summaries of ancestry.

An ancestry-based perspective offers additional benefits for analyzing and interpreting genomic data in hybrid zones. It naturally incorporates correlations among neighboring markers, a challenging task for alternative strategies. Patterns of ancestry switching are directly tied to recombination, the process that enables differential gene flow along a chromosome. Combining ancestry-based analysis with geographic clines and genomic clines could be an especially fruitful approach to dissecting the reproductive barriers that isolate species.