Nanoscale Electrochemical Kinetics & Dynamics: The Challenges and Opportunities of Single-Entity Measurements

Abstract

The development of nanoscale electrochemistry since the mid-1980s has been predominately coupled with steady-state voltammetric (i-E) methods. This research has been driven by the desire to understand the mechanisms of very fast electrochemical reactions, by electroanalytical measurements in small volumes and unusual media, including in-vivo measurements, and by research on correlating electrocatalytic activity, e.g., O₂ reduction reaction, with nanoparticle size and structure. Exploration of the behavior of nanoelectrochemical structures (nanoelectrodes, nanoparticles, nanogap cells, etc.) of a characteristic dimension λusing steady-state i-E methods generally relies on the well-known relationship, λ² ~ Dt, which relates diffusional lengths to time, t, through the coefficient, D. Decreasing λ, by performing measurements at a nanometric length scales, results in a decrease in the effective timescale of the measurement, and provides a direct means to probe the kinetics of steps associated with very rapid electrochemical reactions. For instance, steady-state voltammetry using a nanogap twin-electrode cell of characteristic width, λ~10 nm, allows investigations of events occurring at timescales on the order of ~100 ns. Among many other advantages, decreasing λ also increases spatial resolution in electrochemical imaging, e.g., in scanning electrochemical microscopy, and allows probing of the electric double layer.

This perspective article traces the evolution and driving forces behind the “λ²~ Dt” steady-state approach to nanoscale electrochemistry, beginning in the late 1950s with the introduction of the rotating ring-disk electrode and twin-electrode thin-layer cells, and evolving to current-day investigations using nanoelectrodes, scanning nanocells for imaging, nanopores, and nanoparticles. The recent focus on so-called “single-entity” electrochemistry, in which individual and very short redox events are probed, is a significant departure from the steady-state approach, but provides new opportunities to probe reaction dynamics. The stochastic nature of very fast single-entity events challenges current electrochemical methods and modern electronics, as illustrated using recent experiments from the authors’ laboratory.

Introduction

The electrochemical community is remarkably effective in applying nanostructures for both fundamental investigations and technological applications, providing a resource of tools and methods that have been gleaned from roughly three decades of active research.^{1, 2} Fabricating nearly ideal disk-shaped nanoelectrodes, Figure 1, is now nearly routine.³ These electrodes, of many different sizes, shapes, and composition, have played a vital role in modern measurement of electron-transfer rates⁴ and mechanisms,⁵ as in-vivo probes of neurotransmitter release,^6–8 as probes of the electric double-layer,⁹ in electroanalysis within highly resistive media,¹⁰ as “tips” in high-resolution scanning electrochemical microscopies,¹¹ as contacts to molecules in molecular electronics,¹² and in many other applications.^{2, 13}

Figure 1.

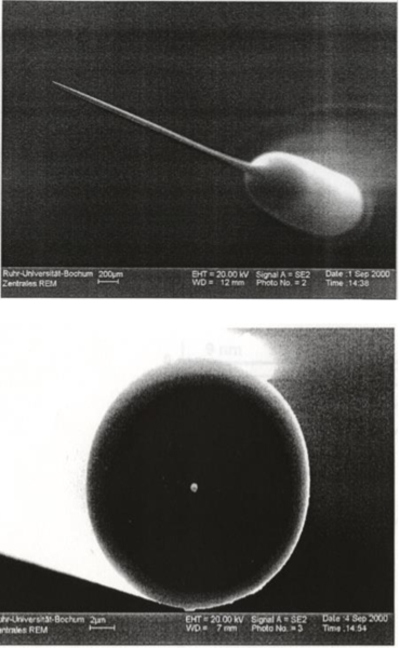
Scanning electron micrographs of a ~250-nm-radius Pt nanodisk electrode formed by heating and pulling a micron-sized Pt wire inside a glass capillary. Top image shows the needle-like geometry of the entire electrode, bottom image shows the tip of the electrode with the bright spot in the center being the Pt nanodisk. Adapted from reference 3.

Not surprisingly, advances in nanoelectrochemistry extend far beyond simply making small electrodes. The advantages of nanoparticles in electrocatalysis and as a high-surface area electrodes have been known for well over a half century,^14–19 but research on preparing exotic nanoparticles (e.g., core-shell and bimetallic nanoparticles) to create more active catalysts has exploded during the past 20 years, with many advances on both the theoretical and synthetic fronts.^20–22 Thin-layer nano-gap cells,^23–25 and scanning electrochemical nanocells²⁶ have been introduced in the past 15 years, with characteristic dimensions well below 100 nm, providing unprecedented sensitivity (single-molecule electrochemistry) and imaging resolution (a few nanometers).²⁷

Nanoelectrochemistry is also a natural companion to the field of single-molecule electronics; both fields developed at approximately the same time, partly because the physics of electron tunneling is basis of both redox chemistry and single molecule electronics (it is not an accident that many molecules studied in molecular electronics are also electroactive), but also because electrochemists are very proficient in attaching molecules to surfaces (through lessons learned in the “chemically modified electrode” era of the 1970s and 80s).^{28, 29} STM break-junction measurements,¹² an example shown in Figure 2, are used to collect single-molecule conductivity data and are representative of this area of research.

Figure 2.

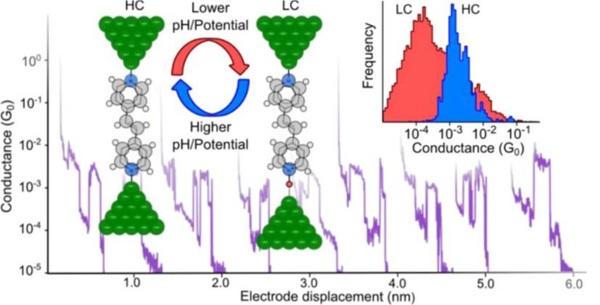
Scanning tunneling microscopy (STM) break junction measurement of the conductivity of a single 4,4′-vinylenedipyridine molecule. Protonation modulates the conductivity between high conductivity (HC) and low conductivity (LC) states. Figure adapted from reference 12.

Electrochemistry beyond “large” nanoparticles is aimed at probing reactions of small clusters of metals atoms (including single atoms!), Figure 3,³⁰ and, while certainly not yet routine, offers the exciting possibility of probing the size and electronic factors that control electrocatalytic activity.^{31, 32}

Figure 3.

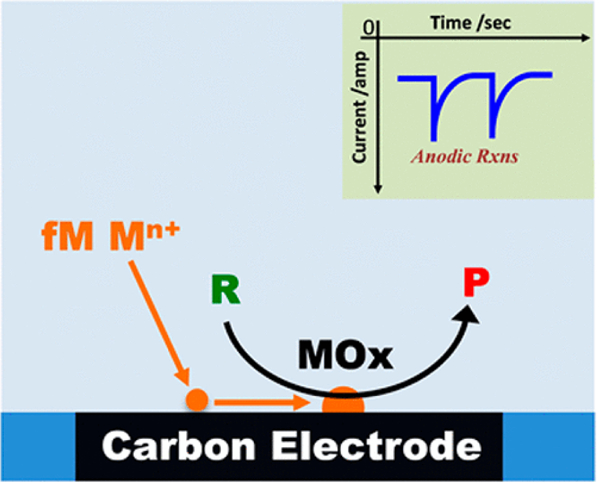
Schematic of the measurement of fM concentrations of metal ions, Mⁿ⁺ (e.g., Co²⁺, Ni²⁺, Pb²⁺), through electrocatalytic amplification. Oxidation of Mⁿ⁺ to metal oxides (MOx) is accompanied by anodic spikes corresponding to electrocatalytic conversion of reactants, R, to products, P; e.g., water oxidation. Figure adapted from reference 30.

An important by-product of nanoelectrochemistry research during the past 20 years has been the strong focus on the electrical properties of nanopores, especially in the theory and applications of ion current rectification,³³ and in the development of “nano” resistive pulse detection (first introduced by Sun and Crooks using carbon nanotubes³⁴). Electrochemists continue to make important contributions to this field, which strongly overlaps with the community using protein ion channels in DNA sequencing technology efforts.³⁵ Today, sophisticated resistive pulse methods have sub-nm resolution in measuring nanoparticle size,^{36, 37} and are often coupled to optical and spectroscopic analysis.³⁸

This Faraday Discussion volume, Nanoelectrochemistry, its 2016 predecessor, Single-Entity Electrochemistry³⁹ and the discussion it prompted,^40–44 are almost exclusively focused on the science and application of methods, materials and theory on nanometer length scales. Thirty years ago, electrochemists made measurements using macroscopic-size electrodes (> 1 millimeter, called a “microelectrode”) and applied “Nicholson and Shain”-type theory^{45, 46} to interpreting cyclic voltammetry to investigate redox mechanisms and emerging materials (e.g., electroactive polymers). Before the 1980s, the term nanoscience did not exist, much less nanoelectrodes^* or nanoelectrochemistry.

What has driven the intense focus on nanoscale electrochemistry?

The appearance of nanoelectrochemistry appears approximately correlated with the invention of scanning tunneling microscopy (STM) in 1981,^47–51 and the general explosion of nanoscience and nanotechnology that immediately followed in the science and engineering communities. The electrochemical community in the late 1980s was enthralled by the possibility of routine in-situ electrochemical STM imaging of electrode interfaces, and numerous electrochemical laboratories rapidly geared up. In-situ electrochemical STM imaging turned out to be a difficult experimental endeavor, but it clearly sparked interest and the rapid development of other types of in-situ imaging of electrode surfaces, e.g., scanning electrochemical microscopy, SECM, initially developed in the Bard laboratories.^{11, 26, 27, 52, 53}

Some aspects of what is now called nanoelectrochemistry¹ existed even before the nanoscience explosion. For instance, the invention of the patch clamp method in 1976 by Sakmann and Neher enabled researchers to isolate a single ion channel in a cell membrane and measure its electrical properties in response to solution agents.⁵⁴ In essence, that is the basic principle underlying much nanopore research today.³⁵ As noted above, electrocatalysis using nanoparticles has been researched for a half century,^{14, 18} by many electrochemists, in connection with the development of fuel cells. It has been understood for many decades that the activity of complex inner-sphere redox reactions often correlate with the particle size and shape.¹⁵

In addition to the backdrop of the general nanoscience explosion, nanoscale electrochemistry also has a less-obvious connection to the development of steady-state voltammetry beginning in the late 1950s.⁵⁵ Steady-state voltammetry was largely developed as a method to probe intermediates of complex redox reactions, e.g., oxygen reduction. A prototypical mechanism of interest would be a simple “E_rC_i” mechanism, Scheme 1, where a primary electron-transfer step, E_r, is followed by irreversible chemical reaction, C_i.

Scheme 1.

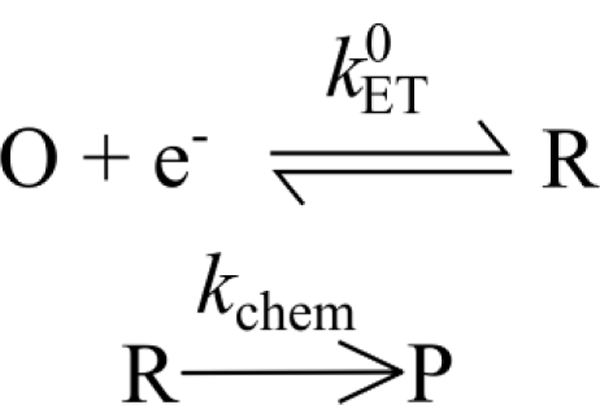
The EC_i reaction, in which an irreversible chemical reaction follows an initial electron-transfer step.

In the 1960s, experimental research led to the development of theoretical descriptions and simulations on the application of (non-steady-state) cyclic voltammetry for unraveling these types of coupled mechanisms, and measuring rate constants of homogeneous chemical reactions.^{45, 46} In parallel with those efforts, there clearly was a growing recognition that steady-state methods using two closely spaced electrodes provided a means to detect intermediates as well as measure their lifetimes. The first example of this approach appears to be the rotating ring-disk electrode (RRDE), initially reported by Frumkin’s laboratory in 1959.^{56, 57} In classical RRDE experiments, the electron-transfer step occurs at the disk electrode and the species R is “collected” at the ring electrode. The amount of R collected at the ring depends on the rate of the following chemical rate, k_chem, the rotation rate, and the “gap” distance between the ring and disk. Clearly, larger values of k_chem (i.e., faster chemical reactions) can be measured when the gap distance is reduced. A key idea of this method is that decreasing the gap thickness between the disk and ring electrodes allowed measurements of short-lived intermediates (or large homogeneous rate constants). Thus, RRDEs were prepared with a gap thickness as small as possible (which were, and remain, macroscopic).

Following the introduction of the RRDE method, Anderson and Reilley in 1965 reported “twin-electrode thin-layer” (TETL) electrochemistry,^{58, 59} Figure 4. This method is analogous to the RRDE in terms of having generator and collector electrodes. However, the TETL cell also introduced the innovative concept of “redox cycling” to create a steady-state response, Figure 4, that results in significant current amplification.

Figure 4.

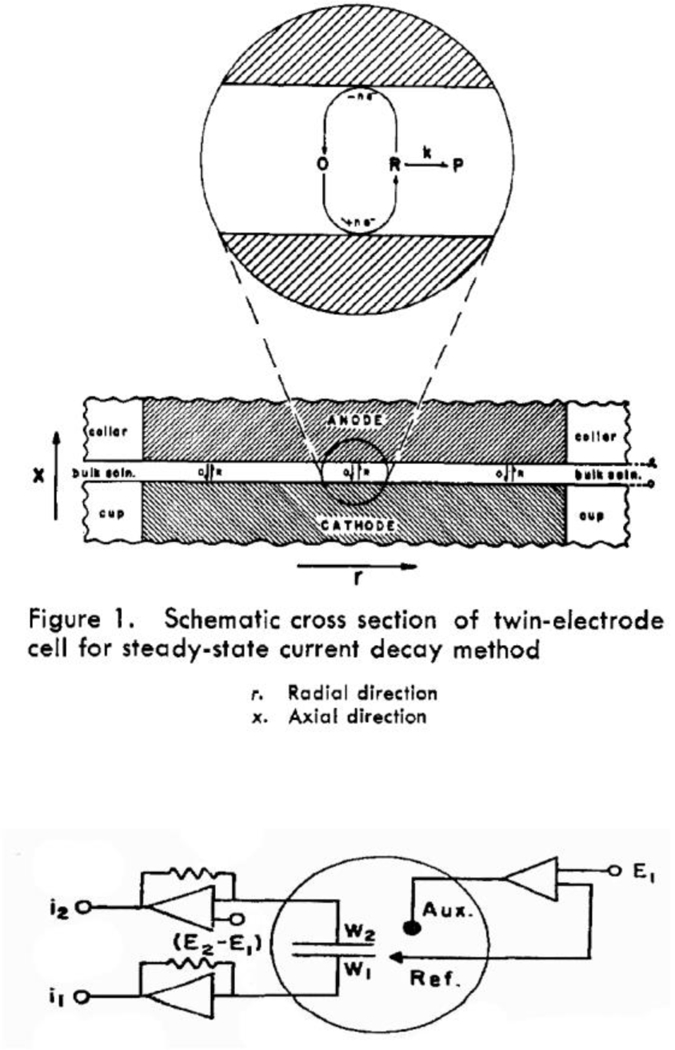
Original drawings of the thin-layer cell and twin-electrode circuitry introduced by Anderson and Reilley and for monitoring rapid chemical processes $(R\stackrel{k}{\to }P)$ during redox cycling. The two working electrodes, W₁ and W₂, were maintained at independent potentials, E₁ and E₂, with a dual op-amp scheme used to measure the two currents. Adapted from references 58 and 59.

Redox cycling remains a central idea in many modern nanoelectrochemical measurements, including SECM imaging.¹¹ In a the TETL cell measurement, an E_rC_i mechanism now is written as shown in Scheme 2, (compare to Scheme 1, which depicts the same chemistry).

Scheme 2.

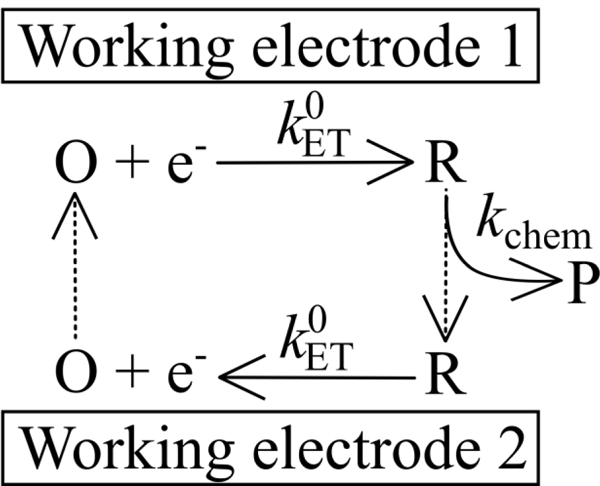
The E_rC_i mechanism of Scheme 1 expressed in context of redox cycling, introduced in the 1965 Anderson-Reilley twin-electrode thin-layer cell.^{58, 59} Redox cycling results in current amplification and the amount of cycling depends on the rate of the following chemical rate, k_chem, and the “gap” distance between the electrodes. Clearly, larger values of k_chem (i.e., faster chemical reactions) can be measured when the gap distance is reduced.

The Anderson-Reilley reports of TETL cell measurements were designed to take advantage of the steady-state approach to measure fast ET reactions, chemical reaction rates, and adsorption. In these thin layer cells, the two electrodes were separated by a solution thickness on the order of 50 μm, which is very large by today’s standards.^60–62 But the basic idea of making the gap as small as possible in order to investigate fast redox and couple chemical phenomena was understood with the publication of these early papers. This idea is now exemplified by single-molecule “two-electrode thin-layer” measurements of Bard,⁶³ Mirkin,⁶⁴ and Lemay,⁶⁰ where the distance between electrodes is reduced by many orders of magnitude from that of the original Anderson-Reilley TETL cells.

A Lemay nanogap electrochemical cell (Figure 5, top) consists of two micron-size parallel electrodes separated by a ~10–100 nm wide gap.²³ With one electrode biased at an oxidizing potential and the other at a reducing potential, redox cycling of a reversible couple with massive current amplification is achieved.⁶⁶ Any molecule residing in the cell will undergo multiple encounters with each electrode in rapid succession, during which electron transfer can occur. The characteristic time to travel between the electrodes is ~1.3 μs (= [40 nm]²/[2×6×10⁻⁶ cm²/s]; L = 40 nm, D = 6 ×10⁻⁶ cm²/s). Thus for a rapid one-electron redox process, each molecule contributes ~60 fA (=1×1.6×10⁻¹⁹ C/[1.3 μs×2]) to the essentially “steady-state” time-averaged current. Redox cycling and fast transport over the very short length scales between the electrodes is the key to single molecule detection.

Figure 5.

(Top) Schematic of a nanogap cell during redox cycling of a single-molecule. (bottom) Experimentally measured current-time trace measured at the top (blue) and bottom (red) electrodes. Occasions where a single FcTMA^0/+ molecule enters the gap and undergoes redox cycling, are visible by correlated increases/decreases in the current at the top/bottom electrode. The ability to detect a single molecule is due to rapid redox cycling. Adapted from reference 65.

In experiments when the concentration of redox mediator is sufficiently low, the volume between the electrodes will almost certainly contain either 0 or 1 molecules, at any one time. In these experiments, the current-time trace (Figure 5, bottom) shows discrete bursts of correlated oxidation/reduction current, with a typical duration of seconds, which are indicative of a single molecule entering the gap and undergoing many (100,000–1,000,000 s⁻¹) individual electron transfer events. Intervening periods of zero Faradaic current occur when no redox molecule resides in the cell. Measuring these miniscule currents (10s fA) requires a high-gain but slow amplifier, which delivers a low temporal response, e.g., 10¹² V/A and 350 ms rise time, respectively, for the amplifier used.⁶⁵

While these experiments represent an ultimate analytical limit, i.e., single-molecule sensitivity, they also represent an average over many hundreds of thousands to millions of single electron transfer events; no dynamic information is gleaned from the measurement except for the entry and exit of the molecule from the thin layer cell, and possibly the decomposition of the molecule. If adequate sensitivity and temporal resolution allowed direct observation of single electron transfer events, what more could one learn about electron transfer or other physical processes? One would expect to observe stochasticity in the time between individual oxidations and reductions, a convolution of the time for molecules to random walk between electrodes and/or the electron transfer rate.⁶⁷ Evidence of heterogeneity between electron transfer rates at different sites on the electrode surface might be expected in addition to physical and mechanistic events occurring on rapid timescales. For example, adsorption/desorption occurring on timescales faster than the amplifiers can presently resolve might also become apparent. For molecules that undergo multiple sequential ET reactions, one would be able to characterize all steps (and not just the rate determining steps). Moreover, one could gain insight into reactions that occur via multiple competing pathways (e.g., electrocatalysis). An ensemble averaged current might show electron transfer with fractional numbers of electrons, while single ET resolution should offer the opportunity to differentiate and characterize the competing mechanisms.

The development of modern nanoelectrochemistry using steady-state voltammetric methods was also greatly accelerated by development of microelectrodes in the 1970s (later coined ultramicroelectrodes or UMEs). A brief, but incomplete definition is that UMEs are electrodes with at least one characteristic dimension small enough to lead to a steady-state response on voltammetric timescales associated with scan rates of 1 V/s or less. Early examples of UME applications include a 1942 report of using a 18-μm diameter Pt disk for measuring O₂ in animal tissues,⁶⁸ and 1970s research using ~10 μm Pt disk UMEs to investigate nucleation phenomena,⁶⁹ and similar size carbon fiber electrodes as implantable sensors for in-vivo detection of neurotransmitter release.⁸

Applications of UME-based electrochemistry exploded in the 1980s. In 1986, a conference dedicated to UME electrochemistry was held in Snowbird, Utah, and attended by researchers world-wide. The conference proceedings, published as the monograph, Ultramicroelectrodes,⁷⁰ was light on actual experimental data, but rather focused on potential applications and concepts that could potentially be investigated by making electrodes as small as possible, including measurements at the nanoscale (see a list of some conference topics in Figure 6). Many of these ideas are still being actively pursued, as exemplified by research reports presented at the current Faraday Discussion on Nanoelectrochemistry. For example, one concept introduced by K. Oldham in Ultramicroelectrodes was the idea that the electric double layer should have a more marked effect on transport rates if the size of the electrode could be reduced sufficiently small, i.e., comparable to the size of the electric double layer.⁹ This prediction has been realized over the past few decades as researchers have learned to make smaller and smaller electrodes and cells, on nanometer length scales.^{62, 71–73} For example, the original Anderson-Reilley TETL cell, reduced to the nanometer scale by Lemay, has been used to very clearly demonstrate how strongly the electric double layer influences molecular transport at nanometer length scales, Figure 7.^{71, 72} Electric fields between two electrodes separated by less than 100 nm have a very strong influence of the shape of the voltammetric wave, resulting in departure from the classical sigmoidal shape of a diffusion-controlled response.

Figure 6.

Ultramicroelectrodes⁷⁰ contained contributions from participants at a conference held in 1986 in Snowbird, Utah), outlining research topics and concepts pursued during the following decades.

Figure 7.

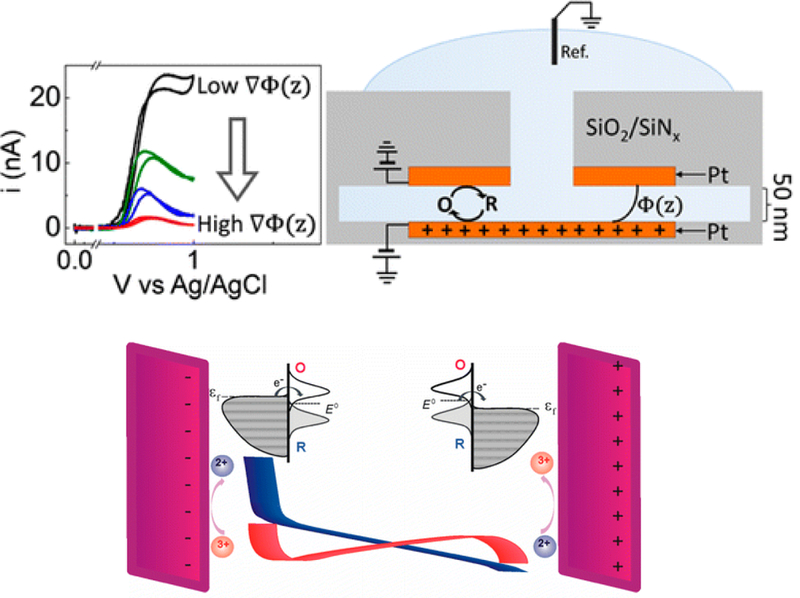
Redox cycling at electrodes separated at distances approaching the Debye length display unusual steady-state voltammetric responses. These measurements have been analyzed using theory describing the electric double-layer and models of electron-transfer kinetics. Adapted from references 71 and 72.

“The advantages of steady state measurements cannot be overemphasized in electrochemistry, especially in cases where fast kinetic parameters are sought.” This statement is from the introductory chapter of Ultramicroelectrodes written by Pons and Fleischmann,⁷⁰ but is also implicit in the early writings on RRDE and TETL cells in the 1950s and 60s.^{58, 59} The correspondence between “steady-state” and “fast kinetics” is not obvious; in fact, it is initially counter intuitive. If you want to measure really fast processes, the least likely successful approach would appear to be to make a steady-state i-V or time averaged measurement. In steady-state measurements, no dynamic information is obtained. So why has the steady-state approach been such a successful means for measuring fast kinetics in electrochemistry?

The answer to this question goes back to the work of Frumkin (RRDE)^{56, 57} and Anderson-Reilley (TETL cells),^{58, 59} in which time and distance were recognized as mutually dependent parameters; more specifically, distance can be manipulated to adjust the timescale of the electrochemical measurement. Decreasing the distance between the disk and ring electrode in RRDE, or the gap between two electrodes in TETL cells, allows one to probe faster kinetics under steady-state conditions. Analogously, UME not only allows steady-state measurements, but measurements of very fast kinetics when the UME is reduced to nanoscale dimensions.⁴ The focus on nanoscale length scales in the 1980s was also driven by the desire, in part, to measure faster rates in electrochemical systems.

Much of the today’s exploration of the behavior of nanoelectrochemical structures is driven by the above ideas. More quantitatively, the concept of using steady-state i-E methods to measure fast processes generally relies on the well-known relationship, λ² ~ Dt, which relates diffusional length to time, t, through the coefficient, D. Decreasing λ using nanoelectrodes, nanoparticles, nanogap cells, etc. results in a decrease in the effective timescale of the measurement, and provides a direct means to probe the kinetics of steps associated with very rapid electrochemical reactions. For instance, steady-state voltammetry using a nanogap twin-electrode cell of characteristic width, λ~10 nm, or a Pt disk electrode of equivalent diameter, allows investigations of events occurring at timescales on the order of ~100 ns. Many of the advantages of nanoscale electrochemistry are also at least partially dependent on this relation between time and distance, including high spatial resolution in electrochemical imaging,^{11, 27} the probing of the electric double layer as noted above,⁹ and the ability to make measurements in the absence of intentionally added electrolyte.¹⁰

Moving Towards Stochastic Electrochemistry and Electrochemical Dynamics

In 2016, a relatively new emphasis of nanoscale electrochemistry, entitled “Single Entity Electrochemistry,” was discussed at the Faraday Discussion in York, England. ^{39, 42} A prototypical example of so-called single-entity electrochemistry are electrochemical measurements of nanoparticle collisions.⁸¹ These stochastic, single entity measurements represent a significant departure from steady-state measurements. The rules that define classical electrochemistry of large ensembles of molecules appear to sometimes become irrelevant in these collision experiments; for example, mass-transport limited currents defined by Fick’s laws are replaced by probability theories of collisions rates.

At the 2016 Faraday Discussion, research groups from three different continents reported evidence of multiple current pulses during the electrooxidation of an individual Ag nanoparticle at a microelectrode, which are interpreted to reflect the dynamic motion of the nanoparticle.^74–76 For instance, Figure 8a shows the i-t response observed during the oxidative collisions of a single Ag nanoparticle at a Au microelectrode held at 1.1 V vs SHE (0.3 V vs E⁰(Ag/Ag⁺)).^{76, 77} The observed current displays discrete events because the nanoparticle spends most of the time in solution and out of contact with the electrode, as modeled by the simulated random walk trajectory in Figure 8b.

Figure 8.

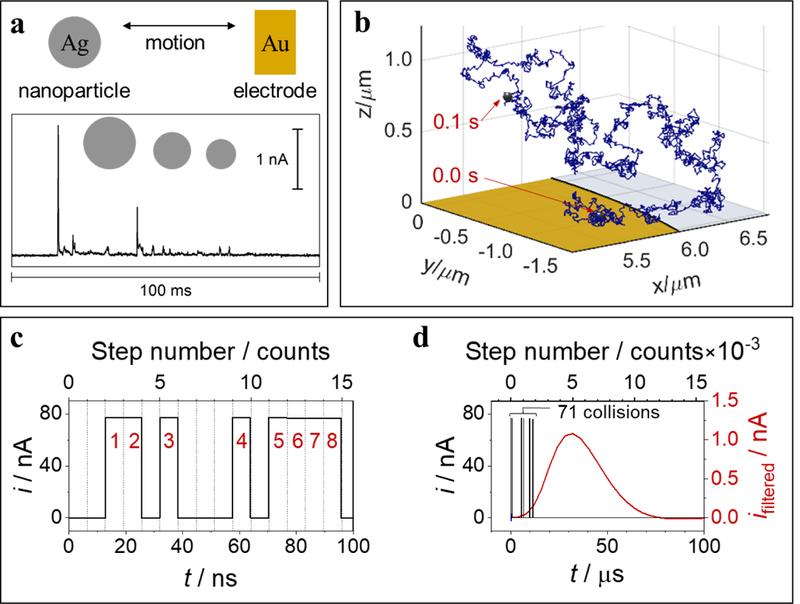
Experimental and simulated results for partial oxidations of an individual Ag nanoparticle, 35 nm radius. (a) Current vs time (i-t) trace (bottom) resulting from multiple partial oxidation/collision events at a Au microelectrode, 6.25 μm radius, held at 600 mV vs Ag/AgCl wire (1.1 V vs SHE), acquired with 3-pole low-pass Bessel filter (10 kHz cutoff) and 50 kHz sampling rate, electrolyte: 20 mM potassium nitrate and 8 mM trisodium citrate. (b) Simulated 3-D motion trajectory over a 0.1 s time interval, starting (0 ms) and ending (100 ms) positions in trajectory trace as labelled. Au electrode (yellow) and glass sheath (light gray) drawn to scale. (c) Results of electrochemical random-walk simulation for a Ag nanoparticle, 35 nm radius, showing resulting i-t traces for ideal unfiltered current (black) over the first 100 ns of electrode-nanoparticle collisions/oxidations, cumulative collision count shown in red numeric labels. (d) Results from same simulation in part (c) shown over longer (0.1 ms) timescale with simulated filtered current (3-pole low-pass Bessel, 10 kHz cutoff frequency, 250 kHz sampling rate) shown in red (right vertical axis). Number of discrete simulated motion steps included in top horizontal axes for parts (c) and (d). Adapted from references 77 and 78.

The discrete timescale of a single nanoparticle/electrode interaction can range from nanoseconds (e.g., thermal collisions),⁷⁷ to effectively infinity (e.g., irreversible particle adsorption).^{79, 80} For the case of Ag nanoparticle oxidation, one observes i-t peaks at the millisecond timescale, but theory^{77, 81, 82} suggests that each observable peak actually represents a set of much faster collisions occurring at the nanosecond timescale. According to our random walk model,⁷⁷ whenever the nanoparticle collides with the electrode, it undergoes partial oxidative dissolution (~1% of total available Ag surface atoms) over a timescale of 6.4 ns and becomes slightly smaller due to the loss of Ag. The electron-transfer rate used to simulate the experimental data (~5 cm s⁻¹) is within one order of magnitude agreement with that estimated from the Butler-Volmer kinetics based on a classically measured standard exchange current using macroscopic Ag electrodes.^{83, 84} This electron transfer rate is comparable to the thermal velocity of a 35 nm radius Ag particle (4.6 cm s⁻¹), which supports the theoretical conjecture that the upper limit of the electron transfer rate is dictated by the thermal velocity of the reactant.^{85, 86}

Theory and simulation suggests that the temporal resolution of the observable peaks in i-t traces is limited entirely by the instrument/cell bandwidth. Figure 8c-d illustrates the juxtaposition of timescales associated with Ag nanoparticle oxidation and the limited information available from the experiment.⁷⁷ Figure 8c shows the predicted i-t trace calculated in the simulation over the first 100 ns of the random walk. The nanoparticle undergoes ~15 motion steps over this time period, 8 of which result in stochastic electrode collisions. Each collision event is marked by a rectangular i-t pulse. The nanoparticle radius (not shown) decreases only slightly after each collision such that the pulse amplitudes barely decrease over time (not noticeable in Figure 8c). Figure 8d simulates the effect of a low-pass filter, such as those used in amplifiers for experimental measurements, on the i-t response. Because of the instrument response limitations, only one i-t peak results from 71 individual nanosecond-scale collisions. Thus, the most interesting information at the nanosecond timescale is essentially filtered out.⁷⁸ One desires to make measurements that are at least a thousand to a million times faster to probe the true dynamics of particle collisions. Such a goal represents a daunting challenge.

Our laboratory has also been performing experiments studying the electrochemical nucleation of small clusters of gasses (H₂) that eventually grow to nanometer size bubbles. The nucleation of bubbles at electrode surfaces represents an interesting model system⁸⁷ of many technological systems involving gas evolution. A single nanobubble can be formed at a 10 – 100 nm radius Pt disk electrode from electrochemical gas generation reactions,⁸⁸ including bubbles of H₂ (from H⁺ reduction),⁸⁹ N₂ (from N₂H₄ oxidation),⁹⁰ and O₂ (from O₂ or H₂O₂ oxidation).^{91, 92} The gas clusters that represent the bubble nuclei contain just a small handful of molecules. Nucleation times, i.e., the time between beginning with the bare Pt nanoelectrode and forming a small cluster of gas molecules at the surface, depends on the electrode potential and ranges from immeasurably slow to immeasurable fast.

Figure 9 shows a study of the nucleation of a H₂ bubble at a Pt nanoelectrode in an acidic solution. The current corresponding to H⁺ reduction to H₂ increases as the potential becomes more negative, resulting in an increase in the surface concentration of H₂. When the surface H₂ concentration becomes sufficiently high, nucleation, the formation of a critical gas bubble nucleus becomes likely. Interestingly, the nucleation rate (J) calculated based on classical nucleation theory increases by 9 orders of magnitude from (10⁻⁶ s⁻¹ to 10³ s⁻¹) within just a minuscule 30 mV voltage range. Because the nucleation rate is highly sensitive to any drift of the electrode potential, we instead controlled the applied current (levels indicated as dashed lines in the top of Figure 9B) and measure the induction time (t_ind) for bubble nucleation to occur. Figure 9c shows the stochasticity in t_ind stemming from the fluctuations that form the critical nucleus. However, at each given supersaturation (i.e., current level), t_ind is well described by a first-order stochastic process, from which we can extract the nucleation rate, J. It can be seen that as the current increases from −30 to −36 nA, the time required for nucleation to occur decreases from several seconds to about 1 ms.⁸⁷ Currently, the fastest measurements we can make are on the 100 μs timescale, corresponding to the RC response time of the electronics/electrode. There is tremendous opportunity in methodology and instrumentation development to push these measurements to shorter times.

Figure 9.

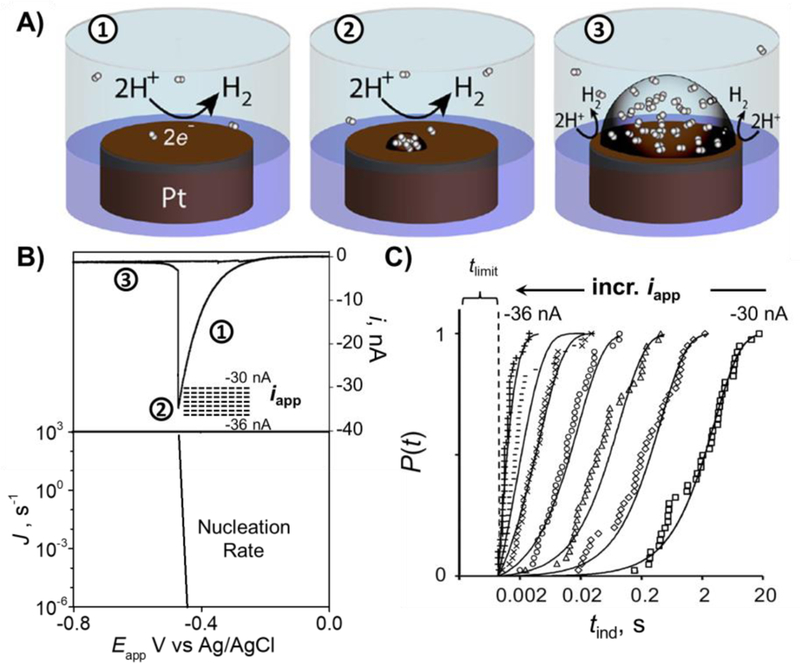
Nucleation and growth of a single H₂ nanobubble at a Pt nanoelectrode. A) Schematic corresponding to: ① H⁺ reduction, ② formation of critical H₂ bubble nucleus, and ③ steady-state bubble sustained at the Pt surface. B) Top: voltammogram corresponding to nucleation and growth of a single H₂ bubble. Dashed lines indicate the range of applied currents (i_app) for nucleation rate measurements. Bottom: Calculated nucleation rates (J) from classical nucleation theory as a function of voltage. Note the log scale for J. C) Cumulative probability distribution of nucleation induction time (t_ind) at different i_app measured from 40 individual nucleation events at each applied current. Figure adapted from reference 87.

Our measurements allow us to determine that the critical nucleus for a H₂ bubble contains between 30 – 50 H₂ molecules. It should be noted that the nucleation induction time we measured is the waiting time for the stochastic process of H₂ molecule clustering. It will be interesting to one day determine if classical nucleation theory breaks down at high supersaturation (via higher applied current), but this will only be possibly if much faster measurement can be achieved, on sub-microsecond timescales. Another interesting aspect of faster measurements is to observe the dynamics of nucleation and the growth of the critical nucleus.

A final example of single entity electrochemical measurements is the use of nanopores in chemical analysis. Nanopore resistive pulse sensing is inherently stochastic, and its applications are largely limited by the ability to measure fast “pulse” events. One sub-area of nanopore measurements is the use of protein ion channels for analyzing single biological molecules.³⁵ In our laboratory, we have recently focused efforts on the detection of single base mismatches/lesions in a DNA sequence.^93–95 We have shown that the “latch zone” of α-HL is an excellent sensing region for measurement of epigenetic modifications in double stranded DNA,⁹⁶ base flipping,⁹⁷ and enzyme kinetics.⁹⁸ In the example of base flipping, mismatch bases within double stranded DNA have the ability to flip in and out of the helix on timescales on the order of milliseconds (at 0.25 M KCl) as shown in Figure 10. The most thoroughly explored base-flipping dynamics are that of a cytosine-cytosine mismatch primarily due to the relatively long timescales (~ 100 ms), which can additionally be modulated by changing the solution pH. Base flipping has also been observed in sequences that contain cytosine-thymine mismatches,⁹⁹ among others,¹⁰⁰ but the kinetics are too fast to be resolved temporally due to the limitations of current instrumentation. We expect that there are many interesting DNA structures where base flipping is just too fast to be observed. Due to the finite bandwidth of our instrumentation, the flipping looks like “noise” in these cases.

Figure 10.

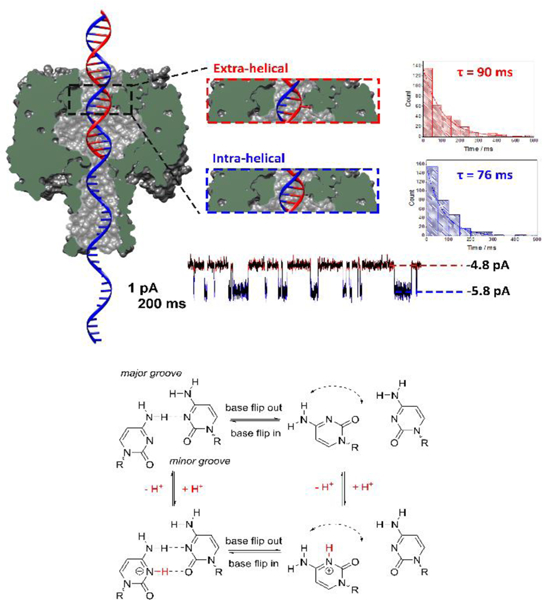
Measuring the dynamics of the motion of an individual DNA base by monitoring the ionic current through a protein nanochannel. (Top) Cross-section of the α-HL protein nanopore with a double-stranded DNA molecule (with a single-stranded tail) captured in the vestibule. The dsDNA contains a cytosine-cytosine mismatch near the latch zone of the protein. The observed current displays a two state modulation on the millisecond timescale resulting from the dynamic base flipping of one of the cytosine bases between intrahelical and extrahelical states. Histograms of the duration times between the two current states, and single exponential fits, are used to measure the first-order lifetimes of the extra-helical (out of the helix) and intra-helical (within the helix) states. (Bottom) Square scheme depicting the protonation/deprotonation and the effect of pH on the number of hydrogen bonds within cytosine-cytosine base pair. Below the pK_a of the cytosine mismatch, an additional hydrogen bond is formed decreasing the rate of base flipping. Although base flipping is a relatively slow process, the protonation/deprotonation that affects the flipping kinetics is immeasurably fast. Figure adapted from reference 99.

Conclusions.

With new nanoscale electrochemistry being reported every week, it is certainly an exciting time for the field. Nanoscale single entity electrochemistry on a sub-millisecond timescale offers great promise for answering fundamental questions and developing new applications. However, the above examples of single entity electrochemical processes are not just fast, but stochastic too. So, the rules of analyzing the data differ significantly from those used for conventional ‘ensemble’ electrochemical measurements. Very little existing electrochemical theory has been formulated for single entity applications, but instead interpretation relies on devising new methods for analyzing data. These are either developed from scratch, applying results from probability theory, or adapted from other single-entity fields (e.g., single molecule optics and STM break-junctions). With new measurements driving theory, new opportunities abound.

However, performing these measurements represents daunting challenges, as one can no longer use steady-state measurements and simply make structures smaller and smaller, an approach that served very well over the past few decades. The approach does not apply because single entity electrochemistry is not at steady state! How to perform ultrafast and dynamic electrochemical measurements? is a tough and open question, which we should strive to answer as a field moving forward.

It is very difficult to eliminate the limitations of RC charging in electrochemical cells. State-of-the-art electronics, with the first amplifier placed very close to the cell minimizes extraneous noise and parasitic currents, is somewhat successful in addressing this issue. Amatore and Compton used such an approach to perform cyclic voltammetry at 10⁶ V/s,^101–104 and more recently CMOS amplifier technology, exemplifying this approach, has delivered even higher bandwidths of low MHz.^{105, 106} Under optimal conditions, these approaches may allow measurements at ~1 μs timescales, which are likely about as fast as you can make in a conventional electrochemical current measurement --- in more typical experiments, even an order of magnitude slower temporal resolution is still challenging to achieve. However, in many of the new experiments, such as the random motion and collision of Ag nanoparticles with an electrode, ^{24, 74, 76} complete characterization of the dynamic motion requires measurement to be down to ~1 ns. Between what is presently measureable and what is desired, there’s a huge gulf waiting to be filled with transformative measurement ideas. An avenue that continues to be actively explored is to couple electrochemistry with optical readouts.^107–112 While it is certainly possible to detect photons on such shorter timescales, a mechanism of electron-transfer-to-photon-transduction is required.