When learning goes beyond statistics: Infants represent visual sequences in terms of chunks

Abstract

Much research has documented infants’ sensitivity to statistical regularities in auditory and visual inputs, however the manner in which infants process and represent statistically defined information remains unclear. Two types of models have been proposed to account for this sensitivity: statistical models, which posit that learners represent statistical relations between elements in the input; and chunking models, which posit that learners represent statistically-coherent units of information from the input. Here, we evaluated the fit of these two types of models to behavioral data that we obtained from 8-month-old infants across four visual sequence-learning experiments. Experiments examined infants’ representations of two types of structures about which statistical and chunking models make contrasting predictions: illusory sequences (Experiment 1) and embedded sequences (Experiments 2-4). In all four experiments, infants discriminated between high probability sequences and low probability part-sequences, providing strong evidence of learning. Critically, infants also discriminated between high probability sequences and statistically-matched sequences (illusory sequences in Experiment 1, embedded sequences in Experiments 2-3), suggesting that infants learned coherent chunks of elements. Experiment 4 examined the temporal nature of chunking, and demonstrated that the fate of embedded chunks depends on amount of exposure. These studies contribute important new data on infants’ visual statistical learning ability, and suggest that the representations that result from infants’ visual statistical learning are best captured by chunking models.

1. Introduction

How do learners make sense of their intricately structured auditory and visual environments? Previous research suggests that both infants and adults are able to identify statistically coherent pieces of information contained within larger sequences presented both aurally and visually (see Krogh, Vlach, & Johnson, 2012 for a review). This “statistical learning” ability may facilitate learners’ detection of important types of environmental structure. For instance, statistical learning is thought to help learners identify words in continuous speech, facilitating language learning (e.g., Saffran, 2001), and help learners segment continuous motion into discrete events, facilitating visual learning and categorization (e.g., Stahl, Romberg, Roseberry, Golinkoff, & Hirsh-Pasek, 2014).

Despite the scope and potential importance of statistical learning ability, the specific processes underlying statistical learning remain unclear. Recent research has investigated how two types of models of the mechanisms underlying statistical learning – statistical models and chunking models – account for adults’ statistical learning performances (see Thiessen, Kronstein, & Hufnagle, 2013 for a review). Though several studies suggested that adults’ statistical learning is best accounted for by chunking models (Fiser & Aslin, 2005; Giroux & Rey, 2009; Orbán, Fiser, Aslin, & Lengyel, 2008; Perruchet & Poulin-Charronnat, 2012; Slone & Johnson, 2015b), at least one study suggested that statistical models may in some cases provide a better fit for adult data (Endress & Mehler, 2009). Moreover, it remains unknown which type of model best accounts for infants’ statistical learning performances. This is an important issue to address, as statistical learning is posited to underlie much early learning, including language acquisition. Additionally, examining possible statistical and chunking processes in infants’ statistical learning allows investigation of the extent to which the mechanisms underlying statistical learning are similar for infants and adults.

1.1 Statistical and Chunking Models of Statistical Learning

In a seminal study of infants’ statistical learning, Saffran, Aslin, and Newport (1996) exposed 8-month-olds to a continuous stream of speech in an artificial language composed of four, three-syllable nonsense “words.” Words were concatenated with no pauses between words, such that word boundaries were marked only by differing statistical relations between syllables within words and between words. After only 2 minutes of exposure to this language, infants were able to distinguish words from “part-words” (syllable sequences spanning word boundaries), demonstrating sensitivity to the statistical structure of the input.

Both statistical (or “transition-finding”) models and chunking (or “clustering”) models (Thiessen et al., 2013) have been proposed to account for such sensitivity to statistical structure (Frank, Goldwater, Griffiths, & Tenenbaum, 2010; Thiessen et al., 2013); however, these models differ in the representations stored in memory. Statistical models can be instantiated with simple recurrent networks (SRNs) (e.g., Elman, 1990) that calculate and represent in memory statistical relations between items. For instance, one statistical relation that models (and human learners) may represent is transitional probability (TP), defined as the probability of event Y given event X (P(Y|X)), a measure of the strength with which X predicts Y. Representing such a statistic would not only inform the model of the likelihood of two items occurring together, but would also allow the model to predict individual items based on previous items in a sequence.

Consider, for instance, the Saffran et al. (1996) sequence composed of four 3-syllable words: A₁A₂A₃, B₁B₂B₃, C₁C₂C₃, and D₁D₂D₃. Statistical models will learn that P(A₂|A₁) and P(A₃|A₂) are high because items A₁, A₂, and A₃ always appear together in that order. In contrast, P(B₁|A₃) will be lower because word A is sometimes followed by word B, but other times followed by words C or D. In this way, statistical models can distinguish statistically coherent units of information contained within a sequence (e.g., A₁A₂A₃) from less coherent units like part-words (e.g., A₃B₁B₂). Statistical models do not explicitly represent statistically coherent units; rather, they represent statistical relations between items.

In contrast, chunking models typically consider sensitivity to statistical relations like TPs to simply be a byproduct of other processes. The general feature separating chunking from statistical models is that chunking models do represent statistically coherent units of information in memory. The mechanisms by which chunking models acquire these representations differ across models. Some of the most common chunking models are Bayesian models (e.g., Goldwater, Griffiths, & Johnson, 2006, 2009; Orbán et al., 2008) and PARSER (Perruchet & Vinter, 1998). Despite their varying learning processes, the representations that result from chunking models are discrete, statistically coherent, “chunks” of information.

PARSER (Perruchet & Vinter, 1998), for instance, is a chunking model designed to account for human behavior by implementing psychologically plausible processes of attention, memory, and associative learning. PARSER joins items perceived within one attentional focus into a representational unit, or chunk. Representations of units whose component items co-occur regularly are progressively strengthened in memory, while representations of units whose component items do not co-occur regularly are forgotten. For instance, consider again the Saffran et al. (1996) sequence, and suppose that at any moment PARSER can only capture up to two items in its attentional focus. PARSER might initially capture the sequence A₁A₂A₃B₁B₂B₃ in three separate chunks: A₁A₂, A₃B₁, and B₂B₃. Over time, chunks A₁A₂ and B₂B₃ will be reinforced in memory because their component items always co-occur. In contrast, chunk A₃B₁ will only be weakly represented because its component items co-occur less frequently. Moreover, once the sequence A₁A₂ is represented as a single chunk rather than as two separate items, it becomes possible for the structure A₁A₂A₃ to be captured in a single attentional focus (i.e., as the aggregate of two items: A₁A₂ and A₃). Thus, with sufficient exposure PARSER will form strong representations of statistically coherent units of information (e.g., A₁A₂A₃) and distinguish them from weakly represented part-words (e.g., A₃B₁B₂).

1.2 Examining Model Fit to Human Data

Recent research has investigated how well statistical and chunking models fit human data (e.g., Endress & Mehler, 2009; Fiser & Aslin, 2005; Frank, Goldwater, Griffiths, & Tenenbaum, 2010; Giroux & Rey, 2009; Orbán et al., 2008; Perruchet & Poulin-Charronnat, 2012; Slone & Johnson, 2015b). Many of these studies have examined the representations that adults store following auditory or visual statistical learning tasks, and whether these representations are best captured by statistical or chunking models. Such studies investigate representations of two types of items. The first type is illusory (or “phantom”) units—units that are never presented to participants, but have the same statistical structure as other units that are presented. For example, if tazepi, mizeru, and tanoru are words presented in a speech stream, and TPs are .50 between syllables within these words (e.g., between ta and ze and between ze and ru), a statistically matched illusory word would be tazeru (Endress & Mehler, 2009). Statistical models could learn, for instance, that P(ze|ta) = P(ru|ze) = P(pi|ze), and would therefore predict that the unit tazepi should be indistinguishable from the illusory word tazeru because the two strings are statistically equivalent. Chunking models, in contrast, predict that learners should fail to recognize illusory units because these units have never been presented, therefore learners could not have extracted from the input a chunk matching an illusory unit.

The second type of item researchers have investigated is embedded units—sub-units that occur only within larger units (Fiser & Aslin, 2005). In terms of linguistic materials, an embedded item could be a group of syllables that occurs within a word, but never occurs independently (e.g., “eleph”, as in “elephant”) (Thiessen et al., 2013). Statistical models predict that, because learners represent statistical relations between all pairs of adjacent elements, as learners become familiar with a unit (e.g., A₁A₂A₃), distinguishing components embedded in that unit (e.g., A₁A₂) should improve relative to less statistically coherent configurations of elements (e.g., A₃B₁). Many chunking models, in contrast, predict that as learners become familiar with a unit, they should become less able to distinguish components embedded in that unit from less statistically coherent configurations of elements (see Giroux & Rey, 2009). This is because an assumption of many chunking models is economy of representation, instantiated as competition between chunks within memory (Fiser & Aslin, 2005; Orbán et al., 2008; Thiessen et al., 2013). For instance, as PARSER learns the unit structure A₁A₂A₃, not only will the chunk A₁A₂A₃ be strengthened in memory, but it will also interfere with memory for embedded chunk A₁A₂, progressively reducing accessibility to A₁A₂ (Giroux & Rey, 2009).

Six studies have recently investigated adults’ representations of illusory and embedded units, and the ability of various models to account for this performance. Specifically, these studies have investigated adults’ representations of illusory units presented in auditory sequences (Endress & Mehler, 2009; Perruchet, & Poulin-Charronnat, 2012) and visual sequences (Slone & Johnson, 2015b), and embedded units presented in auditory sequences (Giroux & Rey, 2009), visual sequences (Slone & Johnson, 2015b), and visual scenes (Fiser & Aslin, 2005; Orbán et al., 2008). Though one study (Endress & Mehler, 2009) suggested that statistical models may provide a better fit for adult statistical learning performances, the majority of these studies suggest that adults’ statistical learning is best accounted for by chunking models.

It remains unknown, however, which type of model best accounts for infants’ statistical learning performances. Two major types of chunking models (Bayesian models and PARSER) rely on assumptions about learners’ priors (e.g. Goldwater et al., 2006, 2009) and attention, memory, and associative learning (Perruchet & Vinter, 1998)—factors that likely change between infancy and adulthood. For instance, PARSER is typically endowed with the ability to process up to three chunks simultaneously. This parameter seems plausible for modeling adults’ learning, as much research suggests that adult short-term and working memory capacities fall in the range of 3 to 5 chunks (see reviews by Cowan, 2001, 2010). However, recent research suggests that during the first 6 months after birth, infants’ short-term memory capacity encompasses only a single item, and expands to encompass two items by 8-10 months of age, and possibly up to four items by an infant’s first birthday (e.g., Kwon, Luck, & Oakes, 2014; Oakes, Baumgartner, Barrett, Messenger, & Luck, 2013; Ross-Sheehy & Newman, 2015; Ross-Sheehy, Oakes, & Luck, 2003). Thus, for an 8-month-old capable of holding only up to two items in memory, computing pairwise statistics might be a more efficient strategy than trying to build up representations of chunks that could consist of many more than two items.

The current set of experiments investigated whether statistical or chunking models best account for infants’ statistical learning performances. Because most work comparing these models’ fits to adult statistical learning data has employed visual stimuli, we focused on infants’ visual statistical learning. Experiment 1 and Experiments 2-3 examined infants’ learning of illusory and embedded visual sequences, respectively, and asked: Are infants’ representations of visual sequences best predicted by statistical models or chunking models? Following up findings in favor of chunking models, Experiment 4 then examined the processes by which infants may form and maintain representations of chunks.

2. Experiment 1

2.1 Material and Method

2.1.1 Participants

Eighteen healthy full-term 8-month-olds (14 females; M age 7 months 24 days, range = 6;28 to 8;17) were tested with a familiarization paradigm. Data from an additional nine infants were excluded from the final sample due to fussiness (n = 4), parental interference (n = 3), or sleepiness (n = 2). Infants were recruited by letter and telephone from hospital records and given a small gift (a toy or baby t-shirt) for their participation.

2.1.2 Apparatus and stimuli

An Eyelink 1000 eye tracker (SR Research) with a 55.9-cm color monitor displayed stimuli and collected eye-tracking data.¹ A PC computer running Experiment Builder software controlled stimulus presentation and collected looking time data.

Stimuli consisted of a five-location spatial array and five colored shapes (Figure 1). Infants viewed a continuous sequence of shapes, presented one at a time for 750 ms each and looming from 1.5 to 5.5 cm in height (about 8.0°-10.0° visual angle) within one of the five locations on the monitor. The familiarization sequence consisted of a continuous sequence of three randomly ordered units: two shape triplets (e.g., triplet 1: red circle, blue square, orange diamond; triplet 2: lime green plus, red circle, orange diamond), and one shape pair (e.g., blue square, yellow triangle). Units could repeat and there were no breaks or delays between units such that units were defined solely by distinctions in TPs. Because each shape could appear in more than one unit, TPs between shapes within units were either 1.0 or .50, and TPs between shapes spanning unit boundaries were .33 (Figure 2A).

Figure 1.

Sample spatial array and shapes presented in Experiments 1-3. Only one shape appeared at a time during familiarization and test.

Figure 2.

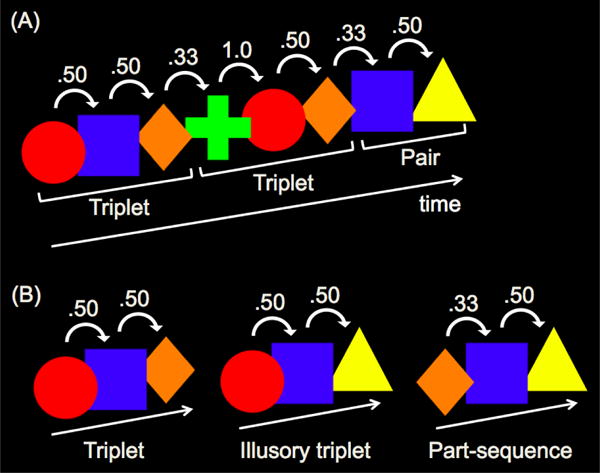
Sample (A) familiarization sequence and (B) test sequences presented in Experiment 1. Numbers above shapes represent TPs during familiarization. Brackets below shapes indicate the unit structure of the familiarization sequence.

2.1.3 Procedure

Infants sat on a caretakers’ lap approximately 60 cm from the monitor. Caretakers were instructed not to interact with the infant or attend to the monitor. During familiarization and test, a trained observer who was unaware of the stimulus sequence observed the infant via a video feed from a camera placed directly below the monitor and coded looking behavior online. Prior to familiarization, an attention-getter was presented to attract infants’ attention to the center of the monitor. Familiarization began when the experimenter pressed a keyboard key to indicate that the infant was looking at the monitor. When the infant fixated away from the monitor, the experimenter released the key, causing the familiarization sequence to pause. If the infant returned attention to the monitor within 2 s, the familiarization sequence resumed. Otherwise, an attention-getter was shown to attract infants’ gaze back to the monitor, whereupon the experimenter immediately resumed the familiarization sequence.

Familiarization continued until the full five-minute familiarization sequence (50 presentations of each unit) had been seen. Following familiarization, infants were presented with two blocks of three unique test trials, for a total of six test trials (see Figure 2B). Trial order within each block was randomized. Each test trial consisted of a repetition of three shapes, with a 750 ms pause separating repetitions. Triplet test trials presented the triplet with .50 TPs between shapes during familiarization (e.g., red circle, blue square, orange diamond). Illusory triplet test trials presented a three-shape sequence that was never seen in its entirety during familiarization, but which had .50 TPs between adjacent shapes during familiarization (e.g., red circle, blue square, yellow triangle). Thus, triplet and illusory triplet test sequences were equivalent in terms of TPs between adjacent shapes. Part-sequence test trials presented the last shape of a triplet followed by the pair from familiarization (e.g., orange diamond, blue square, yellow triangle), such that TP was .33 between the first two shapes and .50 between the latter two shapes. Thus, part-sequences had lower internal TPs compared to triplets and illusory triplets. An attention-getter was presented prior to the first test trial, and every subsequent trial, to center infants’ gaze. Each test sequence was presented until the infant looked away from the monitor for over 2 s or until 90 s had elapsed.

2.1.4 Coding and predicted results

Mean durations of looking to each of the three test types (triplet, illusory triplet, part-sequence) were computed. Looking time measures capitalize on the tendency for infants’ general interest in a visual stimulus to decline upon repeated exposure over the familiarization period. When followed by presentation of test sequences that either bear resemblance to the original stimulus (i.e., triplet from familiarization), or differ along one or more dimensions (i.e., illusory triplet, part-sequence), significantly different durations of looking to these test types indicates discrimination between them, whereas equal durations of looking to the test types suggests no discrimination. The present study used a familiarization design, rather than an infant-controlled habituation design, to equate infants’ exposure to the familiarization stimulus prior to test. One limitation of using familiarization rather than habituation, however, is that we cannot accurately predict a priori whether infants will exhibit a familiarity or a novelty preference as an index of learning (see Hunter & Ames, 1988). Thus, while we predicted discrimination between test types, we did not have a priori predictions about the directions of infants’ preferences.

Both statistical and chunking models predict that successful learning should be indicated by significantly different durations of looking on triplet (high TP) compared to part-sequence (lower TP) test trials. Statistical and chunking models differ, however, in their predictions about infants’ relative looking durations on illusory triplet test trials. Statistical models predict that infants should show similar durations of looking to triplet and illusory triplet test sequences, because these sequences had equivalent TPs between adjacent shapes during familiarization (TPs = .50). In contrast, chunking models predict that infants should show different durations of looking to triplet and illusory triplet test sequences because, with enough exposure, infants should represent the highest-level units from the input (e.g., the triplets) most strongly in memory. Thus, illusory triplets should seem relatively novel to infants because these units were never presented in their entirety during learning.

2.2 Results and Discussion

As can be seen in Figure 3, infants looked longer during the familiar triplet test trials than the illusory triplet or part-sequence test trials. Familiarity preferences have been demonstrated in some infant statistical learning experiments (e.g., Fiser & Aslin, 2002; Graf Estes, 2012, Experiment 1; Thiessen, Hill, & Saffran, 2005, Experiment 1), and have been taken to indicate that infants did not fully habituate to the familiarization stimulus, often due to stimulus complexity, and therefore continued to look to the familiar stimulus during test trials (Hunter and Ames, 1988). This is in contrast to preferences for part-sequences, which are typically expected following habituation of looking, and may indicate more complete stimulus processing such that infants shift their looking toward more novel stimuli during test trials (e.g., Aslin, Saffran, & Newport, 1998; Saffran et al., 1996; Slone & Johnson, 2015a; Thiessen et al., 2005). Thus, prior to analyzing infants’ test performance, we first examined the extent to which infants had become habituated to the familiarization stimulus. If only a minority of the infants in Experiment 1 habituated to the sequence by the end of familiarization, this could explain why a familiarity preference was observed at test.

Figure 3.

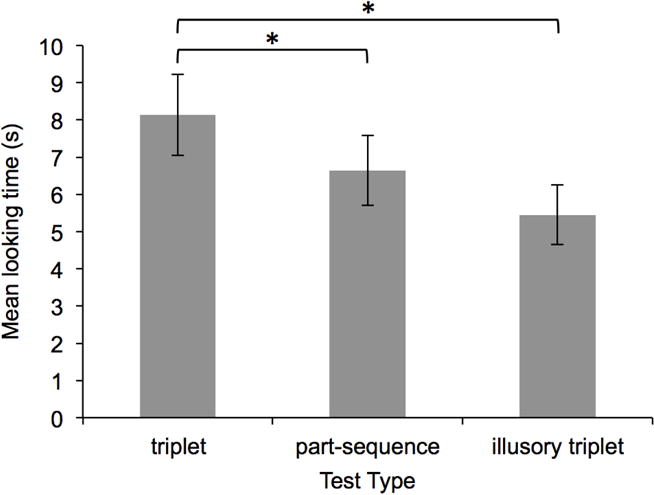
Infants’ mean looking duration to each of the three test types in Experiment 1. Error bars represent standard error of the mean.

Habituation is typically operationalized as a 50% or greater decrement in looking duration between early and later trials. For each infant we divided the five-minute familiarization period into trials based on when the infant looked away from the monitor for >2 s, which ended a trial. Infants completed the five-minute familiarization phase in an average of 25.9 trials (SD = 9.4, range = 9 to 45). Each infant’s habituation score was computed by dividing the sum looking duration during the second half of familiarization trials by the sum looking duration during the first half of familiarization trials²; we considered infants with habituation scores less than .50 (i.e., a 50% or greater decrement in looking) to have habituated. By this criterion, only 2 of the 18 infants in Experiment 1 habituated. Infants’ habituation scores were negatively skewed in this and the other experiments reported in this paper, thus for all further analyses we used an exponential transformation of each infant’s habituation score. Infants’ mean habituation score was 1.26 (SD = 0.35), which is equivalent to only 23% shorter look durations on average during the second half compared to the first half of familiarization. Thus, the familiarity preferences we observed during test trials may have stemmed from infants’ lack of habituation to the familiarization stimulus.

Preliminary analyses of infants’ looking times during test trials revealed non-normal distributions in all four experiments reported in this paper. Thus, we calculated log transformations of each infant’s mean looking duration to each test type, and used these log-transformed measures for all further analyses (Csibra, Hernik, Mascaro, Tatone, & Lengyel, 2016; Figures 3, 5, 6, and 8 show raw looking times for ease of interpretation). A repeated measures analysis of variance (ANOVA) revealed a main effect of test type: F(1,17) = 18.95, p < .001, partial η² = .527. Planned paired samples t-tests (this and all subsequent t-tests were two-tailed) revealed that infants looked significantly longer during triplet test trials, compared to both part-sequence and illusory triplet test trials: ts(17) > 2.68, ps < .05, ds > 0.63. Non-parametric binomial tests confirmed these results. The numbers of infants looking longer during triplet compared to part-sequence (14 out of 18) and illusory triplet (17 out of 18) test trials were greater than the numbers expected by chance (i.e., 9 out of 18), ps < .031. Paired samples t-tests also revealed a marginally significant difference in looking durations during part-sequence and illusory triplet test trials, t(17) = 1.90, p = .07, d = 0.45 (Figure 3); however, this finding was not confirmed by a binomial test, as only 11 of the 18 infants looked longer during part-sequence compared to illusory triplet test trials, p = .481.

Figure 5.

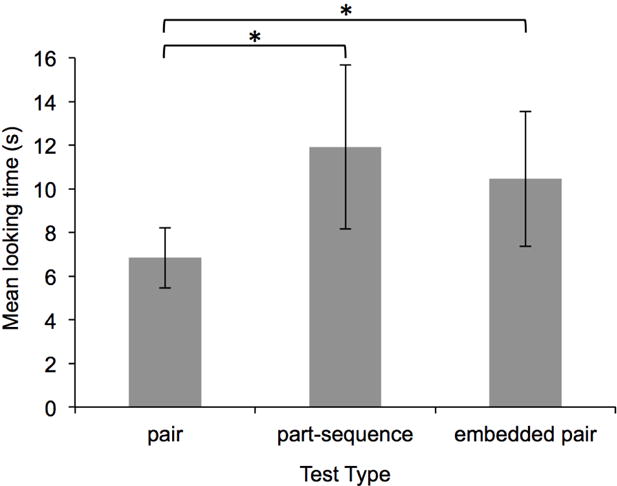
Infants’ mean looking duration to each of the three test types in Experiment 2. Error bars represent standard error of the mean.

Figure 6.

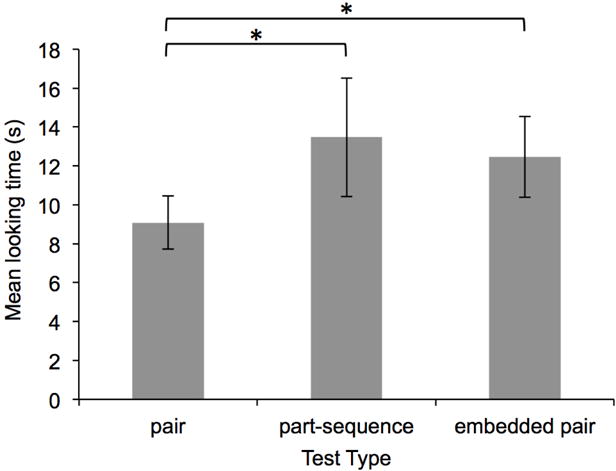
Infants’ mean looking duration to each of the three test types in Experiment 3. Error bars represent standard error of the mean.

Figure 8.

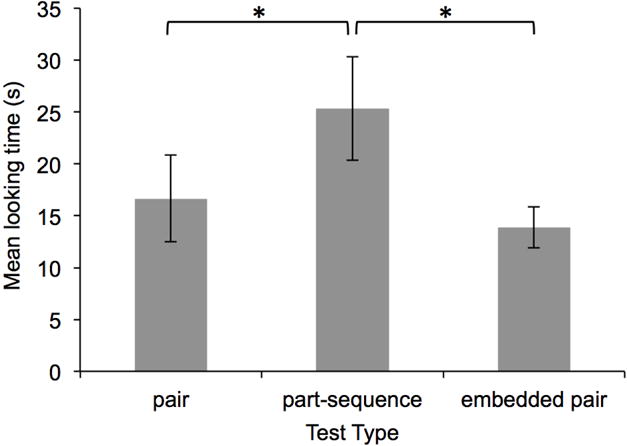
Infants’ mean looking duration to each of the three test types in Experiment 4. Error bars represent standard error of the mean.

Infants provided evidence of discriminating triplets from both part-sequences and illusory triplets. In contrast to the predictions of statistical models, infants did not appear to represent the familiarization sequence primarily in terms of TPs between adjacent items. Rather, infants discriminated between test sequences containing equal TPs (that is, between triplets and illusory triplets), suggesting that infants represented the familiarization sequence in terms of extracted units, not statistical relations.

Additionally, there was some evidence of a difference in looking to part-sequences and illusory triplets, such that part-sequence looking durations fell part-way between triplet and illusory triplet looking durations. The direction of this weak effect also aligns with the predictions of chunking models, as part-sequences would have been encountered in their entirety less often than triplets, but more often than illusory triplets (which had never appeared). In contrast, statistical models would predict the opposite ordering of looking durations; specifically, infants should have distinguished part-sequences from illusory triplets by exhibiting illusory sequence looking durations that were more, not less, similar to triplet looking durations.

This interpretation prioritizes relations between adjacent items on account of data suggesting that non-adjacent relations are more difficult for learners to identify compared to adjacent relations (Newport & Aslin, 2004). It is possible, however, that a statistical model allowing for computation of non-adjacent relations could also account for the data from Experiment 1. For instance, both triplet and illusory triplet test sequences had .50 TPs between adjacent shapes during familiarization. Triplet test sequences also had .50 TP between nonadjacent shapes during familiarization (i.e., red circle predicted orange diamond appearing two items later with .50 accuracy), whereas illusory triplet test sequences had .00 TP between nonadjacent shapes during familiarization (i.e., red circle never predicted yellow triangle appearing two items later). Additionally, part-sequences had .33 TP between non-adjacent shapes during familiarization (i.e., orange diamond predicted yellow triangle appearing two items later with .33 accuracy). It is possible, therefore, that discrimination between triplet test trials and both illusory and part-sequence test trials could have resulted from infants’ representing statistical relations between non-adjacent shapes (either independently or in addition to representing relations between adjacent shapes), rather than representing chunks.

Experiment 2 was designed to address this possibility by examining infants’ representations of embedded sequences. In contrast to illusory sequences, embedded sequences in Experiment 2 consisted of only two shapes, such that only adjacent relations could be used to distinguish embedded sequences from other test sequences. If infants discriminate such embedded pairs from statistically matched non-embedded pairs in Experiment 2, this is further evidence in favor of chunking, rather than statistical models. If, however, without added nonadjacent statistical cues, infants do not discriminate embedded pairs from statistically matched non-embedded pairs, this suggests that performance in Experiment 1 may in fact have resulted from representations of non-adjacent statistical relations.

3. Experiment 2

3.1 Material and Method

3.1.1 Participants

Eighteen healthy full-term 8-month-olds (5 females; M age 8 months 9 days, range = 7;7 to 8;27) were recruited as in Experiment 1. Data from an additional 10 infants were excluded from the final sample due to fussiness (n = 6), parental interference (n = 2), failure to look at the monitor (n = 1), or excessive squirming (n = 1).

3.1.2 Apparatus and stimuli

The apparatus and stimuli were identical to those of Experiment 1, except for the unit structure of the familiarization sequence. In Experiment 2, the familiarization stimulus consisted of a continuous sequence of two randomly ordered units: a shape triplet (e.g., yellow triangle, blue square, orange diamond), and a shape pair (e.g., lime green plus, red circle). Units could repeat and there were no breaks or delays between units such that units were defined solely by distinctions in TPs. Because each shape appeared in only one unit, TPs between shapes within units were 1.0, and TPs between shapes spanning unit boundaries were .50 (Figure 4A).

Figure 4.

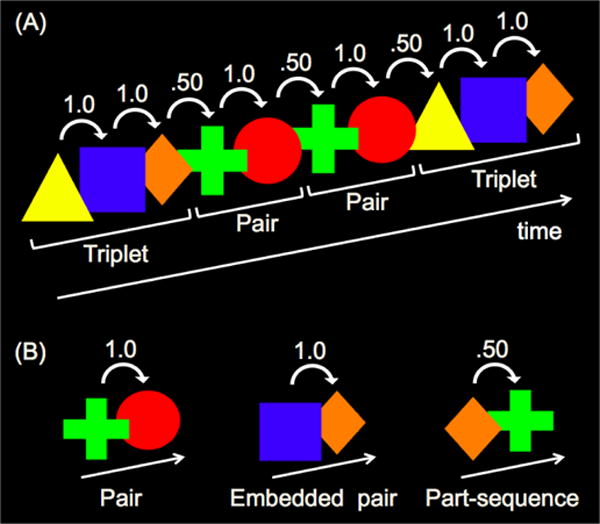
Sample (A) familiarization sequence and (B) test sequences presented in Experiments 2 and 3. Numbers above shapes represent TPs during familiarization. Brackets below shapes indicate the unit structure of the familiarization sequence.

3.1.3 Procedure

The procedure was identical to that of Experiment 1, with two exceptions. First, because only two units were presented in Experiment 2 (compared to three units in Experiment 1), infants saw 80 presentations of each unit (compared to 50 in Experiment 1) during the five-minute familiarization. Second, different test types were presented (Figure 4B). Pair test trials presented the pair from familiarization (e.g., lime green plus, red circle; TP=1.0), embedded pair test trials presented the latter two shapes of the triplet from familiarization (e.g., blue square, orange diamond; TP=1.0), and part-sequence test trials presented the last shape of the triplet followed by the first shape of the pair from familiarization (e.g., orange diamond, lime green plus; TP=.50). Thus, pairs and embedded pairs had equal TPs between shapes, and higher TPs than part- sequences.

3.1.4 Predicted results

Both statistical and chunking models predict that successful learning should be indicated by significantly different durations of looking on pair (high TP) compared to part-sequence (lower TP) test trials. Statistical and chunking models differ, however, in their predictions about infants’ relative looking durations on embedded pair test trials. Statistical models predict that infants should show similar durations of looking to pair and embedded pair test sequences because these sequences had equivalent TPs between shapes during familiarization (TP=1.0). In contrast, chunking models posit that a representation of the embedded pair will be progressively interfered with in memory as a representation of the encompassing triplet is formed, such that the embedded pair may be represented relatively weakly compared to the pair (which was not embedded and therefore did not compete with encompassing representations), resulting in different durations of looking to pair versus embedded pair test sequences.

3.2 Results and Discussion

As in Experiment 1, prior to analyzing infants’ test performance, we first examined the extent to which infants became habituated to the familiarization stimulus. Infants in Experiment 2 completed the five-minute familiarization phase in an average of 27.3 trials (SD = 18.0, range = 2 to 80). Ten of the 18 infants in Experiment 2 showed evidence of habituating, which was significantly greater than the number of habituating infants in Experiment 1 (i.e., 2 out of 18; Fisher’s exact test, p = .012). Moreover, infants’ mean habituation score in Experiment 2 (M = 1.64, SD = 0.47) was significantly greater than that of Experiment 1 (t[34] = 2.75, p < .01, d = 0.92), suggesting that infants in Experiment 2 might be more likely to exhibit novelty preferences, compared to the infants in Experiment 1.

Preliminary analyses of infants’ looking durations during test trials confirmed this prediction. As can be seen in Figure 5, infants looked longer during part-sequence and embedded pair test trials compared to familiar pair test trials. A repeated measures ANOVA revealed a main effect of test type: F(1,17) = 4.54, p < .05, partial η² = .211. Planned paired samples t-tests revealed that infants looked significantly longer during both part-sequence and embedded pair test trials, compared to pair test trials: ts(17) > 2.13, ps < .05, ds > 0.50. Non-parametric binomial tests confirmed that a significant number of infants looked longer during embedded pair compared to pair test trials (14 out of 18 infants, p = .031), but revealed that only 12 of the 18 infants looked longer to part-sequence compared to pair test trials (p = .238). Paired samples t-tests revealed no significant differences in looking durations on embedded pair compared to part-sequence test trials: t(17) = 0.42, p = .68, d = 0.10 (Figure 5); this null effect was corroborated by a binomial test: only 11 of the 18 infants looked longer during part-sequence compared to embedded pair test trials, p = .481.

These findings suggest that infants discriminated the pair from both the part-sequence and the embedded pair. In contrast to the predictions of statistical models, infants did not represent the familiarization sequence primarily in terms of TPs between adjacent items. Rather, infants discriminated between test pairs containing equal TPs (that is, between pairs and embedded pairs), suggesting that infants represented the non-embedded pair differently (and likely more strongly) than the embedded pair, supporting the predictions of chunking models. Moreover, infants’ ability to discriminate sequences with equivalent statistical relations between adjacent items and no additional non-adjacent statistical cues suggests that performance in Experiment 1 may also have been due to infants’ representations of chunks rather than non-adjacent statistical relations.

Given the theoretical importance and counterintuitive nature of this finding – as the predominant explanation of infants’ performance in these types of statistical learning tasks has historically been that infants discriminate test sequences based on differences in transitional probabilities, not chunked units – we conducted Experiment 3 as an internal replication of Experiment 2.

4. Experiment 3

4.1 Material and Method

4.1.1 Participants

Thirty-one healthy full-term 8-month-olds (21 females; M age 7 months 26 days, range = 6;9 to 8;30) were recruited as in Experiments 1 and 2. Power analyses based on the effect size (d = 0.51) for infants’ looking time differences observed in Experiment 2 indicated that a sample size of 31 infants would yield power = 0.79. Data from an additional 5 infants were excluded from the final sample due to fussiness (n = 2), parental interference (n = 1), failure to look at the monitor (n = 1), or experimenter error (n = 1).

4.1.2 Apparatus, stimuli, and procedure

The apparatus, stimuli, and procedure were identical to those of Experiment 2.

4.2 Results and Discussion

As in Experiments 1 and 2, prior to analyzing infants’ test performance, we first examined the extent to which infants became habituated to the familiarization stimulus. Infants in Experiment 3 completed the five-minute familiarization phase in an average of 18.3 trials (SD = 11.5, range = 2 to 53). Eleven of the 31 infants in Experiment 3 showed evidence of habituating, which was marginally significantly greater than the number of habituating infants in Experiment 1 (2 out of 18; Fisher’s exact test, p = .095), and not significantly different from the number of habituating infants in Experiment 2 (10 out of 18; Fisher’s exact test, p = .234). Moreover, infants’ mean habituation score in Experiment 3 (M = 1.49, SD = 0.49) was marginally significantly greater than that of Experiment 1 (t[47] = 1.79, p = .081, d = 0.55) and not significantly different from that of Experiment 2 (t[47] = 0.99, p = .326, d = −0.30). This suggests that infants in Experiment 3 might be more likely to exhibit novelty preferences, as in Experiment 2, than to exhibit familiarity preferences, as in Experiment 1.

Preliminary analyses of infants’ looking durations during test trials confirmed this prediction. As can be seen in Figure 6, infants looked longer during part-sequence and embedded pair test trials compared to familiar pair test trials. A repeated measures ANOVA revealed a main effect of test type: F(1,30) = 5.92, p < .05, partial η² = .165. Planned paired samples t-tests revealed that infants looked significantly longer during both part-sequence and embedded pair test trials, compared to pair test trials: ts(30) > 2.10, ps < .05, ds > 0.37. Non-parametric binomial tests, however, revealed that 20 of the 31 infants looked longer during embedded pair compared to pair test trials (p = .150), and that 18 of the 31 infants looked longer to part-sequence compared to pair test trials (p = .473). Paired samples t-tests revealed no significant differences in looking durations on embedded pair compared to part-sequence test trials: t(17) = 0.14, p = .89, d = 0.02 (Figure 6); this null effect was corroborated by a binomial test: only 15 of the 31 infants looked longer during part-sequence compared to embedded pair test trials, p = 1.00.

Though the patterns of data in this replication study were not as consistent as those of Experiment 2, the results nonetheless suggest that infants discriminated the pair from the part-sequence as well as the embedded pair. In addition, these data lend further evidence that infants represented the non-embedded pair differently (and likely more strongly) than the embedded pair, despite their identical TPs, supporting the predictions of chunking models. This second demonstration of infants’ ability to discriminate sequences with equivalent statistical relations between adjacent items and no additional non-adjacent statistical cues corroborates our hypothesis that performance in Experiment 1 was also due to infants’ representations of chunks rather than non-adjacent statistical relations.

Together, results of Experiments 1-3 provide strong evidence that infants represented the visual sequences in terms of chunks rather than TPs. Experiment 4 was designed to examine the processes by which infants may form and maintain representations of chunks. A strategy shared by several chunking models (e.g., Giroux & Rey, 2009; Perruchet & Vinter, 1998; Robinet, Lemaire, & Gordon, 2011) is a progressive building up of larger chunks as stimulus exposure increases, combined with competition between chunks. These models predict that embedded pairs may initially be represented and recognized, but later not recognized as their representations are supplanted by representations of larger triplet structures. Nevertheless, not all chunking models propose a progressive building up of larger chunks (e.g., Goldwater et al., 2006, 2009) and it is unknown how infants’ recognition of chunks might relate to stimulus exposure.

Experiment 4 was designed to test the prediction that infants’ recognition of embedded chunks depends on stimulus exposure. Specifically, Experiment 4 kept familiarization duration at 5 minutes as in Experiments 2-3 but presented four, rather than two, units such that infants were exposed to each unit half the number of times as in Experiments 2-3. If a greater number of exposures to each unit is required for infants to build up representations of triplets compared to representations of pairs and embedded pairs, reducing the number of exposures to each unit by half could capture a point at which infants have not yet formed robust enough representations of triplets to have suppressed their representations of embedded pairs. If that is the case, infants in Experiment 4 should discriminate part-pairs from pairs as in Experiments 2-3, but should not discriminate embedded pairs from pairs. If, however, infants form representations of pairs and triplets equally rapidly, representations of triplets should interfere with representations of embedded pairs to the same extent in Experiment 4 as in Experiments 2-3. That is, infants in Experiment 4 should behave similarly to those in Experiments 2-3 by distinguishing pairs from both part-sequences and embedded pairs. It is also possible, however, that half the number of exposures to each unit is insufficient for infants to form strong representations of either pairs or triplets, such that infants might not show evidence of discriminating between any of the test stimuli in Experiment 4.

5. Experiment 4

5.1 Material and Method

5.1.1 Participants

Eighteen healthy full-term 8-month-olds (3 females; M age 8 months 1 day, range = 7;7 to 9;5) were recruited as in Experiments 1-3. Data from an additional six infants were excluded from the final sample due to fussiness (n = 3), failure to look at the monitor (n = 2), or sleepiness (n = 1).

5.1.2 Apparatus and stimuli

The apparatus and stimuli were identical to those of Experiments 2-3, except for the number of units employed and the size of the spatial array (Figure 7A). In Experiment 4, the familiarization sequence consisted of a continuous sequence of four randomly ordered units: two shape triplets (e.g., triplet 1: yellow triangle, blue square, orange diamond; triplet 2: gray heart, magenta arrow, cyan banner), and two shape pairs (e.g., pair 1: lime green plus, red circle; pair 2: brown hourglass, forest green star). Units could repeat, there were no breaks or delays between units, and units were defined solely by distinctions in TPs. Because each shape appeared in only one unit, TPs between shapes within units were 1.0, and TPs between shapes spanning unit boundaries were .25 (Figure 7B).

Figure 7.

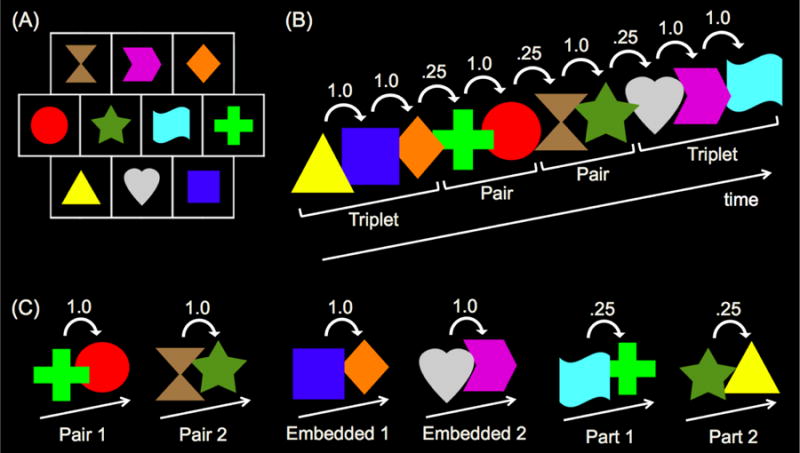
Sample (A) spatial array and shapes presented in Experiment 4. Only one shape appeared at a time during familiarization and test. Sample (B) familiarization sequence and (C) test sequences presented in Experiment 4. Numbers above shapes represent TPs during familiarization. Brackets below shapes indicate the unit structure of the familiarization sequence.

5.1.3 Procedure

The procedure was identical to that of Experiments 2-3, with two exceptions. First, because four units were presented in Experiment 4 (compared to two units in Experiments 2-3), infants saw 40 presentations of each unit (compared to 80 in Experiments 2-3) during the five-minute familiarization. As in Experiments 2-3, infants saw two pair test trials, two embedded pair test trials, and two part-sequence test trials; however, due to the greater number of shapes employed in Experiment 4, we were able to make each test trial in Experiment 4 unique (Figure 7C). That is, each of the two pair test trials presented a different pair from familiarization (e.g., test pair 1: lime green plus, red circle; test pair 2: brown hourglass, forest green star). Moreover, one embedded pair test trial presented the latter two shapes of one triplet from familiarization as in Experiments 2-3 (e.g., embedded test 1: blue square, orange diamond), and the other embedded pair test trial presented the first two shapes of the other triplet from familiarization (e.g., embedded test 2: gray heart, magenta arrow). Additionally, one part-sequence test trial presented the last shape of a triplet followed by the first shape of a pair from familiarization as in Experiments 2-3 (e.g., part test 1: cyan banner, lime green plus), and the other part-sequence test trial presented the last shape of a pair followed by the first shape of a triplet from familiarization (e.g., part test 2: forest green star, yellow triangle). As in Experiments 2-3, test trial order was randomized with the constraint that each of the two test blocks consist of one pair test trial, one embedded test trial, and one part-sequence test trial.

5.2 Results and Discussion

As in Experiments 1-3, prior to analyzing infants’ test performance, we first examined the extent to which infants became habituated to the familiarization stimulus. Infants in Experiment 4 completed the five-minute familiarization phase in an average of 15.17 trials (SD = 8.8, range = 2 to 31). Eight of the 18 infants in Experiment 4 showed evidence of habituating, which was marginally significantly greater than the number of habituating infants in Experiment 1 (2 out of 18; Fisher’s exact test, p = .060), and not significantly different from the number of habituating infants in Experiment 2 (10 out of 18; Fisher’s exact test, p = .740) and Experiment 3 (11 out of 31; Fisher’s exact test, p = .559). This suggests that infants in Experiment 4 might be more likely to exhibit novelty preferences, as in Experiments 2-3, than to exhibit familiarity preferences, as in Experiment 1. Nevertheless, infants’ mean habituation score in Experiment 4 (M = 1.38, SD = 0.64) did not differ significantly from that of Experiments 1, 2, or 3 (ts < 1.39, ps > .175, ds < 0.47).

As can be seen in Figure 8, infants exhibited a novelty preference, looking longer during part-sequence test trials compared to pair and embedded pair test trials. Three infants failed to complete the second block of test trials. For the 15 infants that completed both test blocks, we found no evidence that looking durations differed by test block for any of the three test types (ts[14] < 0.39, ps > .70, ds < 0.23); therefore we (1) computed and used these 15 infants’ mean looking durations to each test type for further analyses, and (2) included in this dataset looking durations from the first test block for the three infants that did not complete the second test block. A repeated measures ANOVA revealed a main effect of test type: F(1,17) = 5.91, p < .05, partial η² = .258. Planned paired samples t-tests revealed that infants looked significantly longer during part-sequence test trials, compared to both pair and embedded pair test trials: ts(17) > 2.43, ps < .05, ds > 0.57. Non-parametric binomial tests confirmed these results. A significant number of infants looked longer during part-sequence compared to pair (14 out of 18) and embedded pair (15 out of 18) test trials, ps < .031. Looking durations did not differ significantly on pair compared to embedded pair test trials: t(17) = 0.20, p = .84, d = 0.05 (Figure 8); this null effect was corroborated by a binomial test: only 7 of the 18 infants looked longer during embedded pair compared to pair test trials, p = .481.

These findings demonstrate that, after 40 exposures to each pair and triplet, infants discriminated pairs from part-sequences but not from embedded pairs. This is in contrast to Experiments 2-3, in which infants discriminated pairs from both part-sequences and embedded pairs, after 80 exposures to each pair and triplet. These findings support the idea that embedded pairs may be indistinguishable from pairs until sufficient exposure has allowed opportunity for larger units (e.g., triplets) to be represented, which then interfere with representations of embedded chunks.

6. General Discussion

We compared predictions from statistical and chunking models of statistical learning mechanisms in four experiments with 8-month-old infants. We assessed infants’ responses to illusory and embedded visual sequences to examine two contrasting possibilities concerning infants’ processing of visual sequences: first, that infants solely represent statistical relations, and second, that infants solely represent chunks. Understanding mechanisms of statistical learning has been an important goal for many researchers investigating language acquisition and cognitive development (Romberg & Saffran, 2010; Saffran & Kirkham, 2018), because statistical learning operates rapidly and efficiently over multiple sources of information and from an early age, implying a powerful contribution to real-world learning. In both laboratory and real-world contexts, learning and memory comprise multiple processes and systems (Gómez, 2017). Our findings provide evidence that visual statistical learning may comprise at least two distinct processes—computation of statistical relations among items and chunking of items into larger units—as opposed to a single mechanism that does not retain statistical information (cf. Mareschal & French, 2017), a possibility we elaborate subsequently.

The infants we observed appeared to discriminate between units (i.e., triplets in Experiment 1, pairs in Experiments 2-4) and part-sequences, providing strong evidence of visual statistical learning. Infants discriminated units from statistically matched illusory triplets (Experiment 1) and embedded pairs (Experiments 2-4), suggesting representations of coherent chunks from familiarization. Moreover, Experiments 2-4 provide insight into the temporal nature of chunking processes, demonstrating that the fate of embedded chunks depended on exposure. This finding implies that pair and triplet chunks were not formed at equal rates, but rather that the larger (triplet) chunks were built up progressively from smaller (embedded) chunks.

6.1 Are Statistical Computation and Chunking Mutually Exclusive?

Recently, a model of auditory and visual statistical learning in infancy demonstrated that a single computational system (a partially recurrent distributed neural network implementing Hebbian learning) formed chunks following exposure to items in sequence without learning transitional probabilities, leading to the claim that statistical and chunking modes of learning may stem from a unitary mechanism (Mareschal & French, 2017). It is also possible, however, that statistical computation and chunking are distinct but not mutually exclusive (Perruchet & Pacton, 2006). Tracking statistical regularities and forming chunks could be independent processes, or could represent successive steps in the learning process. We consider each of these possibilities in turn.

6.1.1 Independent processes

If infants in the present studies tracked statistical relations and formed chunks independently, we would expect both types of information to have influenced looking responses during test trials. For instance, in Experiment 1 we would expect infants’ looking times to illusory sequences (strong statistical relations, weak chunks) to fall partway between looking to familiarized triplet sequences (strong statistical relations, strong chunks), and looking to part-sequences (weak statistical relations, weak chunks). Similarly, in Experiments 2-3 we would expect infants’ looking times to embedded pairs (strong statistical relation, weak chunk) to fall partway between looking to familiarized pairs (strong statistical relation, strong chunk) and looking to part-sequences (weaker statistical relation, weak chunk). However, we did not observe either of these patterns. These null findings do not conclusively rule out the possibility that statistical computation and chunking are independent processes; for instance, as suggested recently (Tummeltshammer, Amso, French, & Kirkham, 2016), it is possible that infants selectively recruit these processes independently as needed, such that only one type of process is employed in any given context. Although this possibility accords with our data (assuming that the present experimental context should elicit a chunking strategy), and could be used to explain discrepancies across studies in terms of the processes employed by participants, a clear demarcation of the contexts in which one type of processes should prevail over the other is lacking. In the absence of such specifications, this explanation has a distinct post-hoc feel.

6.1.2 Successive steps

A more plausible explanation for our results is that statistical computation and chunk formation might represent successive steps in the learning process. Indeed, even proponents of learning via statistical computation have argued that such learning results in some kind of psychological unit. For instance, Saffran and colleagues argued that infants treat the representations resulting from statistical learning as actual linguistic items (Saffran, 2001), even mapping them as labels for objects (e.g., Graf Estes, Evans, Alibali, & Saffran, 2007).

Assuming that infants’ chunk representations emerge from sensitivity to statistical regularities, one might ask what happens to the statistics once chunks are formed. One possibility is that infants maintain statistical information in memory, along with chunks, for future use. If infants represent both statistical relations and chunks, this would lead to expectations that both types of representations influence infants’ looking times. However, Experiments 1-3 yielded no evidence of sensitivity to statistical relations.

An alternate possibility that accords better with the data observed in the present experiments is that representations of statistical relations among stimulus items may be forgotten once chunks are formed. This possibility is consistent with our lack of any observed influence of statistical relations on looking times in Experiments 1-3. Findings from Experiment 4 also align with this possibility. Infants in Experiment 4 were exposed to the familiarization units half the number of times as in Experiment 2-3 in an attempt to capture a point at which the chunking process was not yet complete (i.e., infants would have formed 2-item chunks but not 3-item chunks). The manipulation appeared successful as infants in Experiment 4 exhibited similar looking durations to familiar pairs and embedded pairs, indicating that infants did not respond to test trials on the basis of having formed 3-item chunks. If representations of statistical relations are not forgotten until chunk formation is complete, statistical relation information might have been accessible at test to infants in Experiment 4. Indeed, infants’ discrimination of both familiar and embedded pairs from part-sequences suggests infants recognized 2-item chunks, but is also consistent with what one would expect had infants been guided by sensitivity to statistical relations. The task in Experiment 4 was considerably more complex than that of Experiments 2-3 (half the exposure to each item, twice as many distinct items, and twice as many locations), increasing the memory load and perhaps slowing learning down such that infants had not yet extracted chunks. An additional test of the process of chunk formation could come from an experiment that increased exposure to the stimuli in Experiment 4 (e.g., doubling exposure to match exposure durations per item of Experiments 2-3). Discrimination of pairs from embedded pairs in such an experiment would provide further evidence that triplet chunks progressively supplant representations of embedded chunks, even with more complex stimuli, though infants may not tolerate extended familiarization times much beyond the five minutes tested here.

Thus, the present experiments suggest that infants engage in chunking, particularly by building up representations of larger chunks with increased exposure, but our data do not rule out the possibility that infants computed statistics in the process of chunk formation. Thus, we do not aim to suggest that learners never compute statistical relations or to argue directly against findings that learners can track these relations (e.g., Endress & Mehler, 2009). Rather, we contend that the distinction between statistical computation and chunking processes may not be as clear-cut as it is often portrayed in the literature, and that, because statistical computations appeared to be discarded (if they were ever computed) once chunks are formed, the most parsimonious account of the data from the present series of experiments is that infants engaged in chunking.

6.2 Implications for Statistical Learning and Cognition More Broadly

The present experiments add to a growing body of literature suggesting that infants can detect statistically coherent sequences of information contained within larger visual sequences (e.g., Kirkham, Slemmer, & Johnson, 2002; Marcovitch & Lewkowicz, 2009; Slone & Johnson, 2015a; Stahl et al., 2014). Previous studies have demonstrated infants’ ability to detect pairs of shapes within a continuous sequence of shapes. The present experiments are the first to demonstrate infants’ ability to also detect and represent triplets of shapes.

The present experiments are also the first to examine infants’ representations of illusory and embedded items and to compare statistical and chunking models as the best accounts of how those representations are formed. Investigations of model fit to human data are an important part of the effort to characterize human learning (Frank et al., 2010), and observations with infants add important developmental considerations to the best way to model cognition. For instance, research on both infants’ (Graf Estes et al., 2007; Jusczyk, Houston, & Newsome, 1999; Saffran, 2001) and adults’ (Giroux & Rey, 2009; Perruchet, & Poulin-Charronnat, 2012) processing of auditory sequences suggests that words seem to have a special status in sequence learning. This intuitively makes sense, as words in natural languages are associated with particular meanings and therefore necessarily have a different role than illusory units or sublexical units. The same intuition is not present in regards to visual units. That is, it is difficult to postulate what a sequence like red square-blue triangle-yellow diamond might be used for. And yet, the present findings with infants, and previous findings with adults (Fiser & Aslin, 2005; Orbán et al., 2008; Slone & Johnson, 2015b), suggests that visual units also reach a special status compared to illusory units or sublexical units. These findings suggest that the formation of chunks is not reliant upon an association with semantic content, and may correspond to a more general feature of perceptual learning (see Giroux & Rey, 2009).

Our finding that infants’ performances align most closely with the predictions of chunking models is consistent with many previous findings with adults (Fiser & Aslin, 2005; Giroux & Rey, 2009; Slone & Johnson, 2015b). Moreover, the time course of infants’ formation of 2-item and 3-item chunks appears similar to that of adults (Giroux & Rey, 2009). Giroux and Rey exposed adults to continuous lexical sequences of 2- and 3-syllable words, presented either 29 times or 143 times each. Participants were subsequently tested on recognition of 2-syllable words and 2-syllable sublexical (embedded) units. Similar to our infant findings, adults recognized words and sublexical units equally well after fewer exposures, but recognized words better than sublexical units after greater exposures. These similarities in infants’ and adults’ processing of sequential information suggest that the chunking mechanisms observed in adults may be present early in development. Moreover, these findings suggest that chunking proceeds similarly among populations with different memory capacities. Thus, chunking processes based on principles of associative learning and memory, as in PARSER (Perruchet & Vinter, 1998), might be feasible even with the limited memory capacities of infants.

6.3 Familiarization vs. Habituation

The present experiments used familiarization, rather than infant-controlled habituation, to ensure that infants had: (1) substantial exposure to the familiarization stimuli (i.e., five minutes is much longer than infants typically expose themselves to these types of stimuli in habituation studies), and (2) equal amounts of time to form representations of the familiarization stimuli in each experiment. One limitation of using familiarization rather than habituation, however, is that we cannot accurately predict a priori whether infants will exhibit familiarity or novelty preferences as indices of learning (see Hunter & Ames, 1988). Infants in all three experiments discriminated units from part-sequences, indicating that they learned the structure of the familiarization sequence. Nevertheless, infants showed familiarity preferences in Experiment 1, and novelty preferences in Experiments 2-4. These different directions of preference were likely due to different degrees of habituation to the familiarization stimulus across experiments, as fewer infants habituated in Experiment 1 compared to Experiments 2-4.

To further investigate the proposed explanation for infants’ shift in direction of preference across experiments, we conducted correlational analyses to assess whether individual habituation scores were correlated with preference for the (more novel) part-sequence relative to the familiar triplet (Experiment 1) or familiar pair (Experiments 2-4) test sequence. We operationalized novelty preference as the difference in log mean looking time to the part-sequence minus log mean looking time to the familiar triplet or pair sequence. We predicted positive correlations between habituation scores and novelty preference across experiments (i.e., infants who habituated more should show greater novelty preferences). Habituation scores significantly positively predicted novelty preference in Experiment 2 (r = .56, p < .05), but not in Experiments 1, 3, or 4 (rs = −.03 to -.10, ps = .73 to .91). Though it is possible that these data reflect the lack of a true underlying relation between infants’ level of habituation and their preference for the novel test stimuli, we believe this is unlikely due to the aforementioned finding that the numbers of infants counted as “habituators” in the present experiments related to direction of preference across experiments. Rather, we believe that these predominantly null correlational results are more likely due to the less precise nature of the unconventional operationalizations of “habituation” and “novelty preference” used in these familiarization experiments compared to the traditional measures of these constructs used in the field (for which there are also mixed findings of strong correlations; see Csibra et al., 2016).

Differences in item predictability may be responsible for these differences in the number of infant habituators across experiments. Kidd, Piantadosi, and Aslin (2012) demonstrated a U- shaped relation between the predictability of an event and the likelihood that an 8-month-old would look away from that event. That is, infants were significantly more likely to look away from an event sequence during both highly predictable and highly unpredictable events, compared to events of intermediate predictability. In the present Experiment 1, shapes could appear in more than one unit such that most events in the familiarization sequence were of intermediate predictability (i.e., .50 and .33 probability; see Figure 2). In contrast, each shape in Experiments 2-4 appeared in only one unit such that the most common events in these familiarization sequences were perfectly predictable (see Figures 4 and 7). If 8-month-olds’ likelihood to look away from the familiarization sequence in the present experiments was influenced by event predictability as in Kidd and colleagues (2012), we would expect infants to become more likely to look away from the highly predictable events of Experiments 2-4 over time, compared to those of intermediate predictability in Experiment 1. This would explain the higher habituation rates in Experiments 2-4, compared to Experiment 1.

7. Conclusion

The experiments described in the present paper were designed to examine the representations that infants store following visual statistical learning, and whether these representations are best accounted for by statistical or chunking models. The cumulative evidence of four experiments lends strong support to chunking models, particularly those that posit progressive building up of larger chunks with increased exposure, and provides motivation to reconsider the current prevalence of explanations based on the notion of transitional probability computations in the field of infant statistical learning. Moreover, the similarity between our findings and those obtained in similar experiments with adults and experiments of infant auditory statistical learning suggests that the chunking observed in this research may correspond to a more general feature of perceptual learning that is available across development.

Highlights.

• Infants’ visual statistical learning is best captured by chunking models.

• Infants discriminated units from statistically matched illusory and embedded units.

• Infants built up representations of larger chunks with increased stimulus exposure.

• Chunking may represent a general feature of perceptual learning.