Direct Cortical Recordings Suggest Temporal Order of Task-Evoked Responses in Human Dorsal Attention and Default Networks

Abstract

The past decade has seen a large number of neuroimaging studies focused on the anticorrelated functional relationship between the default mode network (DMN) and the dorsal attention network (DAN). Due principally to the low temporal resolution of functional neuroimaging modalities, the fast-neuronal dynamics across these networks remain poorly understood. Here we report novel human intracranial electrophysiology data from six neurosurgical patients (four males) with simultaneous coverage of well characterized nodes of the DMN and DAN. Subjects performed an arithmetic processing task, shown previously to evoke reliable deactivations (below baseline) in the DMN, and activations in the DAN. In this cohort, we show that DMN deactivations lag DAN activations by approximately 200 ms. Our findings suggest a clear temporal order of processing across the two networks during the current task and place the DMN further than the DAN in a plausible information-processing hierarchy.

SIGNIFICANCE STATEMENT The human brain contains an intrinsic and strictly organized network architecture. Our understanding of the interplay across association networks has relied primarily on the slow fluctuations of the hemodynamic response, and as such it has lacked essential evidence regarding the temporal dynamics of activity across these networks. The current study presents evidence from high spatiotemporal methods showing that well studied areas of the default mode network display delayed task-induced activity relative to divergent responses in dorsal attention network nodes. This finding provides direct and critical evidence regarding the temporal chronology of neuronal events across opposing brain networks.

Introduction

One of the most striking findings that has emerged from the human network neuroscience literature is the seemingly antagonistic relationship between the default mode network (DMN) and dorsal attention network (DAN). Evidence from resting-state neuroimaging studies suggests that the time courses of hemodynamic responses across these networks are anticorrelated (Fox et al., 2005). Furthermore, regions in the DAN are consistently activated during externally focused, attention-demanding tasks (Shulman et al., 1997; Corbetta and Shulman, 2002). In contrast, sites within the DMN, which are more engaged during internally oriented task conditions, deactivate during the same attention-demanding tasks (Shulman et al., 1997; Raichle et al., 2001; Buckner et al., 2008; Foster et al., 2015). Due primarily to the low temporal resolution of contemporary neuroimaging modalities, critical information regarding the relative timing of opposing task-related changes in activity across these networks remains unknown.

Investigating the temporal organization of responses across the DMN and DAN would provide important evidence regarding their internetwork interactions and differential roles in human cognition. A clear temporal chronology, or lack thereof, could motivate hypotheses into possible causal interplay across these networks. For instance, in the case that responses in region A consistently follow responses in region B during a given experimental condition, it can be inferred that region B does not initiate the activity observed in region A during that particular condition.

Prior electrophysiological and imaging studies have demonstrated that the strength and duration of DMN deactivations directly scale with task complexity and difficulty, implicating DMN suppressions in maintaining attention (Weissman et al., 2006; Ossandón et al., 2011). Moreover, increased task demands are associated with reductions in self-reported mind wandering (McKiernan et al., 2003; Mason et al., 2007). However, it is unknown whether deactivation of the DMN is necessary for the DAN to become engaged, whether the DAN actively inhibits the DMN, or whether a third set of regions controls both the DAN and DMN during externally focused, attention-demanding tasks. Determining the timing of DMN deactivations relative to DAN activations would serve to support or oppose these models.

Recently, neuroimaging studies have revealed that DMN regions are anatomically more distant from sensorimotor networks than areas of the DAN (Margulies et al., 2016). In addition, evidence from effective connectivity analysis of neuroimaging data (Nyberg et al., 1996; Sridharan et al., 2008) and noninvasive stimulation with concurrent fMRI (Chen et al., 2013) suggest that activations in non-DMN regions may serve to suppress activity in the DMN. Based on this evidence, we hypothesized that task-evoked deactivations in the DMN would be temporally delayed relative to activations in the DAN.

To explore the fine-grained timing across these two functional networks, we took advantage of the high temporal resolution (on the order of milliseconds) and signal-to-noise ratio (SNR) of intracranial electroencephalography (iEEG; Parvizi and Kastner, 2018). Subjects performed an experimental task, shown previously to deactivate the DMN and activate the DAN (Foster et al., 2015; Daitch et al., 2016), to estimate the relative timing of opposing task-evoked responses in the posteromedial cortex (PMC) and superior parietal lobe (SPL), well characterized regions of the DMN and DAN, respectively. While we did not define these functional networks within an individual subject's brain, we identified sites based on their anatomical locations in either the PMC or SPL, as well as additional functional response criteria across task conditions. In line with previous work from our group and others (Arsalidou and Taylor, 2011; Dastjerdi et al., 2011, 2013; Foster et al., 2012; Daitch et al., 2016), we first aimed to isolate known stimulus-nonspecific and stimulus-selective responses within the SPL and PMC. We used high-frequency broadband (HFB) power (70–170 Hz), also known as high gamma, as a surrogate measure of averaged neuronal population activity and a reliable correlate to BOLD activation (Mukamel et al., 2005; Nir et al., 2007; Manning et al., 2009; Winawer et al., 2013). This information was obtained through simultaneous recordings across the lateral and medial parietal cortices, and was also anchored with direct recordings of neuronal populations in the early visual cortex when available. Lastly, we probed the relative timing of activations and suppressions in the PMC. Considering the well established characteristic of DMN regions to exhibit opposite responses during internal versus external task conditions, this explorative analysis aimed to reveal the consistency of task-related response timing (of either activations or deactivations) in the PMC during these distinct attentional states.

Materials and Methods

Demographics and recordings.

Six patients (four males; demographic and coverage information is included in Table 1) with medicine-resistant epilepsy were implanted with intracranial electrodes (Adtech Medical Instruments) as part of their presurgical evaluation at the Stanford University Medical Center. Each patient was monitored in the hospital for ∼6–10 d and provided written informed consent to participate in the study, which was approved by the Stanford Institutional Review Board. The location of the electrodes was determined by clinical needs. Data were obtained at ≥1000 Hz [subject 1 (S1) = 3051.8 Hz, S2 = 3051.8 Hz, S3 = 3051.8 Hz, S4 = 3051.8 Hz, S5 = 1000 Hz, S6 = 1000 Hz] through a 128-channel recording system (Tucker Davis Technologies; http://www.tdt.com). For subdural grids and strips, electrode size was commonly 2.3 mm in diameter with a center-to-center interelectrode spacing of 10 mm, or 5 mm for higher-density arrays. The diameter of depth electrodes was 0.86 mm, height was 2.29 mm, and the distance between the centers of two adjacent electrodes was 5 mm.

Table 1.

Demographic and recording information

Subject	Sex	Age (years)	Handedness	Epileptic zone	Duration of epilepsy (years)	Number of electrodes implanted, hemisphere
S1	Female	36	Right	Left primary motor cortex (foot area)	13	122 (subdural), left
S2	Female	22	Right	Left mesial pre-SMA	6	106 (subdural), left
S3	Male	46	Ambidextrous	Right lateral motor cortex	20	128 (subdural), right
S4	Male	38	Right	Insula	21	112 (subdural), left
S5	Male	30	Right	Left medial temporal lobe	5	130 (depth), bilateral
S6	Male	30	Right	Left somatosensory cortex	9	73 (depth), left

Anatomical locations of electrodes.

Imaging data were acquired using a GE Healthcare 3 tesla SIGNA scanner at Stanford University equipped with a head coil. A T1-weighted SPGR pulse sequence was anterior commissure–posterior commissure aligned and was resampled at 1 mm isotropic voxels, then segmented to distinguish gray and white matter using Freesurfer (Fischl, 2012). Postimplant CT scans were coregistered to the preoperative MRI anatomical brain volume (Hermes et al., 2012). For each subject, electrodes were localized in BioImage Suite (Papademetris et al., 2006) and displayed on the subjects' own reconstructed 3D cortical surface using the iELVis MATLAB toolbox (Groppe et al., 2017) allowing for the accurate anatomical localization of electrodes. Finally, for subdural grid cases only, we corrected the electrode positions for postimplantation brain shift (Dykstra et al., 2012).

Task paradigm.

We implemented an experimental task that is known from our past studies to reliably engage DAN and DMN sites (Foster et al., 2015; Daitch et al., 2016). The task was administered at patient bedside using Psychophysics Toolbox (http://psychtoolbox.org/) running on the Apple Macintosh OSX operating system. The laptop was positioned ∼70 cm from subjects' eyes at chest level. Subjects were instructed to make true or false judgments on a series of visually presented statements, requiring either memory (e.g., “I ate fruit yesterday”) or arithmetic (e.g., “48 + 9 = 57”) processing. Each subject performed 80–120 math trials and 50–120 memory trials. Math equations always consisted of a two-digit number and a one-digit number to reduce the likelihood that subjects were relying on memorized addition tables to perform the task. Subjects had up to 15 s to respond to each statement by pressing one of two keypad buttons; however, trials were terminated upon a subject's response. These conditions were interspersed with fixation periods (5 or 10 s), during which subjects were instructed to fixate at a center crosshair. A 200 ms intertrial interval (ITI) separated trials, which was used as a baseline period for subsequent analyses. Task-related onset times were tagged using a photodiode for subjects 1–4, while an RTBox was used for subjects 5 and 6. In both cases, the tag was sent to an empty channel on the EEG montage and triggered within our task codes. The photodiode signal was initiated using a bright rectangle at the corner of the laptop screen, whereas the RTBox sent a TTL (transistor–transistor logic) pulse through custom MATLAB commands (Li et al., 2010).

Signal preprocessing.

Preprocessing steps were completed using MATLAB (http://www.mathworks.com) and SPM12 (http://www.fil.ion.ucl.ac.uk/spm/) EEG/MEG toolbox in custom routines (https://github.com/LBCN-Stanford/Preprocessing_pipeline). First, the data were filtered for power-line noise (band-stop between 57 and 63 Hz) and harmonics (117–123 Hz,177–183 Hz). Sites then underwent an automatic signal quality assessment in which sites with raw power five times greater or smaller than the mean raw power across all sites (within an individual subject) were marked as “bad channels.” Sites with three times more “jumps” (i.e., changes in the signal derivative >100 μV) than the mean of the number of jumps across sites were labeled as “spiky” channels. Sites marked as pathological (postclinical evaluation), bad, or spiky were discarded from further analyses. The signal was then rereferenced to the mean over all the nonexcluded channels. Each event was epoched in the −300 to 2200 ms time window around the stimulus onset time, and a baseline (i.e., −200 to 0 ms time window) correction was performed (i.e., the across-trial prestimulus interval was subtracted from the signal). In addition, we identified and omitted individual trials with spikes, which could skew our estimates of HFB power. We marked events (i.e., individual trials) as corrupted if they contained any spike of >100 μV, and excluded these events from further analysis (i.e., a trial displaying such a jump was discarded across all channels). Note that although the jump size threshold used here is equivalent to that implemented for bad channel detection, the latter eliminates channels based on the frequency of jumps, while this trial-level rejection depends on the existence of any jump. Next, time–frequency decomposition was performed on the rereferenced signal at each electrode using 5 cycle Morlet wavelet transforms, with frequencies ranging from 70 to 170 Hz (HFB; 10 Hz steps). The amplitude of each wavelet output was computed by taking the absolute value of the complex signal, and these amplitude time courses were then averaged across frequencies within the HFB range. To reduce ambiguity in timing information, no temporal smoothing was performed. The HFB signal in the −200 to 2000 ms time window around stimulus onset was considered in further analysis.

Category-specific HFB responses.

For each subject, epoched trials were averaged across trials for all time points to obtain the mean HFB time course for each condition (i.e., math and memory, respectively). The signal within a 300–2000 ms poststimulus window was used to evaluate significance of category-specific HFB responses. This time window was chosen based on previously observed late-onset activity in the parietal regions for the current task (Foster et al., 2015; Daitch et al., 2016; Foster and Parvizi, 2017). Sites presumed to lie within the DAN or DMN were identified both based on their anatomical location and on their functional profile of responses across task conditions (response criteria are summarized in Table 2). First, we identified electrode sites located in the superior parietal cortex (SPL; bounded anteriorly by the postcentral sulcus and ventrally by the intraparietal sulcus), PMC (bordered posteriorly by the parieto-occipital sulcus, dorsally and anteriorly by the cingulate and marginal branch of the cingulate sulcus, and ventrally by callosal sulcus), or early visual cortex (V1, V2, and V3). The visual cortex was used as a control region since these sites should exhibit earlier responses across task conditions, relative to both the SPL and PMC.

Table 2.

Response types and their criteria

PMC			SPL
Memory-active	Memory > math	Math-selective	Math > memory
	Memory > baseline		[Math >2 SDs * memory]
			Math > baseline
Math-deactive	Math < memory	Math-active	Math > Memory
	Math < baseline		[Math <2 SDs * memory]
			Math > baseline
			Memory > baseline

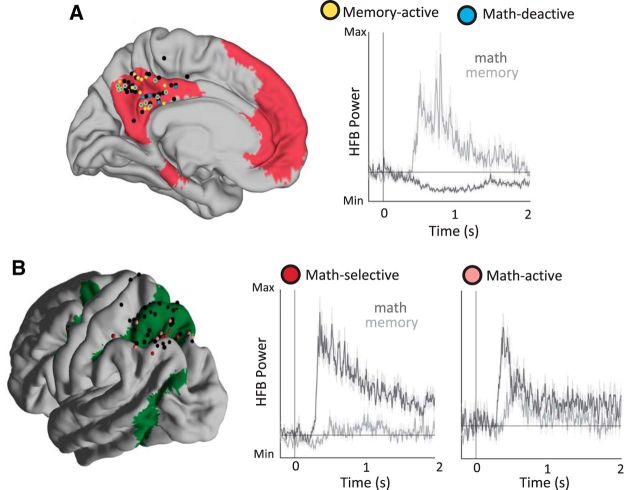
Comparisons in square brackets (i.e., “[…]”) represent numerical (rather than statistical) criteria, while those without brackets denote significant differences based on nonparametric permutation tests. The math and memory HFB time courses for each response type are visually displayed in Figure 1.

Within the SPL, we identified two classes of sites; those responding selectively during the math condition (SPL_{math-selective}), and those responding more during the math than memory condition, but with less selective responses (SPL_math-active). Specifically, SPL_{math-selective} sites exhibited (1) a significant math HFB response compared with the pooled baseline (i.e., −200 to 0 ms prestimulus window across conditions), (2) a significantly higher HFB response during the math condition relative to the memory condition, and (3) mean HFB power during the math condition (within the 300–2000 ms time window) at least 2 SDs above the mean HFB response during the memory condition. The last criterion was implemented to isolate selective sites during mathematical processing, which are commonly found near the intraparietal sulcus (Eger et al., 2003; Daitch et al., 2016). SPL_math-active sites exhibited (1) a significant math HFB response compared with the pooled baseline and (2) a significant memory HFB response compared with the pooled baseline; however (3) math responses did not surpass 2 SDs above the mean of memory-related HFB responses. Within the PMC, we identified two response profiles typical of the DMN; activation during autobiographical memory (PMC_{memory-active}) and deactivation during math (PMC_{math-deactive}). Importantly, unlike the two classes of SPL responses, these two PMC response profiles could (and often did) occur within the same site (Figs. 1, 2A) as our previous publications have also shown (Dastjerdi et al., 2011; Daitch and Parvizi, 2018). PMC_{math-deactive} sites displayed significantly lower HFB responses during the math condition relative both to the pooled baseline period and the memory condition. PMC_{memory-active} sites exhibited significantly higher HFB activity during memory trials relative both to the pooled baseline and the math condition. Finally, “visually active” sites in early visual cortex were defined as having significant math and memory activations above the pooled baseline. In early visual cortical sites, the math-specific HFB response was used in the subsequent temporal analyses. To evaluate the statistical criteria for the response types described above, we first averaged the HFB power within a particular time window (either 300–2000 ms for math or memory trials, or the −200 to 0 ms prestimulus period for baseline) in each trial. We then performed unpaired nonparametric unpaired permutation tests (50,000 repetitions) to compare the distributions of HFB power between a pair of conditions or between a single condition and baseline [p < 0.05, false discovery rate (FDR) corrected for the number of sites tested within an individual subject].

Figure 1.

Electrode coverage and exemplar time courses. A, Electrode coverage in the PMC (left) and task-evoked response types (right). Exemplar HFB time courses represent math and memory responses for a math-deactive and memory-active site in the PMC of S1. The shaded area denotes SEM across trials for each condition. The cortical mask shows DMN (magenta) boundaries using the Yeo et al. (2011) seven-network atlas along with sites identified in subject-specific anatomical space and transformed to MNI space. PMC sites that display both a math and memory response (e.g., the exemplar site presented on the right) are denoted with a blue fill and yellow boundary. Black dots represent sites that did not fall into one of the categories of interest. B, Electrode coverage in the SPL (left) and task-evoked response types (right). Exemplar HFB time courses during the math and memory conditions in the SPL of S1, signifying previously reported math-selective and math-generic responses (Daitch et al., 2016). The shaded area denotes SEM across trials for each condition. Note that math-selective sites display a significantly larger response during the math relative to the memory condition, while math-generic sites display both math- and memory-induced responses. The cortical mask shows DAN boundaries along with sites selected within subjects' anatomical space and projected into MNI space.

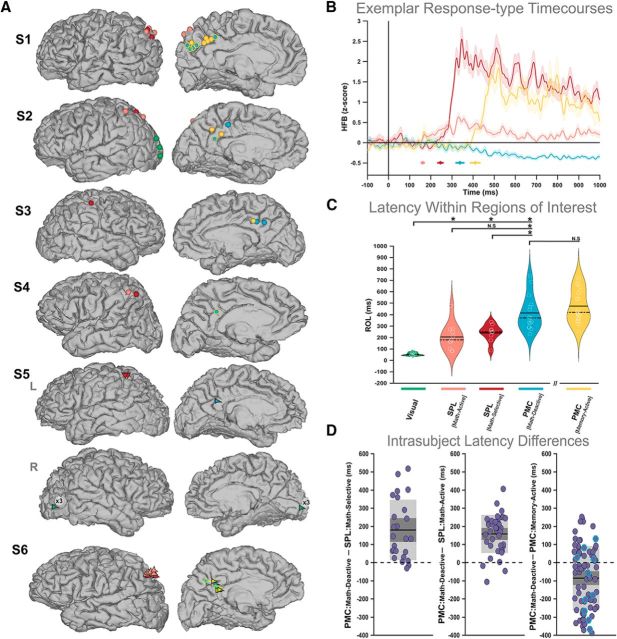
Figure 2.

Spatiotemporal distribution of memory and math responses in parietal and visual cortices. A, Lateral and medial views of electrode positions on subject-specific brain masks. Electrode colors represent specific functional response types as shown in Figure 1. Visually active electrodes are shown in green for two pertinent subjects (S2 and S5). Note that six visually active contacts were found in the right hemisphere for S5 and their equivalent trajectory is denoted on each cortical view with a single green arrow. B, Average (across trials) HFB time courses for four exemplar contacts from a single subject (S1), representing each response type in the lateral and medial parietal cortex. The shaded area denotes the SEM across trials for each condition. The colored circles below the responses denote the ROL estimates for those signals, while their corresponding horizontal lines indicate the 95% confidence interval across bootstrap iterations (see Materials and Methods). Importantly ROL values were estimated as the median across bootstrapped trials and, therefore, do not directly characterize the average signals displayed. C, ROL values for ROI-specific responses. The width of violin plots represents kernel density, and white circles denote individual data points. The violin plot representing memory-active sites is spatially separated (along the x-axis) to distinguish these temporal findings from those acquired during the math condition. D, ROL differences calculated within-subjects between distinct response types. Across comparisons, shaded dark gray indicates SEM, shaded light gray denotes SD, the black line demarcates the mean across difference values, and the dotted line distinguishes the zero value. For the last comparison (far right), we indicate differences for responses within the same electrode (i.e., those showing both a memory activation and a math deactivation) with a blue edge.

Response onset latency.

This technique, which was modified from previously published methods (Foster et al., 2015; Daitch et al., 2016), estimates the time of the inflection point of a task-related activation or deactivation. Since it is difficult to estimate onsets of single-trial time courses (given lower SNR), we estimated a distribution of measures for each electrode site using a bootstrap resampling procedure (repeated 1000 times), in which we selected a subset of trials in each repetition, and approximated the onset based on the average time course across this subset of trials. For each bootstrap sample, we divided the poststimulus signal (0–1000 ms) into 60 ms bins with 58 ms overlap, and the data within each bin were averaged and fitted linearly to estimate slope. Next, a threshold was defined as the mean plus (or minus for deactivation) 1 SD of the baseline distribution to isolate signal fluctuations above the baseline period (i.e., 200 ms ITI before stimulus onset across all trials in the bootstrap repetition), and we identified the earliest 50 consecutive bins in which the average power amplitude exceeded this threshold.

From this set, we noted the bin with the steepest slope and averaged this slope with the overall slope of the baseline period to define a threshold. In a stepwise manner, backward from the window containing the steepest slope, we marked the first bin to show a slope smaller than the slope threshold (for activations) or larger than the slope threshold (for deactivations). The earliest time point of this bin is marked as the signal onset in a bootstrap iteration. We defined the onset for a site as the median value across bootstrap estimates. This analysis was implemented on nonsmoothed HFB signals to minimize confounds associated with temporal smoothing. Unpaired nonparametric permutation tests were used to compare response onset latency (ROL) values within and across our regions of interest (ROIs; p < 0.05, FDR corrected for number of comparisons).

Time-to-peak.

We implemented a time-to-peak (TTP) analysis, which is often applied to human electrophysiology data (Bar et al., 2006; Burke et al., 2014), to evaluate the robustness of the temporal progression revealed using our ROL technique. In line with our ROL analysis, we estimated TTP using a bootstrapping procedure (repeated 1000 times) to estimate a distribution of measures for each significant site. For each bootstrapped sample, we binned the poststimulus signal (0–1000 ms) into 60 ms bins with 58 ms overlap, and data within each bin was averaged. In this way, we aimed to capture the peak amplitude within a larger window rather than a single point, which may be susceptible to transient HFB fluctuations. The first time point of the bin containing the maximum (for activations) and minimum (for deactivation) HFB amplitudes is defined as the peak latency for that bootstrap iteration. Finally, the median peak time across bootstrap samples was identified as the TTP for a site. Unpaired nonparametric permutation tests were used to compare TTP values within and across our ROIs (p < 0.05, FDR corrected for number of comparisons).

Statistical testing.

In this work, statistical testing was implemented using nonparametric permutation tests. We used unpaired permutation tests when comparing a single condition and baseline (using the pooled baseline periods across math and memory trials) and when assessing metrics across conditions, as well as for testing significant differences in latency (ROL and TTP) between response types. Across these comparisons, we implemented 50,000 permutations to ensure a reliable estimation of the null distribution. Significance was evaluated at p < 0.05, and FDR correction was used when multiple comparisons were tested for the same effect (e.g., when testing for significant HFB power across pertinent sites).

Results

Intracranial EEG data were recorded from six patients in whom focal epilepsy had been diagnosed and who had been implanted with electrodes as part of their presurgical evaluation (Table 1). These patients had simultaneous medial and lateral parietal cortical coverage with subdural (four patients) or depth electrodes (two patients). None of the subjects had a seizure focus in the PMC or SPL, and sites with epileptic activity were identified and discarded from subsequent analysis.

Patients performed a self-paced task that consisted of true-false judgments of math and autobiographical memory statements (see additional details in Materials and Methods; behavioral performance is shown in Table 3). We selected the recording sites that fell within either SPL or PMC based on well defined structural boundaries (see Materials and Methods) in subject-specific anatomical space. In addition, two subjects had visually active sites within the occipital lobe, which were used as control sites for the ROL analysis, since these sites should display earlier responses than those in the SPL or PMC. In total, we considered information from 50 sites in the SPL, 41 recording sites in the PMC, and 22 sites in the occipital lobe.

Table 3.

Behavioral performance

	Math: percentage correct	Math: mean (SD) reaction time (s)	Memory: mean (SD) reaction time (s)
S1	97.5%	3.6930 (1.1836)	2.0976 (0.8148)
S2	90%	5.7782 (2.1068)	3.1176 (0.8183)
S3	93.75%	5.3112 (2.0991)	3.3762 (1.1094)
S4	78.12%	3.7132 (2.5498)	3.4825 (1.8246)
S5	73.75%	8.47 (3.7256)	5.5201 (2.072)
S6	95.83%	1.8657 (0.821)	1.7248 (0.7275)

For sites falling within the subject-specific anatomical boundaries of our ROIs, we implemented nonparametric permutation tests to evaluate significant task-evoked changes in HFB activity during each task condition (p < 0.05, FDR corrected). Within the SPL, we identified two types of neuronal population responses, which we would expect of those falling within the DAN: “math-active” sites [11 of 50 recording sites (22%) within the SPL] had greater HFB activity during the math than the memory condition; however, they still exhibited significantly greater HFB responses during both math and memory conditions relative to baseline. In contrast, “math-selective” sites [9 of 50 recording sites (18%) within the SPL] had significantly greater HFB responses during math relative to both baseline and memory conditions. Within the PMC, we identified two response profiles that would be expected of neuronal populations in the DMN. First, “memory-active” sites exhibited higher HFB activity during the memory condition relative to both baseline and math [22 of 41 PMC sites (54%)]. Further, “math-deactive” sites [15 of 41 PMC sites (37%)] displayed lower HFB power during the math condition relative to both baseline and memory. Notably, several sites in the PMC showed both a significant activation during the memory condition and a significant deactivation during the math condition, consistent with previous work (Foster et al., 2012). In two subjects (S2 and S5), we also identified nine sites within the occipital cortex that were placed in the early visual cortices and showed significant activations during both math and memory relative to baseline, and were likely engaged in visual processing of the written stimuli.

As shown in Figure 1, the SPL and PMC sites studied here were mostly clustered within the network boundaries of the DAN and DMN as defined based on a population-level atlas (Yeo et al., 2011). Importantly, though, sites were chosen based on their location in subject-specific anatomical space and not based on individual-subject functional connectivity analysis, which might more directly map these networks in each subject (Kucyi et al., 2018). Furthermore, the electrode sites are prone to shifts in their position when displayed in MNI space. Figure 2A shows the distribution of math- and memory-induced responses in subject-specific anatomical space.

Simultaneous recordings of time-locked responses provided a unique opportunity to determine the relative timing between the DAN and DMN nodes. To capture this temporal information, we implemented an HFB ROL method to estimate the inflection point at which an averaged signal activates or deactivates relative to the time of stimulus onset (see Materials and Methods). Figure 2B shows time-locked data for four exemplar sites representing each response type as well as their temporal onsets. At the group level (Fig. 2C), we found a clear temporal gradient of activity across our ROIs. During the math condition, we observed the earliest response onsets in the visual cortex (mean = 52 ms; SEM = 4.36), followed by activations in the SPL_math-active (mean = 205 ms; SEM = 34.36) and SPL_{math-selective} sites (mean = 239 ms; SEM = 24.98), and deactivations in PMC_{math-deactive} (mean = 414 ms; SEM = 39.1) sites. When measuring the relative timing of opposing responses within PMC sites exhibiting typical DMN response types (i.e., memory activations and math deactivations in PMC_{memory-active/math-deactive} sites), we found that memory activations displayed later onset times (mean = 474 ms; SEM = 31.95) than math deactivations. Based on nonparametric unpaired permutation tests (p < 0.05, FDR corrected; 50,000 repetitions), we established that during the math condition, visual cortex responses occurred significantly earlier than SPL_math-active (p < 4.00E-05) and SPL_{math-selective} (p < 4.00E-05) responses, as well as before PMC_{math-deactive} deactivations (p < 4.00E-05). Likewise, SPL_math-active and SPL_{math-selective} activations took place significantly before PMC_{math-deactive} (p = 4.40E-04, p = 8.80E-04) deactivations. Within the PMC, we observed that PMC_{memory-active} sites showed generally later onset times during the memory condition compared with the time of deactivation at PMC_{math-deactive} sites during the math condition, although this difference was not statistically significant (p = 0.2301). It is important to note that this comparison describes data from distinct trial types (math and memory) and thus is most likely driven by distinct neural processes in each case. Similarly, there was no significant difference in latency between the activation times at SPL_math-active and SPL_{math-selective} sites during the math condition (p = 0.4465).

Next, we inspected the extent to which this temporal pattern was maintained at the individual subject level. Within each subject, we paired each PMC_{math-deactive} site with every SPL_math-active, SPL_{math-selective}, and PMC_{memory-active} site. We then calculated the difference in latency for all pairs and binned the differences for each comparison (Fig. 2D). Within subjects, deactivation times at PMC_{math-deactive} sites were later than both SPL_math-active site activations (92.5% of 40 pairs; mean = 157.8 ms; SEM = 16.48) and SPL_{math-selective} site activations (92% of 25 pairs; mean = 179 ms; SEM = 33). Within the PMC, we found that only 37.65% of 85 pairs showed later deactivations in PMC_{math-deactive} relative to activations at PMC_{memory-active} sites (mean = −86 ms; SEM = 19.11). These findings indicate that, within subjects, math-induced deactivations in the PMC were consistently initiated after math-induced activations in the SPL.

To assess the robustness of our temporal findings across brain regions, we also implemented a TTP analysis to see whether we could replicate the findings from the ROL analyses. For each significantly activated or deactivated site, we estimated the time of maximum (for activations) or minimum (for deactivations) HFB response (see Materials and Methods). Across subjects, we found that the temporal progression of peak times closely matched the temporal pattern outlined with our ROL method. Namely, the earliest peak times were detected in the visual cortex (mean = 118 ms; SEM = 4.28), lagged by stimulus nonspecific (SPL_math-active) contacts (mean = 458 ms; SEM = 63.02) before engagement in math-selective (SPL_{math-selective}) sites (mean = 479 ms; SEM = 45.07) in the lateral parietal cortex, and finally deactivation of the DMN node in PMC_{math-deactive} sites (mean = 819 ms; SEM = 15.01). Within the PMC, we found that stimulus-specific activation (PMC_{memory-active}) displayed earlier peak latencies (mean = 659 ms, SEM = 30.89) relative to deactivations seen in the PMC_{math-deactive} sites. However, this result should be taken cautiously given methodological and practical considerations associated with TTP (see next paragraph). We then applied nonparametric tests (p < 0.05, FDR corrected; 50,000 repetitions) to statistically compare peak latencies across response types. In line with our ROL findings, this TTP method revealed that peak latencies in the visual cortex were significantly earlier than SPL_math-active (p < 4.00E-05) and SPL_{math-selective} (p < 4.00E-05) responses, as well as PMC_{math-deactive} deactivations (p < 4.00E-05). In addition, SPL_math-active and SPL_{math-selective} activations exhibited significantly earlier peak latencies than PMC_{math-deactive} (p < 4.00E-05, p < 4.00E-05) deactivations. Likewise, we observed no significant difference in peak latency between SPL_math-active and SPL_{math-selective} responses (p = 0.7888) within the SPL.

When comparing divergent responses within the PMC, we found that PMC_{math-deactive} suppression displayed significantly longer peak latencies than PMC_{memory-active} responses (p = 6.00E-04). Interestingly, this comparison deviates from our ROL findings in that inflection points (ROL) did not differ significantly in its latency across these response types. This deviation is likely due to the specific features isolated with the two methods. Two activity profiles may have the same inflection point (which would be measured with the ROL method), while exhibiting differential peak latencies. Further, peak latencies may be distorted by signal slope, in that response profiles with a steep slope exhibit earlier peaks, while those with a shallower slope exhibit later peaks. Together, the TTP results corroborate the temporal pattern we found between our ROIs (as identified with our ROL analysis) and contribute complementary information regarding the peak latencies across response types.

Discussion

The ability of fMRI to survey the entire cerebral cortex has been essential for uncovering the antagonistic relationship between the human DMN and DAN. However, the low temporal resolution of fMRI has presented significant ambiguity in understanding whether these opposing responses display a consistent temporal order. The current study sheds new light on this issue by providing direct electrophysiological evidence of divergent internetwork timing of task-evoked responses. Specifically, we show that task-induced PMC deactivations occur ∼200 ms after activations in the SPL. This suggests that a third structure may not be simultaneously mediating the divergent responses observed in the two networks. Our findings also suggest that the deactivations in the DMN occur only after a significant degree of processing within the DAN has taken place. Thus, DMN deactivations cannot be causally important for initiating DAN activations. The current findings are in line with recent reports suggesting that the DMN is positioned further in a hierarchy across associative brain networks (Margulies et al., 2016; Huntenburg et al., 2018) and specifically provides important and hitherto unknown evidence supporting this notion in the temporal domain.

The temporal pattern found here could be consistent with a direct or indirect inhibitory relationship from the DAN to the DMN, although our study did not directly test for such a causal interaction. Prior tract-tracing evidence in the macaque brain shows that regions of the PMC display reciprocal connections to the SPL (Parvizi et al., 2006), which could enable a direct inhibitory connection from the DAN to the DMN. Evidence from effective connectivity neuroimaging studies have implicated salience network (SN) regions in activating the DAN and deactivating the DMN (Sridharan et al., 2008; Menon and Uddin, 2010). Our findings suggest that the SN may not be simultaneously modulating opposing responses across the DAN and DMN, or rather the signal from the SN may take longer to reach the DMN.

Single pulses of electrical stimulation in one region [also known as corticocortical evoked potentials (CCEPs); Matsumoto et al., 2004], while recording in the other region, could assist in providing information about the causal interactions across the DAN and DMN. A recent study from our group using this methodology aimed to identify patterns of effective connectivity across the DMN, frontoparietal network (FPN), and SN (Shine et al., 2017). The findings indicated that stimulation in FPN and SN sites elicited robust responses in the DMN during early processing stages (<70 ms), while stimulation in DMN nodes engaged the SN and FPN at a significantly later stage of processing (>100 ms). The current results indicate that single-pulse stimulation to the DAN may evoke similar early responses in the DMN; in addition, CCEP analyses could provide critical information regarding signal directionality and possible inhibitory/excitatory influences across the two networks (Keller et al., 2014).

Resting-state fMRI studies have revealed reliable anticorrelated activity between the DMN and DAN, at least when using certain data preprocessing strategies (Murphy and Fox, 2017). More recently, the anticorrelation noted using the BOLD response has been shown to covary with that of resting state HFB signals recorded directly from the cortex (Keller et al., 2013). The task-evoked latency differences reported here suggest that an analogous temporal lag could exist across the DMN and DAN during rest. In this case, the temporal delay would contribute to an overall weaker zero-lag anticorrelation in the BOLD data. Prior resting-state fMRI studies have identified a consistent lag structure across associative brain networks, providing supporting evidence for a possible temporal offset across the DMN and DAN (Mitra et al., 2015). More recently, a resting-state iEEG study using cross-correlation techniques demonstrated consistent temporal lags across the hippocampus and association cortex (Mitra et al., 2016). Future resting-state studies could apply a similar approach to examine whether an intrinsic temporal delay exists between the DMN and DAN during wakeful rest and other behavioral states.

In the current work, we used the arithmetic processing condition as a single, well characterized task, to examine the relative timing of divergent responses across the SPL and PMC. However, iEEG studies have reported DMN HFB deactivations and DAN activations during tasks such as visual search (Ossandón et al., 2011) and attentive reading (Lachaux et al., 2008). Subsequent studies using other externally oriented tasks will be necessary to ensure the current findings are due to intrinsic dynamics across the two networks rather than specific features of the arithmetic processing per se. We note that our own preliminary work with other tasks suggests the former rather than the latter.

The current study focused primarily on the relative timing between opposing responses in the SPL and PMC during arithmetic calculation. Nevertheless, we also report the temporal onset of autobiographical memory activations with respect to math-induced deactivations in the PMC. The DMN has been extensively shown to display opposing responses during internal versus external modes of processing (Dixon et al., 2014). Recent work has also indicated that switching between internal/external attentional states may serve as a mechanism for learning internal models of sensory input (Honey et al., 2018). Here, we show that the temporal onsets of PMC responses—both positive and negative—are similarly delayed relative to stimulus onset. In other words, divergent math-induced deactivations and memory-induced activations in the DMN show comparable latencies even though mathematical cognition and autobiographical memory retrieval recruit largely distinct anatomical circuitries in the brain before they engage the PMC. This highlights a potentially important fact about the relative timing of DMN engagement across tasks and hence its hierarchical position across association networks. We are currently exploring this issue with more granular task designs that enable precise timing of electrophysiological activations in the PMC during different stages of memory retrieval and arithmetic processing.