Skip to main content
PMC home page
Ecology and Evolution logoLink to Ecology and Evolution
. 2018 Oct 30;8(22):11224–11234. doi: 10.1002/ece3.4594

Combining Bayesian genetic clustering and ecological niche modeling: Insights into wolf intraspecific genetic structure

Pietro Milanesi 1,2,✉, Romolo Caniglia 2, Elena Fabbri 2, Felice Puopolo 3, Marco Galaverni 4, Rolf Holderegger 5,6
PMCID: PMC6262746  PMID: 30519439

Abstract

The distribution of intraspecific genetic variation and how it relates to environmental factors is of increasing interest to researchers in macroecology and biogeography. Recent studies investigated the relationships between the environment and patterns of intraspecific genetic variation across species ranges but only few rigorously tested the relation between genetic groups and their ecological niches. We quantified the relationship of genetic differentiation (F ST) and the overlap of ecological niches (as measured by n‐dimensional hypervolumes) among genetic groups resulting from spatial Bayesian genetic clustering in the wolf (Canis lupus) in the Italian peninsula. Within the Italian wolf population, four genetic clusters were detected, and these clusters showed different ecological niches. Moreover, different wolf clusters were significantly related to differences in land cover and human disturbance features. Such differences in the ecological niches of genetic clusters should be interpreted in light of neutral processes that hinder movement, dispersal, and gene flow among the genetic clusters, in order to not prematurely assume any selective or adaptive processes. In the present study, we found that both the plasticity of wolves—a habitat generalist—to cope with different environmental conditions and the occurrence of barriers that limit gene flow lead to the formation of genetic intraspecific genetic clusters and their distinct ecological niches.

Keywords: Canis lupus, genetic clustering, human disturbance, landscape genetics, mixed‐effects models, n‐dimensional hypervolume

1. INTRODUCTION

Genetic variation is key for the long‐term persistence and survival of species and populations. Its distribution across species ranges can reveal intraspecific information that is not necessarily represented in simple species occurrence patterns (Harrisson et al., 2016; Kovach et al., 2015). For instance, understanding the distribution of intraspecific genetic variation and how it relates to environmental factors can assist conservation management to assess species responses to environmental conditions and global change (Thomassen et al., 2010).

Recently, Gotelli and Stanton‐Geddes (2015) proposed the use of ecological niche models (ENMs), also known as habitat suitability models or species distribution models, for intraspecific genetic groups identified by Bayesian clustering, in order to account for the genetic diversity occurring within species. ENMs are widely used in various fields of ecology, evolution, biogeography, conservation biology, and landscape genetics (Beaumont et al., 2009; Guisan et al., 2013; Milanesi, Holderegger, Caniglia, Fabbri, & Randi, 2016; Milanesi, Breiner, Puopolo, & Holderegger, 2017; Milanesi, Holderegger, Bollmann, Gugerli, & Zellweger, Spear, Balkenhol, Fortin, McRae, & Scribner, 2010; Wang, Yang, Bridgman, & Lin, 2008). Gotelli and Stanton‐Geddes (2015) suggested that ENMs should be run for each intraspecific genetic cluster separately to provide insight into macroecological patterns caused by the heterogeneous evolutionary history across species’ distribution ranges (Marcer, Méndez‐Vigo, Alonso‐Blanco, & Picó, 2016). Species often display adaptation to particular combinations of environmental conditions in different parts of their whole range (Keller, Holderegger, & Strien, 2013). It is important to note that the approach of Gotelli and Stanton‐Geddes (2015) relies on simple correlations between genetic clusters and environmental factors. Thus, linking genetic patterns within species with ENMs does not necessarily assume that there is a causal effect between environmental factors and intraspecific genetic variation in terms of adaptation. In addition, most genetic markers (microsatellites, SSRs, or single‐nucleotide polymorphism, SNPs) used in genetic clustering are selectively neutral (Holderegger, Kamm, & Gugerli, 2006; Rellstab, Gugerli, Eckert, Hancock, & Holderegger, 2015). In summary, genetic clusters could either be caused by selective processes, caused by different environmental conditions (an adaptive process), or simply caused by restricted gene flow among clusters occurring in areas with different ecological conditions (a neutral process).

The approach of Gotelli and Stanton‐Geddes (2015) has so far only been applied in handful of studies (Harrisson et al., 2016; Ikeda et al., 2017; Marcer et al., 2016; Shinneman, Means, Potter, & Hipkins, 2016) , and the relationship between genetic distances among genetically defined clusters (e.g., genetic differentiation F ST; Dupanloup, Schneider, & Excoffier, 2002; Jombart, Devillard, Dufour, & Pontier, 2008) and distances or similarities among their ecological niches (e.g., niche overlap) has not been tested so far. Moreover, none of these studies specifically investigated the environmental factors differing among genetic clusters. However, in cases of low ecological niche overlap among intraspecific genetic clusters—that is, clusters showing cluster‐specific ecological niches—a given species could be considered as an assemblage of genetic or evolutionary lineages differing in their spatial distribution and their environments (Marcer et al., 2016).

Thus, in this study, we (a) estimated the pairwise ecological niche overlap between genetic groups resulting from spatial Bayesian clustering, (b) determined the relationship between genetic distances (F ST) and ecological niche overlap between identified genetic clusters, and (c) identified the ecological factors related to the spatial location of genetic clusters. For this purpose, we used a genetic data set on wolves (Canis lupus), which were molecularly identified during multiyear large‐scale monitoring projects based on carcasses, live‐trapped individuals, and non‐invasively collected samples from the central Apennines to the western Alps in Italy (Caniglia et al., 2012, 2013 ; Caniglia, Fabbri, Galaverni, Milanesi, & Randi, 2014; Fabbri et al., 2007). The population of wolves in Italy experienced a demographic bottleneck in the 1970s (Zimen & Boitani, 1975), which reversed in the 1980s due to legal protection, the occurrence of ample habitat in diverse landscapes abandoned by humans and the abundant availability of wild prey (Meriggi, Brangi, Schenone, Signorelli, & Milanesi, 2011). In about 40 years, the wolf population re‐expanded from south‐central Italy to the entire Apennine chain (including adjacent lower hills and plains) and the Italian and French western Alps (Caniglia et al., 2013; Fabbri et al., 2007; Galaverni, Caniglia, Fabbri, Milanesi, & Randi, 2016).

2. METHODS

2.1. Study area

Data collection was carried out from the central Apennines to the western Alps in Italy, in a study area of 97,044 km2 (6°62′–13°91′E; 46°46′–42°39′N; Figure 1). The study area was characterized by a large altitudinal range (0–4,634 m a.s.l.), distinct climatic gradients (from temperate to alpine), and diverse human land uses. It was characterized by a high diversity of habitats, such as different types of meadows, pastures, rocky surfaces, and even glaciers in high mountains. In the lower mountains and foothills, abandoned fields currently changing into semi‐natural shrublands and deciduous, mixed or evergreen forests were most abundant. In the valleys, plains, and at the coast, agricultural fields and urban areas were dominant.

Figure 1.

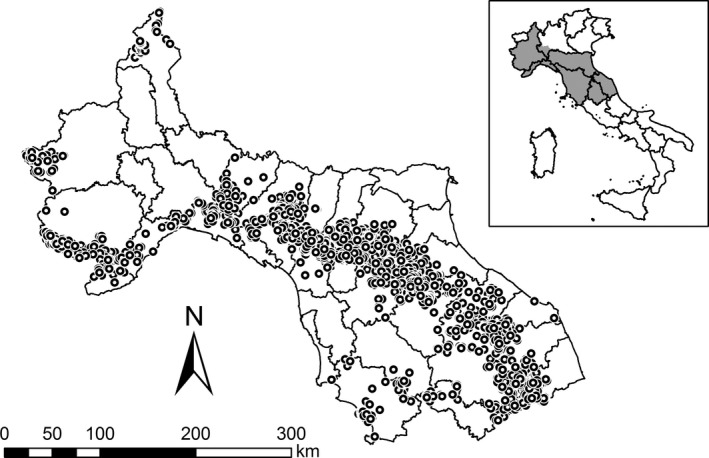
Figure 1

Open in a new tab

Study area in Italy (black lines indicate provincial and regional borders) and wolf sampling locations (white dots with black circles)

2.2. Genetic data set

Putative wolf samples (mainly feces but also blood or muscular tissues from carcasses as well as saliva, urine, and hairs; N = 9,317) were collected by more than 400 trained operators (Italian State Forestry Corps, park rangers and technicians, wildlife managers, researchers, students, and volunteers). Training was done by wolf experts, and operators were instructed to collect samples as fresh‐looking as possible, excluding degraded ones. Samples were collected along randomly chosen trails and country roads across all habitat types, at least once per season. Sampling was part of a long‐term monitoring program on wolves in Italy (from 2000 to 2011; Caniglia et al., 2012, 2014 ; Fabbri et al., 2007). Samples were stored at −20°C in 10 volumes of 95% ethanol or Tris/SDS buffer (Caniglia et al., 2012). The MULTIPROBE IIEX Robotic Liquid Handling System of Perkin Elmer and the QIAGEN stool and tissue extraction kits were used to extract DNA. Multi‐locus genotypes, gender, and taxon (i.e., wolf, dog, or hybrid) were determined using 12 unlinked neutral microsatellites, a sex‐specific restriction site and taxon‐specific markers following the methods described in Caniglia et al., (2014, 2013 . PCR amplification of each sample was carried out four to eight times. A total of 3,815 samples were reliable genotyped at all markers and belonged to 923 unrelated wolf individuals (Figure 1), 93 dogs and 118 wolf ×dog hybrids (Milanesi et al., 2016, Milanesi, Holderegger, Bollmann, et al., ).

2.3. Genetic clustering

To identify genetic clusters of Italian wolves, we considered the 923 wolf individuals and used the Bayesian genetic clustering method implemented in TESS 2.3 (Chen, Durand, Forbes, & François, 2007), incorporating spatial information on sampling locations (considering the spatial coordinates of the location where a given wolf has been sampled for the first time). We used the admixture model to calculate 10 runs for K max = 2–6 clusters (500,000 sweeps, 100,000 burn‐in) using three different values of the spatial interaction parameter h (0, 0.6—the default value—and 0.99 indicating no spatial, medium, and high spatial dependence, respectively).

The optimal number of clusters was estimated through the deviance information criterion (DIC) plot (Chen et al., 2007). For the most likely number of clusters, mean cluster membership probabilities of the 10 runs were estimated with CLUMPP 1.1.2 (Jakobsson & Rosenberg, 2007) and average cluster membership probabilities were then interpolated across the whole study area by thin plate spline function (Tps) in the R package FIELDS (v. 3.3.1; Furrer, Nychka, & Sain, 2009; again only considering the spatial coordinates of the location where a given wolf has been sampled for the first time).

We estimated genetic differentiation between the identified genetic clusters with pairwise F st‐values calculated in GENALEX (9,999 permutations; Peakall & Smouse, 2006).

2.4. Predictor variables

We collected a total of 13 predictor variables encompassing environmental, topographic, and anthropogenic factors. Specifically, we estimated habitat diversity and the percentages of six land cover types derived from CORINE Land Cover 2006 IV Level, with a minimum mapping unit/width of 25 ha/100 m and a thematic accuracy ≥85% (https://www.sinanet.isprambiente.it/it/sia-ispra/download-mais/corine-land-cover/corine-land-cover-2006-iv-livello/view; Table 1). From a digital elevation model of Italy (20 m spatial resolution; https://www.sinanet.isprambiente.it/it/sia-ispra/download-mais/dem20/), we obtained the topographic variables altitude, slope, and landscape roughness (Table 1). We also considered human population density (at a spatial resolution of 1 km; https://ec.europa.eu/eurostat/web/gisco/geodata/reference-data/population-distribution-demography) as well as the presence and distance from human settlements (i.e., urban areas, villages, derived from CORINE Land Cover 2006 IV Level).

Table 1.

Environmental factors used in generalized linear models

Feature Variable Units VIF
Land cover Coniferous forests Percentage (%) 1.128
Mixed woods Percentage (%) 1.101
Shrublands Percentage (%) 1.188
Deciduous forests Percentage (%) 1.337
Meadows Percentage (%) 1.551
Cultivated fields Percentage (%) > 3
Shannon index of habitat diversity Sum of natural logarithm of each category proportion in the sample grid 1.301
Topography Altitude Meter a.s.l. (m) 2.486
Slope Degree (°) >3
Landscape roughness Ratio of the average length of isolines in the sample grid over sample grid side length >3
Anthropogenic factors Human population density Number per km2 1.198
Human settlements Percentage (%) 1.313
Distance from human settlements Meter (m) 1.791
Open in a new tab

Variables with a variance inflation factor (VIF) >3 were removed from further analysis due to multi‐collinearity with other variables.

We calculated the variance inflation factor (VIF) for all the variables and removed predictor variables with values higher than 3 (i.e., highly correlated to other predictors; Zuur, Ieno, & Elphick, 2010; Table 1) to avoid multi‐collinearity among predictors. Specifically, we removed cultivated fields, slope, and landscape roughness, because they all exhibited a VIF >3, and only considered the remaining 10 variables in further analyses (Table 1). We also estimated spatial autocorrelation within each predictor variable through Moran's I index (Table S1) using the R package RASTER (v. 2.5‐8. Hijmans, 2011). We found relatively high and positive Moran's I values considering the entire study area (indicating positive spatial autocorrelation, e.g., clustering; Cliff & Ord, 1981) but low values (close to zero, indicating a random pattern with no spatial autocorrelation; Cliff & Ord, 1981) considering only the values of the predictor variables at the locations were wolves where sampled (Supporting Information Table S1).

2.5. Relating genetic differentiation and ecological niche overlap

We estimated the ecological niche of each genetic cluster considering the locations of wolves belonging to a particular cluster by n‐dimensional hypervolumes (Blonder, Lamanna, Violle, & Enquist, 2014; Blonder, Lamanna, Violle, & Enquist, 2017; see Supporting Information Table S2 for details on model parameters), which, in contrast to other ENMs, allows estimation of the ecological hyperspace considering the whole set of predictors (Blonder et al., 2014). We quantified pairwise ecological niche overlap between clusters of wolves as the intersection of two shared/summed ecological niches in the hyperspace. We performed these analyses in the R package HYPERVOLUME (v. 2.0.8; Blonder et al., 2014). We also provided minimum, mean, and maximum values of the predictor variables of the hypervolume in the minimum convex polygon estimated for each wolf cluster (Supporting Information Table S3).

We then compared the pairwise F st‐values between genetic clusters (response variable) and the corresponding ecological niche overlap between two clusters (fixed effect) in a linear mixed‐effects model (a Toeplitz covariance matrix was considered as random effect to account for the non‐independence of distance measurements between pairs of clusters; Milanesi et al., 2016; Milanesi, Breiner, et al., 2017; Milanesi, Holderegger, Bollmann, et al., ; Selkoe et al., 2010; Van Strien, Keller, & Holderegger, 2012). Actually, linear mixed‐effects models have recently been identified as the best performing among several landscape genetics technics (Shirk, Landguth, & Cushman, 2018). Specifically, our approach is conceptually similar to an isolation by environment test (Wang & Bradburd, 2014; Wang, Glor, & Losos, 2013), but instead of relate pairwise genetic and environmental distances (often derived by least‐cost paths) among populations, we related pairwise genetic distances with ecological niche overlap between clusters. In our approach, high standardized regression coefficient (β) values correspond to a large presumed effect of the predictor on the response variable. We expected an inverse relationship between Fst‐values and ecological niche overlap (and thus a negative standardized β value), as genetic differentiation should decrease with increasing niche overlap. We used 10,000 permutations to assess significance of linear mixed‐effects models using the PGIRMESS package (v. 1.6.7; Giraudoux, 2013) in R.

2.6. Relating cluster distribution and predictor variables

To identify the particular environmental factors related to the spatial distribution of the different genetic clusters of wolves in Italy, we developed spatial conditional autoregressive models (CAR) developed using the SPDEP package in R (v. 0.6‐15; Bivand et al., 2011), which consider autocorrelation among locations (while low at our wolf locations; Supporting Information Table S1), using the cluster membership of each individual wolf as dependent variable. To identify the best model(s) per cluster, we applied an information theoretic approach (Burnham & Anderson, 2004) through model selection and multi‐model inference (testing all possible combinations of predictor variables). Specifically, the Akaike information criterion (AIC; Akaike, 1974) was used, and models were ranked based on ΔAIC (considering only models with ΔAIC < 2; Burnham & Anderson, 2004). We estimated standardized regression β‐coefficients (and their standard errors) as well as significance and importance (calculated as the sum of the Akaike weights, W) of all the predictor variables entered in the best model(s) per genetic cluster through model averaging. We carried out these analyses using the R package MUMIN (v. 1.0.0. Barton, 2009). We also calculated sampling effort through Gaussian kernel density (Elith, Kearney, & Phillips, 2010) based on all sampling locations (i.e., including wolves, dogs, and hybrids locations) and used the resulting values as case weights in the above‐mentioned CAR models.

3. RESULTS

Bayesian genetic cluster analysis suggested the existence of four genetic clusters (Figure 2), as indicated by the lowest DIC value at K max = 4 (49,805.75; 95% confidence interval: ±34.15; Figure 3) in the DIC plot (Figure 2). These four clusters were consistent across the three different spatial interaction factors (h) tested. We thus based further analyses on the default spatial interaction factor of h = 0.6 and the resulting four genetic clusters. The highest number of wolf individuals was recorded in cluster 1 (N = 329), followed by cluster 3 (N = 239), cluster 4 (N = 217), and cluster 2 (N = 138). Cluster 1 was located on the eastern side of the central Apennines (EC hereafter), cluster 2 occurred in the western Alps (WA), cluster 3 on western side of the central Apennines (WC), and cluster 4 in the northern Apennines (NA; Figure 4).

Figure 2.

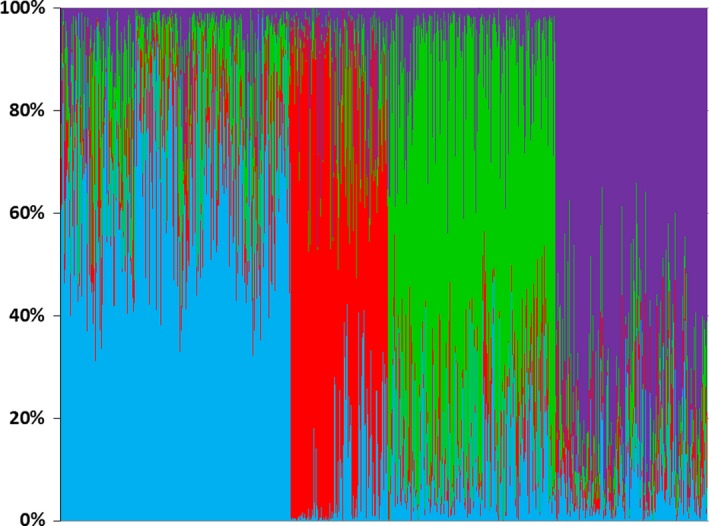
Figure 2

Open in a new tab

Bayesian clustering analysis showing barplots for the proportion of cluster memberships assigned to individual wolves under the estimated optimal numbers of clusters (K max  = 4). Different colors indicate different clusters

Figure 3.

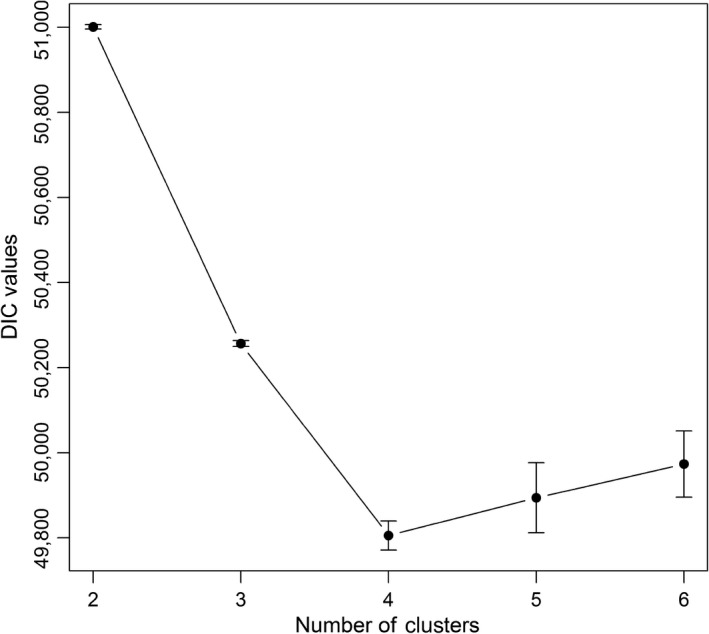
Figure 3

Open in a new tab

Estimation of the number of genetic clusters (K max = 2–6) of wolves in Italy based on the mean (±95% confidence intervals from 10 runs) deviance information criterion (DIC)

Figure 4.

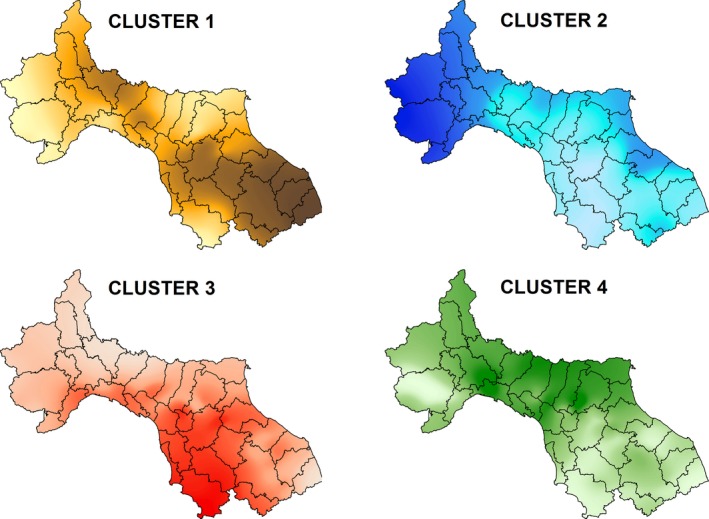
Figure 4

Open in a new tab

Genetic clusters of wolves in Italy. Interpolation maps of membership coefficients of four genetic clusters of wolves are shown (dark to light color shadings indicates higher to lower cluster membership probabilities)

Pairwise comparisons showed statistically significant (p < 0.001) genetic differentiation among clusters. Ecological niche overlap between clusters was moderate, with values ranging between 0.361 and 0.451 (Table 2). These are relative values (ranging from 0 to 1), and hence, the overlap is somewhere in the middle between low and high.

Table 2.

Pairwise genetic differentiation Fst (below diagonal) and pairwise ecological niche overlap (above diagonal) between clusters of wolves

Eastern‐central Apennines (EC) Western Alps (WA) Western‐central Apennines (WC) Northern Apennines (NA)
EC – 0.438 0.361 0.415
WA 0.031* – 0.428 0.451
WC 0.055* 0.042* – 0.401
NA 0.033* 0.018* 0.013* –
Open in a new tab

* p < 0.001.

Linear mixed‐effects models with pairwise genetic differentiation F ST as dependent variable showed a significant relationship (p < 0.001) with ecological niche overlap between clusters with a standardized β‐coefficient of 0.557.

Considering EC, the best models (N = 11; AIC ranging between 995.43 and 997.42, better than a random model at AIC = 1,029.28) included altitude, meadows, and habitat diversity, which were all positively related to cluster membership and had the highest W and p < 0.001 (Table 3), while deciduous and coniferous forests, human population density, shrublands, mixed woods, and human settlements showed lower values of W and were non‐significant (Table 3). The best models of WA (N = 9; AIC ranging between 278.41 and 280.40, better than a random model at AIC = 300.67) included altitude, shrublands, coniferous, and deciduous forests (only the latter with negative β value) with the highest W and p < 0.001 (Table 3), while habitat diversity, mixed woods, meadows, human settlements, and human population density showed lower values of W and were non‐significant (Table 3). In contrast, the best models of WC (N = 16; AIC ranging between 933.04 and 935.04, better than a random model at AIC = 1,018.07) included deciduous forests and mixed woods, both positively related to cluster membership, with the highest W and p < 0.001 (Table 3), while human settlements, coniferous forests, altitude, human population density, habitat diversity, meadows, and shrublands density showed lower values of W and were non‐significant (Table 3). Finally, in the best models of NA (N = 12; AIC ranging between 680.43 and 682.42, better than a random model at AIC = 701.18) altitude, deciduous forests, and meadows (only the latter with negative β value) showed the highest W and p < 0.001 (Table 3), while habitat diversity, human settlements, mixed woods, coniferous forests, shrublands, and human population density showed lower values of W and were non‐significant (Table 3).

Table 3.

Average standardized coefficients (β), standard errors (SE), p‐values (p) and relative importance from Akaike weights (W) based on averaging spatial conditional autoregressive model (CAR) for cluster membership (considering only models with ΔAIC < 2)

Cluster Variable β SE p W
EC (Intercept) −1.33 0.35 <0.001 –
Altitude 0.64 0.01 <0.001 0.99
Meadows 0.71 0.01 <0.001 0.99
Shannon index of habitat diversity 0.92 0.24 <0.001 0.99
Deciduous forests 0.01 0.00 0.361 0.15
Human population density −0.01 0.00 0.471 0.13
Coniferous forests 0.01 0.01 0.550 0.12
Shrublands 0.01 0.00 0.586 0.12
Mixed woods 0.01 0.00 0.729 0.11
Human settlements −0.01 0.01 0.800 0.10
WA (Intercept) −2.84 0.42 <0.001 –
Altitude 0.91 0.01 <0.001 0.99
Shrublands 0.77 0.02 <0.001 0.99
Coniferous forests 0.89 0.02 <0.001 0.99
Deciduous forests −0.61 0.01 <0.001 0.99
Shannon index of habitat diversity −0.33 0.36 0.364 0.18
Mixed woods 0.01 0.01 0.496 0.15
Meadows 0.01 0.00 0.659 0.13
Human settlements −0.01 0.02 0.788 0.12
Human population density −0.01 0.00 0.887 0.12
WC (Intercept) −1.45 0.28 <0.001 –
Deciduous forests 0.93 0.01 <0.001 0.99
Mixed woods 0.86 0.01 <0.001 0.99
Human settlements −0.02 0.01 0.071 0.83
Coniferous forests −0.01 0.01 0.258 0.36
Altitude 0.01 0.00 0.225 0.29
Human population density −0.01 0.00 0.339 0.18
Shannon index of habitat diversity 0.23 0.27 0.390 0.15
Meadows 0.01 0.00 0.362 0.11
Shrublands 0.01 0.01 0.689 0.05
NA (Intercept) −0.39 0.47 0.412 –
Altitude 0.84 0.01 <0.001 0.99
Deciduous forests 0.91 0.01 <0.001 0.99
Meadows −0.62 0.02 <0.001 0.99
Shannon index of habitat diversity 0.49 0.29 0.090 0.73
Human settlements −0.02 0.01 0.160 0.67
Mixed woods −0.01 0.01 0.211 0.39
Coniferous forests −0.01 0.01 0.285 0.30
Shrublands −0.01 0.01 0.288 0.24
Human population density −0.01 0.00 0.969 0.08
Open in a new tab

4. DISCUSSION

In this study, through the analysis of neutral genetic markers (i.e., microsatellites), we identified four genetic clusters of wolves in Italy and developed cluster‐specific ENMs to estimate niche overlap between them. We found moderate ecological niche overlap between the resulting clusters, which was nevertheless significantly related to the genetic distances between them, suggesting that genetically different clusters live in different environmental conditions. Accordingly, we identified cluster‐specific combinations of environmental factors influencing wolf occurrence in Italy.

4.1. Genetic clusters of wolves in Italy

Why should genetic clusters reflect differences in ecological niches among clusters? There are two main possible explanations: (a) genetic clusters might reflect differential adaptation to different environments (as detected by ENMs) caused by selection; (b) genetic clusters occupy different ecological niches, but the genetic differences among them are caused by restricted gene flow. Though the two processes are different in nature, they are not mutually exclusive (Hoffmann & Willi, 2008).

Genetic clusters are often identified based on a small number of microsatellite (SSRs) markers or a larger number of SNPs. While the majority of SSRs is neutral by definition and is usually not linked to adaptive regions within the genome of a study species, a smaller or larger proportion of SNPs (usually about 5%; Schoville et al., 2012) is of adaptive relevance (i.e., is located in adaptive genes or is closely linked to adaptive regions). In both cases, most or all of the genetic markers used for genetic clustering behave neutrally, suggesting that there probably is no direct adaptive relationship between genetic clusters and the ecological niches they occupy. In fact, demographic spatial patterns can mimic and confound adaptive signals (Beaumont & Nichols, 1996; Foll & Gaggiotti, 2008; Holderegger et al., 2008; Rellstab et al., 2015).

If so, intraspecific genetic clusters can also be caused by limited movement, dispersal, and gene flow among different regions within the distribution range of a species (Gotelli & Stanton‐Geddes, 2015), and the genetic differentiation among them is then affected by the interplay of gene flow and genetic drift (Hutchison & Templeton, 1999; Slatkin, 1987). Restricted gene flow among clusters could be caused by many factors affecting movement and dispersal, especially by geographical or landscape barriers—a topic widely explored in evolution, biogeography, landscape ecology, and landscape genetics (Andrew, Ostevik, Ebert, & Rieseberg, 2012; Holderegger & Wagner, 2008; Manel, Schwartz, Luikart, & Taberlet, 2003; McCairns & Bernatchez, 2008; Storfer et al., 2007; Storfer, Murphy, Spear, Holderegger, & Waits, 2010; Temple, Hoffman, & Amos, 2006). Especially in mammals, intrinsic factors such as behavior or the specific use of food resources could also cause limited movement and dispersal among clusters (Pilot et al., 2006; Vonholdt et al., 2010).

The four genetic clusters identified in this study largely coincided with the topology of the main mountain regions occupied by wolves in Italy (parts of the Apennines and the Alps; Figure 3, Supporting Information Figure S1), occupying four continuous areas located on the eastern and western sides of the central Apennines, in the northern Apennines and in the western Alps (Figure 3). A previous study on the history and dynamics of the wolf recolonization in the Apennines detected only three clusters in Italy, namely the central Apennines, the northern Apennines and the western Alps (Fabbri et al., 2007), based on a different genetic data set than the present one. Thus, an interesting result of our analyses was the splitting of the central Apennine wolf population into two distinct genetic clusters, one on the western and one on the eastern slope of the Apennines (Figure 3). The discovery of another cluster in the Italian wolf population was rather unexpected due to the assumed high mobility of wolves. However, the two separated genetic clusters of wolves on opposite slopes of the Apennines could be the result of recent re‐colonization of low‐mountain or hilly areas close to the Tyrrhenian and the Adriatic Sea, originating from the former core habitat of wolves at higher altitudes in the central Apennines (Caniglia et al., 2013; Galaverni et al., 2017; Giacchini, Scotti, & Zabaglia, 2012). The cluster in the western Alps was mainly founded by long‐distance dispersal from the Apennines at the onset of the re‐colonization process of the Alps, followed by the setting of territorial behavior of reproducing packs there (Fabbri et al., 2007; Valière et al., 2003). Such a scenario is supported by similar patterns of genetic structure found for wild cats (Felix silvestris) in Italy (Mattucci et al., 2013).

4.2. Different niches of wolf clusters in Italy

The four identified clusters of wolves were related to different ecological factors. Specifically, we found significant and positive relationships between WC and mixed woods and deciduous forests, while WA was positively related to coniferous forests and NA was positively related to deciduous forests. Thus, our results highlighted the importance of woods and forests in providing suitable habitat and shelter for wolves (Bassi, Willis, Passilongo, Mattioli, & Apollonio, 2015; Jędrzejewski, Niedzialkowska, Mysłajek, Nowak, & Jędrzejewska, 2005; Llaneza, López‐Bao, & Sazatornil, 2012; Meriggi et al., 2011; Milanesi, Meriggi, & Merli, 2012). However, deciduous forests were negatively related to WA. Actually, the areas of occurrence of EC and NA were characterized by a low percentage of coniferous forests, but a high percentage of deciduous forests and mixed woods, while those of WA were mainly covered by coniferous forests. These results suggest that wolves simply are related to the main regional forest type, irrespective of its nature. Moreover, EC, WA, and NA were positively related to altitude, probably because of the abundance of prey, availability of safe areas, and lower disturbance by human activities at higher altitudes (Bassi et al., 2015; Glenz, Massolo, Kuonen, & Schlaepfer, 2001; Jędrzejewski et al., 2005; Llaneza et al., 2012; Pilot et al., 2006).

Shrublands were positively related to WA, probably because of high amounts of open shrublands consisting of land used as pastures by freely roaming livestock in the corresponding region (Eggermann, Costa, Guerra, Kirchner, & Petrucci‐Fonseca, 2011). Meadows were positively related to EC, as a large share of meadows in a region potentially translates into a high availability of livestock as prey. Thus, meadows become important for wolves, in regions where forests are sparse (Jędrzejewski et al., 2005). In contrast, meadows were negatively related to the distribution of NA due to small extension of meadows or low accessibility of livestock as prey in this area (Meriggi et al., 2011). EC was positively related to habitat diversity, because wolves tend to use different habitat types for different activities (Houle, Fortin, Dussault, Courtois, & Ouellet, 2010) and because habitat heterogeneity is a known driver of wild ungulate diversity and distribution (Cromsigt, Prins, & Olff, 2009). In summary, wolf clusters in Italy seem to be simply associated with the most abundant land cover types of their respective area, showing that high ecological flexibility of wolves enabling them to cope with diverse and even fragmented landscapes (Llaneza et al., 2012).

Genetic clusters of animals should also be affected by anthropogenic factors. For instance, animals could show avoidance behavior against human settlements or roads. Such avoidance has been assessed in several wild animals (Cushman, McKelvey, Hayden, & Schwartz, 2006) and is well known to also affect wolf occurrence (Gaillard et al., 2010). Indeed, we found that human disturbance, in terms of human population density and human settlements, tended to be related to genetic clusters in Italian wolves, but not in a consistent and statistically significant way. Nevertheless, in agreement with other studies (Jędrzejewski et al., 2005; Llaneza et al., 2012; Milanesi et al., 2016), the distribution of the four different clusters were negatively related to human population density and human settlements, while distance from human settlements was not included in any of the best models for all clusters.

4.3. Conclusions, management implications, and future research

In this study, we found that different genetic clusters of wolves in Italy are differently related to land cover types, probably caused by two main effects. First, the plasticity of the wolf—a distinct habitat generalist (Llaneza et al., 2012)—which allows it to adapt to diverse regions and landscapes with different environmental conditions. Second, the occurrence of geographical barriers limiting gene flow among wolf clusters. While the former can be inferred from the different relationships between different wolf clusters, and different environment factors, the latter is proved by wolf clusters being mainly separated by mountainous terrains. As long dispersal distances in wolves have been recorded—also across human‐dominated landscapes (Andersen et al., 2015)—wolf clusters in Italy are probably still linked by some gene flow (F ST 0.055). In addition, the wolf is a territorial carnivore living in hierarchical packs and the occurrence of established packs can thus result in moving animals not settling down, because of aggressive behavior and competition of resident individuals, resulting in limited gene flow, finally contributing to genetic clustering in Italian wolves.

Finally, we remark that when using genetic clusters based on neutral loci in combination with ENMs, one pitfall is to simply interpret the results in the light of adaptation. However, there is no direct link between neutral and adaptive genetic diversity or differentiation (Merilä & Crnokrak, 2001; Reed & Frankham, 2001). Differences in the ecological niches of genetic clusters should thus be interpreted in light of neutral processes that influence movement, dispersal, and gene flow among genetic clusters (Gotelli & Stanton‐Geddes, 2015), as done in the present study. However, further studies should compare genetic clusters separately based on neutral and adaptive genetic markers and relate them to ecological niches (as identified by ENMs; Deagle, Jones, Absher, Kingsley, & Reimchen, 2013; Manel & Holderegger, 2013). Since adaptive markers do not have to be in Hardy–Weinberg equilibrium nor in linkage equilibrium, commonly used Bayesian genetic clustering techniques cannot be applied. Nevertheless, assumption‐free methods are now available and can be used for this purpose (e.g. TESS 3; Caye, Deist, Martins, Michel, & François, 2016). Environmental association analyses (linking potentially adaptive genes to particular environmental factors; Rellstab et al., 2015) can then be combined with ENMs to tests whether genetic clusters based on adaptive genes are related to different ecological factors. In such analyses, spatial coincidence of adaptive and neutral genetic clusters would make a strong case for adaptively relevant differences among genetic clusters.

CONFLICT OF INTEREST

None declared.

AUTHORS CONTRIBUTIONS

P.M. and R.H. designed the analyses; R.C., E.F., and M.G. produced the Italian canid database and shared ideas to realize the article; P.M. carried out analyses and wrote the manuscript; R.H. and F.P. shared in the writing of the manuscript. All authors approved the final version of the manuscript.

DATA ACCESSIBILITY

Due to sensitive information (locations of an endangered species), the data of the present study cannot be made openly accessible.

Supporting information

 

Click here for additional data file. (29.7MB, tif)

 

Click here for additional data file. (19.6KB, docx)

 

Click here for additional data file. (15.2KB, docx)

 

Click here for additional data file. (16.8KB, docx)

ACKNOWLEDGMENTS

We thank Chris Foote and two anonymous reviewers for their useful comments and suggestions which greatly improved the previous version of this manuscript. This research would not have been possible without the help of many collaborators, who collected and provided wolf samples. The authors greatly thank the following institutions and collaborators: University of Bologna (E. Randi), Ministero dell'Ambiente e della Tutela del Territorio, Italian Forestry Corp; Progetto Lupo Piemonte, Regione Piemonte (in particular, E. De Biaggi), Parco Naturale delle Alpi Marittime (in particular, G. Canavese and F. Marucco), Regione Emilia‐Romagna (in particular, M. L. Bruschini, E. Valbonesi and M. L. Zanni), Parco Nazionale delle Foreste Casentinesi, Monte Falterona e Campigna (M. Mencucci, N. Cappai, C. Pedrazzoli), Parco Nazionale dell'Appennino Tosco‐Emiliano (W. Reggioni), University of Rome (P. Ciucci), Parco Regionale Naturale dell'Antola and Regione Liguria, Parco Regionale Naturale della Gola della Rossa e di Frasassi and Regione Marche (in particular, M. Scotti and C. Zabaglia), Regione Umbria (in particular, U. Sergiacomi and R. Mazzei) and Parco Naturale Regionale della Maremma (G.P. Sammuri).

Milanesi P, Caniglia R, Fabbri E, Puopolo F, Galaverni M, Holderegger R. Combining Bayesian genetic clustering and ecological niche modeling: Insights into wolf intraspecific genetic structure. Ecol Evol. 2018;8:11224–11234. 10.1002/ece3.4594

Funding information

WSL Swiss Federal Research Institute in Birmensdorf; Italian Ministry of Environment at ISPRA, Ozzano dell’Emilia.

REFERENCES

  1. Akaike, H. (1974). A new look at the statistical model identification. IEEE Transactions on Automatic Control, 19, 716–723. 10.1109/TAC.1974.1100705 [DOI] [Google Scholar]
  2. Andersen, L. W. , Harms, V. , Caniglia, R. , Czarnomska, S. D. , Fabbri, E. , Jędrzejewska, B. , … Pertoldi, C. (2015). Long‐distance dispersal of a wolf, Canis lupus, in northwestern Europe. Mammal Research, 60, 163–168. 10.1007/s13364-015-0220-6 [DOI] [Google Scholar]
  3. Andrew, R. L. , Ostevik, K. L. , Ebert, D. P. , & Rieseberg, L. H. (2012). Adaptation with gene flow across the landscape in a dune sunflower. Molecular Ecology, 21, 2078–2091. 10.1111/j.1365-294X.2012.05454.x [DOI] [PubMed] [Google Scholar]
  4. Barton, K. (2009). MuMIn: Multi‐model inference. R package version 1.0.0. [Google Scholar]
  5. Bassi, E. , Willis, S. G. , Passilongo, D. , Mattioli, L. , & Apollonio, M. (2015). Predicting the spatial distribution of wolf (Canis lupus) breeding areas in a mountainous region of central Italy. PLoS One, 10, e0124698. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Beaumont, L. J. , Gallagher, R. V. , Thuiller, W. , Downey, P. O. , Leishman, M. R. , & Hughes, L. (2009). Different climatic envelopes among invasive populations may lead to underestimations of current and future biological invasions. Diversity and Distributions, 15, 409–420. 10.1111/j.1472-4642.2008.00547.x [DOI] [Google Scholar]
  7. Beaumont, M. A. , & Nichols, R. A. (1996). Evaluating loci for use in the genetic analysis of population structure. Proceedings of the Royal Society of London B: Biological Sciences, 263, 1619–1626. [Google Scholar]
  8. Bivand, R. , Anselin, L. , Berke, O. A. , Bernat, A. , Carvalho, M. , Chun, Y. , … Lewin‐Koh, N. (2011). spdep: Spatial dependence: weighting schemes, statistics and models. R package version 0.6‐15.
  9. Blonder, B. , Lamanna, C. , Violle, C. , & Enquist, B. J. (2014). The n‐dimensional hypervolume. Global Ecology and Biogeography, 23, 595–609. [Google Scholar]
  10. Blonder, B. , Lamanna, C. , Violle, C. , & Enquist, B. J. (2017). Using n‐dimensional hypervolumes for species distribution modelling: a response to Qiao et al. (2016). Global Ecology and Biogeography, 26, 1071–1075. [Google Scholar]
  11. Burnham, K. P. , & Anderson, D. R. (2004). Multimodel inference: Understanding AIC and BIC in model selection. Sociological Methods & Research, 33, 261–304. 10.1177/0049124104268644 [DOI] [Google Scholar]
  12. Caniglia, R. , Fabbri, E. , Cubaynes, S. , Gimenez, O. , Lebreton, J.‐D. , & Randi, E. (2012). An improved procedure to estimate wolf abundance using non‐invasive genetic sampling and capture–recapture mixture models. Conservation Genetics, 13, 53–64. 10.1007/s10592-011-0266-1 [DOI] [Google Scholar]
  13. Caniglia, R. , Fabbri, E. , Galaverni, M. , Milanesi, P. , & Randi, E. (2014). Noninvasive sampling and genetic variability, pack structure, and dynamics in an expanding wolf population. Journal of Mammalogy, 95, 41–59. 10.1644/13-MAMM-A-039 [DOI] [Google Scholar]
  14. Caniglia, R. , Fabbri, E. , Greco, C. , Galaverni, M. , Manghi, L. , Boitani, L. , … Randi, E. (2013). Black coats in an admixed wolf× dog pack is melanism an indicator of hybridization in wolves? European Journal of Wildlife Research, 59, 543–555. 10.1007/s10344-013-0703-1 [DOI] [Google Scholar]
  15. Caye, K. , Deist, T. M. , Martins, H. , Michel, O. , & François, O. (2016). TESS3: Fast inference of spatial population structure and genome scans for selection. Molecular Ecology Resources, 16, 540–548. 10.1111/1755-0998.12471 [DOI] [PubMed] [Google Scholar]
  16. Chen, C. , Durand, E. , Forbes, F. , & François, O. (2007). Bayesian clustering algorithms ascertaining spatial population structure: A new computer program and a comparison study. Molecular Ecology Resources, 7, 747–756. [Google Scholar]
  17. Cliff, A. D. , & Ord, J. K. (1981). Spatial processes: Models and applications (pp. 266). London: Pion. [Google Scholar]
  18. Cromsigt, J. P. , Prins, H. H. , & Olff, H. (2009). Habitat heterogeneity as a driver of ungulate diversity and distribution patterns: Interaction of bodymass and digestive strategy. Diversity and Distribution, 15, 513–522. 10.1111/j.1472-4642.2008.00554.x [DOI] [Google Scholar]
  19. Cushman, S. A. , McKelvey, K. S. , Hayden, J. , & Schwartz, M. K. (2006). Gene flow in complex landscapes: Testing multiple hypotheses with causal modeling. The American Naturalist, 168, 486–499. 10.1086/506976 [DOI] [PubMed] [Google Scholar]
  20. Deagle, B. E. , Jones, F. C. , Absher, D. M. , Kingsley, D. M. , & Reimchen, T. E. (2013). Phylogeography and adaptation genetics of stickleback from the Haida Gwaii archipelago revealed using genome‐wide single nucleotide polymorphism genotyping. Molecular Ecology, 22, 1917–1932. 10.1111/mec.12215 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Dupanloup, I. , Schneider, S. , & Excoffier, L. (2002). A simulated annealing approach to define the genetic structure of populations. Molecular Ecology, 11, 2571–2581. 10.1046/j.1365-294X.2002.01650.x [DOI] [PubMed] [Google Scholar]
  22. Eggermann, J. , da Costa, G. F. , Guerra, A. M. , Kirchner, W. H. , & Petrucci‐Fonseca, F. (2011). Presence of Iberian wolf (Canis lupus signatus) in relation to land cover, livestock and human influence in Portugal. Mammalian Biology, 76, 217–221. 10.1016/j.mambio.2010.10.010 [DOI] [Google Scholar]
  23. Elith, J. , Kearney, M. , & Phillips, S. (2010). The art of modelling range‐shifting species. Methods in Ecology and Evolution, 1, 330–342. 10.1111/j.2041-210X.2010.00036.x [DOI] [Google Scholar]
  24. Fabbri, E. , Miquel, C. , Lucchini, V. , Santini, A. , Caniglia, R. , Duchamp, C. , … Fumagalli, L. (2007). From the Apennines to the Alps: Colonization genetics of the naturally expanding Italian wolf (Canis lupus) population. Molecular Ecology, 16, 1661–1671. [DOI] [PubMed] [Google Scholar]
  25. Foll, M. , & Gaggiotti, O. (2008). A genome‐scan method to identify selected loci appropriate for both dominant and codominant markers: A Bayesian perspective. Genetics, 180, 977–993. 10.1534/genetics.108.092221 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Furrer, R. , Nychka, D. , & Sain, S. (2009). fields: Tools for spatial data. R package version 3.3.1. [Google Scholar]
  27. Gaillard, J.‐M. , Hebblewhite, M. , Loison, A. , Fuller, M. , Powell, R. , Basille, M. , & van Moorter, B. (2010). Habitat–performance relationships: Finding the right metric at a given spatial scale. Philosophical Transactions of the Royal Society of London. Series B, Biological Sciences, 365, 2255–2265. [DOI] [PMC free article] [PubMed] [Google Scholar]
  28. Galaverni, M. , Caniglia, R. , Fabbri, E. , Milanesi, P. , & Randi, E. (2016). One, no one, or one hundred thousand: How many wolves are there currently in Italy? Mammal Research, 61, 13–24. 10.1007/s13364-015-0247-8 [DOI] [Google Scholar]
  29. Galaverni, M. , Caniglia, R. , Pagani, L. , Fabbri, E. , Boattini, A. , & Randi, E. (2017). Disentangling timing of admixture, patterns of introgression, and phenotypic indicators in a hybridizing wolf population. Molecular Biology and Evolution, 34, 2324–2339. 10.1093/molbev/msx169 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Giacchini, P. , Scotti, M. , & Zabaglia, C. (2012).Il Lupo nelle marche. ieri, oggi… e domani?, Pesaro. Regione Marche, Pages 98.
  31. Giraudoux, P. (2013). pgirmess: data analysis in ecology. R package version 1.5. 8. [Google Scholar]
  32. Glenz, C. , Massolo, A. , Kuonen, D. , & Schlaepfer, R. (2001). A wolf habitat suitability prediction study in Valais (Switzerland). Landscape and Urban planning, 55(1), 55–65. [Google Scholar]
  33. Gotelli, N. J. , & Stanton‐Geddes, J. (2015). Climate change, genetic markers and species distribution modelling. Journal of Biogeography, 42, 1577–1585. 10.1111/jbi.12562 [DOI] [Google Scholar]
  34. Guisan, A. , Tingley, R. , Baumgartner, J. B. , Naujokaitis‐Lewis, I. , Sutcliffe, P. R. , Tulloch, A. I. T. , … Mantyka‐Pringle, C. (2013). Predicting species distributions for conservation decisions. Ecology Letters, 16, 1424–1435. 10.1111/ele.12189 [DOI] [PMC free article] [PubMed] [Google Scholar]
  35. Harrisson, K. A. , Yen, J. D. , Pavlova, A. , Rourke, M. L. , Gilligan, D. , Ingram, B. A. , … Sunnucks, P. (2016). Identifying environmental correlates of intraspecific genetic variation. Heredity, 117, 155–164. 10.1038/hdy.2016.37 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Hijmans, R. J. (2011). Raster. R package version 2.5‐8. [Google Scholar]
  37. Hoffmann, A. A. , & Willi, Y. (2008). Detecting genetic responses to environmental change. Nature Reviews Genetics, 9, 421–432. 10.1038/nrg2339 [DOI] [PubMed] [Google Scholar]
  38. Holderegger, R. , Herrmann, D. , Poncet, B. , Gugerli, F. , Thuiller, W. , Taberlet, P. , … Aubert, S. (2008). Land ahead: Using genome scans to identify molecular markers of adaptive relevance. Plant Ecology & Diversity, 1, 273–283. 10.1080/17550870802338420 [DOI] [Google Scholar]
  39. Holderegger, R. , Kamm, U. , & Gugerli, F. (2006). Adaptive vs. neutral genetic diversity: Implications for landscape genetics. Landscape Ecology, 21, 797–807. 10.1007/s10980-005-5245-9 [DOI] [Google Scholar]
  40. Holderegger, R. , & Wagner, H. H. (2008). Landscape genetics. AIBS Bulletin, 58, 199–207. [Google Scholar]
  41. Houle, M. , Fortin, D. , Dussault, C. , Courtois, R. , & Ouellet, J. P. (2010). Cumulative effects of forestry on habitat use by gray wolf (Canis lupus) in the boreal forest. Landscape Ecology, 25, 419–433. 10.1007/s10980-009-9420-2 [DOI] [Google Scholar]
  42. Hutchison, D. W. , & Templeton, A. R. (1999). Correlation of pairwise genetic and geographic distance measures: Inferring the relative influences of gene flow and drift on the distribution of genetic variability. Evolution, 53, 1898–1914. 10.1111/j.1558-5646.1999.tb04571.x [DOI] [PubMed] [Google Scholar]
  43. Ikeda, D. H. , Max, T. L. , Allan, G. J. , Lau, M. K. , Shuster, S. M. , & Whitham, T. G. (2017). Genetically informed ecological niche models improve climate change predictions. Global Change Biology, 23, 164–176. 10.1111/gcb.13470 [DOI] [PubMed] [Google Scholar]
  44. Jakobsson, M. , & Rosenberg, N. A. (2007). CLUMPP: A cluster matching and permutation program for dealing with label switching and multimodality in analysis of population structure. Bioinformatics, 23, 1801–1806. 10.1093/bioinformatics/btm233 [DOI] [PubMed] [Google Scholar]
  45. Jędrzejewski, W. , Niedzialkowska, M. , Mysłajek, R. W. , Nowak, S. , & Jędrzejewska, B. (2005). Habitat selection by wolves Canis lupus in the uplands and mountains of southern Poland. Acta Theriologica, 50, 417–428. 10.1007/BF03192636 [DOI] [Google Scholar]
  46. Jombart, T. , Devillard, S. , Dufour, A. B. , & Pontier, D. (2008). Revealing cryptic spatial patterns in genetic variability by a new multivariate method. Heredity, 101, 92–103. 10.1038/hdy.2008.34 [DOI] [PubMed] [Google Scholar]
  47. Keller, D. , Holderegger, R. , & Strien, M. J. (2013). Spatial scale affects landscape genetic analysis of a wetland grasshopper. Molecular Ecology, 22, 2467–2482. 10.1111/mec.12265 [DOI] [PubMed] [Google Scholar]
  48. Kovach, R. P. , Muhlfeld, C. C. , Wade, A. A. , Hand, B. K. , Whited, D. C. , DeHaan, P. W. , … Luikart, G. (2015). Genetic diversity is related to climatic variation and vulnerability in threatened bull trout. Global Change Biology, 21, 2510–2524. 10.1111/gcb.12850 [DOI] [PubMed] [Google Scholar]
  49. Llaneza, L. , López‐Bao, J. V. , & Sazatornil, V. (2012). Insights into wolf presence in human‐dominated landscapes: The relative role of food availability, humans and landscape attributes. Diversity and Distributions, 18, 459–469. 10.1111/j.1472-4642.2011.00869.x [DOI] [Google Scholar]
  50. Manel, S. , & Holderegger, R. (2013). Ten years of landscape genetics. Trends in Ecology & Evolution, 28, 614–621. 10.1016/j.tree.2013.05.012 [DOI] [PubMed] [Google Scholar]
  51. Manel, S. , Schwartz, M. K. , Luikart, G. , & Taberlet, P. (2003). Landscape genetics: Combining landscape ecology and population genetics. Trends in Ecology & Evolution, 18, 189–197. 10.1016/S0169-5347(03)00008-9 [DOI] [Google Scholar]
  52. Marcer, A. , Méndez‐Vigo, B. , Alonso‐Blanco, C. , & Picó, F. X. (2016). Tackling intraspecific genetic structure in distribution models better reflects species geographical range. Ecology and Evolution, 6, 2084–2097. 10.1002/ece3.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
  53. Mattucci, F. , Oliveira, R. , Bizzarri, L. , Vercillo, F. , Anile, S. , Ragni, B. , … Lyons, L. A. (2013). Genetic structure of wildcat (Felis silvestris) populations in Italy. Ecology and Evolution, 3, 2443–2458. [Google Scholar]
  54. McCairns, R. J. , & Bernatchez, L. (2008). Landscape genetic analyses reveal cryptic population structure and putative selection gradients in a large‐scale estuarine environment. Molecular Ecology, 17, 3901–3916. 10.1111/j.1365-294X.2008.03884.x [DOI] [PubMed] [Google Scholar]
  55. Meriggi, A. , Brangi, A. , Schenone, L. , Signorelli, D. , & Milanesi, P. (2011). Changes of wolf (Canis lupus) diet in Italy in relation to the increase of wild ungulate abundance. Ethology Ecology & Evolution, 23, 195–210. [Google Scholar]
  56. Merilä, J. , & Crnokrak, P. (2001). Comparison of genetic differentiation at marker loci and quantitative traits. Journal of Evolutionary Biology, 14, 892–903. 10.1046/j.1420-9101.2001.00348.x [DOI] [Google Scholar]
  57. Milanesi, P. , Breiner, F. T. , Puopolo, F. , & Holderegger, R. (2017). European human‐dominated landscapes provide ample space for the recolonization of large carnivore populations under future land change scenarios. Ecography, 40, 1359–1368. 10.1111/ecog.02223 [DOI] [Google Scholar]
  58. Milanesi, P. , Holderegger, R. , Caniglia, R. , Fabbri, E. , Galaverni, M. , & Randi, E. (2017). Expert‐based versus habitat‐suitability models to develop resistance surfaces in landscape genetics. Oecologia, 183, 67–79. 10.1007/s00442-016-3751-x [DOI] [PubMed] [Google Scholar]
  59. Milanesi, P. , Holderegger, R. , Caniglia, R. , Fabbri, E. , & Randi, E. (2016). Different habitat suitability models yield different least‐cost path distances for landscape genetic analysis. Basic and Applied Ecology, 17, 61–71. 10.1016/j.baae.2015.08.008 [DOI] [Google Scholar]
  60. Milanesi, P. , Meriggi, A. , & Merli, E. (2012). Selection of wild ungulates by wolves Canis lupus (L. 1758) in an area of the Northern Apennines (North Italy). Ethology Ecology & Evolution, 24, 81–96. [Google Scholar]
  61. Peakall, R. O. , & Smouse, P. E. (2006). GENALEX 6: Genetic analysis in Excel. Population genetic software for teaching and research. Molecular Ecology Resources, 6, 288–295. [DOI] [PMC free article] [PubMed] [Google Scholar]
  62. Pilot, M. , Jedrzejewski, W. , Branicki, W. , Sidorovich, V. E. , Jedrzejewska, B. , Stachura, K. , & Funk, S. M. (2006). Ecological factors influence population genetic structure of European grey wolves. Molecular Ecology, 15, 4533–4553. 10.1111/j.1365-294X.2006.03110.x [DOI] [PubMed] [Google Scholar]
  63. Reed, D. H. , & Frankham, R. (2001). How closely correlated are molecular and quantitative measures of genetic variation? A meta‐analysis. Evolution, 55, 1095–1103. 10.1111/j.0014-3820.2001.tb00629.x [DOI] [PubMed] [Google Scholar]
  64. Rellstab, C. , Gugerli, F. , Eckert, A. J. , Hancock, A. M. , & Holderegger, R. (2015). A practical guide to environmental association analysis in landscape genomics. Molecular Ecology, 24, 4348–4370. 10.1111/mec.13322 [DOI] [PubMed] [Google Scholar]
  65. Schoville, S. D. , Bonin, A. , François, O. , Lobreaux, S. , Melodelima, C. , & Manel, S. (2012). Adaptive genetic variation on the landscape: Methods and cases. Annual Review of Ecology, Evolution, and Systematics, 43, 23–43. 10.1146/annurev-ecolsys-110411-160248 [DOI] [Google Scholar]
  66. Selkoe, K. A. , Watson, J. R. , White, C. , Horin, T. B. , Iacchei, M. , Mitarai, S. , … Toonen, R. J. (2010). Taking the chaos out of genetic patchiness: Seascape genetics reveals ecological and oceanographic drivers of genetic patterns in three temperate reef species. Molecular Ecology, 19, 3708–3726. 10.1111/j.1365-294X.2010.04658.x [DOI] [PubMed] [Google Scholar]
  67. Shinneman, D. J. , Means, R. E. , Potter, K. M. , & Hipkins, V. D. (2016). Exploring climate niches of ponderosa pine (Pinus ponderosa Douglas ex Lawson) haplotypes in the western United States: Implications for evolutionary history and conservation. PLoS One, 11, e0151811. [DOI] [PMC free article] [PubMed] [Google Scholar]
  68. Shirk, A. J. , Landguth, E. L. , & Cushman, S. A. (2018). A comparison of regression methods for model selection in individual‐based landscape genetic analysis. Molecular Ecology Resources, 18, 55–67. 10.1111/1755-0998.12709 [DOI] [PubMed] [Google Scholar]
  69. Slatkin, M. (1987). Gene flow and the geographic structure of natural populations. Science, 236, 787–792. 10.1126/science.3576198 [DOI] [PubMed] [Google Scholar]
  70. Spear, S. F. , Balkenhol, N. , Fortin, M. , McRae, B. H. , & Scribner, K. I. (2010). Use of resistance surfaces for landscape genetic studies: Considerations for parameterization and analysis. Molecular Ecology, 19, 3576–3591. 10.1111/j.1365-294X.2010.04657.x [DOI] [PubMed] [Google Scholar]
  71. Storfer, A. , Murphy, M. A. , Evans, J. S. , Goldberg, C. S. , Robinson, S. , Spear, S. F. , … Waits, L. P. (2007). Putting the 'landscape' in landscape genetics. Heredity, 98, 128 10.1038/sj.hdy.6800917 [DOI] [PubMed] [Google Scholar]
  72. Storfer, A. , Murphy, M. A. , Spear, S. F. , Holderegger, R. , & Waits, L. P. (2010). Landscape genetics: Where are we now? Molecular Ecology, 19, 3496–3514. 10.1111/j.1365-294X.2010.04691.x [DOI] [PubMed] [Google Scholar]
  73. Temple, H. J. , Hoffman, J. I. , & Amos, W. (2006). Dispersal, philopatry and intergroup relatedness: Fine‐scale genetic structure in the white‐breasted thrasher, Ramphocinclus brachyurus . Molecular Ecology, 15, 3449–3458. 10.1111/j.1365-294X.2006.03006.x [DOI] [PubMed] [Google Scholar]
  74. Thomassen, H. A. , Cheviron, Z. A. , Freedman, A. H. , Harrigan, R. J. , Wayne, R. K. , & Smith, T. B. (2010). Spatial modelling and landscape‐level approaches for visualizing intra‐specific variation. Molecular Ecology, 19, 3532–3548. [DOI] [PubMed] [Google Scholar]
  75. Valière, N. , Fumagalli, L. , Gielly, L. , Miquel, C. , Lequette, B. , Poulle, M.‐L. , … Taberlet, P. (2003). Long‐distance wolf recolonization of France and Switzerland inferred from non‐invasive genetic sampling over a period of 10 years. Animal Conservation, 6, 83–92. 10.1017/S1367943003003111 [DOI] [Google Scholar]
  76. Van Strien, M. J. , Keller, D. , & Holderegger, R. (2012). A new analytical approach to landscape genetic modelling: Least‐cost transect analysis and linear mixed models. Molecular Ecology, 21, 4010–4023. 10.1111/j.1365-294X.2012.05687.x [DOI] [PubMed] [Google Scholar]
  77. Vonholdt, B. M. , Stahler, D. R. , Bangs, E. E. , Smith, D. W. , Jimenez, M. D. , Mack, C. M. , … Wayne, R. K. (2010). A novel assessment of population structure and gene flow in grey wolf populations of the Northern Rocky Mountains of the United States. Molecular Ecology, 19, 4412–4427. 10.1111/j.1365-294X.2010.04769.x [DOI] [PubMed] [Google Scholar]
  78. Wang, I. J. , & Bradburd, G. S. (2014). Isolation by environment. Molecular Ecology, 23, 5649–5662. 10.1111/mec.12938 [DOI] [PubMed] [Google Scholar]
  79. Wang, I. J. , Glor, R. E. , & Losos, J. B. (2013). Quantifying the roles of ecology and geography in spatial genetic divergence. Ecology Letters, 16, 175–182. 10.1111/ele.12025 [DOI] [PubMed] [Google Scholar]
  80. Wang, Y.‐H. , Yang, K.‐C. , Bridgman, C. L. , & Lin, L.‐K. (2008). Habitat suitability modelling to correlate gene flow with landscape connectivity. Landscape Ecology, 23, 989–1000. 10.1007/s10980-008-9262-3 [DOI] [Google Scholar]
  81. Zimen, E. , & Boitani, L. (1975). Number and distribution of wolves in Italy. Zeitschrift Für Säugetierkunde, 40, 102–112. [Google Scholar]
  82. Zuur, A. F. , Ieno, E. N. , & Elphick, C. S. (2010). A protocol for data exploration to avoid common statistical problems. Methods in Ecology and Evolution, 1, 3–14. 10.1111/j.2041-210X.2009.00001.x [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

 

Click here for additional data file. (29.7MB, tif)

 

Click here for additional data file. (19.6KB, docx)

 

Click here for additional data file. (15.2KB, docx)

 

Click here for additional data file. (16.8KB, docx)

Data Availability Statement

Due to sensitive information (locations of an endangered species), the data of the present study cannot be made openly accessible.

Articles from Ecology and Evolution are provided here courtesy of Wiley

RESOURCES