The role of acquisition and quantification methods in myocardial blood flow estimability for myocardial perfusion imaging CT

Abstract

In this work, we clarified the role of acquisition parameters and quantification methods in myocardial blood flow (MBF) estimability for myocardial perfusion imaging using CT (MPI-CT). We used a physiologic model with a CT simulator to generate time-attenuation curves across a range of imaging conditions, i.e. tube current-time product, imaging duration, and temporal sampling, and physiologic conditions, i.e. MBF and arterial input function width. We assessed MBF estimability by precision (interquartile range of MBF estimates) and bias (difference between median MBF estimate and reference MBF) for multiple quantification methods. Methods included: six existing model-based deconvolution models, such as the plug-flow tissue uptake model (PTU), Fermi function model, and single-compartment model (SCM); two proposed robust physiologic models (RPM1, RPM2); model-independent singular value decomposition with Tikhonov regularization determined by the L-curve criterion (LSVD); and maximum upslope (MUP). Simulations show that MBF estimability is most affected by changes in imaging duration for model-based methods and by changes in tube current-time product and sampling interval for model-independent methods. Models with three parameters, i.e. RPM1, RPM2, and SCM, gave least biased and most precise MBF estimates. The average relative bias (precision) for RPM1, RPM2, and SCM was ≤11% (≤10%) and the models produced high-quality MBF maps in CT simulated phantom data as well as in a porcine model of coronary artery stenosis. In terms of precision, the methods ranked best-to-worst are: RPM1 > RPM2 > Fermi > SCM > LSVD > MUP >> other methods. In terms of bias, the models ranked best-to-worst are: SCM > RPM2 > RPM1 > PTU > LSVD >> other methods. Models with four or more parameters, particularly 5-parameter models, had very poor precision (as much as 310% uncertainty) and/or significant bias (as much as 493%) and were sensitive to parameter initialization, thus suggesting the presence of multiple local minima. For improved estimates of MBF from MPI-CT, it is recommended to use reduced models that incorporate prior knowledge of physiology and contrast agent uptake, such as the proposed RPM1 and RPM2 models.

Introduction

In the coronary artery disease (CAD) workup, noninvasive tests are recommended to guide diagnosis, risk stratification, and management plans (Fraker and Fihn 2007, Montalescot et al 2013). However, current noninvasive tests show a low positive predictive value for CAD. In a study of patients with stable angina, atypical chest pain, or no symptoms, nearly one-third of patients with a high-risk finding from noninvasive testing showed no obstructive disease in follow-up invasive coronary angiography (ICA) (Patel et al 2014). In the same report, more than half of the patients with low- or intermediate-risk noninvasive test results were found to have no obstructive disease on ICA. These shortcomings highlight the need for a gatekeeper exam that is more effective than existing strategies.

Myocardial perfusion imaging (MPI) is a noninvasive test that can be performed by different modalities, each with advantages and disadvantages, to detect the physiologic evidence of clinically significant ischemia. Nuclear MPI techniques include single photon emission computed tomography (SPECT) and positron emission tomography (PET), with SPECT being more widely available and most commonly used (Duvall et al 2015). MPI-SPECT is often interpreted in terms of relative radiotracer uptake where regions of low signal are suggestive of disease. Despite advancements in SPECT imaging, such as ECG-gating, hybrid SPECT/CT, and improved count sensitivity (Piccinelli and Garcia 2016), PET is generally considered a superior modality for MPI (Ardle et al 2012). PET is currently the preferred modality for noninvasive perfusion quantification with the potential to assess multi-vessel disease (Desiderio et al 2018). However, major disadvantages of PET are cost and limited availability. Another option for MPI is magnetic resonance imaging (MRI) which has better spatial resolution and diagnostic accuracy than SPECT (Chung et al 2010), can provide quantitative perfusion assessment (Schwab et al 2015), and does not expose patients to ionizing radiation. However, lengthy imaging time, operator dependency, limited availability, patient contraindications due to implants or other factors, and cost have prevented MRI from becoming the standard MPI modality (Varga-Szemes et al 2015).

CT has great potential for noninvasive assessment of CAD as it can rapidly and reliably image the coronary arteries, provide measurements of myocardial perfusion (Rochitte et al 2014), and is more widely available than other imaging modalities (Eurostat 2017). Coronary CT angiography can even be used to measure a CT-derived fractional flow reserve (FFR_CT, such as from HeartFlow (Min et al 2015)), although this gives no indication of absolute myocardial blood flow. Whereas single-shot MPI-CT provides relative, qualitative perfusion evaluation suitable for assessment of single-vessel disease, dynamic MPI-CT can be used to quantitatively assess perfusion. Quantitative perfusion evaluation using MPI-CT could serve a similar role as MPI-PET in the assessment of single- and multi-vessel CAD and potentially also in the assessment of microvascular disease (MVD), something not assessed by FFR_CT. The combination of MPI-CT and CT angiography could make CT an ideal gatekeeper to ICA.

Interest in MPI-CT has grown as scanning-related technical challenges have been addressed. Some scanners now have the coverage to acquire whole-heart 3D images in a single heartbeat (Hubbard et al 2016). Challenges with spatial mis-registration have been addressed via the use of registration and spatio-temporal filtering (Huber et al 2013, Muenzel et al 2013, Isola et al 2010, Fahmi et al 2014). Fast rotation speeds and ECG-gating mitigate reconstruction artifacts (Barrett and Keat 2004, Ritchie et al 1992). Energy-sensitive CT minimizes beam hardening artifacts (So et al 2011, Fahmi et al 2016) which can be misconstrued as perfusion defects and lead to false positives. Iterative model-based reconstructions can significantly reduce image noise and enable low x-ray dose protocols (Beister et al 2012, Eck et al 2015, Gramer et al 2012). The current technical landscape creates the potential for CT to become a standard platform for MPI.

A number of techniques exist to quantify myocardial blood flow (MBF) from dynamic, contrast-enhanced scans (Lee 2002). The three categories are: upslope-based methods, model-independent deconvolution methods, and model-based methods. The maximum-upslope method (Peters et al 1987) assumes no contrast agent efflux and thus typically underestimates MBF (Bindschadler et al 2014). Recently, a first pass analysis (FPA) technique has been reported which sums Hounsfield Unit (HU) values over large myocardial regions and assesses contrast agent flux over a short time scale (Hubbard et al 2016, Ziemer et al 2015), thereby improving MBF estimates compared to maximum-upslope. While promising, FPA requires whole-heart coverage scanners and likely depends upon the two image frames chosen for analysis. These upslope-based methods do not capture other tissue properties likely involved in CAD and MVD (i.e., blood volume and vascular permeability). Deconvolution enables one to obtain the tissue impulse response function (IRF) and derive blood flow, mean transit time, and blood volume (Lee 2002). Model-independent deconvolution, such as Tikhonov-regularized singular value decomposition (SVD), mitigates the need for explicit physiologic assumptions but requires careful selection of regularization parameters (Fieselmann et al 2011). However, IRFs produced by SVD can exhibit non-physiologic properties and can significantly bias MBF (Eck et al 2016). Alternatively, model-based flow estimation methods can incorporate model constraints and prior knowledge to address these problems.

The variability in parameter estimates across different processing methods highlights the need to assess techniques. Different algorithms, different implementations of the same algorithm, different commercial software applications, and even upgrades to the same software can yield significantly different quantitative estimates from the same data (Kudo et al 2013, Goh et al 2011, 2007, Eck et al 2016). When deriving MBF from parametric models, a recurring challenge is that of model selection which must consider a number of factors such as data quality, administered contrast agent, and underlying physiologic processes. Reports have described such considerations from theoretical and practical perspectives (Sourbron and Buckley 2012, Schwab et al 2015, Kershaw and Cheng 2010, Luypaert et al 2011, Jerosch-Herold et al 1998). MBF, and other parameters, are estimable if values can be precisely and accurately estimated in the presence of noise. In MRI, a two-compartment exchange model and a two-compartment uptake model have been ruled out due to poor MBF estimability (Schwab et al 2015). Similar studies have ruled out complex models in PET in favor of robust, reduced models (Coxson et al 1997). For MPI-CT, only recently have flow estimation models been compared for appropriateness. In one report (Bindschadler et al 2014), authors evaluated three models: a two-compartment model, an axially-distributed model, and the adiabatic approximation to the tissue homogeneity model. Authors observed similar precision and bias of MBF estimates between models over a range of dose and temporal sampling conditions. Authors concluded that there was no particular advantage between the three models. However, there were important limitations in this study that influence MBF estimability: a single imaging duration was used (30 s) which can vary in clinical practice, residual beam hardening artifacts may have strongly influenced MBF estimates which can be mitigated by dual-energy imaging (So et al 2011, Fahmi et al 2016), and the tested models had similar, limited parameterizations. Further investigation into MPI-CT acquisition and quantification methods can help to elucidate advantages and pitfalls, thus leading to more robust assessment than previous techniques.

In this study, we examine the role of MPI-CT acquisition conditions and quantification methods in MBF estimability, as assessed by precision and bias. We include new robust physiologic models that incorporate prior knowledge of microvasculature and contrast agent extraction, develop a novel semi-analytic model implementation which mitigates parameter estimation problems that arise due to numerical errors, improve upon a physiologic simulator from the literature, and assess a range of acquisition conditions relevant to MPI-CT. Our principal approach is to use a model-to-models test whereby we generate time-attenuation curves (TACs) from a physiologic model and CT simulator and then determine the ability of multiple computational methods to estimate the known simulated flow. A preliminary report indicated that some methods can significantly overestimate flow values (Eck et al 2016), leading us to this more thorough examination of MBF estimability. As patient x-ray dose is an issue in CT, we investigated relevant acquisition parameters including x-ray tube current-time product, sampling interval, and scan duration. Understanding the role of acquisition parameters and MBF quantification methods can guide the development of low-dose scanning protocols as well as processing for robust and accurate MPI.

Computational Methods for Myocardial Blood Flow Estimation

Model-based MBF estimation

We evaluate eight perfusion models: six from the literature and two newly proposed. We use the term “MBF” to refer to the amount of blood flow to a mass of myocardial tissue, given in units of mL/min-100g. MBF is estimated by iteratively optimizing parameters until an estimated model time-concentration curve best fits the measured tissue time-concentration curve in the least squares sense. The model time-concentration curve, C_m(t) (mg/mL), is calculated by convolution of a measured arterial input function (AIF), C_a(t) (mg/mL), with the unit-less model impulse response function (IRF) scaled by MBF, R_MBF(t) (mL/min-100g), and multiplied by a tissue density scaling, ρ (g/mL). Note that HU values in MPI-CT change linearly with contrast agent concentration (Fahmi et al 2016). HU values from measured TACs are used as a surrogate measure for contrast agent concentration after subtraction of a pre-contrast baseline value. Mathematically, the convolution is given by the integral:

$$C_m\left(t_i\right)=\underset{t_1}{\overset{t_i}{{\displaystyle \int }}}{C}_a\left(\tau \right)\cdot \rho \cdot R_{MBF}\left(t_i-\tau \right)\text{d}\tau ,$$ (1)

where t_i is the time of a sampled data point ranging from time index i=1,2,…, N for N scans. We used ρ=1.05 g/mL (Vinnakota and Bassingthwaighte 2004).

We briefly describe the eight tested perfusion models for R_MBF(t). Models 1–7 can be described as reduced forms of two-region, intravascular-extravascular contrast agent exchange models (Figure 1) in which both regions contribute to the CT signal. In the adiabatic approximation to the tissue homogeneity model (AATH), contrast agent, also referred to as indicator, enters the intravascular compartment (red) after time delay, t_d, from the AIF. Assuming plug flow, contrast agent moves through the region in infinitesimally small, discrete increments from left to right with characteristic intravascular transit time (ITT) related to MBF and v_b, ITT=v_b/MBF, in units of mL/g and s, respectively. Before leaving the intravascular space, a proportion of contrast agent, described by the extraction fraction, E, extravasates into the well-mixed extravascular space. The remaining intravascular contrast agent portion then leaves the observation region. The extravascular contrast agent then exchanges back into the intravascular region and washes out with characteristic decay constant, k=(E∙MBF)/v_e in units of s⁻¹, where v_e is the extravascular volume in units of mL/g. An alternative two-region model, the two-compartment exchange model (2CXM), consists of two well-mixed regions with exchange governed by the permeability-surface area product (PS, units of mL/min-g). Simplifications of the two-region models lead to the other models tested. These include: (A) Contrast agent does not wash out of the extravascular space, giving the plug-flow tissue uptake model (AATH → PTU) and compartmental tissue uptake model (2CXM → CTU); (B) Physiologic constraints on ITT and E give proposed robust physiologic models (AATH → RPM1, RPM2); (C) The observation region is a single, well-mixed region, giving the single-compartment model (2CXM → SCM). Impulse response models and free parameters are listed in Table 3 and described in the Appendix.

Figure 1.

Conceptual representations of the AATH and 2CXM models (top-left, bottom-left) and their corresponding impulse response functions (top-right, bottom-right). In the AATH model (top-left), contrast agent passes into and through the intravascular space (red), exchanges with the well-mixed extravascular space (blue), and exits the observation region (grey) giving rise to an impulse response function (top-right) with a box-like intravascular portion and exponential decay extravascular portion. In the 2CXM model (bottom-left), the intravascular compartment is well-mixed and exchanges with the extravascular space according to the rate described by PS which gives rise to an impulse response that is the sum of two exponentials (bottom-right). The y-axes of the impulse response function plots denote normalized indicator concentration scaled by MBF which has units of mL/min-100g. This conceptual representation is adapted from (Sourbron and Buckley 2012).

Table 3.

Impulse response models and free parameters.

Model	Free parameters
AATH	td, MBF, ITT, E, k
2CXM	td, A, B, k+, k−
PTU	td, MBF, ITT, E
CTU	td, MBF, E, k
RPM1	td, MBF, k
RPM2	td, MBF, k
SCM	td, MBF, k
Fermi	td, MBF, t0, k

Model-independent MBF estimation

We applied two model-independent techniques from the literature, singular value decomposition (SVD) and maximum-upslope (MUP), giving a total of ten quantitative methods evaluated in this work. The SVD method has been previously applied to MPI-CT and uses Tikhonov regularization where the regularization factor is determined by the L-curve criterion (LSVD) (Fahmi et al 2016). We use an established method to estimate the maximum-upslope which has been applied to MPI-CT (Bindschadler et al 2014). More details are in the Appendix.

Implementing the impulse response models

For all impulse response models, the convolution was implemented semi-analytically. This approach minimizes numerical errors which can appear when using other methods such as discrete convolution. The AIF is expressed as a piecewise polynomial, i.e. a sequence of polynomials defined for adjacent time intervals to pass through the measured data values (De Boor 1978). Model output is a sum of the convolution integrals, one for each polynomial piece. Each convolution integral is calculated by analytically integrating the product of the polynomial and the IRF for a selected model. Parameter estimation was performed using an unweighted sum-of-squared difference objective function and gradient-based optimization algorithm with analytically determined gradients. Implementation details are in the Appendix.

Experimental Methods

Physiologic simulator

The physiologic simulator was adopted from the literature (Bindschadler et al 2014). It simulates the concentration-time dynamics of a contrast agent as it passes through the large blood pools in the heart and eventually through the myocardial tissue. The simulator assumes constant flow and includes dispersion and delay between large blood pools. The input to the simulator is the iodine concentration in the right atrium modeled as a gamma-variate function (see Figure 2). Downstream toward the myocardium, large blood pools, i.e. the right ventricle, left atrium, left ventricle, and coronary artery, exhibit delay and dispersion as contrast agent passes from one blood pool to another. Within the myocardium there are 20 flow-paths, each containing an arteriole, capillary, and venule, and with different flow rates ranging from 0.05 to three times the mean flow to the myocardium, as sampled from a lagged normal density curve. Capillary permeability to the contrast agent is flow-dependent, as previously described (Appendix of Bindschadler et al 2014). This generalized physiologic simulator can generate data with dispersive effects, time delays, varied cardiac output, varied coronary blood flow, and varied MBF.

Figure 2.

Comparison of in vivo porcine TAC measurements to the standard and modified physiologic simulator. (a) CT image with MBF map overlay from RPM1 is shown for a pig with partial balloon-induced LAD coronary artery occlusion (FFR=0.59). Large ROIs are drawn in the LV cavity, normal, and flow-deprived myocardia in (a), giving AIF and myocardial TACs, respectively in (b). With MBF∝MBV², the modified physiologic simulator generates TACs similar to measured porcine data, as shown in (c), with the exception of recirculation effects. With the standard simulator having fixed MBV, there is little observed change between TACs at significantly different MBF levels (d). MBF is in units of mL/min-100g. TACs are shown after subtraction of baseline HU values.

We modified the simulator above to account for changes in vascular volume at different perfusion levels. It is known that MBF is mediated by changes in vascular tone and resistance, with dilated vessels leading to higher MBF; for example, it has been observed that MBF is proportional to the square of myocardial blood volume (MBV) (Wu et al 1992). We include this relationship to adjust arteriole, capillary, and venule volumes. We changed capillary volume to ${\text{V}}_{\text{cap}}={\beta }_{\text{cap}}\sqrt{\text{MBF}}$, arteriole volume to ${\text{V}}_{\text{art}}={\beta }_{\text{art}}\sqrt{\text{MBF}}$, and venule volume to ${\text{V}}_{\text{ven}}={\beta }_{\text{ven}}\sqrt{\text{MBF}}$ Proportionality constants were chosen such that at MBF=100 mL/min-100g we obtained the same values as in (Bindschadler et al 2014) i.e., V_art= 0.05 mL/g V_cap=0.016 mL/g and V_ven= 0.06mL/g. This provides β_art= 0.005, β_cap= 0.0016, and β_ven= 0.006, all with units $\sqrt{\text{min}\cdot 100\text{g}/\text{mL}}\cdot \text{mL}/\text{g}$.

The concentration of the contrast agent in the right ventricle (RV) was driven by a gamma-variate function similar to the observed pig data (see Figure 2), except without recirculation:

$$C_{RV}\left(t\right)=\{\begin{array}{cc}0,& t<t_{d,RV}\\ y_{\text{max}}{\left(\frac{t-t_{d,RV}}{t_{peak}}\right)}^{\alpha }\text{exp}\left(\alpha -\alpha \left(\frac{t-t_{d,RV}}{t_{peak}}\right)\right),& t<t_{d,RV}\end{array}$$ (2)

with parameters set to y_max=270 HU, t_peak=7 s, and t_d,RV=0 s (Bindschadler et al 2014). The parameter α determines the width of the RV TAC which is varied in AIF simulation experiments. Larger α corresponds to a narrower TAC.

Digital MPI-CT phantom

We created simulated dynamic perfusion data with realistic CT noise using the physiologic simulator described above and a CT simulator, giving what we call the digital MPI-CT phantom. The numerical CT simulator (Radonis software, Philips Research and Development, Hamburg, Germany) has been applied in previous publications (Riviere and Vargas 2008, Hansis and Shao 2011) and models a realistic CT scanner (Brilliance 64, Philips), with cone beam source, finite width detector grid, x-ray pre-filtration, and Poisson noise sampling. In this work, we used only 70 keV photons in the CT simulation to generate a true mono-energetic MPI-CT data set in order to avoid confounding effects of beam-hardening artifacts. Line integrals are computed based on analytic object geometries with defined mass-attenuation coefficients from NIST (Hubbell and Seltzer 1995). The numerical CT simulator accounts for Poisson noise in the projections but does not include x-ray scatter or electronic noise. The digital MPI-CT phantom is anthropomorphic and contains major structures in the field of view, i.e. the left ventricle, right ventricle, myocardium, ribs, and spine. Homogeneous contrast agent dynamics were generated in the right ventricle, left ventricle, descending aorta, and myocardium using the physiologic simulator described above.

Simulation experiments and analysis

MPI-CT simulation experiments were performed to assess the role of acquisition conditions on MBF estimability. Five simulation experiments, with a total of 11 unique data conditions, were performed with independent variables varied as indicated in Table 4. Nominal simulation conditions used an RV TAC α=2.2 (LV FWHM=13 s), 40 s imaging duration, 1 s sampling interval, 100 mAs tube current-time product, and MBF=100 mL/min-100g. The noise level experiments were selected to evaluate the effect of changes in x-ray dose on MBF estimability. The nominal tube current-time product of 100 mAs was selected based on previous work (Fahmi et al 2016). The 50 mAs and 200 mAs tube current-time products led to image SNR values in the LV myocardium at peak enhancement of 8.6 and 17.1, respectively, within the range evaluated in a previous study (Figure 4 of (Eck et al 2015)). Imaging duration conditions were selected to evaluate the range of possible scan durations given that MPI-CT acquisitions are typically ECG-gated at once-per-heartbeat for 30–50 scans. The sampling interval conditions were selected based on potential dose reduction strategies where data could be acquired every-other heartbeat or every-third heartbeat given a 60 beat-per-minute heart rate. The AIF conditions were selected to assess the effect of AIFs with different widths which can vary in patients due to variability in cardiac output or contrast agent injection rates. The simulated MBF conditions were selected to span a range from ischemic (MBF=50 mL/min-100g), to normal at-rest (MBF=100 mL/min-100g), and normal at-stress (MBF=200 mL/min-100g).

Table 4.

Simulation experiments and conditions.

Simulation Experiment	Conditions (units)
Noise level (Tube current-time product)	[50, 100, 200] mAs
Imaging duration	T=[30, 40, 50] s
Sampling interval	Δt=[1, 2, 3] s
Arterial input function width	α=[1.1, 2.2, 4.4] FWHM=[18, 13, 10] s
MBF	MBF=[50, 100, 200] mL/min-100g

The same simulated data and results were used for the underlined conditions to serve as a reference as individual imaging parameters varied.

The full-width at half-max (FWHM) of the left ventricle enhancement curve corresponds to the α value, e.g. α=1.1 has FWHM=18 s.

Figure 4.

Median and interquartile range of the MBF estimates for quantification methods under different acquisition conditions. Each row indicates the effects of change in a given acquisition condition (first: tube current-time product; second: imaging duration; third: sampling interval; fourth: AIF FWHM). For each quantification method, bar heights and error bars depict the median and interquartile range (25% to 75%), respectively, of MBF estimates. The red dashed horizontal lines indicate the known simulated MBF=100 mL/min-100g. MBF precision generally improves as the tube current-time product increases, imaging duration lengthens, and sampling interval shortens. Quantification methods marked with * indicate median and/or 75% MBF estimate (upper error bar) is greater than 200 mL/min-100g. Aside from the condition of interest, nominal simulation parameters were used. MBF is in units of mL/min-100g.

Simulations and analyses were conducted as follows. Under each condition, a digital MPI-CT phantom data set was generated and subsequently processed by the ten quantification methods. LV myocardium was manually segmented once in the digital phantom and the same mask was used for all analyses. Spatial smoothing was applied to voxels within the mask using a 5×5 pixel averaging kernel (3.4×3.4 mm) to reduce noise prior to MBF estimation. Voxels on the edge of the myocardium were not averaged with non-myocardium voxels and were thus somewhat noisier. No temporal smoothing was performed. Each voxel was then processed as an individual TAC. In total, there were 33,605 TACs for this simulation analysis (11 unique conditions × 3,055 voxels per condition).

Perfusion SNR (SNR_P) was used to quantify the overall quality of TACs. SNR_P for each condition was calculated from the average TAC over all of the myocardium, I_mean(t), and the noise standard deviation at the initial time point, σ_noise,

$$SN{R}_P=\frac{\text{max}\left({\text{I}}_{mean}\left(t\right)\right)-{\text{I}}_{mean}\left(t_1\right)}{{\sigma }_{noise}}.$$ (3)

For each measured TAC, MBF was estimated by iteratively optimizing model parameters in order to minimize the unweighted least-squares objective function. The function “fmincon,” a gradient-based, interior-point optimizer from the MATLAB Optimization Toolbox (Mathworks.com, 2016), was used to optimize model parameters. The following stopping criteria for the optimizer were used: default first-order optimality tolerance (“OptimalityTolerance”=1e-6), default constraint tolerance (“ConstraintTolerance”=1e-6), and strict parameter step size tolerance (“StepTolerance”=1e-20). If a maximum number of objective function evaluations or iterations were reached (3,000) the optimization was re-initialized at another randomized set of initial parameters and repeated until the tolerance criteria were met. Parameters were constrained to feasible values, e.g. non-negative MBF, non-negative decay constants, non-negative t_d and ITT, and k₊>k_-. Optimal parameters were recorded for each TAC and MBF values were analyzed.

MBF estimability was assessed by the precision and bias of MBF estimates. Precision was assessed by the interquartile range, IQR, calculated by taking the difference between the 75^th and the 25^th percentile estimates. Bias was assessed by the median estimate minus the known, true simulated MBF. Relative precision was also used to assess variation in MBF estimates and was calculated by dividing the IQR by the median MBF and expressed as a percentage. Robust statistics, such as median and IQR, were used rather than mean and standard deviation to mitigate the effects of outlier flow values which could be similarly rejected in visual and quantitative analysis of perfusion maps. Since the myocardium was uniformly perfused in simulations, any variation in MBF estimates across the myocardium was due to the effects of data acquisition, image reconstruction, and/or quantification method.

Parameter initialization experiment

An experiment was performed to evaluate the presence of local minima and whether final parameter estimates were dependent on initialization. A subset of 50 voxels was randomly selected from the digital phantom myocardium under nominal simulation conditions. The TAC from each voxel was fit using impulse response models with 200 different parameter initializations giving 200 sets of estimated parameters. Parameter initializations for each model were randomly selected and spanned a broad range of physiologically relevant values. Best-fit parameters with the smallest sum-of-squared differences were recorded as the optimum. Estimated parameters from other initializations were compared to the optimum and considered to have converged if they were within a defined tolerance level, i.e. within 0.1 s for time-related parameters, 1 mL/min-100g for MBF, 0.01 for extraction fraction, and 0.01 s⁻¹ for decay parameters. We assessed optimum convergence by the percent of parameter initializations that converged to the optimum, e.g. if 180 parameter initializations converged to the optimum and 20 initializations terminated elsewhere, a value of 90% would be recorded. This process was repeated for all 50 TACs and the average optimum convergence was recorded. Details regarding parameter initialization are provided in Appendix 6 of (Eck 2018).

Arterial input function and model output experiment

The ability to distinguish model tissue curves after convolution with the AIF was assessed. The fast-changing intravascular portion of IRFs may not be excited by the low-frequency content of AIFs present in MPI-CT, prompting this assessment. Two AIFs were used, i.e. a typical AIF (FWHM=13 s, α=2.2) and a hypothetical narrow AIF (FWHM=4 s, α=100). The AATH model was used to generate IRFs and corresponding model output curves for both AIFs. Three sets of parameters were used with MBF values spanning a range from healthy resting MBF to healthy, pharmacologically-induced stress MBF (Prior et al 2012): [t_d=1 s, MBF=100 mL/min-100g, ITT=2 s, E=0.6, k=0.05 s⁻¹]; [t_d=1 s, MBF=200 mL/min-100g, ITT=1 s, E=0.3, k=0.05 s⁻¹]; [t_d=2.5 s, MBF=400 mL/min-100g, ITT=0.5 s, E=0.15, k=0.05 s⁻¹].

In vivo experiment, porcine model of coronary stenosis

A representative porcine MPI-CT data set was used for comparison of the standard and modified physiologic simulator as well as for comparison to MBF maps from the digital phantom. We used a percutaneous, closed-chest porcine model of coronary stenosis guided by fractional flow reserve (FFR) (Fahmi et al 2016). MPI-CT data was acquired using a spectral detector CT scanner (SDCT, prototype of the IQon product, Philips) while the pig had a partial angioplastic, balloon-induced stenosis in the left anterior descending (LAD) coronary artery with FFR=0.59. Acquisition conditions used a tube voltage of 120 kVp, tube current-time product of 100 mAs per scan, 45 scans, 4 cm coverage, 0.27 s rotation speed, ECG-gating at 45% R-R interval (end systole), 360 degree, 120 mm field-of-view, ventilator off to avoid breathing motion, and 22.6 mSv total effective dose. Starting 4 s before initiation of CT scans, 20 mL of iodinated contrast agent (Omnipaque 350, 350 mg/mL Iodine) was intravenously injected at 5 mL/s and followed by 20 mL of saline. Virtual mono-energetic 70 keV images were reconstructed using a projection-based material decomposition (Fahmi et al 2016). Non-rigid registration (Modat et al 2010) was applied to reduce motion between dynamic frames. Myocardium was segmented using commercial research software (QMass research version 25 June, 2013; http://www.medis.nl/). Spatial noise was reduced using a 5×5 pixel (1.2×1.2 mm) averaging kernel on the myocardium. Pig MPI-CT data were used to evaluate whether the modified physiologic simulator with changing blood volume more accurately represents observed data than the standard physiologic simulator. MBF maps were generated using all 10 quantification methods and compared to simulation results with regard to trends between quantification methods.

Results

Standard vs modified physiologic simulator

The modified physiologic simulator matches the pig MPI-CT data more closely than the standard simulator (Figure 2). The separation between ischemic and healthy myocardium in pig is much larger than that observed from the standard physiologic simulator with fixed MBV. Furthermore, the standard simulator provides TACs that saturate above approximately MBF=150 mL/min-100g. Peak enhancement for the standard simulator at MBF=500 mL/min-100g was only 11% greater than peak enhancement at MBF=150 mL/min-100g, whereas the peak enhancement for the modified simulator at MBF=500 mL/min-100g was 78% greater than the value at MBF=150 mL/min-100g. With the flow-dependent MBV relationship in the modified simulator (MBF ∝ MBV²), we observed a larger separation of healthy and ischemic TACs which more closely matched the pig data.

Digital MPI-CT phantom experiments

Figure 3 shows representative fits of models to TACs from three different voxels in the digital phantom at nominal acquisition conditions and simulated MBF=100 mL/min-100g. The average SNR_P over the myocardium was 3.3 before 5×5 pixel spatial averaging. TACs shown in Figure 3 are after spatial averaging in which average SNR_P=10.3. Although AATH has the best visual fit to data and the lowest sum-of-squared difference value, MBF estimates vary widely, i.e. from 81 to 227 mL/min-100g. PTU fits the data nearly as well as AATH, although MBF estimates also vary widely, i.e. from 80 to 147 mL/min-100g. Of the three models, RPM1 has the poorest visual fit in the regions of rapid upslope and contrast agent wash-out, although MBF estimates tend to be much closer to the actual flow than PTU and AATH, i.e. from 103 to 105 mL/min-100g, thus suggesting an improvement in both accuracy and precision.

Figure 3.

Model fits to different noise realizations and variation of MBF estimates. Best-fit curves of AATH, PTU, and RPM1 to TACs from three different voxels in the digital phantom are shown. The AATH model visually fits each curve very well but has a wide variation in estimated MBF. The PTU model has a slightly poorer fit to data but has less variation in estimated MBF. RPM1 has a narrow range of MBF estimates at the cost of a poorer fit to data. Nominal parameters were used in the simulation. MBF is in units of mL/min-100g.

Figure 4 shows MBF estimates for all 10 quantification methods as a function of noise level (tube current-time product), imaging duration, sampling interval, and AIF width, as obtained from the digital MPI-CT phantom. There are notable differences in bias (median estimate minus actual MBF=100 mL/min-100g) and precision (IQR of estimates). Overall, we observe that 5-parameter models (2CXM, AATH) are severely biased and imprecise across all tested conditions, thus indicating that they are inappropriate. Two of the 4-parameter models (CTU, PTU) are sensitive to acquisition conditions, whereas the other 4-parameter model, Fermi, is more robust. As a result of these observations, 2CXM, AATH, CTU, and PTU are eliminated from further analysis of precision and bias. For other methods, we observe trends in precision and bias across acquisition conditions. As tube-current time product was reduced (top-row), precision degraded but the effect on bias differed between quantification methods. For SCM, RPM1, RPM2, Fermi, and MUP, median MBF was unchanged across the mAs levels, indicating robustness to noise. The median MBF for LSVD increased by 5% from 200 mAs to 50 mAs, indicating its bias is dependent on noise level. Across imaging durations (second row), shorter duration worsened precision and bias compared to longer durations. Among model-based methods, RPM1 had the best relative precision at 30 s imaging duration (10%) and had the least change in median MBF (22%) when the duration was changed from 50 s to 30 s. At the 50 s duration, RPM1 and RPM2 were least biased among the model-based methods (2%). Changes in sampling interval (third row) affected quantification methods to varying degrees; the 3-parameter models (SCM, RPM1, RPM2) had slightly degraded precision and unchanged bias, LSVD had a large change in relative precision from 13% at 1 s to 25% at 3 s, and MUP was robust to sampling interval. Changes in the AIF width (bottom row) did not have significant effects on the MBF bias or precision. Overall, regarding the effect of acquisition conditions on MBF bias and precision, imaging duration had the greatest effect on the model-based methods, sampling interval had the largest effect on LSVD, and noise level (tube current-time product) had the largest effect on MUP.

Figure 5 and 6 show model fits and MBF estimates at different simulated MBFs. In Figure 5, TACs at different simulated MBFs share characteristics with TACs observed in pig experiments; at higher MBF levels, e.g. 200 vs 50 mL/min-100g, TACs have greater peak enhancement and more rapid wash-out (see Figure 2(b)). Similar to Figure 3, a better model fit does not indicate a more accurate and precise MBF estimate. Although RPM1 had a slightly worse fit to data than PTU and AATH, estimates were more precise (Figure 6). With the exception of 2CXM, all quantification methods properly identified increasing MBF although with different amounts of bias. The 3-parameter models (SCM, RPM1, RPM2) were least biased and most precise.

Figure 5.

Model fits to TACs obtained from the same voxel location at multiple simulated MBF levels. TACs are shown after 5×5 pixel spatial averaging. (Left-to-right) Simulated MBF values are 50, 100, and 200 mL/min-100g, and the SNR_P values are 7.7, 10.3, and 16.3, respectively. Ranking models by quality of fits, as assessed visually and from sum-of-squared differences, gives AATH>PTU>RPM1. However, RPM1 generally provides more precise MBF estimates than PTU or AATH, as shown in Figure 6. Aside from MBF, nominal simulation parameters were used.

Figure 6.

Median and interquartile range of MBF estimates from quantification methods at different simulated MBF levels. Bar heights for each quantification method indicate the median MBF estimated in the myocardium. The red dashed horizontal lines indicate the known simulated MBF values. With the exception of 2CXM, all methods have median MBF estimates that increase with simulated MBF. Aside from simulated MBF, nominal simulation parameters were used. The * indicates that the median and/or 75% MBF estimate was greater than 400mL/min-100g.

Figure 7 shows the overall bias (median MBF – simulated MBF) and precision (MBF IQR) characteristics of quantification methods across the simulation conditions shown in Figure 4 and Figure 6. In the left panel, all ten quantification methods are shown. Note that CTU, PTU, 2CXM, and AATH, had relative MBF precision >100% of median MBF in at least one condition. In the right panel, six of the better-performing models are shown, all with relative precision <25% (SCM, RPM1, RPM2, Fermi, MUP, LSVD). Of these six methods, model-based methods had better average relative precision than model-independent methods (≤10% vs >15%). Fermi had the poorest bias, over-estimating MBF on average by 67%. Model-independent methods were also significantly biased, underestimating MBF on average by 51% and 18% for MUP and LSVD, respectively. The 3-parameter models were least biased and most precise. Ranked in order of best-to-worst for average relative precision, models were RPM1 (7.2%), RPM2 (8.5%), and SCM (9.8%). Ranked in order of best-to-worst for average magnitude of the relative bias, models were SCM (10.3%), RPM2 (10.6%), and RPM1 (11.0%).

Figure 7.

MBF precision and bias characteristics of quantification methods across all 11 simulation conditions. Units are mL/min-100g. (Left) Some model-based methods, i.e. 2CXM, AATH, CTU, and PTU, have poor absolute precision (>100 mL/min-100g) and relative precision (>100%) in at least one condition. (Right) Over all tested conditions, Fermi, the 3-parameter models (RPM1, RPM2, SCM), and both model-independent methods (MUP, LSVD) had acceptable absolute precision (<25mL/min-100g). RPM1, RPM2, and SCM were overall less biased and more precise than Fermi, MUP, and LSVD.

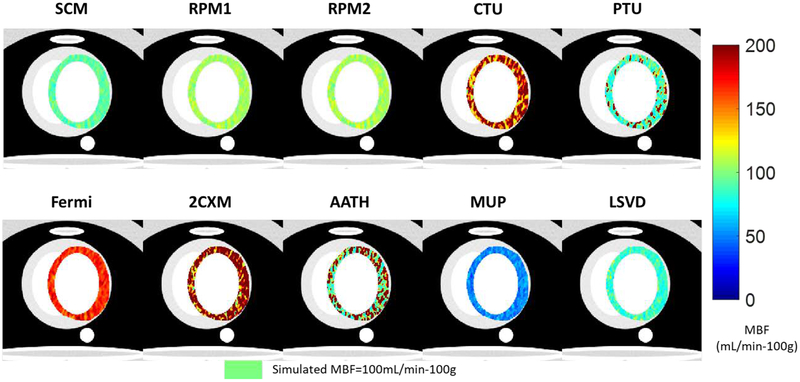
Figure 8 shows MBF maps obtained by the ten quantification methods in digital MPI-CT phantom data at nominal conditions. General trends from the precision and bias assessments (Figure 4, Figure 6, and Figure 7) are observed. The 3-parameter models (SCM, RPM1, RPM2) were closest to the simulated MBF value and maps were least noisy. CTU over-estimated MBF and had an extremely noisy map. PTU had median MBF near the simulated value but with a noisy map. Fermi had little noise in its map but significantly over-estimated MBF. Model-independent methods (MUP, LSVD) had relatively little noise in their maps but under-estimated MBF. The 5-parameter models (2CXM, AATH) produced extremely noisy maps and overestimated MBF. Overall, the 3-parameter models and model-independent LSVD produced high-quality MBF maps.

Figure 8.

MBF maps estimated on digital phantom MPI-CT data. Simulated MBF was uniform in the myocardium with MBF=100 mL/min-100g (light green color) using the physiologic simulator. From left to right: (Top) SCM, RPM1, RPM2, CTU, PTU (Bottom) Fermi, 2CXM, AATH, MUP, LSVD. The same color bar is used for all images. Nominal acquisition parameters were used.

Parameter initialization experiment

Differences between models in terms of convergence to optimal, best-fit parameters were observed. SCM, RPM1, and CTU had optimum convergence percentages of 100%. RPM2 and PTU gave >99% optimum convergence. Other models differed in their tendency terminate in local minima. Optimum convergence percentages were: AATH (98%), Fermi (96%), and 2CXM (61%). Therefore, 2CXM was the most sensitive to parameter initialization. However, even when optimal parameters were obtained they did not necessarily provide accurate MBF; for 2CXM, the median MBF estimate from the best-fit optima was 321 mL/min-100g, much higher than the known, simulated MBF of 100 mL/min-100g.

Arterial input function and model output experiment

Figure 9 demonstrates that typical AIFs blur high-frequency components of IRFs which may contribute to the poor MBF estimability of some models. Three unique IRFs from the AATH model with MBFs ranging from 100 to 400 mL/min-100g give nearly identical model outputs when excited by the typical broad AIF. Models which simultaneously estimate multiple parameters related to the fast-changing intravascular portion of the IRF would thus have poor MBF estimability in this case. A hypothetical narrow AIF led to distinct model outputs; however, this AIF could not clinically be created with a venous injection of contrast.

Figure 9.

AIF properties and MBF estimability. The typical AIF does not excite fast dynamics of IRFs, thus leading to poor MBF estimability in some models. (a) A typical AIF is plotted alongside a hypothetical narrow pulse. (b) IRFs from the AATH model are shown with different MBF, time delay, intravascular transit time, and extraction fraction. The y-axis denotes normalized indicator concentration scaled by MBF. (c) TACs obtained by convolving IRFs in (b) with the typical AIF in (a). (d) TACs after convolution with the narrow AIF in (a) that excites fast dynamics. Model output curves from the three unique impulse responses are nearly identical with the typical “broad” AIF, thus rendering MBF not estimable in the presence of noise. The high-frequency content of the narrow AIF leads to distinguishable TACs.

In vivo experiment, porcine model of coronary stenosis

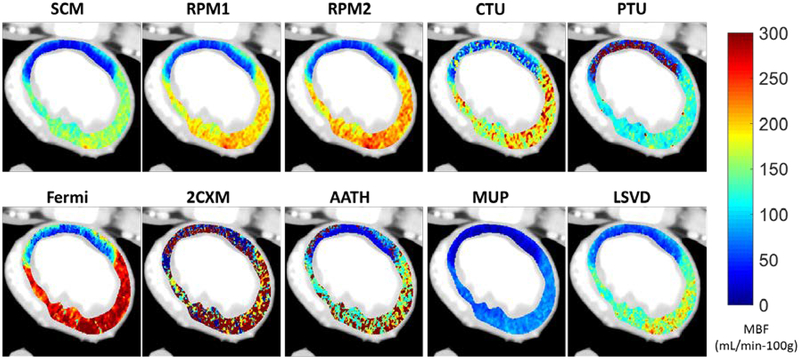
Figure 10 shows MBF maps from the porcine model with partial LAD occlusion (FFR=0.59). Similar overall trends can be observed as compared to the digital phantom perfusion maps shown in Figure 8. Models with more than three free parameters are generally noisier than the 3-parameter models, with the exception of the Fermi model. PTU yields MBF estimates in healthy myocardium with relatively low noise, however the estimates in the ischemic myocardium are noisy. Fermi produced high MBF estimates relative to SCM, RPM1, and RPM2, which was also observed in simulations. MUP and LSVD under-estimated MBF relative to 3-parameter models, also observed in simulations. Overall, the 3-parameter models (SCM, RPM1, RPM2), 4-parameter Fermi model, and model-independent methods (LSVD, MUP) have little noise in their MBF maps and clearly delineate healthy and ischemic flow distributions.

Figure 10.

MBF maps estimated in a porcine ischemic model at FFR=0.59. MBF estimates follow relative trends as observed in simulation experiments. A flow deficit in the large LAD myocardial territory is clear with all methods, except 2CXM, and a transmural perfusion gradient can also be observed with RPM1, RPM2, and Fermi.

Discussion

We found that accurate and precise MBF estimates from MPI-CT data were best obtained using 3-parameter models that include prior information regarding tissue physiology and contrast agent extraction (RPM1, RPM2). Models with more than three free parameters and the model-independent quantification methods had significant bias and/or poor precision across the range of acquisition and physiologic conditions. With a sufficiently long imaging duration, at least 40 s, the 3-parameter models, i.e. SCM, RPM1, and RPM2, were robust to decreases in x-ray exposure, lengthened sampling intervals, and broader arterial input functions, thus providing the lowest overall MBF bias (≤11% on average) and best overall precision (<10% on average). RPM1 provided the best relative precision in every condition which translated to low-noise MBF maps. The 3-parameter models also provided low-noise MBF maps in in vivo pig data with clear delineation of a flow deficit.

MBF estimability was dependent on acquisition condition and quantification method which has implications for protocol design and dose reduction. For model-based methods, imaging durations greater than 30 s were important for estimating parameters related to contrast agent extraction and wash-out. In order to minimize x-ray dose without sacrificing MBF precision and accuracy, dose reduction in model-based methods should retain longer imaging duration and either use fewer image frames or lower exposure per image frame. Regarding the model-independent methods, LSVD and MUP, reductions in imaging duration did not hamper MBF precision or accuracy whereas longer sampling intervals or lower tube current-time product degraded precision. Therefore, imaging duration should be minimized when processing data with LSVD or MUP as long as the baseline myocardium HU and peak myocardium HU are captured.

There is a bias toward underestimation among the best models as the simulated flow is increased (Figure 6). A similar phenomenon has been observed in PET imaging where low order models, e.g. one-tissue compartment model with spillover correction having three parameters, provide uptake parameter estimates which are approximately linearly proportional to MBF at low flows but nonlinear at higher flows (Lortie et al 2007). An accepted solution in PET is to correct uptake values for the flow-dependent extraction fraction via a characterized relationship, an option which could be followed in MPI-CT. In terms of the RPM1 and RPM2 models, the underlying issue in our MPI-CT data is that the lumped parameter extraction fraction does not account for reduced extraction at high flow rates. Simply adding another free parameter would not be advisable as every additional free parameter contributes to imprecision in the presence of noise. Correcting values after the fact might be the preferred option in order to maintain precise MBF estimation.

We observed advantages and disadvantages of model-independent techniques. Maximum-upslope was found to provide relatively precise MBF estimates but significantly underestimated MBF, as seen in a previous report (Bindschadler et al 2014). LSVD also tended to underestimate MBF, possibly due to overly aggressive regularization of the impulse response function. The L-curve criterion in LSVD provides a heuristic for choosing the Tikhonov regularization parameter but does not guarantee selection of a physiologically relevant value. Under-estimation in LSVD may be due to the low frequency content of the AIFs which will influence LSVD to restrain the IRF to smooth forms. This behavior of LSVD differs from our previous preliminary study in pig experiments in which LSVD tended to overestimate MBF (Eck et al 2016). However, CT imaging artifacts, such as motion (Pack et al 2016), were more prevalent in that study. Such artifacts may have introduced high-frequency noise in the AIF which would not have been filtered by LSVD, leading to high-frequency oscillations in the IRF and over-estimation of MBF. Therefore, it may be that LSVD under-estimates MBF under conditions with minimal imaging artifacts but may over-estimate MBF when artifacts are increasingly severe.

The low frequency content of AIFs appears to hamper parameter estimation when modeling the fast intravascular portion of IRFs. It was observed that realistic input functions can lead to model outputs that are nearly indistinguishable across a broad physiologic range of flow values. Although the narrow input function alleviated this effect, it is not possible to produce such an input in practice as venous injections of contrast agent are dispersed before reaching the left ventricle and myocardium. In order to estimate MBF using models that contain fast intravascular kinetics, constraints on model parameters are required, such as those in RPM1 and RPM2.

We observed that models were generally robust to parameter initialization. All models except 2CXM had generally favorable convergence to optimal parameters. Conversely, the poor convergence of 2CXM is suggestive of multiple local minima. Even when analyzing only the best-fit 2CXM parameters, MBF was still biased and imprecise, suggesting fundamental limitations of the model. Furthermore, the use of robust statistics in this work, i.e. median and interquartile range, helps ensure that observed trends in MBF precision and bias across the simulations are due to model behaviors and not due to the parameter optimization procedure.

The use of additional prior information or model constraints could improve parameter estimability and/or enable assessment of other tissue properties. Model parameters could be estimated other means, as has been done with time delay (Cheong et al 2003), and used as constraints. The use of blood pool contrast agents (Hainfeld et al 2006, Kroft and de Roos 1999, Jerosch-Herold et al 1999) would eliminate extraction fraction and wash-out decay constants along with the uncertainty they introduce into parameter estimation, which may significantly improve MBF accuracy and precision. Prior information on parameter values could be used with a Bayesian approach, such as max a posteriori estimation, as has been applied in PET cerebral perfusion (Rizzo et al 2013), acting as a softer constraint than the rigid E=0.6 in RPM1 and RPM2 used in this work. The use of other objective functions, such as weighted sum of squares, could also improve parameter estimates by incorporating knowledge of artifacts or noise magnitude. However, careful selection of weights is important, as improper weights can negatively impact parameter estimates (Muzic and Christian 2006).

We note the limitations of this work. First, the majority of analyses were carried out on simulation data which will differ from in vivo data. While the physiologic simulator accounts for aspects such as myocardial flow heterogeneity, flow-dependent capillary permeability, and now flow-dependent vascular volume, patients may differ. Patients may have different vascular volume or capillary permeability than that which is assumed in the physiologic simulator. In pathologic cases, capillary permeability is likely to change in the presence of prolonged ischemia (Lardo 2006, Zhu et al 2009). In the presence of a significant stenosis, there can be additional time delay and dispersion of the AIF (Calamante et al 2000, 2003). However, it is encouraging that the trends in the MBF map appearance across quantification methods are similar between the porcine data and the simulated data. Another limitation is that the CT simulator used in this work did not include artifacts such as beam hardening, scatter, motion, or partial scan, nor did it have electronic noise. However, this work provides a “best case” baseline for MBF quantification and characterizes the behavior of quantification methods when artifacts are corrected. Further investigation into the effects of specific artifacts on MBF precision and bias is warranted. Despite these limitations, the physiologic simulator and CT simulator enable controlled, reproducible experiments for evaluation of acquisition and quantification methods which may otherwise be confounded by numerous factors in in vivo experiments.

Conclusion

Using numerical simulations and model-to-models tests, we found that reduced, 3-parameter models, i.e. RPM1, RPM2, and SCM, provide the most precise and accurate MBF estimates across a range of MPI-CT acquisition conditions and physiologic conditions. Models with four or more free parameters had poor MBF precision and/or significant bias. Bias was more pronounced at the shortest tested imaging duration, i.e. 30 s, for model-based methods than at the longer imaging durations, i.e. 40 s and 50 s, thus indicating that MPI-CT acquisitions ≥40 s should be preferred. Model-independent LSVD and maximum-upslope provided relatively precise MBF estimates, although tended to greatly underestimate MBF. Considering the precision and bias for MBF estimation using model-based methods, reducing temporal sampling and reducing exposure per image frame seems to be preferable to reducing imaging duration for dose reduction. We recommend reduced, 3-parameter models that incorporate prior information of physiology and contrast agent extraction for typical MPI-CT datasets. The two proposed robust physiologic models, RPM1 and RPM2, and the single-compartment model were found to be best for MBF estimation, with little overall bias, ≤11%, and precise estimation, ≤10%, over the tested conditions. This work provides a foundation for the development and application of quantification methods and acquisition protocols for precise, accurate MBF estimation in MPICT.

Table 1.

List of acronyms and definitions.

Acronym	Definition
AATH	Adiabatic Approximation of the Tissue Homogeneity model
AIF	Arterial Input Function
CTU	Compartmental Tissue Uptake model
Fermi	Fermi model
FFR	Fractional Flow Reserve
FWHM	Full-Width at Half Maximum
IQR	Interquartile Range
IRF	Impulse Response Function
LAD	Left Anterior Descending coronary artery
LSVD	SVD with Tikhonov regularization determined by the L-curve criterion
LV	Left Ventricle of the heart
MPI-CT	Myocardial Perfusion Imaging with Computed Tomography
MUP	Maximum Upslope
MVD	Microvascular Disease
PTU	Plug-flow Tissue Uptake model
RPM1	Robust Physiologic Model with fixed E, fixed ITT
RPM2	Robust Physiologic Model with fixed E, MBF-dependent ITT
SCM	Single-Compartment Model
SVD	Singular Value Decomposition
TAC	Time-Attenuation Curve
2CXM	Two-Compartment Exchange Model

Table 2.

List of parameters and definitions.

Parameter	Definition
A	Scaling parameter for the slowly decaying exponential (2CXM)
α	Width parameter of gamma-variate function
B	Scaling parameter for the quickly decaying exponential (2CXM)
β	Proportionality constant for the flow and blood volume relationship
Ca(t)	Arterial time-concentration curve
Cm(t)	Model tissue time-concentration curve
CRV(t)	Right ventricle time-concentration curve from the gamma-variate function
Ct(t)	Measured tissue time-concentration curve
E	Extraction Fraction
ITT	Intravascular Transit Time
k	Decay constant for contrast agent wash-out
k−	Decay constant of the slowly decaying exponential (2CXM)
k+	Decay constant of the quickly decaying exponential (2CXM)
MBF	Myocardial Blood Flow
MBV	Myocardial Blood Volume
Φ	Unweighted sum-of-squared difference objective function
PS	Permeability-Surface Area product
ρ	Tissue density
RMBF(t)	Flow-scaled tissue impulse response function
SNRP	Perfusion Signal-to-Noise Ratio
T	Mean voxel transit time
Tc	Mean capillary transit time
td	Time delay between arterial input and tissue curve
td,RV	Time delay parameter of the gamma-variate function
Te	Mean extravascular transit time
θ	Generalized variable for model parameters
tpeak	Peak time parameter of the gamma-variate function
t0	Width parameter in the Fermi model
Vart	Arteriole volume
vb	Intravascular (blood) volume
Vcap	Capillary volume
ve	Extravascular volume
Vven	Venule volume
ymax	Maximum value of the gamma-variate function

Appendix

Model-based MBF estimation

The impulse response functions and free parameters for the eight models are described. Further information about these models and their derivation can be found in these references: (Sourbron and Buckley 2012, So et al 2012, Jerosch-Herold et al 1998, Luypaert et al 2011).

• 1)
  Adiabatic approximation of the tissue homogeneity model (AATH). The observation region is composed of intravascular and extravascular regions. Assumptions include plug flow through the intravascular space and that contrast agent concentrations in the extravascular space change much more slowly than in the intravascular space, thus allowing the aggregate extraction of contrast agent from the intravascular space to be represented by the extraction fraction. AATH is also known as an approximation to the Johnson-Wilson model with five free parameters: t_d (s), MBF, ITT (s), E (unit-less), and k (s⁻¹). The corresponding IRF is given by:

  $$R_{MBF}\left(t\right)=MBF\cdot \{\begin{array}{cc}0,& t<t_d\\ 1,& t_d\le t<t_d+ITT\\ E\cdot \text{exp}\left(-k\cdot \left(t-\left(t_d+ITT\right)\right)\right),& t\ge t_d+ITT\end{array}.$$ (4)
• 2)
  Two-compartment exchange model (2CXM). The myocardium consists of well-mixed intravascular and extravascular compartments with exchange between them. This model does not assume plug flow which may not be valid when considering that myocardium has a relatively chaotic spatial arrangement of capillaries, arterioles, and venules with heterogeneous volumes and individual flows (Sourbron and Buckley 2012). The IRF is given by the sum of two exponentials with five free parameters: t_d, A (mL/min-100g), B (mL/min-100g), k_- (s⁻¹), and k₊ (s⁻¹):

  $$R_{MBF}\left(t\right)=\{\begin{array}{cc}0,& t<t_d\\ A\cdot \text{exp}\left(-k_{-}\cdot \left(t-t_d\right)\right)+B\cdot \text{exp}\left(-k_{+}\cdot \left(t-t_d\right)\right),& t\ge t_d\end{array}$$ (5)

  where A is the scale factor of the slowly decaying exponential with decay constant k_- and B is the scale factor of the quickly decaying exponential with decay constant k₊ (see Figure 1). These parameters are related to underlying tissue properties such as MBF; intravascular volume (v_b, mL/g tissue); extravascular volume (v_e, mL/g tissue); and permeability-surface area product (PS, mL/min-g tissue). The relationships are:

  $A=\frac{MBF}{\left(k_{+}-k_{-}\right)}\left(\text{T}{k}_{+}-1\right)k_{-}$,

  $B=\frac{MBF}{\left(k_{+}-k_{-}\right)}\left(1-\text{T}{k}_{-}\right)k_{+}$,

  $k_{-}=\left(\left(T+T_e\right)-\sqrt{{\left(T+T_e\right)}^2-4T_c{T}_e}\right)/\left(2{\text{T}}_c{T}_e\right)$,

  $k_{+}=\left(\left(T+T_e\right)+\sqrt{{\left(T+T_e\right)}^2-4T_c{T}_e}\right)/\left(2{\text{T}}_c{T}_e\right)$,

  T_c = v_b/MBF, mean capillary transit time,

  T_e = v_e/PS, mean extravascular transit time,

  T = (v_b+v_e)/MBF, mean voxel transit time.

• 3)Plug-flow tissue uptake model (PTU). Contrast agent remains trapped in the extravascular space after entering, i.e. equivalent to k=0 in AATH (Sourbron and Buckley 2012). The PTU model has four free parameters: t_d, MBF, ITT, and E.
• 4)
  Compartmental tissue uptake model (CTU). Myocardium is described as two lumped compartments in which contrast agent extracts from the intravascular compartment to the extravascular compartment where it becomes trapped. The difference between CTU and PTU is that CTU is the sum of an exponential and a step function, whereas PTU is a piecewise step function (Sourbron and Buckley 2012). The CTU model has four free parameters: t_d, MBF, E, and k.

  $$R_{MBF}\left(t\right)=MBF\cdot \{\begin{array}{cc}0,& t<t_d\\ \left(1-\text{E}\right)\cdot \text{exp}\left(-k\cdot \left(\text{t}-{\text{t}}_d\right)\right)+\text{E}& t\ge t_d\end{array}$$ (6)
• 5)Robust physiologic model with fixed E and ITT (RPM1). This model is a reduced form of AATH with parameters fixed to E=0.6 and ITT=2 s. These values were selected when considering CT contrast agent extraction in the literature which can range from E=0.3 to E=0.8 (Idée et al 2002), CT voxel size and capillary flow velocity (Kiyooka et al 2005), goodness-of-fit to preclinical data, and parameter estimability across imaging conditions. The RPM1 model has three free parameters: t_d, MBF, and k.
• 6)Robust physiologic model with fixed E and flow-dependent ITT (RPM2). The parameter E is set to a constant and the parameter ITT is a function of MBF. In this work, E=0.6 and $\text{ITT}=\beta /\sqrt{\text{MBF}}$ where β is a proportionality constant. This functional relationship between ITT and MBF is based on observations in the literature that MBF is a quadratic function of myocardial blood volume, MBF∝MBV² (Wu et al 1992), and on the Central Volume Principle, ITT=MBV/MBF (Sourbron and Buckley 2012). Presumably, the quadratic relationship between MBF and MBV is due to the dilation of small blood vessels which decreases microvascular resistance and increases blood flow rates. A value of $\beta =20\text{s}\cdot \sqrt{\text{mL}/\left(\text{min}\cdot 100\text{g}\right)}$ was selected to give the same IRF as RPM1 at MBF=100 mL/min-100g. The RPM2 model has three free parameters: t_d, MBF, and k.
• 7)
  Single-compartment model (SCM). The observation region is described by a single lumped compartment in which the contrast agent enters and resides until leaving according to an exponential decay function (Luypaert et al 2011) which is described by three free parameters: t_d, MBF, and k.

  $$R_{MBF}\left(t\right)=MBF\cdot \{\begin{array}{cc}0,& t<t_d\\ \text{exp}\left(-k\cdot \left(t-t_d\right)\right),& t\ge t_d\end{array}$$ (7)
• 8)
  Fermi model (Fermi). The IRF is defined by a Fermi function (Jerosch-Herold et al 1998), and is described by four free parameters: t_d; MBF; width parameter (t₀, s); and k.

  $$R_{MBF}\left(t\right)=MBF\cdot \{\begin{array}{cc}0,& t<t_d\\ 1/\left(\text{exp}\left(k\cdot \left(t-t_d-t_0\right)\right)+1\right),& t\ge t_d\end{array}$$ (8)

Model-independent MBF estimation

The two model-independent MBF estimation algorithms, LSVD and MUP, are described.

• 9)SVD with Tikhonov regularization determined by the L-curve criterion (LSVD). In this implementation, the convolution is discretized in order to formulate the matrix equation for SVD computation. The t_i time points are equally spaced with average Δt time increment. The values of C_t(t) and C_a(t) are measured and the convolution is transformed into an algebraic form which is then solved by SVD with Tikhonov regularization to obtain R_MBF(t). The regularization factor is determined by the L-curve criterion which balances the effects of noise in R_MBF(t) with fit to the original data. The regularization factor is independently determined for each individual TAC for the analysis in this work. As R_MBF(t) is flow-scaled and represents the retention of a unit bolus of contrast material, MBF is obtained by taking the maximum value of R_MBF(t) (Fieselmann et al 2011).
• 10)
  Maximum Upslope (MUP). Using an established method (Bindschadler et al 2014), the maximum upslope, dC_t/dt, was estimated by fitting a line segment to TAC data from 4 s before the AIF peak to either the minimum of the time-of-peak HU of the myocardial TAC or 7 s after the AIF peak. MBF is computed by the equation below where max(C_a) is the measured peak of the AIF.

  $$MBF=\frac{\text{max}\left(d{C}_t/dt\right)}{\text{max}\left(C_a\right)}\cdot \frac{1}{\rho }$$ (9)

Semi-analytic model implementation

The convolution integral in equation (1) is computed using analytic forms of both R_MBF(t) and C_a(t). We used first-order polynomials to construct a linear spline representation of C_a(t) (De Boor 1978) equivalent to linear interpolation between measured data points:

$$\begin{array}{cc}{C}_a\left(t\right)=a_i+{\text{b}}_i\cdot \left(\text{t}-{\text{t}}_i\right),& t_i\le t\le t_{i+1}\end{array},$$ (10)

$$a_i=C_a\left(t_i\right)$$

$$b_i=\frac{C_a\left(t_{i+1}\right)-C_a\left(t_i\right)}{t_{i+1}-t_i}$$

where a_i is the constant coefficient in the linear equation, b_i is the first-order coefficient or slope, and t_i is the time of a sampled data point for time index i=1,2,…,N for N scans. The linear spline is selected over higher-order splines in order to avoid oscillations, i.e. under- or overshoot, between sampled data points and as a tradeoff between computational efficiency and accuracy given the typical noise levels in the data. (However, the method generalizes to higher-order polynomial splines.) Using this approach, the linear spline from equation (10) can be substituted for C_a(t) in the convolution, equation (1), giving the model output corresponding to the impulse response R_MBF(t),

$$C_m\left(t\right)={\displaystyle \sum }_{j=1}^{N-1}\left[\underset{t_j}{\overset{t_{j+1}}{{\displaystyle \int }}}\left(a_j+b_j\cdot \left(\tau -t_j\right)\right)\cdot \rho \cdot R_{MBF}\left(t-\tau \right)d\tau \right]$$ (11)

where the index j denotes the lower bounded time index for each piece of the linear spline, index j+1 represents the upper bounded time index, and t is on the interval t₁≤t≤t_N. Each integral has a closed-form analytic solution that depends on the impulse response model used (see Appendix 5 of (Eck 2018)). The model TAC (C_m) is compared to the measured tissue curve (C_t) at sample times t_i using the unweighted sum-of-squared difference objective function,

$$\Phi ={\displaystyle \sum }_{i=1}^N{\left({\text{C}}_m\left(t_i\right)-{\text{C}}_t\left(t_i\right)\right)}^2,$$ (12)

which is minimized when the model curve has reached an optimal fit to the data set across all N scans.

We used a gradient-based optimization algorithm to minimize Φ with respect to model parameters. For robust and efficient performance, analytically determined gradients are supplied (Bard 1974). First, the objective function is differentiated with respect to each model parameter, θ_s,

$$\frac{\partial \Phi }{\partial {\theta }_s}=2{\displaystyle \sum }_{i=1}^N\frac{\partial {\text{C}}_m\left(t_i\right)}{\partial {\theta }_s}\cdot \left({\text{C}}_m\left(t_i\right)-{\text{C}}_t\left({\text{t}}_i\right)\right),$$ (13)

in which C_m(t_i) is the model output and ∂C_m(t_i)/∂θ_s is the dynamic sensitivity function of the model-predicted TAC with respect to parameter θ_s. The sensitivity function is computed in a similar fashion as Cm(t),

$$\frac{\partial {\text{C}}_m\left(t_i\right)}{\partial {\theta }_s}={\displaystyle \sum }_{j=1}^{N-1}\left[\underset{t_j}{\overset{t_{j+1}}{{\displaystyle \int }}}\left(a_j+b_j\cdot \left(\tau -t_j\right)\right)\cdot \rho \cdot \frac{\partial R_{MBF}\left(t-\tau \right)}{\partial {\theta }_s}d\tau \right],$$ (14)

in which the derivative $\frac{\partial R_{MBF}\left(t_i-\tau \right)}{\partial {\theta }_s}$ is derived analytically from the model impulse response function (see Appendix 5 of (Eck 2018)).