Hercules: a profile HMM-based hybrid error correction algorithm for long reads

Abstract

Choosing whether to use second or third generation sequencing platforms can lead to trade-offs between accuracy and read length. Several types of studies require long and accurate reads. In such cases researchers often combine both technologies and the erroneous long reads are corrected using the short reads. Current approaches rely on various graph or alignment based techniques and do not take the error profile of the underlying technology into account. Efficient machine learning algorithms that address these shortcomings have the potential to achieve more accurate integration of these two technologies. We propose Hercules, the first machine learning-based long read error correction algorithm. Hercules models every long read as a profile Hidden Markov Model with respect to the underlying platform’s error profile. The algorithm learns a posterior transition/emission probability distribution for each long read to correct errors in these reads. We show on two DNA-seq BAC clones (CH17-157L1 and CH17-227A2) that Hercules-corrected reads have the highest mapping rate among all competing algorithms and have the highest accuracy when the breadth of coverage is high. On a large human CHM1 cell line WGS data set, Hercules is one of the few scalable algorithms; and among those, it achieves the highest accuracy.

INTRODUCTION

High Throughput Sequencing (HTS) technologies have revolutionized the field of genomics, and yet they suffer from two fundamental limitations. First and foremost, no platform is yet able to generate a chromosome-long read. Average read length ranges from 100 bp to 20 kb depending on the platform. Second, reads are not error-free. The most ubiquitous platform, Illumina, produces the most accurate (∼0.1% error rate), yet the shortest (100–150 bp) reads (1). Short read lengths present challenges in accurate and reproducible analyses (2,3), as well as in building reliable assemblies (4–6). On the other hand, Pacific Biosciences Single Molecule, Real-Time (SMRT) sequencing technology is capable of producing >10 kb-long reads on average, though with a substantially higher (∼15%) error rate (7). Similarly, the Oxford Nanopore Technologies (ONT) platform can generate longer reads (up to ∼900 kb). However, their error rate is also higher (>15%) (8). While one can still achieve high basepair accuracy using PacBio or ONT reads, this requires a very high coverage (9), which, given the relatively higher costs associated with long read platforms make this approach prohibitive.

The strengths and weaknesses of the platforms discussed above makes it attractive to combine them. Such combination enables researchers to utilize the longer reads generated by PacBio and ONT platforms while obtaining the same accuracy as the Illumina reads provide. However, downside is that this approach cannot correct regions of the genome with little or no Illumina read coverage. Still, several hybrid error correction methods have been developed that fall into two major categories. The first approach starts with aligning short reads onto long reads generated from the same sample, implemented by several tools such as PacBioToCA (10), LSC (11), proovread (12) and Colormap (13). Leveraging the relatively higher coverage and accuracy of short reads, these algorithms fix the errors in long reads by calculating a consensus of the short reads over the same segment of the nucleic acid sequence. The second approach aligns long reads over a de Bruijn graph constructed using short reads, and the k-mers on the de Bruijn graph that are connected with a long read are then merged into a new, corrected form of the long read. Examples of this approach are LoRDEC (14), Jabba (15) and HALC (16). Despite being a de Bruijn graph-based algorithm, LoRMA (17) is not a hybrid tool as it only uses long reads for correction.

While both approaches work well in some cases, they also suffer from several drawbacks. Alignment based approaches are highly dependent on the performance of the aligner. Therefore, accuracy, run time, and memory usage of the aligner will directly affect the performance of the downstream correction tool. The use of de Bruijn graphs by the second approach eliminates the dependence on external aligners, and implicitly moves the consensus calculation step into the graph construction. However, even with the very low error rate in short reads and the use of shorter k-mers when building the graph, the resulting de Bruijn graph may contain bulges and tips, that are typically treated as errors and removed (18). Accurate removal of such graph elements relies on the availability of high coverage data to be able to confidently discriminate real edges from the ones caused by erroneous k-mers (19,20).

Here, we introduce a new alignment-based Hybrid ERror Correction algorithm, Hercules, to improve basepair accuracy of long reads. Hercules is the first machine learning-based long read error correction algorithm. Hercules models each long and erroneous read as a template profile hidden Markov model (dubbed profile HMM or pHMM). It uses short reads as observations to train the model via Forward-Backward algorithm (21), and learns posterior transition and emission probabilities. Finally, Hercules decodes the most probable sequence for each profile HMM using Viterbi algorithm (22). Although HMMs have been used in short read error correction before (23,24), this is the first use of HMMs in long read error correction.

The main advantage of Hercules over other alignment-based tools is the novel use of pHMMs to (i) reduce dependency on aligner performance, (ii) directly incorporate experimentally observed error profiles of long reads that can be updated when the underlying sequencing technology improves, or adapted to new long read sequencing platforms. Alignment-based methods are dependent on the aligner’s full CIGAR string for each basepair to correct. They perform majority voting to resolve discrepancies among short reads with the assumption that all error types are equally likely to happen during correction. Despite the fact that aligners can take likelihoods of different error types into account, correction step is dependent on the aligner’s choice. In contrast, while Hercules uses the starting positions obtained from an aligner, it does not depend on any other information provided by the aligner. It sequentially and probabilistically accounts for the evidence provided per short read, instead of just independently using majority voting per base-pair. In addition, using the HMM prior probabilities for error types can be configured based on the error profile of the platform to be processed. As prior probabilities are not uniform, the algorithm is better positioned to predict the posterior outcome. Thus, it can also be adapted based on the long read technologies.

We compared Hercules with other methods on the following data sets: (i) two BAC clones of complex regions of human chromosome 17, namely, CH17-157L1 and CH17-227A2 (7), and (ii) a human hydatidiform mole cell line (CHM1) (25) As the ground truth, (i) for BAC clones, we used finished assemblies generated from Sanger sequencing data from the same samples and (ii) for the human data we used CHM1_1.1 assembly (25).

Results on BAC clones show that when the short read coverage is high, Hercules produces reads with the highest mapping rate and, should long reads have high short read breadth of coverage (i.e., 90%), Hercules outputs the largest set of most accurate reads (i.e. >95% accuracy). Unlike BAC clone data sets (short genome, high short read coverage), CHM1 data reflects a more realistic scenario (large genome, moderate short read coverage—639 673 210 paired-end short and 817 410 long reads). We compare the performances of the tools on CHM1 data set that best perform with moderate short read coverage on BAC clones. We show that Hercules is one of the two algorithms that can scale to such a large problem size. Despite moderate short read coverage (<40×), Hercules produces most accurate reads (i.e. >95%) with 128% improvement over LoRDEC.

MATERIALS AND METHODS

Overview of Hercules

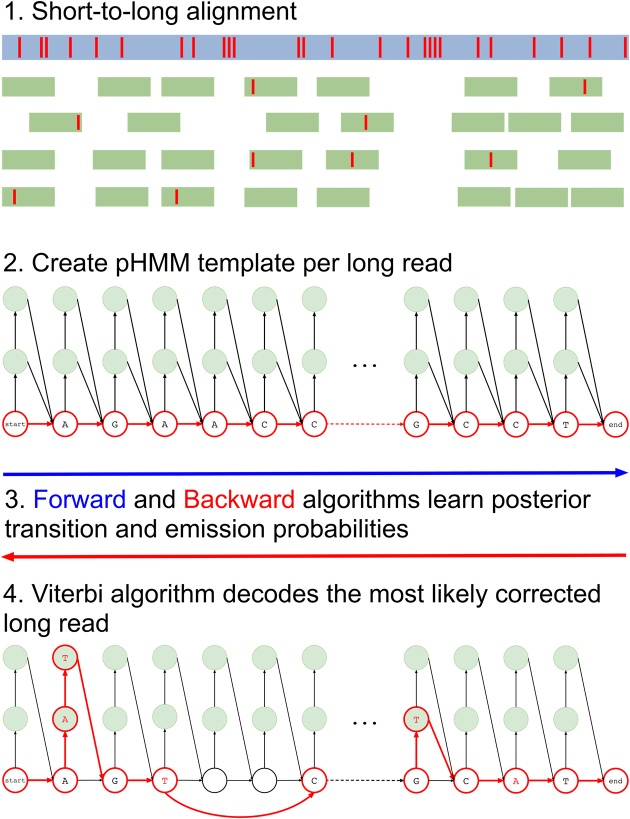
Hercules corrects errors (insertions, deletions, and substitutions) present in long read sequencing platforms such as PacBio SMRT (26) and Oxford Nanopore Technologies (8), using reads from a more accurate orthogonal sequencing platform, such as Illumina (27). We refer to reads from the former as ‘long reads’ and the latter as ‘short reads’ in the remainder of the paper. The algorithm starts with preprocessing the data and obtains the short-to-long read alignment. Then, for each long read, Hercules constructs a pHMM template using the error profile of the underlying platform as priors. It then uses the Forward–Backward algorithm to learn the posterior transition/emission probabilities, and finally, uses the Viterbi algorithm to decode the pHMM to output the corrected long read (Figure 1).

Figure 1.

Overview of the Hercules algorithm. Initially (1), short reads are aligned to long reads using an external tool. Here, red bars on the reads correspond to erroneous locations. Then (2), for each long read Hercules creates a pHMM with priors set according to the underlying technology. Using the starting positions of the aligned short reads, Forward-Backward algorithm learns posterior transition and emission probabilities in (3). Finally (4), Viterbi algorithm finds the most likely path of transitions and emissions as highlighted with red colors. The prefix and the suffix of the input long read in this example is ‘AGAACC...GCCT’. After correction, substring ‘AT’ inserted right after the first ‘A’. Third ‘A’ is changed to ‘T’ and following two base-pairs are deleted. Note that deletion transitions are omitted other than this arrow, and only two insertion states are shown for clarity of the figure. On the suffix, a ‘T’ is inserted and second to last base-pair is changed from ‘C’ to ‘A’.

Preprocessing

Compression

Similar to the approach of LSC (11), Hercules starts with compressing both short and long reads using a run-length encoding scheme. That is, it compresses repeating base-pairs to a single base-pair (e.g., AAACTGGGAC → ACTGAC). This is because PacBio and ONT platforms are known to produce erroneous homopolymer runs, especially when the homopolymer lengths are longer, i.e. consecutive bases may be erroneously repeated (28), which affects the short read alignment performance drastically. Furthermore, when homopolymer compression is enabled, overlapping quality of PacBio reads improves (29). Hercules, then, recalculates the original positions based on the original long reads. Even though this option is performed by default, it is still possible to skip the compression phase.

Short read filtering

After the step described above, the nominal length of some compressed reads may be substantially shortened. This would in turn cause such reads to be ambiguously aligned to the long reads, which is already a common problem in short read sequencing due to repeats (2,3). To overcome this problem, Hercules removes any compressed short read, if its number of non-N characters is less than a specified threshold (set to 40 by default). In addition to PCR and optical duplicates inherent in short read data, it is also highly likely that compression step will generate new duplicate sequences. If the multiple alignment option is enabled by an aligner, these duplicates may cause generating large number of identical alignments. Such identical alignments might be useful in better learning the parameters, but they may also increase the running time of an aligner as well. Therefore, after compression, Hercules may remove these duplicates using a Bloom filter with 0.0001 false positive rate, keeping only a single read as the representative of the group. This may help the aligner to reduce its running time if the short read input size is large. Duplicate removal is an optional phase, and we do not remove duplicates by default.

Alignment and decompression

Hercules is an alignment-based error correction tool. It outsources the alignment process to a third party aligner, and it is compatible with any aligner that provides output in SAM/BAM format (30). However, we suggest mappers that can report multiple possible alignments such as Bowtie2 (31) as we would prefer to cover most of the long read with short reads. Even though this might cause incorrect mappings, Hercules is able to probabilistically downplay the importance of such reads during the learning stage given sufficient short read depth. Hercules also assumes that the resulting alignment file is sorted. Thus, the file in SAM/BAM format must be coordinate sorted in order to ensure a proper correction with Hercules. Alignments are calculated using either compressed or original long and short reads (those that pass filtering step for the latter) as described in previous sections. After receiving the alignment positions from the aligner, Hercules decompresses both short and long reads and recalculates alignment start locations.

All other alignment-based error correction methods in the literature use the CIGAR string provided by the aligner. CIGAR string specifies where each basepair of the short read is mapped on the long read and where insertions and deletions have occurred. Then, per base-pair on the long read, they perform a majority vote among covering short reads. Hence, learning of correct basepairs is actually performed by the aligner, which makes the performance of such tools fully dependent on the aligner choice. In contrast, the only information Hercules receives from the aligner is the starting position of the mapping. The Forward algorithm learns posterior probabilities starting from that position and it can go beyond the covered region. Thus, despite using the starting point information from the aligner, the algorithm can decide that the short read is aligned beyond that point and also that the alignment is essentially different than what is claimed by the aligner in the CIGAR string. This minimizes the dependency of the algorithm on the aligner and makes Hercules the first alignment-based approach to reclaim the consensus learning procedure from the aligner.

The profile HMM structure

Hercules models each long read as a pHMM. In a traditional profile HMM (32), there are three types of states: deletion, insertion and match (mismatch) states. The aim is to represent a family of proteins (amino acid sequences) and then to use it to decide if an unknown protein is likely to be generated from this model (family). Our goal in representing a long read as a template pHMM is different. We use short reads that we know are generated from the source (e.g., same section of RNA/DNA), to update the model (not the topology but the transition and emission probabilities). While the goal of the original application is to calculate the likelihood of a given query sequence, in our case there is no given sequence. Our goal is to calculate the most likely (consensus) sequence the model would produce, among all possible sequences that can be produced using the letters in the alphabet Σ. While the consensus sequence generated by a traditional pHMM is only based on the match states, in our case we would like to generate a different consensus that takes insertions and deletions in to account after the training. This requires us to impose some restrictions on the standard pHMM concept for reasons detailed in later sections. First, we remove the self loop over insertion states. Instead, our model has multiple insertions states per position (basepair) on the long read. The number of insertion states is an input to the algorithm. Second, we substitute deletion states with deletion transitions. The number of possible consecutive basepairs that can be deleted is an input parameter to the algorithm as well.

After we construct the model, we use the error profile of the underlying technology to initialize the prior transition and emission probabilities. Hercules first learns posterior transition and emission probabilities of each ‘long read profile HMM’ using short reads that align to the corresponding long read (Supplementary Equations S1–S4). Then, it decodes the pHMM using the Viterbi algorithm (22) to generate the most probable (i.e. corrected, or consensus) version of the long read (Supplementary Equation S7).

It should be noted that the meanings of insertion and deletion is reversed in the context of the pHMM. That is, an insertion state would insert a basepair into the erroneous long read. However, this means that the original long read did not have that nucleotide and had a deletion in that position. A similar principle applies to deletions.

Next, we first define the structure of the model (states and transitions) and explain how we handle different types of errors (i.e. substitutions, deletions, and insertions).

Match states

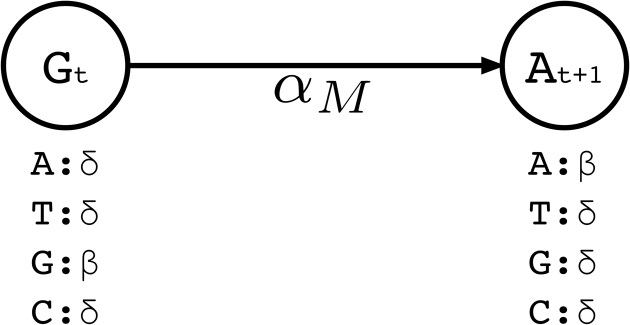
Similar to traditional pHMM, we represent each basepair in the long read by a match state. There are four emission possibilities in a match state (Σ = {A, C, G, T}). The basepair that is observed in the uncorrected long read for that position t is initialized with the highest emission probability (β), while the probabilities for emitting the other three basepairs are set to the expected substitution error rate for the long read sequencing technology (δ) (Note that β ≫ δ and β + 3δ = 1).

We then set transition probabilities between consecutive match states t and t + 1 as ‘match transitions’ with probability α_M. Figure 2 exemplifies a small portion of the profile HMM that shows only the match states and match transitions. From a match state at position t, there are also transitions to (i) the first insertion state at position t (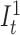), and (ii) to all match states at positions t + 1 + x where 1 ≤ x ≤ k and k determines the number of possible deletions.

Figure 2.

A small portion of the profile HMM built by Hercules. Here, two match states are shown, where the corresponding long read includes G at location t, followed by nucleotide A at location t + 1. At state t, the emission probability for G is set to β, and emission probabilities for A, C, T are each set to the substitution error rate δ. Match transition probability between states t and t + 1 is initialized to α_M.

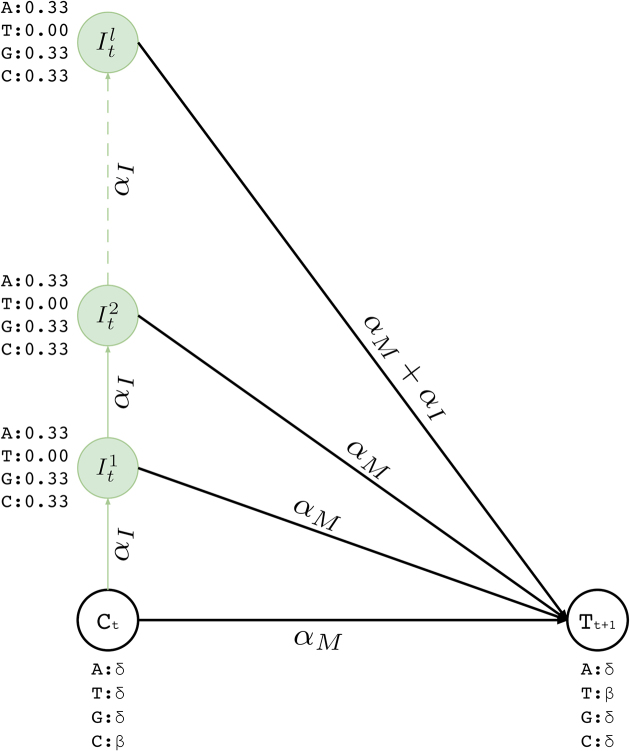
Insertion states

Insertion states have self-loop transitions in standard profile HMMs to allow for multiple insertions at the same site, which creates ambiguity for error correction for two reasons. First, self-loops do not explicitly specify the maximum number of insertions. Thus, it is not possible predetermine how many times that a particular self-loop will be followed while decoding. Second, each iteration over the loop has to emit the same basepair. Since decoding phase prefers most probable basepair at each state, it is not possible for a standard profile HMM to choose different nucleotides from the same insertion state.

Instead of a single insertion state with a self loop per basepair in the long read, we construct l multiple insertion states for every match state at position t (e.g., 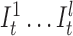). We replace self-loops with transitions between consecutive insertion states (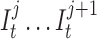) for position t (see Figure 3). The probability for each of such transitions is α_I and the number of insertion states per position l determines the maximum number of allowed insertions between two match states, which are set through user-specified parameters. All insertion states at position t have transitions to the match state at positions t + 1 (the end state is also considered as a match state). For 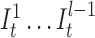the probability of those transitions are α_M, and for 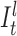, it is α_M + α_I. All those states also have transitions to all match states at positions t + 1 + x where 1 ≤ x ≤ k and k determines the number of possible deletions.

Figure 3.

Insertion states for position t. Here, we show two match states (C_t and T_{t + 1}) and l insertion states (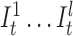). The number of insertion states limit the insertion length to at most l after basepair t of the corresponding long read. We also incorporate equal emission probabilities for all basepairs, except for the basepair represented by the corresponding match state t + 1 (T in this example).

We also set emission probabilities for the insertion states and assume they are equally likely. However, for the insertion states at position t, we set the probability of emitting the nucleotide X ∈ Σ to zero, if X is the most likely nucleotide at the match state of position t + 1. This makes the insertion more likely to happen at the last basepair of the homopolymer run. Otherwise, the likelihood of inserting a basepair is shared among all insertions states of the run, and it is less likely for any them to be selected during the decoding phase. All other basepairs have their emission probabilities set to 0.33 (i.e. 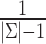)—see Figure 3. Note that these values are prior values and the posterior values would be different after training.

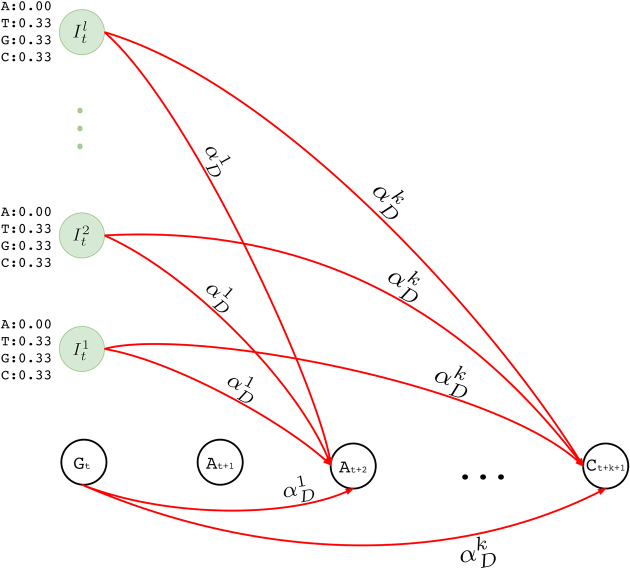
Deletion transitions

In standard pHMM, a deletion state needs to be visited to skip (delete) a basepair, which does not emit any characters. However, as described in the supplementary sections, calculation of the forward and backward probabilities for each state is based on the basepair of the short read considered at that time. This means at each step, the Forward-Backward algorithm consumes a basepair of the short read to account for the evidence the short read provides for that state. As deletion states do not consume any basepairs of the short read, this in turn results in an inflation on the number of possibilities to consider and substantially increases the computation time. In an extreme case, the mapped region of the short read on the long read may be completely deleted. Since we are using an external aligner, such extreme cases are unlikely. Thus, we model deletions as transitions, instead of having deletion states. In our model, a transitions to (1 + x)-step away match states is established to delete x basepairs. As shown in Figure 4, match and insertion states at tth position have a transition to all match states at positions t + 1 + x, where 1 ≤ x ≤ k and k is an input parameter determining maximum number of deletions per transition. We calculate the probability of a deletion of x basepairs, 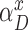, as shown in Equation (1).

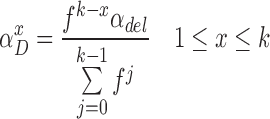(1)

Figure 4.

Deletion transitions (red) in Hercules pHMM. Insertion states of position t have the same deletion transitions with the match state of the same position, t. Any transition from position t to t + 1 + x removes x characters, skipping the match states between t and t + 1 + x, with 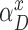probability, where 1 ≤ x ≤ k

Equation (1) is a normalized version of a polynomial distribution where α_del is the overall deletion probability (i.e. α_del = 1 − α_M − α_I), and f ∈ [1, ∞). As f value increases, probabilities of further deletions decrease accordingly.

Training and decoding

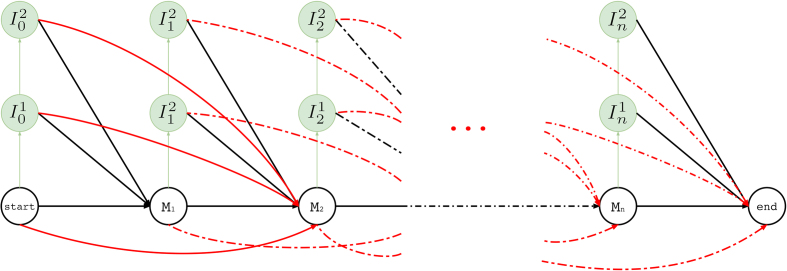
An overall illustration of a complete pHMM for a long read of length n is shown in Figure 5 where (i) match states are labeled with M_t where M ∈ Σ, (ii) insertion states are labeled with 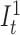and 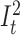, and (iii) deletion transitions for k = 1 are shown. Note that tth basepair of a long read has one match state and two insertion states where 1 ≤ t ≤ n. There are also deletion transitions from every state at tth position to (t + 2)th match state where (t + 2) ≤ n. This example structure allows only one character deletion at one transition since it is only capable of skipping one match state.

Figure 5.

Hercules profile HMM in full. Here we show the overall look at the complete graph that might be produced for a long read M where its tth character is M_t and M_t ∈ {A, T, G, C} 1 ≤ t ≤ n and n is the length of the long read M (i.e. |M| = n). In this example, there are n many match states and two insertion states for each match state. Only one character deletion is allowed at one transition because transitions may only skip one match state.

Let the complete pHMM for a long read be the graph G(V, E). Per each mapped short read s, we extract a sub-graph G_s(V_s, E_s). Here, G_s corresponds to the covered region of the long read with that short read. Hercules may not consider some of the short reads that align to same position in a long read to reduce computational burden. We provide max coverage, mc, option to only consider mc many number of short reads for a position during a correction, where mc = 1 by default. Short reads are selected based on their edit distance.

States that will be included in V_s are determined by several factors. Assume that s is aligned to start from the qth character of the long read. First, all match and insertion states between positions [q − 1, q + m) are included, where m is the length of the short read. If there are insertion errors, deletion transitions might be followed which may require the training phase to consider r more positions where r is a parameter to the algorithm, which is fixed to ⌈m/3⌉. Thus all match and insertion states between [q + m, q + m + r) are also added. Finally, the match state at position q + m + r is also included (end state), and M_{q − 1} acts as the start state. Every transition E_ij ∈ E connecting state i and state j are included in E_s if i ∈ V_s and j ∈ V_s. Each E_ij ∈ E_s is associated with a transition probability α_ij as described in previous subsections. For every pair of states, i ∈ V_s and j ∈ V_s, α_ij = 0 if .

We train each G_s using the Forward-Backward algorithm (21). As we explain above, updates of emission and transition probabilities are exclusive for each sub-graph G_s. Details of the Forward-Backward algorithm can be found in Supplementary Text 1.1. Thus, there can be overlapping states and transitions that are updated within multiple sub-graphs, independently using the prior probabilities. For such cases, updated values are averaged with respect to posterior probabilities from each subgraph. Details of joining the posterior probabilities can be found in Supplementary Text 1.2. Uncovered regions keep prior transition and emission probabilities, and G is updated with the posterior emission and transmission probabilities.

Finally, we use the Viterbi algorithm (22) to decode the consensus sequence. We define the consensus sequence as the most likely sequence the pHMM produces after learning new parameters. The algorithm takes G for each long read and finds a path from the start state to the end state, which yields the most likely transitions and emissions using a dynamic programming approach. Details of the Viterbi algorithm can be found in Supplementary Text 1.3.

RESULTS

Experimental setup

We implemented Hercules in C++ using the SeqAn library (33). The source code is available under the BSD 3-clause license https://github.com/BilkentCompGen/Hercules. We compared Hercules to prior methods proposed for the integration of short and long reads: HALC, LoRDEC (de Bruijn graph-based) and LSC, proovread, Colormap (aligner-based). We ran all tools on a server with four processors with a total of 56 cores (Intel Xeon E7-4850 2.20 GHz), and 1TB of main memory. We assigned 60 threads to all programs including Hercules.

We used Bowtie2 for BAC clones and Minimap2 (29) for the human CHM1 data set to align the reads, and then we sorted resulting alignment files using SAMtools (30) (Supplementary Table S6). For Hercules, we set our parameters as follows: max insertion length (l = 3), max deletion length (k = 10), match transition probability (a_M = 0.75), insertion transition probability (a_I = 0.20), deletion transition probability (a_del = 0.05), deletion transition probability distribution factor (f = 2.5), match emission probability (β = 0.97), max coverage (mc = 1), max filter size (mf = 100). We ran all other programs with their default settings. We demonstrate that Hercules is robust to parameter choices (Supplementary Tables S4 and S5) with up to 8.3% accuracy loss in the most extreme settings for initial transition probabilities.

In our benchmarks we did not include the self-error correction tool, LoRMA, as it does not use short reads, which makes it not comparable to rest of the hybrid error correction tools. Furthermore, HALC uses LoRDEC to further refine its corrected reads (ordinary mode). We would like to note that if short read coverage is not low (i.e. >30×), HALC runs LoRDEC using almost all of the corrected reads for further correction for the second time (Supplementary Table S2). Thus, corrected reads do not only reflect HALC’s error correction performance but also LoRDEC’s performance on HALC-corrected reads as this is the final output of HALC. To compare the benefit of this behavior, an ideal experiment would be providing LoRDEC with the outputs of each correction tool so that these reads are also further corrected by LoRDEC. However, it is possible to turn off this option as well (repeat-free mode), therefore we benchmarked HALC with and without LoRDEC. We also exclude Jabba in our comparisons because it only provides corrected fragments of long reads and clips the uncorrected prefix and suffixes, which results in shorter reads. All other methods consider the entire long read. Additionally, several error correction tools such as LSC and proovread do not report such reads that they could not correct. Others, however, such as Hercules, LoRDEC, and Colormap report both corrected and uncorrected reads, preserving the original number of reads. In order to make the results of all correction tools comparable, we re-insert the original versions of the discarded reads to LSC and proovread output. We ran Colormap with its additional option (OEA) that incorporates more refinements on a corrected read. We observed that there was no difference between running OEA option or not in terms of the accuracy of its resulting reads (Supplementary Table S1), although Colormap with OEA option required substantially higher run time. Last, we tested the performance of three leading algorithms on a large genome data set given a moderate short read coverage (i.e. 42×). Our choices included Hercules, LSC, and LoRDEC as these tools performed well with a moderate short read coverage. However, LSC failed to finish its job even after running for 2 months. The reason was the use of default aligner that comes with LSC as it only produced nearly 50 million alignments in two months and prevented LSC to make its correction in a reasonable time limit. Thus, we subsampled human CHM1 long reads and run LSC with the small data.

Data sets

To compare Hercules’ performance with other tools we used three DNA-seq data sets. First two DNA-seq data sets were generated from two bacterial artificial chromosome (BAC) clones, previously sequenced to resolve complex regions in human chromosome 17 (7). These clones are sequenced with two different HTS technologies: CH17-157L1 (231 kb) data set includes 93,785 PacBio long reads filtered by a minimum length of 200 (average 2576 bp; 1047× coverage, SRA SRR1171743) and 372 272 Illumina paired-end reads (76 bp each, 245× coverage); and CH17-227A2 (200 kb) data set includes 100 729 PacBio long reads filtered by a minimum length of 200 (average 2663 bp; 1338× coverage, SRA SRR1171785) and 342 528 Illumina paired-end reads (76 bp each, 260× coverage). Illumina paired-end reads of the BAC clones are available at http://eichlerlab.gs.washington.edu/pacbio-complex-regions. Additionally, sequences and finished assemblies generated with the Sanger platform are also available for the same BAC clones (GenBanks AC243627.3 and AC243685.2), which we use as the gold standard to test the correction accuracy. We also randomly subsampled the short read inputs of these BAC clones into 10×, 20× and 30× coverage to test the performance of the tools under such circumstances. Human CHM1 cell line WGS data includes 817 410 PacBio long reads (SRA SRR1304331–SRR1304335, 7.89 Gbp, 2.6×) and 639 673 210 Illumina paired-end short reads (101 bp each, 129.2 Gbp, 42× coverage, SRA SRX652547). We measured error correction accuracy using the assembly of human CHM1 genome (25) (NCBI AssemblyDB GCA_000306695.2) as the gold standard.

Correction accuracy

After correction, we align the corrected reads to the corresponding ground truth using BLASR (34) with the bestn=1 and noSplitSubreads options, which forces entire read to align, if possible or otherwise outputs the best local alignment. Then, we denote the accuracy of a read as the alignment identity reported by BLASR. We report the number of reads that align to the gold standard, and the alignment accuracy in four different accuracy brackets.

We observe that the number of mappable reads were the highest (or tightly close to LSC) in both Hercules-corrected BAC clones, given any level of short read coverage (Tables 1 and 3). LoRDEC returned the largest set of reads with the highest accuracy (>95%), when the short read coverage is low (i.e. 10×–30×) in five out of six tests (see Table 1). Hercules was the best in one setting and always ranked in top three. Whereas, when the short read coverage is extremely high, HALC produced largest set of most accurate reads (Table 3). We investigated the reason why HALC’s ordinary mode produced similar results with the repeat-free mode when the short read coverage is low (10×) and why the difference gap increased given high short read coverage. We found that HALC sends 0.2–2% of long reads for further correction by LoRDEC when the coverage is low. However, as the coverage starts increasing, the number of the HALC-corrected reads sent for further correction reaches 99.8%, if coverage is greater than 30× (Supplementary Table S2). Therefore, we claim that if short read coverage is moderate, HALC corrects almost all reads twice in ordinary mode whereas a repeat-free mode cannot attempt to correct them well. We conclude that HALC requires high short read coverage, and its accuracy is lower than its competitors for low short read coverage.

Table 1.

Error correction with multiple short read coverages

	CH17-157L1 BAC clone – number of aligned reads
	10×				20×				30×
Tool	Mapped	80–90%	90–95%	>95%	Mapped	80–90%	90–95%	>95%	Mapped	80–90%	90–95%	>95%
Uncorrected	33 842	17 582	1 974	461	33 842	17 582	1 974	461	33 842	17 582	1 974	461
Colormap	34 215	15 622	4 979	1 579	34 515	14 882	5 989	2 585	34 710	14 428	6 528	3 263
HALC (w/ LoRDEC)	33 933	17 656	1 870	569	35 287	13 250	5 708	5 390	37 217	12 040	6 948	8 845
HALC (w/o LoRDEC)	33 908	17 662	1 867	537	34 242	17 919	1 627	816	34 908	18 360	1 986	1 360
Hercules	36 585	14 539	6 675	3 917	40 863	14 165	7 067	8 498	41 549	13 880	7 162	9 631
LoRDEC	36 604	13 752	7 050	6 270	37 098	11 249	7 302	10 953	36 965	10 597	7 157	12 118
LSC	35 991	14 465	6 234	3 939	40 368	13 939	6 901	8 571	41 254	13 774	6 957	9 788
proovread	34 191	16 881	3 301	1 013	34 361	16 534	3 851	1 380	34 604	16 324	4 223	1 821
	CH17-227A2 BAC clone - Number of aligned reads
Uncorrected	45 625	25 356	7 385	219	45 625	25 356	7 385	219	45 625	25 356	7 385	219
Colormap	45 679	22 878	9 295	1 223	45 712	21 701	9 897	2 072	45 758	21 019	10 269	2 590
HALC (w/ LoRDEC)	45 772	25 460	7 058	627	46 929	14 570	8 843	14 061	48 682	13 118	9 207	18 122
HALC (w/o LoRDEC)	45 679	22 878	9 295	1 223	45 943	26 399	6 414	656	47 038	25 223	8 453	1 833
Hercules	50 090	15 883	11 007	13 256	54 551	14 800	10 546	19 741	54 666	14 421	10 329	20 645
LoRDEC	46 467	14 787	10 010	13 053	46 893	11 422	8 301	20 332	46 956	10 329	7 719	22 597
LSC	50 162	16 206	11 727	12 385	53 762	15 071	10 805	18 568	53 887	14 624	10 578	19 501
proovread	45 700	23 444	8 869	1 139	45 797	22 612	9 289	1 833	45 919	22 044	9 467	2 489

We applied Hercules to correct PacBio reads generated from two BAC clones (CH17-157L1 and CH17-227A2) using Illumina reads from the same resource. We subsampled the Illumina reads into 10×, 20× and 30× to test the performance of the tools for both low and moderate short read coverage. We report the accuracy as the alignment identity as calculated by the BLASR (34) aligner. Mapped refers to the number of any reads aligned to the Sanger-assembled reference for these clones with any identity, where the other columns show the number of alignments within respective identity brackets.

Table 3.

Error correction with original short read coverages

	Number of aligned reads
	CH17-157L1 BAC clone				CH17-227A2 BAC clone				Homo Sapiens (CHM1)
Tool	Mapped	80–90%	90–95%	>95%	Mapped	80–90%	90–95%	>95%	Mapped	80–90%	90–95%	>95%
Uncorrected	33 842	17 582	1 974	461	45 625	25 356	7 385	219	516 983	279 387	27 909	22 851
Colormap	36 391	13 586	7 904	6 235	46 209	18 398	12 364	4 715	NA	NA	NA	NA
HALC (w/ LoRDEC)	43 678	7 989	6 408	24 453	53 017	8 068	6 070	34 407	NA	NA	NA	NA
HALC (w/o LoRDEC)	40 866	9 509	9 643	17 025	52 069	10 201	10 628	26 352	NA	NA	NA	NA
Hercules	44 229	13 609	7 569	12 583	56 140	13 433	9 809	24 269	530 973	168 906	105 012	99 600
LoRDEC	36 812	10 320	7 397	12 167	47 304	8 875	7 010	25 844	534 713	266 257	26 395	43 617
LSC*	43 431	13 534	7 511	12 277	55 853	13 619	10 205	23 509	NA	NA	NA	NA
proovread	38 962	14 918	6 714	7 956	47 344	17 460	9 233	11 140	NA	NA	NA	NA

We applied Hercules to correct PacBio reads generated from two BAC clones (CH17-157L1 and CH17-227A2) and a human CHM1 cell-line (WGS) using Illumina reads from the same resource. We report the accuracy as the alignment identity as calculated by the BLASR (34) aligner. Mapped refers to the number of any reads aligned to the assembly reference for these clones with any identity, where the other columns show the number of alignments within respective identity brackets. NA is set for the tools that we did not run for CHM1 cell-line. We picked the three algorithms that performed best given moderate short read coverage. * We ran LSC with a subsampled human CHM1 data set as it did not scale to large data set as it is reported in Supplementary Table S3.

We investigated the reasons for lower Hercules performance for the BAC clones, and we found that only ∼10% of the reads had >90% short read breadth of coverage. This low percentage of well-covered reads is due to higher error rate in this data set than expected (Supplementary Figure S1). With better short read coverage, LSC and Hercules performed better than all other correction tools and Hercules edged LSC out (Table2 and Supplementary Table S1). This result shows that our HMM-based algorithm performs better given high short read breadth of coverage. Finally, for the human CHM1 data set, Hercules produced the largest set of most accurate reads (i.e. >95% accuracy) even though LoRDEC produced slightly more mappable reads (Table 3).

Table 2.

Correction accuracy given high breadth of coverage (>90%) in CH17-227A2

	No. of aligned reads
Tool	Mapped	80-90%	90-95%	>95%
Uncorrected	4 429	2 135	2 093	26
Colormap	4 432	668	2 345	1 271
HALC (w/ LoRDEC)	4 438	168	219	3 994
HALC (w/o LoRDEC)	4 441	267	897	3 246
LoRDEC	4 425	124	224	4 006
LSC	4 473	45	149	4 264
Hercules	4 476	43	142	4 273
proovread	4 434	1 722	1 665	880

The input included 9449 PacBio reads which had at least 90% of their length covered by short reads. We report the accuracy as the alignment identity as calculated by the BLASR (34) aligner. Mapped column refers to the number of any reads aligned to the Sanger-assembled reference for this clone, where the other columns show the number of alignments within respective identity brackets.

Run time and memory requirements

Finally, we benchmarked computational requirements for each tool for BAC clones with their original data set. Furthermore, we assessed the scalability of the three leading methods (Hercules, LoRDEC, and LSC) and compared their performance on whole genome-sized problem using the human CHM1 cell line WGS data. A highly accurate aligner, Bowtie2, was not able to scale for such a large data set. Therefore, we used Minimap2 to be able to make the corrections even though it is less accurate than Bowtie2. This also prevented LSC to make its corrections in its default mode. Our attempts to modify LSC to provide it with Minimap2 alignment results were also unsuccessful as a single batch only ran in single thread. Therefore, for only accuracy comparison purposes, we subsampled the long read data to successfully run LSC and Hercules with Bowtie2 aligner (Supplementary Table S3). We found that LSC produces slightly more most accurate reads even though Hercules produced reads with a highest mapping rate.

For the BAC clones, we observed that de Bruijn graph based methods were at least three times faster than the alignment-based methods, LoRDEC and HALC were the fastest algorithms, and the run times of alignment-based tools were similar (Table 4). The only exception for this case is Colormap without its OEA refinement as its running time is similar to de Bruijn graph based methods. Running time of Hercules is still on the same scale even though the learning procedure is more time consuming because of per-read calls to Forward Backward and Viterbi algorithms. Interestingly, Hercules runs faster than LoRDEC on the large human genome data set. Since error correction is an offline and one-time task we argue that these run times are acceptable given the gain in accuracy.

Table 4.

Requirements of computational resources for all methods we compared

	CH17-1571		CH17-227A2		Homo Sapiens (CHM1)
Tool	Run time	Memory (GB)	Run time	Memory (GB)	Run time	Memory (GB)
Colormap	22m 17s	9.88	25m 20s	8.79	NA	NA
Colormap (OEA)	1h 36m 57s	9.82	2h 45m 51s	9.23	NA	NA
HALC (w/ LoRDEC)	16m 25s	26.29	25m 09s	23.09	NA	NA
HALC (w/o LoRDEC)	20m 22s	38.97	22m 47s	44.69	NA	NA
Hercules	1h 07m 49s	3.20	2h 10m 09s	3.16	82h 59m 53s	278.74
LoRDEC	12m 43s	1.20	26m 19s	1.33	112h 6m 34s	52.34
LSC*	1h 04m 55s	11.08	1h 40m 51s	9.00	NA	NA
proovread	1h 34m 24s	7.91	2h 39m 57s	4.03	NA	NA

We ran all tools on the same server using 60 threads. We report wall clock run times, and peak memory usage (GB) for each tool. NA is set for the tools that we did not run for CHM1 cell-line. We picked the three algorithms that performed best given a moderate short read coverage. * We ran LSC with a subsampled human CHM1 data set as it did not scale to large data set as it is reported in Supplementary Table S3.

We also investigated the memory requirements of the tools we benchmarked (Table 4). For BAC clones, we find that Hercules uses only a modest amount of memory, second to only LoRDEC. In the BAC clone data sets, the maximum memory Hercules required was 3.2GB, which makes it usable on commodity desktop computers if the size of the data set is not large such as human genome. We found that LoRDEC scales better than Hercules in terms of memory given a human genome data set as Hercules required five times more memory than that of LoRDEC. We note that the memory requirements of Hercules scale linearly with the short read depth of coverage and the number of the long reads to be corrected simultaneously in multiple threads, and the LoRDEC memory usage depends on the size of the de Bruijn graph. Note that LoRDEC is alignment-free, and it builds a de Bruijn graph to cover the entire short read data set. Thus, its memory usage will be determined by the graph size of the input DNA.

DISCUSSION

Long reads such as PacBio are attractive alternatives to short Illumina reads due to the ability to span across common repeats and complete gene fusions, which present analytical and computational challenges to accurately characterize and assemble genomes and transcripts. However, their error rate is also substantially higher than that of short reads making it hard to align them to reference genomes, or infer the fused genes. Therefore, it is useful to correct short indel and substitution errors either using very high coverage long read data, which substantially increases sequencing cost, or by using orthogonal and less expensive short read sequencing data. Here we introduced a new algorithm, Hercules, which uses a hidden Markov model based method to correct erroneous long reads using short but accurate Illumina data.

Profile HMMs have been successfully used for multiple sequence alignment and protein classification (35). In this paper, we modified the standard pHMM to leverage their probabilistic basepair consensus representation to correct long reads given set of aligned short reads. Our proposed pHMM-like structure offers a flexible approach since its initial parameters can be redefined based on the error profile of any other error-prone sequencing technology, such as Oxford Nanopore.

Hercules is slightly slower and more memory demanding compared to LoRDEC for small genome sizes, however, it returns more mappable reads. Hercules is also robust in terms of short read coverage and the genome size. It produces comparable results with low coverage data. It also scales well for large genome data set such as human genome. Furthermore, as we discussed above, the requirement of Bowtie2 aligner becomes a running time bottleneck for large genomes, which renders it inapplicable for mammalian genomes. Even though it may be possible to prevent a memory bottleneck of an aligner by partitioning long and short reads into smaller sizes, a running time bottleneck cannot be solved without either changing the parameters of an aligner or switching to a less accurate but faster aligner. For such cases, the aligner-flexible methods such as Hercules become more advantageous as it can adapt to any applicable aligner. In terms of run time, the main bottleneck for Hercules lies in the pHMM training for each long read. There are several algorithms proposed to improve running time and memory requirements of the standard Viterbi algorithm and Forward/Backward likelihood calculations that may be used to improve run time (36–38). Additionally Hercules may further be accelerated through SIMD vectorization of pHMM training and decoding (39–41) that we leave as future work.

SUPPLEMENTARY DATA

Supplementary Data are available at NAR Online.

FUNDING

TÜBİTAK [TÜBİTAK-1001-215E172 to C.A.]; Marie Curie Career Integration Grant [303772 to C.A.].

Conflict of interest statement. None declared.