Abstract
The analysis of neuroimaging data is frequently used to assist the diagnosis of neurodegenerative disorders such as Alzheimer’s disease (AD) or Parkinson’s disease (PD) and has become a routine procedure in the clinical practice. During the past decade, the pattern recognition community has proposed a number of machine learning-based systems that automatically analyse neuroimaging data in order to improve the diagnosis. However, the high dimensionality of the data is still a challenge and there is room for improvement. The development of novel classification frameworks as TensorFlow, recently released as open source by Google Inc., represents an opportunity to continue evolving these systems. In this work, we demonstrate several computer-aided diagnosis (CAD) systems based on Deep Neural Networks that improve the diagnosis for AD and PD and outperform those based on classical classifiers. In order to address the small sample size problem we evaluate two dimensionality reduction algorithms based on Principal Component Analysis and Non-Negative Matrix Factorization (NNMF), respectively. The performance of developed CAD systems is assessed using 4 datasets with neuroimaging data of different modalities.
Keywords: Multivariate analysis, machine learning, TensorFlow, deep neural networks, principal component analysis, non-negative matrix factorization, Alzheimer’s disease, Parkinson’s disease
1 Introduction
The diagnosis of neurodegenerative disorders such as Alzheimer’s disease (AD) or Parkinson’s disease (PD) is usually corroborated by means of neuroimaging data of different modalities. Magnetic resonance imaging, single-photon emission computed tomography (SPECT) or positron emission tomography (PET) are commonly used to this end. For AD, the structural data is used not only to determine a possible AD state but also to exclude other treatable or reversible causes of dementia such as normal-pressure hydrocephalus, subdural hematoma or tumours. Tomography techniques use radiotracers as 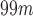 Tc-ECD and
Tc-ECD and 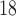 F-FDG for SPECT and PET scanners, respectively. In case of PD, most of the radiotracers focus on the dopaminergic transporters located at the striatum, since they are known to be affected by the disease.
F-FDG for SPECT and PET scanners, respectively. In case of PD, most of the radiotracers focus on the dopaminergic transporters located at the striatum, since they are known to be affected by the disease.
Initially these data were visually analysed by experienced clinicians but nowadays the analysis through computer systems is becoming a routine procedure [11, 23, 28]. Computer-aided diagnosis (CAD) systems are able to successfully manage the huge amount of information contained in the neuroimages and allow reducing the human factor in the data examination.
Two approaches have been proposed to develop a CAD system that analyse neuroimaging data. On the one hand, the most familiar approach to the neuroimaging community concerns mass univariate statistical testing, which models data at the scale of individual voxel, i.e. each voxel is analysed separately and relationships amongst distant voxels are not considered. The well-known Statistical Parametric Mapping (SPM) software [6] has become a standard to perform univariate analyses on neuroimaging data. However, SPM and other univariate approaches were not specifically developed to study a single image but to compare groups. Despite of this, univariate methods have been widely used to assist the diagnosis of AD and PD. For example, in [3] Foster and colleagues reported a diagnostic accuracy of 89.6% and a very high specificity (97.6%) in the differential diagnosis between AD and normal subjects and between AD and patients with frontotemporal degeneration.
On the other hand, multivariate approaches based on machine learning analyse a neuroimage as a single observation and explicitly consider the inter-relationships across voxels. Here, effects due to brain structure or function as well as confounding and error effects are assessed statistically both at each voxel and as interactions among voxels [5]. Research in this field has benefited from recent advances in machine learning such as semi-supervised learning based on the transductive concept [9], which have allowed new algorithms with a higher generalization ability and able to deal with the small sample size problem [2, 8]. In this regard, the research branch of the multinational technology company, Google Inc., has recently released as open-source a machine learning environment known as TensorFlow [1]. Provided as an API for Python and C/C++, the purpose of this software is to train neural networks to detect and decipher patterns and correlations. TensorFlow is currently used by many Google services such as Google Search or Gmail but its effectiveness in the classification of neuroimaging data remains still poorly studied [17].
In this work we analyse the use of Deep Neural Networks (DNN), as they are implemented on TensorFlow, to assist the diagnosis of neurodegenerative disorders. Specifically, we demonstrate several CAD systems to perform the differential diagnosis of AD and PD using different neuroimaging modalities. During the past years, deep neuronal networks have earned significant attention in different fields such as speech recognition, computer vision and bioinformatics [20]. In general, this classification procedure has been successfully applied to problems with availability of large samples. However, the validity of these models in problems with reduced samples, such as neuroimaging classification, has still been poorly analysed. In addition, in this work we evaluate two algorithms to address the small sample size problem by reducing the dimensionality of the data. These techniques allow us to summarize the information contained in neuroimages and are almost mandatory in this field. Due to the limitations to gather large samples of neuroimages (expensive procedures and equipment and need for clinical evaluations, which involves experienced clinicians) most of the neuroimaging studies use reduced datasets of a few tens of examples. Since each neuroimage contains several hundred thousand voxels, fitting the classification function is really challenging. Dimensionality reduction techniques reduce the input space to a few tens of dimensions, making the classifier training affordable.
The main contributions of this work are (i) the proposal of a CAD system implemented on TensorFlow and based on Principal Component Analysis (PCA) and DNN that improve the accuracy of previous systems based on classical classifiers, (ii) the comparison of two different dimensionality reduction approaches using the same data and classification algorithms and (iii) the analysis of the performance of several CAD systems on 4 datasets composed by data of different modality, which gives a general idea of the performance of these systems on the wide problem we are addressing: the diagnosis of neurodegenerative disorders using CAD systems.
2 Material and methods
2.1 Datasets
Four datasets, 2 for AD and 2 for PD, were used to evaluate the systems implemented in this work. Each dataset contains data of different modality. A brief description of each database is shown below:
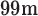 Tc-ECD SPECT database. Ninety-seven SPECT images from AD patients and healthy subjects were collected from a recent study carried out by the ‘Virgen de las Nieves’ hospital (Granada, Spain). The data were acquired by means of a Picker Prism 3000 gamma camera and reconstructed using a filtered back-projection (FBP) algorithm in combination with a Butterworth noise removal filter. The neuroimages were labelled by three experienced clinicians after visually analysing the data. As a result, 41 images were labelled as ‘normal’, 30 as ‘possible AD’, 22 as ‘probable AD’ and 4 as ‘certain AD’. In our experiments, patients belonging to any of the AD categories were considered as positive and the remaining subjects (labelled as ‘normal’) were considered negative.
Tc-ECD SPECT database. Ninety-seven SPECT images from AD patients and healthy subjects were collected from a recent study carried out by the ‘Virgen de las Nieves’ hospital (Granada, Spain). The data were acquired by means of a Picker Prism 3000 gamma camera and reconstructed using a filtered back-projection (FBP) algorithm in combination with a Butterworth noise removal filter. The neuroimages were labelled by three experienced clinicians after visually analysing the data. As a result, 41 images were labelled as ‘normal’, 30 as ‘possible AD’, 22 as ‘probable AD’ and 4 as ‘certain AD’. In our experiments, patients belonging to any of the AD categories were considered as positive and the remaining subjects (labelled as ‘normal’) were considered negative.DaTSCAN database. Neuroimaging data from 189 subjects were used to differentiate between healthy subjects and patients with Parkinsonian syndromes (PS). The images were acquired by the ‘Virgen de la Victoria’ hospital (Málaga, Spain) from January 2003 until December 2008. The data corresponds to patients that attended the hospital redirected by primary care services and who had symptoms that could be considered as Parkinsonism. The images were obtained between 3 and 4 h after the intravenous injection of 185 MBq (5 mCi) of Ioflupane-I-123 with prior thyroid blocking with Lugols solution. A General Electric gamma camera (Millennium model) equipped with a dual head was used to acquire the data. Then, the transaxial image slices were reconstructed using the FBP algorithm without attenuation correction and a Hanning filter (cut-off frequency equal to 0.7). Finally, the neuroimages were visually labelled by three nuclear medicine specialists from the hospital using only the information contained in the images, without any other medical information. As a result, 95 neuroimages were labelled as ‘normal’ and the remaining ones (94) as ‘PS’. Although PD is the most representative pathology of the PS group, it contains other pathologies with similar symptoms such as multi-system atrophy (MSA), progressive supra-nuclear palsy (PSP) and corticobasal degeneration.
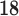 F-DMFP-PET database. This database was collected in a longitudinal study carried out in the University of Munich [13]. Eighty-seven patients with parkinsonism, previously confirmed by a
F-DMFP-PET database. This database was collected in a longitudinal study carried out in the University of Munich [13]. Eighty-seven patients with parkinsonism, previously confirmed by a 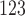 I-FP-CIT SPECT scan according to widely accepted criteria [12], undergone
I-FP-CIT SPECT scan according to widely accepted criteria [12], undergone 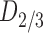 receptor imaging with
receptor imaging with 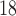 F-DMFP. This radioligand allows us to distinguish between different PS. The neuroimaging data were acquired 60 min after the radiopharmaceutical injection using a ECAT EXACT HR
F-DMFP. This radioligand allows us to distinguish between different PS. The neuroimaging data were acquired 60 min after the radiopharmaceutical injection using a ECAT EXACT HR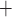 PET scanner (Siemens/CTI). As usual, the neuroimages were reconstructed by means of the FBP algorithm and a Hann filter with a cut-off frequency of
PET scanner (Siemens/CTI). As usual, the neuroimages were reconstructed by means of the FBP algorithm and a Hann filter with a cut-off frequency of 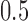 Nyquist and corrected for randoms, dead time and scatter. The patients were clinically monitored during the following years. Two years after the data acquisition, the neuroimages were labelled by experienced clinicians on the basis of last observations. According to the United Kingdom Parkinson Disease Society Brain Bank Diagnostic Criteria for Parkinson Disease [10], the second consensus statement on the diagnosis of multiple-system atrophy [7] and the established criteria for the diagnosis of progressive supranuclear palsy [15], 2 groups were defined: idiopathic PD (39 subjects) and non-idiopathic PD (48 subjects). The latter group contained 24 subjects with MSA and 24 subjects with PSP.
Nyquist and corrected for randoms, dead time and scatter. The patients were clinically monitored during the following years. Two years after the data acquisition, the neuroimages were labelled by experienced clinicians on the basis of last observations. According to the United Kingdom Parkinson Disease Society Brain Bank Diagnostic Criteria for Parkinson Disease [10], the second consensus statement on the diagnosis of multiple-system atrophy [7] and the established criteria for the diagnosis of progressive supranuclear palsy [15], 2 groups were defined: idiopathic PD (39 subjects) and non-idiopathic PD (48 subjects). The latter group contained 24 subjects with MSA and 24 subjects with PSP.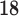 F-FDG-PET database. Alzheimers Disease Neuroimaging Initiative (ADNI) is a global research intended to test whether neuroimaging data and other biological markers can be combined to measure the progression of mild cognitive impairment and AD. ADNI is the resulting effort of many investigators from a broad range of academic institutions and private corporations. Subjects who participated in the study were recruited on more than 50 sites across the U.S. and Canada. To build this dataset, we used a subset of 420 neuroimages from AD patients and controls subjects.
F-FDG-PET database. Alzheimers Disease Neuroimaging Initiative (ADNI) is a global research intended to test whether neuroimaging data and other biological markers can be combined to measure the progression of mild cognitive impairment and AD. ADNI is the resulting effort of many investigators from a broad range of academic institutions and private corporations. Subjects who participated in the study were recruited on more than 50 sites across the U.S. and Canada. To build this dataset, we used a subset of 420 neuroimages from AD patients and controls subjects.
The neuroimaging data from all the 4 databases were spatially normalized to ensure that any given voxel in different images refers to the same anatomical position across the brains. To this end, the well-known template matching approach implemented in the SPM software (version 8) was used. The intensities of the neuroimages were also normalized with respect to a value, 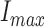 , computed by averaging the 1% of the voxels with highest intensity [22].
, computed by averaging the 1% of the voxels with highest intensity [22].
2.2 Dimensionality reduction of the data
The multivariate analysis of neuroimaging data usually suffers from the small sample size problem [2]. In order to address this problem, we used two dimensionality reduction approaches, one based on Principal Component Analysis and the other based on Non-Negative Matrix Factorization [16, 19]. Given a matrix 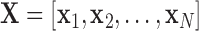 composed as a set of
composed as a set of 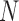 neuroimages in vector form (
neuroimages in vector form (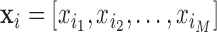 ), these algorithms proceed as follows:
), these algorithms proceed as follows:
- Dimensionality reduction based on PCA: After normalizing the data, X, to have zero mean and unitary norm, PCA performs the decomposition:
where
(1) 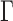 and
and 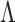 are known as eigenvectors and eigenvalues, respectively. Because the dimensionality of the patterns is greater than the number of patterns (
are known as eigenvectors and eigenvalues, respectively. Because the dimensionality of the patterns is greater than the number of patterns (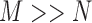 ), diagonalizing
), diagonalizing 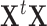 instead of
instead of 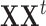 reduces the computational burden. In this case, the PCA decomposition should be reformulated as [28]:
reduces the computational burden. In this case, the PCA decomposition should be reformulated as [28]: 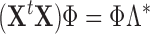
(2)
where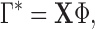
(3) 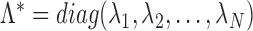 and
and 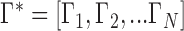 are the first
are the first 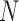 eigenvalues and eigenvectors, respectively.
eigenvalues and eigenvectors, respectively. - Dimensionality reduction based on NNMF: This algorithm computes two non-negative matrices
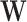 and
and 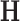 such that [14]
such that [14]
where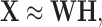
(4) 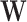 and
and 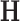 have dimension
have dimension  and
and  , respectively, being
, respectively, being 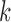 a design parameter which will determine the depth of the dimensionality reduction. In our experiments this parameter was set to commonly use value of
a design parameter which will determine the depth of the dimensionality reduction. In our experiments this parameter was set to commonly use value of 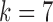 . Mathematically, the factors
. Mathematically, the factors  and
and 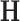 are chosen to minimize a reconstruction error,
are chosen to minimize a reconstruction error,  , that can be estimated as (Frobenius approach)
, that can be estimated as (Frobenius approach)
subject to the non-negativity constraints
(5)  .
.
After decomposition, a reduced dataset is obtained by projecting the original data over the new coordinate space defined by the eigenvectors (in case of PCA) or the matrix 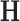 (in case of NNMF).
(in case of NNMF).
2.3 Classification based on TensorFlow
TensorFlow is a machine learning library developed by Google and released as open source on November 2015 [1]. It provides an interface for expressing and executing machine learning algorithms. These algorithms are described by directed graph composed of a set of nodes, which represent the instantiation of an operation and have zero or more inputs and zero or more outputs. The graph represents a dataflow computation, with extensions for allowing some kinds of nodes to maintain and update persistent state and for branching and looping control structures within the graph in a manner similar to Naiad [18].
One of the key feature of TensorFlow is its ability to run on multiple CPU and devices, reducing the computation times for complex problems. Additionally, it could use CUDA extensions for general-purpose computing on graphics processing units. The library is currently used in dozens of commercial Google products such as speech recognition, Gmail, Google Photos and Google Search [27]. It is available as a Python API as well as a C/C++ API.
In this work we used the Python API provided by the SkFlow project, which allows building DNN using the interface of Scikit Learn [21]. Specifically, we used a 3 layers DNN with 5 hidden units per layer. The Adagrad algorithm was used as optimizer.
3 Experiments and results
After the dimensionality reduction based either on PCA or NNMF, a DNN implemented on TensorFlow was used to separate the groups of each dataset. Accuracy measures were computed using a 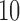 -fold cross-validation (CV) approach and the parameters shown in Table 1. The results were compared with the ones obtained by other statistical classifiers used in previous works to assist the diagnosis of neurodegenerative disorders, i.e. Naive Bayes (NB), Decision Tree (DT) and Support Vector Machine (SVM). In order to avoid biased results, the dimensionality reduction step was carried out using only the training data, i.e. inside the CV loop and therefore it was repeated for each fold. Table 2 shows the results for the 4 datasets used in this work. The range of the intermediate accuracy rates obtained in each fold of the CV procedure is shown in Figure 1.
-fold cross-validation (CV) approach and the parameters shown in Table 1. The results were compared with the ones obtained by other statistical classifiers used in previous works to assist the diagnosis of neurodegenerative disorders, i.e. Naive Bayes (NB), Decision Tree (DT) and Support Vector Machine (SVM). In order to avoid biased results, the dimensionality reduction step was carried out using only the training data, i.e. inside the CV loop and therefore it was repeated for each fold. Table 2 shows the results for the 4 datasets used in this work. The range of the intermediate accuracy rates obtained in each fold of the CV procedure is shown in Figure 1.
Table 1.
Algorithm parameters used in this work. Remaining parameters for listed algorithms and parameters for the remaining classifiers were set to their default values. Variable 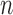 in first row stands for the number of examples in a given dataset
in first row stands for the number of examples in a given dataset
| Algorithm | Parameter | Value |
|---|---|---|
| PCA | Number of eigenvectors |
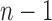
|
| NNMF | Rows of 
|
7 |
| SVM | Cost (C) | 1 |
| DNN | Number of layers | 5 |
| DNN | Units per layers | 5 |
| DNN | Optimizer | Adagrad |
Table 2.
Accuracy rate obtained with the proposed method when used to assist the diagnosis of AD, PS and PD (standard deviation is given in parentheses). The results are compared with the ones obtained by other systems based on NB, DTs and SVMs classification. Datasets 1, 2, 3 and 4 contain 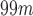 Tc-ECD SPECT (AD diagnosis), DaTSCAN (PS diagnosis),
Tc-ECD SPECT (AD diagnosis), DaTSCAN (PS diagnosis), 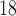 F-DMFP-PET (PD diagnosis) and
F-DMFP-PET (PD diagnosis) and 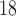 F-FDG-PET (AD diagnosis) data, respectively
F-FDG-PET (AD diagnosis) data, respectively
| PCA | NNMF | ||
|---|---|---|---|
| Dataset 1 | DNN (TensorFlow) | 83.51 (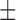 13.23) % 13.23) % |
70.10 (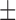 15.88) % 15.88) % |
| NB | 81.44 (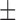 11.21) % 11.21) % |
70.10 (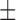 15.77) % 15.77) % |
|
| DTs | 82.47 (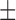 9.29) % 9.29) % |
75.25 ( 8.10) % 8.10) % |
|
| SVM | 82.47 (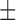 9.79) % 9.79) % |
57.73 ( 2.47) % 2.47) % |
|
| Dataset 2 | DNN (TensorFlow) | 87.30 (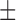 7.77) % 7.77) % |
76.19 ( 16.94) % 16.94) % |
| NB | 75.66 ( 7.47) % 7.47) % |
86.24 (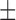 7.24) % 7.24) % |
|
| DTs | 77.25 (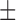 6.09) % 6.09) % |
85.19 (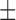 8.89) % 8.89) % |
|
| SVM | 91.53 (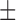 8.40) % 8.40) % |
59.78 (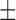 13.19) % 13.19) % |
|
| Dataset 3 | DNN (TensorFlow) | 70.11 (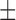 19.47) % 19.47) % |
57.47 (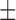 11.42) % 11.42) % |
| NB | 66.67 (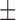 14.91) % 14.91) % |
55.17 ( 15.94) % 15.94) % |
|
| DTs | 62.06 (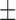 14.02) % 14.02) % |
57.47 (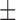 15.10) % 15.10) % |
|
| SVM | 67.82 (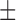 21.19) % 21.19) % |
55.17 (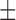 3.47) % 3.47) % |
|
| Dataset 4 | DNN (TensorFlow) | 96.19 (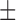 4.08) % 4.08) % |
70.71 (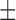 7.19) % 7.19) % |
| NB | 85.48 (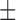 5.55) % 5.55) % |
85.48 (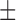 5.55) % 5.55) % |
|
| DTs | 87.38 (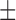 6.64) % 6.64) % |
86.19 (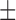 4.87) % 4.87) % |
|
| SVM | 95.47 ( 3.06) % 3.06) % |
66.67 ( 0.00) % 0.00) % |
Figure 1.
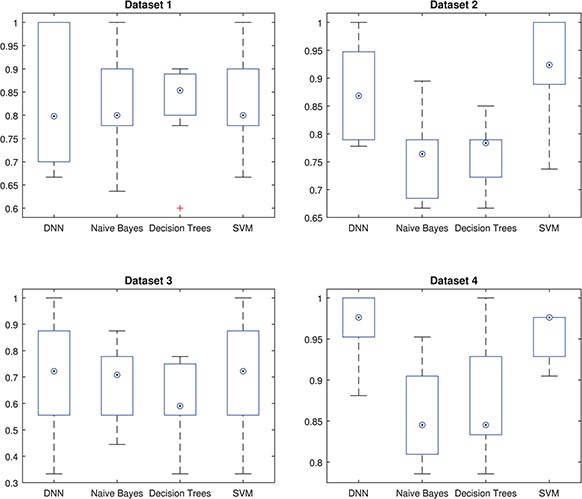
Intermediate accuracies obtained in the cross-validation procedure. Blue boxes and circled dots represent accuracies’ range and median, respectively.
Besides the accuracy, sensitivity and specificity (respectively related with true and false positive rate) are of great relevance in CAD systems. Receiver Operating Characteristic (ROC) curves allow us to analyse the trade-off between these two measures. In a ROC curve, the optimal solution is located in the upper-left corner and corresponds to a true positive rate of 100% and a false positive rate of 0. Therefore, the closer the ROC curve is to the upper-left corner, the higher the overall accuracy of the procedure. The area under the curve (AUC) is a good indicator of this accuracy. Figure 2 shows the ROC curves corresponding to the best systems (one per classifier) for each database.
Figure 2.
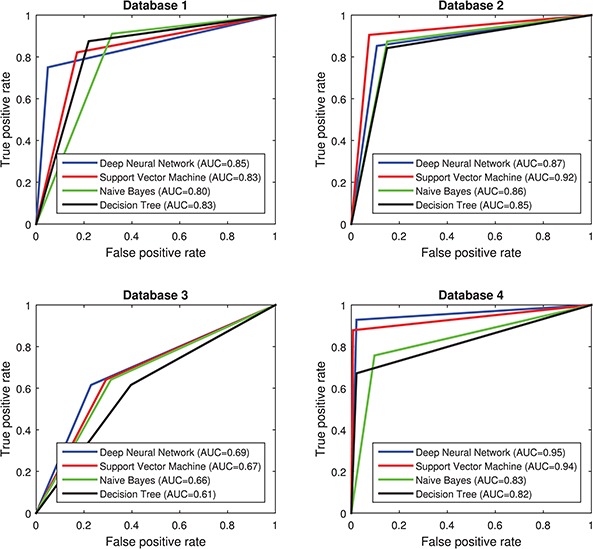
ROC curves for the best systems for each database. The AUC measure is included in the legend. Datasets 1, 2, 3 and 4 contain  Tc-ECD SPECT (AD diagnosis), DaTSCAN (PS diagnosis),
Tc-ECD SPECT (AD diagnosis), DaTSCAN (PS diagnosis),  F-DMFP-PET (PD diagnosis) and
F-DMFP-PET (PD diagnosis) and 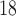 F-FDG-PET (AD diagnosis) data, respectively.
F-FDG-PET (AD diagnosis) data, respectively.
4 Discussion and conclusions
The results presented in previous section suggest that TensorFlow is a suitable framework to develop CAD systems for neurodegenerative disorders. The proposed systems based on DNN provided high accuracy and for 3 databases, these systems along with PCA dimensionality reduction techniques achieved the highest accuracy. Nevertheless, as shown in Figure 1 the accuracy measure obtained by DNN-based systems is more fluctuating than those obtained by other classifiers. This is especially significant for dataset 1 where rates oscillate between 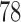 and
and 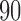 for NB, DT and SVM but are between
for NB, DT and SVM but are between 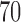 and
and 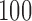 for DNN. This fact can be due to DNN has more parameters that should be optimized during the training produce and probably requires larger training samples. In spite of that, the accuracy rate obtained by the DNN-based system in the whole CV procedure for dataset 1 is higher than that obtained by other systems. High accuracy rates obtained in general in this work are partly due to the dimensionality reduction carried out by the algorithms based on PCA and NNMF. They made the classification problem affordable and allowed us to develop full-automatic systems that did not require initialization steps based on previous knowledge, such as a region selection.
for DNN. This fact can be due to DNN has more parameters that should be optimized during the training produce and probably requires larger training samples. In spite of that, the accuracy rate obtained by the DNN-based system in the whole CV procedure for dataset 1 is higher than that obtained by other systems. High accuracy rates obtained in general in this work are partly due to the dimensionality reduction carried out by the algorithms based on PCA and NNMF. They made the classification problem affordable and allowed us to develop full-automatic systems that did not require initialization steps based on previous knowledge, such as a region selection.
The relatively low accuracy rates obtained for the third dataset by most of the systems are explained by the problem addressed in this study. Distinguishing among PS is very difficult because of the disorders of this family produce similar neurological hallmarks and patients show similar symptoms [25, 26]. In addition, all the data included in this dataset correspond to subjects with early stage diseases. The analysis of the classification measures reported in previous section should also considered the error inherent to the labelling procedure. In classification studies related with clinical diagnosis there often exists an error due to possible labelling errors. Only high confident labels such as those corroborated by autopsy in AD patients are not affected by this problem.
It is worth noting that the accuracy values reported in Table 2 should be independently analysed for each dataset. It would make no sense to compare the accuracy values obtained with different dataset, even if they are intended to study the same disorder, because they were acquired from different populations, with different disease stages and were labelled using different criteria. Thus, e.g. the first dataset was labelled taking into account both the results of neuropsyhological tests and the visual examination of the neuroimages. In contrast, dataset 4 was labelled without considering the neuroimaging data.
An important matter in the development of CAD systems is parameter optimization. The more sophisticated is a system, the more parameters should be optimized. The parameter optimization requires additional data and if they are limited, simple systems often perform better than sophisticated ones. The proposed systems are not exempt from this problem. For example, the number of features resulting from the dimensionality reduction procedure (parameter 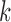 in NNMF or number of principal components in PCA) can be optimized. Similarly classification parameters such as the cost parameter of the SVM classifier,
in NNMF or number of principal components in PCA) can be optimized. Similarly classification parameters such as the cost parameter of the SVM classifier, 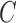 , or the number of units of the DNN algorithm can also be optimized. However, this optimization would require additional data and the number of samples in most of the neuroimaging studies (including the ones used in this work) is reduced. For this reason we decided to keep these parameters to their common/default values. In our opinion, the value of the results is not affected by this decision because all the systems were evaluated under the same conditions, so they can be fairly compared.
, or the number of units of the DNN algorithm can also be optimized. However, this optimization would require additional data and the number of samples in most of the neuroimaging studies (including the ones used in this work) is reduced. For this reason we decided to keep these parameters to their common/default values. In our opinion, the value of the results is not affected by this decision because all the systems were evaluated under the same conditions, so they can be fairly compared.
Funding
This work was supported by and the MINECO under the TEC2015-64718-R project and the Vicerectorate of Research and Knowledge Transfer of the University of Granada.
Data collection and sharing for this project was funded by the Alzheimer’s Disease Neuroimaging Initiative (ADNI) (National Institutes of Health Grant U01 AG024904) and DOD ADNI (Department of Defense award number W81XWH-12-2-0012). ADNI is funded by the National Institute on Aging, the National Institute of Biomedical Imaging and Bioengineering and through generous contributions from the following: Alzheimers Association; Alzheimers Drug Discovery Foundation; Araclon Biotech; BioClinica, Inc.; Biogen Idec Inc.; Bristol-Myers Squibb Company; Eisai Inc.; Elan Pharmaceuticals, Inc.; Eli Lilly and Company; EuroImmun; F. Hoffmann-La Roche Ltd and its affiliated company Genentech, Inc.; Fujirebio; GE Healthcare; IXICO Ltd.; Janssen Alzheimer Immunotherapy Research & Development, LLC.; Johnson & Johnson Pharmaceutical Research & Development LLC.; Medpace, Inc.; Merck & Co., Inc.; Meso Scale Diagnostics, LLC.; NeuroRx Research; Neurotrack Technologies; Novartis Pharmaceuticals Corporation; Pfizer Inc.; Piramal Imaging; Servier; Synarc Inc.; and Takeda Pharmaceutical Company. The Canadian Institutes of Health Research is providing funds to support ADNI clinical sites in Canada. Private sector contributions are facilitated by the Foundation for the National Institutes of Health (www.fnih.org). The grantee organization is the Northern California Institute for Research and Education, and the study is coordinated by the Alzheimer’s Disease Cooperative Study at the University of California, San Diego. ADNI data are disseminated by the Laboratory for Neuro Imaging at the University of Southern California.
References
- Abadi M., Agarwal A., Barham P., Brevdo B., Chen Z., Citro C., Corrado G. S., Davis A., Dean J., Devin M., Ghemawat S., Goodfellow I., Harp A., Irving G., Isard M., Jia Y., Jozefowicz R., Kaiser L., Kudlur M., Levenberg J., Mané D., Monga R., Moore S., Murray D., Olah C., Schuster M., Shlens J., Steiner B., Sutskever I., Talwar K., Tucker P., Vanhoucke V., Vasudevan V., Viégas F., Vinyals O., Warden P., Wattenberg M., Wicke M., Yu Y. and Zheng X.. . TensorFlow: large-scale machine learning on heterogeneous systems. Software available from https://www.tensorflow.org/ (Nov. 2015).
- Duin R. Classifiers in almost empty spaces. In 15th International Conference on Pattern Recognition. Proceedings, vol. 2, pp. 1–7. Barcelona, Spain: IEEE; 2000. doi:10.1109/ICPR.2000.906006. [Google Scholar]
- Foster N. L., Heidebrink J. L., Clark C. M., Jagust W. J., Arnold S. E., Barbas N. R., DeCarli C. S., Turner R. S., Koeppe R. A., Higdon R. and Minoshima S... FDG-PET improves accuracy in distinguishing frontotemporal dementia and Alzheimer’s disease. Brain, 130, 2616–2635, 2007. doi:10.1093/brain/awm177. [DOI] [PubMed] [Google Scholar]
- Friston K. J., Ashburner J. T., Kiebel S. J., Nichols T. E. and Penny W. D.. Statistical Parametric Mapping: The Analysis of Functional Brain Images, 1st edn. Academic Press, Amsterdam, 2006. [Google Scholar]
- Friston K. and Stephan K.. Chapter 03 - Modelling brain responses. In Statistical Parametric Mapping, John Ashburner Karl Friston, Thomas Nichols Stefan Kiebel and William Penny, , pp. 32–45. Academic Press, London, 2007. [Google Scholar]
- Gilman S., Wenning G. K., Low P. A., Brooks D. J., Mathias C. J., Trojanowski J. Q., Wood N. W., Colosimo C., Dürr A., Fowler C. J., Kaufmann H., Klockgether T., Lees A., Poewe W., Quinn N., Revesz T., Robertson D., Sandroni P., Seppi K. and Vidailhet M... Second consensus statement on the diagnosis of multiple system atrophy. Neurology, 71, 670–676, 2008. doi:10.1212/01.wnl.0000324625.00404.15. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Górriz J. M., Ramírez J., Suckling J., Illán I. A., Ortiz A., Martinez-Murcia F. J., Segovia F., Salas-González D. and Wang S... Case-based statistical learning: a non-parametric implementation with a conditional-error rate SVM. IEEE Access, 5, 11468–11478, 2017. doi:10.1109/ACCESS.2017.2714579. [Google Scholar]
- Gorriz J. M., Ramirez J., Suckling J., Martinez-Murcia F. J., Illán I. A., Segovia F., Ortiz A., Salas-González D., Castillo-Barnés D. and Puntonet C. G... A semi-supervised learning approach for model selection based on class-hypothesis testing. Expert Systems with Applications, 90, 40–49, 2017. doi:10.1016/j.eswa.2017.08.006. [Google Scholar]
- Hughes A. J., Daniel S. E., Ben-Shlomo Y. and Lees A. J... The accuracy of diagnosis of parkinsonian syndromes in a specialist movement disorder service. Brain, 125, 861–870, 2002. doi:10.1093/brain/awf080. [DOI] [PubMed] [Google Scholar]
- Illán I. A., Górriz J. M., Ramírez J., Segovia F., Jiménez-Hoyuela J. M. and Lozano S. J. O.. Automatic assistance to Parkinson’s disease diagnosis in DaTSCAN SPECT imaging. Medical Physics, 39, 5971–5980, 2012. doi:10.1118/1.4742055. [DOI] [PubMed] [Google Scholar]
- Koch W., Radau P. E., Hamann C. and Tatsch K.. Clinical testing of an optimized software solution for an automated, observer-independent evaluation of dopamine transporter SPECT studies. Journal of Nuclear Medicine: Official Publication, Society of Nuclear Medicine, 46, 1109–1118, 2005. [PubMed] [Google Scholar]
- la Fougère C., Pöpperl G., Levin J., Wängler B., Böning G., Uebleis C., Cumming P., Bartenstein P., Bötzel P. and Tatsch K.. The value of the dopamine D2/3 receptor ligand 18F-desmethoxyfallypride for the differentiation of idiopathic and nonidiopathic parkinsonian syndromes. Journal of Nuclear Medicine, 51, 581–587, 2010. doi:10.2967/jnumed.109.071811. [DOI] [PubMed] [Google Scholar]
- Lee D. D. and Seung H. S... Learning the parts of objects by non-negative matrix factorization. Nature, 401, 44565, 1999. doi:10.1038/44565. [DOI] [PubMed] [Google Scholar]
- Litvan I., Agid Y., Calne D., Campbell G., Dubois B., Duvoisin R. C., Goetz C. G., Golbe L. I., Grafman J., Growdon J. H., Hallett M., Jankovic J., Quinn N. P., Tolosa E. and Zee D. S... Clinical research criteria for the diagnosis of progressive supranuclear palsy (Steele-Richardson-Olszewski syndrome): report of the NINDS-SPSP international workshop. Neurology, 47, 1–9, 1996. [DOI] [PubMed] [Google Scholar]
- Lopez M., Ramirez J., Gorriz J., Salas-Gonzalez D., Alvarez I., Segovia F. and Puntonet C. G.. . Automatic tool for alzheimer’s disease diagnosis using PCA and bayesian classification rules. Electronics Letters, 45, 389–391, 2009. doi:10.1049/el.2009.0176. [Google Scholar]
- Martinez-Murcia F. J., Ortiz A., Górriz J. M., Ramírez J., Segovia F., Salas-Gonzalez D., Castillo-Barnes D. and Illán I. A... A 3D convolutional neural network approach for the diagnosis of Parkinson’s disease. In Natural and Artificial Computation for Biomedicine and Neuroscience, pp. 324–333. Springer, Cham, 2017. doi:10.1007/978-3-319-59740-9.32. [Google Scholar]
- Murray D. G., McSherry F., Isaacs R., Isard M., Barham P. and Abadi M... Naiad: a timely dataflow system. In Proceedings of the Twenty-Fourth ACM Symposium on Operating Systems Principles, SOSP ’13, pp. 439–455. Association for Computing Machinery, New York, NY, USA. 2013. doi:10.1145/2517349.2522738.
- Padilla P., Górriz J. M., Ramírez J., Lang E. W., Chaves R., Segovia F., López M., Salas-González D. and Álvarez I... Analysis of SPECT brain images for the diagnosis of Alzheimer’s disease based on NMF for feature extraction. Neuroscience Letters, 479, 192–196, 2010. doi:10.1016/j.neulet.2010.05.047. [DOI] [PubMed] [Google Scholar]
- Pastur-Romay L. A., Cedrón F., Pazos A. and Porto-Pazos A. B... Deep artificial neural networks and neuromorphic chips for big data analysis: pharmaceutical and bioinformatics applications. International Journal of Molecular Sciences, 17, 2016. doi:10.3390/ijms17081313. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pedregosa F., Varoquaux G., Gramfort A., Michel V., Thirion B., Grisel O., Blondel M., Prettenhofer P., Weiss R., Dubourg V., Vanderplas J., Passos A., Cournapeau D., Brucher M., Perrot M. and Duchesnay É... Scikit-learn: machine learning in Python. Journal of Machine Learning Research, 12, 2825–2830, 2011. [Google Scholar]
- Saxena P., Pavel D. G., Quintana J. C. and Horwitz B.. An automatic threshold-based scaling method for enhancing the usefulness of Tc-HMPAO SPECT in the diagnosis of Alzheimer’s disease. In Medical Image Computing and Computer-Assisted Interventation—MICCAI’98, Wells W. M., Colchester A., Delp S., eds, pp. 623–630. Lecture Notes in Computer Science, Cambridge MA, USA.Springer Berlin, Heidelberg, 1998. [Google Scholar]
- Segovia F., Bastin C., Salmon E., Górriz J. M., Ramírez J. and Phillips C.. Combining PET images and neuropsychological test data for automatic diagnosis of Alzheimer's disease. In PLoS ONE, 9, e88687, 2014 doi:10.1371/journal.pone.0088687. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Segovia F., Salas-Gonzalez D., Górriz J. M., Ramírez J. and Martínez-Murcia F. J.. Analysis of 18F-DMFP-PET data using hidden Markov random field and the Gaussian distribution to assist the diagnosis of Parkinsonism. In Proceeding of SPIE Medical Imaging 2017 , vol. 10134, pp. 101342B–101342B–7. Orlando, FL, USA: 2017 doi:10.1117/12.2250281. [Google Scholar]
- Segovia F., Górriz J. M., Ramírez J., Martínez-Murcia F. J., Levin J., Schuberth M., Brendel M., Rominger A., Bötzel K., Garraux G. and Phillips C.. Multivariate analysis of 18F-DMFP PET data to assist the diagnosis of Parkinsonism. Frontiers in Neuroinformatics, 11, 2017. doi:10.3389/fninf.2017.00023. [DOI] [PMC free article] [PubMed] [Google Scholar]
- TensorFlow-Google’s latest machine learning system, open sourced for everyone (Nov. 2015).
- Towey D. J., Bain P. G. and Nijran K. S.. Automatic classification of 123I-FP-CIT (DaTSCAN) SPECT images. Nuclear Medicine Communications, 32, 699–707, 2011. doi:10.1097/MNM.0b013e328347cd09. August 2011. [DOI] [PubMed] [Google Scholar]
- Trambaiolli L. R., Lorena A. C., Fraga F. J., Kanda P. A. M., Anghinah R. and Nitrini R.. Improving Alzheimer’s disease diagnosis with machine learning techniques. Clinical EEG and Neuroscience, 42, 160–165, 2011. doi:10.1177/155005941104200304. [DOI] [PubMed] [Google Scholar]
- Turk M. and Pentland A.. Eigenfaces for recognition. Journal of Cognitive Neuroscience, 3, 71–86, 1991. doi:10.1162/jocn.1991.3.1.71. [DOI] [PubMed] [Google Scholar]


