Microfluidic flow-free generation of chemical concentration gradients

Abstract

This paper presents a class of novel microfluidic concentration gradient generation (CGG) devices that create temporally stable chemical concentration gradients with complex shapes in a flow-free environment. The devices feature a two-layer channel design and the incorporation of a semipermeable membrane, which effectively segregates the concentration gradient region in the lower layer from the flow of reagent sample (simply “sample” onward) and buffer in the upper layer. In the mean time, free diffusion across the membrane constantly replenishes sample and buffer to maintain a stable concentration. The shapes of the concentration gradients are controlled by the geometries of the micro-channels and chambers. Concentration gradients with complex shapes can be achieved by piecewise combining constituent gradients with elementary shapes. Capable of generating concentration gradients in a flow-free environment, our devices eliminate undesirable flow stimulation on biological cells under investigation, while maintaining a stable chemical environment for cell studies.

1. Introduction

Chemical concentration gradients play an important role in cell growth and differentiation [1–3], signaling [4–6], chemotaxis [7–9], and other cell biology studies that involve exogenous chemical stimulation and cell response. Compared to conventional methods for generating chemical concentration gradients, microfluidic concentration gradient generation (CGG) device is of particular interest, thanks to their advantages in low reagent consumption and ease of control and automation. In stem cell research, for instance, microfluidic CGG was used to generate different gradient profiles of growth factors for controlling the growth and differentiation of human neural stem cells [10]. In pharmacological screening, gradients of drug molecules were also created using a microfluidic device for lead optimization in drug discovery processes [11]. In a high-throughput microfluidic cell culture array, the integration of a gradient generator enabled different cell lines to be cultured and treated with a variety of chemical concentrations in a single setup [12], substantiating the role of CGG devices in cell culture and treatment.

Currently, microfluidic CGG devices most commonly exploit molecular diffusion between multiple streams of laminar flow [7,8,10,13–17]. To generate a chemical gradient, streams of buffer and sample with different concentrations are introduced into a network of microchannels at carefully determined flow rates. The streams are joined at appropriately selected positions such that after the junctions, chemical molecules will diffuse between the streams for a predetermined time and distance depending on the flow rates. As a result, a desired concentration gradient profile will form across the channel width further downstream; the shape of the gradient profile is determined by a combination of the channel network configuration and sample concentration and flow rate of each stream. While such microfluidic devices using multi-stream laminar flow are capable of generating relatively complex gradient profiles, the presence of bulk fluid flow significantly limits their use in cell biology studies. For example, the bulk flow may introduce undesired shear force to cells under investigation, and the presence of continuous fluid flow may flush away cells that do not attach to surfaces. Even for adherent cells, cell-secreted growth factors essential for intercellular signaling may be carried away by fluid flow, leading to failure of signaling between cells. Moreover, the stability of the concentration gradient profiles is limited by flow rate stability; that is, as the shape of the gradient profiles critically depends on flow rates, it could be significantly changed by even slight disturbances to the flow. Finally, when relatively high flow rates are required, sample and reagent consumption becomes significant, especially when cells need to be cultured in the concentration gradients for extended period of time.

There have been a number of notable attempts to eliminatebulk fluid flow in microfluidic concentration gradient generation. For example, two parallel channels respectively containing sample and buffer solutions can be perpendicularly connected by another channel in which a linear gradient of the chemical concentration results [18]. Bulk flow is drastically reduced in the perpendicular gradient forming channel when identical flow rates were used in the parallel sample and buffer channels, allowing the study of non-adherent cells. To generate concentration profiles more complex than linear gradient profiles, the shape of the gradient forming channel can be modified to generate nonlinear, yet monotonically varying gradient profiles [19]. However, such designs, relying on precisely matching sample and buffer flow rates, remain susceptible to mechanical disturbances to the microfluidic system.

Alternatively, a straight gradient forming channel lies between two large, stationary reservoirs, each respectively containing sample and buffer solutions [6]. The channel is coupled to the reservoirs through a semipermeable membrane, which eliminates bulk flow while allowing molecular diffusion. This approach is more effective in eliminating fluid disturbances in the gradient forming channel, but is limited to linear concentration profiles, which also diminish over an extended period of time. These limitations can be over-come by using a hydrogel as a medium in which concentration gradients are established [20,21]. For example, parallel sample and buffer streams may be separated by a sheet of hydrogel, through which sample molecules diffuse and a concentration gradient is created, and a gradient forming channel is placed in contact with the hydrogel to sample different concentration gradients depending on the location and shape of the channel [20]. This effectively eliminatesflow disturbancesin the gradient forming channel, and is capable of maintaining temporally non-diminishing gradient profiles with constant replenishment of sample and buffer, and by design of the gradient forming channel shape, allows generation of more complex concentration gradients. Unfortunately, due to slow molecular diffusion in hydrogels, this approach requires prolonged setup times for the concentration gradients (e.g., about 10 h [20]).

This paper presents an approach to microfluidic concentration gradient generation that is capable of generating temporally stable chemical concentration gradients with various shapes in a flow-free environment. The approach is based on two microfluidic layers separated by a semipermeable membrane. Bulk fluid flow of chemical sample and buffer solutions is contained within the upper layer, and chemical concentration gradients are generated within a flow-free microchamber in the lower layer. Cross-membrane diffusion of sample molecules allows continuous replenishment of sample and buffer from the upper-layer channels to the lower-layer gradient forming microchamber, whose shape can be designed to allow the generation of concentration gradient profiles of different shapes. Such flow-free gradient profiles will be useful for cell biology applications, especially those that involve non-attachable cells.

2. Principle and design

2.1. Generation of flow-free concentration gradients

Our approach to microfluidic concentration generation is based on a two-layer device configuration (Fig. 1). The upper layer consists of two parallel microchannels respectively containing a sample and a buffer solution, while the lower layer contains a gradient forming microchamber. The sample and buffer channels are connected to the microchamber through a semipermeable membrane, which is sandwiched between the two microfluidic layers, allowing molecular diffusion while preventing bulk fluid flow across the membrane. The microchamber is connected through the membrane pores to the sample and buffer channels at selected chamber boundaries (referred to as “control boundaries”). At these control boundaries, the fluid concentrations in the gradient forming microchamber are kept constant by the fluid flowing in the overlaying sample and buffer channels by means of molecular diffusion across the membrane at these boundaries.

Fig. 1.

Device configuration. (a) Exploded view of the device: an upper PDMS layer containing sample and buffer channels, a bottom layer containing a gradient forming microchamber, and a semipermeable membrane sandwiched in between. (b) A sealed final device. Marked in red are the control boundaries where the concentration in the gradient forming chamber is controlled to be constant by the running sample and buffer solutions in the respective overlaying channels. (c) Fluidic path and molecular diffusion path. The solid arrows denote fluidic path, and the dotted arrows denote diffusion path. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

During operation, sample and buffer are supplied in their respective channels at a flow rate enough for replenishment. At the control boundaries, due to the concentration difference across the membrane, sample molecules will diffuse from the sample channel into the gradient forming microchamber and then into the buffer channel. Fig. 1c illustrates the fluidic path in the sample and buffer channels, as well as the path for molecular diffusion across the membrane pores and the gradient forming microchamber. As sample and buffer are replenished at a constant flow rate in the upper layer, constant concentrations are imposed at the control boundaries of the gradient forming microchamber, with a higher concentration at the boundaries coupled to the sample channel and a lower concentration at those connected to the buffer channel. In the mean time, sample molecules also diffuse within the gradient forming microchamber. After an initial transition time, a concentration gradient will evolve and reach a steady state in the gradient forming microchamber. This gradient profile will not diminish over time thanks to the continuous replenishment of the sample and buffer solutions.

Due to the large cross-membrane flow resistance resulting from the small pore size, bulk flow is limited to the upper layer only, creating a flow-free environment in the gradient forming microchamber. The large cross-membrane flow resistance also makes the gradient forming microchamber virtually unaffected by flow disturbances inside the sample and buffer channels. As sample molecules inside the gradient forming microchamber move only through diffusion and not through convection, the resulting concentration gradient will not be distorted by fluid flow once the gradient is established.

2.2. Facilitating concentration gradient setup

In order to facilitate the establishment of concentration gradients, we did not solely rely on passive diffusion across the membrane during the initial gradient forming period. While setting up the gradient, we applied a higher pressure at the sample channel than the buffer channel, which, in the gradient forming chamber, created a very slight fluid movement carrying sample molecules in the same direction of molecular diffusion. This fluid movement was very slow due to the large fluidic resistance of the semipermeable membrane, so it would not cause potential disturbance to cells. When the front of the sample solution reached halfway through the gradient forming chamber, we changed both sample and buffer to the same flow rate to stop the fluid movement in the gradient forming chamber. Subsequently, molecular diffusion started to happen from the middle of the gradient forming chamber where the concentration gradient is the sharpest, and the gradient was developing in both directions along the chamber. This not only reduced the diffusion length L by half and hence diffusion time t by 75% (t~L²), but also avoided the diffusion bottleneck at the semipermeable membranes.

Comparing to Ref. [20], we also used Alexa Fluor as the sample. However, we used water instead of hydrogel as medium, and the diffusivity of Alexa 488 in water is D = 4.3e10⁻⁶ cm²/s. Assuming we have the same length of concen tration gradient generation chamber as in [20], i.e. 2.8 mm. Using our method, the diffusion length L becomes half of the chamber length, i.e. 1.4 mm. Thus, the diffusion time t = L²/2D = 2279 s, i.e. 38 min (comparing to 10 h in [20]). Also, in our method, the concentration gradient across the membranes is almost zero while the gradient is developing from the middle of the gradient forming chamber, therefore the diffusion across the membrane is nearly negligible.

2.3. Control of concentration gradient shape

Concentration gradients with different shapes can be generated using different geometries of the sample and buffer channels and the gradient forming microchamber, combined with proper choice of control boundaries. When the height of the gradient forming microchamber is small compared to its in-plane dimensions, diffusion in the z-direction can be negligible compared to that in the x- and y-directions. Thus, the steady-state concentration distribution inside the gradient forming microchamber can be reduced to two dimensional, and is governed by the steady-state diffusion equation

$$\frac{{\partial }^{2}c}{\partial x^2}+\frac{{\partial }^{2}c}{\partial y^2}=0$$ (1)

where c is the local concentration, and x and y indicate the positions inside the gradient forming microchamber. The boundary conditions associated with Eq. (1) are: c = 1 at the control boundaries replenished with sample, c = 0 at those replenished with buffer, and $\partial c/\partial \vec{n}=0$ ( being the normal vector at the boundaries) at the remaining gradient forming microchamber boundaries, respectively.

Given different choices of control boundaries and different shapes of sample and buffer channels, different solutions will be obtained corresponding to different concentration distributions in the gradient forming microchamber. For example, to obtain simple linear gradients, control boundaries are chosen to be the two short edges, and both the sample and buffer channels assume a rectangular shape (Fig. 2a). To obtain parabola-like gradients with concave or convex shape, the one of the two control boundaries assumes a rectangular shape and the other assumes a trapezoidal shape, with the sample and buffer channels shaped with the same convexity (Fig. 2b and c).

Fig. 2.

Geometry designs of sample and buffer channels and gradient forming microchamber for various concentration gradients: (a) linear profile; (b) concave parabola-like profile; (c) convex parabola-like profile; (d) sawtooth-shaped profile; and (e) bell-shaped profile.

Based on the same principle, gradient profiles with more complex shapes can be constructed from the elementary linear and parabola-like gradient profiles as building blocks. For this purpose, CGG devices may incorporate multiple straight or trapezoidal sample or buffer channels to produce the desired constituent linear or parabola-like gradients. For example, a sawtooth-shaped concentration profile can be created by connecting a series of linear concentration profiles using a CGG device with multiple sets of straight sample and buffer channels laid out in Fig. 2d, while a bell-shaped concentration profile can be constructed by joining multiple parabola-like profiles using a symmetric arrangement of trapezoidal channel (Fig. 2e). As the shapes of the piece-wise profile segments constituting a final concentration gradient profile are independent from each other, each profile segment can be tuned without interfering with other segments. Utilizing the simulation tool COMSOL Multiphysics v3.4 (COMSOL, Inc., Burlington, MA), the choice of control boundaries and the geometries of the sample and buffer channels can be determined for concentration gradient profiles with complex shapes.

3. Experimental

The CGG devices were fabricated according to the optimized microchamber design determined from the simulation. The devices consisted of two poly(dimethylsiloxane) (PDMS) sheets bonded to each other with a polycarbonate (PCTE) semipermeable membrane sandwiched in between. The microfluidic channels and chambers were fabricated in the PDMS sheets using soft lithography. Briefly, a 100-µm layer of SU-8 2100 photoresist (MicroChem, MA) was spin-coated and patterned through lithography on a silicon wafer, which upon curing on a hotplate formed a master defining the negative of the desired microfluidic features. A PDMS prepolymer (Sylgard 184, Dow Corning, MI) was then cast against the master and cured on a hotplate to form 100-µm-thick micro-channels and chambers. The resulting PDMS sheet was then peeled off from the master, cut into suitably sized pieces, and punched with inlet and outlet holes. Next, the PDMS sheets were bonded with the semipermeable membrane as follows [22]. The two PDMS sheets were first stamped against a glass slide with a 0.5-µm layer of pre-cured PDMS diluted in toluene. A PCTE semipermeable membrane (pore diameter 0.4 µm; Sterlitech, WA) was applied on the stamped side of one of the PDMS sheets, which was then aligned and brought in contact with the stamped side of the other PDMS piece. The PDMS-PCTE membrane assembly was then placed on a hotplate so that the pre-cured PDMS between the layers acting as adhesive cross-links and solidified to form a sealed device. A photograph of a fabricated device is shown in Fig. 3, with ink filled in the channel to aid visualization.

Fig. 3.

A fabricated device for the linear profiles. Channels are filled with ink for visualization.

Before gradient generation experiments, devices were pre-filled with water to remove the air from the CGG device. During operation, filtered sample and buffer were driven to their respective inlets using a syringe pump (KD230P; KD Scientific, MA) via Tygon tubes (Saint-Gobain Performance Plastics, OH) at a flow rate of 0.1 µL/min. The sample and buffer were filtered to prevent clogging of semimembrane pores. We used 10-µM Alex 488 (Sigma–Aldrich, MO) fluorescent stock solution and water as the model sample and buffer, respectively. Different profiles of concentration gradients were observed under an inverted epi-fluorescent microscope (Diaphot 3000; Nikon Instruments, NY). Fluorescent images were recorded using a CCD camera (Model 190CU; Micrometrics, NH). Fluorescent intensity profiles, representing concentration profiles, were observed along the centerline of the gradient forming microchamber and analyzed using ImageJ (http://rsb.info.nih.gov/ij/).

4. Results and discussion

4.1. Flow resistance of the semipermeable membrane

We verify whether the flow resistance provided by the semipermeable membrane is sufficiently high to eliminate fluid flow across the membrane and the gradient forming microchamber. At the control boundaries of the microchamber, fluids may follow two possible paths: (a) they may continue to flow through in the sample or buffer channels in the upper layer, i.e. the “fluidic path” in Fig. 1c (denoted as “Path 1”), or (b) they may cross the semipermeable membrane from one channel, enter and traverse the gradient forming microchamber, and cross the membrane again and reach the other channel, i.e. the “diffusion path” in Fig. 1c (denoted as “Path 2”). We now estimate and compare the flow resistances associated with Path 1 and Path 2 (denoted as R₁ and R₂, respectively). Given the length of sample or buffer control boundaries l, channel width w and height h, gradient forming microchamber length L (numerically equal to the distance between sample and buffer channels) and chamber width W and height H, membrane thickness t, pore diameter d and number of pores connecting the sample or buffer channel and the gradient forming microchamber n, R₁≈12ηl/wh³(1–0.63h/w), and R₂≈2 × (128ηt/nπd⁴) + (12ηL/WH³(1 − 0.63H/W)), where η is the dynamic viscosity of the fluid. Design parameters in our devices result in R₁ ~ 1010 Pa s m⁻³, and R₂ ~ 101⁴ Pa s m⁻³. Since R₂ is four orders of magnitude larger than R₁, fluid flowing via Path 2 is negligible, and hence the semipermeable membrane is effective in eliminating fluid flow in the gradient forming microchamber and allowing undisturbed concentration gradient therein.

Next, we examine the various concentration gradients generated by our CGG devices. We first validate our CGG approach for generating flow-free concentration gradients with elementary gradient profiles, i.e. linear and parabola-like gradients. Next, we demonstrate the capability of our approach to use the elementary gradient profiles as building blocks to generate concentration gradient profiles with more complex shapes, using sawtooth- and bell-shaped profiles as examples. For each gradient profile, we first discuss the designs of the sample and buffer channels as well as the gradient forming microchamber, and then present results from the CGG devices, with each experimentally generated gradient profile compared with the corresponding design profile obtained from simulation. To facilitate the examination of the results, the fluorescent intensity in the channels and chambers is normalized based on the fluorescent intensity of the stock solution, while the position along the centerline of the gradient forming microchamber is normalized against the length of the microchamber centerline.

4.2. Linear concentration profiles

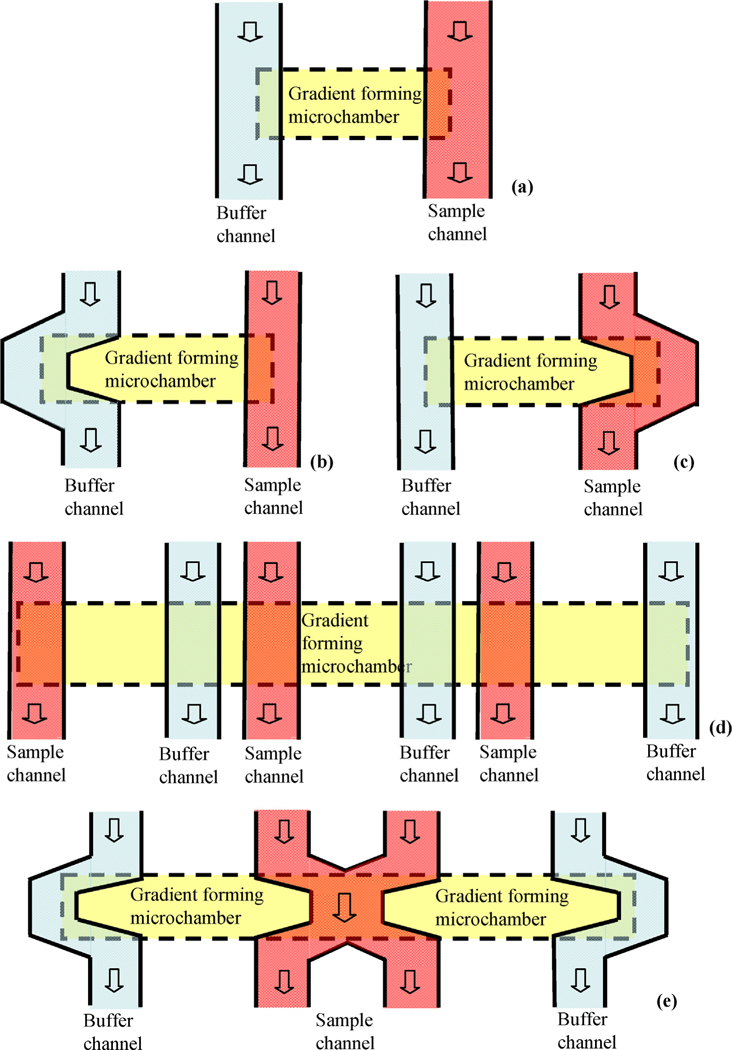
The first set of elementary gradient profiles we demonstrate are the linear concentration gradients. The CGG devices generating linear gradients consisted of straight sample and buffer channels and a gradient forming microchamber with orthogonal control boundaries. Three rectangular gradient forming microchambers each of which was 100 µm wide and spanned distances of 500 µm, 1000 µm, and 1500 µm, respectively, between the sample and buffer channels. The fluorescent image was captured in Fig. 5a after the gradients had stabilized, showing that linear gradients were established along the length of each gradient forming microchamber section. Fluorescence intensity profiles were extracted along the microchamber length and compared with the corresponding design concentration profile from simulation. All three linear gradients were achieved with high linearity and accuracy, agreeing with simulation results within 2.4%, 2.7% and 3.9% for the 500-µm, 1000-µm, and 1500-µm long microchambers, respectively (Fig. 4b–d). Additionally, once the gradients had stabilized, they did not show any tendency to diminish over time as observed in reservoir-based methods where sample and buffer were not replenished [6]. Indeed, fluctuations in the gradient profile over 12 h were within 5%, demonstrating a high temporal stability.

Fig. 5.

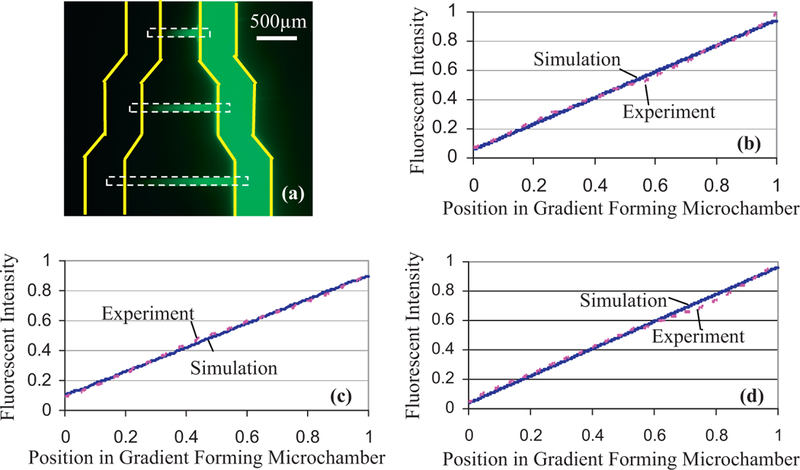
Fluorescent images and intensities of the concave and convex parabola-like profiles. Fluorescent images: (a) concave profile; (b) convex profile. Intensity profiles: (c) concave profile; (d) convex profile. The yellow solid lines in the fluorescent images represent the boundaries of the sample and buffer channels in the top layer, and the white dashed lines represent the boundaries of the gradient forming microchamber in the bottom layer. Intensity profiles are observed along the centerline (red) inside the gradient forming microchamber. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

Fig. 4.

Fluorescent image and intensities of the linear profiles. (a) Fluorescent image. (b)–(d) Intensity profiles inside the 500 µm, 1000 µm, and 1500 µm gradient forming microchambers, respectively. The yellow solid lines in the fluorescent image represent the boundaries of the sample and buffer channels in the top layer, and the white dashed lines represent the boundaries of the gradient forming microchamber in the bottom layer. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

4.3. Parabola-like concentration profiles

The other set of elementary profiles we chose to demonstrate are parabola-like gradient profiles. To generate a concave and a convex parabola-like profile, we designed devices with the sample and buffer channels and the gradient forming microchambers having geometries determined from simulation as shown in Fig. 2b and c, respectively. For both profiles, the shape of the buffer channel or the sample channel was modified, which defined the geometry of the control boundaries of the gradient forming microchambers. The control boundaries formed a trapezoidal shape on one end and a rectangular shape on the other end of the gradient forming microchamber. Note that the sample and buffer channels are complimentary for the concave and convex profiles. As determined by diffusion equation, along the symmetry axis (or “centerline”) inside the gradient forming microchamber, the generated gradient profile would have a larger curvature close to the trapezoidal control boundaries; whereas near the rectangular control boundaries, the gradient profile would approximate a straight line. The curvature transitioned smoothly along the gradient profile, whose shape resembled a parabola. For the concave profile, buffer flowed along the trapezoidal control boundaries on top of the gradient forming microchamber, and sample flowed along the rectangular control boundaries. The convex profile can be achieved by switching the buffer and sample supplies.

Concentration gradients were generated along the gradient forming microchambers, including a 200-µm long rectangular section and a 400-µm long trapezoidal section. The width of the microchambers was 400 µm on the rectangular end and 120 µm on the trapezoidal end. Fluorescent images are shown in Fig. 5a and b for the concave and convex parabola-like profiles, respectively. Intensity profiles were observed along the centerline of the gradient forming microchamber as marked by the red line. Experimentally obtained concentration gradients were compared with the simulated profiles in Fig. 5c and d. Indeed, larger curvature was observed for the profile section on the trapezoidal end of the microchamber, whereas the profile section on the rectangular end of the microchamber was close to linear. For both concave and convex parabola-like profiles, excellent agreement can be observed between the experimental and simulation results, with errors less than 2.8% and 2.2%, respectively.

4.4. Sawtooth-shaped concentration profiles

Having demonstrated the generation of linear and parabola-like gradient profiles, we now construct more complex gradient profiles with these elementary profiles as building blocks. We first created sawtooth-shaped profiles which contain three linear profiles with sharp slopes at the transitions between single linear profiles. Three pairs of straight sample and buffer channels were juxtaposed in parallel, which were all connected by a rectangular gradient forming microchamber in the perpendicular direction. The distance between the pairing sample and buffer channels was 400 µm, and adjacent pairs of channels were placed closely with a 100-µm gap to realize the sharp slope at the transitions. Here, we created two sawtooth-shaped profiles, one containing three identical linear sections, i.e. constant-peak sawtooth, and the other containing three linear sections with decreasing peak magnitudes, i.e. varying-peak sawtooth. For the constant-peak sawtooth profile, the same fluorescent stock solution was supplied in all three sample channels, whereas for the varying-peak sawtooth profile, the solutions supplied in the three sample channels were made to have 100%, 60%, and 20% of the concentrations of the stock solution, respectively. Water was supplied in the three buffer channels.

Both gradient profiles were generated as shown in the fluorescent images (Fig. 6a and b). Intensity profiles along the gradient forming microchamber were compared with simulation results in Fig. 6c and d. The errors between the experimental and simulated profiles for the constant-peak and varying-peak sawtooth profiles agreed within 6.0% and 4.9%, respectively. For both the constant-peak and the varying-peak sawtooth-shaped profiles, linear concentration gradients were created between each pair of sample and buffer channels. The slope of each linear profile segment was determined by the distance between the sample and buffer channels. Sharp slopes were also achieved between the closely juxtaposed buffer and sample channels. The peaks and valleys of the sawtooth-shaped profiles were slightly blunted due to molecular diffusion in the channels. For the varying-peak sawtooth-shaped profile, the height of each peak was effectively controlled by the concentration of the sample solution flowing in each sample channel. Of the four intersections between the sample or buffer channels and the gradient forming microchamber, two were located at the ends of the microchamber and two in the middle. At the two intersections at the ends, molecules could only diffuse in one direction in the microchamber; whereas at the two middle intersections, molecules were able to diffuse along both directions in the microchamber, which resulted in a slight decrease in the peaks and increase in the valleys at the middle intersections. This phenomenon becomes more pronounced when the sample and buffer channels are placed too closely to each other because of the short molecular diffusion path. Thus, a trade-off exists between the sharpness of the profile slopes and the accuracy of the peak and valley concentrations.

Fig. 6.

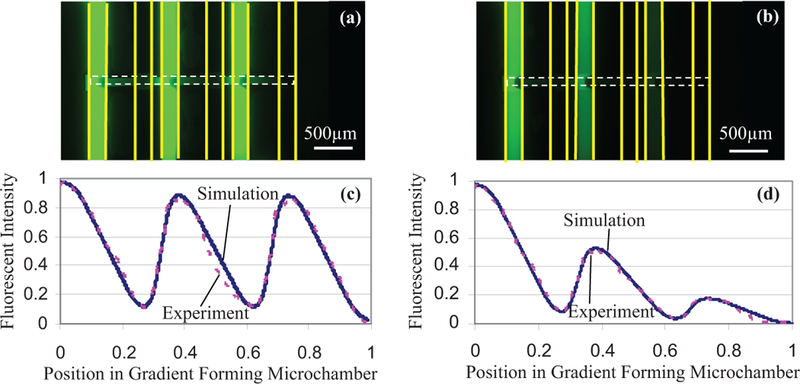
Fluorescent images and intensities of the sawtooth-shaped profiles. Fluorescent images: (a) iso-peak profile; (b) varying-peak profile. Intensity profiles: (c) iso-peak profile; (d) varying-peak profile. The yellow solid lines in the fluorescent images represent the boundaries of the sample and buffer channels in the top layer, and the white dashed lines represent the boundaries of the gradient forming microchamber in the bottom layer. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

4.5. Bell-shaped concentration profiles

Finally, we demonstrated the generation of bell-shaped concentration profiles from elementary parabola-like profiles. The bell-shaped profile can be constructed by smoothly connecting four piecewise parabola-like constituent profiles: two mirrored convex profiles in the middle and two mirrored concave profiles on the sides. Sample and buffer channels are configured into proper trapezoidal shapes to generate each of the four parabola-like profile segments. The symmetric channel arrangement reflected the symmetry of the bell-shaped profile. Fluorescent stock solution was supplied in the sample channels in the middle, and water as pure buffer was supplied in the buffer channels on two sides.

The fluorescent image of the bell-shaped profile generated along the 2200-µm long gradient forming microchamber is shown in Fig. 7a, with the intensity value along the centerline shown and compared with simulation in Fig. 7b. A symmetric bell-shaped gradient profile was generated with high accuracy, with an error within 1.5%. The shape of each of the four parabola-like profile segments resembles that achieved individually, without interference among each other. Meanwhile, smooth transitions were achieved between adjacent parabola-like profile segments. At both ends as well as the middle section of the bell-shaped profile, larger curvature was observed, and thus trapezoidal control boundaries and channel shapes were adopted. Whereas for the monotonically ascending and descending profile sections where the concentration gradient approximated linear, the linear channels that were present in the earlier cases of generating individual parabola-like profiles were no longer necessary. Instead, the linearity in these sections of the bell-shaped profile was achieved due to the linear shape of the gradient forming microchamber boundaries at corresponding locations, as well as the symmetric arrangement of the trapezoidal channels.

Fig. 7.

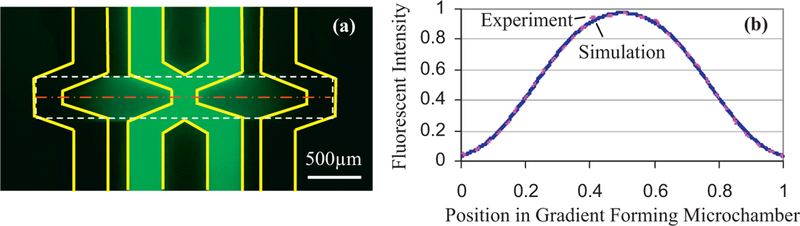
Fluorescent image and intensity of the bell-shaped profile. (a) Fluorescent image. (b) Intensity profile. The yellow solid lines in the fluorescent image represent the boundaries of the sample and buffer channels in the top layer, and the white dashed lines represent the boundaries of the gradient forming microchamber in the bottom layer. Intensity profiles are observed along the centerline (red) inside the gradient forming microchamber. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of the article.)

5. Conclusion

A class of novel microfluidic CGG devices generating temporally stable, flow-free concentration gradients with complex shapes has been presented. The elimination of fluid flow in the gradient generation region is achieved through the design of micro-channels and chambers in two layers and the incorporation of a semipermeable membrane between the layers. This device structure makes diffusion the only means of mass transport in the gradient generation region, i.e. the gradient forming microchamber, limiting fluid flow to the other side of the membrane. The temporal stability of the gradient profiles is ensured by the continuous replenishment of the sample and buffer and cross-membrane diffusion of sample molecules. Since only minimal flow rate is required for sample and buffer replenishment, sample consumption is largely reduced compared to those CGG methods based on diffusion between laminar streams.

The steady-state concentration distribution in the gradient forming microchamber is governed by the two dimensional diffusion equation. By varying the geometry of the sample and buffer channels and that of the gradient forming microchamber, concentration gradients with different shapes have been realized. Gradients with complex shapes can be constructed by combining simpler gradients in a modular fashion.

Devices have been designed through simulation and fabricated for different gradient profiles, and gradient generation experiments have been carried out. First, a set of the linear gradients and a pair of parabola-like gradient profiles have been achieved to validate our proposed CGG method. Then a pair of sawtooth-shaped profile and a bell-shaped profile have been designed through combining multiple linear or parabola-like profiles, and then successfully generated in the experiment. All the experimentally achieved gradient profiles agree with simulation results within 6%.

Our devices are especially advantageous when fluid flow is critically undesirable during gradient generation, such as experiments with cells that do not attach to surfaces, which has not been possible for other CGG devices involving laminar flow. The flow-free concentration gradients enabled by our devices will lead to better control over the microfluidic environment in current cell experiments.

Biographies

Yao Zhou received his B.S. degree in mechanical engineering from Tsinghua University, Beijing, China, M.S. degree in manufacturing engineering from Worcester Polytechnic Institute, Worcester, MA, and Ph.D. degree in mechanical engineering from Columbia University, New York, NY. He is currently conducting postdoctoral research in the High-Throughput Neurotechnology Group at MIT. His research interests include designing and developing automated platforms and BioMEMS devices to interrogate neural system in a high-throughput fashion. He is currently working on single-cell-resolution gene analysis of brain tissue.

Qiao Lin received Ph.D. degree in mechanical engineering from the California Institute of Technology, Pasadena, in 1998, with thesis research in robotics. He conducted postdoctoral research in microelectromechanical systems (MEMS) at the Caltech Micromachining Laboratory from 1998 to 2000 and was an assistant professor of mechanical engineering at Carnegie Mellon University, Pittsburgh, PA, from 2000 to 2005. He has been an associate professor of mechanical engineering at Columbia University, New York, NY, since 2005. His research interests are in designing and creating integrated micro/nanosystems, particularly MEMS and microfluidic systems, for biomedical applications.