Revealing sub-voxel motions of brain tissue using phase-based amplified MRI (aMRI)

Abstract

Purpose

Amplified Magnetic Resonance Imaging (aMRI) was recently introduced as a new brain motion detection and visualization method. The original aMRI approach used a video-processing algorithm, Eulerian Video Magnification (EVM), to amplify cardio-ballistic motion in retrospectively cardiac-gated MRI data. Here we strive to improve aMRI by incorporating a phase-based motion amplification algorithm.

Methods

Phase-based aMRI was developed and tested for correct implementation and ability to amplify sub-voxel motions using digital phantom simulations. The image quality of phase-based aMRI was compared with EVM-based aMRI in healthy volunteers at 3T, and its amplified motion characteristics were compared with phase-contrast MRI. Data were also acquired on a patient with Chiari I malformation, and qualitative displacement maps were produced using free form deformation (FFD) of the aMRI output.

Results

Phantom simulations showed that phase-based aMRI has a linear dependence of amplified displacement on true displacement. Amplification was independent of temporal frequency, varying phantom intensity, Rician noise, and partial volume effect. Phase-based aMRI supported larger amplification factors than EVM-based aMRI, and was less sensitive to noise and artifacts. Abnormal biomechanics were seen on FFD maps of the Chiari I malformation patient.

Conclusion

Phase-based aMRI might be used in the future for quantitative analysis of minute changes in brain motion, and may reveal subtle physiological variations of the brain due to pathology using processing of the fundamental harmonic, or by selectively varying temporal harmonics. Preliminary data shows the potential of phase-based aMRI to qualitatively assess abnormal biomechanics in Chiari I malformation.

Introduction

As a very soft and complex biomaterial, the human brain is under constant motion and deformation due to different physiological dynamics. As the heart contracts and relaxes during the cardiac cycle, periodic variations in arterial blood pressure are transmitted along the vasculature, resulting in relatively localized motions and deformations of the brain [1–5]. Pulsatile brain motion is regarded as a crucial mechanical element, linking the blood flow and cerebrospinal fluid (CSF) dynamics, making it a prime candidate to investigate brain diseases such as Chiari I Malformation and hydrocephalus.

Several methods have been introduced in order to visualize this pulsatile motion. Phase-contrast MRI, which uses a set of bipolar gradients to encode blood/brain velocity [4–5] combined with cardiac synchronization, achieves high temporal resolution and enables the measurements of the brain tissue motion, blood and CSF flow [4–7]. This method has been used widely in clinical applications, to diagnose disorders such as hydrocephalus (including normal pressure hydrocephalus), cystic CSF collections, and Chiari I malformation [8]. Hofmann et al. [9], used phase-contrast MR imaging of the cervical CSF and spinal cord, showing that the obstruction of the foramen magnum in patients with Chiari I malformation causes an abrupt systolic downward displacement of the spinal cord and impairs the recoil of CSF during diastole. Forner et al. [10] used quantitative phase-contrast MR imaging of CSF flow in order to calculate maximum diastolic velocity, mean flow, and stroke volume to identify patients with normal pressure hydrocephalus. A more recent quantitative tissue motion imaging technique, Displacement Encoded imaging with Stimulated Echoes (DENSE) MRI, encodes tissue displacement in the phase of the stimulated echo [11–16]. Zhong et al. [15] used DENSE-MRI to track brain motion of healthy volunteers during the cardiac cycle, and found the smallest detected motion to be 0.04 mm in the occipital lobe. Soellinger et al. [16], used DENSE-MRI for brain motion measurements in all three spatial directions, revealing tissue displacement in the order of 0.01 mm.

Recently, an ‘amplified MRI’ (aMRI) approach was introduced [17] to visualize the multi-directional biomechanical response of the brain tissue due to cardiac-induced blood pulsation, and reveal subtle brain motions. aMRI is based on the use of retrospectively cardiac-gated (‘cine’ MRI) data, followed by amplification of the resulting cine images using the Eulerian Video Magnification (EVM) algorithm [18]. aMRI has a shorter scan time than phase-contrast and DENSE-MRI, and may have a further advantage in its ability to reveal smaller motions. aMRI also has a higher temporal resolution than phase-contrast MRI, does not require phase-encoding in multiple directions to capture the full extent of brain motion, and is independent of the velocity encoding gradient aliasing effect. In addition, aMRI has other advantages over DENSE-MRI, since the latter is prone to error from cardiac frequency variations, and has decreasing contrast to noise ratio (CNR) with decreasing displacement amplitudes [16].

In this study, we introduce a more advanced aMRI method which utilizes phase-based video motion processing originally developed (as for EVM [18]) for use in real-world videography applications [19]. In comparison to the EVM-based method, phase-based video motion processing has been reported to support larger amplification factors and is significantly less sensitive to noise and artifacts [19]. As the amplification factor is increased, noise is translated rather than amplified, as opposed to the original EVM-based approach. Phase-based aMRI is also less sensitive to non-motion-induced voxel intensity changes, since the amplification is done by manipulating the temporal phases changes instead of the temporal brightness changes as in EVM.

The new phase-based aMRI is compared to the original EVM-based aMRI method in in vivo data. Additionally, as a first step in determining whether phase-based aMRI can reliably reveal sub-voxel brain motion, simple digital phantom simulations were tested. Very early preliminary aMRI data was acquired on a patient with known craniocervical dysmorphia and obstructive features (consistent with Chiari I Malformation), and on a normal control, to test the potential diagnostic value of phase-based aMRI in identifying disease-induced biomechanical differences.

Methods

Human Subjects

With institutional review board approval (IRB-28674) and informed consent, experiments were conducted on two healthy adult volunteers (one male 32 years old and one women 30 years old) using a 3T whole-body GE MR750 Discovery MRI system (GE Healthcare, Milwaukee, WI, gradient strength=50 mT/m and slew rate=200 T/m/s) and an eight-channel head coil. With IRB approval, data were also acquired on two patients during clinical diagnostic scans: 1) one with abnormal anatomy (4Y male), clinical symptoms of headaches and cerebellar ataxia, and obstructive features at the craniocervical junction, including peg-like, low-lying cerebellar tonsils and narrow foramen magnum, associated with Chiari I malformation and basilar invagination; and 2) one control with normal structural MRI (3Y male).

MRI Acquisition

aMRI experiments used the cardiac-gated balanced steady state free precession (bSSFP) sequence [20], a common imaging sequence that is typically used to capture and record the motion of the heart. This sequence produces a short cine MRI ‘movie’ of the tissue of interest over the different phases of the cardiac cycle (that is, over a single heart beat) using cardiac-gated MRI. Here, the entire cardiac cycle is ultimately sampled independent of variations of the heart rate. Any data that is acquired during an irregular heartbeat is discarded, and therefore it is assumed that the temporal phases (which corresponds to heart harmonics) is matched with the real temporal heart beat frequency content. For each scan, a 2D mid-sagittal slice of the brain was obtained using the following imaging parameters: matrix size = 192 – 224 × 192 – 224 (Zero-filling to 512 × 512), flip angle = 45°, TR/TE = 3.6/1.3 ms, ± 125 KHz bandwidth, FOV = 220–240 mm², slice thickness ranging from 4 – 5 mm, parallel imaging with an acceleration parameter = 2, number of views/segment = 6, retrospective rebinning to 75–150 cardiac phases, and a scan time per slice on the order of 30 – 40 s (depending on the heart rate). External photoplethysmography (PG) gating was used as the cardiac triggering mechanism.

In order to further validate the ability of phase-based aMRI to perform a realistic amplification of brain motion, a dataset was acquired using a phase-contrast sequence – a well-established method of tracking brain motion. 2D cine phase-contrast data were acquired using the following parameters: matrix size = 192 × 192, flip angle =15°, TR/TE = 11.8/5.7 ms, ± 125 KHz bandwidth, FOV = 220 mm², slice thickness = 4 mm, parallel imaging with an acceleration parameter = 2, number of views/segment = 6, velocity encoding factor (venc) = 5 cm/sec, encoding in all 3 directions, retrospective rebinning to 75 cardiac phases, and scan time per slice = 1:20 min.

Motion Amplification

With the cine MRI images as ‘video input’, the phase-based algorithm [19] was used to amplify and thereby enable visualization of the biomechanical motion of the brain during the cardiac cycle, explained in more detail below.

Both the linear Eulerian [18] and phase-based [19] video magnification algorithms follow the Eulerian perspective for the flow field, where the properties of a voxel of fluid, such as pressure and velocity, evolve over time. (This differs from the Lagrangian perspective, where the trajectory of particles is tracked over time.) In the Eulerian approach to motion magnification, the motion is not explicitly estimated, but rather magnified by amplifying temporal intensity changes at fixed positions [18]. In the original EVM-based aMRI approach, the images are decomposed as a Laplacian pyramid, which performs spatial low-pass filtering on the frames of the video, followed by downsampling for computational efficiency. Here, the goal of the spatial processing is to increase the temporal signal to noise ratio [18], and magnification is achieved by manipulating the linear approximation of the intensity value at each spatial location of the pyramid levels using the first two terms of the Taylor series.

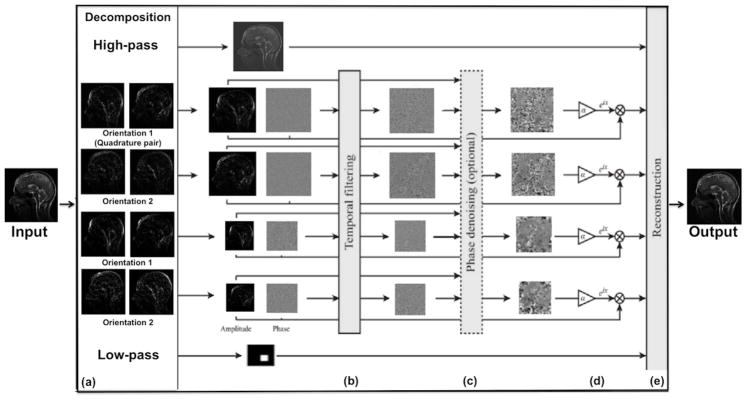
Unlike EVM-based aMRI, phase-based aMRI instead decomposes the images into scale and orientation components (Figure 1), by using a linear complex-valued steerable pyramid [19]. Temporal variations in the phase of the coefficients of a complex-valued steerable pyramid correspond to motion, and can be temporally processed and amplified to reveal imperceptible motions, or attenuated to remove distracting changes. Just as the phase variation of the Fourier basis function (sine wave) is related to translation via the Fourier shift theorem, the phase variation of the complex steerable pyramid correspond to local motions in spatial subbands of an image [19]. Because EVM-based aMRI amplifies temporal brightness changes, the amplitude of noise is amplified linearly. In contrast, phase-based modifies phases (not amplitudes), and as such does not increase the magnitude of spatial noise.

Figure 1.

The phase-based motion processing algorithm, described by Wadhwa et al [19], applied to MRI cine data. (a) The cine MRI (short video) is decomposed by the complex steerable pyramid into scales and orientations. (b) The phases are independently temporally filtered at each spatial location, orientation, and scale. (c) Optional step: the filtered phases can be “spatially” filtered again to increase the phase SNR using amplitude-weighted Gaussian spatial smoothing. (d) The filtered phases are multiplied by an amplification parameter and added to the original phase components, and finally the video is reconstructed (e).

In phase-based aMRI, the local phase is computed for each component over time at every spatial scale and orientation of the steerable pyramid, and then a temporal bandpass filter is used to isolate specific temporal frequencies relevant to the desired application. An optional amplitude-weighted Gaussian spatial smoothing can be performed on the filtered phases in order to increase the phase SNR and to support a larger amplification parameter. The filtered phases are multiplied by an amplification parameter and added to the original phase components. The image is then reconstructed, resulting in an amplified movie exhibiting the desirable range of frequencies. The amplification parameter, α was as defined in the original phase-based study [19] as $\alpha \delta (t)<\frac{\lambda }{4}$. By assuming a maximum displacement, δ(t), of the brainstem (midbrain, pons, and medulla) with peak displacements of approximately 0.20 mm [7] and calculating the maximum spatial wavelength, λ = 4mm, of the first image (assuming that when the image undergoes translations and/or deformations the intensity remains relatively constant), we choose an α within this boundary, $\alpha <\frac{4}{4\times 0.2}=5$, that supports sufficient amplification and with minimum artifacts and distortions. The condition above allows one to selectively amplify different temporal harmonics depending on the physiological information one is interested in. In this case, small displacement amplitudes (such as what typically occurs for higher temporal harmonics) can be amplified to a greater degree than large displacement amplitudes (such as what typically occurs for lower temporal harmonics).

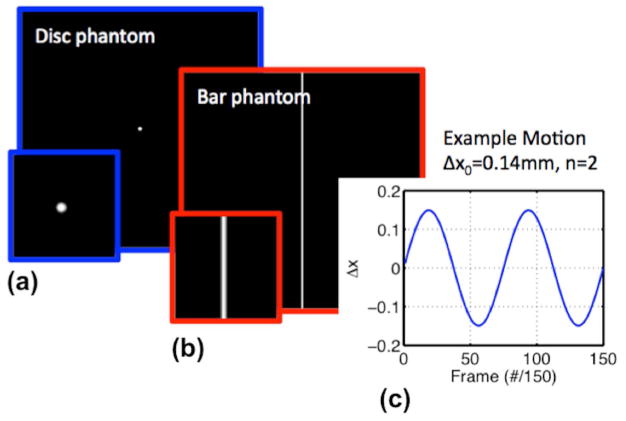
Digital Phantom Simulation

We characterized the phase-based aMRI algorithm using digital phantom simulations with known motion. Two Gaussian filtered 2D digital phantoms, with a pixel intensity between 0 and 1, consisting of a vertical bar with width d and a disc with radius r were simulated in MATLAB [21] (Figure 2). Note that, given the clinical interest in (and prevalence of) obstructive disorders that alter motion at the level of the midbrain and lower, this phantom was designed to mimic two brain structures, with the vertical bar mimicking the spinal cord, and the disc mimicking the cerebellum. The simulations were similarly designed to be a simple first step toward validation and quantification of the method. The phantom moved over time, t, with 1D displacement $\mathit{\Delta }x=\mathit{\Delta }{x}_0\times \mathit{sin}(\frac{2\pi n}{150}t)$, amplitude, Δx_0, and harmonic number, n. Rician noise was added, along with sinusoidal intensity variations to emulate the partial volume effect (PVE). The data simulation was converted into DICOM images with the same matrix size as the acquired cine MRI (512 × 512), and was then amplified by the phase-based algorithm. The amplified displacement was measured using a custom algorithm. For each frame (cardiac phase), the phantom’s intensity profile was extracted (middle row or column sum), then each frame below a chosen threshold of 0.05 was discarded and the phantom position was calculated. The overall amplification factor was calculated as the peak-to-peak amplified displacement divided by 2Δx₀. Table 1 shows the different simulations that were performed. For the Rician noise simulation, the position-time curve was low pass filtered before calculating the amplification factor. We investigated the dependence of amplification factor on: varying amplification parameter (α ) using a range of 0 – 10, varying original displacement ranging from 0 – 0.95 mm, varying harmonic number ranging from 0 – 10, varying disc phantom size ranging from 1.875 – 30 mm, varying bar phantom size ranging from 3.75 – 30 mm, varying background contrast ranging from 0.1 – 1, varying phantom intensity (mimicking in- and out-of plane motions), varying Rician noise parameter, s, ranging from 0 – 0.01. We also investigated the coupling between motion and partial volume effects (PVE).

Figure 2.

The two digital phantoms: (a) A disc (mimicking the cerebellum) with radius r and (b) a vertical bar (mimicking CSF around the midbrain and spinal cord) with width d, were simulated in MATLAB. (c) 1D sinusoidal motion, $\mathit{\Delta }x=\mathit{\Delta }{x}_0\times \mathit{sin}(\frac{2\pi n}{150}t)$, with amplitude, Δx₀, and harmonic number, n.

Table 1.

Phantom simulation results demonstrated that phase-based aMRI exhibited expected and desired behavior. This suggests that future quantitation (accurate displacement measurements) of brain tissue motion might be feasible.

Purpose of simulation	Parameter space	Results
Dependence on varying alpha	α: [0 – 10]	Linear correlation with r squared= 0.99
Dependence on varying initial displacement	Δx0: [0 – 0.95] mm	Linear correlation with r squared = 0.99 (indicating constant amplification factor)
Dependence on varying harmonics	n: [0 – 10]	Different harmonics were amplified equally
Dependence on varying disk radius	r: [1.875 – 30] mm	Different phantom size were amplified equally
Dependence on varying bar width	d: [3.75 – 60] mm	Different phantom size were amplified equally
Dependence on varying phantom intensity over time	n: [0 – 10]	Varying phantom intensity did not effect the amplification
Dependence on varying Rician noise	Rician noise parameter s:[0 – 0.01] mm	Different noise parameter were amplified equally
Investigate coupling between motion and partial volume effect (PVE)	n: [0 – 4] Δl0: [0 – 0.2]	Amplification parameter is independent of partial volume effect

Qualitative Displacement Maps

In order to visualize the displacement of the brain tissue, a free form deformation (FFD) [22] image registration algorithm was used to produce normalized temporal average displacement fields of the amplified data. Image registration consists of deforming a floating image by matching each frame of the amplified volume ‘movie’ to a reference image (the first frame). The amplified volume was first converted to NIFTI format and each frame (slice) was extracted. To eliminate CSF, a brain mask was generated for every frame through several processing steps including sharpening, median filtering, skull stripping and Otsu thresholding. A deformable B-spline registration algorithm was employed, as implemented in NiftyReg (https://sourceforge.net/projects/niftyreg) [23], to compute deformations between every frame and the reference first frame. The algorithm used normalized mutual information for measuring interframe similarity and a two level pyramidal approach for optimization. Normalized average displacement maps were then generated for the amplified volume ‘movie’. No rigid or affine initialization was utilized.

In Vivo data

Artifact, noise, and normalized temporal variance maps were produced for visualization and comparison of brain tissue motion among the input data, EVM-based aMRI, and phase-based aMRI outputs, and among different temporal harmonics (frequencies). The phase-based aMRI algorithm was validated in a healthy volunteer, by comparing the overall motion characteristics with phase-contrast MRI. Phase-contrast data were converted from velocity into net displacement by integrating the cine frames over time [7]. Additionally, the T2*-weighted data (the magnitude images extracted from the phase-contrast sequence) were amplified to show that the algorithm can be employed over other contrast mechanisms; or in other words, that aMRI is not just restricted to amplifying T1/T2 contrast MRI data based off the bSSFP sequence (Supporting Video S3). To further validate the aMRI pipeline and highlight its utility in the clinical domain, we investigated its ability to differentiate between amplified volumes ‘movie’ of a Chiari I Malformation pediatric patient and a normal control.

Results

Phantom Simulations

As shown in Table 1, phase-based aMRI demonstrated several ideal behaviors, at least when applied to simplified numerical phantoms, including: 1) linear dependence of amplified displacement on true displacement (i.e. constant amplification), 2) independence of amplification on temporal frequency, phantom size, varying phantom intensity (mimicking in- and out-of plane motions), Rician noise, and partial volume effect. We also observed non-ideal, slight dependence of amplification on phantom shape (the standard deviation of the amplification factor was ~5% of the mean).

Phase-Based versus EVM-Based aMRI

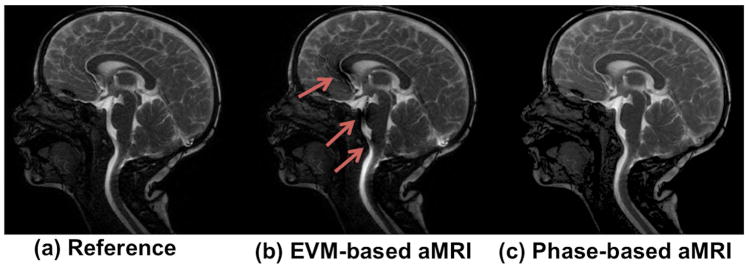
There were several advantages of phase-based aMRI compared to EVM-based aMRI, the main three of which are shown in Figures 3–5. Phase-based aMRI was less sensitive to artifacts compared to EVM-based aMRI, showing superior image quality, with an overall reduction in shading over the cerebral cortex and spinal cord, and fewer CSF flow artifacts (Figure 3 and Supporting Video S1). In particular, diminished blooming and pulsation artifacts were seen in the basilar cistern, basilar artery, anterior corpus callosum, anterior cerebral artery, and straight sinus. Anterior cingulate motion was also better defined on phase-based aMRI without an artifact associated with the CSF and anterior cerebral artery.

Figure 3.

A snapshot of the cardiac cycle of the original cine MRI data, EVM-based aMRI, and phase-based aMRI. The first harmonic was amplified with an amplification parameter of 6 (other harmonics were attenuated to zero). Arrows denote shading, blooming, and CSF pulsation artifacts seen on EVM-based aMRI.

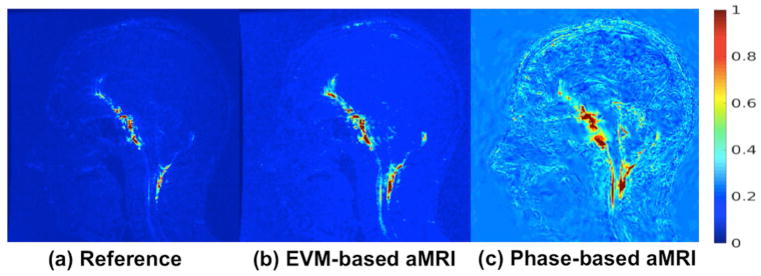
Figure 5.

Normalized temporal standard deviation of (a) the original (reference) cine MRI data, (b) EVM-based aMRI, and (c) phase-based aMRI. The data was amplified with an amplification parameter of 10 for the temporal harmonics 1–5 (with no spatial filtering). By computing the unamplified cine images, both EVM-based and phase-based aMRI methods magnify near-imperceptible motion near the midbrain, spinal cord, and cerebellum, but phase-based aMRI also reveals subtle motion in the cerebrum.

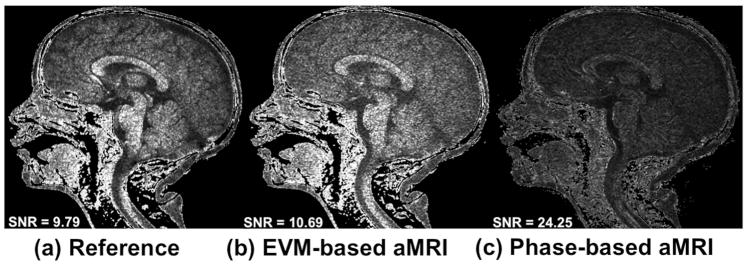
Phase-based aMRI was found to be less sensitive to noise compared to EVM-based MRI, as shown in Figure 4. The noise maps and SNR calculated from the original data (9.8) and EVM-based aMRI (10.7) were similar. On the other hand, the SNR of phase-based aMRI (24.3) was approximately 2.5 times larger than EVM-based aMRI.

Figure 4.

Noise maps of (a) the original cine images, (b) EVM-based aMRI, and (c) phase-based aMRI. The SNR in the original data and EVM-based aMRI are close in value due to the fact that the EVM algorithm amplifies the motion and the noise all together. On the other hand, the SNR of phase-based aMRI is approximately 2.5 times larger than EVM-based aMRI, since EVM-based aMRI amplifies temporal brightness changes and the amplitude of noise is amplified linearly. In contrast, phase-based modifies phases (not amplitudes), and as such does not increase the magnitude of spatial noise.

While the movement of the brain was barely perceptible in the reference data, it was significantly amplified in both the EVM-based and phase-based output data, especially near the brainstem, cerebellum and spinal cord. However, phase-based aMRI revealed subtle motion that was not seen in EVM-based aMRI (Figure 5).

Frequency Analysis

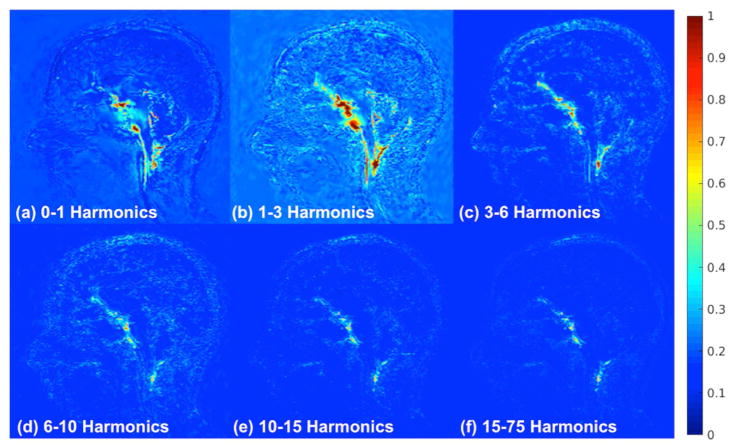
Figure 6 shows normalized temporal standard deviation maps for different temporal harmonics (frequency) bands. These results reveal the different displacement response of the brain for different temporal frequencies (Supporting Video S2). The most motion was picked up for the fundamental frequency (that is, 1Hz – the heart rate of the patient), although higher temporal frequencies also produced some subtle brain displacement.

Figure 6.

Normalized temporal variance maps for different harmonic bands as follows: (a) 0–1 (b) 1–3 (c) 3– 6 (d) 6–10 (e) 10–15, and (f) 15–75. The amplification parameter is 10 and the other harmonics are attenuated to zero. The highest amplification achieved can be seen in the 1–3 harmonic band. This was as expected since this band encompasses the natural frequency of the heart beat, however, we can still see that there are contributions by the higher harmonics.

In-vivo comparison with phase-contrast MRI

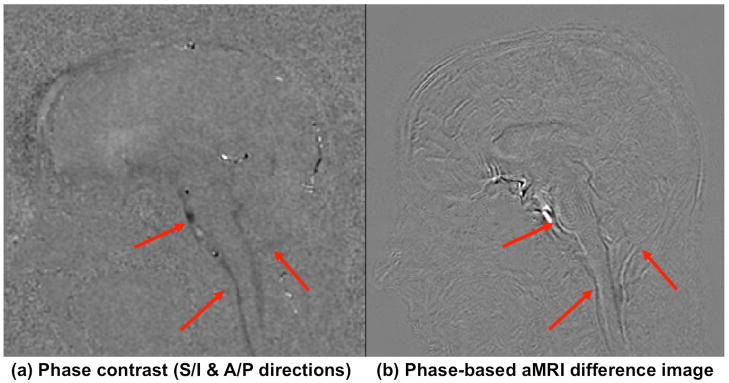
Brain motion in phase-based aMRI was found to closely resemble the displacement maps produced from phase-contrast MRI in the mid-brain, spinal cord, and cerebellar region – but the motion was more pronounced overall on phase-based aMRI, with subtle motion being detected in the cortex (Figure 7). Amplified magnitude images taken from the cine T2*-weighted phase-contrast sequence show that the amplification algorithm can be applied to image contrast mechanisms other than the T1/T2-weighted bSSFP approach (Supporting Video S3).

Figure 7.

(a) Phase contrast (maximum displacement) and (b) phase-based aMRI (maximum difference from the first frame) maps showing similar motion characteristics in the mid-brain, spinal cord, and cerebellar region (arrows), but with more subtle motion seen in the cortex on phase-based aMRI.

Patient data

For both the patient and normal control, the input cine images displayed near-imperceptible motion, while the phase-based aMRI output showed amplified motion, particularly near the midbrain, frontal lobe, spinal cord, and cerebellum (Supporting Video S4). Compared with the normal patient, the phase-based aMRI output from the Chiari I Malformation patient – who had obstructive anatomic features of low-lying cerebellar tonsils (11 mm below foramen magnum) – showed increased caudal midbrain tissue displacement, and downward displacement at the level of the brainstem and craniocervical junction. For the phase-based aMRI data, we used an ideal narrow band filter with passband of 1Hz, amplification parameter of 6, and amplitude weighted gaussian spatial smoothing with σ=5. These factors were chosen empirically to emphasize the ‘piston-like’ motion of the cerebellum without the creation of significant artifacts.

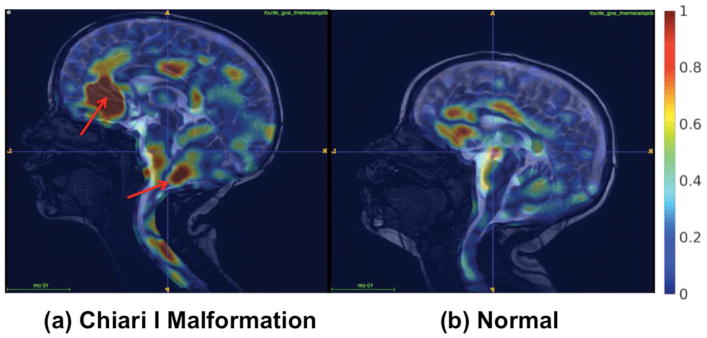
FFD maps produced from the phase-based aMRI data for both the structurally abnormal Chiari I Malformation and control patient (Figure 8) also revealed considerable differences in displacement in regions of the spinal cord, midbrain, and cerebellum.

Figure 8.

Natural motion of brain structures and spinal cord may be disrupted by pathologies that alter intracranial pressure and/or cerebrospinal fluid (CSF) flow dynamics at the craniocervical junction. Thus, visualization of brain motion may provide clinicians with invaluable information on the nature and extent of the disease. Here, free form deformation (FFD) maps represent the normalized average displacement, and show the potential of the method to differentiate a pediatric patient Chiari I malformation (4yr male) from a normal control (3yr male).

Discussion

This work introduces a new phase-based aMRI method, a promising quantitative and visualization tool for assessing sub-voxel brain motion due to arterial pulsation during the cardiac cycle.

Through phantom simulations, phase-based aMRI mostly demonstrated ideal behaviors, at least when applied to simplified numerical phantoms. While there was a slight dependence of amplification on phantom shape (the standard deviation of the amplification factor was ~5% of the mean), phase-based aMRI showed a linear dependence of amplified displacement with true displacement (that is, constant amplification for different amplitude displacements). Amplification was also independent of temporal frequency, phantom size, varying phantom intensity (mimicking in and out-of plane motions), Rician noise, and partial volume effect. These phantom simulation results are a promising first step, implying that phase-based aMRI accurately represents real brain motion within realistic brain displacement amplitudes. This characterization of phase-based aMRI demonstrates that it might be possible to quantify sub-voxel brain motion by constructing a more advanced brain-like phantom. Using a calibration curve produced by such phantom simulations, accurate amplified displacement measurements could be mapped to the real in vivo displacement.

In vivo data showed that phase-based aMRI revealed subtle motions that were not picked up by the EVM-based aMRI method. Since phase-based aMRI modifies phase rather than amplitude, it can achieve higher amplification factors with reduced vulnerability to spatiotemporal noise and other artifacts, and it is less sensitive to non-motion-induced voxel intensity changes (such as the partial volume effect). These features of phase-based aMRI are increasingly important for detecting small brain motions.

Through phantom simulations, we observed that phased-based aMRI is capable of revealing sub-voxel motions. In spite of this promising result, caution is advised regarding its interpretation. Although the phantom simulations were not affected by varying phantom intensity (that emulate in- and out-of plane motion and the partial volume effect), the amplification algorithm may not be immune to these effects in vivo. As a result, a full validation of the new method will require the expansion of the phase-based aMRI pulse sequence and algorithm to three dimensions, which will enable the acquisition of data with a smaller slice thickness and subsequent processing of motion in 3D.

A further advantage of phase-based aMRI is in its ability to explore brain dynamics at different frequencies. The motion in the higher temporal frequencies exists due to the non-linearity of brain tissue [24]. In practice, amplification of the whole range of temporal frequencies to extract the ‘real’ amplified brain motion (within the boundaries of the temporal resolution) is feasible and will depend on the application. For example, in this work we found empirically that an amplification factor (α) of 6 applied to the first harmonic emphasized the motion of midbrain, spinal cord, and cerebellar structures without introduction of confounding image artifacts. This enabled us to qualitatively differentiate between normal and Chiari I malformation patients. However, by judicious amplification of higher harmonics in phase-based aMRI, one may be able to extract even more subtle motion to reveal microscopic changes associated with other brain pathologies, opening up both qualitative and quantitative applications for phase-based aMRI.

A disadvantage of aMRI is that, unlike phase-contrast MRI, it lacks the straightforward ability to directly quantify motion. While the ability of phase-based aMRI to be accurately quantified for in vivo applications needs to be further validated, there are some potential advantages of phase-based aMRI as a motion detection tool: it has a shorter scan duration than phase-contrast MRI (up to 3 times shorter depending on the number of velocity encoding gradients used in phase-contrast MRI) and can achieve a higher resolution than DENSE-MRI since it does not rely on the Echo Planar Imaging (EPI) trajectory. It also could overcome other limitations of phase-contrast MRI: it has a higher temporal resolution, and does not require multiple velocity encoding directions and values to capture motion in all relevant directions and velocities. In addition, phase-based aMRI can be used as another tool to dramatically enhance motion in images acquired with a variety of contrast mechanisms, including T1/T2-weighted images and T2*-weighted images explored in this work, which may be useful depending on the application of interest. The amplification of the phase maps acquired from phase-contrast MRI data could also be a future possibility, however, care must be taken to ensure that the intensity variation across the temporal frames is smooth enough for accurate amplification.

Using free form deformation (FFD) to qualitatively visualize tissue displacement maps, this study showed promise in the ability of phase-based aMRI to differentiate a pediatric patient with Chiari I malformation from a normal patient. In the one case represented in this study, the Chiari I Malformation patient exhibited increased caudal midbrain tissue displacement, and downward displacement at the level of the brainstem and craniocervical junction in the amplified data. These findings support the notion of deranged biomechanics at the brainstem and cerebellum which is thought to occur in patients with Chiari I malformation [9].

There are other potential important applications of phase-based aMRI. Since the algorithm can amplify subtle motions, it may allow one to reveal subtle changes in the underlying biomechanical properties of brain tissue – a promising biomarker for conditions such as mild traumatic brain injury [25]. With the increasing use of MR Elastography (MRE) to extract in vivo biomechanical properties of the brain (such as stiffness) using phase-contrast MRI, phase-based aMRI may also find a home in this arena. This promising application is supported by a recent study by Weaver et al. [26], in which intrinsic activation of the brain using a standard cine phase-contrast MRI sequence was shown to be a viable alternative to traditional MRE for measuring the biomechanical properties of brain tissue (obviating the need for specialized MRE hardware and software). With the accurate quantification of brain displacements in phase-based aMRI to similarly allow the extraction of the biomechanical properties, this would make in vivo MRE more cost effective and accessible for the clinics, while also reducing scan time and increasing patient comfort.

Our improved aMRI method works on the assumption that the motions induced by the heart pulsation during the cardiac cycle are small and subtle – that is, the variation of the intensity in the same voxel over time cannot be too big. Additionally, rigid body motion may pose a concern, however a promising means of motion correction has been demonstrated by a method that analyzes the derivative of the phases [27]. Another limitation of this work is that through-plane motion detection was not possible, since the phase-based imaging processing algorithm was only performed in two dimensions. Further work needs to be done to extend the algorithm to three dimensions to accurately represent motion in all directions.

Because we have relied on qualitative heuristics to achieve motion amplification while controlling for confounding artifacts such as banding and shading, further work is needed to quantify the maximum motion amplification that can be achieved without accruing significant artifacts. It should also be noted that the phase-based aMRI algorithm can be used to selectively amplify different brain structures (that is, if specific regions of the brain have either different spatial wavelengths or different maximum displacements, these regions can be selectively amplified to emphasize motion). Thus, in order to maximize the performance of the method, one should take into consideration the spatial and temporal frequencies of the part of the brain that is being amplified.

Conclusion

This study presents a new phase-based aMRI method that enables more accurate visualization of brain motion, with fewer noise and artifacts than EVM-based aMRI. Phase-based aMRI amplifies minute changes in brain motion through spatio-temporal processing of cardiac-gated cine MRI, and may provide a means of revealing subtle physiological variations of the brain due to pathology. Preliminary data shows the potential of phase-based aMRI to assess abnormal biomechanics in patients with Chiari I malformation. Application of phase-based aMRI to the clinical in vivo assessment of brain biomechanical properties has the potential for a wide-range of clinical implications, not only in the pre-surgical assessment of craniocervical and skull base dysplasias, but also other clinical conditions impacting brain biomechanics, such as brain injury, hydrocephalus, and other conditions associated with abnormal intracranial pressure.

Supplementary Material

Supp VideoS1. Suppurting Video S1.

The entire cardiac cycle for the three datasets shown in Figure 3 clearly demonstrates that phase-based aMRI produces better dynamic image quality than the original EVM-based aMRI, with fewer shading, blooming, and CSF pulsation artifacts seen on EVM-based aMRI.

Supp VideoS2. Suppurting Video S2.

Normalized temporal variance maps for different harmonic bands as follows: (a) 0–1 (b) 1–3 (c) 3–6 (d) 6–10 (e) 10–15, and (f) 15–75. The amplification parameter is 10 and the other harmonics are attenuated to zero. The highest amplification achieved can be seen in the 1–3 harmonic band. This was as expected since this band encompasses the natural frequency of the heart beat, however, we can still see that there are contributions by the higher harmonics.

Supp VideoS3. Suppurting Video S3.

Motion characteristics of phase-based aMRI applied to T1/T2-weighted data (acquired with a cine bSSFP sequence) is similar to that of T2*-weighted data (acquired with a cine phase-contrast sequence)

Supp VideoS4. Suppurting Video S4.

Animated movie output for the original (reference) cine MRI data and the amplified output images for both patient and control in Figure 8. Natural motion of brain structures and spinal cord may be disrupted by pathologies that alter intracranial pressure and/or cerebrospinal fluid (CSF) flow dynamics at the craniocervical junction. Thus, visualization of brain motion may provide clinicians with invaluable information on the nature and extent of obstructive diseases.