Abstract
Diagnosing pleiotropy is critical for assessing the validity of Mendelian randomization (MR) analyses. The popular MR-Egger method evaluates whether there is evidence of bias-generating pleiotropy among a set of candidate genetic instrumental variables. In this article, we propose a statistical method—global and individual tests for direct effects (GLIDE)—for systematically evaluating pleiotropy among the set of genetic variants (e.g., single nucleotide polymorphisms (SNPs)) used for MR. As a global test, simulation experiments suggest that GLIDE is nearly uniformly more powerful than the MR-Egger method. As a sensitivity analysis, GLIDE is capable of detecting outliers in individual variant-level pleiotropy, in order to obtain a refined set of genetic instrumental variables. We used GLIDE to analyze both body mass index and height for associations with colorectal cancer risk in data from the Genetics and Epidemiology of Colorectal Cancer Consortium and the Colon Cancer Family Registry (multiple studies). Among the body mass index–associated SNPs and the height-associated SNPs, several individual variants showed evidence of pleiotropy. Removal of these potentially pleiotropic SNPs resulted in attenuation of respective estimates of the causal effects. In summary, the proposed GLIDE method is useful for sensitivity analyses and improves the validity of MR.
Keywords: causal inference, direct effect, instrumental variables, sensitivity analysis
Editor’s note: An invited commentary on this article appears on page 2681.
Mendelian randomization (MR) (1–4) is an inferential method that uses germ-line genotypes (e.g., single nucleotide polymorphisms (SNPs)) as instrumental variables (IVs) to assess the causal effect of an exposure on a disease outcome, and it is increasingly popular in genetic epidemiology. By exploiting the random assortment of genes from parents to offspring during gamete formation and conception, which has been likened to “Nature’s randomized experiment” (2, 5), MR holds promise for removing the potential confounding and reverse causation that loom over observational epidemiology. While this is conceptually appealing, skepticism has persisted on whether the strong assumptions required by MR (6–9) are plausible. Stated informally, these assumptions require that genetic variants are independent of any confounder of the exposure-disease relationship, that genetic variants are associated with the exposure (preferably strongly), and that there is no direct effect from the genetic variants to the disease outcome other than through the pathway mediated by the exposure—also known as “no pleiotropy.”
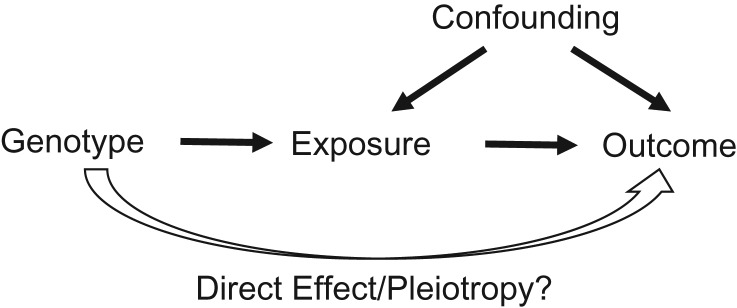
Pleiotropy, or more specifically, horizontal pleiotropy, refers to the phenomenon wherein a gene or mutation affects multiple phenotypes via independent biological pathways (10, 11). Figure 1 illustrates the concept of MR and the critical no-pleiotropy assumption. As the founding principle, the independence between genotypes and confounding variables is backed up in theory by the random assortment of genes from parents to offspring, and in practice it is further aided through adjustment for population substructures. The strength of the IV’s association with the exposure can be improved by increasing the sample size and including additional known risk loci. Perhaps the Achilles’ heel of MR is the potential for pleiotropic effects among the genetic risk variants associated with complex diseases, given the biological plausibility of pleiotropy in complex biological pathways and networks. Indeed, recent genome-wide association studies have shown that pleiotropy is pervasive in complex traits, with evidence of numerous genetic variants’ affecting multiple traits, some of which represent horizontal pleiotropy (12–14).
Figure 1.
Causal diagram for Mendelian randomization. The goal is to use genotypes as instrumental variables to infer the causal effect of an exposure on a disease outcome. One critical assumption is that there is no direct effect from the genotype to the disease (no pleiotropy).
Methods for detecting pleiotropy and, more ambitiously, estimating the causal effect in the presence of pleiotropy, have been under active development. Notably, Egger regression—a tool for detecting small-study bias in meta-analysis—has been adapted to test for the impact of pleiotropy on the casual effect of interest (15). This test exploits the observation that if there is no pleiotropy, a dosage relationship should be present between the individual genetic associations with the exposure and the corresponding genetic associations with the outcome (16). A linear regression model is fitted between the 2 sets of genetic associations, and a nonzero intercept suggests that there is evidence of pleiotropy. In the presence of direct effects, and under the “instrument strength independent of direct effect” (InSIDE) assumption, the MR-Egger test yields a valid causal effect estimate, though such an assumption is untestable and may be difficult to justify. Along the same lines, it has been shown that the causal effect can be estimated unbiasedly when fewer than 50% of IVs are invalid, either by the median estimator (17) or by the shrinkage estimation procedure (18).
When a number of SNPs are used as candidate IVs in MR, it is possible that some variants are valid IVs but others are not. Several informal diagnostic statistics for detecting outliers and investigating pleiotropy have been proposed in MR-Egger and other meta-analytical methods—for example, the heterogeneity in dependent instrument (HEIDI) outlier test (19–21). There is a pressing need to develop more rigorous significance tests for global and individual-variant pleiotropy. Such analyses will lead to sensitivity analyses that remove variants exhibiting evidence of pleiotropy and estimate causal effects with a more justified set of IVs. This is a challenging task because, without additional constraints, the IV regression approach cannot assess simultaneously the causal effect of primary interest and the individual direct effects.
Binary outcomes pose additional modeling challenges. Most of the existing approaches were formulated for a quantitative trait by linear regression, a feature inherited from the classical 2-stage least-squares regression approaches in the econometrics literature. Strictly speaking, these methods cannot be immediately used for MR analyses with binary disease outcomes. While logistic regression has been the workhorse and the odds ratio is the de facto association estimate for binary outcomes, using an odds ratio as the causal estimand is difficult for causal inference (22–24). This is mostly due to the noncollapsibility of the odds ratio (25), meaning that the stratum-specific odds ratio is not equal to the marginal odds ratio ignoring strata even when the stratification variable is not related to the exposure. The use of 2-stage IV approaches in logistic regression yields approximations of causal odds ratios for rare disease outcomes (8, 26).
In this article, we propose a statistical method—global and individual tests for direct effects (GLIDE)—with which to assess pleiotropy and conduct sensitivity analyses for MR when a number of SNPs were used as candidate IVs, assuming that genetic variants are indeed independent of confounding variables. The novel contribution of GLIDE is a rigorous significance analysis for global and individual-variant pleiotropy, using a quantile-quantile (Q-Q) plot and a permutation procedure. Causal effects are defined in terms of relative risk, a measure that is collapsible and well interpretable for binary disease endpoints (27). Though individual direct effects are not simultaneously identifiable through the IV regression, we show that “surrogate direct effects”—the direct effects for one individual variant at a time, not conditional on other variants—are estimable and provide valid tests for individual direct effects under plausible conditions. Using the proposed GLIDE method, investigators can determine whether the set of genetic variants being evaluated for IVs show any evidence of global pleiotropy and, if so, which variants exhibit evidence of pleiotropy and therefore should be removed in a sensitivity analysis. We conduct extensive simulation studies to evaluate the performance of the proposed GLIDE method relative to the MR-Egger method. Finally, we use GLIDE to analyze the associations of body mass index (BMI; weight (kg)/height (m)2) and height with colorectal cancer risk in data from the Genetics and Epidemiology of Colorectal Cancer (GECCO) Consortium and the Colon Cancer Family Registry.
METHODS
Consider an MR study with a binary disease outcome Y and a set of m independent genetic variants , denoted by , that have been identified as candidate IVs to infer the causal effect of the intermediate exposure X on the outcome Y. Typically, these genetic variants are independent loci derived from prior genome-wide association studies. For an MR analysis, X is not required to be measured in the study, as long as X can be predicted by the set of genotypes G and the previously reported association parameters. Suppose the causal effect of X on Y is confounded by a collection of unmeasured variables U. Assume that the independence assumption for G holds, so that . For simplicity of notation, additional measured confounding variables are omitted, but the formulation follows immediately when measured confounding variables are added. The interest herein is to test the third IV assumption of no pleiotropy that there is no direct effect of G on Y other than the hypothesized mediation effect through X. In what follows, the notions of “direct effect” and “pleiotropic effect” will be used interchangeably.
The causal effect of the intermediate exposure X on the outcome Y is defined on the relative risk scale through a log-linear model:
| (1) |
where is the causal effect of X on Y and is the direct effect of the jth variant . This is a structural equation model in which causal effects are conditional on unmeasured confounding variables U. The global null hypothesis of interest is that there is no direct effect for any genetic variant, expressed as
If this global null hypothesis is rejected, the interest is to then assess which individual variants show evidence of a direct effect and therefore should be deleted in the subsequent analysis. However, neither testing the global hypothesis nor diagnosing individual variants can be accomplished by regressing Y on because of the presence of the unmeasured confounding, U.
Suppose a genetic risk score has been developed externally to predict X from G, denoted by , where is the previously derived nonzero weight (coefficient) associated with . The variability of estimating in prior studies when X is a quantitative trait can be negligible in IV estimation (28). By definition, , and is independent of the error term . Plugging the expression of X into model 1 (equation 1), we have
Since G is independent of and U, integration of and U leads to
| (2) |
The fundamental problem in estimating direct effects through the IV regression approach is that there are m IVs but now causal effects to be estimated in model 2 (equation 2). The design matrix for model 2 is rank-deficient, since is a linear combination of ’s. Therefore ’s are not identifiable. Instead, one has to devise tests for nonzero indirectly under some constraints—for example, the MR-Egger test (15). If for all , then the genetic effects on , expressed as in our notation, and the genetic effects on should have a dose-response relationship and form a straight line with the intercept 0. This forms the basis for indirect tests of global pleiotropy through testing of the intercept in the MR-Egger method. As informal ways to assess individual pleiotropy, other methods have been developed that involve assessment of heterogeneity in causal effect estimates based on individual genetic variants one at a time (19–21).
While the direct effects in model 2 (equation 2) are not simultaneously identifiable, we propose GLIDE, an indirect method with which to test the global null hypothesis and at the same time provide diagnostics for pleiotropy for individual variants. The key novelty is the development of an individual-level significance test of pleiotropy for each SNP under suitable conditions. Specifically, a sequence of log-linear models are fitted to , each assessing the “marginal” direct effect for one genetic variant at a time:
| (3) |
We call the “surrogate direct effect,” which is related to the true direct effect and is directly testable. In Web Appendix 1 (available at https://academic.oup.com/aje), we show that ’s can be expressed explicitly as functions of , , and some distributional parameters for ’s. We derive 3 results that form the basis of our proposed test procedure. First, if the global null hypothesis is true (i.e., if for all ), then for all . Second, if for all , then for the jth variant. Third, when the majority of ’s are zero or when is positive for some and negative for others, is numerically close to .
These results delineate a test procedure for the unidentifiable parameters through the estimable quantities, the ’s. The core of our GLIDE procedure is to evaluate the P values associated with , denoted by , with respect to their null distributions derived from Monte Carlo simulations. The benefit of diagnosing pleiotropy by means of P values is that they are agnostic to the sign of direct effects, thereby circumventing the issue in balanced pleiotropy where some direct effects are positive and others are negative. To summarize the evidence for global pleiotropy, we combine the P values by Fisher’s method, , and compare the observed value with its null distribution to compute the P value for global pleiotropy. A unique feature of GLIDE is that it gives an intuitive Q-Q plot of ’s for diagnosing individual variant pleiotropy. To perform a sensitivity analysis with the set of more justified IVs, the procedure can be applied iteratively by deleting potentially pleiotropic variants.
The null distributions of under require careful derivation. First, because each is conditional on , which is shared across models, the z scores associated with ’s, denoted by ’s, are correlated even though the ’s are mutually independent. As such, a naive Bonferroni test for variants that ignores the correlation structure may not be optimal. In Web Appendix 2, we derive the asymptotic distribution of ’s from the estimating equation theory. Second, although each is an estimable quantity, the joint distribution of ’s is degenerate with rank , meaning that if ’s are first obtained, then the one left out is not stochastic and indeed completely determined from previous ’s. This is formally proven in Web Appendix 2. This observation is reminiscent of the rank deficiency of in model 2 (equation 2). On the basis of these results, a parametric Monte Carlo simulation program is devised to obtain the null distribution of ’s, accounting for both correlation and rank deficiency in the multivariate asymptotic null distribution (Web Appendix 3). The null distributions of the quantiles of observed P values are obtained and compared with the observed quantiles. Testing of the global null hypothesis can then be achieved by comparing the Fisher’s combination statistic with its null distribution. The familywise error rate or false discovery rate can be used to perform significance tests for individual pleiotropic effects.
For case-control MR studies, fitting model 3 (equation 3) while accounting for case-control sampling could be accomplished by means of the inverse probability weighting method using estimation procedures for relative risk models as discussed previously, if such weights are known or can be derived from the population incidence of the disease (27). For many cancers, the incidence is low and the odds ratio estimates from standard logistic regression approximate the relative risk estimates, so any software that implements logistic regression can be used to derive surrogate direct effects and associated P values. The crux of computation in the GLIDE procedure is to generate null distributions of surrogate direct effects, particularly when there are a large number of candidate IV SNPs. We have developed an R package (R Foundation for Statistical Computing, Vienna, Austria) for GLIDE, freely available from the Comprehensive R Archive Network (https://cran.r-project.org/), with which to implement and disseminate the proposed method.
RESULTS
Simulation to assess validity and power
A case-control MR study was simulated to assess the performance of the proposed GLIDE procedure. The data vector for a subject contains a binary outcome , an exposure that has a normal distribution, 25 SNPs as candidate IVs, and a variable representing unmeasured confounding between and . The SNPs were generated from a multinomial distribution at , with probabilities corresponding to minor allele frequencies randomly selected from a uniform distribution with a range from 0.1 to 0.4. The data-generating models for are
| (4) |
| (5) |
| (6) |
where is the causal effect of on (set to be either 0 or 0.5), ’s represent the strength of IVs, ’s are the direct effects to be tested, and are drawn from independent normal distributions with mean 0 and variance 0.25. We assume that is independent of in the simulation study shown in the main text, and we left the scenario with being dependent on in Web Appendix 4 as a sensitivity analysis. We generated ’s from a uniform distribution with a range from 0.1 to 0.2. The direct effects ’s are zero under the null hypothesis or drawn from a uniform distribution under the alternative hypothesis, which may be correlated with ’s. In all simulation settings, we chose the value of to achieve a disease prevalence 0.01 and generate a population of 50,000 or 250,000 individuals. All cases and an equal number of controls were sampled in the case-control study. The case-control sampling scheme was accounted for in analyses by the inverse probability weighting method.
Control of type I error rate.
Table 1 shows the empirical type I error rates in 2,000 simulated data sets when for all , so that there is no direct effect for any of the 25 genetic variants. For GLIDE, we evaluate whether the Fisher’s combination statistic for the surrogate direct effects attains the type I error level at 0.05. For the MR-Egger method, we test whether the intercept of the Egger regression is zero, using the weighted least squares procedure (15). As expected, both tests achieve proper control of the type I error rate for the 2 sample sizes considered, whether or not there is a causal effect of on . The validity of the 2 methods requires the independence between ’s and , as additional simulations in Web Appendix 4 (Web Table 1) show.
Table 1.
Type I Error Rate for the Proposed GLIDE Test and the MR-Eggera Test When the Nominal P Value Is 0.05
| Sample Size, no. | Causal Effect () | Test | ||
|---|---|---|---|---|
| Cases | Controls | GLIDE | MR-Egger | |
| 500 | 500 | 0 | 0.0436 | 0.0489 |
| 0.5 | 0.0457 | 0.0505 | ||
| 2,500 | 2,500 | 0 | 0.0482 | 0.0494 |
| 0.5 | 0.0484 | 0.0503 | ||
Abbreviations: GLIDE, global and individual tests for direct effects; MR, Mendelian randomization.
a Egger’s test for assessing pleiotropy in MR.
Statistical power for testing for global pleiotropy
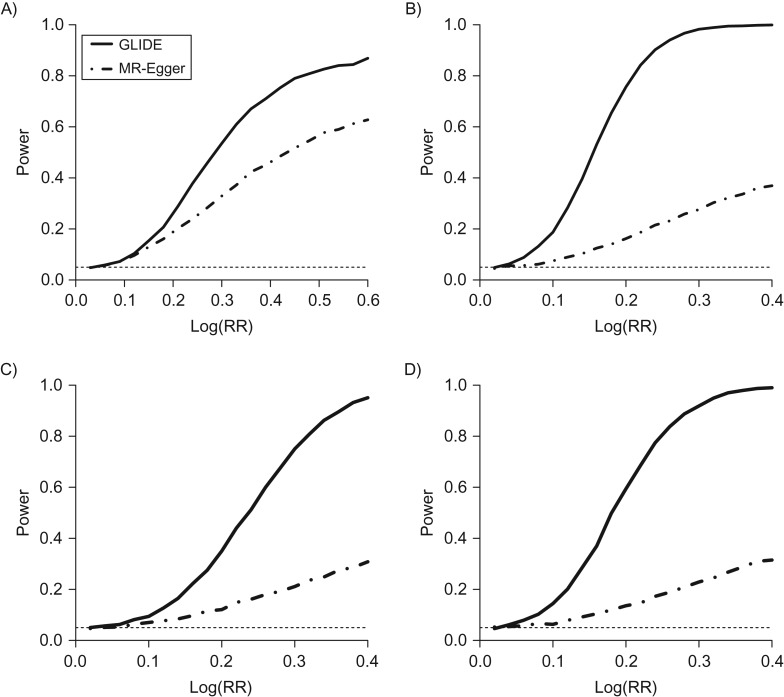
In Figure 2 and Web Figure 1, we show the statistical power achieved for detection of global pleiotropy under a variety of distributions of ’s. The details of the parameter settings in these simulation experiments are described in Web Appendix 5. Figure 2 shows scenarios where there is a causal effect of on , namely in model 6 (equation 6), among which Figures 2A–2C show scenarios where the distributions of the direct effects and the instrumental strengths are uncorrelated and 2D shows a scenario where the direct effects and the instrumental strengths are indeed correlated. In Figure 2A, the direct effects are all positive. In Figure 2B, some direct effects are negative and others are positive, representing a scenario close to “balanced pleiotropy” (15). In Figure 2C, only a subset of variants (15 out of the 25 (60%)) have pleiotropic effects. Note that even if the distributions of the direct effects and the instrumental strengths are probabilistically uncorrelated in Figures 2A–2C, in each simulated data set the covariance of and in the sample is not exactly zero; therefore a naive inverse-variance–weighted estimate of the causal effect will be biased in all 4 scenarios (simulation results not shown).
Figure 2.
Statistical power, in simulations, of the global and individual tests for direct effects (GLIDE) and Mendelian randomization (MR)-Egger methods to test the global null hypothesis that there is no direct effect for any genetic variant. The sold line represents results of the GLIDE test, and the dotted-dashed line represents results of the MR-Egger test. A) The direct effects are all positive; B) some direct effects are positive and some are negative; C) a proportion of single nucleotide polymorphisms (SNPs) (60%) have pleiotropic effects; D) all SNPs have direct effects that are correlated with the genetic associations with the intermediate exposure. RR, relative risk.
In all 4 scenarios shown in Figure 2, GLIDE outperforms MR-Egger substantially. The power improvement can reach as much as 20% when all direct effects are positive in Figure 1A, while a much greater power gain is seen in Figures 2B and 2D. The improvement stems from the MR-Egger test suffering reduced power performance when some direct effects are negative and others are positive, since the intercept in the MR-Egger regression tends to get close to 0 (but not exactly 0), as negative and positive effects may cancel out in the overall impact on the intercept. It is important to note that balanced pleiotropy that does not distort estimation in the MR-Egger method is a numerical coincidence and is rarely exactly satisfied in practice. When the causal effect was set to be zero while all other parameters remained unchanged (Web Figure 1), the power comparisons showed no difference from Figure 2.
Estimation of individual direct effects
A simulation study was conducted to evaluate the bias of the estimated surrogate direct effect for a particular genetic variant in model 3 (equation 3) as estimates of true individual direct effects . The degree of approximation between and is critical to the use of the Q-Q plot as a means to identify individual variants with potentially pleiotropic effects. The models and results of this simulation study were relegated to Web Appendix 6 (Web Table 2). Under diverse simulation settings, the results in Web Table 2 suggest that the estimated surrogate direct effect captures the corresponding true direct effect and the bias is largely negligible.
GECCO data analyses
We analyzed epidemiologic and genetic data from 10,226 colorectal cancer cases and 10,286 population-based controls of European ancestry from 11 studies (6 cohort studies and 5 case-control studies) included in the GECCO Consortium and the Colon Cancer Family Registry (Web Appendix 7). Full details on these consortia (GECCO and the Colon Cancer Family Registry) have been published elsewhere (29). We previously reported results for 77 BMI-linked SNPs and 696 height-linked SNPs identified in the Genetic Investigation of Anthropometric Traits (GIANT) Consortium as IVs in MR analyses using GECCO and Colon Cancer Family Registry data (30, 31). These results suggested that genetically determined BMI and height are both associated with the risk of colorectal cancer, indicating evidence of causality (30, 31).
We now investigate the validity of these 77 BMI-linked SNPs and 696 height-linked SNPs as IVs, using both GLIDE and the MR-Egger regression approaches. Two genetic risk scores were computed on the basis of association estimates in the GIANT Consortium (32, 33). Because colorectal cancer is a rare disease in these populations, surrogate direct effect estimates and their respective P values in model 3 (equation 3) were obtained via a logistic regression model approximating a log-linear model for relative risk estimates. The null distribution of P values was obtained from 50,000 simulated data sets following the degenerate multivariate normal distribution.
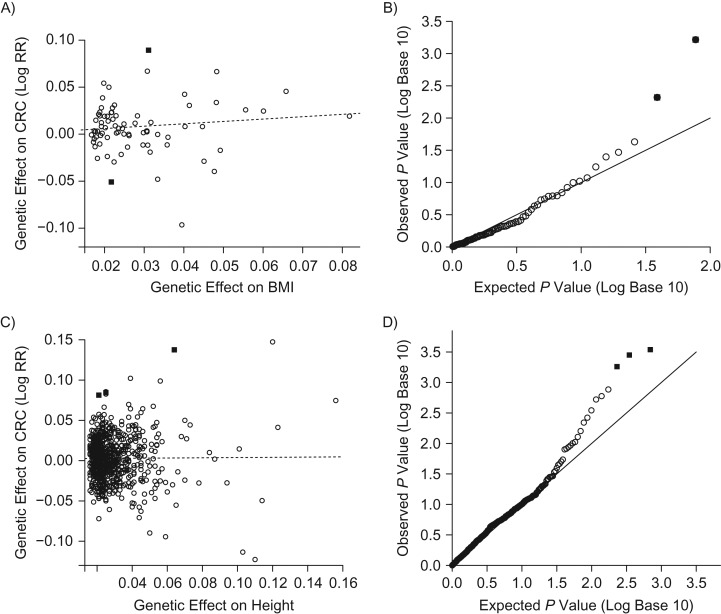
Figures 3A and 3C show scatterplots of the reported genetic associations from the GIANT genome-wide association study (30, 31) and the associations with risk of colorectal cancer in GECCO, respectively. Figures 3B and 3D show the respective Q-Q plots of P values derived from the GLIDE method. MR-Egger regression suggests that there is no evidence of pleiotropy for either analysis (BMI: intercept = 0.001, P = 0.89; height: intercept = 0.002, P = 0.33). The P values for testing of global pleiotropy from GLIDE are 0.55 (BMI) and 0.02 (height), indicating that there is evidence of global pleiotropy for the height MR analysis. The Q-Q plots are more informative for diagnosing individual variants. Figure 3 shows that there are 2 BMI-linked variants (rs16951275 and rs12286929) with evidence of a direct effect (solid squares; false discovery rate < 0.2) and 3 height-linked SNPs (rs3923086, rs11144688, and rs6085662) with evidence of a direct effect (solid squares; false discovery rate < 0.2). We use a false discovery rate of 0.2 as the significance cutoff because we want to be conservative in selecting valid IVs for MR. As such, these results suggest that these SNPs should be omitted in the subsequent refined MR estimation. For clarity, these SNPs with evidence of pleiotropy are also highlighted in Figures 3A and 3C as solid squares.
Figure 3.
Application of Menedelian randomization (MR)-Egger regression and the proposed global and individual tests for direct effects (GLIDE) test to data from the Genetics and Epidemiology of Colorectal Cancer (GECCO) Consortium in a study of body mass index (BMI; weight (kg)/height (m)2) and height in colorectal cancer (CRC) risk. The solid squares represent single nucleotide polymorphisms (SNPs) with some evidence of pleiotropy detected by GLIDE; the open circles represent SNPs which did not exhibit evidence of pleiotropy. A) MR-Egger regression results showing the intercept and slope for 77 SNPs previously shown to be linked to BMI in the Genetic Investigation of Anthropometric Traits (GIANT) Consortium (30, 31). B) Proposed GLIDE test results showing the quantile-quantile (Q-Q) plot for P values derived from assessment of surrogate direct effects for BMI. C) MR-Egger regression results showing the intercept and slope for 696 SNPs previously shown to be linked to height in the GIANT consortium. D) Proposed GLIDE test results showing the Q-Q plot for P values derived from assessment of surrogate direct effects for height. RR, relative risk.
These 5 SNPs and their associated genes are listed in Table 2, each having a small surrogate direct effect estimate in relative risk. Notably, in annotation work in the GIANT studies, Locke et al. (32) and Wood et al. (33) have reported that the genes associated with these SNPs are linked to important cellular functions and multiple pathways: The mitogen-activated protein kinase kinase 5 gene (MAP2K5) is in the MAP kinase signaling pathway involved in growth factor–stimulated cell proliferation and muscle cell differentiation; the cell adhesion molecule 2 gene (CADM2) involves cell-to-cell adhesion and synaptic function in neuronal development and the immune system; the axis inhibition protein 2 gene (AXIN2) is a negative regulator of wingless/integrated (Wnt)/β-catenin signaling; the proprotein convertase subtilisin/kexin type 5 gene (PCSK5) is involved in endopeptidase activities, abnormal skeleton development, basal cell carcinoma, and Wnt-protein binding; and the bone morphogenetic protein 2 gene (BMP2) encodes a secreted ligand of the transforming growth factor β family of proteins, which are involved in a number of cellular functions. In either analysis, the MR-Egger test was not able to detect any evidence of pleiotropic effects (Figure 3).
Table 2.
Estimates of Surrogate Direct Effects for Single Nucleotide Polymorphisms With Some Evidence of Pleiotropy Detected via the GLIDE Method in Analyses of Body Mass Index and Height Associations With Colorectal Cancer Riska
| Study and SNP ID No. | Gene | Surrogate Direct Effect (RRb) | Nominal P Value | FDR |
|---|---|---|---|---|
| BMIc | ||||
| rs16951275 | MAP2K5 | 1.09 | 0.0006 | 0.046 |
| rs12286929 | CADM2 | 0.94 | 0.0048 | 0.183 |
| Height | ||||
| rs3923086 | AXIN2 | 1.08 | 2.9 × 10−4 | 0.12 |
| rs11144688 | PCSK5 | 1.14 | 3.5 × 10−4 | 0.12 |
| rs6085662 | BMP2 | 1.08 | 5.5 × 10−4 | 0.13 |
Abbreviations: AXIN2, axis inhibition protein 2 gene; BMI, body mass index; BMP2, bone morphogenetic protein 2 gene; CADM2, cell adhesion molecule 2 gene; FDR, false discovery rate; GLIDE, global and individual tests for direct effects; ID, identification; MAP2K5, mitogen-activated protein kinase kinase 5 gene; PCSK5, proprotein convertase subtilisin/kexin type 5 gene; RR, relative risk; rs, reference SNP; SNP, single nucleotide polymorphism.
a Data were obtained from 11 studies (6 cohort studies and 5 case-control studies) included in the Genetics and Epidemiology of Colorectal Cancer Consortium and the Colon Cancer Family Registry (Web Appendix 7).
b The RR was calculated per 5-unit increment for BMI and per 10-cm increment for height.
c Weight (kg)/height (m)2.
Next, as a sensitivity analysis, we removed the 5 SNPs with some evidence of pleiotropy and recomputed the genetic risk scores and estimated surrogate direct effects for the remaining 75 BMI SNPs and 693 height SNPs, respectively. The Q-Q plots of the P values suggested that the refined sets of SNPs exhibit little evidence of pleiotropy in either analysis (Web Figure 2). Table 3 shows the resulting causal estimates obtained when the SNPs with evidence of pleiotropy were excluded in the refined 2-stage IV regression. The estimates were adjusted for age, sex, the top 3 principal components in the GECCO genome-wide association study data, and the 11 GECCO studies (included as indicator variables in the regression). In both the BMI analyses and the height analyses, excluding the violating SNPs results in an attenuated effect size for the causal estimate and an increased P value, because those deleted SNPs are typically the outliers of genetic association. This data example showcases the utility of the proposed method: It enables assessment of individual variants and leads to sensitivity analyses that remove potentially invalid IVs, thereby improving the validity of MR analysis.
Table 3.
Causal Effect Estimates Obtained With and Without the 2 Single Nucleotide Polymorphisms Showing Evidence of Pleiotropy in Analyses of Body Mass Index and Height Associations With Colorectal Cancer Riska
| Study and IV | Causal Effect Estimate (RRb) | 95% CI | P Value |
|---|---|---|---|
| BMIc | |||
| Original 77 SNPs | 1.32 | 1.10, 1.58 | 0.003 |
| Refined 75 SNPs | 1.26 | 1.06, 1.51 | 0.009 |
| Height | |||
| Original 696 SNPs | 1.07 | 1.01, 1.14 | 0.017 |
| Refined 693 SNPs | 1.06 | 1.00, 1.13 | 0.053 |
Abbreviations: BMI, body mass index; CI, confidence interval; GECCO, Genetics and Epidemiology of Colorectal Cancer; IV, instrumental variable; RR, relative risk; SNP, single nucleotide polymorphism.
a Data were obtained from 11 studies (6 cohort studies and 5 case-control studies) included in the GECCO Consortium and the Colon Cancer Family Registry (Web Appendix 7).
b The RR was calculated per 5-unit increment for BMI and per 10-cm increment for height. Estimates were adjusted for age, sex, the top 3 principal components in GECCO genome-wide association study data, and the 11 GECCO studies (included as indicator variables in the regression).
c Weight (kg)/height (m)2.
DISCUSSION
In this article, we have proposed a diagnostic tool, GLIDE, for assessing global and individual pleiotropy in MR studies. Our method is formulated for estimating causal relative risk in a log-linear model and therefore is tailored specifically for binary disease outcomes. The unique feature of our method with respect to existing methods is that it provides a rigorous assessment of pleiotropy for individual genetic variants, therefore allowing sensitivity analyses with a more justified subset of IVs. Furthermore, for assessment of global pleiotropy, our simulations and data examples show that the power of GLIDE is uniformly better than the MR-Egger regression method.
In analyses evaluating associations of BMI and height with the risk of colorectal cancer, GLIDE detected 2 BMI-linked SNPs and 3 height-linked SNPs that showed evidence of pleiotropy. Removing these SNPs in subsequent MR analyses resulted in attenuated causal effects, since those SNPs often present as outliers in genetic associations. These examples highlight the importance of evaluating and diagnosing IVs before causal testing. As we elaborated in the Introduction, pleiotropic effects can be common for genes and mutations that affect complex traits. Assessment of any direct effects of genotypes on the outcome (i.e., the presence of pleiotropy) can also be tested using mediation analysis, if the information on the intermediate exposure and all confounders is available. However, such an analysis yields inaccurate results when the exposure is measured with error, which is often the case when a single measurement per subject (e.g., blood pressure) is used to represent a long-term average of the exposure (e.g., blood pressure) over time. Thus, the mediation analysis approach is limited in practice, and our method does not have these limitations.
GLIDE works best for MR analyses with many independent variants, where a Q-Q plot of P values can be informative. If there are only a few variants (<10), it becomes difficult to visualize and assess evidence of violations from a Q-Q plot and subsequently remove individual variants that may drive the violation. Paradoxically, more SNPs in the IV would increase the statistical power of testing the causal effect but at the same time lower the power of GLIDE to assess the potential of individual variants’ pleiotropic effects due to multiple testing. One possible extension of GLIDE is to group variants by pathways or chromosomes and test pleiotropy by group.
GLIDE assumes that genetic variants are independent of confounding variables. Violation of this independence assumption will lead to false-positive findings in assessing pleiotropy (Web Table 1). GLIDE does not solve the fundamental problem when estimating direct effects through the IV regression approach, as these individual causal direct effects are not identifiable together with the causal effect of interest. The surrogate direct effects estimated through GLIDE are merely approximations of the direct effects when there are many variants, and when there are positive and negative direct effects. Though GLIDE is generally more sensitive than MR-Egger regression for detecting pleiotropy, it does not always detect direct effects. There are scenarios in which surrogate direct effects are zero yet true direct effects are not all zero. This limitation is inevitable, because individual causal direct effects are not identifiable without additional constraints.
Genetic epidemiology is advancing from discovering genome-wide associations to more functionally characterizing genetic associations. In this context, causal inference and mediation analyses are becoming important tools for epidemiologic analysis, providing a stronger, causal interpretation rather than a mere association. However, investigators need to exert caution and carefully examine the underlying assumptions of IVs before engaging in causal estimation. The proposed GLIDE method is useful for assessing variants for evidence of pleiotropy and improving the validity of the MR approach.
Supplementary Material
ACKNOWLEDGMENTS
Author affiliations: Division of Public Health Sciences, Fred Hutchinson Cancer Research Center, Seattle, Washington (James Y. Dai, Ulrike Peters, Xiaoyu Wang, Jonathan Kocarnik, Emily White, Li Hsu); Department of Biostatistics, School of Public Health, University of Washington, Seattle, Washington (James Y. Dai); Department of Epidemiology, School of Public Health, University of Washington, Seattle, Washington (Ulrike Peters, Emily White); Division of Cancer Epidemiology, German Cancer Research Center, Heidelberg, Germany (Jenny Chang-Claude); Genetic Cancer Epidemiology Group, University Cancer Center Hamburg, University Medical Center Hamburg-Eppendorf, Hamburg, Germany (Jenny Chang-Claude); Department of Internal Medicine, University of Utah Health Sciences Center, Salt Lake City, Utah (Martha L. Slattery); Division of Gastroenterology, Massachusetts General Hospital and Harvard Medical School, Boston, Massachusetts (Andrew Chan); Channing Division of Network Medicine, Brigham and Women’s Hospital and Harvard Medical School, Boston, Massachusetts (Andrew Chan); Ontario Institute for Cancer Research, MaRS Centre, Toronto, Ontario, Canada (Mathieu Lemire); Division of Cancer Epidemiology and Genetics, National Cancer Institute, Bethesda, Maryland (Sonja I. Berndt); USC Norris Comprehensive Cancer Center, University of Southern California, Los Angeles, California (Graham Casey); Department of Epidemiology, Harvard School of Public Health, Boston, Massachusetts (Mingyang Song); Melbourne School of Population and Global Health, The University of Melbourne, Melbourne, Victoria, Australia (Mark A. Jenkins); Division of Clinical Epidemiology and Aging Research, German Cancer Research Center, Heidelberg, Germany (Hermann Brenner); Division of Preventive Oncology, German Cancer Research Center and National Center for Tumor Diseases, Heidelberg, Germany (Hermann Brenner); German Cancer Consortium, German Cancer Research Center, Heidelberg, Germany (Hermann Brenner); and Department of Medicine and Dan L Duncan Comprehensive Cancer Center, Baylor College of Medicine, Houston, Texas (Aaron P. Thrift).
This work was supported by National Institutes of Health grants R01 CA233588, R01 HL114901, and P01 CA53996.
Conflict of interest: none declared.
Abbreviations
- BMI
body mass index
- GIANT
Genetic Investigation of Anthropometric Traits
- GECCO
Genetics and Epidemiology of Colorectal Cancer
- GLIDE
global and individual tests for direct effects
- IV
instrumental variable
- MR
Mendelian randomization
- Q-Q
quantile-quantile
- SNP
single nucleotide polymorphism
REFERENCES
- 1. Katan MB. Apolipoprotein E isoforms, serum cholesterol, and cancer. Lancet. 1986;1(8479):507–508. [DOI] [PubMed] [Google Scholar]
- 2. Smith GD, Ebrahim S. ‘Mendelian randomization’: can genetic epidemiology contribute to understanding environmental determinants of disease? Int J Epidemiol. 2003;32(1):1–22. [DOI] [PubMed] [Google Scholar]
- 3. Thomas DC, Conti DV. Commentary: the concept of ‘Mendelian randomization’. Int J Epidemiol. 2004;33(1):21–25. [DOI] [PubMed] [Google Scholar]
- 4. Didelez V, Sheehan N. Mendelian randomisation as an instrumental variable approach to causal inference. Stat Methods Med Res. 2007;16(4):309–330. [DOI] [PubMed] [Google Scholar]
- 5. Nitsch D, Molokhia M, Smeeth L, et al. . Limits to causal inference based on Mendelian randomization: a comparison with randomized controlled trials. Am J Epidemiol. 2006;163(5):397–403. [DOI] [PubMed] [Google Scholar]
- 6. Hernán MA, Robins JM. Instruments for causal inference: an epidemiologist’s dream? Epidemiology. 2006;17(4):360–372. [DOI] [PubMed] [Google Scholar]
- 7. Bochud M, Chiolero A, Elston RC, et al. . A cautionary note on the use of Mendelian randomization to infer causation in observational epidemiology. Int J Epidemiol. 2007;37(2):414–416. [DOI] [PubMed] [Google Scholar]
- 8. Didelez V, Meng S, Sheehan NA. Assumptions of IV methods for observational epidemiology. Stat Sci. 2010;25(1):22–40. [Google Scholar]
- 9. VanderWeele TJ, Tchetgen Tchetgen EJ, Cornelis M, et al. . Methodological challenges in Mendelian randomization. Epidemiology. 2014;25(3):427–435. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10. Hodgkin J. Seven types of pleiotropy. Int J Dev Biol. 1998;42(3):501–505. [PubMed] [Google Scholar]
- 11. Stearns FW. One hundred years of pleiotropy: a retrospective. Genetics. 2010;186(3):767–773. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Sivakumaran S, Agakov F, Theodoratou E, et al. . Abundant pleiotropy in human complex diseases and traits. Am J Hum Genet. 2011;89(5):607–618. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Solovieff N, Cotsapas C, Lee PH, et al. . Pleiotropy in complex traits: challenges and strategies. Nat Rev Genet. 2013;14(7):483–495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Pickrell JK, Berisa T, Liu JZ, et al. . Detection and interpretation of shared genetic influences on 42 human traits. Nat Genet. 2016;48(7):709–717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Bowden J, Davey Smith G, Burgess S. Mendelian randomization with invalid instruments: effect estimation and bias detection through Egger regression. Int J Epidemiol. 2015;44(2):512–525. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16. Dai JY, Chan KC, Hsu L. Testing concordance of instrumental variable effects in generalized linear models with application to Mendelian randomization. Stat Med. 2014;33(23):3986–4007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17. Bowden J, Davey Smith G, Haycock PC, et al. . Consistent estimation in Mendelian randomization with some invalid instruments using a weighted median estimator. Genet Epidemiol. 2016;40(4):304–314. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18. Kang H, Zhang A, Cai TT, et al. . Instrumental variables estimation with some invalid instrument and its application to Mendelian randomization. J Am Stat Assoc. 2016;111(513):132–144. [Google Scholar]
- 19. Corbin LJ, Richmond RC, Wade KH, et al. . BMI as a modifiable risk factor for type 2 diabetes: refining and understanding causal estimates using Mendelian randomization. Diabetes. 2016;65(10):3002–3007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20. Bowden J, Del Greco MF, Minelli C, et al. . A framework for the investigation of pleiotropy in two-sample summary data Mendelian randomization. Stat Med. 2017;36(11):1783–1802. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21. Zhu Z, Zheng Z, Zhang F, et al. . Causal associations between risk factors and common diseases inferred from GWAS summary data. Nat Commun. 2018;9:224. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Vansteelandt S, Goetghebeur E. Causal inference with generalized structural mean models. J R Stat Soc Ser B. 2003;65(4):817–835. [Google Scholar]
- 23. Vansteelandt S, Bowden J, Babanezhad M, et al. . On instrumental variables estimation of causal odds ratio. Stat Sci. 2011;26(3):403–422. [Google Scholar]
- 24. Clarke PS, Windmeijer F. Instrumental variable estimators for binary outcomes. J Am Stat Assoc. 2012;107(500):1638–1652. [Google Scholar]
- 25. Greenland S, Robins JM, Pearl J. Confounding and collapsibility in causal inference. Stat Infer. 1999;14(1):29–46. [Google Scholar]
- 26. Dai JY, Zhang XC. Mendelian randomization studies for a continuous exposure under case-control sampling. Am J Epidemiol. 2015;181(6):440–449. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27. Lumley T, Kronmal R, Ma S Relative risk regression in medical research: models, contrasts, estimators and algorithms. (UW Biostatistics Working Paper Series, working paper 293). Berkeley, CA: Berkeley Electronic Press; 2006. https://biostats.bepress.com/uwbiostat/paper293/. Accessed March 15, 2017.
- 28. Burgess S, Butterworth A, Thompson SG. Mendelian randomization analysis with multiple genetic variants using summarized data. Genet Epidemiol. 2013;37(7):658–665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Peters U, Jiao S, Schumacher FR, et al. . Identification of genetic susceptibility loci for colorectal tumors in a genome-wide meta-analysis. Gastroenterology. 2013;144(4):799–807. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30. Thrift AP, Gong J, Peters U, et al. . Mendelian randomization study of body mass index and colorectal cancer risk. Cancer Epidemiol Biomarkers Prev. 2015;24(7):1024–1031. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31. Thrift AP, Gong J, Peters U, et al. . Mendelian randomization study of height and risk of colorectal cancer. Int J Epidemiol. 2015;44(2):662–672. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32. Locke AE, Kahali B, Berndt SI, et al. . Genetic studies of body mass index yield new insights for obesity biology. Nature. 2015;518(7538):197–206. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33. Wood AR, Esko T, Yang J, et al. . Defining the role of common variation in the genomic and biological architecture of adult human height. Nat Genet. 2014;46(11):1173–1186. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.