Abstract
Especially for larger molecules relevant to life sciences, vibrational self-consistent field (VSCF) calculations can become unmanageably demanding even when only first and second order potential coupling terms are considered. This paper investigates to what extent the grid density of the VSCF’s underlying potential energy surface can be reduced without sacrificing accuracy of the resulting wavenumbers. Including single-mode and pair contributions, a reduction to eight points per mode did not introduce a significant deviation but improved the computational efficiency by a factor of four. A mean unsigned deviation of 1.3% from the experiment could be maintained for the fifteen molecules under investigation and the approach was found to be applicable to rigid, semi-rigid and soft vibrational problems likewise. Deprotonated phosphoserine, stabilized by two intramolecular hydrogen bonds, was investigated as an exemplary application.
Keywords: VSCF, grid density, spectroscopy, anharmonicity, MP2, infrared, vibrational self-consistent field, phosphoserine
1. Introduction
The continuously increasing availability of computational resources as well as the development of accurate and efficient quantum chemical approaches have made computational vibrational spectroscopy an indispensable field complementing experimental techniques. Nowadays, almost every quantum chemical software package enables the analysis of second-order properties of the energy (e.g., IR and Raman absorptions, IR intensities, electric dipole polarizabilities, nuclear magnetic resonance chemical shifts, spin-spin coupling constants). Arguably, the prediction of IR and Raman absorptions is among the most important applications considering the prevalence of these technique. While most fundamental IR absorptions can be assigned quite satisfyingly on an empirical basis or via normal coordinate analysis, especially the near-infrared region is cluttered by overtones and combination excitations that are cumbersome to assign.
With regard to computational approaches, the harmonic oscillator approximation (HOA) is the most fundamental technique for obtaining vibrational spectroscopic data. However, due to the rigorous assumption introduced, in that the bond potential exhibits a harmonic shape, significant deviation from experiment is frequently observed. The most simple solution accounting for the lack of anharmonicities is to introduce empirical scaling factors that are multiplied with the harmonically approximated absorptions. Scott and Radom derived scaling factors for a vast number of ab initio and semi-empirical methods and a large number of basis sets [1,2]. It has to be stressed, however, that an empirical scaling may not be applied on a system-independent basis, even though the scaling factors have been derived for a rather large set of molecules. Noteworthy, a harmonic bond potential cannot be assumed a proper basis for considerations towards excitations involving more than one quantum of energy.
Especially due to these fundamental deficiencies, further corrective techniques have been developed that account for anharmonicities in an explicit manner. The two most prominent approaches are the vibrational self-consistent field (VSCF) method [3,4,5,6,7,8] and the vibrational second order perturbative ansatz (VPT2) [9,10]. VPT2 is a technique that relies on the computation of higher-order derivatives of the energy. Gaussian [11] is probably the most prominent commercial software package incorporating a VPT2 algorithm which relies on third and semi-diagonal fourth derivatives of the energy with respect to the nuclear coordinates. This method is applied regularly [12,13] but it may only be employed safely to vibrational problems where the harmonic part of the potential is dominant. Moreover, the computationally demanding generation of third and fourth derivatives limits the approach to rather small systems. VSCF on the other hand utilizes a separability ansatz which enables the anharmonicity of each mode to be accounted for by screening the respective potential in a point-wise manner. Mode interactions may be evaluated by computing d dimensional grids and the maximum possible dimensionality is determined by the number of vibrational degrees of freedom (N ) featured by the molecule under investigation. In a conventional VSCF calculation, each mode’s potential is characterized by 16 grid points [14]. In the past, scientific papers have been reported that employed grids of higher (r = 32) [15] and lower resolutions (r = 8) [16,17,18]. Roy et al. [19] recently presented data based on a variety of grid densities ranging from 8 to 16 points. Since they reported overall deviations summed over a set of reference molecules, one could conclude that this rather diverse choice of grid resolutions does not impose a significant error on the wavenumbers. However, to date there still seem to exist ambiguities with regard to a generally applicable grid density that is computationally feasible. Hence, and considering the massive computational effort involved in high resolution VSCF calculations, it seemed promising to conduct a systematic study addressing these issues. 15 reference molecules are investigated in detail and an application to the lowest energy conformer of phosphoserine is presented. At this point it seems worth mentioning that while many quantum chemical software packages such as GAMESS [20], NWChem [21] and MOLPRO [22] incorporate VSCF implementations, GAMESS is the program employed in this work due to the fact that it is freely available and compatible with the most prominent computer operating systems.
2. Methods
In this section, a brief overview describing the procedures underlying a VSCF evaluation is given. Particularities of the involved techniques are presented while reference to the original literature is given for further details.
2.1. Energy Minimization
A prerequisite for every computational spectroscopic analysis is a proper structural ensemble. For the majority of cases, the user would want to obtain absorption data corresponding to an equilibrium structure and thus, an energetically favorable reference geometry is required. This implies that at least a local energy minimum (or the global energy minimum) is obtained and this is reflected by a nearly zero gradient of the energy g(q)∆q with respect to the nuclear coordinates q. While the program’s default criteria suffice for energetical and structural considerations in many cases, a VSCF calculation requires a thoroughly minimized geometry. This condition is realized by setting up rigorous cutoff tolerances for g(q)∆q. We considered a molecular geometry properly minimized when each gradient contribution is smaller than 0.000001 Eh· Bohr−1. Every calculation reported herein was performed at the Møller-Plesset level of theory, accounting for electron correlation effects via a perturbative ansatz [23,24,25]. The frozen-core approximation [26] was employed, explicitly correlating all but the core electrons. Dunning’s correlation-consistent polarized basis set of triple-ζ quality has been utilized since it can be considered a routinely employed set of functions that is known to deliver results of acceptable accuracy [27]. The appropriate point group was imposed onto the molecular geometry where applicable in order to make use of the efficient symmetry optimized SCF algorithm in GAMESS.
2.2. Second Derivatives of the Energy
A potential V(q) may be expressed as a Taylor series
| (1) |
and for the case that the reference geometry resembles an energy minimum and assuming a harmonic potential shape, all but the first and third terms vanish. This simplified approach enables the evaluation of the elements of ℍr,s by analytical or numerical analysis:
| (2) |
A transformation into mass-weighted coordinates and diagonalization of the Hessian matrix ℍr,s yields the eigenvectors corresponding to the normal modes. At this point, computational spectroscopic data at the HOA level is available. It seems worth mentioning that the further description of extended vibrational analysis is based on mass-weighted normal coordinates or other non-redundant coordinates for the sake of clarity, whereas the expansion of the potential energy surfaces was realized in rectilinear coordinates (Section 3.1). VSCF calculations require a Hessian corresponding to the equilibrium geometry, as will be discussed in the next paragraph. The Hessian matrices in this work have been obtained semi-numerically involving two displacements of ±0.01 Bohr about the reference geometry for each atom.
2.3. The VSCF Routine
Even though VSCF accounts for anharmonicities explicitly, it still requires ℍr,s as a reference state. This is owed to the fact, that VSCF assumes a molecule’s vibrational wave function Ψ(Q1,..,N) to be separable into single mode wave functions :
| (3) |
While this product ansatz can be implemented rather efficiently, it inherently limits the accuracy of the VSCF technique since it represents decoupled vibrational modes. There are, besides the methods mentioned in Section 2.4, techniques available which are able to circumvent this limitation [28,29]. Introducing the variational principle [30,31], the single mode VSCF equation [6,32] is formulated as:
| (4) |
where is mode Qi’s effective potential. Equation (4) neglects parts of the full Watson Hamiltonian for non-linear molecules [33] which accounts for N vibrational degrees of freedom:
| (5) |
The second and third part of the Hamiltonian represent the generalized inverse of the effective moment of inertia µαβ and the vibrational angular momentum operator . Given that the full Watson Hamiltonian is cumbersome to implement computationally, most implementations resort to neglecting the last two terms of Ĥ. The error introduced is small especially for fundamental excitations as has been shown by Bowman et al. [34].
The VSCF equations are solved in an iterative manner until self-consistency is achieved. Illustratively, VSCF may be seen as an approach where each vibration is influenced by the mean field of the surrounding modes. However, especially when certain mode interactions exhibit unique properties, this mean field ansatz does no longer properly describe the vibrational problem sufficiently well. A number of post-VSCF techniques accounting for this deficiency have been presented and they are discussed in the subsequent section.
Since the VSCF technique involves a grid-based screening of bond potentials and their interactions, a discussion of the so-called hierarchical expansion is justified. For a system exhibiting N normal modes, the VSCF expansion is denoted as:
| (6) |
A complete interaction scheme is realized by imposing N -dimensionality onto Equation (6) but obviously, such a treatment scales unfavorably with the studied system size. Noteworthy, most applications of VSCF theory truncate the expansion largely by including only and contributions [35,36,37,38]. This simplification is valid for a large number of applications and the inclusion of higher-order interaction terms is hardly justifiable for other than the smallest molecules or for cases, where convergence is only achieved when including such terms. Programs such as MULTIMODE [34,39], Molpro [22] and MIDAScpp enable coupling orders of d > 3 yielding IR bands of exceptional accuracy [7,40]. In this article, we confine our discussion to and contributions since this study aims at larger molecules where an incorporation of higher coupling terms would be prohibitive. The number of grid points due (Np) is calculated via Equation (7) .
| (7) |
Assuming r = 16 and taking glycine as an example, the pair-wise approximation would require 71,040 points to be computed while a VSCF calculation involving also three-mode interactions already gives rise to 8,361,344 energy evaluations, a nearly 120 fold increase in computational burden. Herein, we will examine the impact of the grid density on the quality of the absorption data by conducting VSCF calculations involving between 6 and 16 grid points per mode. For the displacements underlying the PES scan, a symmetric grid range of [−4, +4], with ωi being the harmonic frequency of the i-th normal mode, was chosen. The grid points within these boundaries have been set-up in an equidistant manner which implies that for even grid densities (i.e., 6, 8, 10, 12, 14 and 16 points), equilibrium is located between the two innermost grid points. For odd grid densities (i.e., 7, 9, 11, 13 and 15 points), equilibrium is described by one distinct grid point. For every resolution r < 16, the grid points are interpolated to the original resolution of r = 16 by a polynomial fit.
2.4. Extensions of the VSCF Approach
As mentioned earlier, the VSCF assumption does not hold for many applications. Therefore, a perturbative approach has been suggested, accounting for the error introduced by the mean-field VSCF ansatz [15,41,42]. A prerequisite is that the difference between the "true" energy and the mean-field VSCF energy is small. An expansion known from electronic structure theory [23] is then formulated for the energy and wave function of a state n that is truncated at second order:
| (8) |
| (9) |
with H = + λ∆V and an insertion of En and Ψn in H Ψn = EnΨn, the energy contribution at second order may be formulated as:
| (10) |
Herein, and are the unperturbed vibrational product wave functions and and are the unperturbed VSCF energies. This technique, which is commonly abbreviated as second order perturbation theory augmented (PT2)-VSCF or correlation-corrected (CC)-VSCF, has proven useful for many applications. However, since obtaining correlation-corrected VSCF energies requires significant computational resources, the basic PT2-VSCF approach is limited to small systems. Due to the inherent need for an efficient solution of Equation (10), Gerber’s work group developed a solution based on the assumption of orthogonal vibrational single mode wave functions (Equation (3)) which leads to the annihilation of diagonal elements in Equation (10) [43]. Tests involving Glyn peptides showed that the runtime improvement is greater for larger molecules: for monomeric Gly, a speedup factor close to 6 was observed while the correlation-corrected wavenumbers of tetraglycine have been evaluated more than 16 times faster as with the conventional PT2-VSCF ansatz. This acceleration technique, and also the fact that this accelerated PT2-VSCF technique is readily implemented in GAMESS [20], are probably the main reasons for PT2-VSCF being a routinely employed VSCF correction. It has to be stressed, however, that the evaluation of the VSCF equations with its further corrections may not be confused with the preceding and highly demanding evaluation of the potential energy grid (vide supra).
Problems may arise when degenerate vibrational states are present. PT2-VSCF can fail here due to a close to zero denominator in Equation (4) which can lead to a largely overestimated perturbative correction. Hence, the degenerate PT2-VSCF method has been developed [44] but to date it has been implemented in GAMESS exclusively for degeneracies arising from fundamental excitations. A more generally available simple solution available in the GAMESS program code is that contributions involving denominators falling below a critical value are excluded from the treatment. Most applications reporting PT2-VSCF derived data rely on this simplification and therefore, we will also confine our calculations to this simplified technique.
Besides perturbation theory augmented VSCF, significant effort is put into post-VSCF techniques involving configuration interaction [45,46,47,48], coupled-cluster [49,50,51] and multi-configurational SCF theory [52,53]. While such methods yield highly accurate data, they are to date only applicable to small vibrational problems with less than 20 atoms.
Due to the popularity of the PT2-VSCF method and the fact that results of good quality at manageable computational cost are available also for larger molecules, all data presented in this paper is corrected exclusively with this perturbative ansatz.
3. Results and Discussion
The fifteen molecules under investigation gave rise to 176 distinct vibrational degrees of freedom, considering all fundamental stretching, deformation and torsional vibrations. PT2-VSCF can yield questionable or sometimes even divergent results for very low-lying and floppy torsions, which is due to the fact that the PES expansion is conventionally carried out in Cartesian coordinates [18,19,54]. The error induced through an anharmonic correction of such a vibration can exceed the boundaries of accuracy known from the HOA [54]. Hence, the usual procedure is to either treat such vibrations harmonically or to describe the underlying displacements in internal coordinates. A substitution for physically more meaningful internal coordinates was proposed by Njegic and Gordon [54] and could be shown to yield good results for formamide and thioformamide [55] as well as for H2O2 but by introducing a new expansion technique for the kinetic energy operator [56]. Nonetheless, setting up internal coordinates that properly describe the displacements underlying a VSCF treatment is by no means a trivial task. The GAMESS code is able to identify each normal mode’s contributions to particular internal coordinates [57], but the user still has to input a balanced description of each vibrational degree of freedom which can become unmanageably difficult for larger systems. Hence, and especially when large molecules are investigated, the majority of users of VSCF theory resort to a PES expansion in Cartesian coordinates and the contributions of critical torsions are omitted when self-consistency is not achieved.
For glycine (C2H5NO2), three normal modes (i.e., the N-Cα-Ccarb-O torsion, the NH2 group torsion and δCcarbO2,oop) had to be excluded from the VSCF treatment since they are known to lead to divergence during a perturbation theory corrected VSCF evaluation [19]. Similarly, for methanol (CH3OH) the CO axis torsion has been omitted from the PT2-VSCF treatment due to an inadequate description of this particularly floppy torsional mode within the VSCF framework [58]. Dimethylether also exhibits two floppy torsions involving the C-O axes that have been excluded likewise. For ethane, one normal mode near 290 cm−1 [59,60,61,62] was omitted due to its floppy character but the other six missing modes did arise from degenerate states in νCH3,as, δCH3,as and ρCH3. Experimentally, these degeneracies cannot be distinguished and since the PT2-VSCF derived values did not exhibit significant numerical discrepancies, each pair of degeneracies is presented as a single mean value for the sake of visibility.
3.1. Performance of the PT2-VSCF Approach
The computationally obtained absorption data are compared to experimental data in Table 1. The column headers indicate the employed number of grid points during the VSCF evaluations. As a measure of quality, the mean absolute percentage error µ for each molecule and each grid density is calculated according to Equation (11):
| (11) |
Table 1.
Computed and experimental absorption data and the calculated values for µ in %. n.a. means “not applicable” and n.o. means “not observed”.
| H2O (C2v) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,71,72] |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| νOH2 ,as | B2 | 2875 | 3997 | 3731 | 3772 | 3766 | 3766 | 3765 | 3765 | 3765 | 3765 | 3765 | 3756 |
| νOH2 ,s | A1 | 3041 | 3785 | 3657 | 3691 | 3684 | 3683 | 3683 | 3682 | 3682 | 3682 | 3682 | 3652 |
| δOH2 | A1 | 1216 | 1688 | 1570 | 1590 | 1586 | 1586 | 1586 | 1586 | 1586 | 1586 | 1586 | 1595 |
| μ | 21.3 | 5.3 | 0.8 | 0.6 | 0.6 | 0.6 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 | n.a. | |
| CO2 (D∞h) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,73,74] |
| νCO2,as | 1791 | 2547 | 2359 | 2391 | 2386 | 2386 | 2385 | 2385 | 2385 | 2385 | 2385 | 2349 | |
| νCO2,s | 993 | 1408 | 1255 | 1319 | 1316 | 1315 | 1315 | 1315 | 1315 | 1315 | 1315 | 1285 | |
| δCO2 | ∏μ | 487 | 699 | 645 | 654 | 653 | 653 | 653 | 653 | 653 | 653 | 653 | 667 |
| δCO2 | ∏μ | 487 | 699 | 645 | 654 | 653 | 653 | 653 | 653 | 653 | 653 | 653 | 667 |
| μ | 25.1 | 6.9 | 2.3 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | n.a. | |
| CH2O (C2v) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,75,76,77] |
| νCH2,as | B1 | 2184 | 3000 | 2809 | 2837 | 2833 | 2833 | 2833 | 2832 | 2832 | 2832 | 2832 | 2843 |
| νCH2,s | A1 | 2250 | 2905 | 2801 | 2823 | 2818 | 2818 | 2818 | 2817 | 2817 | 2817 | 2817 | 2782 |
| νCO | A1 | 1312 | 1855 | 1719 | 1745 | 1741 | 1740 | 1740 | 1740 | 1740 | 1740 | 1740 | 1746 |
| δCH2 | A1 | 1157 | 1614 | 1502 | 1521 | 1518 | 1518 | 1518 | 1518 | 1518 | 1518 | 1518 | 1500 |
| ρCH2 | B1 | 945 | 1340 | 1240 | 1257 | 1254 | 1254 | 1254 | 1254 | 1254 | 1254 | 1254 | 1249 |
| ωCH2 | B2 | 891 | 1250 | 1162 | 1176 | 1174 | 1173 | 1173 | 1173 | 1173 | 1173 | 1173 | 1167 |
| μ | 23.0 | 6.4 | 0.8 | 0.8 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | n.a. | |
| C2H2 (D∞h) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,60,78,79,80] |
| νC2H2,s | 2699 | 3490 | 3375 | 3390 | 3384 | 3380 | 3384 | 3384 | 3384 | 3384 | 3384 | 3374 | |
| νC2H2,as | 2523 | 3405 | 3199 | 3233 | 3228 | 3227 | 3227 | 3227 | 3227 | 3227 | 3227 | 3289 | |
| νCC | 1469 | 2046 | 1912 | 1937 | 1932 | 1932 | 1932 | 1932 | 1932 | 1932 | 1932 | 1974 | |
| δC2H2,s | ∏u | 557 | 792 | 733 | 746 | 743 | 743 | 743 | 743 | 743 | 743 | 743 | 730 |
| δC2H2,s | ∏u | 557 | 792 | 733 | 746 | 743 | 743 | 743 | 743 | 743 | 743 | 743 | 730 |
| δC2H2,as | ∏g | 443 | 638 | 589 | 602 | 598 | 598 | 598 | 598 | 598 | 598 | 598 | 612 |
| δC2H2,as | ∏g | 443 | 638 | 589 | 602 | 598 | 598 | 598 | 598 | 598 | 598 | 598 | 612 |
| μ | 24.5 | 5.2 | 2.0 | 1.7 | 1.8 | 1.8 | 1.8 | 1.8 | 1.8 | 1.8 | 1.8 | n.a. | |
| HCOOH (Cs) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,81,82,83,84] |
| νOH | A' | 2841 | 3682 | 3530 | 3559 | 3550 | 3557 | 3552 | 3552 | 3552 | 3552 | 3552 | 3570 |
| νCH | A' | 2246 | 3134 | 2959 | 2983 | 2978 | 2977 | 2977 | 2977 | 2977 | 2977 | 2977 | 2943 |
| νC=O | A' | 1337 | 1910 | 1764 | 1790 | 1786 | 1786 | 1786 | 1785 | 1785 | 1785 | 1785 | 1770 |
| δCH | A' | 1043 | 1480 | 1367 | 1384 | 1381 | 1381 | 1381 | 1381 | 1381 | 1381 | 1381 | 1387 |
| δOH | A' | 982 | 1367 | 1265 | 1280 | 1277 | 1277 | 1277 | 1277 | 1277 | 1277 | 1277 | 1387 |
| νC-O | A' | 848 | 1148 | 1077 | 1089 | 1086 | 1086 | 1086 | 1086 | 1086 | 1086 | 1086 | 1105 |
| δCH | A" | 786 | 1114 | 1029 | 1042 | 1040 | 1040 | 1040 | 1040 | 1040 | 1040 | 1040 | 1033 |
| δOH,oop | A" | 515 | 631 | 588 | 623 | 609 | 608 | 609 | 609 | 609 | 609 | 609 | 638 |
| δOCO | A' | 469 | 659 | 611 | 619 | 617 | 617 | 617 | 617 | 617 | 617 | 617 | 625 |
| μ | 22.8 | 6.0 | 2.1 | 1.4 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 | n.a. | |
| CH4 (Td) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,60,85,86] |
| νCH3,as | F2 | 2333 | 3210 | 3000 | 3035 | 3029 | 3029 | 3028 | 3028 | 3028 | 3028 | 3028 | 3019 |
| νCH3,as | F2 | 2299 | 3177 | 2990 | 3020 | 3015 | 3015 | 3014 | 3014 | 3014 | 3014 | 3014 | 3019 |
| νCH3,as | F2 | 2330 | 3209 | 2999 | 3033 | 3028 | 3027 | 3027 | 3027 | 3027 | 3027 | 3027 | 3019 |
| νCH4,s | A1 | 2588 | 2968 | 2948 | 2943 | 2945 | 2944 | 2943 | 2943 | 2943 | 2943 | 2943 | 2917 |
| δCH4,as | E | 1166 | 1641 | 1523 | 1542 | 1539 | 1539 | 1539 | 1539 | 1539 | 1539 | 1539 | 1534 |
| δCH4,as | E | 1166 | 1641 | 1523 | 1542 | 1539 | 1539 | 1539 | 1539 | 1539 | 1539 | 1539 | 1534 |
| δCH3,s | F2 | 993 | 1390 | 1293 | 1309 | 1306 | 1306 | 1306 | 1306 | 1306 | 1306 | 1306 | 1306 |
| δCH3,s | F2 | 992 | 1390 | 1293 | 1309 | 1306 | 1306 | 1306 | 1306 | 1306 | 1306 | 1306 | 1306 |
| δCH3,s | F2 | 993 | 1390 | 1294 | 1309 | 1307 | 1307 | 1307 | 1306 | 1306 | 1306 | 1306 | 1306 |
| µ | 22.3 | 5.9 | 0.9 | 0.4 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | n.a. | |
| CH3Cl (C3v) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,87,88,89,90] |
| νCH3,as | E | 2338 | 3203 | 3002 | 3035 | 3030 | 3029 | 3029 | 3029 | 3029 | 3029 | 3029 | 3039 |
| νCH3,as | E | 2306 | 3192 | 2974 | 3019 | 3016 | 3015 | 3015 | 3015 | 3015 | 3015 | 3014 | 3039 |
| νCH3,s | A1 | 2339 | 3074 | 2964 | 2989 | 2987 | 2986 | 2986 | 2985 | 2985 | 2985 | 2985 | 2937 |
| δCH3,as | E | 1106 | 1555 | 1445 | 1463 | 1460 | 1460 | 1460 | 1460 | 1460 | 1460 | 1460 | 1452 |
| δCH3,as | E | 1106 | 1556 | 1444 | 1462 | 1460 | 1459 | 1459 | 1459 | 1459 | 1459 | 1459 | 1452 |
| δCH3,s | A1 | 1036 | 1464 | 1357 | 1375 | 1372 | 1372 | 1371 | 1371 | 1371 | 1371 | 1371 | 1355 |
| ρCH3 | E | 773 | 1099 | 1017 | 1031 | 1028 | 1028 | 1028 | 1028 | 1028 | 1028 | 1028 | 1017 |
| ρCH3 | E | 776 | 1099 | 1020 | 1033 | 1031 | 1031 | 1031 | 1031 | 1031 | 1031 | 1031 | 1017 |
| νCCl | A1 | 585 | 802 | 749 | 760 | 758 | 758 | 758 | 758 | 758 | 758 | 758 | 732 |
| µ | 23.0 | 7.0 | 0.9 | 1.4 | 1.2 | 1.2 | 1.2 | 1.2 | 1.2 | 1.2 | 1.2 | n.a. | |
| CH3OH (Cs) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,60,91,92,93] |
| νOH | A’ | 2812 | 3900 | 3646 | 3694 | 3687 | 3686 | 3686 | 3686 | 3686 | 3686 | 3686 | 3681 |
| νCH3,as | A’ | 2301 | 3198 | 2984 | 3035 | 3030 | 3029 | 3028 | 3028 | 3028 | 3028 | 3028 | 3000 |
| νCH3,as | A” | 2230 | 3091 | 2881 | 2912 | 2908 | 2908 | 2907 | 2907 | 2907 | 2907 | 2907 | 2960 |
| νCH3,s | A’ | 2363 | 2951 | 2849 | 2957 | 2947 | 2942 | 2941 | 2941 | 2941 | 2941 | 2941 | 2844 |
| δCH3,as | A’ | 1130 | 1587 | 1475 | 1493 | 1490 | 1490 | 1490 | 1490 | 1490 | 1490 | 1490 | 1477 |
| δCH3,as | A” | 1116 | 1574 | 1459 | 1478 | 1475 | 1475 | 1475 | 1475 | 1474 | 1474 | 1474 | 1477 |
| δCH3,s | A’ | 1104 | 1563 | 1447 | 1466 | 1463 | 1463 | 1463 | 1463 | 1463 | 1463 | 1463 | 1455 |
| δOH | A’ | 1020 | 1458 | 1342 | 1362 | 1359 | 1359 | 1358 | 1358 | 1358 | 1358 | 1358 | 1345 |
| ρCH3 | A” | 843 | 1178 | 1069 | 1083 | 1081 | 1081 | 1080 | 1080 | 1080 | 1080 | 1080 | 1060 |
| νCO | A’ | 789 | 1060 | 1015 | 1028 | 1026 | 1026 | 1025 | 1025 | 1025 | 1025 | 1025 | 1033 |
| µ | 22.9 | 6.4 | 0.9 | 1.3 | 1.2 | 1.2 | 1.2 | 1.2 | 1.1 | 1.1 | 1.1 | n.a. | |
| CH3CN (C3v) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,94,95,96,97,98,99,100] |
| νCH3,as | E | 2281 | 3153 | 2940 | 2972 | 2967 | 2967 | 2967 | 2966 | 2966 | 2966 | 2966 | 3009 |
| νCH3,as | E | 2322 | 3172 | 2976 | 2994 | 2990 | 2989 | 2989 | 2988 | 2988 | 2988 | 2988 | 3009 |
| νCH3,s | A1 | 2322 | 3059 | 2951 | 2970 | 2968 | 2967 | 2967 | 2967 | 2967 | 2967 | 2967 | 2954 |
| νCN | A1 | 1656 | 2308 | 2152 | 2178 | 2174 | 2174 | 2173 | 2173 | 2173 | 2173 | 2173 | 2267 |
| δCH3,as | E | 1099 | 1547 | 1438 | 1456 | 1453 | 1453 | 1453 | 1453 | 1453 | 1453 | 1453 | 1454 |
| δCH3,as | E | 1099 | 1550 | 1437 | 1456 | 1453 | 1453 | 1453 | 1453 | 1453 | 1453 | 1453 | 1454 |
| δCH3 ,s | A1 | 1047 | 1487 | 1378 | 1397 | 1394 | 1394 | 1394 | 1393 | 1393 | 1393 | 1393 | 1389 |
| ρCH3 | E | 788 | 1121 | 1037 | 1052 | 1049 | 1049 | 1049 | 1049 | 1049 | 1049 | 1049 | 1041 |
| ρCH3 | E | 789 | 1122 | 1038 | 1053 | 1050 | 1050 | 1050 | 1050 | 1050 | 1050 | 1050 | 1041 |
| νCC | A1 | 692 | 983 | 923 | 932 | 930 | 930 | 930 | 930 | 930 | 930 | 930 | 920 |
| δCCN | E | 270 | 395 | 361 | 367 | 366 | 366 | 366 | 366 | 366 | 366 | 366 | 361 |
| δCCN | E | 268 | 395 | 359 | 365 | 364 | 364 | 364 | 364 | 364 | 364 | 364 | 361 |
| µ | 24.4 | 6.4 | 1.1 | 1.1 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | n.a. | |
| C2H4(D2h) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,60,101,102] |
| νCH2,as | B2u | 2399 | 3358 | 3122 | 3161 | 3155 | 3154 | 3154 | 3154 | 3154 | 3154 | 3154 | 3106 |
| νCH2,as | B1g | 2379 | 3328 | 3095 | 3133 | 3127 | 3126 | 3126 | 3126 | 3126 | 3126 | 3126 | 3103 |
| νCH2,s | Ag | 2297 | 3152 | 3047 | 3055 | 3052 | 3051 | 3051 | 3051 | 3051 | 3051 | 3051 | 3026 |
| νCH2,s | B3u | 2318 | 3253 | 3023 | 3060 | 3055 | 3054 | 3054 | 3054 | 3054 | 3054 | 3054 | 2989 |
| νCC | Ag | 1273 | 1750 | 1628 | 1648 | 1644 | 1644 | 1644 | 1644 | 1644 | 1644 | 1644 | 1623 |
| δCH2 | B3u | 1095 | 1554 | 1439 | 1458 | 1455 | 1455 | 1455 | 1455 | 1455 | 1455 | 1455 | 1444 |
| δCH2 | Ag | 1051 | 1432 | 1345 | 1361 | 1359 | 1358 | 1358 | 1358 | 1358 | 1358 | 1358 | 1342 |
| ρCH2 | B1g | 922 | 1318 | 1217 | 1235 | 1232 | 1232 | 1232 | 1232 | 1232 | 1232 | 1232 | 1236 |
| τCH2 | Au | 795 | 1129 | 1046 | 1060 | 1058 | 1058 | 1058 | 1058 | 1058 | 1058 | 1058 | 1023 |
| ωCH2 | B1u | 730 | 1036 | 960 | 973 | 971 | 971 | 971 | 971 | 971 | 971 | 971 | 949 |
| ωCH2 | B2g | 712 | 1013 | 939 | 951 | 949 | 949 | 949 | 949 | 949 | 949 | 949 | 943 |
| ρCH2 | B2u | 619 | 893 | 824 | 836 | 834 | 834 | 834 | 834 | 834 | 834 | 834 | 826 |
| µ | 23.4 | 7.7 | 0.8 | 1.5 | 1.4 | 1.4 | 1.3 | 1.3 | 1.3 | 1.3 | 1.3 | n.a. | |
| C2H4O (C2v) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,60,103,104] |
| νCH2,as | B2 | 2372 | 3313 | 3083 | 3120 | 3114 | 3114 | 3113 | 3113 | 3113 | 3113 | 3113 | 3065 |
| νCH2,as | A2 | 2361 | 3296 | 3067 | 3104 | 3098 | 3098 | 3097 | 3097 | 3097 | 3097 | 3097 | n.o. |
| νCH2,s | A1 | 2378 | 3097 | 2939 | 3047 | 3064 | 3058 | 3057 | 3056 | 3056 | 3056 | 3056 | 3018 |
| νCH2,s | B1 | 2295 | 3214 | 2988 | 3024 | 3019 | 3018 | 3018 | 3018 | 3018 | 3018 | 3018 | 3006 |
| δCH2,s | A1 | 1153 | 1634 | 1500 | 1518 | 1515 | 1515 | 1515 | 1515 | 1515 | 1515 | 1515 | 1498 |
| δCH2,as | B1 | 1121 | 1590 | 1472 | 1492 | 1489 | 1489 | 1489 | 1489 | 1489 | 1489 | 1489 | 1472 |
| νCC | A1 | 1070 | 1328 | 1277 | 1288 | 1286 | 1285 | 1285 | 1285 | 1285 | 1285 | 1285 | 1270 |
| ρCH2 | A2 | 876 | 1253 | 1157 | 1174 | 1171 | 1171 | 1171 | 1171 | 1171 | 1171 | 1171 | n.o. |
| τCH2 | B2 | 871 | 1244 | 1149 | 1166 | 1163 | 1163 | 1163 | 1163 | 1163 | 1163 | 1163 | 1142 |
| ωCH2 | B1 | 859 | 1229 | 1135 | 1152 | 1149 | 1149 | 1149 | 1149 | 1149 | 1149 | 1149 | 1151 |
| ωCH2 | A1 | 882 | 1203 | 1128 | 1141 | 1139 | 1138 | 1138 | 1138 | 1138 | 1138 | 1138 | 1148 |
| τCH2 | A2 | 783 | 1117 | 1032 | 1047 | 1044 | 1044 | 1044 | 1044 | 1044 | 1044 | 1044 | n.o. |
| νOC2,s | A1 | 669 | 946 | 877 | 889 | 887 | 887 | 887 | 887 | 887 | 887 | 887 | 877 |
| νOC2,as | B1 | 624 | 891 | 822 | 833 | 832 | 831 | 831 | 831 | 831 | 831 | 831 | 872 |
| ρCH2 | B2 | 615 | 885 | 816 | 829 | 827 | 827 | 827 | 827 | 827 | 827 | 827 | 821 |
| µ | 23.3 | 6.5 | 1.2 | 1.4 | 1.4 | 1.3 | 1.3 | 1.3 | 1.3 | 1.3 | 1.3 | n.a. | |
| CH3NH2(Cs) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,105,106,107] |
| νNH2,as | A” | 2629 | 3517 | 3318 | 3348 | 3343 | 3343 | 3343 | 3343 | 3343 | 3343 | 3343 | 3411 |
| νNH2,s | A’ | 2539 | 3431 | 3362 | 3352 | 3347 | 3347 | 3346 | 3346 | 3346 | 3346 | 3346 | 3349 |
| νCH3,as | A” | 2283 | 3110 | 2919 | 2947 | 2943 | 2942 | 2942 | 2942 | 2942 | 2942 | 2942 | 2985 |
| νCH3,as | A’ | 2283 | 3079 | 2907 | 2960 | 2957 | 2956 | 2956 | 2956 | 2955 | 2955 | 2955 | 2963 |
| νCH3,s | A’ | 2201 | 3010 | 2833 | 2889 | 2911 | 2906 | 2904 | 2904 | 2904 | 2904 | 2904 | 2816 |
| δNH2 | A’ | 1223 | 1733 | 1596 | 1610 | 1608 | 1608 | 1608 | 1608 | 1608 | 1608 | 1608 | 1642 |
| δCH3,as | A” | 1132 | 1601 | 1483 | 1503 | 1500 | 1494 | 1500 | 1500 | 1500 | 1500 | 1500 | 1481 |
| δCH3,as | A’ | 1119 | 1581 | 1467 | 1487 | 1484 | 1483 | 1483 | 1483 | 1483 | 1483 | 1483 | 1463 |
| δCH3,s | A’ | 1083 | 1534 | 1421 | 1440 | 1437 | 1437 | 1436 | 1436 | 1436 | 1436 | 1436 | 1450 |
| ρCH3 | A” | 998 | 1420 | 1314 | 1331 | 1328 | 1328 | 1328 | 1328 | 1328 | 1328 | 1328 | n.o. |
| ρCH3 | A’ | 891 | 1237 | 1152 | 1169 | 1167 | 1167 | 1167 | 1167 | 1167 | 1167 | 1167 | 1144 |
| νCN | A’ | 845 | 1109 | 1045 | 1059 | 1057 | 1057 | 1057 | 1057 | 1057 | 1057 | 1057 | 1050 |
| τNH2 | A” | 725 | 1052 | 967 | 981 | 979 | 979 | 979 | 979 | 979 | 979 | 979 | n.o. |
| ωNH2 | A’ | 637 | 909 | 840 | 852 | 851 | 850 | 850 | 850 | 850 | 850 | 850 | 816 |
| CN axis torsion | A” | 245 | 316 | 345 | 337 | 307 | 313 | 316 | 313 | 313 | 314 | 314 | 304 |
| µ | 22.8 | 5.9 | 2.4 | 2.3 | 1.6 | 1.7 | 1.8 | 1.7 | 1.7 | 1.7 | 1.7 | n.a. | |
| C2H6(D3d) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,60,61,62,108,109] |
| νCH3,as | Eu | 2309 | 3221 | 2999 | 3037 | 3031 | 3030 | 3030 | 3030 | 3030 | 3030 | 3030 | 2985 |
| νCH3,as | Eg | 2290 | 3185 | 2967 | 3011 | 3007 | 3006 | 3006 | 3006 | 3006 | 3006 | 3006 | 2969 |
| νCH3,s | A1g | 2470 | 3006 | 2950 | 2981 | 3004 | 2996 | 2995 | 2995 | 2994 | 2994 | 2994 | 2954 |
| νCH3,s | A2u | 2250 | 3172 | 2943 | 2982 | 2976 | 2975 | 2975 | 2975 | 2975 | 2975 | 2975 | 2896 |
| δCH3,as | Eg | 1123 | 1596 | 1474 | 1494 | 1491 | 1491 | 1491 | 1491 | 1491 | 1491 | 1491 | 1468 |
| δCH3,as | Eu | 1123 | 1593 | 1475 | 1496 | 1493 | 1493 | 1492 | 1492 | 1492 | 1492 | 1492 | 1469 |
| δCH3,s | A1g | 1059 | 1501 | 1393 | 1411 | 1408 | 1408 | 1408 | 1408 | 1408 | 1408 | 1408 | 1388 |
| δCH3,s | A2u | 1042 | 1482 | 1372 | 1392 | 1389 | 1389 | 1388 | 1388 | 1388 | 1388 | 1388 | 1379 |
| ρCH3 | Eg | 909 | 1294 | 1197 | 1215 | 1212 | 1212 | 1212 | 1212 | 1212 | 1212 | 1212 | 1190 |
| νCC | A1g | 818 | 1051 | 1003 | 1010 | 1008 | 1008 | 1008 | 1008 | 1008 | 1008 | 1008 | 995 |
| ρCH3 | Eu | 620 | 899 | 828 | 842 | 839 | 839 | 839 | 839 | 839 | 839 | 839 | 822 |
| µ | 22.3 | 7.5 | 0.6 | 1.7 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 | n.a. | |
| CH3OCH3(C2v) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [59,60,110,111] |
| νCH3,as | A1 | 2339 | 3142 | 2945 | 3016 | 3013 | 3012 | 3012 | 3011 | 3011 | 3011 | 3011 | 2996 |
| νCH3,as | B1 | 2313 | 3145 | 2949 | 2976 | 2976 | 2976 | 2975 | 2975 | 2975 | 2975 | 2975 | 2996 |
| νCH3,as | A2 | 2242 | 3126 | 2906 | 2942 | 2936 | 2936 | 2936 | 2936 | 2936 | 2936 | 2935 | 2952 |
| νCH3,as | B2 | 2236 | 3117 | 2899 | 2934 | 2928 | 2928 | 2928 | 2928 | 2928 | 2928 | 2928 | 2925 |
| νCH3,s | A1 | 2206 | 2949 | 2825 | 2869 | 2852 | 2856 | 2855 | 2855 | 2855 | 2855 | 2854 | 2817 |
| νCH3,s | B1 | 2200 | 3080 | 2861 | 2897 | 2891 | 2891 | 2891 | 2891 | 2891 | 2891 | 2891 | 2817 |
| δCH3,as | A1 | 1142 | 1597 | 1488 | 1506 | 1503 | 1503 | 1503 | 1503 | 1503 | 1503 | 1503 | 1464 |
| δCH3,as | B2 | 1122 | 1587 | 1475 | 1494 | 1492 | 1491 | 1491 | 1491 | 1491 | 1491 | 1491 | 1464 |
| δCH3,as | B1 | 1118 | 1589 | 1475 | 1494 | 1491 | 1491 | 1491 | 1491 | 1491 | 1491 | 1491 | 1464 |
| δCH3,as | A2 | 1111 | 1579 | 1466 | 1485 | 1482 | 1482 | 1482 | 1482 | 1482 | 1482 | 1482 | 1464 |
| δCH3,s | A1 | 1114 | 1574 | 1460 | 1479 | 1476 | 1475 | 1475 | 1475 | 1475 | 1475 | 1475 | 1452 |
| δCH3,s | B1 | 1082 | 1541 | 1426 | 1445 | 1442 | 1442 | 1442 | 1442 | 1442 | 1442 | 1442 | 1452 |
| ρCH3 | A1 | 944 | 1349 | 1248 | 1265 | 1263 | 1262 | 1262 | 1262 | 1262 | 1262 | 1262 | 1244 |
| ρCH3 | B1 | 897 | 1275 | 1181 | 1197 | 1194 | 1194 | 1194 | 1194 | 1194 | 1194 | 1194 | 1227 |
| ρCH3 | B2 | 893 | 1273 | 1180 | 1194 | 1195 | 1190 | 1189 | 1188 | 1188 | 1188 | 1188 | 1179 |
| ρCH3 | A2 | 871 | 1245 | 1153 | 1168 | 1166 | 1166 | 1166 | 1166 | 1166 | 1166 | 1166 | 1150 |
| νC2O,as | B1 | 839 | 1207 | 1113 | 1129 | 1127 | 1127 | 1126 | 1126 | 1126 | 1126 | 1126 | 1102 |
| νC2O,s | A1 | 780 | 988 | 941 | 950 | 949 | 949 | 949 | 948 | 948 | 948 | 948 | 928 |
| δC2O | A1 | 333 | 452 | 423 | 429 | 428 | 428 | 428 | 428 | 428 | 428 | 428 | 418 |
| µ | 23.0 | 7.2 | 1.1 | 1.7 | 1.6 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | n.a. | |
| C2H5NO2(Cs) | Sym. | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | Expt. [112,113] |
| νOH | A’ | 2773 | 3737 | 3524 | 3557 | 3552 | 3551 | 3551 | 3550 | 3550 | 3550 | 3550 | 3560 |
| νNH2,as | A” | 2609 | 3556 | 3337 | 3370 | 3365 | 3364 | 3364 | 3364 | 3364 | 3364 | 3364 | 3410 |
| νNH2,s | A’ | 2629 | 3480 | 3346 | 3357 | 3352 | 3351 | 3351 | 3351 | 3351 | 3350 | 3350 | n.o. |
| νCH2,as | A” | 2268 | 3101 | 2907 | 2937 | 2932 | 2932 | 2932 | 2931 | 2931 | 2931 | 2931 | n.o. |
| νCH2,s | A’ | 2265 | 3059 | 2982 | 2957 | 2953 | 2952 | 2952 | 2952 | 2952 | 2952 | 2952 | 2958 |
| νC=O | A’ | 1346 | 1921 | 1777 | 1802 | 1798 | 1798 | 1798 | 1798 | 1798 | 1798 | 1798 | 1779 |
| δNH2 | A’ | 1228 | 1750 | 1602 | 1620 | 1617 | 1617 | 1617 | 1617 | 1617 | 1617 | 1617 | 1630 |
| δCH2 | A’ | 1085 | 1532 | 1421 | 1440 | 1437 | 1437 | 1437 | 1437 | 1437 | 1437 | 1437 | 1429 |
| νC−O | A’ | 1043 | 1482 | 1372 | 1391 | 1388 | 1388 | 1388 | 1387 | 1387 | 1387 | 1387 | 1373 |
| τCH2,NH2 | A” | 1030 | 1466 | 1355 | 1374 | 1371 | 1371 | 1371 | 1371 | 1370 | 1370 | 1370 | n.o. |
| ωCH2 | A’ | 968 | 1382 | 1275 | 1293 | 1290 | 1290 | 1290 | 1290 | 1290 | 1290 | 1290 | n.o. |
| δCCN,oop | A” | 881 | 1262 | 1164 | 1181 | 1178 | 1178 | 1178 | 1178 | 1178 | 1178 | 1178 | n.o. |
| νCN | A’ | 905 | 1245 | 1156 | 1172 | 1169 | 1169 | 1169 | 1169 | 1169 | 1169 | 1169 | 1136 |
| δCO2 | A’ | 832 | 1186 | 1097 | 1113 | 1110 | 1110 | 1110 | 1110 | 1110 | 1110 | 1110 | 1101 |
| δCNH2 | A’ | 716 | 1002 | 922 | 938 | 935 | 935 | 934 | 934 | 934 | 934 | 934 | 907 |
| δC=O,oop | A” | 685 | 990 | 910 | 924 | 922 | 922 | 922 | 922 | 922 | 922 | 922 | 883 |
| νC −C | A’ | 658 | 863 | 815 | 823 | 822 | 822 | 822 | 822 | 822 | 822 | 822 | 801 |
| δC=O,ip | A’ | 486 | 678 | 629 | 637 | 636 | 636 | 636 | 636 | 636 | 636 | 636 | 619 |
| C-O axis torsion | A” | 369 | 529 | 475 | 485 | 483 | 483 | 483 | 483 | 483 | 483 | 483 | 500 |
| O-C2N axis shear | A’ | 365 | 495 | 461 | 467 | 466 | 466 | 466 | 466 | 466 | 466 | 466 | 463 |
| O=C2N axis shear | A’ | 194 | 286 | 262 | 266 | 266 | 266 | 266 | 266 | 266 | 266 | 266 | n.o. |
| µ | 22.8 | 7.5 | 1.5 | 1.8 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 | n.a. |
The obtained values for µ are generally smaller than 2%, which is in good agreement with the recent work by Roy et al. [19] who concluded that MP2/cc-pVTZ based PT2-VSCF evaluations exhibit a mean unsigned error of under 2%. MP2 is a topical ab initio method that accounts for electron correlation effects to a certain extent and it seems as if for most molecules, this method indeed delivers satisfactory results. Acetonitrile is an exception due to its CN triple bond. However, the particularities of this molecule are discussed elsewhere [63] and it was found that state-of-the-art quantum chemical methods [64,65,66,67,68,69] are required for a proper description of νCN. Importantly, the more or less ubiquitous stretching motions arising from a methyl group are not described in a reliable manner and this has been recently ascribed to the nature of the MP2 method [19]. Conversely, it was shown that when higher order coupling terms (i.e., ) are included in a DPT2-VSCF [44] treatment, MP2 indeed seems to be a viable ab initio method of choice [63]. VSCF data relies on the HOA and hence makes use of the rigid rotor approximation [70] which inherently is co-responsible for discrepancies between experiment and theory. Considering that still a large number of approximations are involved even in state-of-the-art VSCF calculations and their underlying ab initio energy evaluations, it must be concluded that computationally derived spectroscopic data are prone to a certain degree of fortuitous error compensation. However, both the data presented by Roy et al. [19] and our results indicate that triple-ζ based MP2 calculations in a VSCF treatment rather reliably deliver data with no more than 2% of unsigned error.
3.2. Performance at Reduced Grid Densities
As a VSCF evaluation with 16 grid points per mode is computationally highly demanding, a reduction of the grid density is desirable. From the data in Table 1 it becomes evident that for most cases, a reduction to 10 grid points yields identical results as the corresponding calculation with 16 grid points, indicating that the computational demand in a VSCF treatment of and contributions can be reduced safely by more than 50%. It has to be kept in mind, however, that for every set of reduced densities, the grid is interpolated to the original resolution and the displacement boundaries are not affected by the reduction. Hence, as long as the points on the potential energy surface are chosen properly, the accuracy of the VSCF results is not affected. Noteworthy, the default routine in GAMESS chooses the displacement boundaries in dependence to the underlying normal mode’s wavenumber but the user is nonetheless able to alter these settings if desired.
Reviewing the values for µ in Table 2 permits the conclusion that major errors are starting to appear at grid densities <8 points. The GAMESS manual states that the VSCF code is “thought to give accuracy to 50 cm−1 for the larger fundamentals” when MP2 with a triple-ζ basis set is employed and hence, the boundaries of accuracy are wider than the error inflicted by a reduction of the grid density to 8 points. In order to provide statistical evidence as to what extent a reduction of the grid density is viable, paired t-tests [114] of the obtained values for µ have been conducted with the following equation:
| (12) |
Table 2.
Obtained values for µ in %, their arithmetic means and the corresponding t-values according to Equation (12). n.a. means “not applicable”.
| Number of Grid Points | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Molecule | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| H2O | 21.3 | 5.3 | 0.8 | 0.6 | 0.6 | 0.6 | 0.5 | 0.5 | 0.5 | 0.5 | 0.5 |
| CO2 | 25.1 | 6.9 | 2.3 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 | 2.0 |
| CH2O | 23.0 | 6.4 | 0.8 | 0.8 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 |
| C2H2 | 24.5 | 5.2 | 2.0 | 1.7 | 1.8 | 1.8 | 1.8 | 1.8 | 1.8 | 1.8 | 1.8 |
| HCOOH | 22.8 | 6.0 | 2.1 | 1.4 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 |
| CH4 | 22.3 | 5.9 | 0.9 | 0.4 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 | 0.3 |
| CH3Cl | 23.0 | 7.0 | 0.9 | 1.4 | 1.2 | 1.2 | 1.2 | 1.2 | 1.2 | 1.2 | 1.2 |
| CH3OH | 22.9 | 6.4 | 0.9 | 1.3 | 1.2 | 1.2 | 1.2 | 1.2 | 1.1 | 1.1 | 1.1 |
| CH3CN | 24.4 | 6.4 | 1.1 | 1.1 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| C2H4 | 23.4 | 7.7 | 0.8 | 1.5 | 1.4 | 1.4 | 1.3 | 1.3 | 1.3 | 1.3 | 1.3 |
| C2H4O | 23.3 | 6.5 | 1.2 | 1.4 | 1.4 | 1.3 | 1.3 | 1.3 | 1.3 | 1.3 | 1.3 |
| CH3NH2 | 22.8 | 5.9 | 2.4 | 2.3 | 1.6 | 1.7 | 1.8 | 1.8 | 1.7 | 1.7 | 1.7 |
| C2H6 | 22.3 | 7.5 | 0.6 | 1.7 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 | 1.6 |
| CH3OCH3 | 23.0 | 7.2 | 1.1 | 1.7 | 1.6 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 |
| C2H5NO2 | 22.8 | 7.5 | 1.5 | 1.8 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 | 1.7 |
| Mean µ | 23.1 | 6.5 | 1.3 | 1.4 | 1.3 | 1.3 | 1.3 | 1.3 | 1.3 | 1.3 | 1.3 |
| t-Value | 102.96 | 25.59 | 0.09 | 2.43 | 0.81 | 0.78 | 1.71 | 1.34 | 0.66 | 2.39 | n.a. |
In Equation (12), µref is the reference value at a grid density of 16 points. µcalc is the mean absolute percentage deviation at the examined grid density. χ is the number of investigated molecules and the t-value is calculated with sd as the corrected sample standard deviation of the respective grid density. For a two-tailed problem, critical values for t can be specified according to Table 3.
Table 3.
Critical boundaries according to Student’s t-distribution for a two-tailed problem.
| t-Value | Difference |
|---|---|
| t ≤ 2.145 | Insignificant |
| 2.145 < t ≤ 2.977 | Probable |
| 2.977 < t ≤ 4.140 | Significant |
| 4.140 < t | Highly significant |
Except for the data obtained at grid densities of 6 and 7 points, no significant deviations from the reference data are observed, indicating that even a reduction to 8 grid points is a very viable option. The computational effort involved in a pair-approximated VSCF evaluation (Equation (7)) may thus be reduced by a factor of nearly 4. It has to be stressed, however, that the obtained t-value for r = 8 (i.e., 0.09) may not be confused as to indicate the objectively best agreement with the reference values since the statistical analysis is based on unsigned error values. Moreover, the anharmonic correction seems to be slightly over-estimated at r = 8, yielding more red-shifted absorptions, as can be learned from Table 1. This over-correction is responsible for a slightly improved agreement with experiment for most of the molecules, especially since it is known that MP2 tendentially yields blue-shifted IR absorptions [19]. Overall, it may be concluded that VSCF treatments involving at least 8 grid points reproduce the experimental values within the same boundaries of accuracy as the reference values with a mean absolute percentage deviation from experiment of ~1.3% (Table 2).
In their recent paper, Roy et al., reported that soft and semi-rigid molecules have to be treated at higher grid densities than rigid molecules and they mention ethylene oxide as a particular example where the VSCF equations converge at no less than 12 grid points. Our results contradict this statement since our VSCF calculations of ethylene oxide did indeed converge for grid densities ≥6 points and a density of 8 points yielded the same quality of results as observed for the other molecules. Given the fact that the identical code, the same ab initio method and the same basis set were employed, this outcome is rather puzzling. This disagreement may be ascribed to the use of symmetry during our VSCF calculations and the underlying reference geometries having been minimized to the most stringent criterion available. Overall, none of our VSCF evaluations exhibited convergence problems apart from the few excluded torsional degrees of freedom that have been mentioned earlier.
3.3. Application to Deprotonated Phosphoserine
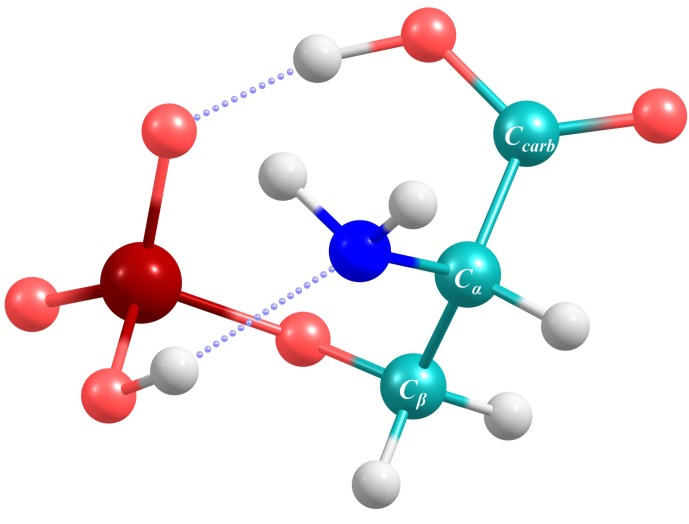
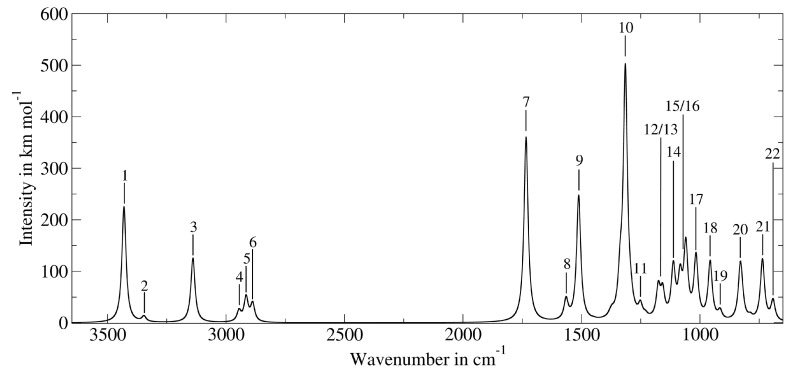
Phosphorylation of proteins is considered a major signal transduction mechanism, mainly occurring at the OH terminus of the amino acids serine, threonine and tyrosine. As a major constituent of biofluids, phosphoserine was subject of a gas-chromatographic investigation of human urine samples [115]. In autopsied Alzheimer’s disease brain tissue, l-phosphoserine was found in elevated concentrations [116] and only very recently, plasma phosphoserine levels were found to be upregulated in sepsis patients [117]. Deprotonated phosphoserine, abbreviated as [pSer-H]−, was investigated via infrared multiple photon dissociation (IRMPD) spectroscopy and hence, experimental data of a few major gas phase IR absorptions of the molecule is available [118]. The authors identified the lowest energy conformer of [pSer-H]− as the one exhibiting hydrogen bonds between the carboxylic OH and the phosphate O as well as between the phosphate OH and the amino N. This conformer was chosen as a benchmark for the 8 point VSCF analysis due to the fact that it represents rigid and weak structural motifs likewise. Figure 1 shows the minimum geometry obtained at the MP2/cc-pVTZ level of theory which served as a reference state for the VSCF evaluation. Table 4 lists the PT2-VSCF computed absorptions of [pSer-H]−, the respective intensities and the available experimental data [118]. Due to the cage-like structure, many normal modes couple among each other and hence, especially lower vibrations cannot be ascribed to distinct normal modes. In such cases, the main vibrational contributions are given in Table 4. For illustrative purposes, the calculated IR spectrum of [pSer-H]− is shown in Figure 2. The intensities have been computed using harmonic dipole derivatives at the MP2/cc-pVTZ level of theory and band broadening was introduced via a Lorentzian function using a band width at half height of 20 cm−1.
Figure 1.
The lowest energy conformer of [pSer-H]− exhibits a hydrogen bond between the carboxylic OH and the phosphate O and between the phosphate OH and the amino N.
Table 4.
The main absorptions of [pSer-H]− and the experimentally obtained [118] values.
| Band Number | PT2-VSCF (cm−1) | Intensity (km mol−1) | IRMPD (cm−1) [118] | Main Contributions |
|---|---|---|---|---|
| 1 | 3430 | 225 | n.o. | νOH |
| 2 | 3346 | 11 | n.o. | νNH2,as |
| 3 | 3139 | 125 | n.o. | νNH2,s |
| 4 | 2945 | 21 | n.o. | νCαH |
| 5 | 2915 | 47 | n.o. | νCβH2,s |
| 6 | 2888 | 35 | n.o. | νCβH2,as |
| 7 | 1734 | 359 | 1728 | νCcarb =O |
| 8 | 1565 | 39 | 1610 | δNH2 |
| 9 | 1512 | 244 | 1461 | δCcarbOH,ip |
| 1449 | 1 | 1419 | δCβH2 | |
| 1380 | 4 | n.o. | τNH2 and δNCαH | |
| 1371 | 9 | n.o. | ωCβH2 | |
| 1337 | 68 | n.o. | νCcarb−O and τCβH2 | |
| 10 | 1315 | 484 | 1291 | νP =O |
| 1292 | 21 | n.o. | ωCβH2 and δCcarbCαH and νCcarb−O | |
| 11 | 1251 | 24 | n.o. | νCα − Cβ and δCβCαH and νCα−N and τNH2 |
| 1230 | 6 | n.o. | νCcarbCα and δCcarbCαH and τNH2 | |
| 12 | 1176 | 60 | n.o. | δCcarbOH,oop |
| 13 | 1157 | 51 | n.o. | νCβO |
| 14 | 1113 | 99 | 1108 | δPOH |
| 15 | 1084 | 74 | n.o. | νNCαCcarb,as and νCβO |
| 16 | 1060 | 141 | 1052 | ωNH2 |
| 17 | 1017 | 121 | 1028 | νP − OH −bonded |
| 18 | 957 | 113 | n.o. | νNCαCβ,as |
| 19 | 915 | 17 | n.o. | νNCαCβ,s and νNCαCcarb,as and νCcarbCαCβ,as |
| 20 | 830 | 98 | 836 | νP −OH |
| 823 | 24 | 812 | δCcarbCαCβ and δCcarbO2,oop | |
| 787 | 7 | n.o. | δCcarbO2 and δCcarbCαCβ | |
| 21 | 736 | 120 | 738 | νP −OCβ and δCcarbO2 |
| 22 | 692 | 39 | n.o. | δCαNCβCcarb,umbrella and νP − OCbeta |
| 513 | 41 | n.o. | δPOH,oop |
Figure 2.
The computed IR spectrum of [pSer-H]−. For band assignments, refer to Table 4.
Considering the 11 available experimental values, µ was computed for the corresponding VSCF data as 1.38%. Since we did calculate the IR absorptions of [pSer-H]− exclusively using 8 grid points per mode, no definitive conclusion can be drawn whether higher grid densities would enable an improved accuracy for this larger molecule. A re-evaluation of the potential energy surface at grid densities up to 16 points would be unmanageably expensive but nonetheless, the data presented fits well into the error boundaries as observed for the 15 molecules discussed earlier.
The band assignment in Table 4 clearly shows that empirical considerations are only applicable to the large fundamentals. For a proper description of low lying vibrations that are determined by a number of torsions, computational approaches are an important option aiding the spectroscopist. In their experimental work, Scuderi et al., have employed computational techniques during their band assignment of [pSer-H]− as well, but they resorted to scaled HOA absorption data at the B3LYP/6-311+G(d,p) level of theory.
4. Conclusions
VSCF theory has grown an important field in computational spectroscopy and this is owed to the increasingly available computational resources and to efficient and easily applicable algorithms. With this systematic study it has been demonstrated that a largely reduced grid density in a VSCF evaluation does not only spare considerable resources but also does not significantly affect the resulting absorption data. It was found that the convergence of VSCF equations is not impaired by such a reduced-effort technique even when highly problematic densities of <8 grid points are employed. While further investigations are required with regard to the role of symmetry in a VSCF treatment, it was found that reduced grid densities may be safely applied to a wide set of molecular entities. Application to [pSer-H]− showed that a 8 point VSCF calculation yields accurate data for a molecule exhibiting weak interactions. The routine presented herein should, in conjunction with other recent developments [35], prove valuable for larger molecules relevant to life sciences where a conventional VSCF treatment with 16 grid points per mode is not feasible.
Author Contributions
O.M.D.L., B.M.R., G.K.B. and C.W.H. designed research; O.M.D.L. performed research; O.M.D.L. analyzed data; O.M.D.L. wrote the paper. All authors read and approved the final manuscript.
Conflicts of Interest
The authors declare no conflict of interest.
Footnotes
Sample Availability: Not available.
References
- 1.Scott A.P., Radom L. Harmonic Vibrational Frequencies: An Evaluation of Hartree-Fock, Møller-Plesset, Quadratic Configuration Interaction, Density Functional Theory, and Semiempirical Scale Factors. J. Phys. Chem. 1996;100:16502–16513. [Google Scholar]
- 2.Sinha P., Boesch S.E., Gu C., Wheeler R.A., Wilson A.K. Harmonic Vibrational Frequencies: Scaling Factors for HF, B3LYP, and MP2 Methods in Combination with Correlation Consistent Basis Sets. J. Phys. Chem. A. 2004;108:9213–9217. doi: 10.1021/jp048233q. [DOI] [Google Scholar]
- 3.Bowman J.M. Self-Consistent Field Energies and Wavefunctions for Coupled Oscillators. J. Chem. Phys. 1978;68:608–610. doi: 10.1063/1.435782. [DOI] [Google Scholar]
- 4.Cohen M., Greita S., McEarchran R. Approximate and Exact Quantum Mechanical Energies and Eigenfunctions for a System of Coupled Oscillators. Chem. Phys. Lett. 1979;60:445–450. doi: 10.1016/0009-2614(79)80609-0. [DOI] [Google Scholar]
- 5.Gerber R., Ratner M. A Semiclassical Self-Consistent Field (SC SCF) Approximation for Eigenvalues of Coupled-Vibration Systems. Chem. Phys. Lett. 1979;68:195–198. [Google Scholar]
- 6.Bowman J.M. The Self-Consistent-Field Approach to Polyatomic Vibrations. Acc. Chem. Res. 1986;19:202–208. doi: 10.1021/ar00127a002. [DOI] [Google Scholar]
- 7.Carter S., Culik S.J., Bowman J.M. Vibrational Self-Consistent Field Method for Many-Mode Systems: A New Approach and Application to the Vibrations of CO Adsorbed on Cu(100) J. Chem. Phys. 1997;107:10458–10469. doi: 10.1063/1.474210. [DOI] [Google Scholar]
- 8.Carney G.D., Sprandel L.L., Kern C.W. Variational Approaches to Vibration-Rotation Spectroscopy for Polyatomic Molecules. In: Prigogine I., Rice S.A., editors. Advances in Chemical Physics. Volume 37. John Wiley & Sons,Inc.; Hoboken, NJ, USA: 2007. pp. 305–379. [Google Scholar]
- 9.Barone V. Vibrational Zero-Point Energies and Thermodynamic Functions Beyond the Harmonic Approximation. J. Chem. Phys. 2004;120:3059–3065. doi: 10.1063/1.1637580. [DOI] [PubMed] [Google Scholar]
- 10.Barone V. Anharmonic Vibrational Properties by a Fully Automated Second-order Perturbative Approach. J. Chem. Phys. 2005;122 doi: 10.1063/1.18248810. [DOI] [PubMed] [Google Scholar]
- 11.Frisch M.J., Trucks G.W., Schlegel H.B., Scuseria G.E., Robb M.A., Cheeseman J.R., Scalmani G., Barone V., Mennucci B., Petersson G.A., et al. Gaussian Inc.; Wallingford, CT, USA: 2013. Gaussian 09, Revision D.01. [Google Scholar]
- 12.Barone V., Biczysko M., Bloino J. Fully Anharmonic IR and Raman Spectra of Medium-Size Molecular Systems: Accuracy and Interpretation. Phys. Chem. Chem. Phys. 2014;16:1759–1787. doi: 10.1039/c3cp53413h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Biczysko M., Bloino J., Carnimeo I., Panek P., Barone V. Fully Ab Initio IR Spectra for Complex Molecular Systems from Perturbative Vibrational Approaches: Glycine as a Test Case. J. Mol. Struct. 2012;1009:74–82. doi: 10.1016/j.molstruc.2011.10.012. [DOI] [Google Scholar]
- 14.Chaban G.M., Jung J.O., Gerber R.B. Ab Initio Calculation of Anharmonic Vibrational States of Polyatomic Systems: Electronic Structure Combined with Vibrational Self-Consistent Field. J. Chem. Phys. 1999;111:1823–1829. doi: 10.1063/1.479452. [DOI] [Google Scholar]
- 15.Jung J.O., Gerber R.B. Vibrational Wave Functions and Spectroscopy of (H2O)n, n = 2, 3, 4, 5: Vibrational Self-Consistent Field with Correlation Corrections. J. Chem. Phys. 1996;105:10332–10348. doi: 10.1063/1.472960. [DOI] [Google Scholar]
- 16.Chaban G.M., Jung J.O., Gerber R.B. Anharmonic Vibrational Spectroscopy of Hydrogen-Bonded Systems Directly Computed from Ab Initio Potential Surfaces: (H2O)n, n = 2, 3; Cl−(H2O)n, n = 1, 2; H+(H2O)n, n = 1, 2; H2O-CH3OH. J. Phys. Chem. A. 2000;104:2772–2779. doi: 10.1021/jp993391g. [DOI] [Google Scholar]
- 17.Chaban G.M., Jung J.O., Gerber R.B. Anharmonic Vibrational Spectroscopy of Glycine: Testing of Ab Initio and Empirical Potentials. J. Phys. Chem. A. 2000;104:10035–10044. doi: 10.1021/jp002297t. [DOI] [Google Scholar]
- 18.Miller Y., Chaban G., Gerber R. Theoretical Study of Anharmonic Vibrational Spectra of HNO3, HNO3-H2O, HNO4: Fundamental, Overtone and Combination Excitations. Chem. Phys. 2005;313:213–224. doi: 10.1016/j.chemphys.2005.01.012. [DOI] [Google Scholar]
- 19.Roy T.K., Carrington T., Gerber R.B. Approximate First-Principles Anharmonic Calculations of Polyatomic Spectra Using MP2 and B3LYP Potentials: Comparisons with Experiment. J. Phys. Chem. A. 2014;118:6730–6739. doi: 10.1021/jp5060155. [DOI] [PubMed] [Google Scholar]
- 20.Schmidt M.W., Baldridge K.K., Boatz J.A., Elbert S.T., Gordon M.S., Jensen J.H., Koseki S., Matsunaga N., Nguyen K.A., Su S., et al. General Atomic and Molecular Electronic Structure System. J. Comput. Chem. 1993;14:1347–1363. doi: 10.1002/jcc.540141112. [DOI] [Google Scholar]
- 21.Valiev M., Bylaska E., Govind N., Kowalski K., Straatsma T., Dam H.V., Wang D., Nieplocha J., Apra E., Windus T., et al. NWChem: A Comprehensive and Scalable Open-Source Solution for Large Scale Molecular Simulations. Comput. Phys. Commun. 2010;181:1477–1489. doi: 10.1016/j.cpc.2010.04.018. [DOI] [Google Scholar]
- 22.Werner H., Knowles P.J., Knizia G., Manby F.R., Schütz M., Celani P., Korona T., Lindh R., Mitrushenkov A., Rauhut G., et al. MOLPRO, Version 2012.1, A Package of Ab Initio Programs. 2012. [(accessed on 15 December 2014)]. Available online: http://www.molpro.net/
- 23.Møller C., Plesset M.S. Note on an Approximation Treatment for Many-Electron Systems. Phys. Rev. 1934;46:618–622. doi: 10.1103/PhysRev.46.618. [DOI] [Google Scholar]
- 24.Fletcher G.D., Schmidt M.W., Gordon M.S. Developments in Parallel Electronic Structure Theory. In: Prigogine I., Rice S.A., editors. Advances in Chemical Physics. Volume 110. John Wiley & Sons, Inc.; Hoboken, NJ, USA: 2007. pp. 267–294. [Google Scholar]
- 25.Aikens C.M., Gordon M.S. Parallel Unrestricted MP2 Analytic Gradients Using the Distributed Data Interface. J. Phys. Chem. A. 2004;108:3103–3110. doi: 10.1021/jp031142t. [DOI] [Google Scholar]
- 26.Sachs E.S., Hinze J., Sabelli N.H. Frozen Core Approximation, a Pseudopotential Method Tested on Six States of NaH. J. Chem. Phys. 1975;62:3393–3398. doi: 10.1063/1.430993. [DOI] [Google Scholar]
- 27.Dunning T.H. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron Through Neon and Hydrogen. J. Chem. Phys. 1989;90:1007–1023. doi: 10.1063/1.456153. [DOI] [Google Scholar]
- 28.Bowman J.M., Carrington T., Meyer H.D. Variational Quantum Approaches for Computing Vibrational Energies of Polyatomic Molecules. Mol. Phys. 2008;106:2145–2182. doi: 10.1080/00268970802258609. [DOI] [Google Scholar]
- 29.Chan M., Carrington T., Manzhos S. Anharmonic Vibrations of the Carboxyl Group in Acetic Acid on TiO2: Implications For Adsorption Mode Assignment in Dye-Sensitized Solar Cells. Phys. Chem. Chem. Phys. 2013;15:10028–10034. doi: 10.1039/c3cp00065f. [DOI] [PubMed] [Google Scholar]
- 30.Sakurai J.J., Tuan S.F. Modern Quantum Mechanics. Volume 1 Addison-Wesley; Boston, MA, USA: 1985. [Google Scholar]
- 31.Griffiths D.J., Harris E.G. Introduction to Quantum Mechanics. Volume 2 Prentice Hall; Upper Saddle River, NJ, USA: 1995. [Google Scholar]
- 32.Ratner M.A., Gerber R.B. Excited Vibrational States of Polyatomic Molecules: The Semiclassical Self-Consistent Field Approach. J. Phys. Chem. 1986;90:20–30. doi: 10.1021/j100273a008. [DOI] [Google Scholar]
- 33.Watson J.K. Simplification of the Molecular Vibration-Rotation Hamiltonian. Mol. Phys. 1968;15:479–490. doi: 10.1080/00268976800101381. [DOI] [Google Scholar]
- 34.Bowman J.M., Carter S., Huang X. MULTIMODE: A Code to Calculate Rovibrational Energies of Polyatomic Molecules. Int. Rev. Phys. Chem. 2003;22:533–549. doi: 10.1080/0144235031000124163. [DOI] [Google Scholar]
- 35.Roy T.K., Gerber R.B. Vibrational Self-Consistent Field Calculations for Spectroscopy of Biological Molecules: New Algorithmic Developments and Applications. Phys. Chem. Chem. Phys. 2013;15:9468–9492. doi: 10.1039/c3cp50739d. [DOI] [PubMed] [Google Scholar]
- 36.Gregurick S.K., Fredj E., Elber R., Gerber R.B. Vibrational Spectroscopy of Peptides and Peptide-Water Complexes: Anharmonic Coupled-Mode Calculations. J. Phys. Chem. B. 1997;101:8595–8606. doi: 10.1021/jp971587f. [DOI] [Google Scholar]
- 37.Gregurick S.K., Liu J.H.Y., Brant D.A., Gerber R.B. Anharmonic Vibrational Self-Consistent Field Calculations as an Approach to Improving Force Fields for Monosaccharides. J. Phys. Chem. B. 1999;103:3476–3488. doi: 10.1021/jp9826221. [DOI] [Google Scholar]
- 38.Kowal A.T. First-principles Calculation of Geometry and Anharmonic Vibrational Spectra of Thioformamide and Thioformamide-d2. J. Chem. Phys. 2006;124 doi: 10.1063/1.2139995. [DOI] [PubMed] [Google Scholar]
- 39.Carter S., Bowman J.M., Handy N.C. Extensions and Tests of MULTIMODE: A Code to Obtain Accurate Vibration/Rotation Energies of Many-Mode Molecules. Theor. Chem. Acc. 1998;100:191–198. [Google Scholar]
- 40.Rheinecker J., Bowman J.M. The Calculated Infrared Spectrum of Cl H2O Using a New Full Dimensional Ab Initio Potential Surface and Dipole Moment Surface. J. Chem. Phys. 2006;125 doi: 10.1063/1.2209675. [DOI] [PubMed] [Google Scholar]
- 41.Norris L.S., Ratner M.A., Roitberg A.E., Gerber R.B. Møller-Plesset Perturbation Theory Applied to Vibrational Problems. J. Chem. Phys. 1996;105:11261–11267. doi: 10.1063/1.472922. [DOI] [Google Scholar]
- 42.Pele L., Gerber R.B. On the Number of Significant Mode-Mode Anharmonic Couplings in Vibrational Calculations: Correlation-Corrected Vibrational Self-Consistent Field Treatment of Di-, Tri-, and Tetrapeptides. J. Chem. Phys. 2008;128 doi: 10.1063/1.2909558. [DOI] [PubMed] [Google Scholar]
- 43.Pele L., Brauer B., Gerber R. Acceleration of Correlation-Corrected Vibrational Self-Consistent Field Calculation Times for Large Polyatomic Molecules. Theor. Chem. Acc. 2007;117:69–72. doi: 10.1007/s00214-006-0132-2. [DOI] [Google Scholar]
- 44.Matsunaga N., Chaban G.M., Gerber R.B. Degenerate Perturbation Theory Corrections for the Vibrational Self-Consistent Field Approximation: Method and Applications. J. Chem. Phys. 2002;117:3541–3547. [Google Scholar]
- 45.Bowman J.M., Christoffel K., Tobin F. Application of SCF-SI Theory to Vibrational Motion in Polyatomic Molecules. J. Phys. Chem. 1979;83:905–912. doi: 10.1021/j100471a005. [DOI] [Google Scholar]
- 46.Christoffel K.M., Bowman J.M. Investigations of Self-Consistent Field, SCF CI and Virtual Stateconfiguration Interaction Vibrational Energies for a Model Three-Mode System. Chem. Phys. Lett. 1982;85:220–224. doi: 10.1016/0009-2614(82)80335-7. [DOI] [Google Scholar]
- 47.Christiansen O., Luis J.M. Beyond Vibrational Self-Consistent-Field Methods: Benchmark Calculations for the Fundamental Vibrations of Ethylene. Int. J. Quantum Chem. 2005;104:667–680. doi: 10.1002/qua.20615. [DOI] [Google Scholar]
- 48.Neff M., Rauhut G. Toward Large Scale Vibrational Configuration Interaction Calculations. J. Chem. Phys. 2009;131 doi: 10.1063/1.3243862. [DOI] [PubMed] [Google Scholar]
- 49.Kaulfuss U.B., Altenbokum M. Anharmonic Oscillator as a Test of the Coupled-Cluster Method. Phys. Rev. D. 1986;33:3658–3664. doi: 10.1103/PhysRevD.33.3658. [DOI] [PubMed] [Google Scholar]
- 50.Nagalakshmi V., Lakshminarayana V., Sumithra G., Prasad M.D. Coupled Cluster Description of Anharmonic Molecular Vibrations. Application to O3 and SO2. Chem. Phys. Lett. 1994;217:279–282. doi: 10.1016/0009-2614(93)E1380-Y. [DOI] [Google Scholar]
- 51.Thomsen B., Yagi K., Christiansen O. Optimized Coordinates in Vibrational Coupled Cluster Calculations. J. Chem. Phys. 2014;140 doi: 10.1063/1.4870775. [DOI] [Google Scholar]
- 52.Culot F., Liévin J. A Multiconfigurational SCF Computational Method for the Resolution of the Vibrational Schrödinger Equation in Polyatomic Molecules. Theor. Chim. Acta. 1994;89:227–250. doi: 10.1007/BF01225116. [DOI] [Google Scholar]
- 53.Meyer H.D. Studying Molecular Quantum Dynamics With the Multiconfiguration Time-Dependent Hartree Method. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2012;2:351–374. doi: 10.1002/wcms.87. [DOI] [Google Scholar]
- 54.Njegic B., Gordon M.S. Exploring the Effect of Anharmonicity of Molecular Vibrations on Thermodynamic Properties. J. Chem. Phys. 2006;125 doi: 10.1063/1.2395940. [DOI] [PubMed] [Google Scholar]
- 55.Bounouar M., Scheurer C. The Impact of Approximate VSCF Schemes and Curvilinear Coordinates on the Anharmonic Vibrational Frequencies of Formamide and Thioformamide. Chem. Phys. 2008;347:194–207. [Google Scholar]
- 56.Strobusch D., Scheurer C. Hierarchical Expansion of the Kinetic Energy Operator in Curvilinear Coordinates for the Vibrational Self-Consistent Field Method. J. Chem. Phys. 2011;135 doi: 10.1063/1.3637629. [DOI] [PubMed] [Google Scholar]
- 57.Boatz J.A., Gordon M.S. Decomposition of Normal-Coordinate Vibrational Frequencies. J. Phys. Chem. 1989;93:1819–1826. doi: 10.1021/j100342a026. [DOI] [Google Scholar]
- 58.Yagi K., Hirao K., Taketsugu T., Schmidt M.W., Gordon M.S. Ab Initio Vibrational State Calculations with a Quartic Force Field: Applications to H2CO, C2H4, CH3OH, CH3CCH and C6H6. J. Chem. Phys. 2004;121:1383–1389. doi: 10.1063/1.1764501. [DOI] [PubMed] [Google Scholar]
- 59.Shimanouchi T. Tables of Molecular Vibrational Frequencies Consolidated Volume I. Natl. Bur. Stand. 1972;1:1–164. [Google Scholar]
- 60.Herzberg G. Infrared and Raman Spectra of Polyatomic Molecules. Van Nostrand; New York, NY, USA: 1949. [Google Scholar]
- 61.Smith L.G. The Infra-Red Spectrum of C2H6. J. Chem. Phys. 1949;17:139–167. doi: 10.1063/1.1747206. [DOI] [Google Scholar]
- 62.Weiss S., Leroi G.E. Direct Observation of the Infrared Torsional Spectrum of C2H6, CH3CD3, and C2D6. J. Chem. Phys. 1968;48:962–967. doi: 10.1063/1.1668849. [DOI] [Google Scholar]
- 63.Lutz O.M., Rode B.M., Bonn G.K., Huck C.W. The Impact of Highly Correlated Potential Energy Surfaces on the Anharmonically Corrected IR Spectrum of Acetonitrile. Spectrochim. Acta Part A. 2014;131:545–555. doi: 10.1016/j.saa.2014.04.067. [DOI] [PubMed] [Google Scholar]
- 64.Bartlett R.J., Purvis G.D. Many-Body Perturbation Theory, Coupled-Pair Many-Electron Theory, and the Importance of Quadruple Excitations for the Correlation Problem. Int. J. Quantum Chem. 1978;14:561–581. doi: 10.1002/qua.560140504. [DOI] [Google Scholar]
- 65.Pople J.A., Krishnan R., Schlegel H.B., Binkley J.S. Electron Correlation Theories and Their Application to the Study of Simple Reaction Potential Surfaces. Int. J. Quantum Chem. 1978;14:545–560. doi: 10.1002/qua.560140503. [DOI] [Google Scholar]
- 66.Gauss J., Stanton J.F. Perturbative Treatment of Triple Excitations in Coupled-cluster Calculations of Nuclear Magnetic Shielding Constants. J. Chem. Phys. 1996;104:2574–2583. doi: 10.1063/1.471005. [DOI] [Google Scholar]
- 67.Pople J.A., Head-Gordon M., Raghavachari K. Quadratic Configuration Interaction. A General Technique for Determining Electron Correlation Energies. J. Chem. Phys. 1987;87:5968–5975. doi: 10.1063/1.453520. [DOI] [Google Scholar]
- 68.Piecuch P., Włoch M. Renormalized Coupled-Cluster Methods Exploiting Left Eigenstates of the Similarity-Transformed Hamiltonian. J. Chem. Phys. 2005;123 doi: 10.1063/1.2137318. [DOI] [PubMed] [Google Scholar]
- 69.Piecuch P., Włoch M., Gour J.R., Kinal A. Single-Reference, Size-Extensive, Non-Iterative Coupled-Cluster Approaches to Bond Breaking and Biradicals. Chem. Phys. Lett. 2006;418:467–474. doi: 10.1016/j.cplett.2005.10.116. [DOI] [Google Scholar]
- 70.Dennison D.M. The Infrared Spectra of Polyatomic Molecules Part I. Rev. Mod. Phys. 1931;3:280–345. doi: 10.1103/RevModPhys.3.280. [DOI] [Google Scholar]
- 71.Barker E.F., Sleator W.W. The Infrared Spectrum of Heavy Water. J. Chem. Phys. 1935;3:660–663. doi: 10.1063/1.1749572. [DOI] [Google Scholar]
- 72.Benedict W.S., Gailar N., Plyler E.K. Rotation-Vibration Spectra of Deuterated Water Vapor. J. Chem. Phys. 1956;24:1139–1165. doi: 10.1063/1.1742731. [DOI] [Google Scholar]
- 73.Amat G., Pimbert M. On Fermi Resonance in Carbon Dioxide. J. Mol. Spectrosc. 1965;16:278–290. doi: 10.1016/0022-2852(65)90123-2. [DOI] [Google Scholar]
- 74.Suzuki I. General Anharmonic Force Constants of Carbon Dioxide. J. Mol. Spectrosc. 1968;25:479–500. doi: 10.1016/S0022-2852(68)80018-9. [DOI] [Google Scholar]
- 75.Davidson D.W., Stoicheff B.P., Bernstein H.J. The Infrared and Raman Spectra of Formaldehyde-d1 Vapor. J. Chem. Phys. 1954;22:289–294. doi: 10.1063/1.1740054. [DOI] [Google Scholar]
- 76.Blau H.H., Nielsen H.H. The Infrared Absorption Spectrum of Formaldehyde Vapor. J. Mol. Spectrosc. 1957;1:124–132. doi: 10.1016/0022-2852(57)90015-2. [DOI] [Google Scholar]
- 77.Nakagawa T., Kashiwagi H., Kurihara H., Morino Y. Vibration-Rotation Spectra of Formaldehyde: Band Contour Analysis of the ν2 and ν3 Fundamentals. J. Mol. Spectrosc. 1969;31:436–450. doi: 10.1016/0022-2852(69)90373-7. [DOI] [Google Scholar]
- 78.Lafferty W.J., Thibault R.J. High Resolution Infrared Spectra of H2, C12C13H2, and H2. J. Mol. Spectrosc. 1964;14:79–96. doi: 10.1016/0022-2852(64)90101-8. [DOI] [Google Scholar]
- 79.Scott J., Rao K. Infrared Absorption Bands of Acetylene: Part I. Analysis of the Bands at 13.7µ. J. Mol. Spectrosc. 1965;16:15–23. doi: 10.1016/0022-2852(65)90081-0. [DOI] [Google Scholar]
- 80.Scott J., Rao K.N. Infrared Absorption Bands of Acetylene: Part III. Analysis of the Bands at 3µ. J. Mol. Spectrosc. 1966;20:438–460. doi: 10.1016/0022-2852(66)90015-4. [DOI] [Google Scholar]
- 81.Williams V.Z. Infra-Red Spectra of Monomeric Formic Acid and Its Deuterated Forms. I. High Frequency Region. J. Chem. Phys. 1947;15:232–242. doi: 10.1063/1.1746487. [DOI] [Google Scholar]
- 82.Wilmshurst J.K. Vibrational Assignment in Monomeric Formic Acid. J. Chem. Phys. 1956;25:478–480. doi: 10.1063/1.1742947. [DOI] [Google Scholar]
- 83.Millikan R.C., Pitzer K.S. Infrared Spectra and Vibrational Assignment of Monomeric Formic Acid. J. Chem. Phys. 1957;27:1305–1308. doi: 10.1063/1.1743996. [DOI] [Google Scholar]
- 84.Miyazawa T., Pitzer K.S. Internal Rotation and Infrared Spectra of Formic Acid Monomer and Normal Coordinate Treatment of Out-Of-Plane Vibrations of Monomer, Dimer, and Polymer. J. Chem. Phys. 1959;30:1076–1086. doi: 10.1063/1.1730085. [DOI] [Google Scholar]
- 85.Allen H.C., Plyler E.K. ν3 Band of Methane. J. Chem. Phys. 1957;26:972–973. doi: 10.1063/1.1743458. [DOI] [Google Scholar]
- 86.Herranz J., Morcillo J., Gómez A. The ν2 Infrared Band of CH4 and CD4. J. Mol. Spectrosc. 1966;19:266–282. doi: 10.1016/0022-2852(66)90250-5. [DOI] [Google Scholar]
- 87.King W.T., Mills I.M., Crawford B. Normal Coordinates in the Methyl Halides. J. Chem. Phys. 1957;27:455–457. doi: 10.1063/1.1743745. [DOI] [Google Scholar]
- 88.Jones E., Popplewell R., Thompson H. Vibration—Rotation Bands of Methyl Chloride. Spectrochim. Acta. 1966;22:669–680. [Google Scholar]
- 89.Maki A.G., Thibault R. Analysis of Some Perturbations in the ν4 Band of Methyl Chloride. J. Chem. Phys. 1968;48:2163–2167. doi: 10.1063/1.1669407. [DOI] [Google Scholar]
- 90.Morillon-Chapey M., Graner G. Fine Structure in the ν1 Band of CH3Cl near 2970 cm−1. J. Mol. Spectrosc. 1969;31:155–169. doi: 10.1016/0022-2852(69)90348-8. [DOI] [Google Scholar]
- 91.Tanaka C., Kuratani K., Mizushima S.I. In-Plane Normal Vibrations of Methanol. Spectrochim. Acta. 1957;9:265–269. doi: 10.1016/0371-1951(57)80141-6. [DOI] [Google Scholar]
- 92.Van Thiel M., Becker E.D., Pimentel G.C. Infrared Studies of Hydrogen Bonding of Methanol by the Matrix Isolation Technique. J. Chem. Phys. 1957;27:95–99. doi: 10.1063/1.1743725. [DOI] [Google Scholar]
- 93.Falk M., Whalley E. Infrared Spectra of Methanol and Deuterated Methanols in Gas, Liquid, and Solid Phases. J. Chem. Phys. 1961;34:1554–1568. doi: 10.1063/1.1701044. [DOI] [Google Scholar]
- 94.Nakagawa I., Shimanouchi T. Rotation-Vibration Spectra and Rotational, Coriolis Coupling, Centrifugal Distortion and Potential Constants of Methyl Cyanide. Spectrochim. Acta. 1962;18:513–539. doi: 10.1016/S0371-1951(62)80163-5. [DOI] [Google Scholar]
- 95.Tolonen A., Koivusaari M., Paso R., Schroderus J., Alanko S., Anttila R. The Infrared Spectrum of Methyl Cyanide Between 850 and 1150 cm−1: Analysis of the ν4, ν7, and 3ν18 Bands with Resonances. J. Mol. Spectrosc. 1993;160:554–565. doi: 10.1006/jmsp.1993.1201. [DOI] [Google Scholar]
- 96.Venkateswarlu P. The Rotation-Vibration Spectrum of Methyl Cyanide in the Region 1.6 µ–20 µ. J. Chem. Phys. 1951;19:293–298. doi: 10.1063/1.1748197. [DOI] [Google Scholar]
- 97.Venkateswarlu P. The Infrared Spectrum of Methyl Cyanide. J. Chem. Phys. 1952;20:923–923. doi: 10.1063/1.1700606. [DOI] [Google Scholar]
- 98.Thompson H.W., Williams R.L. The Infra-red Spectra of Methyl Cyanide and Methyl Isocyanide. Trans. Faraday Soc. 1952;48:502–513. [Google Scholar]
- 99.Parker F., Nielsen A., Fletcher W. The Infrared Absorption Spectrum of Methyl Cyanide Vapor. J. Mol. Spectrosc. 1957;1:107–123. doi: 10.1016/0022-2852(57)90014-0. [DOI] [Google Scholar]
- 100.Huet T. The ν1 and ν5 Fundamental Bands of Methyl Cyanide. J. Mol. Struct. 2000;517:127–131. doi: 10.1016/S0022-2860(99)00243-4. [DOI] [Google Scholar]
- 101.Arnett R.L., Crawford B.L. The Vibrational Frequencies of Ethylene. J. Chem. Phys. 1950;18:118–126. doi: 10.1063/1.1747428. [DOI] [Google Scholar]
- 102.Allen H.C., Plyler E.K. The Structure of Ethylene from Infrared Spectra. J. Am. Chem. Soc. 1958;80:2673–2676. [Google Scholar]
- 103.Lord R.C., Nolin B. Vibrational Spectra of Ethylene Oxide and Ethylene Oxide-d4. J. Chem. Phys. 1956;24:656–658. [Google Scholar]
- 104.Potts W. The Fundamental Vibration Frequencies of Ethylene Oxide and Ethylene Imine. Spectrochim. Acta. 1965;21:511–527. doi: 10.1016/0371-1951(65)80143-6. [DOI] [Google Scholar]
- 105.Kirby-Smith J.S., Bonner L.G. The Raman Spectra of Gaseous Substances 1. Apparatus and the Spectrum of Methylamine. J. Chem. Phys. 1939;7:880–883. doi: 10.1063/1.1750337. [DOI] [Google Scholar]
- 106.Gray A.P., Lord R.C. Rotation-Vibration Spectra of Methyl Amine and Its Deuterium Derivatives. J. Chem. Phys. 1957;26:690–705. doi: 10.1063/1.1743369. [DOI] [Google Scholar]
- 107.Tsuboi M., Hirakawa A.Y., Ino T., Sasaki T., Tamagake K. Amino Wagging and Inversion in Methylamines. J. Chem. Phys. 1964;41:2721–2734. doi: 10.1063/1.1726344. [DOI] [Google Scholar]
- 108.Cole A., Lafferty W., Thibault R. Rotational Fine Structure of the Perpendicular Band, ν7, of Ethane. J. Mol. Spectrosc. 1969;29:365–374. doi: 10.1016/0022-2852(69)90113-1. [DOI] [Google Scholar]
- 109.Nakagawa I., Shimanouchi T. Rotation-Vibration Spectra and Rotational, Coriolis Coupling and Potential Constants of Ethane, Ethane-d6 and Ethane-1, 1, 1-d3. J. Mol. Spectrosc. 1971;39:255–274. doi: 10.1016/0022-2852(71)90058-0. [DOI] [Google Scholar]
- 110.Taylor R.C., Vidale G.L. Raman Spectrum and Vibrational Assignments of Gaseous Dimethyl Ether. J. Chem. Phys. 1957;26:122–123. doi: 10.1063/1.1743235. [DOI] [Google Scholar]
- 111.Fateley W., Miller F.A. Torsional Frequencies in the Far Infrared-II: Molecules With Two or Three Methyl Rotors. Spectrochim. Acta. 1962;18:977–993. [Google Scholar]
- 112.Stepanian S.G., Reva I.D., Radchenko E.D., Rosado M.T.S., Duarte M.L.T.S., Fausto R., Adamowicz L. Matrix-Isolation Infrared and Theoretical Studies of the Glycine Conformers. J. Phys. Chem. A. 1998;102:1041–1054. doi: 10.1021/jp973397a. [DOI] [Google Scholar]
- 113.Brauer B., Chaban G.M., Gerber R.B. Spectroscopically-Tested, Improved, Semi-Empirical Potentials for Biological Molecules: Calculations for Glycine, Alanine and Proline. Phys. Chem. Chem. Phys. 2004;6:2543–2556. doi: 10.1039/b315326f. [DOI] [Google Scholar]
- 114.Goulden C. Methods of Statistical Analysis. Wiley; New York, NY, USA: 2007. pp. 50–55. [Google Scholar]
- 115.Kataoka H., Nakai K., Katagiri Y., Makita M. Analysis of Free and Bound O-Phosphoamino Acids in Urine by Gas Chromatography with Flame Photometric Detection. Biomed. Chromatogr. 1993;7:184–188. doi: 10.1002/bmc.1130070403. [DOI] [PubMed] [Google Scholar]
- 116.Mason R., Trumbore M.W., Pettegrew J.W. Membrane Interactions of a Phosphomonoester Elevated Early in Alzheimer’s Disease. Neurobiol. Aging. 1995;16:531–539. doi: 10.1016/0197-4580(95)00057-L. [DOI] [PubMed] [Google Scholar]
- 117.Chiarla C., Giovannini I., Siegel J.H. High Phosphoserine in Sepsis: Panel of Clinical and Plasma Amino Acid Correlations. SpringerPlus. 2014;3 doi: 10.1186/2193-1801-3-279. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Scuderi D., Correia C.F., Balaj O.P., Ohanessian G., Lemaire J., Maitre P. Structural Characterization by IRMPD Spectroscopy and DFT Calculations of Deprotonated Phosphorylated Amino Acids in the Gas Phase. ChemPhysChem. 2009;10:1630–1641. doi: 10.1002/cphc.200800856. [DOI] [PubMed] [Google Scholar]