Simplicial closure and higher-order link prediction

Significance

Networks provide a powerful abstraction for complex systems throughout the sciences by representing the underlying set of pairwise interactions, but much of the structure within these systems involves interactions that take place among more than two nodes at once. While these higher-order interactions are ubiquitous, an evaluation of the basic properties and organizational principles in such systems is missing. Here we study 19 datasets from biology, medicine, social networks, and the web and characterize how higher-order structure emerges and differs between domains. We then propose a general framework for evaluating higher-order data models based on link prediction, a task in which we seek to predict future interactions from a system’s structure and past history.

Abstract

Networks provide a powerful formalism for modeling complex systems by using a model of pairwise interactions. But much of the structure within these systems involves interactions that take place among more than two nodes at once—for example, communication within a group rather than person to person, collaboration among a team rather than a pair of coauthors, or biological interaction between a set of molecules rather than just two. Such higher-order interactions are ubiquitous, but their empirical study has received limited attention, and little is known about possible organizational principles of such structures. Here we study the temporal evolution of 19 datasets with explicit accounting for higher-order interactions. We show that there is a rich variety of structure in our datasets but datasets from the same system types have consistent patterns of higher-order structure. Furthermore, we find that tie strength and edge density are competing positive indicators of higher-order organization, and these trends are consistent across interactions involving differing numbers of nodes. To systematically further the study of theories for such higher-order structures, we propose higher-order link prediction as a benchmark problem to assess models and algorithms that predict higher-order structure. We find a fundamental difference from traditional pairwise link prediction, with a greater role for local rather than long-range information in predicting the appearance of new interactions.

Networks are a fundamental abstraction for complex systems and relational data throughout the sciences (1–3). The basic premise of network models is to represent the elements of the underlying system as nodes and to use the links of the network to capture pairwise relationships. In this way, a social network can represent the friendships between pairs of people, a web graph can encode links among web pages or topic categories, and a biological network can represent the interactions among pairs of biological molecules or components (3–6). But much of the structure in these systems involves higher-order interactions between more than two entities at once (7–11): People often communicate or interact in social groups, not just in pairs; associative relations among ideas or topics often involve the intersection of multiple concepts; and joint protein interactions in biological networks are associated with important phenomena (12).

These types of higher-order, group-based interactions are apparent even in the standard genres of datasets used for network analysis. For example, coauthorship networks are built from data in which larger groups write papers together, and similarly, email networks are based on messages that often have multiple recipients. While such higher-order structure is not captured by the topology of a graph, it may be modeled via a collection of formalisms that include set systems (13), hypergraphs (14), simplicial complexes (15), and bipartite affiliation graphs (7, 16). Despite the existence of mathematical formalisms for higher-order structure, there is no unifying study that analyzes the basic higher-order structure of such datasets. This is in sharp contrast to other notions of “higher-order models” generalizing graph data, such as multiplex networks (17) and higher-order Markov chain models (18, 19), which are successful but still rooted in a pairwise representation paradigm. We study the complementary direction of group interactions, as outlined in the examples above, and use the term higher-order model in this sense.

A key reason for the lack of large-scale studies in higher-order models is that data are often collected directly in a network format, thus eliminating higher-order interactions already at the data-collection stage. Another reason is that analyzing higher-order interactions can be computationally challenging for large datasets. Consequently, despite their potential importance, little is known about organizational principles of higher-order structures within real-world datasets. For instance, one question that remains to be answered is whether higher-order interactions enable us to differentiate different kinds of datasets or whether higher-order properties are universal across datasets.

Here, we provide steps in the direction of promoting a broad, rigorous study of higher-order topological interactions across domains. To this end, we study the structure and temporal evolution of 19 datasets from a variety of domains that have higher-order interactions. We find that distinct patterns for different domains are immediately revealed with three-way interaction features that are not available from the graph structure of the networks alone.

Motivated by the importance of triangular structures in network clustering and the theory of triadic closure in social networks (4, 20), we study an extension of this theory via simplicial closure or the way in which groups of nodes evolve until eventually coappearing in a higher-order structure. In this case, we find that strong previous interactions between subsets of a group increase the likelihood of a simplicial closure event, where the nodes appear in a group together. The relative importance of different types of prior interactions depends on the dataset yet remains consistent when considering groups of different sizes for a given dataset. To facilitate future modeling and demonstrate that the higher-order patterns are not simple epiphenomena of the underlying link structure, we introduce a higher-order link prediction problem—the forecasting of future higher-order interactions—as an evaluation framework for models and algorithms that aim to predict the emergence of higher-order structure from existing data.

Structural Analysis of Higher-Order Networks

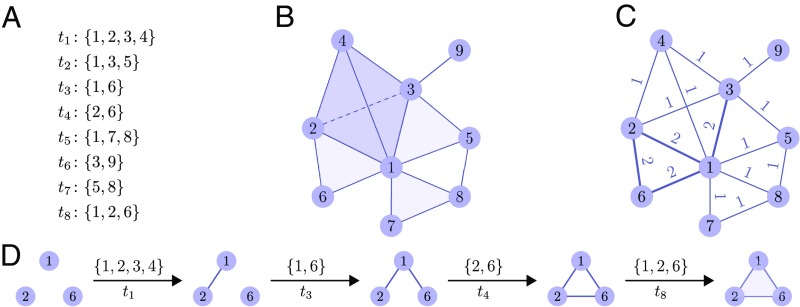
We assembled a diverse collection of 19 datasets, recording the timestamped interactions of groups of entities. Thus, each dataset is a set of timestamped sets of nodes. We call each set of nodes a simplex, and the nodes in each simplex take part in a shared interaction at a given timestamp (Fig. 1A). For example, in a coauthorship network, a simplex corresponds to a set of authors publishing an article at a given time.

Fig. 1.

Higher-order network models, open and closed three-node cliques (triangles), and simplicial closure events. (A) Example of higher-order network dataset consisting of eight timestamped simplices on nine nodes. More than one simplex can appear at a given time, which often occurs in real-world data with coarse-grained temporal measurements. We study 19 real-world datasets of this type (Table 1). (B) Visual representation of the dataset (ignoring timestamps). Shading represents the simplices (to highlight the difference with traditional graphs), and the dashed line between nodes 2 and 3 denotes 3D perspective for the four-node simplex $\left\{\mathrm{1,2,3,4}\right\}$ (this four-node simplex also has darker shading). Nodes 1, 2, and 3 form a closed three-node clique (i.e., closed triangle) since all three nodes appeared in the same simplex at time $t_1$, whereas nodes 1, 5, and 8 form an open triangle since all three pairs of nodes coappeared in a simplex (time $t_2$ for nodes 1 and 5, time $t_5$ for nodes 1 and 8, and time $t_7$ for nodes 5 and 8) but no one simplex contains all three nodes. Thus, the region between nodes 1, 5, and 8 is not shaded. In total, the dataset has seven closed triangles—$\left\{\mathrm{1,2,3}\right\}$, $\left\{\mathrm{1,2,4}\right\}$, $\left\{\mathrm{1,3,4}\right\}$, $\left\{\mathrm{2,3,4}\right\}$, $\left\{\mathrm{1,3,5}\right\}$, $\left\{\mathrm{1,2,6}\right\}$, $\left\{\mathrm{1,7,8}\right\}$—and one open triangle—$\left\{\mathrm{1,5,8}\right\}$. We find that the fraction of triangles that are open varies widely depending on the dataset (Fig. 2). (C) The “projected graph” of the dataset. The weight of an edge is the number of times its two end points have appeared in a simplex together. Open and closed triangles are both triangles in the projected graph. Traditional network science ideas often ignore higher-order structure and use only this graph. (D) A simplicial closure event for nodes 1, 2, and 6. Each transition lists the new simplex and the time it appears in the dataset. Before closing, the three nodes induce several subgraphs in the projected graph over time. For example, the nodes form an open triangle at time $t_4$, which persists until time $t_8$ when the simplicial closure event occurs. We study properties of such simplicial closure events and predict their future occurrence as part of a framework for evaluating higher-order network models.

Formally, each dataset consists of $N$ timestamped simplices, ${\left\{\left(S_i,t_i\right)\right\}}_{i=1}^N$, where $t_i\in \mathbb{R}$ is the time at which simplex $S_i$ was observed, and $S_i$ is a set representing the nodes in the $i$th simplex. If $\left|S_i\right|=k$, we say that $S_i$ is a $k$-node simplex. [Such a structure is called a (k − 1)-simplex in algebraic topology, and the set of all its pairs is called a k-clique in graph theory.] This set-based representation provides a natural format for datasets from a range of domains. We briefly describe our datasets below (see SI Appendix for more complete descriptions).

• •Coauthorship data (coauth-DBLP; coauth-MAG-History; coauth-MAG-Geology): Nodes are authors and a simplex is a publication; DBLP spans over 80 years and the other two datasets span about 200 years.
• •Online tagging data (tags-stack-overflow; tags-math-sx; tags-ask-ubuntu): Nodes are tags (annotations) and a simplex is a set of tags for a question on online Stack Exchange forums; the data contain the complete history of the forums.
• •Online thread participation data (threads-stack-overflow; threads-math-sx; threads-ask-ubuntu): Nodes are users and a simplex is a set of users answering a question on a forum; again, the data contain the complete history of the forum.
• •Drug networks from the National Drug Code Directory (NDC-classes): Nodes are class labels (e.g., serotonin reuptake inhibitor) and a simplex is the set of class labels applied to a drug (all applied at one time). (NDC-substances): Nodes are substances (e.g., testosterone) and a simplex is the set of substances in a drug; datasets include the complete history of the directory.
• •US. Congress data [congress-committees (21); congress-bills (22)]: Nodes are members of Congress and a simplex is the set of members in a committee or cosponsoring a bill; the committees dataset spans 1989–2003 and the bills dataset spans 1973–2016.
• •Email networks [email-Enron (23); email-Eu (24)]: Nodes are email addresses and a simplex is a set consisting of all recipient addresses on an email along with the sender’s address; email-Enron spans most of the duration of a company’s lifetime, and email-Eu spans over 2 years.
• •Contact networks [contact-high-school (25); contact-primary-school (26)]: Nodes are persons and a simplex is a set of persons in close proximity to each other.
• •Drug use in the Drug Abuse Warning Network (DAWN): Nodes are drugs and a simplex is the set of drugs reportedly used by a patient before an emergency department visit.
• •Music collaboration (music-rap-genius): Nodes are rap artists; simplices are sets of rappers collaborating on songs.

To provide uniformity across datasets, we restrict to simplices consisting of at most 25 nodes. This is relevant to, e.g., the coauthorship data in which large consortia of hundreds of authors collaborate on a single paper. However, such events are rare and not relevant for our analysis. Table 1 lists some summary statistics of the datasets. The number of unique simplices appearing in the data is minuscule compared with the total number of possible simplices. For example, in the dataset with the smallest number of nodes (email-Enron, 143 nodes), there are nearly 500 million possible simplices of size at most 5, whereas only 1,542 unique simplices appear in the dataset. On the other hand, in most datasets, the number of unique simplices is within an order of magnitude of the number of pairs of nodes that coappear in some simplex (edges in the projected graph; discussed in the next section).

Table 1.

Summary statistics for our datasets

Dataset	Nodes	Edges in projected graph	Timestamped simplices	Unique simplices
coauth-DBLP	1,924,991	7,904,336	3,700,067	2,599,087
coauth-MAG-geology	1,256,385	512,0762	1,590,335	1,207,390
coauth-MAG-history	1,014,734	1,156,914	1,812,511	895,668
music-rap-genius	56,832	123,889	224,878	85,429
tags-stack-overflow	49,998	4,147,302	14,458,875	5,675,497
tags-math-sx	1,629	91,685	822,059	174,933
tags-ask-ubuntu	3,029	132,703	271,233	151,441
threads-stack-overflow	2,675,955	20,999,838	11,305,343	9,705,709
threads-math-sx	176,445	1,089,307	719,792	595,778
threads-ask-ubuntu	125,602	187,157	192,947	167,001
NDC-substances	5,311	88,268	112,405	10,025
NDC-classes	1,161	6,222	49,724	1,222
DAWN	2,558	122,963	2,272,433	143,523
congress-bills	1,718	424,932	260,851	85,082
congress-committees	863	38,136	679	678
email-Eu	998	29,299	234,760	25,791
email-Enron	143	1,800	10,883	1,542
contact-high-school	327	5,818	172,035	7,937
contact-primary-school	242	8,317	106,879	12,799

Each dataset is a collection of timestamped simplices (as in Fig. 1).

Higher-Order Features Reveal Rich Structural Diversity.

Our data representation distinguishes between the observations of different kinds of $k$-way interactions between a set of entities. Stated differently, unlike in a graph representation, we do not break down each simplex into a set of (induced) pairwise interactions. Although the specific representation is not essential provided the information of the group interaction is faithfully encoded, it is convenient to think of our data as an abstract simplicial complex as depicted in Fig. 1B.

The simple encoding of the observed information as a graph is called the projected graph. Formally, in the projected graph, two nodes are joined by an edge of weight $w$ if they coappear in $w$ simplices (Fig. 1C). A $k$-clique in the projected graph is a set of nodes among which an edge is present between all pairs. $k$ cliques appear if (i) the $k$ nodes were all part of some simplex or (ii) each pair was part of some simplex, although all $k$ were never part of the same simplex. In the former case, we say the $k$ nodes form a closed clique, while in the latter case we say they form an open clique.

We first study the occurrence of open and closed 3-cliques or triangles (Fig. 2). This is the simplest higher-order structure present in our datasets that is not captured by a graph. Furthermore, triangles are one of the most important structural patterns in network analysis (4, 8, 27). As discussed above, there are two types of triangles which cannot be distinguished by the weighted projected graph alone. In a closed triangle, all three nodes have coappeared in at least one simplex. Formally, $\left\{u,v,w\right\}$ is a closed triangle if there exists some simplex $S_i$ for which $\left\{u,v,w\right\}\subset S_i$. In an open triangle, on the other hand, every pair of the three nodes has coappeared in at least one simplex, but no single simplex contains all three nodes.

Fig. 2.

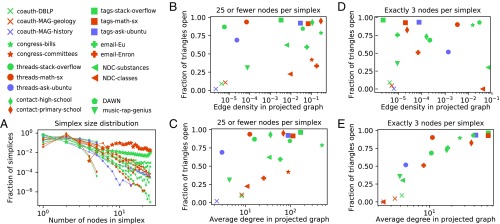
Basic structure of higher-order interaction datasets. (A) Distribution of simplex sizes. In most datasets, small simplices ($\le 4$ nodes) are the most common. (B–E) Dataset landscapes in terms of fraction of triangles that are open and either edge density (B and D) or average degree (C and E) when considering simplices with 25 or fewer nodes (B and C) or just 3-node simplices (D and E). Datasets from the same domain tend to be similar with respect to these features, whether or not we include simplices with greater than 3 nodes. Indeed, we can predict the system domain of some datasets by measuring these statistics on egonets (Table 2 and Fig. 3).

Every simplex with at least three nodes directly creates a closed triangle, while open triangles appear coincidental. Moreover, larger simplices lead to many closed triangles: For instance, a $k$-node simplex contributes $\left(\genfrac{}{}{0ex}{}{k}{3}\right)$ closed triangles. Thus, one might intuit that closed triangles are much more common than open triangles due to the presence of (potentially) large groups. On the other hand, only a small fraction of all possible simplices are present in the network compared with the total number of possible edges in the projected graph, so one might expect that there are more open triangles. Our analysis reveals that, across our datasets, there is a spectrum for the fraction of triangles that are open (Fig. 2 B–E).

While the distribution of simplex sizes is broadly similar in most datasets (Fig. 2A), jointly analyzing the edge density in the projected graph with the fraction of triangles that are open reveals a rich landscape of datasets (Fig. 2B): (i) low density with a small fraction of triangles open (coauthorships and music collaboration), (ii) low density with a large fraction of triangles open (Stack Exchange threads), (iii) high density with a large fraction of triangles open (Stack Exchange tags, contact, bill cosponsorship), and (iv) high density with a medium fraction of triangles open (email, Congress committee membership, NDC substances and classes). These results are not skewed by large simplices—the landscape is broadly preserved when restricting to the three-node simplices (Fig. 2D).

Measuring average unweighted degree along with fraction of open triangles also reveals substantial diversity, and datasets from the same domain continue to exhibit similar features (Fig. 2C). Restricting the data to only three-node simplices, we find a near-linear relationship between the fraction of open triangles and the log of the average degree (Fig. 2E). A linear model of the data in Fig. 2E has $R^2=0.85$, compared with $R^2=0.38$ for a linear model of the data in Fig. 2D. This suggests that larger simplices bring diversity to the data.

Higher-Order Egonet Features Discriminate System Domains.

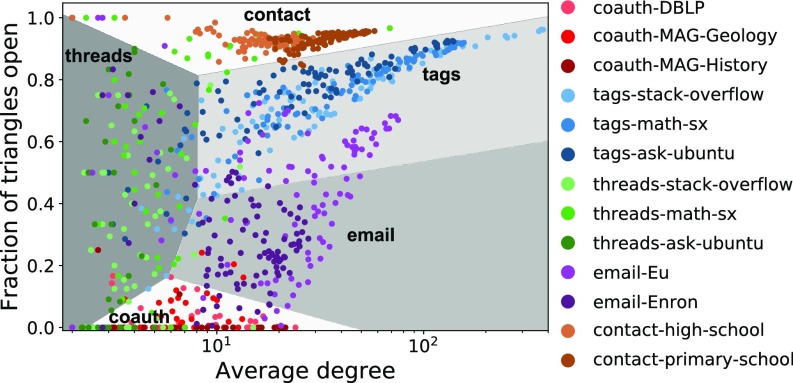
The structural diversity of the datasets is also present at the local level of egonets (1-hop neighborhoods of nodes), and local statistics can identify the “system domain” of datasets. By system domain, we simply mean the categories identified in Fig. 2 that correspond to datasets recorded from the same kind of system. Our collection of datasets has five clear system domains with at least two datasets each: coauthorship, online tags, online thread coparticipation, email, and proximity contact. Using a multinomial logistic regression model to determine system domain with the fraction of triangles that are open and log of the average degree as covariates reveals clustering structure of the system domains (Fig. 3). This simple model can predict system domain with nearly 75% accuracy, compared with approximately 21% accuracy with random guessing. The prediction accuracy provides evidence that there are different organizational mechanisms at play locally for different systems. In conjunction with the structure illustrated in Fig. 2, this suggests that there is not a single “universal” setting of values for simplicial network statistics; the context underlying the network matters, but within a given context the parameters are quite stable.

Fig. 3.

Class decision boundaries of the learned multinomial logistic regression model for predicting five dataset system domains (coauthorship, threads, tags, email, or contact) using the log of the average degree ($\log \left(\overline{d}\right)$) and fraction of triangles that are open ($f$) of egonets (Table 2 and Materials and Methods). Markers correspond to sampled egonets used in model training. The two-feature linear model can predict the five-class dataset domain with 75% accuracy (Table 2). In conjunction with the prediction accuracies in Table 2, our analysis suggests that the fraction of triangles that are open (a higher-order network statistic) is an important covariate for analyzing and modeling the local structure of higher-order interaction data.

We also trained models with the log of the edge density as a covariate, in addition to the log of the average degree and the fraction of triangles that are open; model accuracy mildly increased from 75% to 78% (Table 2). However, discarding the log of the average degree as a covariate decreases model accuracy to 60%, and including only edge density and average degree without the fraction of triangles that are open decreases model accuracy to 50%. The accuracy numbers are guides in how to model higher-order interaction data. For example, we conclude that the fraction of triangles that are open—a network statistic that relies on knowledge of the higher-order structure in the dataset—is a valuable covariate for identifying system domains. Thus, simple higher-order interactions should be used when analyzing or modeling such data. Furthermore, the average degree tends to be more valuable than edge density when considering local organizational mechanisms.

Table 2.

Prediction of dataset type by egonet features

Model features				Accuracy
$\log \left(\rho \right)$	$\log \left(\overline{d}\right)$	$f$	Intercept	Random	Multinomial LR
X	X	X	X	0.21	0.78 $\pm$ 0.02
	X	X	X	0.21	0.75 $\pm$ 0.02
X		X	X	0.21	0.60 $\pm$ 0.02
X	X		X	0.21	0.49 $\pm$ 0.03

For the datasets from coauthorship, threads, tags, email, and contact system domains, we sampled egonets and computed the edge density (ρ), average degree ($\overline{d}$), and fraction of triangles that are open (f). Using these features, we trained a multinomial logistic regression model to predict the system domain of the network (Materials and Methods). Models incorporating the fraction of triangles that are open outperform the one that does not, highlighting the importance of this feature for higherorder organization. Fig. 3 illustrates the model that uses log(ρ) and f as features.

A Simple Generative Model for Open and Closed Triangles.

We have now seen that there is diversity in datasets from global network statistics and that local statistics reveal system domains of the networks. We now provide a simple generative model of simplices that helps describe how diversity in the datasets might arise. The model uses the hypothesis that three-node simplices form independently with a fixed probability. While extreme, this hypothesis indeed leads to diversity in the fraction of triangles that are open. To see this, suppose that a dataset consists only of three-node simplices on $n$ nodes, and any set of three nodes $\left\{u,v,w\right\}$ appears in a simplex with probability $p=1/n^b$, where $b>0$ is a parameter regulating the probability of this event. Let $X_{uvw}$ be the indicator random variable that $\left\{u,v,w\right\}$ is an open triangle. Then, for large $n$, it follows from the independence assumption that

$$\mathbb{E}\left[X_{uvw}\right]\approx {\left(1-{\left(1-1/n^b\right)}^n\right)}^3.$$ [1]

There are two asymptotic regimes here depending on the value of $b$. If $b<1$, then ${\left(1-1/n^b\right)}^n\le e^{-n^{1-b}}$, and $\mathbb{E}\left[X_{uvw}\right]$ approaches 1 as $n$ gets large. If $b>1$, on the other hand,

$$\mathbb{E}\left[X_{uvw}\right]\approx {\left(1-{\left(1-1/n^b\right)}^n\right)}^3=O\left(1/n^{3b-3}\right).$$ [2]

Denote the set of open triangles by $\mathcal{O}$ and the set of closed triangles by $\mathcal{C}$. According to our calculations above, for large $n$, the expected number of open triangles is $\mathbb{E}\left[\left|\mathcal{O}\right|\right]={\sum }_{\left\{u,v,w\right\}}\mathbb{E}\left[X_{uvw}\right]=O\left(n^3\right)$ if $b<1$. For $b>1$, the expected number of open triangles for large $n$ is $\mathbb{E}\left[\left|\mathcal{O}\right|\right]=O\left(n^{3\left(2-b\right)}\right)$. The expected number of closed triangles is always $\mathbb{E}\left[\left|\mathcal{C}\right|\right]=p\cdot \left(\genfrac{}{}{0ex}{}{n}{3}\right)=O\left(n^{3-b}\right)$. Therefore, if $b<3/2$, the number of open triangles grows faster, and if $b>3/2$, the number of closed triangles grows faster. To illustrate this numerically, we generated five random samples from this model for $b=0.8,0.82,0.84,\dots ,1.8$ and $n=\mathrm{25,50,100,200}$. As suggested by the above theory, the samples have a fraction of open triangles spanning the interval between 0 and 1 (Fig. 4).

Fig. 4.

Distribution of the fraction of triangles that are open and edge density in simulations from a model where each triple of $n$ total nodes forms a three-node simplex independently with probability $p=1/n^b$, $b\in \left[0.8,1.8\right]$. Color scales with $b$ so that larger $p$ are lighter and smaller $p$ are darker. Varying $b$ creates datasets spanning all possible values of the fraction of triangles that are open.

We can also use the above procedure to construct datasets with a smaller edge density, while keeping the average degree fixed by patching together $c$ replicates of one of these random datasets; this creates a dataset with $c$ times as many nodes, but the same average degree. More formally, if a dataset with $n$ nodes has average degree $d$ and edge density $\rho$, then the union of $c$ copies of this dataset has $cn$ nodes, average degree $d$, and edge density $c\rho \left(\left(\genfrac{}{}{0.0pt}{}{n}{2}\right)-n\right)/\left(\left(\genfrac{}{}{0.0pt}{}{nc}{2}\right)-nc\right)\approx \rho /c$ (for large $n$). Thus, our simple independent model spans the two-dimensional feature space in Fig. 2 B and D, but this does not imply that our data were generated by this model.

Temporal Dynamics and Simplicial Closure Events

The above analysis already reveals useful information about the organization of closed and open triangles, and studying the temporal dynamics of the networks in detail offers additional insights. A possible hypothesis for strong prevalence of open triangles would be temporal asynchrony in link creation. For example, consider three Congresspersons $u$, $v$, and $w$ in the committee membership dataset, where $u$ is in one committee with $v$ and in another committee with $w$. If $u$ is not reelected, there will be no opportunity for the triple of nodes to form a closed triangle, as $u$ has effectively become inactive. An open triangle may still form if $v$ and $w$ are on the same committee in a future Congress. However, we find that temporal asynchrony does not explain most open triangles. Depending on the dataset, the three edges in 61.1–97.4% of open triangles have an overlapping period of activity (including 89.5% for Congress committees; SI Appendix).

Regardless of how open triangles are created, the three associated nodes may of course appear together in a simplex in the future as the network evolves. Deviating from our above simple model of independent creation of closed triangles, we find that many newly formed simplices in our data consist of $k$ nodes that had previously constituted an open $k$-clique in the projected graph. We say that the appearance of a new simplex containing these $k$ nodes is an instance of a simplicial closure event, i.e., the conversion of an open structure to a closed one, as illustrated in Fig. 1D. [Here we are building on terminology for datasets of static sets of simplices (28). The term “simplicial closure” also appears in the combinatorial topology literature but with a different meaning (29).] In the following, we investigate the simplicial closure mechanism as an organizational principle for higher-order interactions.

Simplicial Closure on Triangles Reveals Competing Features.

Although conceptually similar, three nodes participating in a simplicial closure event is distinct from the well-known phenomenon of triadic closure events in social networks (4). A triadic closure event modifies the structure of the underlying pairwise interactions, whereas a simplicial closure event adds a new higher-order interaction without necessarily changing the pairwise structure of the projected graph.

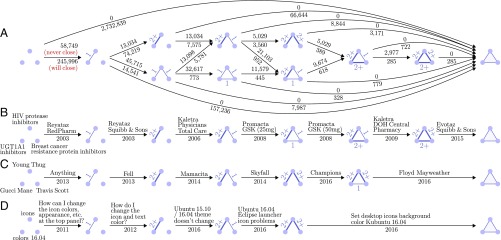
Any induced subgraph on three nodes in the weighted projected graph can change several times before the three nodes appear in a simplex together, i.e., go through a simplicial closure event (Fig. 5). We call this the “lifecycle” of the triple of nodes. There are two changes that a triple of nodes can undergo during its lifecycle before a simplicial closure event. First, a new pairwise link can be added between two nodes $u$ and $v$. This corresponds to an increase in density in this induced subgraph; e.g., the introduction of the drug Promacta adds an edge in Fig. 5B. Second, the projected graph edge weight between nodes $u$ and $v$ can increase, which we interpret as an increase in tie strength. For instance, in Fig. 5C, the tie strength between Gucci Mane and Young Thug increases after they collaborate on “Fell.” To simplify our analysis, we differentiate only between weak ties corresponding to a single interaction ($W_{uv}=1$ in the projected graph; denoted 1) and strong ties corresponding to multiple interactions over time ($W_{uv}\ge 2$; denoted 2+). With this binning, there are 11 possible states in a lifecycle (Fig. 5A).

Fig. 5.

Lifecycles of triples of nodes. Triangle edge weights are from the projected graph binned into weak ties for pairs of nodes appearing in only one simplex together (denoted 1) and strong ties for pairs of nodes appearing in at least two simplices together (denoted 2). (A) Lifecycles in the coauth-MAG-History dataset for all triples that eventually form a triangle. Edges represent transitions between configurations, and the numbers are counts of triples that follow the transition. The top number counts triples of nodes that never experience a simplicial closure event (i.e., never reach the closed state on the far right), and the bottom number counts triples that do go through a simplicial closure event. (B) Lifecycle of classification codes “HIV protease inhibitors,” “UGT1A1 inhibitors,” and “breast cancer resistance protein inhibitors” in the NDC-classes dataset, where simplices consist of the labels applied to drugs. Reyataz and Kaletra—two HIV-1 medications—produced strong ties via multiple drug labelers; RedPharm Drug Inc. and E.R. Squibb & Sons, LLC labeled Reyataz, and Physicians Total Care and DOH Central Pharmacy labeled Kaletra. Promacta, a bone marrow stimulant classified as both a breast cancer resistance protein inhibitor and a UGT1A1 inhibitor, creates the open triangle. A strong tie is due to GlaxoSmithKline plc labeling multiple dosages of Promacta as products (25 mg and 50 mg). The introduction of Evotaz, a combination drug, induces a simplicial closure event for the three labels, six years after the open triangle formed. (C) Lifecycle of rap artists Young Thug, Gucci Mane, and Travis Scott. Mane and Thug first collaborated on the song “Anything” on a Mane mixtape; the two subsequently both featured on Waka Flocka Flame’s track “Fell.” Thug then twice featured on Scott’s 2014 mixtape “Days Before Rodeo,” on the tracks “Mamacita” and “Skyfall.” Both Mane and Scott featured on Kanye West’s ensemble track “Champions,” leading to an open triangle. A simplicial closure event occurred when Scott and Mane both featured on Thug’s track “Floyd Mayweather.” (D) Lifecycle of tags “icons,” “colors,” and “16.04” applied to questions on the Ask Ubuntu question-and-answer forum. The tag 16.04 refers to a 2016 Ubuntu release. There are questions about icons and colors independent of the Ubuntu version, dating back to 2011 (just one year after the forum was created). In 2016, users asked 16.04-specific icon questions related to the new release. Finally, a 16.04-specific question on both icons and colors leads to a simplicial closure event.

To get a first impression of the magnitude of these events, we examine the lifecycle of every triple of nodes that becomes an open or closed triangle in the coauth-MAG-History dataset (Fig. 5A). In this dataset, a closed triangle is more likely to have come from a configuration with exactly two strong tie edges (3,171 cases) than from an open triangle (328 + 779 + 722 + 285 = 2,114 cases). Most closed triangles are formed by nodes that had no previous interaction (2,732,839 cases); however, since the graph is sparse, the fraction of triples of nodes with no prior engagement that go through a simplicial closure event is small (SI Appendix). Additionally, if three nodes induce an open triangle with only weak ties at some point in time, then the three nodes are more likely to gain a strong tie before closure (445 cases) than to close directly from that state (328 cases).

We also analyze the probability of a simplicial closure event conditioned on the state of the three nodes in its lifecycle. To do so, we split each dataset based on the temporal order of appearance of the simplices into a training set, consisting of the first 80% of the simplices (in time) and a test set of the remaining 20% of the simplices. Formally, if $t_{*}$ is the 80th percentile of the timestamps $t_1,\dots ,t_N$, then the training set is the set of timestamped simplices $\left\{\left(S_i,t_i\right)|t_i\le t_{*}\right\}$ and the test set consists of $\left\{\left(S_i,t_i\right)|t_i>t_{*}\right\}$. We then measured the probability that a triple of nodes from the training set is a closed triangle in the test set as a function of its previous configuration in the weighted projected graph, i.e., its lifecycle state in the training data (SI Appendix contains all of the simplicial closure event probabilities).

We highlight four important findings. First, the simplicial closure event probability typically increases with additional edges (Fig. 6A). In other words, as the edge density of the subgraph induced by the three nodes increases, the probability of a simplicial closure event increases. We formally test this by comparing the closure probability of a fixed weighted induced subgraph configuration and the same configuration with an additional unit-weight edge for all suitable cases. The latter has a statistically significant larger simplicial closure event probability in 102 of 113 cases over all datasets and pairs of configurations, whereas the less dense structure is never significantly more likely to close ($P<10^{-5}$; Materials and Methods). (Our goal here is to illustrate general trends rather than to find a single statistically significant result.) This result is consistent with both theoretical (4) and empirical (30) studies of dyadic link formation in social networks. However, several of our datasets are not social networks.

Fig. 6.

Comparison of simplicial closure event probabilities based on configurations of three-node and four-node structures. The simplices appearing in the first 80% of the time spanned by the dataset determine the configuration (appearing as the x-axis and y-axis labels). The scatter plots compare the probability of different configurations going through a simplicial closure event in the final 20% of timestamped simplices. (A–C) Comparison of simplicial closure event probabilities for pairs of three-node configurations that demonstrate how increasing edge density (A) or tie strength (B) increases the probability of a simplicial closure event. However, the relative importance of edge density and tie strength depends on the dataset (C). (D–F) Comparison of simplicial closure event probabilities for pairs of four-node configurations. Each axis has two labels giving two pictorial representations of the configuration. The white nodes in the “flat” representation (left label on x axis; top label on y axis) represents the same node, so the 3D structure can be envisioned by folding the white nodes on top of each other. The other representation (right label on x axis; bottom label on y axis) shows a 3D tetrahedral perspective of this folding. We again see that increasing edge density (D) or tie strength (E) increases the probability of a simplicial closure event. Here, “tie strength” is measured at the level of three-node simplices, i.e., how often three nodes have appeared in a simplex (no times, not shaded; one time, shaded, denoted 1; or at least two times, shaded, denoted 2+). The relative importance of edge density and tie strength depends on the dataset but is consistent with the three-node case. In three of the five datasets for which the configuration on the y axis in F is significantly more likely to go through a simplicial closure event, the open triangle of weak ties is also significantly more likely to close for sets of three nodes (coauth-DBLP, coauth-MAG-Geology, congress-bills; compare with C; $P<10^{-5}$). And in three of the four datasets for which the configuration on the x axis in F is significantly more likely to go through a simplicial closure event the configuration with just two strong ties is also more likely to close than the open triangle with all weak ties (tags-stack-overflow, tags-math-sx, tags-ask-ubuntu; compare with C; $P<10^{-5}$). Moreover, there were no datasets for which tie strength was significantly more indicative of simplicial closure events for one simplex size and density was more important for another (significance level $10^{-5}$).

Second, the probability of a simplicial closure event typically increases with tie strength (Fig. 6B). We test the effect of tie strength by comparing the closure probability of a fixed weighted induced subgraph containing at least one weak tie and the same configuration where the weak tie is converted to a strong tie. Increasing the tie strength significantly increases the probability of a simplicial closure event in 82 of 113 cases over all datasets and significantly decreases the closure probability in just 6 of 113 cases ($P<10^{-5}$). Again, this result is consistent with both theoretical (4) and empirical (27, 31) studies of social networks, even though not all of our networks are social.

Third, neither edge density nor tie strength dominates the likelihood of simplicial closure events (Fig. 6C). In the coauthorship and Congress datasets, an open triangle composed of three weak ties is more likely to close than a three-node subgraph with just two strong ties. The reverse is true for the stack exchange tags and stack exchange threads datasets. Overall, the open triangle of weak ties is significantly more likely to close than the three nodes with two strong ties in 4 of 19 datasets, whereas the opposite is true in 6 of 19 datasets ($P<10^{-5}$).

Fourth, the results reveal varying closure dynamics over the dataset domains. In human social interactions, simplicial closure events appear to be driven by a topological form of triadic closure: Mutual acquaintance between all of the nodes in a set increases the probability of a joint interaction. In contrast, simplicial closure events in the discussion platform networks resemble transitive closure: Once there is a sufficiently strong co-occurrences of tags, they become likely to be used together.

A possible concern with our analysis is that we measured closure probabilities only at one point in time for each dataset. Furthermore, while some of our datasets represent a complete history of the network (tags, threads, NDC) and some span a long duration of time (coauthorship, music, congress-bills), a few contain only a slice of the underlying network’s dynamics (email-Eu, contact). However, we find that the closure probabilities and the results on edge density and tie strength are consistent at different points in time (SI Appendix).

Simplicial Closure Properties Extend Beyond Triangles.

All four of the above findings hold for simplicial closure events on four nodes, so our results are not limited to structure on three nodes (Fig. 6 D–F). Now, a simplicial closure event is all four nodes appearing in a simplex, and tie strength is measured on three-node simplices, i.e., how often the three-node subsets of a four-node structure have appeared together in a simplex (0, “open”; 1, “weak”; or at least two times, “strong”).

To measure the effect of edge density, we compare the closure probability of a configuration consisting of a fixed number of edges to the closure probability of the same configuration with an additional edge, keeping the tie strengths fixed (Fig. 6D shows one such comparison). In 180 of 228 applicable comparisons over all datasets, the closure probability significantly increases with the edge density and significantly decreases in only 2 cases ($P<10^{-5}$). To measure the effect of tie strength, we compare the closure probability of a given configuration to the closure probability of the same configuration where the tie strength increases from an open tie to a weak tie or from a weak tie to a strong tie (Fig. 6E shows a case where the tie strength increases from open to weak). The closure probability significantly increases with simplicial tie strength in 26 of 38 cases for three-edge configurations, 31 of 38 cases for four-edge configurations, 77 of 114 cases for five-edge configurations, and 177 of 359 cases for six-edge configurations, compared with a significant decrease in closure probability in just 2 of 38, 1 of 38, 1 of 114, and 4 of 359 cases ($P<10^{-5}$). Therefore, tie strength is also a positive indicator of simplicial closure in four-node configurations.

There is also tension between the influence of sparser configurations with strong ties and that of denser configurations with weak ties. Fig. 6F shows one such comparison. In this case, three of five datasets for which edge density is significantly more indicative than tie strength in the three-node comparison of Fig. 6C, edge density is also significantly more important in the four-node case ($P<10^{-5}$). And in three of the four datasets for which tie strength is significantly more indicative than edge density in the same three-node case, the same is true in the four-node case. Finally, there is no dataset for which tie strength was significantly more influential for one simplex size and density was significantly more influential for another.

Higher-Order Link Prediction

Thus far, we have shown that higher-order interactions provide a rich source of additional information beyond traditional network modeling. Our analysis leaves open many questions, such as the development of better mechanistic models for the emergence of these interactions. To facilitate this process, we propose an analog of link prediction for higher-order structure.

Model Evaluation Framework.

The basic premise in link prediction—whether pairwise or higher order—is to use structural network properties up to some time $t$ to predict the appearance of new interactions after $t$. In traditional network analysis, link prediction is a cornerstone problem and a highly successful evaluation framework for comparing different models via a well-calibrated prediction task (32, 33). Specifically, link prediction examines data that evolve over time and sees how well a given model predicts the appearance of new links—for example, new coauthorships appearing in a coauthor network or new messages between pairs of people in an email network.

In this context, a model is interpreted broadly and may be mechanistic [e.g., preferential attachment (34)], statistical [e.g., probabilistic hierarchical models (35)], or implicitly encapsulated by a principled heuristic algorithm. For instance, personalized PageRank is a model capturing the fact that a large number of walks between two nodes drive up the connection probability between them (32). A key advantage of link prediction as an evaluation framework is precisely that it can handle these various kinds of models. This holds even in the absence of a likelihood expression, which would be required for a more standard statistical evaluation of goodness of fit. While ultimately we may want to arrive at a generative, causal description of the emergence of higher-order patterns, the flexibility of link prediction enables us to probe the importance of features of the network data in a simple manner without having to create a formal statistical model.

Link prediction has proved valuable for methodological reasons and also in concrete applications. Methodologically, asking whether one model is better than another at predicting new links provides a data-driven way of assessing the effectiveness of the models (32, 36, 37). Link prediction also has a number of direct applications that cut across disciplines, including predicting friendships in social networks (38), inferring new relationships between genes and diseases (39), and suggesting novel connections in the scientific community (40).

Link prediction is also used within model selection tools for evaluating community detection algorithms (41, 42). In these cases, link prediction may be interpreted as the smallest possible test for the fit of a model as we need to predict only one edge at a time. However, if one were to consider all edges in a cross-validation assessment, good link prediction performance indicates a good model fit for other structures in the data. Our higher-order link prediction task probes a larger set of features, in that it requires us to be able to predict more aspects of the data (any higher-order interaction, in principle).

For simplicity of presentation and scalability reasons, we predict simplicial closure events on triples of nodes. Thus, the higher-order link prediction problem examined here is predicting which triples of nodes that have not yet appeared in a simplex together will be a subset of some simplex in the future. Our above analysis suggests that open triangles or triples of nodes with strong ties are the most likely to close in the future. For our experiments, we predict which open triangles will go through a simplicial closure event in the future. Thus, this is a problem completely ignored by traditional link prediction, which would just view the triangle as already part of the graph. From a computational view, this restriction also makes it feasible to enumerate all open structures upon which the algorithms will make a prediction, using only modest computational resources. Thus, we avoid a common problem in link prediction of how to pare down an enormous candidate set of potential links, which itself is an active research topic (43, 44).

Simple Local Features Predict Well.

We first split the data into training (first 80% of simplices in time) and test (final 20%) sets. Then, we evaluated the prediction performance of several models (several inspired from classical link prediction) on each dataset by the area under the precision-recall curve (AUC-PR) metric (Table 3). We use random scores as a baseline, which, with respect to AUC-PR, corresponds to the proportion of open triangles in the training set that go through a simplicial closure event in the test set.

Table 3.

Open triangle closure prediction performance based on eight models: harmonic, geometric, and arithmetic means of the three edge weights; three-way Adamic–Adar coefficient (A-A); preferential attachment (PA); Katz similarity; personalized PageRank similarity (PPR); and a feature-based supervised logistic regression model (Log. reg.)

Dataset	Harmonic mean	Geometric mean	Arithmetric mean	A-A	PA	Katz	PPR	Log. reg.
coauth-DBLP	1.49	1.59	1.50	1.60	0.74	1.51	1.83	3.37
coauth-MAG-history	1.69	2.72	3.20	5.82	2.49	3.40	1.88	6.75
coauth-MAG-geology	2.01	1.97	1.69	2.71	0.97	1.74	1.26	4.74
music-rap-genius	5.44	6.92	1.98	2.10	2.15	2.00	2.09	2.67
tags-stack-overflow	13.08	10.42	3.97	6.63	2.74	3.60	1.85	3.37
tags-math-sx	9.08	8.67	2.88	6.34	2.81	2.71	1.55	13.99
tags-ask-ubuntu	12.29	12.64	4.24	7.51	5.63	4.15	2.54	7.48
threads-stack-overflow	23.85	31.12	12.97	3.19	3.89	11.54	4.06	1.53
threads-math-sx	20.86	16.01	5.03	23.32	7.46	4.86	1.18	47.18
threads-ask-ubuntu	78.12	80.94	29.00	30.82	6.62	32.31	1.51	9.82
NDC-substances	4.90	5.27	2.90	5.97	4.46	2.93	1.83	8.17
NDC-classes	4.43	3.38	1.82	0.99	2.14	1.34	0.91	0.62
DAWN	4.43	3.86	2.13	4.77	1.45	2.04	1.37	2.86
congress-committees	3.59	3.28	2.48	5.04	1.31	2.59	3.89	7.67
congress-bills	0.93	0.90	0.88	0.66	0.55	0.78	1.07	107.19
email-Enron	1.78	1.62	1.33	0.87	0.83	1.28	3.16	0.72
email-Eu	1.98	2.15	1.78	1.37	1.55	1.79	1.75	3.47
contact-high-school	3.86	4.16	2.54	2.00	1.13	2.53	2.41	2.86
contact-primary-school	5.63	6.40	3.96	3.21	0.94	4.02	4.31	6.91

Performance is AUC-PR relative to the random baseline, i.e., relative to the fraction of open triangles that close. The top performance number for each dataset is in boldface type.

We compare eight models here and provide additional comparisons in SI Appendix. Three are heuristics based on our finding that tie strength is indicative of closure; these are the harmonic, geometric, and arithmetic means of the three edge weights in the open triangle. Two more are based on the Adamic–Adar model (45) and the preferential attachment model. The latter has been suggested as a growth mechanism of coauthorship networks (20, 34). Two are based on longer path counts (Katz and personalized PageRank), which are models known for providing good prediction in dyadic link prediction (32). Finally, we use a supervised logistic regression model based on features from the other models.

No single model performs the best over all datasets, but our proposed baseline algorithms can achieve much better performance than randomly guessing which open triangles go through a simplicial closure event. In the threads datasets, we achieve between one and two orders of magnitude performance improvements with the harmonic and geometric means, which indicates that local tie strength is relatively more important for these datasets than for others. The absolute performance of the algorithms is far from perfect (SI Appendix), as the higher-order link prediction is challenging. This finding is consistent with recent research on subgraph prediction in pairwise networks (46). However, our goal here is to identify some of the important structural features of the problem, rather than to predict with perfect accuracy.

The harmonic and geometric means of edge weights perform well across many datasets, which further highlights the importance of tie strength in predicting simplicial closure events. This finding is fundamentally different from traditional link prediction with pairwise interactions (i.e., for the edges in a graph). In traditional link prediction, a key principle is that it is valuable to use information contained in paths of nontrivial length between two nodes $u$ and $v$ for predicting a link between them—for example, PageRank and Katz measures are effective (32, 33). In this sense, higher-order link prediction is fundamentally more local in its overall structure. This arises from the ability of a $k$-tuple of nodes, for $k\ge 3$, to contain rich local information in its interactions among subsets of size $k-1$, a phenomenon that has no natural analogue when $k=2$.

The arithmetic mean performs the worst of the three means in all but one dataset. We further analyze the performance of edge weight means using the generalized mean with parameter $p$ as score functions: $s_p\left(u,v,w\right)={\left[\left(W_{uv}^p+W_{uw}^p+W_{vw}^p\right)/3\right]}^{1/p}$, where $W_{ab}$ is the weight between nodes $a$ and $b$ in the projected graph. The harmonic, arithmetic, and geometric means are the special cases where $p=-1$, $p=1$, and the limit $p\to 0$. Generally, prediction performance is (i) unimodal in $p$, (ii) maximized for $p\in \left[-\mathrm{1,0}\right]$, and (iii) better for $p<-1$ than for $p>1$ (Fig. 7). Two exceptions are NDC-classes and coauth-MAG-History. The former is the only dataset without an open triangle with exactly one strong tie to close. Thus, smaller $p$ should perform better, as this accounts more for the minimum edge weight value. The latter is the dataset with the smallest average degree in the projected graph (Fig. 2C). Therefore, a single strong edge could provide the signal for closure, in which case a larger $p$ is a better score function.

Fig. 7.

AUC-PR relative to random predictions as a function of the parameter $p$ in the generalized mean heuristic model for higher-order link prediction.

The supervised learning approach also performs well broadly, especially in the larger datasets such as the coauthorship datasets, which have sufficient training data to learn a good model. However, even when including the features of the other models, the method does not always perform the best. This is likely a case of overfitting (47). In the case of the congress-bills data, the supervised method captures a unique feature of this dataset—nodes appearing in fewer simplices are more likely to go through a simplicial closure event. This is possibly due to the ambition of junior Congresspersons. The fact that combinations of features prove effective in many domains highlights the richness of the underlying problem, and the array of methods and findings presented here can guide progress on better models.

Discussion

The dyadic network modeling paradigm has been successful but fails to capture natural higher-order interactions. Here, we established the foundation for analyzing the basic structure of temporal networks with higher-order structure. We found rich structural variety in our datasets in terms of the fraction of triangles that are open, the average degree, and the edge density. Local statistics at the level of egonets can identify system domain, which suggests that these features are key to the organizing principles of the systems. Recent research shows the small fraction of triangles that are open in coauthorship networks (28); our results are consistent but reveal that open triangles are extremely common in other domains. Prior research has also identified the distinction between open and closed triangles when projecting bipartite networks but has not studied the idea of simplicial closure events (7, 48).

We found that common principles from dyadic network evolution also hold for higher-order structure; namely, tie strength and edge density are positive indicators of simplicial closure events among sets of three and four nodes. However, there is tension between these features—the more influential feature depends on the dataset, suggesting different mechanisms for simplicial closure events. For example, edge density matters more in human interaction, but tie strength matters more for tagging on online discussion platforms.

Higher-order link prediction provides a general methodology for evaluating models in any data where higher-order structure evolves over time, such as predicting which sets of authors will write a paper together or which sets of people will appear as joint recipients on an email. We anticipate that higher-order link prediction will validate emerging higher-order network modeling techniques, such as multipartite networks (49), metapaths (50), and embeddings (51), and connect to ideas in computational topology, such as random walks on simplicial complexes (52, 53). Related higher-order models for different data (18, 19) can also use higher-order link prediction for model evaluation. For example, in the absence of temporal information, higher-order link prediction could be used to find missing data, similar to how dyadic link prediction can find missing data in static networks (35). Our higher-order link prediction framework also provides a way to study more sophisticated models where the underlying network is also dynamic, e.g., with arrival and departure of nodes. Specifically, such models should be able to predict higher-order links.

Our prediction problem examined a structure that is not even considered in traditional network analysis, where no distinction is made between open and closed triangles. From this setup, we found that simple local measures (generalized means of edge weights) are effective predictors. This finding differs from traditional link prediction, where long paths are important (32), and suggests that the temporal evolution of higher-order network data is fundamentally different from dyadic network evolution.

Materials and Methods

System Domain Prediction from Egonet Statistics.

We computed (i) the fraction of open triangles, (ii) the log of the average degree in the projected graph, and (iii) the log of edge density in the projected graph of 100 egonets sampled uniformly at random (without replacement) from all egonets containing at least one open or closed triangle in each of 13 datasets categorized as coauthorship, stack exchange tags, stack exchange threads, email, or contact. Using 80 samples from each of the 13 datasets as training data, we trained an ${\ell }_2$-regularized multinomial logistic regression classifier to predict the system domain given the three features above and an intercept term. The model was trained using the scikit-learn library (the regularization parameter was set to $C=10$). Test accuracy was computed on the remaining 20 samples for each dataset. This entire process described was repeated 20 times, resulting in 20 different collections of egonet samples. Table 2 reports the mean and SD of test accuracy over the 20 trials. The decision boundary in Fig. 3 comes from one of the 20 trials. Finally, let $p_c$ be the fraction of egonets in a system domain within the training data and $C$ the set of all classes. Then random guessing accuracy is ${\sum }_{c\in C}{p}_c^2$. The square appears because class $c$ appears in a $p_c$ fraction of the data and is guessed correctly with probability $p_c$.

Hypothesis Testing for Simplicial Closure Event Probabilities.

Let $n_c$ and $x_c$ denote the number of instances of an open configuration $c$ in the training set (first 80% of data) and the number of those instances that close in the test set (final 20% of data). For a pair of configurations $c$ and $c^{\prime }$, we use a one-sided hypothesis test for $x_c/n_c<x_{c^{\prime }}/n_{c^{\prime }}$. We use Fisher’s exact test when $max\left(x_c,x_{c^{\prime }}\right)\le 5$; otherwise, we use a one-sample $z$ test.

Data and Software.

Data collection details are in SI Appendix. Software is available at https://github.com/arbenson/ScHoLP-Tutorial. Datasets have been deposited in the GitHub repository, https://github.com/arbenson/ScHoLP-Data.