Emergence of phytoplankton patchiness at small scales in mild turbulence

Significance

Recent observations found that swimming phytoplankton species have a patchy spatial distribution down to the millimeter scale in oceans and lakes. This is rather surprising because it goes against the intuitive expectation that the turbulent flow mixes the microorganisms and spreads them rather homogeneously. Here, we identify the relevant scales that rationalize the observation of patchiness. We find that a mild turbulent field can lead to the formation of small dense patches of motile cells when the typical scales of the turbulence roughly match the scales of the interaction among microorganisms, which is mediated by hydrodynamics.

Abstract

Phytoplankton often encounter turbulence in their habitat. As most toxic phytoplankton species are motile, resolving the interplay of motility and turbulence has fundamental repercussions on our understanding of their own ecology and of the entire ecosystems they inhabit. The spatial distribution of motile phytoplankton cells exhibits patchiness at distances of decimeter to millimeter scales for numerous species with different motility strategies. The explanation of this general phenomenon remains challenging. Furthermore, hydrodynamic cell–cell interactions, which grow more relevant as the density in the patches increases, have been so far ignored. Here, we combine particle simulations and continuum theory to study the emergence of patchiness in motile microorganisms in three dimensions. By addressing the combined effects of motility, cell–cell interaction, and turbulent flow conditions, we uncover a general mechanism: The coupling of cell–cell interactions to the turbulent dynamics favors the formation of dense patches. Identification of the important length and time scales, independent from the motility mode, allows us to elucidate a general physical mechanism underpinning the emergence of patchiness. Our results shed light on the dynamical characteristics necessary for the formation of patchiness and complement current efforts to unravel planktonic ecological interactions.

The spatial distribution of plankton is key to understanding myriad aspects of marine ecology: from the flux of nutrients in the water column, or predation strategies (1, 2), to the global repercussions of harmful algal blooms (3). It is one of the oldest observations in biological oceanography that phytoplankton exhibit a heterogeneous spatial distribution (patchiness) at length scales of kilometers (4, 5). Recent technological advances have ushered in measurements at small scales (decimeters to millimeters) that revealed patchiness also at these smaller scales (6). These small distances form the natural arena where biological and physical processes such as nutrient uptake, growth, and community composition take place (2, 7–10). Due to various factors such as wind or tidal currents, the local, small-scale environment of phytoplankton is nearly invariably turbulent (11), and turbulence has a profound impact on the biology and ecology of plankton (12). For example, turbulent diffusion reduces the size of the concentration boundary layer of depleted nutrients and thus facilitates the nutrient uptake of the microorganism (13–15).

Numerous phytoplankton species are motile, and the vast majority of harmful algal blooms are caused by motile phytoplankton (3, 11). Thus, a comprehension of the consequences of active motion in a turbulent environment can clarify important aspects of the phytoplankton ecology, such as division rates and nutrient retrieval. Recent work has established that gyrotactic plankton swimming in mildly turbulent environments form dense patches (16–19). However, patchiness is exhibited by a myriad of motile species with different motility modes, such as phototaxis, chemotaxis, pattern swimming, and autoregulated aggregation (3, 20–22). Furthermore, flow visualization techniques have demonstrated that motile plankton create microflows which in turn modify the fluid environment (2) and will introduce effective hydrodynamic interactions among individual cells at the scale of about $100\hspace{0.17em}\mathrm{\mu }$m. Recurrent algal blooms produce the initial conditions for the subsequent emergence of patchiness (7). In this context, a basic yet unresolved question is to determine what features of marine turbulence conspire with planktonic motility to engender patchiness.

Here, we combine molecular dynamics simulations and a continuous description of the incompressible Navier–Stokes flow to determine a general mechanism for patchiness in motile phytoplankton cells swimming in a turbulent environment. Unlike previous investigations of gyrotactic plankton, we include a minimal model of cell–cell interactions among the swimmers. Our work explores the fundamental spatial and temporal scales associated to the reorientation of the swim direction when cells encounter each other and the scales associated to the mild turbulent motion. We identify dimensionless numbers that compare the characteristic time scales associated to the small-scale motion of the fluid with the cell–cell interactions and that compare the characteristic length scales associated to the turbulent motion with the active motion of the cells.

Associating time and length scales to turbulent dynamics is a familiar operation from classical studies of turbulence, but the role of these scales in the context of phytoplankton with hydrodynamic coupling is not known. We consider two complementary methods to generate a turbulent flow: (i) a simplified but realistic representation of turbulent flow via random Fourier modes (23, 24), the so-called kinematic simulation method first proposed by Kraichnan (25), and (ii) direct numerical simulations (DNS) of the Navier–Stokes equations with a pseudospectral method. Our investigations are carried out in a parameter range close to the ecologically relevant Taylor-based Reynolds number (26) ${\mathcal{R}}_{\lambda }\approx 20$, which corresponds to realistic conditions found, e.g., at the pycnocline (7).

We find that the correlation length scale associated to the vorticity of the flow constitutes a characteristic scale, and when it matches the length scale associated to the cell–cell interactions, strong patchiness emerges. Experimental evidence at such a level of precision is scarce. However, the current evidence points to the fact that minuscule changes in the cellular morphology can dramatically affect the hydrodynamic cell–cell interactions (27) and how different organisms respond to turbulent microflows (28), thus giving further motivation for our work.

Results

Modeling Phytoplankton Dynamics in Mildly Turbulent Environments.

Consider a motile microorganism, such as phytoplankton, swimming in a turbulent aqueous milieu. A fundamental length scale characterizing the scale where the energy associated with turbulent motion dissipates is the Kolmogorov length scale ${\eta }_K={\left({\nu }^3/\epsilon \right)}^{1/4}$, where $\nu$ is the kinematic viscosity of the fluid (∼$10^{-6}$ ${\mathrm{m}}^2$/s for sea water), and $\epsilon$ is the energy dissipation rate. For realistic values of dissipation rate ($\epsilon \approx 10^{-10}-10^{-5}\hspace{0.17em}{\mathrm{m}}^2$/${\mathrm{s}}^3$) (29, 30), the Kolmogorov length scale ${\eta }_K$ is of the order of hundreds of micrometers. Within dense patches, phytoplankton cells are separated by distances comparable or smaller than ${\eta }_K$ (16). Thus, for typical phytoplankton cell sizes ($1-\mathrm{1,000}\hspace{0.17em}\mathrm{\mu }$m) (31) cell–cell interactions should be directly addressed.

Because of their sizes, the motion of microorganisms in aquatic environments is dominated by viscous forces, which are two to five orders of magnitude larger than the inertial forces (32). This means that the microorganisms’ motion and the small-scale perturbations to the fluid produced by their motility are described by the Stokes equation $\nabla p-\mu {\nabla }^2\mathit{u}=\mathit{f}$, where $p$ is the hydrostatic pressure, $\mathit{u}$ is the fluid velocity, $\mu$ is the fluid viscosity, and $\mathit{f}$ is a body force. The fact that this equation is linear and not explicitly dependent on time allows a great simplification with respect to the full Navier–Stokes equations, and we can write the general solution (in unbounded domains) as $\mathit{u}=\int \mathrm{O}\left(\mathit{r}-\mathit{r}\prime \right)\cdot \mathit{f}d\mathit{r}\prime$, where $\mathrm{O}\left(\mathit{r}\right)=\frac{1}{8\pi \mu r}\left(\mathrm{I}+\frac{\mathit{r}\otimes \mathit{r}}{r^2}\right)$ is the Oseen tensor. Because flagellated microorganisms move autonomously, the hydrodynamic perturbations produced by their active motion can be well described as the sum of two equal and opposite forces $\mathit{f}=\pm f_0\mathit{e}$ separated by a distance $\delta$, i.e., a force dipole. The fluid velocity field generated by a force dipole reads ${\mathit{u}}_{\mathrm{d}\mathrm{i}\mathrm{p}}=\frac{f_0\delta }{8\pi \mu r^2}\left[3{\left(\widehat{\mathit{r}}\cdot \mathit{e}\right)}^2-1\right]\widehat{\mathit{r}}$, where $\widehat{\mathit{r}}$ and $\mathit{e}$ are the unit vectors representing the direction of the position and orientation of the dipolar swimmer, respectively. We note that the expression for ${\mathit{u}}_{\mathrm{d}\mathrm{i}\mathrm{p}}$ has a symmetry: It remains invariant under the exchange $\mathit{e}\to -\mathit{e}$. Hence, hydrodynamically mediated cell–cell interactions among flagellated swimmers generate a flow field which to leading order exhibits up–down symmetry (33, 34). Hydrodynamic interactions between motile cells are in principle long ranged. However, the intrinsic biological stochasticity of the cells’ motility together with the strongly fluctuating conditions of turbulent microflows effectively produce short-range cell–cell interactions (34). The range $ϵ$ of this cell–cell interaction mediated by hydrodynamics has been estimated to be of the same order of magnitude as the cell body length for Chlamydomonas (34, 35). Beyond this length scale $ϵ$ the stochastic nature of the flow prevails. Short- to medium-range cell–cell interactions with up–down symmetry are the key ingredient for our modeling.

We model the cells as particles with swimming speed $v_0$ and orientation $\mathit{e}$. The cells’ reorientation is subject to two torques: (i) $\frac{1}{2}\left(\mathit{\omega }\times \mathit{e}\right)$ induced by the fluid vorticity $\mathit{\omega }=\nabla \times \mathit{u}$, where $\mathit{u}$ is the fluid velocity, and (ii) a torque representing the short-range cell–cell interactions with up–down symmetry. The interaction is restricted to particles within the range $ϵ$ and takes place on a time scale $1/\gamma$. Rotational diffusion is introduced through a stochastic noise $\mathit{\xi }$. For the sake of comparison we also consider select simulations with extended particles to examine the impact of repulsive contact forces. See Materials and Methods for more details.

To model the turbulent flow, we combine results from two complementary techniques to generate a turbulent flow. In the first approach, we use kinematic simulations; that is, the turbulent velocity field is modeled by a sum of unsteady random Fourier modes which obey a prescribed energy spectrum. We refer to this model as the “Kraichnan fluid” after its first proponent (25). In the second approach, we perform DNS of the incompressible Navier–Stokes equations with a pseudospectral method to model the turbulent flow directly (more details in SI Appendix). (We note that the Kolmogorov scale as a measure for the small-scale turbulent motions is meaningful only in the context of 3D Navier–Stokes flow. In that sense, comparisons to real-world data are more sensible for this setting than for simplified 2D flows.)

The orientational dynamics can be characterized by two dimensionless numbers. The first one is the rotational Péclet number $\mathcal{P}=\gamma /D_r$, which describes the ratio between the strength of cell–cell interaction $\gamma$ and the rotational diffusion $D_r$ due to stochastic noise. The second dimensionless number serves to compare the strength of the cell–cell interaction with the turbulent field. The typical vorticity of the turbulent field is quantified by the Kolmogorov shear rate ${\omega }_K=\sqrt{⟨{\mathit{\omega }}^2⟩}=\sqrt{2\int E\left(k\right)k^2\text{d}k}$, where $E\left(k\right)$ is the energy spectrum and $k$ the wavenumber. We define the vortical Stokes number as ${\mathcal{S}}_{\omega }={\tau }_{\text{turb}}/{\tau }_{\text{int}}=2\gamma /{\omega }_K$, where ${\tau }_{\text{turb}}$ and ${\tau }_{\text{int}}$ are the characteristic times of the turbulent field and of the cell–cell interaction.

Phase Diagram of Patchiness.

In our simulations, we observe phytoplankton patchiness as a consequence of the cell motility and the cell–cell interaction for a wide range of parameters. This can be reasoned as follows: The dynamics described by the equations of motion of the swimming cells (Eq. 2 in Materials and Methods) produce a compressing phase-space volume $\mathrm{\Gamma }\equiv {\nabla }_{\mathit{r}}\cdot \dot{\mathit{r}}+{\nabla }_{\mathit{e}}\cdot \dot{\mathit{e}}=-4\gamma \left({\mathit{e}}_{\text{av}}\cdot \mathit{e}\right)$, where ${\mathit{e}}_{\text{av}}$ is the average orientation around a reference cell. Because cells swimming in the same patch will necessarily have a similar orientation, the average $⟨\mathrm{\Gamma }⟩<0$. Thus, the coupling of active motion and turbulence potentially produces regions of increased local density.

For a more detailed picture of the mechanism we map out the nonequilibrium phase diagram of cell patchiness, identifying the relevant length and time scales. To quantify the degree of patchiness in the spatial distribution of swimming cells we calculate the patchiness factor $Q$, which is a normalized local density based on the Voronoi tessellation of the 3D domain (16) (more details in Materials and Methods). Fig. 1A shows the nonequilibrium phase diagram obtained from our molecular dynamics simulation of swimming cells immersed in a Kraichnan fluid. At fixed Péclet number, as the vortical Stokes number ${\mathcal{S}}_{\omega }$ increases to values larger than unity (indicating a dominant reorientational dynamics of the cells), we find that the patchiness factor $Q$ exhibits a sharp increase. At ${\mathcal{S}}_{\omega }\approx 10$ a well-defined maximum occurs. This maximum is robust upon variation over a wide range of Péclet numbers and upon replacing point-like with extended particles. At large values of ${\mathcal{S}}_{\omega }$ the patchiness always saturates to a finite value.

Fig. 1.

(A) Nonequilibrium phase diagram of point-like swimming cells immersed in a Kraichnan turbulent flow field. As the reorientation of the swim direction due to cell–cell interactions increases its strength with respect to the turbulent vorticity (i.e., increasing vortical Stokes number ${\mathcal{S}}_{\omega }$), small-scale patchiness emerges. We calculate the dependence of the patchiness factor $Q$ on ${\mathcal{S}}_{\omega }$ and the Péclet number $\mathcal{P}$ for $N=\mathrm{27,000}$ cells at a number density $\rho {ϵ}^3=4\times 10^{-3}$. For $\mathcal{P}>1$, motile cells swimming in a turbulent field and interacting with each other exhibit a maximum in the patchiness, as ${\mathcal{S}}_{\omega }$ increases. When we consider the ratio $\zeta$ of characteristic turbulent to active length scales, we observe emergence of strong patchiness at $\zeta \approx 1$. The lines indicate the loci $\mathcal{P}=1$ (dotted) and $\mathcal{P}={\mathcal{S}}_{\omega }$ (solid) which serve as boundaries for the region where emergence of patchiness is expected (main text). (B) The maximum in patchiness does not depend on the microscopic details of the interaction, as the emergence of patchiness is robust upon replacing point-like with extended particles (both cases for $\mathcal{P}\to \infty$); nor does the maximum in patchiness depend on the details of the flow field.

The relevant length scales associated to phytoplankton patchiness warrant the investigation of the impact of the cells’ finite size—an aspect so far largely neglected by models of motile particles. The finite extension of the cells induces correlations in their spatial distribution, and these correlations will affect the characteristics of the patches. To study whether our results are robust upon inclusion of more realistic spatial correlations, we perform simulations of extended particles immersed in a Kraichnan fluid. Fig. 1B (circles) shows that patchiness emerges also for extended cells for ${\mathcal{S}}_{\omega }\gtrsim 10$ and exhibits the same qualitative dependence on ${\mathcal{S}}_{\omega }$ as for point-like cells. Due to the spatial extension of the cells, however, the patchiness factor $Q$ reaches lower values than for point-like cells because the local density cannot grow arbitrarily large.

We can derive some limits on the location of the maximum for patchiness in the following way. First, for the cell–cell interaction to overcome the rotational diffusion, the Péclet number $\mathcal{P}$ must be larger than unity (this condition corresponds to the region above the dotted line in Fig. 1A). Second, to have an effect on the dynamics, the vorticity associated to the turbulent flow should be stronger than the rotational diffusion, which is quantified by the condition ${\mathcal{S}}_{\omega }<\mathcal{P}$ (corresponding to the region above the solid line in Fig. 1A). This characterization of patchiness in terms of time scales can be complemented by considering the relevant length scales. To this end, we define a dimensionless number $\zeta \equiv L_{\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{b}}/L_{\text{int}}$ that compares the length scale associated to the turbulent vortical motion $L_{\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{b}}={\tau }_{\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{b}}{u}_{\mathrm{r}\mathrm{m}\mathrm{s}}$ with the length scale $L_{\text{int}}={\tau }_{\text{int}}{v}_0$ associated to the cell–cell interactions. The region of enhanced patchiness is delimited by the two loci described above and as visible in Fig. 1A. In the current setting, we find that the condition $\zeta \approx 1$ marks the emergence of strong patchiness for our system of motile cells for both point-like particles and extended ones (Fig. 1). This fact points to a general mechanism underpinning the emergence of patchiness. The region where cell–cell interactions considerably change cells’ swim directions has characteristic size $L_{\text{int}}$. When $L_{\text{int}}$ roughly matches the size $L_{\mathrm{t}\mathrm{u}\mathrm{r}\mathrm{b}}$, where turbulent vortical motion acts most strongly, dense patches emerge.

Kinematic simulations provide a synthetic flow field with realistic spatiotemporal correlations. However, they lack a number of hallmark features of real hydrodynamic turbulence such as a self-consistent energy spectrum with realistic large- and small-scale cutoffs and non-Gaussian velocity and vorticity fluctuations. Although the degree of non-Gaussianity is low for the mild turbulence considered here, departures could have a sensitive impact on the clustering behavior. We therefore turn to full DNS calculations (SI Appendix) to further corroborate our findings and compare them with the results of the Kraichnan fluid. Fig. 1B (squares) shows the patchiness factor $Q$ for the same range of ${\mathcal{S}}_{\omega }$ as for the Kraichnan fluid ($\mathcal{P}\to \infty$). The emergence of clusters occurs again for $\zeta \approx 1$. It is remarkable to note that a maximum in $Q$ occurs for intermediate values of ${\mathcal{S}}_{\omega }$ close to the maximum found in the Kraichnan fluid. The fully nonlinear Navier–Stokes flow and the Kraichnan flow therefore generate consistent results.

This coincidence corroborates our argument above about the mechanism of patch formation: The cell–cell interactions lead to a patchy distribution of swimming cells provided that the scales associated to turbulent motion and cell–cell interactions match. The height and precise position of the maximum in $Q$ depend on the details of the fluid flow. We find that both the Taylor-based Reynolds number and the ratio of cell–cell interaction length scale to Kolmogorov length scale influence the height of the maximum in $Q$ (details in SI Appendix).

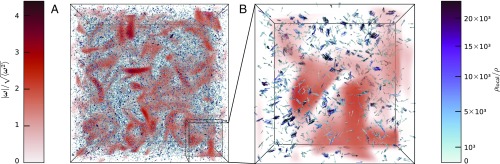
Fig. 2 shows a typical snapshot of the system. The visualization of vorticity fields of the Navier–Stokes flow exhibits the filamentary vortex structures, which are characteristic of turbulent flows. The position and orientation of the phytoplankton cells are indicated with arrows. It appears that the locations of the phytoplankton patches are subtly influenced by the joint effect of active motion and flow vorticity. While there are some events of considerable reorientation of the cells within the vortex cores, in a more typical situation cells are mildly deflected by the local vorticity.

Fig. 2.

(A) Typical steady-state configuration of the motile cells in the Navier–Stokes flow field (at ${\mathcal{S}}_{\omega }=86.52$). Cells are shown as arrows whose color indicates the normalized local density (obtained from a Voronoi tessellation) and whose orientation indicates the local alignment. The background (red) color represents the value of the normalized turbulent vorticity. The elongated, dark red regions correspond to the vortex cores moving through the system. (B) Close-up of the system where the clusters are discernible.

Finally, to bolster our discussion of the influence of the correlation length of the turbulent field compared with the interaction range $ϵ$, we perform simulations of the Kraichnan flow at fixed ${\mathcal{R}}_{\lambda }$ and with varying correlation length scale of the turbulent field. We introduce the correlation length scale of the vorticity

$$L_{\omega }\equiv {\int }_0^{\infty }{f}_{\omega }\left(\lambda \right)\mathrm{d}\lambda ,$$ [1]

where $f_{\omega }\left(\lambda \right)\equiv ⟨{\omega }_x\left(\mathit{r}+\lambda {\mathit{e}}_{\mathrm{x}},t\right){\omega }_x\left(\mathit{r},t\right)⟩/⟨{\omega }_x^2⟩$, ${\omega }_x=\mathit{\omega }\cdot {\mathit{e}}_{\mathrm{x}}$, and ${\mathit{e}}_{\mathrm{x}}$ is one of the unit vectors specifying the Cartesian coordinate axes.

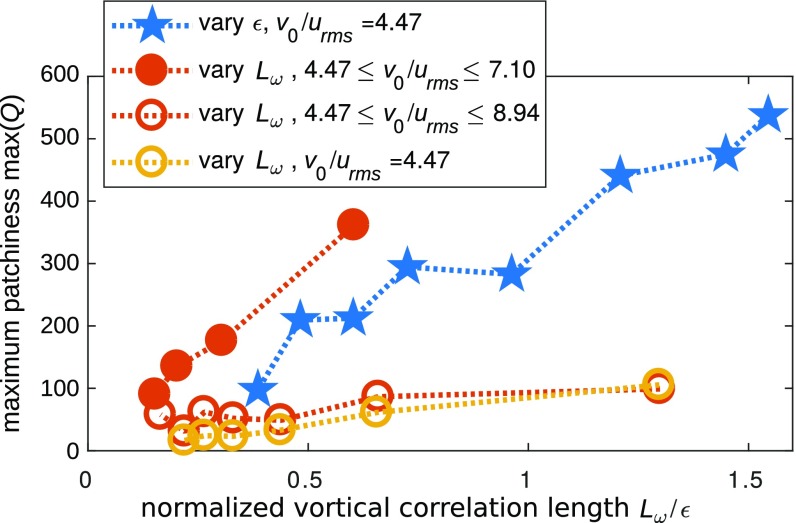
Fig. 3 shows the dependence of the maximum in patchiness factor $Q$ on the ratio of $L_{\omega }$ to the cell–cell interaction length scale $ϵ$ for different cell densities and also physical parameters characterizing the turbulent flow (i.e., the wavenumbers delimiting the inertial regime and turbulent kinetic energies). As $L_{\omega }$ increases, the patchiness in the spatial distribution of motile cells increases monotonically, indicating a stronger influence on the system of the turbulent vorticity that favors cluster formation. This conclusion is robust upon variation of the physical parameters characterizing the system, while the slope of the curve depends on the precise features of the microenvironment.

Fig. 3.

Dependence of the maximum patchiness factor $Q$ on the ratio of correlation length scale of the vorticity and cell–cell interaction range $L_{\omega }/ϵ$. In all these calculations of the Kraichnan flow, we set $k_{max}/k_{min}=63$ and $\mathcal{P}\to \infty$. The patchiness increases as $L_{\omega }/ϵ$ increases. This behavior is robust upon variation of the average filling fraction (solid symbols, $\rho {ϵ}^3=0.41$; open symbols: $\rho {ϵ}^3=0.041$). Furthermore, this conclusion is not altered upon variation of the ratio of length scales—either by changing the cell–cell interaction range $ϵ$ (blue stars) or by changing $L_{\omega }/ϵ$ via a shift of the minimum wavenumber of the turbulent flow (circles). Keeping a fixed (yellow) or variable (red) turbulent kinetic energy also shows the same qualitative result.

Discussion

Noninertial particles in an ergodic incompressible flow can cluster only if they are motile because they can cross the streamlines of the flow. Passively advected particles which initially are homogeneously distributed will be advected following volume-conserving dynamics. We find that small-scale patchiness emerges when hydrodynamic cell–cell interactions couple with the vorticity in a turbulent flow field.

The following physical picture emerges from our results. When the reorientational strength of the cell–cell interaction is stronger than the rotational diffusion of the fluid, the cell–cell interaction leads to (some degree of) alignment of neighboring cells. The turbulent fluctuations may then statistically bring two motile cells closer together. From this point on the cells will experience a similar physical environment and will be very likely to remain at close distance.

When a balance is struck between the length scales where reorientational interactions and turbulence act, marked by $\zeta \approx 1$, patchiness is likely to emerge. Thus, the concerted action of motility, cell–cell interaction, and turbulent microflows approximately produces an absorbing state, that is, a dynamical configuration that remains statistically preserved in time. This is mathematically represented by a negative, average phase-space volume compression factor, $⟨\mathrm{\Gamma }⟩<0$.

The results of Fig. 1, together with Fig. 3, also explain the maximum in clustering observed upon increasing ${\mathcal{S}}_{\omega }$. In the limit of large ${\mathcal{S}}_{\omega }$ and for ${\mathcal{S}}_{\omega }>\mathcal{P}$, the vorticity cannot effectively perturb the orientations, and the spatial distribution of cells remains homogeneous. For very small values of ${\mathcal{S}}_{\omega }$, instead, the turbulent vorticity is much stronger than the cell–cell alignment mechanism, and in this case the turbulent field will decorrelate the orientation of closely neighboring particles and eventually tear them apart. For intermediate values of ${\mathcal{S}}_{\omega }$, the interplay between cell–cell alignment together with the motility of the cells and the effect of the turbulent vorticity leads to patchiness. Larger regions of influence lead to larger amounts of patchiness.

Let us now put our findings in the context of experimental observations. Recent technological advances have expanded the range of length scales we can access and consequently also our view of the problem of plankton patchiness. In situ fluorometry (36, 37), rapid freezing (38, 39), and pneumatically operated sampling (40, 41) allow one to reach submillimeter scales (6) in measurements of planktonic distributions.

Experiments using high-resolution gradient multisamplers can give access to spatial resolutions of the order of decimeters which correspond to the scale of patchiness predicted by our results. Measurements at the pycnocline in the Kattegat found an increase of a factor of 20 with respect to the surface layers and a variation of a factor of 3–5 within 30 cm (7) in Gyrodinium aureolum. Dinobryon species concentrations were observed to vary by up to a factor of 10 in a river estuary within a meter scale (42). Variations in concentration of factors up to 2 or 3 below the meter scale were observed for different species of dinoflagellates in the Aarhus Bay (8). These numbers are in agreement with the predictions of our theory (Fig. 1B).

A combination of traditional turbulence sensors [e.g., shear probes and fast response thermistors (43, 44)] and a backscatter fluorometer measured microstructure in the velocity and in the intensity of chlorophyll concentrations at the centimeter scale (45), so-called biophysical microstructures. As high-frequency acoustic scattering techniques grow in precision (46, 47), additional tools can be deployed to map marine and freshwater environments to increasing accuracy, which may facilitate future experimental confirmations of our findings.

Our results ignore the presence of stratification. While this is an important feature of real-world settings, we do not expect that our conclusions will change qualitatively, as $Q$ will result in a weighted average of the individual strata.

Conclusion

Aiming to identify a minimal model for motile phytoplankton, we investigated the collective behavior of a large number of both point-like and extended, motile cells immersed in a mildly turbulent flow field. We quantify the influence of cell–cell interactions via a dimensionless number, the vortical Stokes number ${\mathcal{S}}_{\omega }$, that measures the ratio of time scales associated to vorticity and cell–cell interaction. Strong patchiness emerges for ${\mathcal{S}}_{\omega }\gtrsim 10$. This points to a balance of time scales underpinning the dynamics of the motile cells.

We explore the microhydrodynamics characterized by a Taylor-based Reynolds number of the order of ${\mathcal{R}}_{\lambda }\approx 20$ which matches the typical conditions found, e.g., in the pycnocline (48). We identify the relevant dimensionless number $\zeta$ which compares the length scales associated to cell–cell interactions and to turbulent dynamics. Patchiness is likely to emerge when $\zeta \approx 1$, indicating the coupling of turbulent structures with the cell–cell spatial correlations. Our results indicate that the coupling of cell–cell interactions with mildly turbulent flows controls the emergence of a patchy spatial distribution of motile phytoplankton.

We confirmed that both models (Kraichnan flow and Navier–Stokes flow) show a near quantitative agreement. We find, however, an influence of the kinematic details, such as the ratio ${\eta }_K/ϵ$, on the magnitude of the maximum patchiness (more details in SI Appendix). This means that the occurrence of small-scale patches strongly depends on the specific turbulent field which acts on the cells.

This finding can complement discussions on the influence of physical forces on marine ecology. Although for smaller phytoplankton species it is conceivable that the local environment is a linear shear field, the microflows change rapidly on the scale of $L_{\omega }$. Our results show that $L_{\omega }$ has considerable impact on the amount of patchiness. Because the correlation length scale of the vorticity may substantially vary in realistic situations, our result can inform future hydrographic and biophysical measurements at small scales.

By addressing the combined effect of turbulent flow and cell–cell interactions, our work paves the way to unravel the complex interplay of physical and biological interactions determining phytoplankton’s microenvironment.

Materials and Methods

Molecular Dynamics Simulations.

Our system is composed of $N$ identical, finite-size particles which are self-propelled and have an up–down symmetric interaction with each other. These self-propelled particles inhabit a cubic box with side length $L$ and periodic boundary conditions. We integrate the equations of motion for particle $i$ at position ${\mathit{r}}_i$ and with orientation ${\mathit{e}}_i$,

$${\dot{\mathit{r}}}_i=v_0{\mathit{e}}_i+\mathit{u}\left({\mathit{r}}_i,t\right)-\frac{1}{{\gamma }_F}\sum _{j=1}^N\frac{\partial U_{\text{WCA}}\left(r_{ij}\right)}{\partial {\mathit{r}}_i}$$ [2a]

$${\dot{\mathit{e}}}_i={\left(-\gamma \frac{\partial U}{\partial {\mathit{e}}_i}+\frac{1}{2}\left(\mathit{\omega }\left({\mathit{r}}_i,t\right)\times {\mathit{e}}_i\right)+{\mathit{\xi }}_i\left(t\right)\right)}_{\perp },$$ [2b]

where the subscript $\perp$ refers to the part of the torque which is perpendicular to ${\mathit{e}}_i$, with ${\mathit{e}}_i^2=1$ at all times. The orientation vector indicates the direction of self-propulsion with speed $v_0$ and can be changed by three different mechanisms: First, each particle interacts with its $n_i$ neighbors within an interaction range $ϵ$, which we take as our unit of length. This interaction is given by the Lebwohl–Lasher potential $U=-\frac{1}{2}{\sum }_i^N{\sum }_{j\in n_i}{\left({\mathit{e}}_i\cdot {\mathit{e}}_j\right)}^2$ (49) together with the relaxation constant $\gamma$. Second, the vorticity $\mathit{\omega }=\nabla \times \mathit{u}$ of the turbulent field changes the particle’s orientation (16); third, a noise ${\mathit{\xi }}_i\left(t\right)$ [uniformly distributed on the surface of a sphere (50)] models rotational diffusion and is delta correlated in time and space: $⟨{\xi }_{i\alpha }\left(t\right){\xi }_{i\beta }\left(t\prime \right)⟩=2D_r\delta \left(t-t\prime \right){\delta }_{\alpha \beta }$. The finite size of the particles is modeled as hard cores through the Weeks–Chandler–Anderson (WCA) potential (51) $U_{\text{WCA}}\left(r_{ij}\right)=4{ϵ}_F\left[{\left(\sigma /r_{ij}\right)}^{12}-{\left(\sigma /r_{ij}\right)}^6\right]+{ϵ}_F$, for $r_{ij}\le \sqrt[6]{2}\sigma$, and 0 otherwise, where $\sigma$ denotes the particle diameter, ${ϵ}_F$ is the strength of the potential, and $r_{ij}\equiv |{\mathit{r}}_i-{\mathit{r}}_j|$.

All simulations are performed in a cubic simulation domain of side length ranging $L=\left(124-374\right)ϵ$. The dimensionless number density is set to $\rho {ϵ}^3=N{\left(ϵ/L\right)}^3=0.0041$, except where stated otherwise (see SI Appendix for discussion on influence of $\rho {ϵ}^3$). The number of particles varies between $\mathrm{8,000}\le N\le \mathrm{216,000}$, depending on the choice of the cell–cell interaction range $ϵ$.

We perform two sets of simulations: In the first one we use ${ϵ}_F=0$, (i.e., point particles). In the second set, the particle diameter is chosen to be half of the cell–cell interaction range ($\sigma =0.0168$) which leads to a packing fraction of $\varphi =N\frac{\pi }{6}{\left(\frac{\sigma }{L}\right)}^3\approx 0.027\%$. For extended particles the relaxation time and the strength of the WCA force are kept fixed (${\gamma }_F=1$, ${ϵ}_F=10^{-3}$). Different values of $\mathcal{P}$ and ${\mathcal{S}}_{\omega }$ are achieved by changing the relaxation constant $\gamma$ and the rotational diffusion constant $D_r$, if not stated otherwise.

Analysis of Patchiness.

To quantify the degree of clustering in a given configuration, we use the patchiness factor defined in ref. 16. To derive this factor, the Voronoi tessellation of a given configuration is calculated, which attaches a volume $v_i$ to every particle. The local (number) density $C$ is then defined as the inverse of this volume. We use the fraction $f$ of the most dense particles to calculate a mean density $C\left(f\right)={⟨v_i⟩}_{i\in f}^{-1}$. This mean density is compared with a random distribution of cells ($C_{\text{random}}\left(f\right)$) and the overall number density $\rho =N/V$ as $Q\left(f\right)={\rho }^{-1}\left[C\left(f\right)-C_{\text{random}}\left(f\right)\right]$. We take the absolute value of $Q$ which differs from $Q$ only for roughly homogeneously distributed particles (small values). All data shown in this paper are calculated with $f=5\%$.