Standardizing CT lung density measure across scanner manufacturers

Abstract

Purpose

Computed Tomography (CT) imaging of the lung, reported in Hounsfield Units (HU), can be parameterized as a quantitative image biomarker for the diagnosis and monitoring of lung density changes due to emphysema, a type of chronic obstructive pulmonary disease (COPD). CT lung density metrics are global measurements based on lung CT number histograms, and are typically a quantity specifying either the percentage of voxels with CT numbers below a threshold, or a single CT number below which a fixed relative lung volume, nth percentile, falls. To reduce variability in the density metrics specified by CT attenuation, the Quantitative Imaging Biomarkers Alliance (QIBA) Lung Density Committee has organized efforts to conduct phantom studies in a variety of scanner models to establish a baseline for assessing the variations in patient studies that can be attributed to scanner calibration and measurement uncertainty.

Methods

Data were obtained from a phantom study on CT scanners from four manufacturers with several protocols at various tube potential voltage (kVp) and exposure settings. Free from biological variation, these phantom studies provide an assessment of the accuracy and precision of the density metrics across platforms solely due to machine calibration and uncertainty of the reference materials. The phantom used in this study has three foam density references in the lung density region, which, after calibration against a suite of Standard Reference Materials (SRM) foams with certified physical density, establishes a HU‐electron density relationship for each machine‐protocol. We devised a 5‐step calibration procedure combined with a simplified physical model that enabled the standardization of the CT numbers reported across a total of 22 scanner‐protocol settings to a single energy (chosen at 80 keV). A standard deviation was calculated for overall CT numbers for each density, as well as by scanner and other variables, as a measure of the variability, before and after the standardization. In addition, a linear mixed‐effects model was used to assess the heterogeneity across scanners, and the 95% confidence interval of the mean CT number was evaluated before and after the standardization.

Results

We show that after applying the standardization procedures to the phantom data, the instrumental reproducibility of the CT density measurement of the reference foams improved by more than 65%, as measured by the standard deviation of the overall mean CT number. Using the lung foam that did not participate in the calibration as a test case, a mixed effects model analysis shows that the 95% confidence intervals are [−862.0 HU, −851.3 HU] before standardization, and [‐859.0 HU, −853.7 HU] after standardization to 80 keV. This is in general agreement with the expected CT number value at 80 keV of −855.9 HU with 95% CI of [−857.4 HU, −854.5 HU] based on the calibration and the uncertainty in the SRM certified density.

Conclusions

This study provides a quantitative assessment of the variations expected in CT lung density measures attributed to non‐biological sources such as scanner calibration and scanner x‐ray spectrum and filtration. By removing scanner‐protocol dependence from the measured CT numbers, higher accuracy and reproducibility of quantitative CT measures were attainable. The standardization procedures developed in study may be explored for possible application in CT lung density clinical data.

1. Introduction

The Quantitative Computed Tomography (QCT) density measures in Hounsfield Units (HU) have been widely studied^{1, 2, 3, 4, 5} as a quantitative image biomarker for the diagnosis and monitoring of lung density changes due to emphysema, a feature of chronic obstructive pulmonary disease (COPD). QCT has growing importance in both phenotyping and early diagnosis of COPD patients, potentially leading to the detection of treatable COPD subgroups, differential treatments for these subgroups, and reduction in morbidity and mortality due to this disease. It has been shown that progression of emphysema can be identified using quantitative imaging CT.^{6, 7, 8} In studies using both QCT and spirometry (PFT), recently published data have shown a discordance between QCT and routine spirometry. Regan et al. demonstrated that lung disease impairments could be found in a group of smokers using both radiological visual and QCT assessment, even though spirometry was normal. The study concluded that chronic obstructive pulmonary disease has a spirometric definition, but more importantly is expressed in a pathologic and structural pattern (emphysema and large and small airway inflammation with thickening). These findings support the notion that detection of emphysema and structural inflammation (airways) necessitates QCT to correctly determine the full extent of COPD, even in those without spirometric impairment.⁹

CT lung density metrics are global measurements based on lung CT number histograms, and are typically a quantity specifying either the percentage of voxels with CT numbers below a threshold, or a single CT number below which a fixed relative lung volume, nth percentile, falls. To reduce variability in the density metrics specified by CT attenuation, measured in Hounsfield Units (HU), one must adjust for the level of inspiration, which is one of the major sources of variation.^{6, 10, 11, 12} The Quantitative Imaging Biomarkers Alliance (QIBA) Lung Density Committee has organized efforts to summarize longitudinal studies in terms of repeatability by performing meta‐analysis of the published data^{13, 14, 15, 16, 17, 18} and the derived repeatability coefficient (RC). The results of the meta‐analysis are summarized in a Profile.¹⁹ In addition to quantifying the effect of volume adjustment on the RC, it is necessary to assess the sources of variation contributing to a given lung density CT measure in a clinical setting. One way to achieve this is by conducting phantom studies in a variety of scanner models to establish a baseline for assessing the variations in patient studies that can be attributed to scanner calibration and measurement uncertainty.

We report the results of standardization analyses of data obtained from scanning the COPDGene 2 phantom (Phantom Labs, Salem, NY, USA) on four CT scanners (one from each of these manufacturers: GE, Philips, Siemens, and Toshiba), with best‐effort matching protocols at various tube potentials and exposure settings (Table 1). Free from biological noise, these phantom studies provide an assessment of the accuracy and precision of the density metrics across platforms solely due to machine calibration and uncertainty of the reference materials. A previous study by Sieren et al.²⁰ reported on the statistical analysis of multisite scans using the original COPDGene phantom which did not contain standardized reference foams. In the Sieren paper, data was gathered using multiple scanner models, sites, phantoms, and contained longitudinal scanning at 1–2 month intervals. These additional variables were listed as random effects. The study found that the differences across all scanners dominated the contribution to the standard deviations, more than the rest of these random effects. These results prompted the development of a new phantom called the COPDGene 2 phantom that incorporated foam density references in the lung density range (identified by Levine et al. in a previous publication²¹) which was used in a new round of scanning focused on scanner variations, reported here. In addition, the absolute density calibrations of these reference foams were carried out using the Standard Reference Material (SRM) foams,^{22, 23} allowing the establishment of a HU‐electron density relationship. Therefore, this study has the benefit of the additional information needed to remove scanner dependence for the CT lung density measures. We show that this new information combined with a simplified physical model enabled the standardization of the HU values reported across scanner‐protocols, reducing the contribution of scanner effects to the total standard deviation.

Table 1.

Summary of vendor scan parameters. All data were reconstructed using FBP algorithm and the most commonly used standard reconstruction kernel innate to each scanner at the time of scanning

Scanner	Recon kernel	Collimation	kVp (kV)	CTDI dose (mGy)			Slice thickness (mm)	Slice spacing (mm)
				1.5	3	6
1	Standard	64 × 0.625	100	x	x	x	1.25	1.0
			120	x	x	x
2	Standard B	64 × 0.75	120		x		1.0	1.0
3	B35f	64 × 0.60	100	x	x	x	1.0	0.5
			120	x	x	x
			140	x	x	x
4	FC17	80 × 0.50	100		x	x	1.0	0.8
			120		x	x
			135		x	x

2. Materials and methods

The COPDGene2 phantom, shown in a CT slice image in Fig. 1, consists of 3 reference foam inserts (labeled as 4 lb, 12 lb, and 20 lb, correspond to nominal densities of 64.2 kg/m³, 192.6 kg/m³, and 321.0 kg/m³, respectively), as well as air and water, embedded in a larger oval shaped lung density equivalent foam and attenuated by a chest wall equivalent ring.²⁴ Five repeat scans were performed for each protocol, and the slice averaged mean HU value was obtained for each region of interest using the Pulmonary Analysis Software Suite (PASS)²⁵ from the University of Iowa. A brief description of its phantom measurement method is given in the Appendix A. The scanning protocols (a total of 22 combinations of scanner‐protocol) are listed in Table 1. The study parameters also include 3 exposure levels: 1.5 mGy, 3 mGy, and 6 mGy, though not all vendors have acquired all 3 levels for all tube potential settings. With the available data, the SD analysis by mGy was performed to assess the variations influenced by the noise level.

Figure 1.

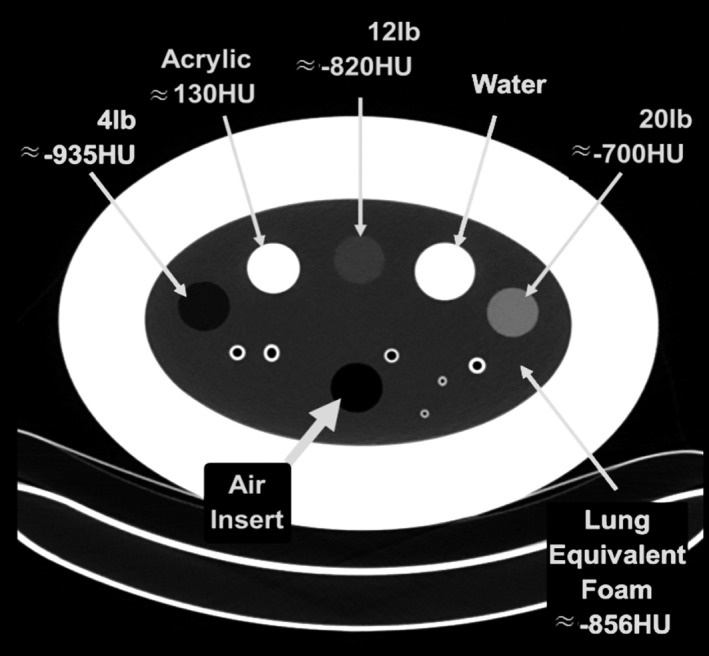
CT slice image of the COPDGene 2 phantom used in this study. The CT numbers labeled are approximate from a typical 120 kV scan.

The preliminary assessment of the current study shows that across scanners, for a subset of the data shown in Table 2 (120 kV with an exposure of 3 mGy), the spread of the HU values as estimated by the standard deviation (SD) of the distribution, is from 1.5 HU to 3 HU depending on the density, with the maximum variations about 3 times greater than the standard deviations (SD). A more complete assessment of the data using the methods described here is used to determine the extent of the differences in scanner beam characteristics and calibrations have on the variations. A standardization scheme has been devised to eliminate scanner dependent parameters such that the comparison can be made based on the phantom's material properties.

Table 2.

Raw CT numbers obtained from all 22 scanner/protocols for the 3 reference foams, air, water, and the lung foam (backing foam), along with the kVp and dose settings. A shifted CT number $H_{raw}$ = (raw CT number)/1000 + 1 is used for subsequent analysis

Scanner	Foam 1	Foam 2	Foam 3	Air	Water	Lung	kVp (kV)	Dose (mGy)
1	−940.53	−823.05	−698.58	−1001.40	1.91	−855.72	100	1.5
	−940.27	−822.26	−697.56	−1001.53	0.84	−855.69	120	1.5
	−940.16	−822.86	−698.28	−1001.61	2.12	−855.14	100	3.0
	−939.83	−822.42	−697.09	−1001.85	1.30	−855.29	120	3.0
	−940.11	−823.04	−698.18	−1001.96	2.55	−855.06	100	6.0
	−940.14	−822.32	−697.23	−1002.13	1.48	−855.24	120	6.0
2	−942.65	−822.21	−698.42	−1002.70	3.88	−859.86	120	3.0
3	−936.48	−820.92	−696.00	−995.38	−0.91	−852.24	100	1.5
	−935.52	−819.08	−695.17	−994.04	−1.14	−851.71	120	1.5
	−935.28	−818.18	−694.68	−993.92	−0.76	−851.70	140	1.5
	−936.78	−820.97	−695.85	−997.35	−1.15	−852.43	100	3.0
	−936.02	−819.73	−695.00	−997.21	−1.29	−852.37	120	3.0
	−935.77	−818.97	−694.45	−996.54	−0.92	−852.01	140	3.0
	−936.50	−820.76	−695.67	−998.37	−1.07	−852.34	100	6.0
	−935.94	−819.40	−694.74	−997.79	−1.45	−852.25	120	6.0
	−935.40	−818.64	−694.29	−997.19	−1.11	−851.90	140	6.0
4	−940.65	−826.08	−699.66	−1002.31	0.44	−858.55	100	3.0
	−940.37	−824.64	−699.18	−1002.44	0.16	−858.03	120	3.0
	−940.38	−823.94	−698.84	−1002.22	−0.08	−857.73	135	3.0
	−940.59	−825.90	−699.83	−1002.23	0.25	−858.28	100	6.0
	−940.55	−824.57	−699.37	−1002.36	0.01	−857.88	120	6.0
	−940.35	−823.86	−699.04	−1002.28	−0.22	−857.55	135	6.0

Raw CT number (HU) reported for each scanner‐protocol.

An initial effort was made using a linear model to fit the HU values vs. the nominal density of the reference foams, and forcing the ratio of the fitted slope to a common value of 0.95 (which is the approximate value of the relative electron density of the reference polyurethane foam with an assumed composition). This simple approach was able to bring the SDs down to sub‐HU levels, but is not suitable for the water value; in fact the model amplifies the deviation of CT number of water. Another model was then attempted to include not only the 3 reference foams but also air and water values which were fitted to a quadratic model. This also gave satisfactory SDs for the foams, as well as for air and water (see Supplementary Material). While the results are acceptable for achieving consistency across vendors, an empirical model does not offer much insight into understanding the nature of the discrepancies. Therefore, these earlier efforts were abandoned in favor of physical models based on electron density ρ _e and effective atomic number Z _eff, or their respective ratio to water, ρ _e* and Z _eff*.

The CT number in Hounsfield Unit is defined as the ratio of the linear attenuation coefficient $\mathit{\mu }$ of a material to that of water:

$$CTnumber=\frac{\mathit{\mu }-{\mathit{\mu }}_w}{{\mathit{\mu }}_w}1000$$ (1)

which is energy dependent. The classic treatment of the CT number is Schneider's²⁶ 2‐parameter formula separating the incoherent, coherent and photoelectric processes that contribute to the attenuation following empirically determined energy dependence for each process. Martinez²⁷ simplified Schneider's treatment by combining the terms into a single machine dependent parameter α, and rewrite (1) into

$$H(E)/{\mathit{\rho }}_e\ast =\mathit{\alpha }(E)(1-{Z_{eff}}^{\ast n})+{Z_{eff}}^{\ast n},$$ (2)

where H(E) is the rescaled and shifted CT number at a given energy E, H = CT number/1000 + 1, and n has been determined to be 3.21 for elements up to calcium. The CT number can be calculated for a given energy by definition (1), using the linear attenuation coefficients calculated from the mass attenuation coefficients as a function of energy tabulated. The CT number can also be calculated for a given x‐ray spectrum using (2), where ρ_e*, the relative electron density, and Z_eff*, the relative effective atomic number, can be calculated based on mixture sum rules.²⁸ The * denotes ratio to water, and ${\mathit{\rho }}_e={\mathit{\rho }}_m{\sum }_i{w}_i\frac{Z_i}{A_i}$, where ${\mathit{\rho }}_m$ is the mass density, and w _i , Z _i , and A _i are mass fraction, atomic number, and atomic mass, respectively, for each element i in the composite material. Similarly, $Z_{eff}={[{\sum }_i{w}_i\frac{Z_i}{A_i}{Z}_i^n/{\sum }_i{w}_i\frac{Z_i}{A_i}]}^{1/n}$. The machine dependent parameter α(Ε) in equation (2) is assumed to follow a universal curve of

$$\mathit{\alpha }(E)=\frac{1}{1+A{E}^{-p}}$$ (3)

with A = 12179 and p = 2.8, for most substances in the low Z region.²⁷ In practice, this parameter is determined by calibration of a known material for a given spectrum with an average energy Ē, depending on the tube potential setting, kVp. This method is known as the single parameter calibration process of the CT machine, which avoids the need to use a look up table. For this work, α(Ē) was obtained by a linear least square fit of the measured H values of the 5 data points: air, 3 reference foams, and water, where the reference foams were calibrated against a suite of 5‐density foams certified as a Standard Reference Material (SRM) for physical density (see Appendices B and C for more information) and are assumed to have known composition. Applying equation (2) to the measured CT number (scaled) H in a spectrum with an average energy Ē, and rearranging (2) into $H-{\mathit{\rho }}_e^{\ast }{Z}_{eff}^{\ast n}=\mathit{\alpha }{\mathit{\rho }}_e^{\ast }\left(1-Z_{eff}^{\ast n}\right),$ a linear least square fit of $H-{\mathit{\rho }}_e^{\ast }{Z}_{eff}^{\ast n}$ vs ${\mathit{\rho }}_e^{\ast }\left(1-Z_{eff}^{\ast n}\right)$ is used to determine α(Ē) for each protocol. This was carried out for all 22 scanner‐protocol combinations. The residuals of the fit become the error of recovering ρ _e* from the measured H. A scanner‐independent ρ _e,m* value is obtained by the following:

$${\mathit{\rho }}_{e,m}^{\ast }=\frac{H_{recal}}{\mathit{\alpha }(\overline{E})(1-Z_{eff}^{\ast n})+Z_{eff}^{\ast n}},$$ (4)

where the subscript m stands for “measured”, $H_{recal}$ is the scaled measured CT number after internal air‐water correction (Appendix D). Assuming the same composition for these reference foams at all densities, i.e., a constant $Z_{eff}^{\ast n}$, ρ _e,m* is then related to the measured CT number linearly with a slope of $1/[\mathit{\alpha }(\overline{E})(1-Z_{eff}^{\ast n})+Z_{eff}^{\ast n}]$ The quantity of ρ_e,m* thus determined can now be used to assess CT number variations for these foams in the lung density region across all 22 vendor‐protocols.

With the protocol dependence removed, the measured electron density can be mapped to a CT number at a monochromatic x‐ray energy in order to assess the variation in HU, a more conventional unit. This is set to E = 80 keV because it is representative of the reported HU values for all the data in this study. $\mathit{\alpha }(80keV)$ is obtained from the universal curve shown in eq. (3).

$$H_{80keV}={\mathit{\rho }}_{e,m}^{\ast }[\mathit{\alpha }(80keV)(1-Z_{eff}^{\ast n})+Z_{eff}^{\ast n}],$$ (5)

with $CTnumbe{r}_{80keV}\text{(HU)}=(H_{80keV}-1)1000$. The SD of H _80keV is an assessment of the variation expected in the normal measurement range. 80 keV is chosen because the CT numbers calculated at this value roughly correspond to the range of CT numbers observed. It is a little high compared to the average energy of a typical 120 kVp CT spectrum in air. However, since we are measuring the objects inside the simulated chest ring which tends to cause spectral hardening, the 80 keV value is not unreasonable. For this study, the choice of the energy value does not really matter; the standardization simply requires that all CT numbers are mapped to a common energy. Terms such as “virtual monochromatic images” were used in the literature often in the context of dual‐energy CT, which is analogous to our “80 keV calibration” here.

In summary, the calibration steps being implemented are as follows:

1. Scale reported CT number (Eq. 1), denoted H _raw

2. Perform internal air and water calibration (Appendix D) to obtain H _recal

3. Linear regression of $H_{recal}-{\mathit{\rho }}_e^{\ast }{Z}_{eff}^{\ast n}$ vs ${\mathit{\rho }}_e^{\ast }\left(1-Z_{eff}^{\ast n}\right)$ (Eq. 2) to obtain $\mathit{\alpha }(\overline{E})$

4. Obtain a “measured” relative electron density ${\mathit{\rho }}_{e,m}^{\ast }$ based on $\mathit{\alpha }(\overline{E})$ (Eq. 4)

5. Map ${\mathit{\rho }}_{e,m}^{\ast }$ to a monochromatic energy 80 keV, H _{80 keV} . (Eq. 5)

3. Results and discussion

The raw CT numbers obtained from all 22 scanner/protocols for the 3 reference foams, air, water, and the lung foam (backing foam) are listed in Table 2, along with the corresponding kVp and dose settings. Following steps 2 and 3, a scanner calibration parameter is obtained for each protocol, listed in Table 3, along with the relative electron density ${\mathit{\rho }}_{e,m}^{\ast }$ obtained from step 4. The CT number scaled from H _80keV following step 5 are listed in Table 4. By carrying out the above 5‐step process, the SD of H _80keV is reduced to about 1/3 of the SD of $H_{raw}$ (Table 5).

Table 3.

Calibration parameter determined from linear regression fit of the measured CT number, and the relative electron density for each foam recovered from the calibration. The estimated standard error of α from the fit is 0.4%

Scanner	α(Ē)	Relative electron density ${\mathit{\rho }}_{e,m}^{\ast }$				kVp (kV)	Dose (mGy)
		Foam 1	Foam 2	Foam 3	Lung foam
1	0.9424	0.0619	0.1815	0.3081	0.1482	100	1.5
	0.9567	0.0621	0.1817	0.3080	0.1478	120	1.5
	0.9469	0.0624	0.1815	0.3080	0.1487	100	3
	0.9613	0.0627	0.1814	0.3080	0.1481	120	3
	0.9488	0.0627	0.1814	0.3080	0.1490	100	6
	0.9624	0.0626	0.1816	0.3079	0.1483	120	6
2	0.9501	0.0607	0.1826	0.3077	0.1445	120	3
3	0.9271	0.0608	0.1802	0.3091	0.1478	100	1.5
	0.9296	0.0605	0.1808	0.3088	0.1471	120	1.5
	0.9345	0.0605	0.1812	0.3086	0.1467	140	1.5
	0.9458	0.0620	0.1806	0.3087	0.1483	100	3
	0.9563	0.0624	0.1810	0.3083	0.1477	120	3
	0.9561	0.0620	0.1812	0.3083	0.1475	140	3
	0.9569	0.0630	0.1809	0.3083	0.1487	100	6
	0.9649	0.0629	0.1813	0.3080	0.1479	120	6
	0.9652	0.0628	0.1815	0.3079	0.1477	140	6
4	0.9358	0.0629	0.1799	0.3089	0.1467	100	3
	0.9468	0.0631	0.1808	0.3083	0.1468	120	3
	0.9504	0.0628	0.1811	0.3082	0.1468	135	3
	0.9353	0.0629	0.1800	0.3088	0.1470	100	6
	0.9453	0.0629	0.1809	0.3083	0.1470	120	6
	0.9504	0.0629	0.1813	0.3081	0.1470	135	6
Ref. value		0.0623	0.1812	0.3082	0.14686

Table 4.

CT numbers calibrated and mapped to 80 keV from all vendor‐protocols

Scanner	Foam 1	Foam 2	Foam 3	Air	Water	Lung	kVp (kV)	Dose (mGy)
1	−939.26	−822.01	−697.80	−1000.00	0.00	−854.62	100	1.5
	−939.12	−821.85	−697.93	−1000.00	0.00	−855.07	120	1.5
	−938.80	−821.99	−697.91	−1000.00	0.00	−854.13	100	3.0
	−938.51	−822.13	−697.89	−1000.00	0.00	−854.70	120	3.0
	−938.49	−822.08	−697.92	−1000.00	0.00	−853.91	100	6.0
	−938.60	−821.90	−698.01	−1000.00	0.00	−854.51	120	6.0
2	−940.44	−820.96	−698.19	−1000.00	0.00	−858.33	120	3.0
3	−940.34	−823.32	−696.82	−1000.00	0.00	−855.05	100	1.5
	−940.68	−822.69	−697.12	−1000.00	0.00	−855.76	120	1.5
	−940.68	−822.27	−697.37	−1000.00	0.00	−856.16	140	1.5
	−939.19	−822.91	−697.29	−1000.00	0.00	−854.51	100	3.0
	−938.78	−822.44	−697.65	−1000.00	0.00	−855.10	120	3.0
	−939.18	−822.29	−697.66	−1000.00	0.00	−855.36	140	3.0
	−938.21	−822.61	−697.67	−1000.00	0.00	−854.15	100	6.0
	−938.35	−822.17	−697.90	−1000.00	0.00	−854.92	120	6.0
	−938.39	−821.98	−698.00	−1000.00	0.00	−855.14	140	6.0
4	−938.28	−823.61	−697.06	−1000.00	0.00	−856.11	100	3.0
	−938.11	−822.72	−697.62	−1000.00	0.00	−856.01	120	3.0
	−938.40	−822.39	−697.76	−1000.00	0.00	−856.06	135	3.0
	−938.27	−823.42	−697.18	−1000.00	0.00	−855.85	100	6.0
	−938.32	−822.59	−697.65	−1000.00	0.00	−855.83	120	6.0
	−938.30	−822.23	−697.87	−1000.00	0.00	−855.80	135	6.0

CT numbers_80keV = (H _{80 kev} − 1) × 1000.

CT number (HU) mapped to 80 keV for each scanner‐protocol.

Table 5.

Mean and standard deviations of the CT numbers from the 22 protocols before and after calibration to 80 keV, showing a reduction in the SD that is a representation of the scanner/protocol variation, for the reference foams and the backing lung foam in the COPDGene 2 phantom

	Foam 1		Foam 2		Foam 3		Lung foam
	Raw	80 keV	Raw	80 keV	Raw	80 keV	Raw	80 keV
Mean CT number (HU)	−938.6	−938.9	−822.0	−822.4	−697.1	−697.6	−855.0	−855.3
SD (HU)	2.4	0.8	2.3	0.6	1.9	0.4	2.7	1.0

The CT number values for each of the 3 steps, converted from H _raw to H _recal and H _80keV are illustrated in Fig. 2, using the middle density foam as an example, to show the reduction in the variation in the HU values at each step. The upper panel is a so‐called “interaction plot” that traces the CT number from each protocol through the calibration steps, showing the overall convergence. The lower panel is a “box plot” visualizing the distribution of the CT numbers at each stage for all protocols, again showing the reduction in the standard deviation, as tabulated at the bottom of the figure.

Figure 2.

Results after executing procedures used to eliminate machine dependent variations for the 22 vendor‐protocols for the middle density foam (nominal density 192.6 kg/m³). Upper panel: trace plot for each of the 22 vendor‐protocols at each of the calibration steps. Lower panel: boxplot representation for each vendor‐protocol. The box represents the first and third quartile of the distribution, and the horizontal bar in the middle of the box is the median value. The upper and lower whiskers are the maximum and minimum values excluding outliers. The data points outside of the whiskers are considered outliers. The reference value (solid line) at 80 keV is calculated based on the SRM foam density and assumed composition, and the mean value (dashed line) is the unweighted mean of the HU value at 80 keV for the entire group. The maximum variation and standard deviation in HU at each step are also listed. All the data analysis and graphics were performed with R (http://www.R-project.org).

The calibration obtained by using the 3 reference foams plus air and water has also enabled the determination of the density of the lung foam (the pink colored foam backing in the COPDGene 2 phantom) to be 153.7 kg/m³ ± 5.1 kg/m³ (uncertainty calculated based on the estimated uncertainty due to the foam composition and the effect on the calibration parameter α). The density derived from the 22‐protocol average of the measured ρ_e,m* is 153.3 kg/m³ ± 2.8 kg/m³. These values are somewhat higher than a previous laboratory test measurement of small samples of the same type foam, determined to be 148.6 kg/m³ ± 1.0 kg/m³. Further investigation is needed, since the composition and density of backing foam has not been directly characterized. Nevertheless, this has served as an assessment of the CT number variation and accuracy in this group of scanner/protocols, and of the adequacy of the physical model and the methods described for an “unknown” foam that was not part of the calibration. Fig. 3 is a boxplot of the distribution for each density, including the lung foam, at H_80keV, showing the variations by scanner, which helps visualizing how within‐scanner variations compared with between‐scanner variation. Scanner 2 had only a single data point (per density), and therefore provides no information on within‐scanner variation.

Figure 3.

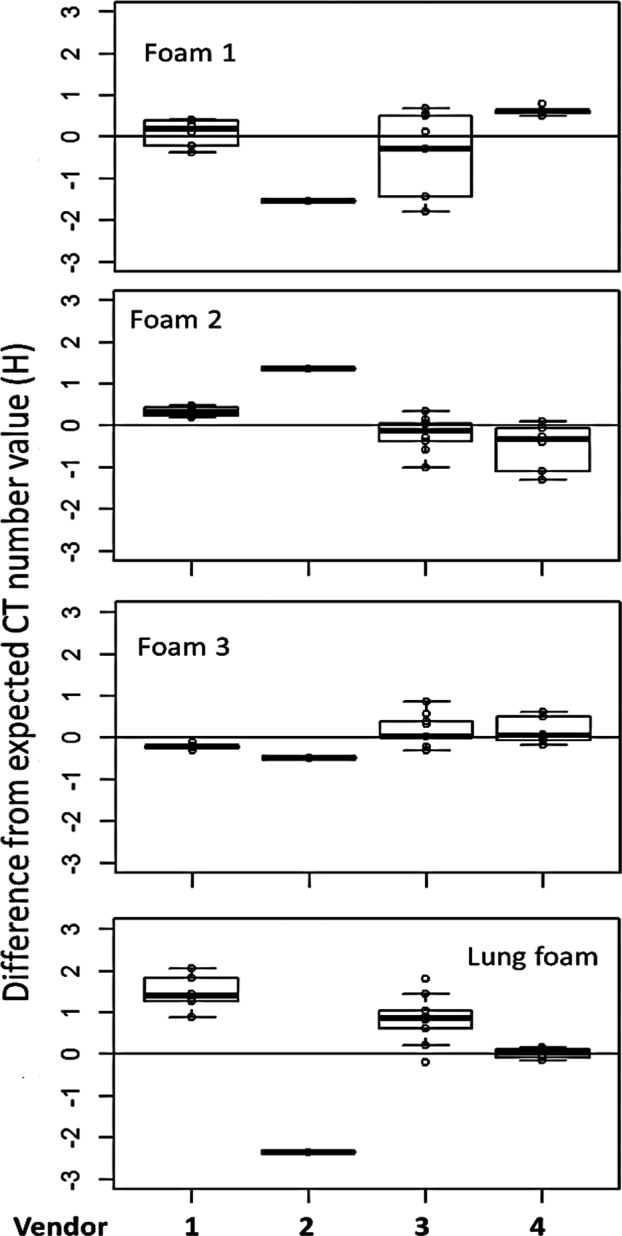
Boxplot showing distribution of the HU value after scanner recalibration of all kVp and mGy settings, mapped to a single energy of 80 keV, plotted by vendor. Foams 1 to 3 are the reference foams, and the lung foam is the foam backing that fills the entire phantom. The lung foam did not participate in the calibration fit, and therefore serves as a test case to assess the variation.

To assess the influence of noise, the data were analyzed by mGy settings and the results are shown in Fig. 4. There are 5, 9, and 8 data points for 1.5 mGy, 3 mGy, and 6 mGy respectively. It is shown that 6 mGy has smallest SD for foams 1, 2, and 3, and for foams 1 and 3 the SD appears to be inversely proportional to the dose as expected due to Poisson counting statistics. However, there is no clear difference for the rest of the densities between 1.5 mGy and 3 mGy. These results may add some insights into the value of low dose scanning in clinical settings. The exceedingly large SD for the lung foam at 3 mGy is due to a single scanner (see Fig. 3 panel 4).

Figure 4.

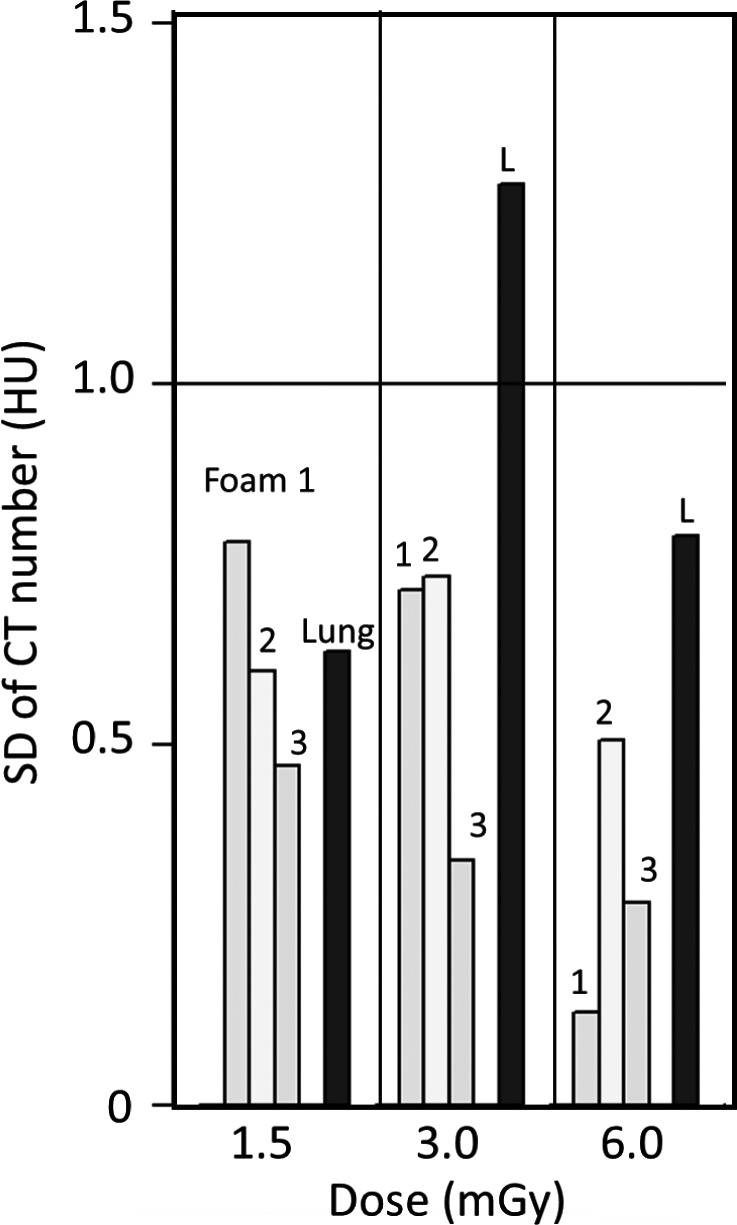
CT number variation by dose levels for each foam, labeled as Foam 1, 2, 3, and Lung (L), for calibrated CT number at 80 keV. The number of data points for each of the dose levels (1.5 mGy, 3 mGy, and 6 mGy) is 5, 9, and 8 respectively. The expected reduction in the SD due to increased dose rate is observed for foams 1 and 3. With the exception of the lung foam at 3 mGy, all the SD's are below 1 HU. The high value for the lung foam at 3 mGy is mostly due to a single scanner, as indicated in the 4th panel of Fig. 3.

The results of mapping all values to 80 keV are shown in Table 4, corresponding to the raw data from Table 1. The CT number values by density from Tables 1 and 4 are summarized as histograms in Fig. 5, showing a more centralized distribution for all 4 densities after the recalibration.

Figure 5.

Histograms showing the relative distributions of the HU values for all scanner‐protocols as measured (light) and corrected to 80 keV (dark) for each of the 4 densities. The more unimodal distribution for all densities illustrates the level of standardization achieved.

Figure 6 shows forest plots summarizing the results of statistical analyses of the data before and after standardization, considering the effects of vendor, tube potential (kVp), and dose (mGy), for the backing lung foam in the phantom (which served as an “unknown”). The statistical analyses are based on fitting mixed effects models²⁹ to the two datasets, using facilities in R package lme4.³⁰ The forest plots show how the standardization procedure greatly reduces uncertainty while hardly changing the estimate of the overall mean, and produces a consensus value (estimate of the overall mean) that agrees well with the expected CT number of −855.9 HU for this foam at 80 keV. The same analysis has been performed for all densities to confirm the reduction in variability across all densities.

Figure 6.

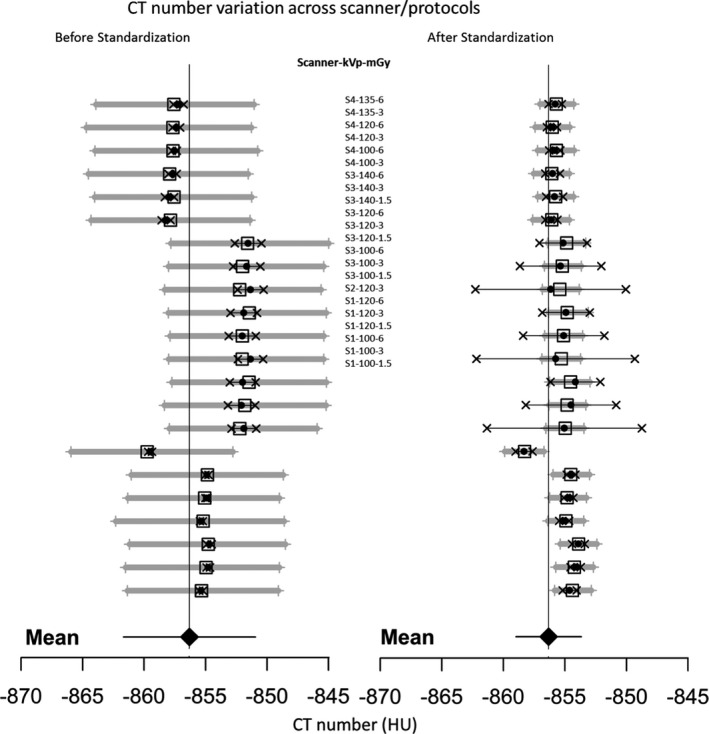
Forest Plots: Left panel – CT number as measured (scaled H _raw ); right panel – CT number after the recalibration standardization procedures (scaled H _80keV ), for the backing lung foam in the phantom (which served as an “unknown”), showing the reduction in variability and improved accuracy. The solid black dots and horizontal thin black line segments with an “x” symbol on both ends represent the measured values and their associated expanded uncertainties (95% confidence). The open squares and horizontal thick gray line segments with a “+” symbol on both ends represent the corresponding values predicted by the fitted models and their associated expanded uncertainties (95% confidence). The large solid diamond at the bottom and the vertical, thin solid line indicate the overall mean (consensus value) determined by a mixed effects model, in both cases fitted to the data taking the effects of scanner, kVp and mGy into account. In this mixed effects model, the overall mean and dose (mGy) are the fixed effects, and scanner and kVp (which is nested within scanner) are the random effects. The expected CT number value at 80 keV is −855.9 HU with 95% CI of [−857.4 HU, −854.5 HU] (based on the propagation of uncertainty in the SRM certified density). This is in general agreement with the information conveyed by the 95% confidence intervals of [−862.0 HU, −851.3 HU] (before standardization) and [−859.0 HU, −853.7 HU] (after standardization), shown as the error bars for the overall mean at the bottom.

The heterogeneity across vendor platforms for each density was assessed by examining the estimate of the standard deviation of the corresponding variance component (which was estimated as a by‐product of fitting the mixed effects models to the data): this heterogeneity was reduced by 50% after calibration, and the residual standard deviation was reduced almost 5‐fold. The standard uncertainty (1 standard deviation, SD) associated with the mean HU value was also reduced by about 50%. The 95% confidence intervals (CI) of the final CT number was within ± 1 HU for all 3 reference foam densities and for the backing lung foam in the phantom. The tube potential (kVp) and dose (mGy) settings did not appear to make significant contributions to the observed variability, with the exception for the foam with the lowest density for which the SD does have a clear quadratic dependence.

With the proposed calibration procedures, the inter‐scanner reproducibility of better than 1 HU is demonstrated in the current phantom study for the reference foam densities, but not yet achieved for a test density. One possible reason could be that the absolute calibration (SRM‐in‐ring scan) was performed retrospectively on one machine only (scanner 4) which was transferred to the COPDGene 2 phantom scanned at the same time. This may have introduced machine‐dependent errors that are not accounted for. Given the inherent uncertainties in the SRM density certification, it is advisable to perform the same scan in future studies with the COPDGene 2 Phantom to evaluate validity of the calibration method. This in fact has been put in practice in the next round of scanning with a certified Standard Reference Material for direct calibration.

The study here employs a phantom with foams in the lung density region, for which the effective atomic number and electron densities are determined based on the best knowledge composition and calibrated physical density. The uncertainties in these properties will affect the value of α. To assess the validity of applying this phantom calibration to tissues in a greater range of combinations of electron density and effective atomic number, a calculation was performed using the tissue composition from ICRP (1975) quoted by the Martinez paper. The estimated change in the calculated CT number in HU per 1% change in the machine calibration parameter α is shown in Fig. 7. According to this model, for certain tissues (and the foams in the current study) the change is in the sub‐HU range, whereas for other tissues the changes can be an order of magnitude greater. Therefore, this method may not be valid for use in calibration for certain tissues, but it is valid for the lung density work, which is the main goal of this study.

Figure 7.

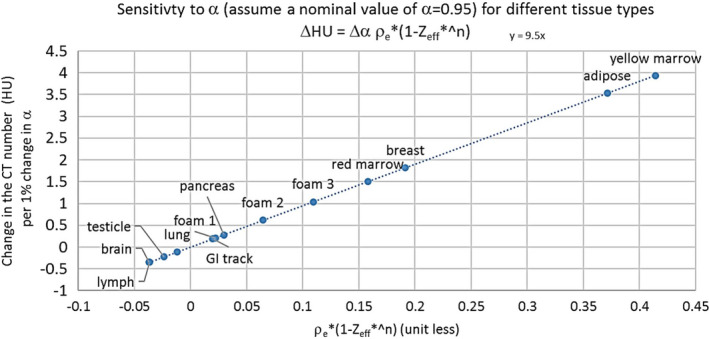
Expected change in CT number for different kinds of tissue due to a 1% change in the calibration parameter α, calculated based on the ICRP (1972) tissue compositions, to illustrate how the calibration error affects the CT number variation, the degree of whcih depending on the electron density and effective atomic number of the particular tissue.

Finally, this study is focused on a single phantom with a fixed wall thickness (a simulated chest ring of 5‐cm thick), and therefore the air‐water correction is valid for the measurement objects inside the phantom with this particular attenuation. In a clinical setting where patient size is of concern, the absolute calibration of the foam density will likely change and therefore affects the accuracy of the density assessment. In fact, the air value as a function of chest ring thickness has been studied and shown systematic variations.¹ However, the primary concern of this study is to assess CT scanner variations as a baseline expectation for patient studies. The variations were shown to be greatly reduced for all densities in the phantom after applying a physical model to remove scanner dependence.

4. Conclusion

The data from a round of multi‐vendor CT scans using the COPDGene2 phantom were analyzed in an effort to standardize the CT lung density measurements. A simplified theoretical model using a single parameter to describe the scanner dependent contribution to the HU value was used to arrive at a common calibration for all scanners at a single energy, chosen to be 80 keV. The CT number values mapped to this common calibration are in agreement with a standard deviation less than 1 HU for all 22 scanner‐protocol settings. This result provides a quantitative assessment of the variations expected in CT lung density measures attributed to non‐biological sources such as scanner calibration and scanner x‐ray spectrum and filtration. This result can be used to set expectations for patient studies conducted across vendor platform and protocols.

Defined CT protocol adherence is an essential aspect for accuracy and reliability of quantitative CT measures. Newell et al. outlined the importance of aligning specific CT vendor parameters with emphasis on proper CT acquisition techniques to reduce amount of HU variability within COPD assessment.³¹ The work of this manuscript builds upon those recommendations and proposes a simplified physical model for standardization, to further reduce the HU variation across multi‐vendor CT scanners. Based on this work, we recommend using a standardized lung density phantom similar to the one used in this study, preferably equipped with reference foams at 3 or more well‐calibrated physical densities in the lung density region, and with some knowledge of the foam composition to carry out the calibration procedures outlined in this study. The scanning protocols can vary, but after removing the scanner dependence from the measured CT numbers, a monochromatic CT number should fall into the 95% confidence interval summarized in Fig. 6.

Conflict of interest

H. Chen‐Mayer and A. Possolo are federal employees and have no conflict of interest to disclose. S. Fain has research funding from GE Healthcare to develop pulmonary MRI techniques. B. Hoppel is an employee of Toshiba Medical Research Institute USA and has financial interest with GE Healthcare. M. Fuld is an employee of Siemens Healthcare for medical device equipment and software. J. Sieren is an employee and shareholder of VIDA Diagnostics Inc., a medical software company. J. Guo is a shareholder in VIDA Diagnostics.

Disclaimer

Any mention of commercial products within this paper is for information only; it does not imply recommendation or endorsement by NIST.

Supporting information

Fig. S1. CT number variation determined by empirical linear or quadratic fit of CT numbers vs nominal physical density of the reference foams, along with air and water.

Appendix A. CT data segmentation algorithm

A.1.

The CT number HU values of some of the three reference foam inserts are very close to the surrounding lung density equivalent foam, making it a challenge task to separate them out, especially when the noise level is high. To achieve this goal, the key regions whose density values were distinguishable from the surrounding lung foam (air hole, water bottle, and acrylic rod) were first segmented using a thresholding method followed by a connected component analysis method. The segmented depth (z‐axis) was 20 mm and located in the center of the phantom. The orientation of the phantom was then accurately located from the central line direction of these key objects and their relative positions. In the end, with the known nominal position and the calculated phantom orientation, the locations of the three foam inserts were determined. The segmented regions were further eroded by 4 pixels from the edge in the x‐y plane to eliminate the partial volume effect near the boundaries before the mean HU and standard deviations were evaluated for each eroded region of interest.

Appendix B. Absolute density calibration using standard reference material (SRM) foams

B.1.

The reference foams inside the COPDGene 2 phantom were originally uncalibrated. Using the manufacturer specified nominal densities, the calibration procedures described in section Methods could still be used to reduce the inter‐scanner variations. However, there is no way of knowing what the correct value should be with these reference foams. This was addressed with the NIST SRM foam suite²² with 5 densities in the range of 65 kg/m³ to 320 kg/m³ (within the range of the 4 lb to 20 lb foams). The SRM foams are certified for physical densities. The composition was nominally polyurethane but uncertain. Best effort was made to determine a composition based on elemental mass ratios of H, C, and N using Prompt Gamma Activation Analysis (Appendix C). Based on this information, the electron density per unit mass relative to water is calculated to be 0.956, and the effective atomic number relative to water is calculated to be 0.871. These values are used in the standardization procedures, and can carry systematic uncertainties (due to the uncertainty assigned to the density values of the SRM) that are estimated to be less than 1%, in addition to the uncertainties from the composition analysis (see Appendix C). By applying the same procedures as mentioned above, a calibration of H vs ρ_e* is obtained and the density values are assigned to the 3 foams in the phantom. These measured density values are +1.7%, −1.2%, and +0.4%, respectively, from their nominal values. These deviations are in such a way that they compensate to make the slope of the fit deviate only negligibly from when the known density is used. Therefore, calibration using the nominal values is very close to the calibration using better information, with the mean value reflecting the true density, even though the nominal density was wrong. However, only when the true density is used can one assess the deviation from the truth, otherwise one can only assess the deviation from the mean, which will change with a different collection of scanner/protocols.

Appendix C. Composition of the SRM foams

C.1.

Composition analysis of the SRM foams using prompt gamma neutron activation analysis (PGAA) was carried by Rick Paul² at the NIST Center for Neutron Research.³² Samples of 5 densities of the polyurethane foams were irradiated by cold neutron beams, producing capture gamma rays characteristic of the main elements of interest. By referencing to standards, molar ratios of H/C and N/C could be determined for these samples. It was determined that the average ratio of H/C and N/C are 1.16 (0.06) and 0.080 (0.004) respectively. Since the composition of the polyurethane foams are not well known, we have compiled 10 possible compositions based on web search, and compared the H/C ratios of each to the measured ratio (Fig. 8). This narrowed down the list to 5 possible choices whose ratio is within 2 standard deviations (dash lines) of the PGAA determined ratio. Of those 5, C₂₅H₃₀N₂O₈ has the N/C ratio of 0.08, closest to the PGAA determined ratio. Therefore, it is assumed to be the composition of these reference foams. However, all 5 compositions were entered into the calculation to assess the effect on the calibration parameter α, which causes variations with a standard deviation of 3%. In addition, because the foam has closed cells, and the density variation is assumed to be achieved by varying mixture of air and foam materials. By neglecting the air inside, the estimated error introduced is about 1.5%.

Figure 8.

Stoichiometric H/C ratio of various possible polyurethane compositions. Dash lines are the upper and lower bound of the 95% confidence interval of the mean value as determined by PGAA measurement. Those compositions that fall within this interval are considered as possibilities, and are used to assess the error associated with the composition.

Appendix D. Internal calibration using air and water values

D.1.

Since the air and water values are measured internally to the phantom, they are unlikely to agree with the scanner's calibration. The following steps are implemented for an internal calibration for each protocol:

$$\mathrm{\Delta }=({\mathit{\delta }}_w-{\mathit{\delta }}_a){\mathit{\rho }}_e\ast +{\mathit{\delta }}_a,$$ (D1)

$$H_{recal}=H_{raw}-\mathrm{\Delta }/1000,$$ (D2)

where δ _a and δ _w are offsets from −1000 and 0 respectively. By subtracting the correction term from the raw H value, the air and water values are recalibrated to 0 and 1, respectively (Δ = δ _a for air, ρ _e* = 0; Δ = δ _w for water, ρ _e* = 1) for all protocols, and the correction to each H values linearly proportional to density of the foam. The SD of H_recal is substantially reduced from SD of H_raw, to about 1 HU for even the lightest foam, but now all air and water are perfectly calibrated. This step eliminates the internal calibration discrepancy.