Abstract
Background
A predictive biomarker for total sugars intake was recently developed under controlled conditions. We used this biomarker to assess measurement error (ME) structure in self-reported total sugars intake in free-living individuals.
Methods
The Observing Protein and Energy Nutrition (OPEN) study involved 484 participants aged 40–69 years. Diet was assessed using two administrations of a food frequency questionnaire (FFQ) and two non-consecutive 24-hour dietary recalls (24HDR). Two 24-hour urine samples checked for completeness were analyzed on sucrose and fructose. We applied the biomarker calibrated in a feeding study to OPEN data to assess the ME structure and the attenuation factors (AFs) for intakes of absolute total sugars and sugars density for the FFQ and 24HDR.
Results
The AFs for absolute sugars were similar for a single FFQ and 24HDR, but attenuation decreased with repeated 24HDRs. For sugars density, the AFs for FFQ (men: 0.39; women: 0.33) were greater than for single 24HDR (men: 0.30; women: 0.24), and similar to two 24HDRs (men: 0.41; women: 0.35). The attenuation associated with both instruments was greater in women than in men.
Conclusions
Both the FFQ and 24HDR were found to be biased; hence incorporation of the sugars biomarker in calibration studies within the cohorts may be necessary in order to more reliably estimate sugars–disease associations.
Impact
In this article we propose a new dietary reference instrument based on the recently defined class of “predictive” biomarkers. Using sugars biomarker, we quantify measurement error in the FFQ- and 24HDR-reported absolute total sugars and total sugars density.
Keywords: predictive biomarkers, urinary sugars, total sugars, diet, OPEN, measurement error
Background
Positive associations between sugars and cancer have long been postulated in nutritional epidemiology (1), yet difficult to study, due to unreliability of self-reported intake. Measurement error (ME) associated with self-reported added sugars, which are particularly prone to misreporting (2–5), may substantially distort estimated disease risk and reduce statistical power to detect an effect (6). Wide recognition of the problem of ME in self-reported diet (7–8) has raised interest in development and use of dietary biomarkers (9–11), which are objective measures of intake that do not depend on a person’s capacity or motivation to accurately report their diet.
In the late 90s, Kaaks et al (12) defined two classes of dietary biomarkers, “recovery” and “concentration” biomarkers. Recovery biomarkers are based on a “known quantitative relationship between intake and output” over a certain period of time and therefore qualify as reference instruments in validation/calibration studies, given that they can be translated into absolute estimates of intake. Unfortunately, only few recovery biomarkers have been identified so far, including 24-hour urinary nitrogen for protein intake (13), doubly-labeled water (DLW) for total energy intake (14), and possibly 24-hour urinary potassium for potassium intake (15). Concentration biomarkers measure concentrations of specific compounds in blood, adipose or other tissues (e.g. serum carotenoids or vitamin C, adipose tissue fatty acids, etc.) (12). These biomarkers “do not have the same quantitative relationship with intake for every individual in a given study population” (16). In addition, they do not have a time dimension, and their between-subject variation “is generally determined not only by dietary intake of a given compound, but also by variations in digestion and absorption, distribution over body compartments, endogenous synthesis and metabolism, and excretion” (16). Thus, although concentration biomarkers are correlates of dietary intake, it is not yet clear how to use them in validation/calibration studies, even though when combined with dietary measures, they were shown to help in the investigation of diet-disease relationships by increasing the statistical power to detect an effect (17).
Recently, the sum of urinary sucrose and fructose in 24-hour urine was proposed as a dietary biomarker for total sugars intake based on data from two feeding studies (18). In the study of constant diets, the biomarker responded to intake in a dose-response and time-sensitive manner, and in the habitual diet study, the 30-day mean of the biomarker was highly correlated with 30-day mean of total sugars intake (r = 0.84). Yet, the overall urinary recovery of the sugars (~0.05% of intake) was much lower than that for 24-hour urinary nitrogen or potassium (both ~80% of intake). Given that the sugars biomarker showed more complex relationship with intake compared to recovery biomarkers, but, unlike concentration biomarkers, its relationship with intake was much stronger, relatively stable, time-related and sensitive to intake in a dose-response manner, the authors proposed a new class which they called “predictive” biomarkers (18). To our knowledge, the sugars biomarker is so far the only member of this class, and its statistical modeling for validation/calibration purposes has not yet been defined.
This article has two aims. First, we propose a novel ME model for predictive biomarkers. With the parameters of the model estimated from feeding studies, the predictive biomarker can be calibrated to meet the requirements for a reference instrument in validation/calibration studies. Second, we apply this novel ME model to the urinary sugars biomarker to investigate misreporting of total sugars intake in the Observing Protein and Energy Nutrition (OPEN) study (19). Under the assumption that the urinary sugars biomarker conforms to the ME model for predictive biomarkers we first use data from the feeding study in which this biomarker was developed to estimate the model parameters and to calibrate the biomarker. Then, we apply the calibrated biomarker in the OPEN study to estimate the ME structure and the attenuation related to intakes of absolute total sugars and total sugars density reported on a food frequency questionnaire (FFQ) and 24-hour dietary recall (24HDR).
MATERIAL AND METHODS
Feeding study
The development of the sugars biomarker in the feeding study is described elsewhere (18). Briefly, the feeding study was a 30-day intervention applied to 7 men and 6 women aged 23 to 66 years residing in a metabolic suite under strictly controlled conditions while consuming their usual diet. Prior to the intervention, participants were asked to keep 7-day estimated food diaries for four consecutive weeks while living at home. These data were then used to provide participants with their usual diet during the intervention. Continuous 24-hour urine collections were made throughout the 30-days. In total, 386 urinary measurements of sucrose and fructose, and 389 days of dietary measurements were available for analysis.
The OPEN Study Design
The OPEN study was conducted by the National Cancer Institute (NCI) from September 1999 to March 2000. Details on the study design have already been reported (19). Briefly, 261 men and 223 women aged 40 to 69 years who were healthy volunteers from Montgomery County, Maryland, took part in the study. Each participant was asked to complete an FFQ and 24HDR twice. The FFQ was first administered within 2 weeks of Visit 1, and then approximately 3 months later, within a few weeks of Visit 3. The 24HDR was administered at Visit 1, and approximately 3 months later at Visit 3. Participants provided two 24-hour urine collections at least 9 days apart and within 2 weeks following Visit 1, verified for completeness by the PABAcheck method. The DLW was administered for 2 weeks from Visit 1 through Visit 2, and the protocol was repeated for 14 male and 11 female volunteers.
Dietary Assessment
The FFQ used in this study was the NCI Diet History Questionnaire, which is a self-administered semi-quantitative FFQ with 124 food items that queried participants about their usual diet over the previous 12 months (20). A question in the FFQ also inquired whether participants usually drank sugar-free or regular-calorie type beverages, and what kind of sweetener they usually added to coffee and tea (sugar or honey, equal or aspartame, saccharin or Sweet-n-Low, or other sweetener). The food items, sex-specific portion sizes and nutrient database for the FFQ were generated using data from the U.S. Department of Agriculture (USDA) Continuing Survey of Food Intake by Individuals (CSFII) 1994 – 1996, as described by Subar et al (21). The 24HDR was a standardized five-pass method, developed by the USDA for use in national dietary surveillance (22). It was conducted by in-person interview, where interviewers used highly standardized probes, food models and coding. Based on the responses from the 24HDR, daily intake was calculated using the Food Intake Analysis Systems version 3.99, which obtains its database from updates to the USDA CSFII 1994–1996 (23). Individual monosaccharides and disaccharides were estimated using Nutrition Data System for Research software version 5.0_35 (2004), developed by the Nutrition Coordinating Center, University of Minnesota, Minneapolis, MN. The group of total sugars was defined as the sum of monosaccharides (glucose, fructose and galactose) and disaccharides (sucrose, lactose, and maltose).
Dietary Biomarkers
Biomarker for sugars intake
24-hour urine samples were preserved with boric acid (up to 2 g/L) during collection. The completeness of the collections was assessed by urinary recovery of three 80 mg tablets of PABA taken by the participants on the urine collection day (PABAcheck, Laboratories for Applied Biology, London, United Kingdom) (24). PABA concentration in urine was measured by a colorimetric technique (24). Urine collections with <70% recovery of the oral dose of PABA were considered incomplete and were excluded from the analyses. Those with PABA recovery of 70 to 85% were retained, but the content of analytes was proportionally adjusted to 93% PABA recovery (25). In case of recovery >110%, PABA was measured by high performance liquid chromatography, to distinguish between PABA and chemically similar compounds, such as acetaminophen, a drug commonly taken by participants (26–27).
Sucrose and fructose in urine were quantitatively determined using a colorimetric method on the Olympus AU640 clinical chemistry analyzer. The method used Olympus glucose reagent, whereas sucrose and fructose reagents and calibrators, and a glucose calibrator were prepared in house (Quotient Bioresearch Ltd.). Control material was prepared using a Fluka fructose standard and Sigma glucose and sucrose standards (1000 mg/L). Lower and upper limits of quantification were 4 mg/L and 133 mg/L for sucrose, and 1.2 mg/L and 88 mg/L for fructose, respectively.
Using the daily urine volume and sucrose and fructose concentration in urine, we estimated daily excretion of urinary sucrose and fructose. The sum of the two was used as a predictive biomarker of total sugars intake to estimate the ME structure of FFQ- and 24HDR-reported total sugars in the OPEN biomarker study.
Biomarker for energy intake
We used the DLW biomarker, which measured total energy expenditure (TEE) over 2 weeks, as a reference measure of participants’ energy intake. The DLW protocol, measurement of isotopes and calculation of TEE have been previously reported in detail (19).
Statistical Methods
Modeling the predictive sugars biomarker
A general model for predictive biomarkers and the details of fitting this model to the sugars biomarker data from the feeding study where this biomarker was developed (19) are described in the Appendix.
Simplifying notations used in the Appendix, for individual i, i = 1,…,n, let Ti denote logarithm of true usual, i.e., long-term average, sugars intake, Tij denote the logarithm of true intake on day j, and Mij denote the log-transformed sugars biomarker value on day j. As detailed in the Appendix, analyzing the feeding study data, we determined that the relationship between Mij and true intake Tij can be approximated by the following model,
| (1) |
where Ai is a log-transformed age, uMi is a person-specific bias (random effect), and εMij is within-person random error. Under certain assumptions discussed in the Appendix, one can use model (1) to specify the relationship between Mij and true usual intake Ti. In the feeding study, we estimated this relationship to be
where Si is an indicator variable that equals 0 for men and 1 for women. As follows from equations (A8), (A11)–(A12) in the Appendix, the calibrated biomarker values that are calculated as
| (2) |
satisfy the following ME model
We also used the feeding study to estimate the ratio of the variance of uMi to the variance of Ti + uMi,
| (3) |
It is assumed that both the parameters of the calibration equation (2) and the ratio (3) are relatively stable and do not change substantially from population to population. Yet, the biomarker ME parameters used here were estimated based on only one feeding study with a limited sample size. More such studies, preferably conducted across different populations, are needed to investigate the stability of the parameters used in this analysis.
Estimating the ME structure in self-reported intake in the OPEN study
For sugars intake, we used a ME model, which is a modification of the model described by Kipnis et al (8). For individual i, i = 1,…,n, let Qij and Rij denote log-transformed reported intake on the jth application of the FFQ and 24HDR, respectively. Denoting by XIi the vector of potential covariates that may affect the relationship between an instrument F = Q, R and true usual intake, the ME model is given by:
| (4) |
| (5) |
| (6) |
where, for a self-reported instrument F = Q, R, βF0 is the overall population intercept and represent constant biases at the population level; slope βFT reflects intake-related bias; slope βFX defines the association of the respective measure with the corresponding vector of covariates; uFi is person-specific bias with mean zero and variance ; and εFij is within-person random error with mean zero and variance . Although FFQ queries about diet over the previous year, whereas 24HDR measures diet on a particular day, we consider both instruments to be measures of usual intake, which is the average intake over 15 months. The 24HDR will then have a greater within-person random error compared to the FFQ due to additional day-to-day variation in intake. We assume that the person-specific biases for the FFQ and 24HDR, i.e. uQi and uRi, respectively, are correlated with each other but are independent of the person-specific bias for the calibrated biomarker, uMi, and that all three are independent from other random variables in the model, whereas the within-person random errors are independent of each other and of all other variables in the model. The log-transformed biomarker was calibrated using equation (2). However, the ME model allows within-person random errors εQij, εRij and εMij to be correlated, if measurements are taken very close in time. Otherwise, the within-person errors are assumed to be independent of each other and of all other variables in the model. In the OPEN study, the first 24HDR and first urinary sugars biomarker were taken at least two days apart, so we initially fitted a model that allowed εRi1 and εMi1 to be correlated. Given that the estimated correlation was small and not statistically significantly different from zero (p-value = 0.95 for men and 0.30 for women), in the final model we assumed they were uncorrelated.
For energy intake, we used the measurement error model in Kipnis et al (8), which is the same as model (4) – (6), except the DLW biomarker on the log scale does not need any calibration and satisfies equation (6) with no person-specific bias.
For all dietary and urinary variables on the log scale, we excluded values, which were below the 25th percentile minus twice the inter-quartile range, or above the 75th percentile plus twice the interquartile range. For each variable and each dietary instrument, no more than nine outlying values for men and seven for women were excluded from the analyses. Under the assumption that data were missing at random, we used the maximum likelihood method, which includes all available data for each subject, to produce unbiased estimates of the model parameters.
As was recently suggested by Willett (28), an evaluation of an FFQ could be invalid unless heterogeneity in the study population due to gender, age, and body size was adjusted for. To address this issue, we stratified the analysis of the ME structure in the FFQ and 24HDR by gender and also included log-transformed age and BMI in the ME model for self-reported sugars and energy intakes as components in the covariate vector XQ = XR.
Taking the fixed value of ratio (3) into account, we used the method of maximum likelihood to estimate the parameters in ME models (4)–(6) for sugars and energy intakes simultaneously under the assumption of normality of the random effects and within-person errors in the models. The simultaneous fitting of ME models for sugars and energy allows one to improve the efficiency of the estimates and to obtain the ME parameters for both absolute, as well as energy-adjusted intake estimates (29). We used the nutrient density method for energy adjustment, where sugars intake was expressed in grams per 1,000 kcal of total energy intake.
Estimation of the Attenuation Factors for the FFQ and 24HDR and the Pearson Correlation Coefficients between self-reported and true intake
When using self-reported dietary intake F measured with error to investigate the association between diet and disease, the observed log relative risk (RR) will be biased (7–9). On an appropriate scale, to a very good approximation, the bias is multiplicative, so that the observed log RR will be the product of the bias factor and the true log RR. The bias factor is given by the slope λF|X for reported intake in the multiple linear regression of true intake on self-reported intake F and covariates X in the ME model for F. In dietary studies, the value λF|X is usually between 0 and 1, so that ME leads to underestimation (attenuation) of the true RR, and λF|X is called the attenuation factor (30). Values closer to zero indicate more serious attenuation of risk.
The attenuation factor for a dietary-assessment instrument F = Q, R was calculated from the parameters in the ME model (4)–(6) as
| (7) |
When the disease model involves intake categorized into quantiles (e.g. quintiles), the observed RR between any two quintiles will be attenuated by the partial Pearson correlation coefficient between the self-reported and true intake (31). The partial correlation between the reported intake F = Q, R and the true intake can be calculated from the parameters in the ME model (4)–(6) as
| (8) |
For the FFQ and 24HDR, we estimated the attenuation factor and correlation with true intake by substituting the estimated parameters from fitting ME model (4)–(6) into equations (7) and (8) for F = Q, R.
RESULTS
Four hundred and seventy nine participants in the OPEN study completed the FFQ and 24HDR on two occasions. Valid DLW data were available from 450 of 484 participants. In total, 704 24-hour urine collections were considered complete and were available for analysis. Of those, 51 collections had PABA recovery between 70 – 85%, and the analytes were readjusted to 93% PABA recovery; 41 of 51 collections were from unique individuals, whereas 10 collections came from five participants. 73 and 90 urine samples had fructose and sucrose values, respectively, below the limit of quantification (<1.2 mg/L for fructose and <4 mg/L for sucrose). In order to retain those samples, we set their respective values to half the limit of quantification. We also conducted a sensitivity analysis where we excluded values below the limit of quantification, which produced virtually the same estimates. Thus, the findings from the analysis which included all the values are reported here.
The geometric means of total sugars and total sugars density by gender as estimated by the two instruments and the biomarker, as well as of urinary sucrose and fructose are presented in Table 1. Compared to the biomarker-based estimate, reported intake of total sugars was about 13.5% lower on the FFQ, for both men and women. Sugars intake reported from 24HDRs was slightly higher than the biomarker in men and nearly identical for women. The self-reported total sugars density intakes as estimated by the FFQ and 24HDRs were greater than the biomarker by approximately 32% and 20%, respectively, for both men and women. It is important to note that the group means indicate the validity of instruments to measure absolute total sugars intake on a group level only and do not necessarily invalidate the use of these self-reported dietary instruments in a cohort study. If participants in a cohort misreport to the same extent and direction, then the instrument would still serve the purpose of ranking individuals with regard to their total sugars intake. The greatest contributors to total sugars intake in our participants were soft drinks (18%) and fruits (15%) as measured by FFQ, and soft drinks (22%) and cookies, cakes and pies (13%) as measured by 24HDR.
Table 1.
Geometric means and 95% confidence intervals (CI) for total sugars intake and total sugars density as assessed by FFQ, 24HDR and urinary sugars biomarker in the OPEN study
| Men (n = 261) | Women (n = 223) | ||||||
|---|---|---|---|---|---|---|---|
| Instrument | N | Geometric Mean |
95% CI | N | Geometric Mean |
95% CI | |
| Total sugars intake (g/day) | FFQ1 | 259 | 107.8 | (101.1, 115.0) | 220 | 94.3 | (88.2, 100.8) |
| FFQ2 | 259 | 99.4 | (93.2, 106.1) | 218 | 87.5 | (82.6, 92.8) | |
| 24HDR1 | 259 | 128.2 | (119.6, 137.5) | 223 | 104.6 | (97.5, 112.1) | |
| 24HDR2 | 260 | 121.8 | (113.4, 130.7) | 220 | 100.7 | (94.0, 107.9) | |
| Biomarker* | 225 | 119.2 | (108.9, 130.6) | 188 | 105.8 | (94.9, 117.9) | |
| Total sugars density (g/1000 kcal) | FFQ1 | 257 | 55.1 | (52.7, 57.7) | 220 | 61.9 | (59.0, 64.9) |
| FFQ2 | 257 | 54.4 | (52.0, 57.0) | 218 | 62.4 | (59.9, 65.0) | |
| 24HDR1 | 259 | 50.7 | (48.0, 53.6) | 223 | 54.5 | (51.3, 57.8) | |
| 24HDR2 | 257 | 49.7 | (46.9, 52.7) | 220 | 54.9 | (51.8, 58.2) | |
| Biomarker*† | 209 | 41.2 | (37.7, 45.0) | 174 | 47.4 | (42.7, 52.7) | |
| Urinary Excretion (mg/day) | Sucrose | 226 | 28.8 | (25.9, 32.0) | 188 | 21.6 | (19.1, 24.5) |
| Fructose | 226 | 11.4 | (10.0, 12.9) | 190 | 13.7 | (11.7, 15.9) | |
Estimated based on the measurement error parameters generated from the feeding study (18).
Expressed on energy intake estimated by DLW measurement of total energy expenditure.
ME parameters for the FFQ and 24HDR are given in Table 2. The slope βRT in the regression of reported intake R on true intake represents part of the instrument’s bias associated with true intake, also called intake-related bias: βRT = 1 means no such bias in the instrument, whereas βRT <1 indicates a tendency to underreport high and over-report low intake (a flattened slope phenomenon) that results in inflation of the risk estimate (32). As shown in Table 2, the slopes for the FFQ were somewhat smaller (less favorable) than for the 24HDR, and for both instruments were much smaller in women than in men. No change in the slopes was observed with energy adjustment. The variance of the person-specific bias was greater for the FFQ compared to the 24HDR absolute intake estimates, and was similar between men and women (Table 2). In men, the variance of the person-specific bias in the FFQ, but not in the 24HDR, was greater than the variance of true intake, whereas in women, for both instruments, it was smaller compared to the variance of true intake. Energy adjustment reduced the person-specific bias in both instruments, although considerably less so in the 24HDR, and made it similar in magnitude between the two. Nevertheless, in all instances the person-specific bias was still substantial and statistically significantly different from zero. We observed a strong positive correlation between the person-specific biases of the FFQ and 24HDR, which remained after energy adjustment and, in women, became even stronger. As expected, the variance of the within-person error was greater in the 24HDR than in the FFQ. The within-person error in 24HDR was also closer to the between-person variation compared to the FFQ. After energy adjustment, the within-person error was somewhat reduced.
Table 2.
Measurement error structure for total sugar intake and total sugars density as assessed by FFQ and 24HDR by gender on log scale*
|
Gender |
Variance of true Intake |
Instrument |
Slope in regression of reported on true intake (βQ1 or βR1) |
Variance of person- specific bias |
Correlation of person- specific biases (ρuQ,uR) |
Variance of within-person error |
|
|---|---|---|---|---|---|---|---|
| Total sugars intake (g/day) | Male | 0.12 (0.04†) | FFQ | 0.66 (0.16) | 0.17 (0.02) | 0.81 (0.08) | 0.06 (0.005) |
| 24HDR | 0.82 (0.18) | 0.08 (0.02) | 0.16 (0.01) | ||||
| Female | 0.25 (0.06) | FFQ | 0.16 (0.06) | 0.16 (0.02) | 0.72 (0.09) | 0.07 (0.01) | |
| 24HDR | 0.22 (0.08) | 0.08 (0.02) | 0.18 (0.02) | ||||
| Total sugars density (g/1000 kcal) | Male | 0.08 (0.03) | FFQ | 0.65 (0.17) | 0.08 (0.01) | 0.82 (0.09) | 0.03 (0.002) |
| 24HDR | 0.82 (0.19) | 0.05 (0.02) | 0.12 (0.01) | ||||
| Female | 0.22 (0.05) | FFQ | 0.16 (0.06) | 0.07 (0.01) | 1.00 (0.08) | 0.04 (0.003) | |
| 24HDR | 0.21 (0.07) | 0.06 (0.01) | 0.12 (0.01) | ||||
All the parameters were estimated using FFQ- and 24HDR-ME models adjusted for BMI and age, and biomarker ME model adjusted for age.
Standard error (all values in parenthesis).
In Table 3, we present the attenuation factors for reported intake, and the correlation coefficients between true and reported intake for FFQ, single 24HDR, and for the average of two 24HDRs. The attenuation factor for FFQ for absolute total sugars intake was rather small, and more favorable in men (≈0.3) than in women (≈0.2). The attenuation factor for a single 24HDR was only slightly greater than that for the FFQ, but further increased when the average of two repeat 24HDRs was used. Similar to the FFQ, the attenuation factor for 24HDR was greater in men than in women. Energy adjustment improved the attenuation associated with the FFQ; the attenuation factors somewhat increased, but still remained substantially smaller than 1, whereas for the 24HDR some improvements were observed in women, but none in men. After energy adjustment, the attenuation factors for a single FFQ were only slightly lower than for two 24HDRs. When we used the 24HDR as a reference instrument for total sugars density, the estimated AFs for the FFQ were considerably closer to 1 compared to the biomarker-based estimates (men: 24HDR-based AF = 0.68 vs. biomarker-based AF = 0.39; women: 24HDR-based AF = 0.71 vs. biomarker-based AF = 0.33).
Table 3.
Correlations of true and reported total sugars intake and total sugars density on log scale, and AFs for reported total sugars intake and total sugars density on log scale from a ME model for the urinary sugars biomarker*
| Men (n = 261) | Women (n = 223) | ||||
|---|---|---|---|---|---|
| Instrument | Attenuation Factor (AF) |
Correlation with true intake |
Attenuation Factor (AF) |
Correlation with true intake |
|
| Total sugars intake (g/day) | FFQ | 0.283 (0.058†) | 0.431 (0.069) | 0.169 (0.068) | 0.163 (0.064) |
| Single 24HDR | 0.304 (0.056) | 0.499 (0.067) | 0.196 (0.069) | 0.206 (0.070) | |
| Avg. of two 24HDR | 0.407 (0.074) | 0.577 (0.076) | 0.291 (0.102) | 0.252 (0.085) | |
| Total sugars density (g/1000 kcal) | FFQ | 0.385 (0.093) | 0.500 (0.090) | 0.331 (0.129) | 0.231 (0.087) |
| Single 24HDR | 0.301 (0.069) | 0.496 (0.079) | 0.238 (0.089) | 0.225 (0.080) | |
| Avg. of two 24HDR | 0.410 (0.092) | 0.578 (0.091) | 0.346 (0.128) | 0.271 (0.096) | |
All the parameters were estimated using FFQ- and 24HDR-ME models adjusted for BMI and age, and biomarker ME model adjusted for age.
Standard error (all values in parenthesis).
The results for the correlation coefficients between true and reported sugars intake were qualitatively similar to the results for the attenuation factors. For absolute sugars intake, they were greater in men than in women, greater for a single 24HDR than for the FFQ, and further increased with two 24HDRs. The correlations of FFQ estimates with true intake improved after energy adjustment, but were still lower than the correlations yielded by two 24HDRs. Similarly to 24HDR-based attenuation estimates, the estimated correlation coefficients between the FFQ and true sugars density based on 24HDR suggest that, using 24HDR as a reference may lead to considerable overestimation of FFQ validity with respect to sugars intake, especially in women (men: 24HDR-based ρ = 0.79 vs. biomarker-based ρ = 0.50; women: 24HDR-based ρ = 0.83 vs. biomarker-based ρ = 0.23).
In further sensitivity analysis (data not shown), after adding smoking and education as covariates in the ME model, the attenuation factors and correlation coefficients between reported and true sugars intake remained virtually the same in men, and only slightly increased in women. Furthermore, replacing the continuous covariate BMI with a categorical one in the ME model produced virtually unchanged results. We also attempted stratified analyses of the ME model by age, BMI, smoking status and alcohol intake. The estimated attenuation factors and correlation coefficients were not statistically significantly different between strata at the nominal level for any of the investigated variables, except for the correlation coefficients stratified by age in men. Nonetheless, these differences became statistically non-significant after adjustment for multiple testing. We emphasize though that the OPEN study was not powered for such stratified analyses. In the future, it would be important to investigate whether differences by characteristics, such as age, BMI, race, etc., do exist, should larger validation studies become available.
DISCUSSION
In this report we propose a ME model for predictive biomarkers and show how it could be calibrated using estimates from feeding studies. The important qualities of a predictive biomarker are that its person-specific bias is uncorrelated with the person-specific biases in the self-report instruments, and that the biomarker ME parameters are reasonably similar for all individuals across different categories in the study population. Although we acknowledge that predictive biomarkers’ level may be affected by genetic, physiological, pathological or other determinants besides diet only (as potential sources for person-specific bias), they ought not to explain a significant portion of the variability in the biomarker, and their effect estimates (calculable from a feeding study) ought to be stable. Though they also may be associated with intake-related and covariate-related bias, their association to intake should be quantifiable, stable, and time-sensitive, i.e. refer to certain period of intake. After calibration, and given that their person-specific bias is stable compared to their intake-related bias (ratio given in (A10) in Appendix), predictive biomarkers, like recovery biomarkers, can be used as reference instruments in validation/calibration studies to estimate the ME structure in self-reported intake and/or adjust estimated diet-disease relationships for measurement error. In fact, recovery biomarkers can be considered a special class of predictive biomarkers, which are known to have no bias.
In this report, we also apply the developed ME model for predictive biomarkers to the recently developed predictive biomarker for sugars intake to investigate misreporting in FFQ and 24HDR in the OPEN study. Based on the physiological mechanisms by which sugars biomarker occur in urine (18), it is plausible to assume that errors in the calibrated sugars biomarker are independent of errors in the self-reporting instruments, i.e. of subject’s capacity or motivation to give an accurate response to the traditional dietary assessment methods, and that it has less non-dietary determinants than concentration biomarkers. In general, urinary measures may be better candidates for predictive or recovery biomarkers, as their levels are less likely to be affected by the complex homeostatic and metabolic mechanisms, and lifestyle factors, that affect blood or tissue measures. Although a study of participants on constant diets showed a certain level of between-subject variability in the urinary sugars biomarker (18), a second study of participants consuming their usual varying diet showed that dietary sugars intake explained a large proportion of the variance in sucrose and fructose excretion (72% of the variance in 30-day mean urinary sucrose and fructose was explained by 30-day mean sugars intake (18)), suggesting that it is very likely that this would be the case in other populations too. The fact that no effect of several commonly investigated characteristics, such as sex, BMI or physical activity, was found on the relationship between the biomarker and true total sugars intake, further suggests that the assumption of stability of the biomarker ME parameters is plausible. It must be stressed though that the sample size of the feeding study was small and the power to detect moderate effects was relatively low. However, another feeding study confirmed the independence of the sugars biomarker from individuals’ body mass index (BMI) (33).
Sucrose and fructose occur in urine in very small amounts; urinary sucrose is possibly a fraction of dietary sucrose that escapes enzymatic hydrolysis in the small intestine, and once in the blood stream, is excreted in the urine, whereas urinary fructose is a portion of fructose, either from dietary fructose or sucrose, that escapes fructose hepatic metabolism. Thus, any person-specific differences in absorption, hepatic metabolism or renal excretion of these two nutrients, determined by genetic factors, physiological or medical conditions, would be possible sources of person-specific bias, and may differ between different populations. For instance, altered intestinal disaccharidase activity (34), gastric damage (35) or high intraluminal concentration of sucrose (36), may facilitate sucrose leakage through the gut and increase its excretion. Although age was found to statistically significantly affect the biomarker-diet relationship in the feeding study, in our sensitivity analysis, excluding age in the biomarker ME model did not significantly affect the biomarker-based attenuation and correlation estimates for the self-report instruments in OPEN (data not shown), suggesting that even a simple ME model may be robust enough for validation purposes.
By using the sugars biomarker, we found sugars reports on both FFQ and 24HDR to be associated with intake-related and person-specific biases. These biases have opposing effects on risk estimates; while intake-related bias leads to inflated estimated risk, person-specific bias attenuates risk (37). In our analysis, intake-related bias was somewhat greater in the FFQ than in the 24HDR, and much greater in women than in men. Yet, the relative variances of the person-specific bias and the within-person error in women were still substantial, and overrode the effect of the intake-related bias resulting in attenuation factors well below 1. Whereas person-specific bias was greater in the FFQ, as expected, the within-person error was greater in the 24HDR due to day-to-day variability in intake.
The attenuation factors, as well as person-specific biases for the FFQ improved after energy adjustment, meaning that errors in FFQ estimates of total sugars and energy were correlated; hence energy adjustment diminished the effect of ME although it still remained substantial. From the attenuation factor estimates shown in Table 3, it can be calculated that in analyses with energy-adjusted FFQ intake, true RR of 2, 1.5 or 1.2 would be observed as 1.3, 1.2 or 1.1, respectively. On the other hand, energy adjustment had very little effect on the attenuation or on the person-specific bias associated with 24HDR, suggesting that errors in sugars estimates were independent of errors in energy reporting. It is therefore possible that errors in sugars estimates from 24HDR and FFQ reports may have different sources, or that, in our data, sugars were major contributors to energy as reported on FFQ, but not as reported on 24HDR. It is also possible that the interrelation of errors among reported macronutrients, i.e. the energy contributors, is different in the FFQ compared to the 24HDR. Yet, the person-specific biases in the two instruments remained highly correlated even after energy adjustment, which makes questionable the use of 24HDR as a reference instrument for absolute or energy-adjusted sugars reported on the FFQ.
In both men and women, the attenuation factors for absolute sugars self-reports were somewhat better for one 24HDR than for one FFQ, and they further improved with repeated 24HDR. Although, compared to the FFQ, the attenuation factors for 24HDR did not improve much with energy adjustment, these values for two 24HDRs were still greater (more favorable) that the attenuation factors for the FFQ. Moreover, as seen from equation (7), with added 24HDR repeats, the attenuation factor will further improve. We also note that the attenuation associated with both instruments was greater in women than in men. In earlier studies, energy underreporting was found to be more common in women than in men (38–39).
From earlier analysis using recovery biomarkers, ME structures for self-reported energy and protein showed somewhat similar patterns with what we are seeing for sugars (7, 31, 40). The attenuation associated with misreporting of sugars intake was similar to that of protein, and smaller (better) than that of energy. One might expect that misreporting of sugars would be greater than misreporting of protein, because of the tendency to misreport foods high in added sugars (2–5). Yet, the sugars biomarker measures not only added sugars (i.e. used as ingredients in processed and prepared foods, or added at the table), but also naturally occurring sugars from fruits and vegetables. It may be that error from possibly under-reporting high added sugars food in parts is canceled-out by over-reporting fruit and vegetables.
In summary, using the newly developed sugars biomarker, we showed that absolute and energy-adjusted total sugars reported on both the FFQ and 24HDR in the OPEN study were associated with substantial error. Based on our findings, in a disease model with absolute total sugars intake, two 24HDRs would provide more accurate risk estimate for the sugars effect than FFQ, whereas in analysis with energy-adjusted intakes, the FFQ seems to perform similarly to two 24HDRs. Women tended to misreport sugars more than men on both instruments. Hence, problematic assessment of sugars in nutritional epidemiology may have prevented us from detecting a causal link between sugars and cancer. As both instruments were found to be biased, incorporation of the sugars biomarker in calibration studies within large cohorts (which will allow for adjusting the risk estimates for ME) may be necessary in order to obtain more definite answers for the role of sugars in cancer.
It is important to note that the ME structure of the self-report instruments was assessed based on biomarker ME parameters estimated from only one feeding study with a limited sample size. More feeding studies across different populations are necessary to investigate the stability of the sugars biomarker ME parameters used in this analysis.
Supplementary Material
APPENDIX
ME Model for Predictive Biomarkers
For person i = 1,…,n, daily measurement j = 1,…,J, let Tij represent true intake of a food/nutrient. Define true usual intake as the within-person mean of daily intakes Ti = E(Tij | i). Consider the following model relating appropriately transformed biomarker measurements gM (Mij) to appropriately transformed true daily intakes gT(Tij)
| (A1) |
where Xi is a vector of covariates that may affect the relationship between the biomarker and true intake, βM0, βMT are the scale parameters that define overall population and intake-related biases, respectively, in biomarker measurements, βMX is the vector of parameters that define covariate-related bias, uMi is the person-specific bias with mean zero and variance that represents the difference between within-person bias and its intake-related and covariate-related components, εMij is within-person random error with mean zero and variance . We assume that random variables Tij, uMi, εMij are mutually independent, and that uMi, εMij are independent from vector Xi. Since, for a given person i, the biomarker measurements are taken on consecutive days, components of vector εMi = (εMi1,…,εMiJ)t may be correlated with the variance-covariance matrix Σε.
Let δij denote within-person deviations of transformed daily intakes for person i from the within-person mean μi = E[gT(Tij) | i], i.e.,
| (A2) |
Note that the deviations δij are uncorrelated with any personal characteristic Vi, including gT(Ti) and Xi, since
For nonlinear transformation,
In general, the difference νi = μi − gT(Ti) could depend on true transformed usual intake, as well as the covariates in the model. Regressing νi onto gT(Ti) and Xi we have
| (A3) |
so that
| (A4) |
Substituting expression (A2) into model (A1) with μi specified according to regression (A4), it follows that the model relating biomarker measurements to transformed true usual intake is given by
| (A5) |
where
If gT(.) is the log transformation, then, under certain conditions, equation (A5) simplifies. We have
or
Since, by definition, Ti = E(Tij|i), it follows that
and
| (A6) |
Under the assumption that E(eδij | i) is a constant, which would be the case if the δij are identically distributed, it follows that νi is a constant. Denoting this constant by ν, it follows from (A5) that
| (A7) |
It is assumed that model (A5) is stable by satisfying the following requirements:
parameters β̃M0, β̃MT, β̃MX are the same for individuals across different populations and can be evaluated in the feeding studies;
the ratio of the variance of the person-specific bias to the variance of the intake-related and person-specific biases is nearly the same for individuals across different populations and can be evaluated in the feeding studies;
person-specific bias ũMi and within-person random error ε̃Mij are independent of any personal characteristics and of self-reported intakes from dietary-assessment instruments.
Under assumptions (i)–(iii), using the parameters evaluated in the feeding studies, the predictive biomarker could be calibrated to remove intake-related and covariate-related biases by calculating
| (A8) |
Denoting , the calibrated predictive biomarker follows the model
| (A9) |
With the ratio
| (A10) |
estimated from the feeding studies, all the parameters of model (A9) are uniquely identifiable in any biomarker validation study, and the calibrated predictive biomarker could be used as a reference instrument to estimate the ME structure of dietary-assessment methods such as the FFQ and 24HDR.
Developing the calibrated sugars biomarker in the feeding study
We first used data from the feeding study in which this biomarker was developed (18), to evaluate the appropriate scales for the biomarker and true daily sugars intakes, covariates Xi related to biomarker-intake relationship, and the covariance structure of within-person errors for ME model (A1). We used the SAS MIXED procedure to fit the model by the method of maximum likelihood under the assumption that random effect and within-person error are normally distributed.
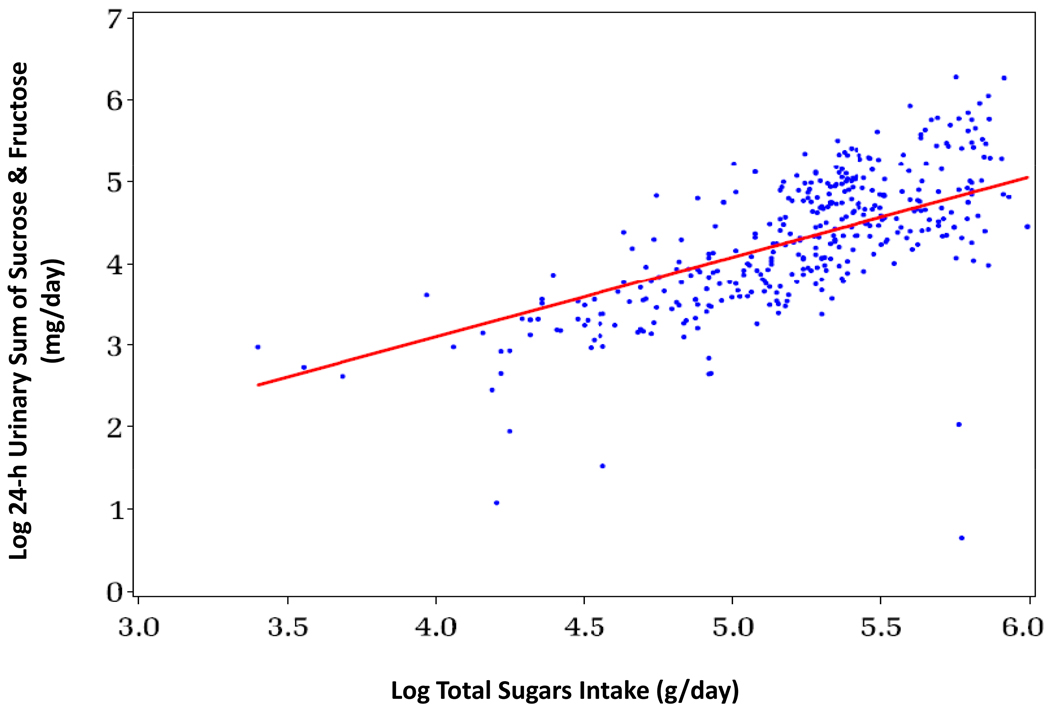
After considering various transformations to approximate the linear relationship between true daily intake and biomarker level in model (A1), we chose both gM(Mij) and gT(Tij) to be the logarithmic transformation. Figure 1 shows the association between log-transformed daily urinary sucrose and fructose measurements and log of daily total sugars intake in the 13 participants. In a previous report of these data (18) the authors used 30-d means of urinary sucrose and fructose, and total sugars intake to assess the characteristics of the biomarker, whereas in this analysis we use all 30 daily measurements of urinary and dietary sugars per participant. Using all daily measurements, we analyzed a set of potential covariates Xi in model (A1) including gender, age, BMI, and true intakes of fat, carbohydrates, protein, and total energy. Only log-transformed age, Ai was identified as a statistically significant covariate in the regression of urinary on dietary sugars (P = 0.003), which was therefore included in the ME model as a single covariate Xi = Ai.
Figure 1.
Association between urinary sucrose and fructose and total sugars intake in the 30-day feeding study (n = 13; 13 subjects × 30 24-h urine collections and 13 × 30-d of diet) (19)
We considered two correlation structures for the variance-covariance matrix Σε: (i) the first order autoregressive structure and (ii) the Toeplitz structure of orders 2 to 4 (41). The second order Toeplitz structure, which assumes that any two consecutive within-person errors εij, εij+1 are correlated with the same correlation coefficient, but non-consecutive within-person errors are uncorrelated, produced the best fit based on the Akaike’s information criterion (42) and was chosen for model (A1).
The estimated parameters for thereby specified model (A1) were: βM0 = 1.71 βMT = 1.00 βMX = −0.71, .
In the feeding study, we checked the assumption that E(eδij | i) is a constant, and found that the mean E(eδij | i) depends on participants’ gender. Stratifying by gender, the individual means E(eδij | i) were not exactly the same, but the differences from the overall gender-specific mean were very small with var(νi) = 0.0006 for both genders. We further fitted regression (A3) to estimated values νi from (A6). None of the considered covariates was statistically significant in the model. Slope γT, although statistically significantly different from zero, was very small at 0.03 compared to βMT = 1.00, and the residual variance was 0.0003. Substituting those values into (A5) did not produce any material difference compared to model (A7). We, therefore, proceeded by using estimated parameters from model (A7) with the gender-specific parameter ν as follows: for women, this parameter was estimated as ν̄ = 0.020 and, for men, as ν̄ = 0.039.
As a result, the fitted in the feeding study ME model for predictive sugars biomarker is given by
| (A11) |
were S = 0 for men and S = 1 for women. The estimated ratio of person-specific bias to the sum of person-specific and intake related biases is
| (A12) |
Footnotes
Supported by the Intramural Research Program of the National Cancer Institute, National Institutes of Health, U.S. Department of Health and Human Services.
References
- 1.WCRF/AICR. Food, Nutrition, Physical Activity and the prevention of Cancer: a Global Perspective. Washington DC: AICR; 2007. [Google Scholar]
- 2.Johansson L, Solvoll K, Bjorneboe GE, Drevon CA. Under- and overreporting of energy intake related to weight status and lifestyle in a nationwide sample. Am J Clin Nutr. 1998;68(2):266–274. doi: 10.1093/ajcn/68.2.266. [DOI] [PubMed] [Google Scholar]
- 3.Poppitt SD, Swann D, Black AE, Prentice AM. Assessment of selective under-reporting of food intake by both obese and non-obese women in a metabolic facility. Int J Obes Relat Metab Disord. 1998;22(4):303–311. doi: 10.1038/sj.ijo.0800584. [DOI] [PubMed] [Google Scholar]
- 4.Pryer JA, Vrijheid M, Nichols R, Kiggins M, Elliott P. Who are the 'low energy reporters' in the dietary and nutritional survey of British adults? Int J Epidemiol. 1997;26(1):146–154. doi: 10.1093/ije/26.1.146. [DOI] [PubMed] [Google Scholar]
- 5.Bingham SA, Cassidy A, Cole TJ, et al. Validation of weighed records and other methods of dietary assessment using the 24 h urine nitrogen technique and other biological markers. Br J Nutr. 1995;73(4):531–550. doi: 10.1079/bjn19950057. [DOI] [PubMed] [Google Scholar]
- 6.Kipnis V, Freedman LS, Brown CC, Hartman AM, Schatzkin A, Wacholder S. Effect of measurement error on energy-adjustment models in nutritional epidemiology. Am J Epidemiol. 1997;146(10):842–855. doi: 10.1093/oxfordjournals.aje.a009202. [DOI] [PubMed] [Google Scholar]
- 7.Kipnis V, Midthune D, Freedman LS, et al. Empirical evidence of correlated biases in dietary assessment instruments and its implications. Am J Epidemiol. 2001;153(4):394–403. doi: 10.1093/aje/153.4.394. [DOI] [PubMed] [Google Scholar]
- 8.Kipnis V, Subar AF, Midthune D, et al. Structure of dietary measurement error: results of the OPEN biomarker study. Am J Epidemiol. 2003;158(1):14–21. doi: 10.1093/aje/kwg091. discussion 2–6. [DOI] [PubMed] [Google Scholar]
- 9.Bingham SA. Biomarkers in nutritional epidemiology. Public Health Nutr. 2002;5(6A):821–827. doi: 10.1079/phn2002368. [DOI] [PubMed] [Google Scholar]
- 10.Potischman N, Freudenheim JL. Biomarkers of nutritional exposure and nutritional status: an overview. J Nutr. 2003;133(Suppl 3):873S–874S. doi: 10.1093/jn/133.3.873S. [DOI] [PubMed] [Google Scholar]
- 11.Jenab M, Slimani N, Bictash M, Ferrari P, Bingham SA. Biomarkers in nutritional epidemiology: applications, needs and new horizons. Hum Genet. 2009;125(5–6):507–525. doi: 10.1007/s00439-009-0662-5. [DOI] [PubMed] [Google Scholar]
- 12.Kaaks R, Riboli E, Sinha R. Biochemical markers of dietary intake. IARC Sci Publ. 1997;(142):103–126. [PubMed] [Google Scholar]
- 13.Bingham SA, Cummings JH. Urine nitrogen as an independent validatory measure of dietary intake: a study of nitrogen balance in individuals consuming their normal diet. Am J Clin Nutr. 1985;42(6):1276–1289. doi: 10.1093/ajcn/42.6.1276. [DOI] [PubMed] [Google Scholar]
- 14.Schoeller DA. Measurement of energy expenditure in free-living humans by using doubly labeled water. J Nutr. 1988;118(11):1278–1289. doi: 10.1093/jn/118.11.1278. [DOI] [PubMed] [Google Scholar]
- 15.Tasevska N, Runswick SA, Bingham SA. Urinary potassium is as reliable as urinary nitrogen for use as a recovery biomarker in dietary studies of free living individuals. J Nutr. 2006;136(5):1334–1340. doi: 10.1093/jn/136.5.1334. [DOI] [PubMed] [Google Scholar]
- 16.Kaaks R, Ferrari P, Ciampi A, Plummer M, Riboli E. Uses and limitations of statistical accounting for random error correlations, in the validation of dietary questionnaire assessments. Public Health Nutr. 2002;5(6A):969–976. doi: 10.1079/phn2002380. [DOI] [PubMed] [Google Scholar]
- 17.Freedman LS, Kipnis V, Schatzkin A, Tasevska N, Potischman N. Can we use biomarkers in combination with self-reports to strengthen the analysis of nutritional epidemiologic studies? Epidemiol Perspect Innov. 2010;7(1):2. doi: 10.1186/1742-5573-7-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Tasevska N, Runswick SA, McTaggart A, Bingham SA. Urinary sucrose and fructose as biomarkers for sugar consumption. Cancer Epidemiol Biomarkers Prev. 2005;14(5):1287–1294. doi: 10.1158/1055-9965.EPI-04-0827. [DOI] [PubMed] [Google Scholar]
- 19.Subar AF, Kipnis V, Troiano RP, et al. Using intake biomarkers to evaluate the extent of dietary misreporting in a large sample of adults: the OPEN study. Am J Epidemiol. 2003;158(1):1–13. doi: 10.1093/aje/kwg092. [DOI] [PubMed] [Google Scholar]
- 20.Subar AF, Thompson FE, Kipnis V, et al. Comparative validation of the Block, Willett, and National Cancer Institute food frequency questionnaires : the Eating at America's Table Study. Am J Epidemiol. 2001;154(12):1089–1099. doi: 10.1093/aje/154.12.1089. [DOI] [PubMed] [Google Scholar]
- 21.Subar AF, Midthune D, Kulldorff M, et al. Evaluation of alternative approaches to assign nutrient values to food groups in food frequency questionnaires. Am J Epidemiol. 2000;152(3):279–286. doi: 10.1093/aje/152.3.279. [DOI] [PubMed] [Google Scholar]
- 22.Moshfegh AJ, Raper N, Ingwersen L, et al. An improved approach to 24-hour dietary recall methodology. Ann Nutr Metab. 2001;45(Suppl 1):156. [Google Scholar]
- 23.Tippett KS, Cypel YS, editors. Nationwide Food Surveys Rep. Beltsville, MD: US Department of Agriculture, Agricultural Research Service; 1997. Design and Operation: The continuing Survey of Food Intakes by Individuals and the Diet and Health Knowledge Survey, 1994–96. Continuing Survey of Food Intakes by Individuals 1994–96. [Google Scholar]
- 24.Bingham S, Cummings JH. The use of 4-aminobenzoic acid as a marker to validate the completeness of 24 h urine collections in man. Clin Sci (Lond) 1983;64(6):629–635. doi: 10.1042/cs0640629. [DOI] [PubMed] [Google Scholar]
- 25.Johansson G, Bingham S, Vahter M. A method to compensate for incomplete 24-hour urine collections in nutritional epidemiology studies. Public Health Nutr. 1999;2(4):587–591. doi: 10.1017/s1368980099000786. [DOI] [PubMed] [Google Scholar]
- 26.Jakobsen J, Ovesen L, Fagt S, Pedersen AN. Para-aminobenzoic acid used as a marker for completeness of 24 hour urine: assessment of control limits for a specific HPLC method. Eur J Clin Nutr. 1997;51(8):514–519. doi: 10.1038/sj.ejcn.1600434. [DOI] [PubMed] [Google Scholar]
- 27.Berg JD, Chesner I, Lawson N. Practical assessment of the NBT-PABA pancreatic function test using high performance liquid chromatography determination of p-aminobenzoic acid in urine. Ann Clin Biochem. 1985;22(Pt 6):586–590. doi: 10.1177/000456328502200606. [DOI] [PubMed] [Google Scholar]
- 28.Willett W. Commentary: Dietary diaries versus food frequency questionnaires-a case of undigestible data. Int J Epidemiol. 2001;30(2):317–319. doi: 10.1093/ije/30.2.317. [DOI] [PubMed] [Google Scholar]
- 29.Carroll RJ, Midthune D, Freedman LS, Kipnis V. Seemingly unrelated measurement error models, with application to nutritional epidemiology. Biometrics. 2006;62(1):75–84. doi: 10.1111/j.1541-0420.2005.00400.x. [DOI] [PubMed] [Google Scholar]
- 30.Kaaks R, Riboli E, van Staveren W. Calibration of dietary intake measurements in prospective cohort studies. Am J Epidemiol. 1995;142(5):548–556. doi: 10.1093/oxfordjournals.aje.a117673. [DOI] [PubMed] [Google Scholar]
- 31.Schatzkin A, Kipnis V, Carroll RJ, et al. A comparison of a food frequency questionnaire with a 24-hour recall for use in an epidemiological cohort study: results from the biomarker-based Observing Protein and Energy Nutrition (OPEN) study. Int J Epidemiol. 2003;32(6):1054–1062. doi: 10.1093/ije/dyg264. [DOI] [PubMed] [Google Scholar]
- 32.Wacholder S. When measurement errors correlate with truth: surprising effects of nondifferential misclassification. Epidemiology. 1995;6(2):157–161. doi: 10.1097/00001648-199503000-00012. [DOI] [PubMed] [Google Scholar]
- 33.Joosen AM, Kuhnle GG, Runswick SA, Bingham SA. Urinary sucrose and fructose as biomarkers of sugar consumption: comparison of normal weight and obese volunteers. Int J Obes (Lond) 2008;32(11):1736–1740. doi: 10.1038/ijo.2008.145. [DOI] [PubMed] [Google Scholar]
- 34.Bjarnason I, Batt R, Catt S, Macpherson A, Maxton D, Menzies IS. Evaluation of differential disaccharide excretion in urine for non-invasive investigation of altered intestinal disaccharidase activity caused by alpha-glucosidase inhibition, primary hypolactasia, and coeliac disease. Gut. 1996;39(3):374–381. doi: 10.1136/gut.39.3.374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Sutherland LR, Verhoef M, Wallace JL, Van Rosendaal G, Crutcher R, Meddings JB. A simple, non-invasive marker of gastric damage: sucrose permeability. Lancet. 1994;343(8904):998–1000. doi: 10.1016/s0140-6736(94)90125-2. [DOI] [PubMed] [Google Scholar]
- 36.Menzies I. Absorption of intact oligosaccharide in health and disease. Bioch Soc Trans. 1974;2:1042–1047. [Google Scholar]
- 37.Thiebaut AC, Kipnis V. Dietary fat underreporting and risk estimation. Public Health Nutr. 2007;10(2):212–213. doi: 10.1017/S1368980007339049. author reply 3–4. [DOI] [PubMed] [Google Scholar]
- 38.Krebs-Smith SM, Graubard BI, Kahle LL, Subar AF, Cleveland LE, Ballard-Barbash R. Low energy reporters vs others: a comparison of reported food intakes. Eur J Clin Nutr. 2000;54(4):281–287. doi: 10.1038/sj.ejcn.1600936. [DOI] [PubMed] [Google Scholar]
- 39.de Vries JH, Zock PL, Mensink RP, Katan MB. Underestimation of energy intake by 3-d records compared with energy intake to maintain body weight in 269 nonobese adults. Am J Clin Nutr. 1994;60(6):855–860. doi: 10.1093/ajcn/60.6.855. [DOI] [PubMed] [Google Scholar]
- 40.Day N, McKeown N, Wong M, Welch A, Bingham S. Epidemiological assessment of diet: a comparison of a 7-day diary with a food frequency questionnaire using urinary markers of nitrogen, potassium and sodium. Int J Epidemiol. 2001;30(2):309–317. doi: 10.1093/ije/30.2.309. [DOI] [PubMed] [Google Scholar]
- 41.Littell RC, Pendergast J, Natarajan R. Modelling covariance structure in the analysis of repeated measures data. Stat Med. 2000;19(13):1793–1819. doi: 10.1002/1097-0258(20000715)19:13<1793::aid-sim482>3.0.co;2-q. [DOI] [PubMed] [Google Scholar]
- 42.Burnbaum KP, Anderson DR. Model Selection and Multimodel Inference. 2nd ed. New York: Springer; 2002. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.