Radiobiological considerations in combining doses from external beam radiotherapy and brachytherapy for cervical cancer

Abstract

The recommended radio-therapeutic treatment for cervix cancer consists of a first phase of external beam radiotherapy (EBRT) plus a second phase of brachytherapy (BT), the combined treatment being delivered within 8 weeks.

In order to assess a comprehensive dosimetry of the whole treatment, it is necessary to take into account that these two phases are characterized by different spatial and temporal dosimetric distributions, which complicates the task of the summation of the two contributions, EBRT and BT. Radiobiology allows to tackle this issue pragmatically by means of the LQ model and, in fact, this is the usual tool currently in use for this matter.

In this work, we describe the rationale behind the summation of the dosimetric contributions of the two phases of the treatment, EBRT and BT, for cervix cancer, as carried out with the LQ model.

Besides, we address, from a radiobiological point of view, several important considerations regarding the use of the LQ model for this task. One of them is the analysis of the effect of the overall treatment time in the result of the global treatment. Another important question considered is related to the fact that the capacity of LQ to predict the treatment outcomes is deteriorated when the dose per fraction of the radiotherapic scheme exceeds 6–10 Gy, which is a typical brachytherapy fractionation. Finally, we analyze the influence of the uncertainty and the variability of the main parameters utilized in the LQ model formulation in the assessment of the global dosimetry.

1. Background

Nowadays, the recommended radiotherapeutic treatment to ensure loco regional control and survival of patients with cervical cancer consists of the combination of external beam radiotherapy (EBRT) and a brachytherapy boost (BT).1, 2, 3, 4, 5 Several studies suggest that a contribution of 50% of either technique to the equivalent dose in 2 Gy per fraction (EQD2) of the global treatment leads to an optimal therapeutic window, reaching to a D90 for the high risk CTV (CTV_HR) of 85–90 Gy EQD2.1, 6, 7, 8, 9 The most relevant organs at risk (OR) are the bladder, whose dose constraint is 90 Gy EQD2, the rectum and sigmoid, whose dose constraints are 75 Gy EQD2, the bowel and the vagina.¹ These constraints are referred to the most exposed 2.0 cc (D2cc) of the mentioned OR.

Currently, there are several schedules in use combining both techniques. The EBRT is usually delivered in 25 fractions of 1.8–2 Gy, separated by enough time to allow normal tissue recovery, typically one day, in such a way that the treatment spans five weeks. On the other hand, the BT may deliver the dose by means of different temporal patterns: a continuous low dose rate regime (LDR) (0.5 Gy h⁻¹), pulsed rate (PDR) for several days (0.5–1 Gy h⁻¹), or high dose rate (HDR) (>12 Gy h⁻¹) by delivering several fractions in several days or weeks.1, 10, 11 Nevertheless, the actual trend reveals preference for the HDR scheme given its advantages over the other techniques.¹² For instance, high dose rate brachyterapy (HDR-BT) is more convenient for the patient, easier to administrate and it allows dose optimization to normal tissues. In addition, it represents an economic benefit for the center in comparison to other BT techniques. For this reason, from this point forward we will consider only the treatment composed by an EBRT and HDR-BT phases.

The schedule proposed by the University of Viena⁸ is widely accepted and commonly used. It consists of an EBRT phase of 45–50 Gy followed by two applications of HDR-BT separated by about one week, with two fractions each (7 Gy nominal per fraction). Other treatment schedules are also put into practice, the main difference between them being the temporal distribution in which the dose fractions of BT are delivered. In any case, the total treatment (EBRT + BT) should not be longer than 8 weeks to achieve better tumor local control and survival.9, 12, 13, 14

The biological effect caused by the dose absorption depends on factors such as the treated volume, the dose and dose rate distributions, the dose per fraction or pulse, the time interval between fractions or pulses, the overall treatment time, the radiation quality (LET), other therapeutic interventions (hyperthermia, chemotherapy, etc.), factors related to the patient (comorbidity) and factors related to the tumor (hypoxia).1, 11, 15 The dose per fraction, the dose rate and the treatment time are important concepts that differ in both techniques, EBRT and BT, regarding the temporal distribution.

Another relevant difference between the EBRT and the BT, which is an important factor in the effect of the radiation, is the different level of homogeneity of the distributions generated. The EBRT aim is to deliver dose as homogeneous as possible in the volume of interest, with variations between 95% and 107%.11, 16, 17, 18 On the other hand, the BT is characterized by high heterogeneous dose distributions even in small target volumes, due to the rapid and continuous dose fall close to the radioactive sources according to the inverse square distance law and the effective absorption of the dose by the tissues.¹⁵ The whole CTV comprehends a minimum dose, and on the inside it receives in great part of the volume a higher dose and dose rate in the vicinity of the radioactive sources.¹⁵ On average, the gross tumor volume (GTV) may receive up to 150% of the dose arriving at the CTV periphery, from which a steep drop of dose and dose rate is produced.¹ Actually, this high heterogeneity produces an important increment in the biological effect.¹⁹

Such differences in the spatial and temporal dosimetric distributions of the EBRT and the BT make the addition of its dosimetric contributions to the total dose distribution a very complex process. Furthermore, even though the register of the image studies of the EBRT and BT phases may be considered as a tool to perform this sum, the variations of the anatomy of the patient during the whole treatment jeopardize this solution, making this task even more complicated. Understanding all the aforementioned differences, radiobiology provides us with proper tools to know how to add the contribution of each treatment phase.

The commonly accepted practice to compute the cumulative sum of the doses delivered by the EBRT and the BT1, 20 implies the assumption of several approximations which make this task easier: the volumes or point of interest in the BT phase are considered to be irradiated uniformly by the prescription dose of the EBRT. This assumes that there is no area in the OR which is irradiated by a dose lower than that prescribed in the EBRT phase, which represents a conservative scenario for the OR, and is also more reasonable for the target, since the CTV_HR defined in the BT is a sub-volume of the PTV defined in the EBRT. Therefore, the summation of the contributions of the two phases of the treatment is based on the mere addition of the doses of the BT phase in the points and volumes of interests plus the prescribed dose in the EBRT phase, being both previously converted to their equivalent in 2 Gy per fraction, a process usually known as parametric sum.21, 22 This strategy facilitates the use of the linear quadratic model (LQ) to perform the assessment of the dosimetric distributions of the EBRT and the BT.²³

It is convenient to take into account that the basic formulation of the LQ model does not consider the effect of the overall treatment time. This model should be corrected in case a comparison were to be made between the different treatment schedules with their corresponding overall treatment times. More importantly, the model should be corrected before assessing the efficacy of the cervical cancer treatment.²⁴ This is one of the questions we are going to analyze in this work from a radiobiological point of view: the influence of the overall treatment time in which the EBRT and the BT are delivered in the result of the global treatment.

Another important feature to be considered is that the LQ model may overestimate the biological effect if the dose per fraction surpasses 6–10 Gy.25, 26 Below this range, we will get proper estimations by assuming a complete repair of the sub-lethal damage between fractions and protocols with similar repopulation processes and cellular redistribution.¹ In this work, we will also study the LQ model in this context, and its application will be analyzed.

Finally, we will also address the effect of the uncertainty and the variability in the parameters used in the LQ model.

2. Theoretical framework: the LQ model

The LQ model is the recommended one for the comparison and evaluation of treatments with different fractionations and dose rates.11, 15, 27, 28, 29 In this model, the cell survival fraction, S, in the presence of radiation exposure, decreases as the delivered dose, d, increases according to the following equation:

$$S=\exp (-\alpha d-\beta d^2)$$ (1)

The parameters α and β specify the sensitivity of the cell to the radiation.

Assuming that each successive fraction of the treatment produces equivalent effects, a biological effect predictor of the radiation is defined within the LQ model context as a function of the dose per fraction, d, the number of fractions, n, and the parameters α and β:

$$E=-\ln {(S)}^n=n(\alpha d+\beta d^2)$$ (2)

This equation is applicable to treatment schedules for which total recovery of normal tissue is assumed, such as EBRT and HDR. There is no need for corrections related to the different dose rates of these techniques, since the biological effects produced by them are similar, except for dose differences resulting from the different dosimetric homogeneities.¹

On the contrary, for LDR and PDR regimes it is necessary to take into account that the repair of sub-lethal damage starts after 15–30 min, this fact is the most influential factor for the radiation effect.¹¹ It is assumed that the repair kinetics is determined by a recovery mean time, T_1/2 (time for half of the DNA damage to be repaired). Therefore, the LQ model is modified as follows:

$$E_{\text{LDR},\text{PDR}}=(\alpha D+g\beta D^2)$$ (3)

where D is the total absorbed dose. The g factor, known as Lea-Catcheside factor,³⁰ is represented, in the case of LDR, by the expression:

$$g_{\text{LDR}}=\frac{2}{\mu t}\left[1-\frac{1-e^{-\mu t}}{\mu t}\right]$$ (4)

where μ = ln 2/T_1/2 is the recovery rate constant and t is the total time.

For PDR, an incomplete repair is assumed between and during fractions, in which the dose is delivered as an accelerated HDR.³¹ The g factor is described by the expression:

$$g_{\text{PDR}}=\frac{2}{\mu t}\left[1-\frac{NY-P{Y}^2}{N\mu t}\right]$$ (5)

where

$$Y=1-e^{-\mu t}$$

$$P=\left[\frac{NK-K-N{K}^2{e}^{-\mu t}+K^{N+1}{e}^{-N\mu t}}{{(1-K{e}^{-\mu t})}^2}\right]$$

with K = exp (−μt).

In this case t is the length of time of each pulse, x is the time between pulses and N is the total number of pulses.

It is usual to consider T_1/2 = 0.5–1 h for early-responding tissues and tumors, and T_1/2 = 1.5 h for late-responding tissues.¹¹

The figure that quantifies the biological effect of the radiation is the biologically effective dose, BED, defined for the fractionated schedule²⁶:

$$\text{BED}=\frac{E}{\alpha }=nd\left(1+\frac{d}{\alpha /\beta }\right)$$ (6)

Mathematically, it is defined as the dose required to yield the effect E produced by n fractions of d Gy in an infinite number of fractions of infinitely small doses. α/β quantifies the tissue sensitivity to fractionation changes. Early-responding tissues, of high α/β (7–20 Gy), are not as sensitive to fractionation changes as late-responding tissues, characterized by lower α/β (0.5–6 Gy). When two treatments lead to the same tissue effect, E and α are constant, and therefore its BED can be equalized in order to compare both treatments.

As previously mentioned, the biological effect of the radiation depends, among other factors, on the temporal schedule in which the dose is delivered, that is, its dose per fraction and dose rate. Therefore, in order to know the total biological or clinical effect of the combination of EBRT and BT, both treatment schedules should be translated into a common treatment schedule. The great clinical experience gathered throughout the history of radiotherapeutic treatments delivered at 2 Gy per fraction makes this schedule the appropriate one to perform comparisons and additions between treatments with different conditions, and consequently it is usual to take it as the reference radiotherapeutic schedule.¹ Hence, the equivalent dose to 2 Gy per fraction, EQD2, is defined as the dose to be delivered with 2 Gy per fraction to obtain the same biological effect as the treatment under consideration obtains. Accordingly, if two treatment schedules with the same LET and similar dose rates, a generic one with total dose D = nd and a reference one, have the same effect, Eq. (6) can be equalized for both, and the following is to be satisfied:

$$D\left(1+\frac{d}{\alpha /\beta }\right)=\text{EQD}2\left(1+\frac{2}{\alpha /\beta }\right)$$ (7)

$$\text{EQD}2=D\left(\frac{\alpha /\beta +d}{\alpha /\beta +2}\right)$$ (8)

3. Addition of EBRT AND BT

As previously mentioned, if we consider that during the EBRT the volumes of interest (D₉₈, D₉₀, D₅₀ regarding the CTV_HR and D_0.1cc, D_1cc y D_2cc for the OR1, 32 and points of interest (A points) are irradiated uniformly by the prescription dose, the LQ model provides a formulation with which it is possible to easily perform the summation of the doses of both treatment phases, EBRT and HDR-BT. The total BED will be the summation of the BED of each of those phases:

$$\text{BED}={\text{BED}}_{\text{EBRT}}+{\text{BED}}_{\text{HDR}-\text{BT}}$$ (9)

The absorbed doses by the points or volumes of interest of the target and OR of both techniques will be used to compute the EQD2 of each of them, in this way simulating treatment phases with identical fractionation and dose rate, making it possible to add these figures in order to obtain the EQD2 of the whole treatment.²² This simple approach is easy to perform in practice, and in fact, it is the scenario recommended to perform the summation of the cumulative dose of both treatments for cervix cancer.1, 15, 32 It is a conservative scenario which tends to over-estimate the dose to the normal tissue, foreseeing the existence of toxicity, but giving a reasonable estimation for the doses to the OR.²¹ Regarding this, worksheets have been supplied for the radiobiological assessment in the clinical practice (http://icru.org/content/reports/prescribing-recording-and-reporting-brachytherapy-for-cancer-of-the-cervix-report-no-89).

However, the most conservative scenario guaranteed by this approximation, although reasonable,20, 21, 33 is not what is really happening. The dosimetric distributions are not perfectly homogeneous and, in fact, in order to describe the shape of a dose-volume histogram (DVH) several values of dose-volume, D_V, are needed, selected in such a way that they can be correlated with the final effect.¹ Specifically regarding techniques such as IMRT or VMAT, in which high conformed dosimetric distributions are intended, but not necessarily uniform in the OR,³³ in general it would not be true that the sub-volumes of the walls of the OR close to the CTV_HR were irradiated the same as the more distant sub-volumes.1, 32, 34 It will also be necessary to consider whether a boost in the parametrial region or a nodal boost is performed as part of the EBRT treatment, since it will contribute additionally to the dose delivered to the volumes of interest at the moment of the HDR-BT.35, 36, 37, 38 In such cases, a more realistic assessment of the relevant dosimetric parameters could allow a dose escalation for the target volumes.²¹ The heterogeneity of the total dose distribution of the combination of EBRT and HDR-BT will depend, to a large extent, on the weight of the contributions of each technique to the global treatment, so that the more the HDR-BT is weighted, the more heterogeneous the distribution will be.¹

In the context of image guided brachytherapy for cervix cancer, the gold standard implies at least one image study per application.¹ The summation of the contributions of the EBRT and the HDR-BT will consider the dosimetric distributions as static in the different image sets performed during the treatment, typically a CT, where the EBRT dosimetry is performed, and the image studies (MR or CT) carried out during the BT phase. Therefore, the most irradiated sub-volume of each OR is supposed to be the same throughout the HDR-BT fractions.22, 32 In reality, during the treatment the ORs move and deform to a greater or lesser extent depending on the organ in question.¹ Also, the hot spots in the OR walls may or may not be continuous.32, 39 In addition, the applicator may modify its position from application to application, changing substantially the topography of the tissue.1, 21, 32 And finally, the tumor changes its volume and configuration, which also influences the OR configuration.32, 40 Additionally, in implants with interstitial component the irradiated target volumes with low doses may be at different locations throughout the different BT fractions. Therefore, the static scenario which is implicit in the approximation assumed when adding EBRT and HDR-BT, would not always be the most representative one, and thus, each particular clinical case should be considered carefully in order to analyze the suitability of the approximation.1, 22, 33

The most suitable and broadly accepted tool to evaluate the dose in the considered volumes and its homogeneity is the DVH, which is usually evaluated in its cumulative form, although its differential form provides relevant information which would be important to take into account also (one example of this is the use of the differential DVH to compute the generalized equivalent uniform dose, gEUD, for OR).⁴¹ The precision of the histograms depends on the treatment planning system (TPS) and the algorithm used in it, and may influence the results of the analysis.¹⁵ Nevertheless, the DVH lacks the information related to the spatial distribution of the dose in a specific volume, which is an intrinsic limitation of the DVH. The fact of adding the dose of EBRT and HDR-BT without taking into account how the spatial distribution of the dose varies in the volumes may over-estimate the EQD2 in the OR, jeopardizing the target coverage during the dose optimization process.1, 39 It is impossible to have a single DVH with totally comprehensive information of both contributions.21, 23, 29 This is the reason why, ideally, the summation of both radiotherapy phases should take into account the radiation effect at a cellular level.¹

The methods based on a voxelized dosimetry do not take into account the changes of the volumes produced throughout the global treatment, thus being insufficient for a precise assessment of the whole treatment effect.¹ But up to now, there has been no method to take into account the temporal evolution of the dose distribution throughout the treatment. Therefore, due to the inter-fraction, intra-fraction and inter-application variations, it is not possible to perform a rigid registration of the different image sets.1, 33, 42, 43 It would be necessary to identify each irradiated voxel in each HDR-BT fraction and match it with the correspondent irradiated voxel in each HDR-BT fraction.1, 32 The deformable register is a technique that tries to trace this historical information of the irradiated volumes of interest, mapping the voxels between the different image sets.22, 44 One of the challenges of the deformable register is to tackle the fact of having an applicator in place in one of the image sets to be registered.1, 45 In the case of EBRT treatments, with or without boost, it seems to provide more realistic results when estimating the dose to the OR than a simple parametric summation.²¹ Although currently this research field is rather active, this technique has not yet been clinically validated in a reliable way.1, 21, 22

3.1. Example: application of the LQ model to assess the dose in the combined treatment of EBRT and HDR-BT in cervix cancer

A cervix cancer patient follows a radiotherapy treatment consisting of 25 fractions of EBRT of 1.8 Gy each, 5 days a week, to achieve 45 Gy. This treatment is combined with 2 HDR-BT applications separated by a week, each composed of two fractions of 7 Gy nominal delivered in two consecutive days. In each HDR-BT fraction, the volumes of interest receive the doses shown in Table 1, figures which are converted into EQD2 considering α/β = 10 Gy for the tumor and α/β = 3 Gy for the ORs. The total dose delivered by EBRT is also transformed to EQD2 and the result, shown in the last column of Table 1, corresponds to the summation in EQD2 of the 4 HDR-BT fractions and the total dose delivered by EBRT. In this example, only the most common ORs, the bladder, rectum and sigmoid, are included.

Table 1.

Illustrative example of the computation of the total dose delivered (in Gy) by the combination of EBRT and HDR-BT phases for a typical scheme of cervix cancer radiotherapy treatment. It is indicated in bold the dosimetric variables and values upon which the recommended dosimetric constraints are referred, that is, D₉₀ for the CTV_HR and D_2cc for the ORs.

		BT, Fraction 1		BT, Fraction 2		BT, Fraction 3		BT, Fraction 4		EBRT		Total
		D	EQD2	D	EQD2	D	EQD2	D	EQD2	D	EQD2	EQD2
CTVHR	D98	5.75	7.55	5.93	7.87	6.24	8.44	6.02	8.04	45	44.24	76.14
	D90	7.08	10.08	7.22	10.36	7.41	10.75	7.15	10.22			85.65
	D50	10.39	17.65	10.41	17.71	10.78	18.67	10.13	16.99			115.26
Bladder	D0.1cc	6.33	11.81	6.35	11.87	6.26	11.59	6.56	12.54	45	43.20	91.01
	D1cc	5.94	10.62	5.97	10.71	5.67	9.83	6.09	11.07			85.43
	D2cc	5.75	10.06	5.83	10.30	5.38	9.02	5.81	10.24			82.82
Rectum	D0.1cc	5.03	8.08	5.05	8.13	5.81	10.24	4.79	7.46			77.11
	D1cc	4.56	6.89	4.59	6.97	4.67	7.16	4.38	6.46			70.68
	D2cc	4.34	6.37	4.38	6.46	4.20	6.05	4.04	5.69			67.77
Sigma	D0.1cc	5.51	9.38	5.53	9.43	5.30	8.80	4.79	7.46			78.27
	D1cc	4.77	7.41	4.80	7.49	4.29	6.25	3.93	5.45			69.80
	D2cc	4.40	6.51	4.42	6.56	3.82	5.21	3.60	4.75			66.23

4. Overall treatment time effect

The cellular proliferation of many tumors has an important influence on the result of radiotherapy,⁴⁶ and it also explains the reason why a prolongation of the total treatment time produces a tumor control probability reduction for patients treated exclusively with radiotherapy, or with surgery and chemotherapy followed by radiotherapy.47, 48, 49 This is so in the case of the cervix,9, 13, 50, 51, 52, 53, 54, 55 even employing chemotherapy,⁵⁶ which is why it is considered to be category 1 according to The Royal College of Radiologist recommendations.⁵⁷ That is to say, they are patients with a cancer type for which it is evident that the prolongation of treatment does affect the results, having been treated with curative intention, particularly in the case of combined treatments. Therefore, patients receiving EBRT plus BT should not have the overall time of their treatments prolonged.

In order to include the effect of the proliferation in the LQ isoeffect equation, a term can be added accounting for the increment of the cell number as time passes. If for that purpose, as usual, the exponential growth model is utilized, the LQ survival equation may be written as⁵⁸:

$$-\ln S=nd(\alpha +\beta d)-\frac{\ln 2}{T_{\text{eff}}}T$$ (10)

where T is the total time to deliver the treatment and T_eff the total effective doubling time. Thus, we obtain:

$$\text{BED}(D,d,T)=D\left(1+\frac{d}{\alpha /\beta }\right)-\kappa T$$ (11)

with κ = ln 2/(αT_eff). κ is known as the time factor and, although it has units of absorbed dose per time, it does not represent the dose needed to compensate for the repopulation effect caused by the addition of treatment days, but the BED required for that compensation. Considering values for the parameter α between 0.2 and 0.4 Gy⁻¹ and values for T_eff between 3 and 6 days,⁵⁴ κ takes an average value of 0.5 Gy/day, and for highly proliferative and radio resistant tumors κ may be bigger than 1 Gy/day.

Some tumors have shown a phenomenon known as accelerated repopulation, which is an increase in the proliferation rate in respect to that of the tumor before the beginning of the therapy, as the treatment progresses.46, 59 Since the accelerated repopulation manifests several weeks after the treatment is initiated, Eq. (11) can be modified to consider this fact:

$$\text{BED}(D,d,T)=D\left(1+\frac{d}{\alpha /\beta }\right)-\kappa \max (T-T_0,0)$$ (12)

That is to say, the total time effect does not occur before a time T₀ from the beginning of the treatment, because max(T − T₀, 0) produces a value other than 0 only if T is greater than T₀. For the cervix tumor, the estimation for T₀ is 19 days (CI95%).⁵⁴

With the change in the LQ model expressed in Eq. (11), we should take into account the total treatment time in the EQD2 assessment. Given a treatment schedule (D, d, T), we can define a biologically effective dose delivered with a schedule of 2 Gy per fraction in a total time T′ as follows:

$$\text{BED}(\text{EQD}{2}_{T^{\prime }},2,T^{\prime })=\text{BED}(D,d,T)$$ (13)

According to Eq. (11) we have:

$$\text{EQD}{2}_{T\text{'}}=\frac{\alpha /\beta }{2+\alpha /\beta }\left[D\left(1+\frac{2}{\alpha /\beta }\right)-\kappa (T-T^{\prime })\right]$$ (14)

In the case of EBRT followed by HDR-BT, we can rewrite Eq. (14) as:

$$\text{EQD}{2}_{T^{\prime }}=\frac{\alpha /\beta }{2+\alpha /\beta }\left[D_{\text{EBRT}}\left(1+\frac{d_{\text{EBRT}}}{\alpha /\beta }\right)+D_{\text{BT}}\left(1+\frac{d_{\text{BT}}}{\alpha /\beta }\right)-\kappa (T-T^{\prime })\right]$$ (15)

where D_EBRT and d_EBRT are, respectively, the total dose and the dose per fraction delivered in EBRT, D_BT and d_BT the total dose and dose per fraction delivered in HDR-BT, T the total time of the combined treatment and T′ the total time of the reference schedule delivered at 2 Gy per fraction.

In order to examine the total time effect in the result over the tumor of the combined treatment of EBRT and HDR-BT, we will contemplate a common clinical situation: a combined schedule consisting of 45 Gy of EBRT, delivered in fractions of 1.8 Gy, plus 4 fractions of 7 Gy of HDR-BT delivered in 2 applications or implants with 2 fractions each, given on Thursday and Friday of 2 consecutive weeks.

We assume that no interruptions happen and that the treatment starts on Monday, but the choice of the 2 weeks in which the HDR-BT is delivered is different between institutions. We are going to study the cases in which the HDR-BT starts, in the earliest case, the third week and it is separated from the beginning of the treatment by one week at a time; that is, the total time will amount to 39 days for the HDR-BT in weeks 3 and 4 or weeks 4 and 5, and will be increased when HDR-BT starts from week 5 on, amounting to 68 days in the longest schedule (Fig. 1). Now it is not necessary to perform a correction like that suggested in Eq. (12), as in this case the total treatment time is always longer than 19 days.

Fig. 1.

Representation of 7 different examples of radiotherapy schedules combining EBRT with HDR-BT. The red bars represent the days of EBRT; the long gray bars represent the weekends, in which there is not treatment; the short gray bars represent days in which there is not EBRT treatment, since it already finished; the black bars represent the days of HDR-BT; the blue line represent the recommended total treatment time limit of 8 weeks. The total treatment time, in days, is also displayed.

For the computation of EQD2, we take a reference time T′ = 39 days, that is, we calculate EQD2_39days. We assume α/β = 10 Gy and two values for κ, 0.5 and 1.0 Gy/day, which reflect situations of moderate and high proliferation, respectively. The results are shown in Table 2, where remember that the recommendations establish a time limit of 8 weeks for the whole treatment.9, 12, 13, 14

Table 2.

Values of EQD2_39days for the treatment schedules of Fig. 1.

BT beginning		Week 3	Week 4	Week 5	Week 6	Week 7	Week 8	Week 9
Overall treatment time (days)		39	39	40	47	54	61	68
EQD239days (Gy)	κ = 0.5 Gy/day	83.9	83.9	83.5	80.6	77.7	74.8	71.8
	κ = 1.5 Gy/day	83.9	83.9	83.1	77.3	71.4	65.6	59.8

Although the EQD2_39days values indicate a reduction of the effectiveness of the treatment when the overall treatment time increases, it is better to estimate this reduction by means of the tumor control probability (TCP) associated to each treatment scheme. To do so, following the previous example, we utilize the logistic model⁶⁰:

$$\text{TCP}(D)={\left[1+{\left(\frac{D_{50}}{D}\right)}^{4\gamma }\right]}^{-1}$$ (16)

where D₅₀ is the total dose needed to reach 50% of control and γ is the gradient of the dose–response relation normalized in D₅₀.

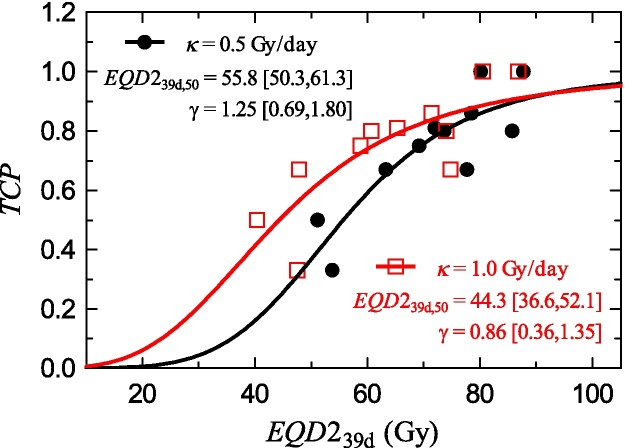
In order to perform the calculations, we need the values of the parameters in Eq. (16). We use the data of the work of Huang et al.⁵⁴ which can be seen in Table 3. Table 3 also includes the computation of the EQD2_39days, which allows fitting the free parameters in Eq. (16) to those data to obtain D₅₀ = EQD2_39days,50 and γ (Fig. 2). The fit has been performed with Mathematica version 10 (Wolfram Research, Inc.). The experimental data and the fit results are shown in Fig. 2. We obtain results for the TCP which are in accordance with the literature.⁹

Table 3.

Data of Huang et al.⁵⁴ for the total dose of a schedule of 1.8 Gy per fraction and control probability for 11 groups of patients with different overall treatment times. In the columns 3 and 4, the values of EQD2_39days are shown for κ = 0.5 and 1.0 Gy/day, respectively.

EQD1.8 (Gy)	Overall treatment time (days)	EQD239days (Gy)		TCP
		κ = 0.5 Gy/day	κ = 1.0 Gy/day
61	54	53.7	47.5	0.33
63	65	51.1	40.3	0.50
81	38	80.1	80.5	1.00
82	46	77.7	74.8	0.67
80	55	72.0	65.3	0.81
81	64	69.2	58.8	0.75
80	76	63.3	47.8	0.67
90	41	87.7	86.8	1.00
87	56	78.5	71.4	0.86
88	70	73.6	60.7	0.80
99	67	85.9	74.0	0.80

Fig. 2.

Probability control data from the work of Huang et al.⁵⁴ transformed to obtain the EQD2_39days equivalence and fits of the control probability model (16) to those data. Red squares correspond to κ = 1.0 Gy/day and black circles to κ = 0.5 Gy/day. The results of the fit of (16) to the data in Table 3 are also shown. The confidence interval is referred to as 95%.

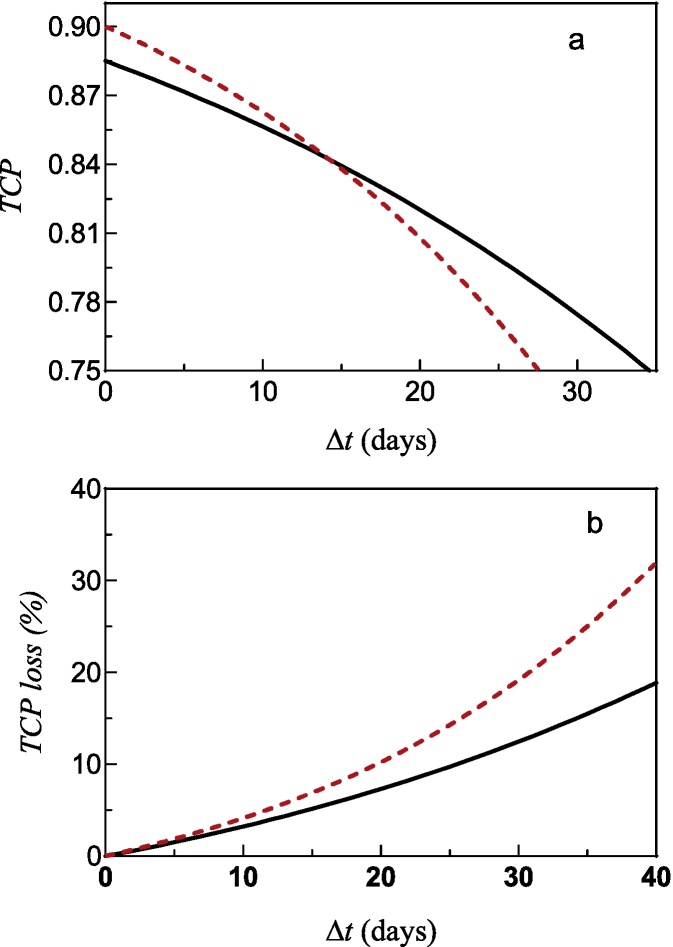
Once these fits have been performed, we can obtain the drop of tumor control associated with the increase of the combined treatment duration. The results are shown in Fig. 3. The lack of linearity of the TCP dependence on the overall treatment time increment implies that the TCP drop grows bigger as the time delay increases (Fig. 3a). Therefore, the TCP reduction becomes more and more important as the overall treatment time raises (Fig. 3b). Consequently, each week of increase in the total treatment time produces a gradually worsening effect.

Fig. 3.

(a) Tumor control as a function of the increase in the total combined treatment time above 39 days. (b) Absolute loss of tumor control with respect to the treatment with duration of 39 days. The results for κ = 1.0 Gy/day are represented by the discontinuous red line and for κ = 0.5 Gy/day, by the continuous black line.

Finally, the total dose (and dose per fraction) of HDR-BT can be computed in order to compensate the tumor control loss produced by the increase in the total treatment time with respect to the one which is 39 days long. This is shown in Table 4, in which it can again be seen that the later the HDR-BT initiates, the bigger the dose per fraction correction will need to be. Such correction points in the same direction as the results obtained by Tanderup et al.⁹ According to our calculations, an increase in EQD2 of 5.83 κ Gy per week is needed to compensate the TCP loss. Tanderup et al.⁹ indicate that 5 Gy are required to compensate an increase of the overall treatment time of 1 week, a result which is within the interval considered here for κ = 0.5 and κ = 1, with a tumor control loss between 1% and 2.5% depending on the tumor size. Other authors report a TCP loss between 0.67% and 1.6% per day of increase of the total treatment time above 55 days.53, 55, 56

Table 4.

Values of dose per fraction and total dose to compensate the tumor control loss, with respect to that achieved with the scheme of 39 days, when the total treatment time increases.

Beginning of HDR-BT		Week 3	Week 4	Week 5	Week 6	Week 7	Week 8	Week 9
Overall treatment time (days)		39	39	40	47	54	61	68
dBT (Gy)	κ = 0.5 Gy/day	7	7	7.1	7.4	7.8	8.1	8.4
	κ = 1.5 Gy/day	7	7	7.1	7.8	8.5	9.1	9.7

In light of the above, if an absorbed dose of 85–90 Gy EQD2 is recommended for this combined treatment, such a recommendation should also consider the overall treatment time.

In addition, it is important to take into account that the EBRT may be prolonged due to treatment interruptions and, therefore, it is essential to manage them adequately.

However, the TCP drop with the overall treatment time may reflect a bad prognosis of the treatment, the relation with cellular proliferation being unclear, that is, patients with bad prognosis would have longer overall treatment times.⁶¹ Some institutions’ experiences indicate that the prolongations of the total treatment time are a result of poor coordination between EBRT and BT.⁵⁵

5. Uncertainties and variability

As Eq. (15) indicates, EQD2 depends on the value considered for α/β. As we have seen, in order to perform the calculations for the combined treatment, generic values of α/β =3 Gy and α/β = 10 Gy are recommended for late-responding normal tissue and tumor response, respectively.¹ Nevertheless, there are several reasons why the generic values taken for α/β may change or be different than the ones employed as the reference. We will address such reasons further on.

These generic values are affected, in the first place, by an important uncertainty in their clinical determination. Besides, their average values may change due to the progress in the state of the art. In fact, this has already happened for the α/β value considered for prostate cancer in recent years⁶² and also for an important tissue in our case, the bladder, for which an α/β value as low as 0.4 Gy is suggested,⁶³ which would imply a much bigger sensitivity of this organ for high doses per fraction than that currently supposed. Another important aspect that should be taken into account is the variability in the response between patients, which makes the use of a generic value for α/β more uncertain.

Considering any of the reasons why the α/β value has such an important uncertainty, one can analyze the influence of this uncertainty in the estimation of EQD2 by means of a simple Monte Carlo simulation, performed in Mathematica version 10 (Wolfram Research, Inc.), in a certain case in which Eq. (15) is utilized. This can now be applied to the example in Section 3.1.

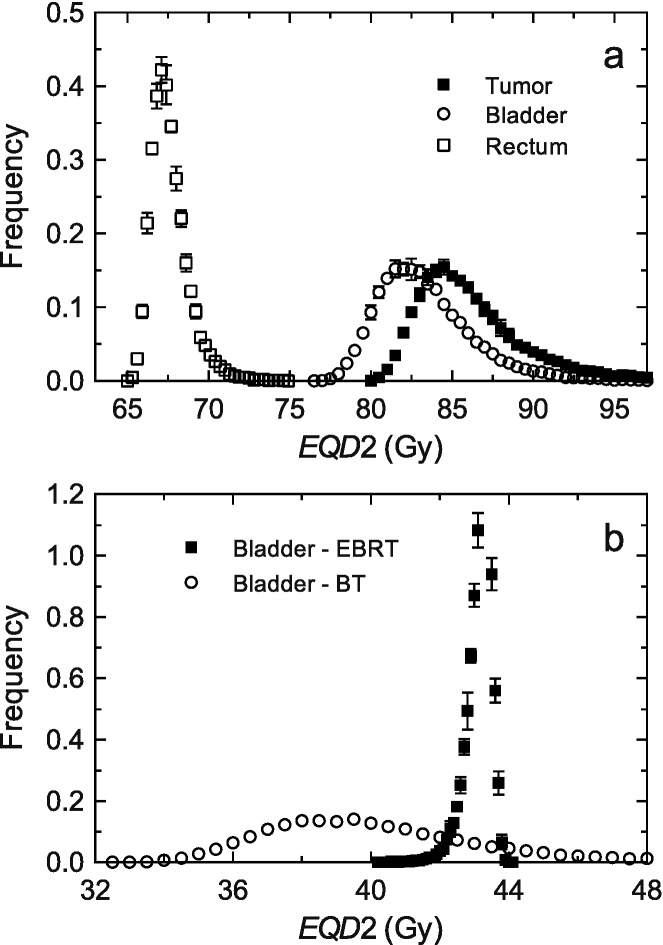
For the HDR-BT with 4 fractions, the following is assumed: for the D₉₀ of the CTV_HR a mean value of dose per fraction of 7.2 Gy, for the D_2cc of the bladder, a mean value of 5.7 Gy per fraction and for the D_2cc of the rectum and sigmoid (we would not distinguish between them since they both receive very similar doses and have the same tolerance) a mean value of 4.2 Gy per fraction, as we can see in Table 1; it is assumed that the dose distribution produced by EBRT is homogeneous for the tumor and ORs. Now it is supposed that α/β may change according to a normal distribution N[α/β,σ], where α/β is the average reference value for each tissue (10 Gy for the tumor tissue and 3 Gy for the normal one) and σ is the standard deviation, which is taken as 30%, a value which has been chosen from the typical uncertainties in the clinical studies that provide estimations of α/β (the reader may take a look at the values for rectal toxicity⁶⁴ or skin fibrosis, intestine late effects and skin and breast cancers as examples in Table 9.1 of Joiner and van der Kogel⁶⁵) and that, therefore, maybe under-estimates the total uncertainty. It will be considered the reference schedule of 39 days long in the previous section. With these assumptions, we will perform a simulation with a high number of events (25,000 of them, so that we have good statistics), which will provide values for the D₉₀ of the CTV_HR, EQD2_tumor, and for the D_2cc of the normal tissues, EQD2_bladder and EQD2_rectum. The contribution of each phase of the total treatment (EBRT plus HDR-BT) to the final EQD2 is also analyzed in the case of the bladder. The obtained distributions are shown in Fig. 4.

Fig. 4.

(a) EQD2 distributions for the D₉₀ of the CTV_HR (black squares), EQD2_bladder and EQD2_rectum for D_2cc of the bladder (white circles) and the rectum (white squares). (b) Contribution of each treatment phase to the final EQD2 for the bladder. Uncertainties correspond to a confidence interval of 95%.

As can be observed in Fig. 4a, the effect of the variability, or the uncertainty, in α/β, in the total EQD2 is relatively small, since, having introduced a standard deviation of 30% in this parameter, the standard deviation obtained for the EQD2 values is 3% for the tumor and the bladder, and 1.4% for the rectum. Therefore, although it is important to consider the uncertainty in our knowledge of α/β, we could conclude that the use of generic values for the tumor and the normal tissues does not have a great influence on the EQD2 calculation, unless the variation of α/β is very important.

Nevertheless, it is necessary to consider that the effect of the change of α/β is almost entirely due to the HDR-BT treatment, as can be observed in Fig. 4b, where the distributions corresponding to the EQD2 produced by EBRT and HDR-BT have been separated. The variability in the case of EBRT is very small, 0.7%, compared to that obtained for HDR-BT, 7%; and since the dose per fraction of EBRT is less than 2 Gy, the tail of the distribution has the opposite direction as the tail of the distribution of the HDR-BT treatment, which produced, because of its influence, the whole tail of the distribution of EQD2. Note that in the case of HDR-BT, an increase in the α/β respect to the one taken as reference (which makes EQD2 drop, left side of the distributions) has a smaller effect in EQD2 than a decrease of the same quantity (which makes EQD2 increase, right side of the distributions), since the absolute value of the derivative of EQD2 with respect to α/β raises more quickly when α/β decreases. For EBRT delivered with doses per fraction smaller than 2 Gy, since the sign of the derivative is positive, the tail of the distribution goes in the opposite direction; now an increase of α/β respect to that taken as reference makes EQD2 increase. In this sense, it can be seen that a drop of the dose per fraction received by the normal tissue in the HDR-BT produces a smaller uncertainty in the determination of EQD2, as can be observed in the histogram of the rectum compared to that of the bladder in Fig. 4a. Finally, note that the considered uncertainty span a range which exceeds the tolerance value of the bladder (90 Gy), while it does not for the rectum (75 Gy), although this applies for this example presented here in particular. Therefore, and as a conclusion, it is convenient to perform an estimation of the uncertainty associated with the computation of EQD2 and consider, if appropriate, the possibility of exceeding the tolerance doses or not reaching the established values for the CTV_HR doses.

Secondly, a way of taking into account the whole biological effect due to the heterogeneity of the dose distribution, so important in BT, and to the dependence with the irradiated volume of the different organs, characterized by a parameter that is usually denoted as n (which varies between 0, for series tissues such as the spinal cord, and 1, for parallel tissues such as the lung), is to use an effective value for α/β, α/β_eff, which allows the employment of the basic equations of the LQ model66, 67 just by replacing the parameter α/β by α/β_eff. Therefore, the effect of the heterogeneity and the type of tissue, regarding the parameter of volume, can be considered by means of a variation in α/β; that is, certain irradiation circumstances of a particular tissue conditions the α/β value. Consequently, it is possible to distinguish between the α/β values corresponding to the EBRT, and the α/β values corresponding to the HDR-BT. In general this distinction will affect normal tissue more, which is usually irradiated with important heterogeneities (even in EBRT when techniques such as IMRT or VMAT are used), than tumor tissue, which irradiation is more homogeneous.

Additionally, the validity of the LQ model has been questioned when the doses per fraction are high, and the doses employed in HDR-BT for the combined treatments in this work (7 Gy per fraction in the given example) are considered to be in the limit of high doses. This is a controversial issue which, it can be said, has not been solved yet,⁶⁷ but it admits a pragmatic approximation which allows a description of the clinical results despite our lack of awareness of the biological mechanisms which produce them. Therefore, it would be sufficient to consider that the survival model LQ is just an empirical approximation which is valid in a limited range of doses. In this way, we could take an adequate fit of the LQ model in the low or intermediate dose region, with a value (α/β)_L, and another one in the intermediate to high doses region, with a value (α/β)_H, so that the predictive capacity of the LQ model holds in each region.

Under this pragmatic perspective, and taking into account the considerations of the two previous paragraphs, the equation for EQD2, without considering the time, could be written in the following way:

$$\text{EQD}{2}_{T^{\prime }}=\frac{{(\alpha /\beta )}_E}{2+{(\alpha /\beta )}_E}\left[D_{\text{EBRT}}\left(1+\frac{d_{\text{EBRT}}}{{(\alpha /\beta )}_E}\right)+D_{\text{BT}}\left(1+\frac{d_{\text{BT}}}{{(\alpha /\beta )}_B}\right)\right]$$ (17)

where the values of (α/β)_E and (α/β)_B represent the adequate values for the conditions of the dose distributions in the cases of the EBRT and the HDR-BT, respectively.

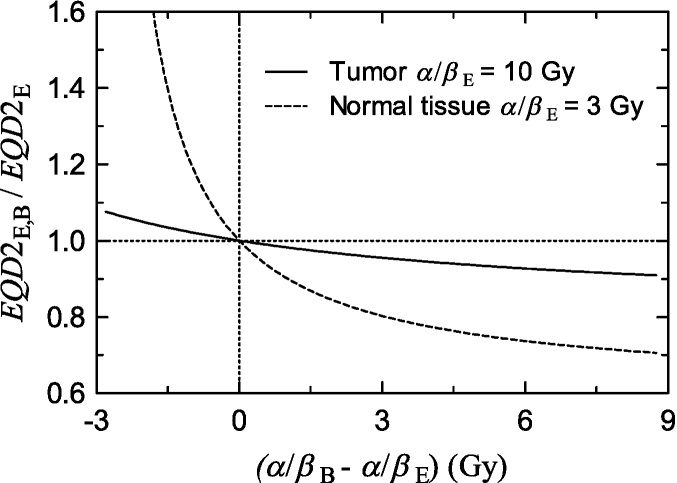
Fig. 5 shows the ratio between the EQD2 computed according to Eq. (17) and the EQD2 computed according to Eq. (15) with κ = 0, considering fixed values for (α/β)_E equal to 3 Gy and 10 Gy for the normal tissue and the tumor, respectively, as a function of the difference between (α/β)_E and (α/β)_B. As can be seen, considering two different values of α/β for EBRT and HDR-BT has an effect which is more important for low values of α/β, which correspond to normal tissues, than in the case of tumors, with higher α/β.

Fig. 5.

Ratio between EQD2 computed with Eq. (17) and EQD2 computed with Eq. (15) considering fixed values for (α/β)_E equal to 3 Gy and 10 Gy for the normal tissue and the tumor, respectively, as a function of the difference between (α/β)_E and (α/β)_B. We have considered an EBRT schedule of 45 Gy in fractions of 1.8 Gy plus 4 fractions of 7 Gy of HDR-BT.

It is usual to consider that the LQ model over-estimates the cellular death in the range of dose per fraction under consideration for HDR-BT,⁶⁸ therefore, if we do not consider the effect of the heterogeneity, (α/β)_B is bigger than (α/β)_E and the EQD2 computed with the usual Eq. (15) will be bigger than that produced by Eq. (17).

In addition to the uncertainty associated to the value of κ and its variability between patients, the overall treatment time effect on the effectiveness of the radiotherapy on cervix cancer, which is only considered in the case of the tumor, it is affected also by the α/β value, since the equivalent dose lost per day of increase in the total treatment time is written as:

$$\Delta \text{EQD}{2}_{T^{\prime }}=\frac{\alpha /\beta }{2+\alpha /\beta }\kappa (T-T^{\prime })$$ (18)

As done previously, an assessment can be made of the effect of the variability in α/β and κ, although it is now much simpler. Since α/β is in the numerator and in the denominator of the quotient, its influence is very small, hence, the uncertainty in κ translates directly to ΔEQD2, since the dependence is linear.

All these considerations should serve as a general warning about the use of generic values of α/β. The uncertainty in α/β is important to determine the dose–response relationships of the different tissues, tumor and normal, and to estimate the final result of the treatment. According to the issues analyzed in this section, the values utilized in the computations may change with respect to the current consensual values and, therefore, it is fundamental to adequately register all the variable dosimetric aspects of the treatments without radiobiological correction, and so its results.¹

6. Conclusions

A radiobiological description of the currently recommended method of summation of the external beam radiotherapy and brachytherapy phases for the treatment of cervix cancer is performed. Some important points regarding the use of the radiobiological LQ model in the assessment of the comprehensive dosimetry of the whole treatment have been addressed.

A prolongation of the overall treatment time above the recommended 8 weeks worsens the tumor control probability considerably. Therefore, it is important to carefully manage the temporal features of the delivery of the treatment, such as interruptions to the treatment and when to begin the BT phase.

It can be concluded that estimation of the EQD2 is not dramatically affected by the uncertainty of the most important parameters of the LQ model, which consolidates the LQ model as a solid tool for the assessment of the relevant dosimetric quantities.

The validity of the LQ model when the dose per fraction is higher than 6–10 Gy is a controversial issue that may be pragmatically solved in view of the analysis performed in this work, which supports the unexplored idea of considering two different α/β values, one for each of the typical regions employed in EBRT (low dose region) and BT (high dose region).

Conflict of interest

None declared.

Financial disclosure

None declared.