Applying the Monod-Wyman-Changeux Allosteric Activation Model to Pseudo–Steady-State Responses from GABA_A Receptors

Abstract

The Monod-Wyman-Changeux (MWC) cyclic model was described as a kinetic scheme to explain enzyme function and modulation more than 50 years ago and was proposed as a model for understanding the activation of transmitter-gated channels soon afterward. More recently, the MWC model has been used to describe the activation of the GABA_A receptor by the transmitter, GABA, and drugs that bind to separate sites on the receptor. It is most interesting that the MWC formalism can also describe the interactions among drugs that activate the receptor. In this review, we describe properties of the MWC model that have been explored experimentally using the GABA_A receptor, summarize analytical expressions for activation and interaction for drugs, and briefly review experimental results.

Introduction

The Monod-Wyman-Changeux (MWC) (Monod et al., 1965) cyclic model was described more than 50 years ago as a kinetic scheme to explain enzyme function and modulation and was proposed as a model for understanding the activation of transmitter-gated channels soon afterward (Karlin, 1967). Subsequent work by J. P. Changeux’s group and others has extended the discussion (Edelstein and Changeux, 1996; Edelstein et al., 1996). Colquhoun and Lape (2012) have discussed the application of the MWC model to channel activation.

The MWC model has been used most extensively to describe the activation of the GABA_A receptor by GABA (Chang and Weiss, 1999) and drugs that bind to separate sites on the receptor including clinically used anesthetic agents (Rüsch et al., 2004; Rüsch and Forman, 2005; Campo-Soria et al., 2006; Ruesch et al., 2012; Ziemba and Forman, 2016; Shin et al., 2017, 2018; Akk et al., 2018; Germann et al., 2018). Of the greatest interest for this review is the finding that use of the MWC formalism can describe interactions among drugs (Rüsch et al., 2004; Rüsch and Forman, 2005; Ruesch et al., 2012; Ziemba and Forman, 2016; Shin et al., 2017, 2018; Akk et al., 2018; Germann et al., 2018). A review by Forman (2012) has covered some of the topics in this review.

MWC Scheme for One Drug

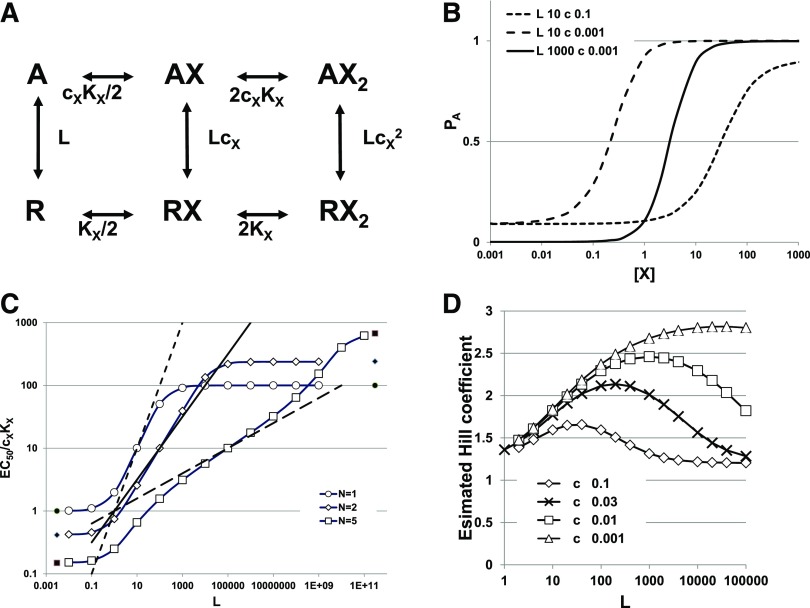
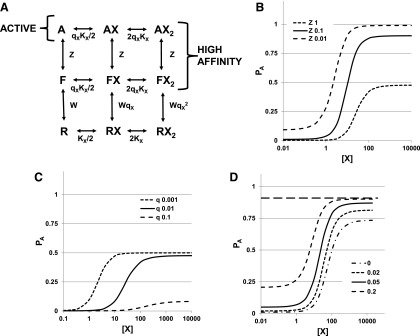
The MWC model is a cyclic model with strong constraints. A receptor has N_X identical sites for a ligand, X. The receptor can exist in two states, R (resting) and A (active), with differing affinities for X (microscopic dissociation constants K_X,R and K_X,A). When the receptor changes state, the properties of all N_X sites change, so the sites always have identical affinities and there cannot be a mixture of sites with the two different affinities on the same receptor at the same time. Another way to put this is that the two states apply to the receptor, rather than to the sites separately. The ratio of affinities is given by c_X = K_X,A/K_X,R. In the absence of X, the relative prevalence of the two states is given by the ratio L = R/A. Figure 1A shows a state diagram for a case when N_X = 2.

Fig. 1.

Model and predictions for one drug. (A) The state diagram for drug X with two sites acting on a receptor after the MWC concerted transition scheme. Inactive receptor states (R) occupy the line at the bottom, whereas active states (A) occupy the line at the top. In the absence of X, the receptor activates with the inverse of the activation equilibrium given as L = R/A. Agonist X binds to its site with dissociation constant K_X,R on the inactive receptor and K_X,A on the active receptor, with c_X = K_X,A/K_X,R. In the scheme, K_X = K_X,_R. The equilibrium between R and A states is determined by c, as dictated by detailed mass action in the coupled cycles. (B) Activation curves (P_A) as a function of [X] for three combinations of parameters. For all the relationships, N_X = 2 and K_X = 100 (K_X = K_X,R). The values for L and c_X were varied as shown in the figure legend. (C) A log-log plot of the normalized EC_50,X against L for three values of N_X with c_X = 0.01 and K_X,R = 100. The lines show slopes of 1/N_X, whereas the filled symbols show the predicted values for the asymptotes. Note that the EC₅₀ value can be less than K_X,A (=1 in the normalized plot) or greater than K_X,R (=100 in the normalized plot). (Panel modified from Akk et al., 2018). (D) The Hill coefficient plotted against L for different values of c_X (0.1, 0.03, 0.01, and 0.001, as indicated) whereas for all plots in the panel N_X = 3, K_X,R = 100. Estimates were made using eq. 1.16.

The focus of this review is receptor activation, so the “state function” is the major topic and very little mention will be made of the “binding function”—the occupancy of sites on the receptor.

The Probability of Being Active.

The probability that a receptor is active (in the A state) with any number of bound X molecules is:

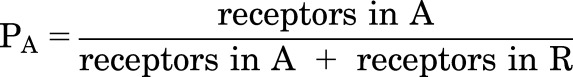(1.1)

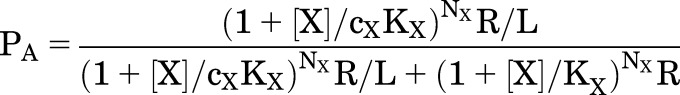(1.2)

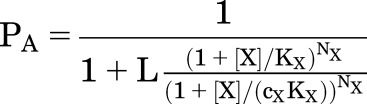(1.3)

where K_X is the dissociation constant for X on the inactive receptor (K_X,R), c_X is the ratio of dissociation constants for active to inactive receptors (K_X,A/K_X,R), N_X is the number of identical sites for X on the receptor, and L is the reciprocal of the equilibrium activation ratio in the absence of X (R/A).

Equation 1.3 differs from the form in the original description (Monod et al., 1965) in that K_X is defined as the dissociation constant for the resting receptor state, while the original description defined it as that for the active state.

A small value for L indicates that the energy difference between active and inactive states is small, so a relatively large proportion of receptors is active even in the absence of drug X. We will use L for the activity in the absence of drug X, although there may be a background drug present. The constitutive activity seen in the absence of any known activator or inhibitor is usually assumed to be an intrinsic property of the receptor, although it is possible that endogenous chemicals (e.g., membrane lipids) or possible post-translational modifications affect the activity in addition to consequences resulting from receptor structure.

The parameter c_X reflects the selectivity of the drug between the two states. Agonists, by definition, bind more tightly to the active state of the receptor; hence, the value for c_X is <1 for an agonist.

In the absence of X, the receptor has a low probability of being active, termed the “constitutive activity” or minimal activity:

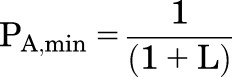(1.4)

whereas in the presence of saturating [X], when all sites are occupied, the probability of being active is:

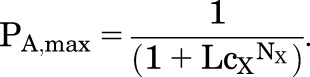(1.5)

The energy difference between active and resting states in the absence of X is RT × ln(L). The “stabilization energy” contributed by the binding of agonist when all sites are occupied is N_XRT × ln(c_X).

Three examples of concentration-activation relationships are shown in Fig. 1B. In each case, N_X = 2, whereas L is 10 or 1000 and c_X is 0.1 or 0.001. P_A,min depends on L, whereas EC_50,X and P_A,max depend on both L and c_X.

The Concentration of Agonist Producing EC₅₀

By definition, the P_A at [A] = EC_50,A (P_{A, γ}) is one-half of the maximal response:

Karlin (1967) gives an expression for the value of EC_50,X normalized to K_X,A:

The value for P_A,γ from eq. 1.3 is:

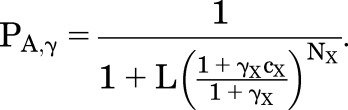Substituting the value for P_A,γ and the definitions for P_A,max and P_A,min, and doing some algebra gives the equation given by Karlin (1967) for “α_1/2” in his Table 1:

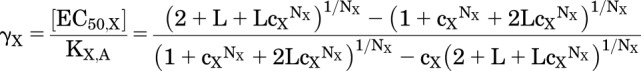(1.6)

Figure 1C shows a plot of γ_X as a function of L for c_X = 0.01 and N_X = 1, 2 or 5.

The predictions in the Fig. 1C cover a large range of values for L, to illustrate that the value for EC₅₀ shows asymptotes at both low and high values of L:

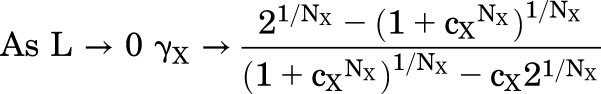(1.7)

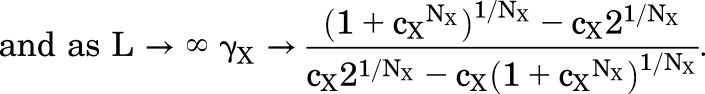(1.8)

Chang and Weiss (1999) were the first to demonstrate the asymptotic value as L → 0, whereas Akk et al. (2018) demonstrated the asymptote as L → ∞. Edelstein and Changeux (1996) provided expressions for the values of these asymptotes in the case that c_x^Nx <<1 (i.e., X is a strong agonist): as L → 0, γ_X → (2^1/Nx -1), and as L → ∞, γ_X → 1/(c_x(2^1/Nx -1)). Inspection of the relationship in Fig. 1C indicates that the curvature toward the asymptotes becomes marked when L < 1 and L > 1/c_x^Nx. When 1/c_x^Nx is much larger than 1, the asymptotes are well separated and the slope of the relationship between log(EC₅₀) and log(L) approaches 1/N_X, as first pointed out by Karlin (1967). The approximation is closer for N_X = 2 than for other values of N, but is not particularly accurate (see Fig. 1C and further discussion in Akk et al. (2018).

In studies of wild-type GABA_A receptors containing α1, β, and γ2 subunits, the experimental ranges of values for c_X and L are narrower than shown in Fig. 1C: c_X is in the range of 0.001–0.1 for an agonist, and estimates for L are in the range of 1000–100,000 for a wild-type receptor in the absence of drugs.

The value for the EC₅₀ can range from less than c_XK_X (higher potency than for binding to the active receptor) to greater than K_X (lower potency than for binding to the resting receptor). It is clear from the definitions of the asymptotic values for γ_X that this is the case for N_X > 1, since (2^1/Nx -1) < 1 (so EC_50,X can be less than K_X,A) and 1/(c_x(2^1/Nx -1)) > 1 (so EC₅₀ can be larger than K_X,R). The reason for this is that γ_X is not directly related to the fundamental binding affinities, and the fractional occupancy of sites at the EC₅₀ can be greater or less than 50%. Essentially, the stabilization energy required to reach P_A at the EC₅₀ depends strongly on the value for L (that sets the P_A,min), and the occupancy of sites by agonist is less when L is small (P_A,min larger) than when L is large (P_A,min smaller).

The Concentration of Antagonist Producing IC₅₀

If c_X = 1, then X binds equally well to an inactive or active receptor and so acts as a pure competitive inhibitor for a drug binding to that site.

If c_X > 1, then X binds to inactive receptors with higher affinity. In this case, X is an antagonist that reduces channel activation from whatever level is seen in the absence of X (Ueno et al., 1997; Chang and Weiss, 1999; Thompson et al., 1999).

The relationship between the IC_50,X and L is given by eq. 1.6. The graph is an inverted version of that for EC_50,X, with IC_50,X decreasing as L increases. The asymptotes at low and high values of L are (when c_x^Nx >>1):

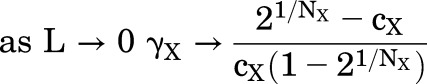(1.9)

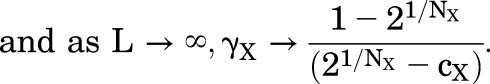(1.10)

The relationship bends over to the asymptotes when L < c_x^Nx and L > 1, and the slope approaches 1/N_X between those values.

Bicuculline and gabazine act as allosteric inhibitors on the GABA_A receptor, as well as competing for the GABA binding site (Ueno et al., 1997; Chang and Weiss, 1999; Thompson et al., 1999). Values for c_X > 1 have not been explicitly reported, but an estimate can be made in the following way. The maximal inhibition is given by eq. 1.5, as for activation. The relative maximal effect can be defined as:

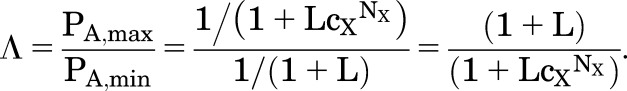(1.11)

So, one way to estimate c_X for an allosteric inhibitor is from the equation

(1.12)

Equation 1.12 produces reasonably accurate estimates for the agonists GABA and propofol, for which there are experimental estimates of c_X: for c_GABA the experimentally estimated value is 0.0033 (Akk et al., 2018); whereas the value calculated from eq. 1.12 using parameters in the article is 0.0029, and the experimental c_Propofol value is 0.22 (Shin et al., 2018) with a calculated value of 0.22. Two articles have examined the ability of bicuculline and gabazine to block constitutive currents of mutated receptors, and the use of eq. 1.12 generated estimates for c_Bicuculline and c_Gabazine of 1.6 and 1.2 (Chang and Weiss, 1999) and 4.6 and 1.2 (Thompson et al., 1999). Finally, currents elicited by pentobarbital and alfaxalone are blocked by these drugs (Ueno et al., 1997), with calculated values for c_Bicuculline of 3.5 and for c_Gabazine of 1.4 for block of pentobarbital-induced currents; and for c_Bicuculline of 5.9 and for c_Gabazine of 1.2 for block of alfaxalone-induced currents. These calculations suggest that c_Bicuculline is about 4 and c_Gabazine about 1.2.

The Hill Coefficient for the Activation Curve

Experimental sigmoid concentration-effect relationships are often fit with the Hill equation:

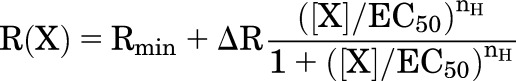(1.13)

where R_min is the response when [X] = 0, ∆R is (R_max − R_min), and n_H is the Hill coefficient.

To predict the value of n_H that would be fit to an activation curve, two approaches can be used. The normalized concentration-effect curve is:

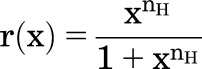(1.14)

where r(x) = (R(X) − R_min)/∆R and x = X/EC₅₀. The derivative at X = EC₅₀ (x = 1) is

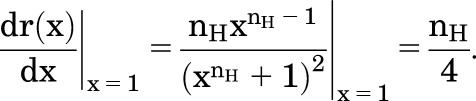(1.15)

Accordingly, the Hill coefficient can be estimated from the slope of the normalized concentration-response relationship at the EC₅₀.

Alternatively, Marzen et al. (2013, their Fig. 2c) present an equation for h_eff, where h_eff is the Hill coefficient that would be fit to the overall data (in our notation, n_H). Using our notation:

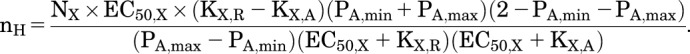(1.16)

The two approaches give the same values for n_H.

The effects of changes in L or c_X on the Hill coefficient are shown in Fig. 1D. n_H is low when L is small, presumably because so little energy difference is present between inactive and active receptors that occupation of a minimal number of sites provides sufficient stabilization energy. When efficacy is high (c_X is small) and L is relatively large (large energy difference between inactive and active), then n_H approaches N_X, presumably because the majority of sites need to be occupied to provide sufficient stabilization energy.

Comments on Section 1

Necessity of Converting Responses to a Probability of Being Open Scale.

The observed membrane current responses (I([X])) must be converted to a probability of being open (P_O) scale (Chang and Weiss, 1999; Rüsch and Forman, 2005). There are two basic reasons for this. First, any analysis in terms of energies requires that the ratio of open to closed receptors be calculable. Second, P_O is used as a proxy for P_A for analysis in terms of the MWC model. To make the conversion, it is necessary to know the constitutive activity (P_O,min) in the absence of any added drug and the maximal activity achievable (P_O,max). In practice P_O,min is estimated by blocking the response using a pore blocker (for GABA_A receptors, usually picrotoxin). P_O,max is estimated from the largest response to a saturating concentration of a strong agonist (usually GABA) plus a potentiating drug (e.g., propofol, alfaxalone, pentobarbital). P_O,min is defined as 0 and P_O,max as 1, and all other responses are normalized to this interval:

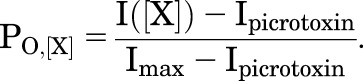The relationship between P_O and P_A is conventionally assumed to be 1:1, so that an estimated P_O of 1 corresponds to a P_A of 1.

Issues in Fitting Data.

In practical terms it can be the case that a wide range of values for L can be used to describe the data for activation (see Akk et al., 2018). This is understandable when the relationship between the concentration-response data and the model is examined: in the data, the two asymptotes are P_A,min and P_A,max. The model defines P_A,min as 1/(1 + L), and P_A,max as 1/(1 + Lc^N). When P_A,min is very low, then both L and c are determined largely by P_A,max. For a given P_A,max value, pairs of L and c are possible as long as L₁c₁^N = L₂c₂^N. These findings are in agreement with previous theoretical studies on the relationships between constitutive activity and MWC parameters (Ehlert, 2014). Similarly, the value for N can vary. Again, if L is set, then pairs of values for c and N are possible provided that c₁^N1 = c₂^N2. However, the value for N is additionally constrained by the shape of the concentration-response curve. The relationship between the EC₅₀ and L can also greatly help in constraining values for N and L, as shown previously (Akk et al., 2018; Shin et al., 2018).

The Relationship between EC₅₀ and L Can Define the Number of Sites for a Drug.

Karlin (1967) pointed out that the slope of the relationship between the logarithms of EC₅₀ and L is approximately 1/N, and this relationship has been used to estimate values for L by extrapolation (e.g., Chang and Weiss, 1999). This approximation is roughly true, as indicated in Fig. 1D. However, analysis of the relationship, especially when coupled with mutations of putative binding sites, can constrain the estimates for N (Akk et al., 2018; Shin et al., 2018).

Interactions among Drugs Acting at Different Sites

This section will cover two drugs that act on the same receptor after an MWC scheme but do not bind to the same sites. A later section will discuss the case when both drugs bind to the same site.

The Probability of Being Active

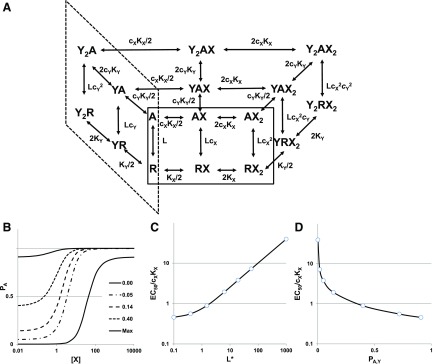
The reaction scheme is shown in Fig. 2A. As can be seen, the receptor can be active with no drug bound, with X alone bound, with Y alone bound, or with X and Y both bound, and similarly for an inactive receptor. The probability of being active is:

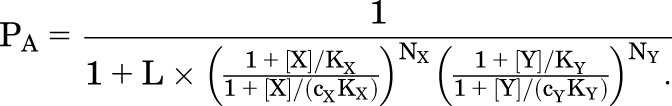(2.1)

Inspection of eq. 2.1 indicates that the presence of a constant concentration of Y is equivalent to a change in L:

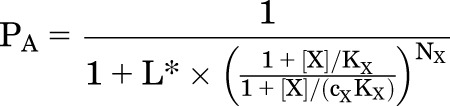(2.2)

where L*, the modified value for L, is:

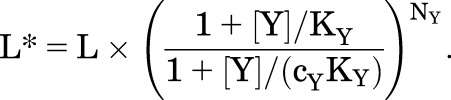(2.3)

This relationship was first pointed out by Rubin and Changeux (1966).

Fig. 2.

The state diagram and concentration-response relationships for two drugs acting at different sites. (A) A partial state diagram for two drugs (X and Y, each with two sites) acting on a receptor. Inactive receptor states (R) occupy the plane at the bottom [note that some states are obscured (e.g., YRX, Y₂RX)], while active states (A) occupy the plane at the top. The diagram is distorted to show states with only agonist X bound (solid line box at front) and only agonist Y bound (short dash line box at left); the other states have both agonists bound. In the absence of both X and Y, the receptor activates constitutively with L = R/A. Agonist X binds to its site with dissociation constant K_X,R on the resting receptor, and K_X,A on the active receptor, with c_X = K_X,A/K_X,R. Agonist Y binds to a different site, with dissociation constant K_Y,R on the resting receptor and K_Y,A on the active receptor, with c_Y = K_Y,A/K_Y,R. In the scheme, K_X = K_X,R and K_Y = K_Y,R. Note that the presence of bound Y does not affect the binding of X or vice versa. The equilibrium between R and A states is determined by the respective values for c, as dictated by detailed mass action in the coupled cycles. (Panel modified from Akk et al., 2018). (B) The activation curve for drug X at various concentrations of drug Y. (The numbers indicate the background P_A elicited by [Y] present.) (C) shows the decrease in the EC₅₀ value for X as [Y] increases, so L* steadily decreases. (D) shows the same data for the EC₅₀, but now plotted as a function of the increasing background P_A elicited by Y. (B–D) L = 1000, N_X = 2, K_X = 100, c_X = 0.01, and N_Y = 2, K_Y = 30, c_Y = 0.01. For (B), the values for [Y] were 0, 2, 4, 10, and saturating, which produced background P_A values of 0, 0.05, 0.14, 0.40, and 0.91, respectively, and resulted in L* values of 1000, 19.4, 6.25, 1.51, and 0.10. In (C and D), additional points are plotted for values of [Y] of 1 and 30, producing P_A values of 0.02 and 0.72, and L* values of 56.9 and 0.39.

The response in the absence of X (P_A,min) is set by Y, and the maximal response (P_A,max) is increased:

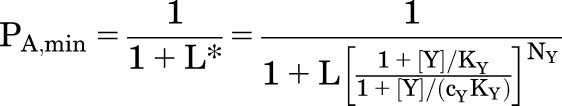(2.4)

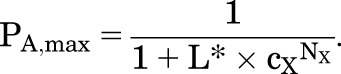(2.5)

The greatest practical utility of the MWC framework is that the use of eq. 2.2 simplifies experimental study. For example, to predict the ability of an allosteric agonist to potentiate activation by GABA, eq. 2.2 indicates that it is not necessary to characterize the concentration-effect curve for the allosteric agent. It is simply necessary to measure the direct activation by the particular concentration: say, drug Y (e.g., propofol) elicits a response of P_A,Y at the test concentration. Then L* = (1 − P_A,[Y])/P_A,[Y] and the concentration-effect curve for X (e.g., GABA) in the presence of that concentration of drug Y can be calculated from eq. 2.2.

The Concentration of Agonist Producing EC₅₀

The relative EC₅₀ value for X in the presence of a given concentration of Y is the same as earlier, with L* replacing L:

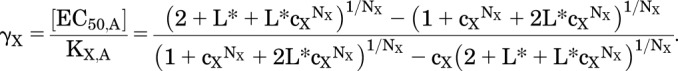(2.6)

Figure 2B shows the activation curve for drug X in the presence of various values of [Y]. As [Y] increases, the baseline activity in the absence of X increases, the EC₅₀ value shifts to lower [X], and the maximal P_A value increases. Figure 2C shows the relative EC₅₀ as L* decreases as a result of the increasing [Y], whereas Fig. 2D shows the decrease in EC₅₀ as a function of the increased background P_A due to Y. When two drugs bind to different sites on the receptor, the addition of a constant concentration of a background drug enhances the response to the primary drug both by increasing the maximal response and by decreasing the EC₅₀ value.

Different Potentiators Applied at Concentrations that Directly Activate to the Same P_A Produce Equivalent Potentiation

For a full agonist such as GABA, the probability of being active is:

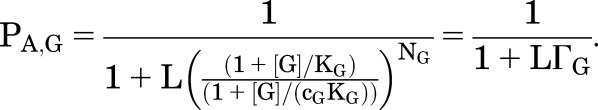(2.7)

Similarly, for a potentiator Y:

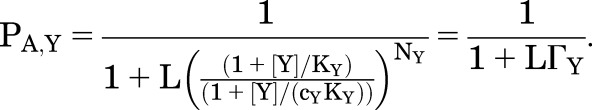(2.8)

Then the response to coapplication of both GABA and Y is:

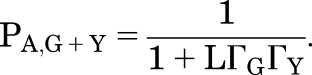(2.9)

This is true for all other potentiators at concentrations that give the same direct response at the appropriate concentration (i.e., Γ_X = Γ_Y). That is, when potentiators X and Y are used at concentrations that produce the same direct activation when applied by themselves, they will produce the same potentiation of a response to GABA.

Potentiation is often characterized in terms of the ratio of the response to GABA in the presence of potentiator X to that in the absence of X. Call this potentiation ratio Θ_X = P_A,G+X/P_A,G:

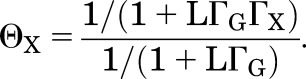(2.10)

So long as the desired value of P_A is constant at different values of L, as L → 0 Θ_X approaches 1 (since all the Γ terms are constant) and as L → ∞ Θ_X approaches 1/Γ_X.

Note that the range of values that can be used for the desired value of P_A is limited, with a minimum set by L and by the P_A,max attainable by a given agonist.

Potentiation Depends on L When the Response Is Measured as a Fraction of the Maximal Response to Agonist

Experimental data are often expressed in terms of the fraction of the maximal response to a given agonist, and the concentration of drug producing that fractional response is referred to as the “effective concentration” (EC) value. For this section, R_G is the normalized response to GABA alone and R_X is the response to X alone at the particular concentrations used, also normalized in terms of the response to GABA:

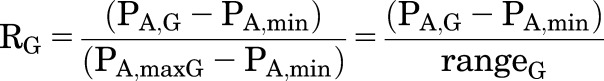(2.11)

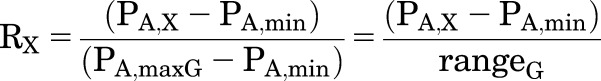(2.12)

and

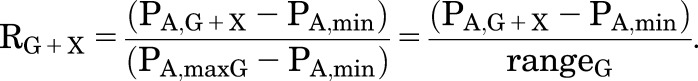(2.13)

A particular protocol is often used in studies of the effects of mutations or interactions among multiple drugs. In this protocol, a constant R_G is elicited as L is changed (although this may require use of a different [GABA]), a constant R_X is elicited, then the combination of GABA and X at those concentrations is tested.

For the particular value of R_G there is a particular value of P_A,G resulting in that value, and produced by a particular value of Γ_G, where P_A,G = 1/(1 + LΓ_G). As L changes at constant c_G and K_G, the concentration of GABA needed will change. Similarly, there will be a particular value of Γ_X to produce the value of R_X. In the scenario considered here, Γ_X = Γ_G = Γ (i.e., the concentration of GABA and the concentration of X directly activate to the same level).

Call the potentiation ratio defined in terms of fractional response Ψ_X = R_G+X/R_G:

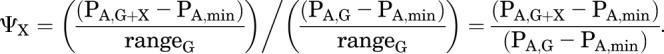(2.14)

Substituting in values for the P_A terms and rearranging gives:

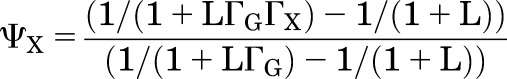(2.15)

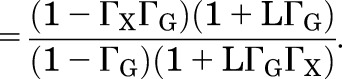(2.16)

Referring back to the definition of Γ_G and Γ_X, we can express them in terms of the particular value of P_A required to reach the initial response (ρ) for GABA and X applied separately:

(2.17)

or

(2.18)

and similarly for X.

Simplification of eq. 2.16 for the case where the initial responses are the same, ρ_G = ρ_X = ρ (so Γ_X = Γ_G = Γ), gives:

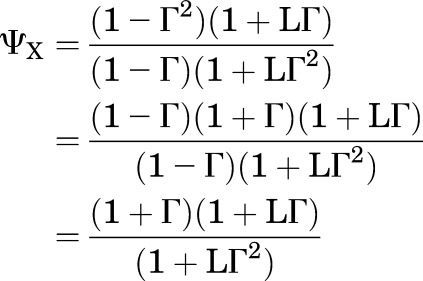(2.19)

and substitution from eq. 2.18 gives:

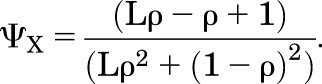(2.20)

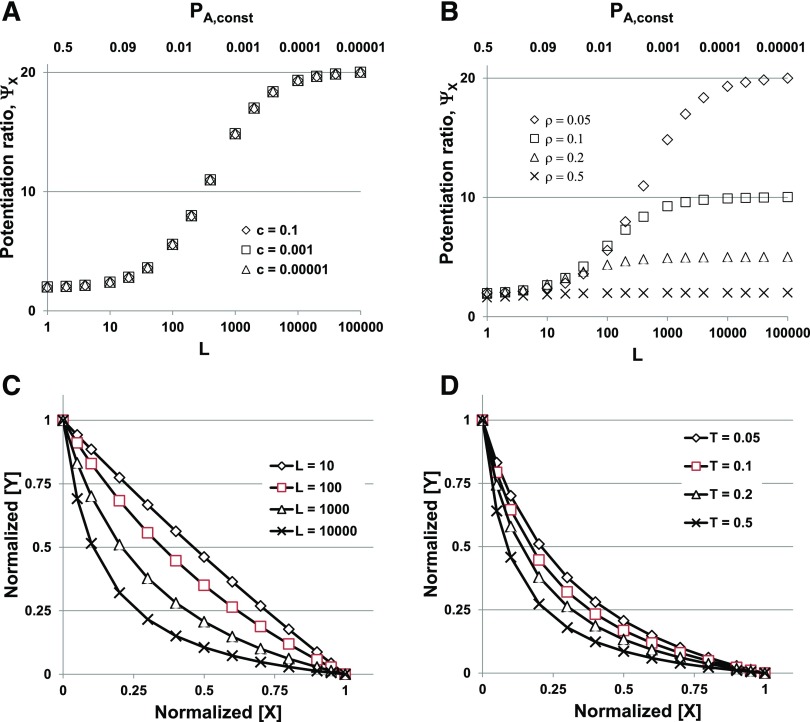
A salient point here is that Ψ_X does not depend on the affinities or efficacies for potentiator (K_X or c_X) for a given initial response. However, when the potentiation ratio is expressed in this way, the potentiation ratio will change as L changes although K_X and c_X values are constant. Similarly, potentiation will depend on the initial response at the same L. Plots of Ψ_X as a function of L are shown in Fig. 3, A and B.

Fig. 3.

Potentiation depends on the level of spontaneous activity and the response amplitude used. (A and B) The potentiation ratio for normalized responses (Ψ_X, eq. 2.20) is plotted against L (lower abscissa scale), whereas the corresponding constitutive background activity [P_A,const = 1/(1 + L)] is shown above the plots. (A) shows that Ψ_X increases as L becomes larger (P_A,min smaller) but does not depend on the affinity ratio (efficacy) for the potentiating drug X (c_X between 0.1 and 0.00001). The value for Ψ_X approaches 2 − ρ as L → 0 and has a plateau at 1/ρ as L increases, then increases to a second plateau at 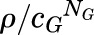as L → ∞ (not shown in this plot). (B) shows that Ψ_X decreases as the value for ρ increases from 5% to 50% of the maximal response to GABA. (C and D) Isobolograms; the concentrations of X and Y are normalized to the concentrations producing the target response in the absence of the other drug (X₀ and Y₀). This is because the values for X₀ and Y₀ varied so much in the different conditions that some of the plots could not be resolved when plotted as actual concentrations. As L increases (C) the degree of curvature also increases, which would be interpreted as increasing synergy. As the target response (Τ) increases (D), the curvature also increases. Note that comparing (B and D) appears to provide different qualitative statements regarding the interactions of the two drugs; the potentiation ratio decreases with increasing initial response, whereas the curvature of the isobologram increases with increasing target response. In (A), T = 0.05, K_G = 300, N_G = 3, and c_G = 1/300, whereas K_X = 300, N_X = 3, and c_X = 0.1, 0.001, or 0.00001, as indicated. In (B), K_G = 300, N_G = 3, and c_G = 1/300; and K_X = 300, N_X = 3, and c_X = 0.001, whereas the target response (T) changes from 0.05 to 0.5, as indicated. In (C and D), K_X = K_Y = 300, N_X = N_Y = 3, and c_X = c_Y = 1/300, whereas L and T change as indicated.

The value for Ψ_X approaches 2 − ρ as L → 0, and has a plateau at 1/ρ as L increases, then increases to a second plateau at T /c_G^N_G as L → ∞.

The Shape of the Isobologram Depends on the Value of L and the Target Response

An isobologram is a two-dimensional (most often) plot with axes showing the doses (or concentrations) of two agonists. The points on the graph are the pairs of concentrations that produce a given response that will be called the “target” response (T). The intersections with the two axes are the concentrations of drug X and drug Y, which when administered alone produce the target effect (call them X₀ and Y₀). When combinations of drugs are tested, for a given value of [X] the concentration of Y that must be added to produce the target effect provides one point of the plot. A straight line between (X₀, 0) and (0, Y₀) is defined as the linear isobologram of additivity and indicates that X and Y substitute for each other on a proportional basis (i.e., one-fifth of X₀ + four-fifths of Y₀ produces a response equivalent to that of X₀ or Y₀). Straight lines can be obtained for some particular cases of preparation, response, and drug combination. A relationship that lies below the straight line is often termed “synergistic” (or supra-additive) since proportionately less Y must be added to produce the target. In contrast, one that lies above the line is “antagonistic” (or subadditive) since more Y must be added. However, the entire concept of the isobologram and its interpretation is rather complex (Geary, 2013; Foucquier and Guedj, 2015; Tallarida, 2016). We have discussed some aspects of this topic previously (Shin et al., 2017; Germann et al., 2018).

An isobologram can be defined using any response metric desired. In the present case, two metrics are most appropriate, either in terms of P_A or the EC for one drug. From the discussion of potentiation ratios, it is apparent that the shape (degree of curvature) of an isobologram can be affected by the value for L and the target response level.

We did not find an analytical expression to allow calculation of the points on an isobologram, but they can be calculated numerically. Figure 3, C and D shows calculated isobolograms for some combinations of parameters, using the EC relative to GABA as the response metric. For a small value of L (i.e., a large constitutive response), the curvature is reduced. Similarly, when the target response is small, the curvature is reduced.

Comments on the Section Interactions among Drugs Acting at Different Sites

Equivalence of Changes in L by a Drug or a Mutation.

Equations 2.1–2.3 imply that a mutation that only changes L or the presence of a drug that produces the same change in L have equivalent effects on the activation produced by an agonist that acts at a different site. Experimental results indicate this is true for activation by GABA (Chang and Weiss, 1999; Akk et al., 2018) and propofol (Shin et al., 2018), and effects of mutations that decrease the energy difference between closed and open states have consistent effects on activation by GABA, etomidate, and benzodiazepines (Chang and Weiss, 1999; Rüsch et al., 2004; Rüsch and Forman, 2005; Campo-Soria et al., 2006).

Of course, there are caveats to each approach. A mutation may affect an activation parameter for a drug (K, c, or N) as well as L. Similarly, an additional drug could interact directly with a binding site for the principal agonist being tested or the drugs might interact in a fashion that is not described by an MWC model (e.g., one drug could alter an activation parameter for another drug).

Parameters for a Weak Agonist Can Be Determined from Potentiation Data.

A weak agonist can have such a high value for c_X that the concentration-response relationship for direct activation cannot be accurately defined. However, in this case the MWC parameters can be determined by analyzing the ability of the weak agonist to potentiate a stronger agonist.

Potentiation Depends on Constitutive Activity and Response.

“Potentiation” can be expressed as a shift in the concentration-response curve for the “primary agonist” to lower concentrations or by an increase in the response to a given concentration of the primary agonist. It is important to note that the enhancement of a response by the addition of a second drug is not invariant. A receptor with a high constitutive activity (low L) shows a lower potentiation ratio than one with higher L, as well as showing reduced curvature in the isobologram. The background activity can depend on several factors, including mutations to the receptor or the presence of additional drugs. Because of the role of constitutive activity, interpretation of the effects of mutations can be confounded. A mutation that decreases L might increase the direct response to a potentiator but appear to make it less effective as a potentiator and thereby suggest a selective effect on activation or potentiation. This possibility has been directly examined and shown to be experimentally observed (Germann et al., 2018).

The degree of interaction also is dependent on the response used to study the interaction. The potentiation ratio measured for a large initial response (large value for ρ) will be lower than for a smaller initial response. This might be expected, since potentiation of a large initial response might be limited by response saturation. In contrast, the isobologram shows more curvature when a large target response is used, indicating that when the desired response is large, the effect of combining the two drugs is enhanced. In many pharmacological applications, the relationship shown by the isobologram would be most relevant, in that the combination producing the desired target is the critical result. This suggests that when the physiologic effect requires that a large fraction of the receptors are activated, two agonists may show more apparent interactions than when only a small fraction must be activated.

Interactions between Two Drugs Acting at the Same Site

Activation Curve in the Presence of a Competing Drug.

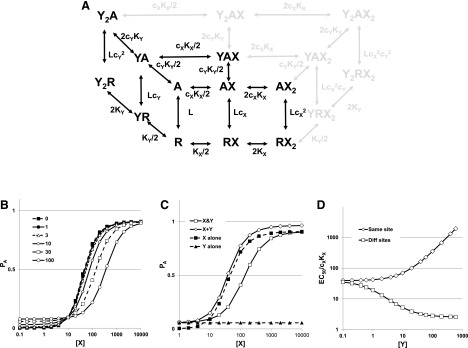
If two drugs (X and Y) bind to the same site or sites, the interaction is basically a standard competitive interaction but with parameters described by the MWC equations. The state diagram shown in Fig. 4A demonstrates that the available states are a subset of the case when X and Y bind to distinct sites (Fig. 2A).

Fig. 4.

The state diagram and concentration-response relationships for two drugs acting at the same sites. (A) The state diagram for drugs X and Y interacting with the same two sites acting on a receptor. Inactive receptor states (R) occupy the plane at the bottom, whereas active states (A) occupy the plane at the top. The inactive state YRX is hidden in the diagram. Note that the scheme shows a restricted set of the states available for the case when X and Y bind to distinct sites (indicated by the gray states and transitions). The parameters have the same definitions as before. (B) The activation curves as a function of [X] in the presence of different concentrations of a lower-efficacy drug Y (indicated in the panel). (C) Activation curves at a single [Y] ([Y] = 30) for [X] in the absence of [Y] (X alone, filled squares), [Y] (Y alone, filled triangles), the sum of the response to X alone and [Y] alone (X + Y, hollow diamonds) and the response to X applied in the presence of [Y] (X & Y, hollow squares). (D) The effect of increasing [Y] on the EC₅₀ for X, if X and Y act at the same sites (diamonds) or different sites (squares). For (B and C): L = 1000, N = 2, K_X = 100, c_X = 0.01, and K_Y = 10, c_Y = 0.1. In (B), [Y] ranged from 0 to 100, as indicated, whereas in (C) [Y] = 30. In (D), for the “same site” calculations L = 1000, N = 2, K_X = 100, c_X = 0.01, and K_Y = 10, c_Y = 0.1, whereas for the “different site” L = 1000, N_X = 2, K_X = 100, c_X = 0.01, and N_Y = 2, K_Y = 10, c_Y = 0.1.

The probability that a receptor is active in the presence of two drugs binding to the same site is:

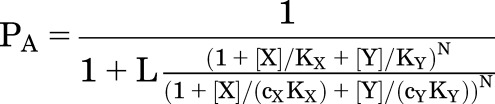(3.1)

where N is the number of identical sites for X and Y on the receptor and other terms are as defined earlier.

If drug Y is present at a constant concentration:

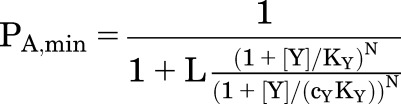(3.2)

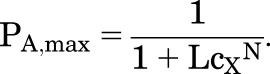(3.3)

P_A,min is set by [Y], whereas P_A,max is the maximal response to X alone. (In contrast, when X and Y bind to different sites, P_A,max is increased by Y.)

Concentration-response curves for drug X in the presence of various concentrations of a lower-efficacy drug (Y) are shown in Fig. 4B. The responses to the combination of X and Y lie above the response to X alone at low concentrations of X but are less than the response to X alone at a higher concentration. At very large values of [X], X fully displaces Y and the maximal response to X is the same in the absence or presence of Y. It is interesting that the curves appear to cross at a single value for [X] for all values of [Y] (Fig. 4B).

This value can be calculated by setting the responses equal:

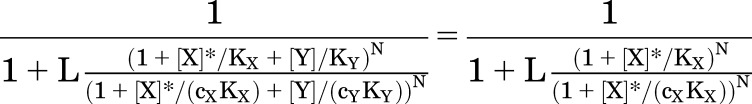(3.4)

where [X]* is the concentration of X where the responses cross over. The solution is:

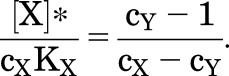(3.5)

The result is positive if both X and Y are agonists and c_Y > c_X, a relationship that is required for Y to be an inhibitor of responses to X. It may be unintuitive that the crossover concentration is independent of [Y], K_Y, and N.

The presence of drug Y inhibits the response to X in the sense that the response to the application of the combination of X and Y is less than or equal to the sum of the response to X alone plus the response to Y alone (Fig. 4C).

EC₅₀.

The normalized EC₅₀ when both drugs bind to the same site is:

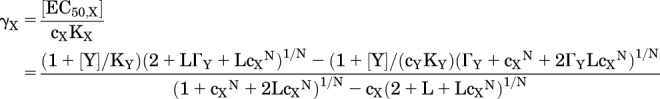(3.6)

where Γ_Y = ((1+[Y]/K_Y)/(1+[Y]/(c_YK_Y))^N for the concentration of Y present and other terms are as defined earlier. [This equation for γ_X differs from the one given in the study by Karlin (1967) that omitted the term Γ_Y.] Figure 4D shows a plot of γ_X as a function of [Y], and for comparison the plot when X and Y act at distinct sites. Y acts as a competitive inhibitor of X when both drugs bind to the same site and as an allosteric potentiator when they bind to distinct sites.

More Complicated Combinations of Drug Actions.

Say we have two drugs, X and Y, and two classes of sites, class I and class II. Drug X binds to all class I sites and class II sites, whereas Y binds only to the class I sites. This situation may well be present for the GABA_A receptor. For example, in the case of propofol and barbiturates, barbiturates may bind to some but not all of the sites for propofol (Jayakar et al., 2014). The overall probability of being active would be analogous to that for two drugs that bind to distinct sites (I and II) but with competition between X and Y at class I sites:

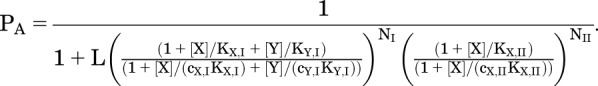(3.7)

Extension of the MWC Model to Include Preactive States Such as the Flip Model

The Two States Can Be Defined by Affinity or Functional Properties

The R state has two attributes: it is inactive and it has a low affinity for agonist. In contrast, the A state is both active and has a higher affinity. So far, the emphasis has been on the functional consequences of the change in state. However, the change in affinity is critical for the properties of the model.

The “flip” model for receptor activation is defined in terms of a change in affinity for the agonist, whereas the receptor remains inactive (Beato et al., 2004; Burzomato et al., 2004; Plested et al., 2007; Lape et al., 2008). That is, there is a preopen, high-affinity state of the receptor, whereas channel opening occurs in a second step. In the flip model, the properties of all binding sites on the receptor change together, retaining the concerted nature of the MWC model. In contrast, for the “Prime” model the properties of the binding sites on the receptor can change independently (Mukhtasimova et al., 2009). The Prime model clearly differs from the MWC scheme.

The flip state is quite brief, lasting less than 10 µs. The fully liganded flip state has an estimated duration of about 7 µs for either glycine or taurine on the wild-type glycine receptor (Lape et al., 2008) and about 9 µs for tetramethyl ammonium or acetylcholine on the muscle nicotinic receptor (Lape et al., 2008). Partially liganded receptors have durations that depend on the agonist concentration and ligation of the receptor, but even at low (1 µM) concentrations the predicted durations are less than 10 µs (Lape et al., 2008). A similar preactive closed state has been incorporated into a number of linear kinetic schemes for receptor activation for both nicotinic and GABA_A receptors (Auerbach, 1993; Haas and Macdonald, 1999; Lema and Auerbach, 2006). This closed state has all binding sites occupied by agonist. However, the affinity for agonist cannot be defined since there are no association and dissociation steps connecting to this state in a linear scheme.

A version of a cyclic scheme incorporating a flip state is shown in Fig. 5A. In addition to the R state (low affinity, resting) and A state (high affinity, active), the receptor can adopt an F state (high affinity, resting). It is assumed that the affinity of the sites is the same for F and A states—all the change occurs when the receptor changes from R to F. In the absence of agonist, W = R/F and Z = F/A. K_X is the affinity of the R state for X (K_X,R) and q_X is the ratio of the affinity of the flip state to that of the resting state (q_x = K_X,F/K_X,R). Note that Z does not change with the binding of X to the receptor. This is required because the affinity of the receptor is postulated to be the same in the F and A states. This model was also proposed by Gielen et al. (2012), but only a restricted version was analyzed.

Fig. 5.

An extension of the MWC model incorporating a high-affinity closed state. (A) A kinetic scheme incorporating a state with high affinity for agonist for a resting receptor. In addition to the R state (low affinity, resting) and A state (high affinity, active), the receptor can adopt an F state (high affinity, resting). In the absence of agonist, W = R/F and Z = F/A. K_X is the affinity of the R state for X (K_X,R) and q_X is the ratio of the affinity of the flipped or active states to that of the closed state (q_X = K_X,A/K_X,R). Note that Z does not change with binding of X to the receptor. (B and C) Activation curves for combinations of parameters; in (B), the effects of altered values for Z are shown, whereas q is changed in (C). [In both (B and C), W = 1000, K_X = 100, and N_X = 2; in (B), q_X = 0.01, whereas Z is changed from 0.01 to 1, as indicated, and in (C), Z = 1 whereas q_X = is changed from 0.001 to 0.1]. (D) The interaction between two drugs acting at different sites. The activation curve for drug X is shown in the absence of Y and in the presence of Y at concentrations eliciting responses with PA of 0.02, 0.05, and 0.2 as indicated (W = 1000, Z = 0.1, N_X = 2, K_X = 100, q_X = 0.05, N_Y = 2, K_Y = 100, q_Y = 0.05).

We will call the scheme in Fig. 5A the flip model, recognizing that the flip model applied in some studies differs from this most general case. In particular, it is often applied in a partially noncyclic form, in which it is assumed that agonist could not bind to or unbind from receptors with open channels (Burzomato et al., 2004).

State Functions for Being High Affinity or Being Active

The probability that a receptor is in a high affinity state (F or A) is P_High:

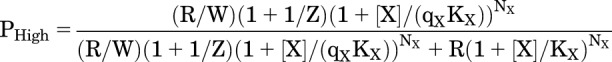(4.1)

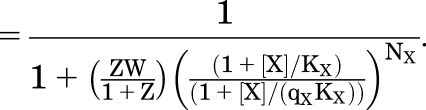(4.2)

This has the same form as the equation for P_A in the WMC model, with L replaced by (ZW)/(1 + Z):

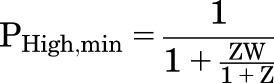(4.3)

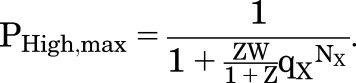(4.4)

The minimal and maximal values for P_High are analogous to the expressions for the MWC model, and hence the calculated EC₅₀ value for P_High is also analogous.

To convert to the fraction of receptors with active channels, multiply the equation for P_high by the probability of being active given that the receptor is either active or flipped:

(4.5)

This gives:

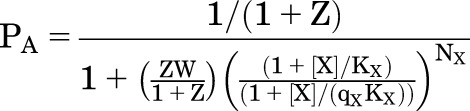(4.6)

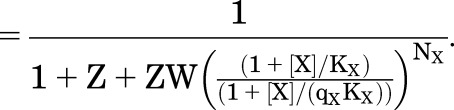(4.7)

The constitutive and maximal activities are:

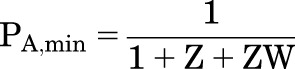(4.8)

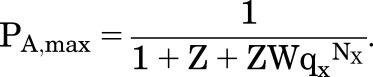(4.9)

In the equations for P_A, it can be appreciated that the activation by agonist will be limited even for highly efficacious agonists (q_X << 1) since as 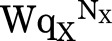approaches 0, P_A,max approaches 1/(1 + Z). In most biologic situations, the majority of receptors is inactive in the absence of agonist (W >> 1), but most receptors can be activated once the receptor enters the high-affinity state (Z < 1). In this case, the equations for P_high and P_A approach each other:

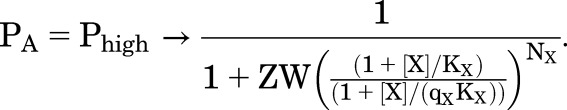(4.10)

This equation has the same form as that for the basic MWC model. The product ZW = R/A (the ratio of low-affinity resting receptors to high-affinity active receptors) is analogous to L for the MWC model. Activation curves are shown in Fig. 5, B and C, an indication of the effects of changes in W and q_X.

The Concentration of Agonist Producing EC₅₀

An expression for the relative EC₅₀ can be derived in a fashion similar to that for the MWC model. To emphasize the similarity, the variable ρ is used in eq. 1.10, where ρ = (1 + Z):

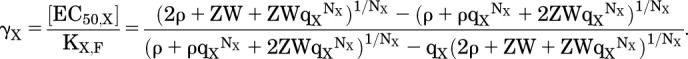(4.11)

For comparison, the equation for the EC₅₀ for the MWC model is:

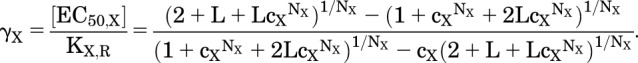The predictions converge as Z → 0, as expected given the earlier discussion of P_A.

Interaction between Two Drugs Acting by a Flip Model

This scheme is readily extended to allow binding of two drugs to distinct sites, X and Y. As is the case for the original MWC model, this is a highly constrained kinetic scheme. Inspection of Fig. 5A indicates that the values for W and Z are properties of the receptor, not of any of the ligands, and so are the same irrespective of which ligands are bound. The ligands can have different affinities (K_X) and efficacies (q_X). However, the fact that W and Z are the same for all ligands means that the equations for high-affinity and active channel receptors retain their similarity to the MWC scheme:

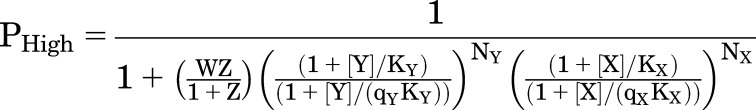(4.12)

and

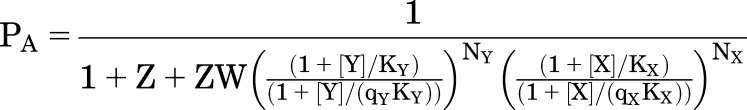(4.13)

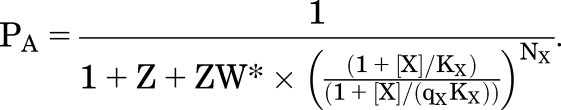(4.14)

An important consideration is that as in the case of a single drug P_A.max cannot exceed 1/(1 + Z).

Figure 5C gives an illustration of the interaction of two drugs acting by the flip model at distinct sites.

Comments on Including a Flip State in an MWC Model

It Can Be Hard to Estimate Parameters for the Flip Model.

It has already been pointed out that the estimation of L and c_X can be difficult for the MWC model, if P_A,min is close to 0. The same is true for the flip model in terms of ZW and q_X. It is also quite important to have an independent estimate for Z, to constrain the values of other parameters.

What Forms of the Flip Model Have Been Fit to Data?

Formally, this form of the flip and MWC models are compatible. However, when the flip model is applied to single-channel data for glycine or muscle nicotinic receptors, it does not seem that the form in Fig. 5A describes the data well. The model actually fit to the data omitted the flip and active states for unliganded receptors and also did not allow ligand association or dissociation for active receptors (Burzomato et al., 2004; Lape et al., 2008). The authors noted that the quality of the fits was not as good when these transitions were included in the model. This can also be seen in the parameter values in various tables: the best-fitting values for Z differed depending on the state of ligation of the receptor, which would not be allowed for the model discussed here.

An even more simplified variant of the flip model has been applied to analysis of the actions of benzodiazepines on GABA_A receptors (Gielen et al., 2012). In this case, the number of sites for GABA binding was reduced to only 1, and openings in the absence of GABA were neglected (so, a linear model was fit comprising R + X ↔ RX ↔ FX ↔ AX). Overall, this scheme provided a good description of whole-cell currents elicited by GABA and the ability of benzodiazepines to potentiate the currents. However, it should be noted that other groups have found that the classic MWC model provides a satisfactory quantitative description of the actions of benzodiazepines (Downing et al., 2005; Rüsch and Forman, 2005; Campo-Soria et al., 2006).

Overall, in the cases that have been examined thoroughly the highly constrained model provided by the MWC-like flip scheme is not able to describe single-channel data as well as an only partially cyclic scheme.

Addition of a Desensitized State Has a Similar Form.

If a receptor can move from the active state to a desensitized (inactive) state, whereas the active and desensitized states have the same (higher) affinity for agonist, similar equations result. The expression for P_high is the same as for the flip model. The P_A is determined by multiplying P_high by P {Active|Active or Desensitized} = Q/(1+Q), where Q = fraction active / fraction densitized. Again, this ratio is independent of ligation and is the same for all agonists.

Discussion

Application of the Model to the GABA_A Receptor.

A study by Chang and Weiss (1999) pioneered the application of the MWC model to the GABA_A receptor. A series of gain-of-function mutations were studied and the relationship between the EC₅₀ for activation by GABA and the level of constitutive current was analyzed. The model gave a quantitative description of the relationship. Work from Forman’s laboratory (Rüsch et al., 2004, Rüsch and Forman, 2005; Forman, 2012; Ruesch et al., 2012; Ziemba and Forman, 2016) analyzed interactions between allosteric agonists (etomidate, propofol, and pentobarbital) and GABA in activation of the GABA_A receptor. The results demonstrated that the MWC model provides a quantitative description of the relationship between activation by single drugs and activation by pairwise combinations of drugs. Finally, work from our laboratory has extended the analysis of the activation and potentiation by orthosteric and allosteric agonists (Shin et al., 2017, 2018; Akk et al., 2018; Germann et al., 2018). In this work, the MWC model could give a quantitative description of the effects of mutations that affected either receptor constitutive activity or the number of binding sites for a drug, and for the interactions of several allosteric and orthosteric agents.

Overall, the model can give a good description of the pharmacology of the GABA_A receptor, although possibly not of the effects of benzodiazepines (Gielen et al., 2012; Goldschen-Ohm et al., 2014; but see also Downing et al., 2005; Rüsch and Forman, 2005; Campo-Soria et al., 2006). At present, the MWC framework appears to be a simple and relatively accurate scheme for understanding the activation of the GABA_A receptor and interactions among drugs that bind to different sites on the receptor.

An interesting point is that to date there is no support for the idea that drug interactions at the GABA_A receptor require that a drug directly alters either the binding or intrinsic efficacy of another drug. The MWC model does not include such effects. Even in the analysis of actions of benzodiazepines when is has been concluded that the MWC model is inadequate, it has not been necessary to postulate a specific effect on binding or the efficacy of other drugs (Gielen et al., 2012; Goldschen-Ohm et al., 2014).

Strengths of the Model.

The strength of the model is its simplicity. The MWC model reduces the complexity of channel activation to four parameters. The small number of parameters reflects the simplicity of the kinetic scheme for activation. The receptor undergoes the state transition between active and inactive as a whole, so all subunits (sites) change state simultaneously. The concerted transition means that “mixed” receptors that have sites of different affinity do not occur. This assumption significantly reduces the number of states in the reaction scheme. All sites for an agent are independent and identical so that the occupation of any site provides an identical increment of stabilization energy. Finally, receptors in any state of ligation can activate, including receptors with no bound agonist. Application of Hess’ law then determines all of the equilibrium constants for the individual steps in the overall scheme.

There is no pairwise specific interaction among agents (except competition for occupancy between compounds that bind to the same site); all interactions are mediated through the overall energy available to stabilize one state or the other of the receptor.

Accordingly, interactions between two agonists that bind to different sites occur by changes in the stabilization energy required to reach a given level of activity. If drug X is considered the principal agonist, then the stabilization energy contributed by the background drug Y reduces the energy difference to be overcome by drug X. The effect of an allosteric inhibitor (or “inverse agonist”) is mediated by an increase in the energy difference to be overcome.

The model explicitly considers both the intrinsic activity of the receptor in the absence of drugs (in the parameter L) and the ability of a drug to enhance (or reduce) activity (in the parameter c). The energy difference between the active and inactive states is:

(5.1)

The intrinsic energy difference between the active and inactive states of the receptor is:

(5.2)

The energetic contribution of a drug is defined in a single parameter (c_X) scaled by the number of sites for the agent (N_X). Activation is enhanced by the increased affinity of agonist for its sites in the active state, and drug binding is reflected in a stabilization energy ∆G_X:

(5.3)

where

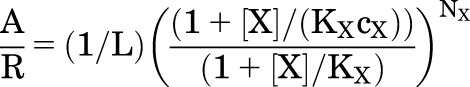(5.4)

so

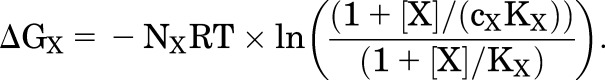(5.5)

The maximal stabilization energy as [X] → ∞ and all sites are occupied is:

(5.6)

Particular Parameters of the Model

Meaning of N.

The parameter N in the original formulation of the model was the number of identical subunits in a multimeric protein. We, and others, have adapted N to indicate the number of sites available to bind an agent irrespective of the number of subunits. This seems quite appropriate, as the parameter N determines the maximal free energy available as a result of drug binding to the receptor rather than any unique property of a subunit per se. This idea does, however, depart from the original philosophical idea of structural symmetry of a multimeric protein as an essential aspect of the mechanism.

Only Two States?

Even discarding physiologic phenomena such as desensitization that occur on a relatively slow time scale, how can channel activation be described with so few parameters? At a detailed microscopic (single-channel) level, it seems impossible that the MWC model is correct for any of the receptors in the pentameric ligand-gated channel family. However, it does appear to describe macroscopic results, and for the related muscle nicotinic receptors even microscopic data (Auerbach, 2012). A possibility is that receptor activity can be partitioned into two interconnected collections of states, one with a low affinity for agonist and low average probability that the channel is active, and the other with a high affinity and a high average probability. It is then possible to associate “inactive” with low average P_A + low affinity and “active” with high average P_A + high affinity. This brings up the question of which collection of states belongs to the inactive set and which to the active. The available kinetic models for GABA_A receptor activation that are based on single-channel recordings do not lend themselves to any simple transformation to a “two-state” (inactive/active) model (Haas and Macdonald, 1999; Lema and Auerbach, 2006). At this point, it can only be speculated that the partitioning could be based on the definition of a preferred path for channel activation, in which rarely occupied states are neglected and the remaining states are arranged in two groups.

There has been strong evidence for a “preopen” receptor state that is high affinity but has a closed channel (Burzomato et al., 2004; Plested et al., 2007; Lape et al., 2008; Mukhtasimova et al., 2009). Such a state can be included in an extended version of the MWC model, but to date it seems that data are better described by a version of the kinetic scheme that does not conform to the assumptions of the MWC model in that some of the kinetic cycles are broken and agonist association/dissociation is not allowed for receptors with open channels.

Relating Open to Active?

The possibility that the active state may include closed channel states raises a question: what is the probability that a channel is open given that the receptor is active (P{Open|Active})?

In the analysis it is assumed that P{Open|Active} is 1 for all agonists. Even if the assumption is relaxed so that P{Open|Active} < 1, the model assumes it is identical for all agonists. However, single-channel recordings indicate that P_O in a “cluster” at high drug concentrations may differ for different agents. This has consequences for analysis in terms of the MWC scheme. If drug A has P{Open|Active} = 1 and drug B has P{Open|Active} = 0.5, then the maximal inferred P_A value for drug B would be only half that of drug A. This is of importance for two reasons. Empirically, the L assigned to a given response elicited by drug B would actually be twofold higher than appropriate due to the low value for P{Open|Active}, which would distort the predicted relationship of EC₅₀ for drug A to L. In addition, the value for c_B would be artificially low, because the determination of the value of c_B is strongly influenced by the maximal P_A.

The data suggest that this problem is not of major importance: for example, propofol has a low maximal response compared with GABA (approximately one-half), and yet the observed EC₅₀ values for GABA at L* values set by propofol fall on the appropriate line for GABA EC₅₀ versus L (Akk et al., 2018). This is also true for alfaxalone and pentobarbital, which differ greatly in relative maximal response (Akk et al., 2018). GABA and P4S alter the EC₅₀ value for propofol in similar fashion, although they differ in maximal response (Shin et al., 2018). It is interesting that kinetic analysis using the prime or flip models of preopen, high-affinity states indicates that for glycine (Burzomato et al., 2004) and nicotinic (Lape et al., 2008; Mukhtasimova et al., 2009) receptors the opening and closing rates for full and partial agonists are quite similar. This suggests that 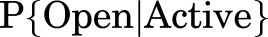is similar if the MWC active state were defined as the flip (or prime) + open states.

Does the MWC Model Work for Activation Kinetics?

The short answer is no. This was first noted by Sheridan and Lester (1977), who reported that the current relaxations after voltage jumps applied to nicotinic receptors did not conform to the predictions for the MWC model (Colquhoun and Hawkes, 1977). For single-channel studies, Colquhoun and Lape (2012) have considered the issue and reached the same conclusion.

Abbreviations

MWC

Monod-Wyman-Changeux

Authorship Contributions

Participated in research design: Steinbach, Akk.

Contributed new reagents or analytic tools: Steinbach, Akk.

Performed data analysis: Steinbach, Akk.

Wrote or contributed to the writing of the manuscript: Steinbach, Akk.