Abstract
Purpose
The purpose of this study was to enhance the deformation range of demons‐based deformable image registration (DIR) for large respiration‐induced organ motion in the reconstruction of time‐resolved four‐dimensional magnetic resonance imaging (TR‐4DMRI) for multi‐breath motion simulation.
Methods
A demons‐based DIR algorithm was modified to enhance the deformation range for TR‐4DMRI reconstruction using the super‐resolution approach. A pseudo demons force was introduced to accelerate the coarse deformation in a multi‐resolution (n = 3) DIR approach. The intensity gradient of a voxel was applied to its neighboring (5 × 5 × 5) voxels with a weight of Gaussian probability profile (σ = 1 voxel) to extend the demons force, especially on those voxels that have little intensity gradience but high‐intensity difference. A digital 4DMRI phantom with 3–8 cm diaphragmatic motions was used for DIR comparison. Six volunteers were scanned with two high‐resolution (highR: 2 × 2 × 2 mm3) breath‐hold (BH) 3DMR images at full inhalation (BHI) and full exhalation (BHE) and low‐resolution (lowR: 5 × 5 × 5 mm3) free‐breathing (FB) 3DMR cine images (2 Hz) under an IRB‐approved protocol. A cross‐consistency check (CCC) (BHI→FB←BHE), with voxel intensity correlation (VIC) and inverse consistency error (ICE), was introduced for cross‐verification of TR‐4DMRI reconstruction.
Results
Using the digital phantom, the maximum deformable magnitude is doubled using the modified DIR from 3 to 6 cm at the diaphragm. In six human subjects, the first 15‐iteration DIR using the pseudo force deforms 200 ± 150% more than the original force, and succeeds in all 12 cases, whereas the original demons‐based DIR failed in 67% of tested cases. Using the pseudo force, high VIC (>0.9) and small ICE (1.6 ± 0.6 mm) values are observed for DIR of BHI&BHE, BHI→FB, and BHE→FB. The CCC identifies four questionable cases, in which two cases need further DIR refinement, without missing true negative.
Conclusions
The introduction of a pseudo demons force enhances the largest deformation magnitude up to 6 cm. The cross‐consistency check ensures the quality of TR‐4DMRI reconstruction. Further investigation is ongoing to fully characterize TR‐4DMRI for potential multi‐breathing‐cycle radiotherapy simulation.
Keywords: deformable image registration (DIR), image‐guided radiotherapy (IGRT), multi‐breath motion assessment, time‐resolved four‐dimensional magnetic resonance image (TR‐4DMRI)
1. Introduction
Respiration‐induced tumor motion is one of the major uncertainties in radiotherapy of a thoracic or abdominal tumor and commonly occurring breathing irregularities have not been fully accounted for in the current radiotherapy planning process.1, 2 Attempts to incorporate tumor motion variation and statistics in treatment planning have been reported using the probability density function of tumor motion3, 4, 5 or a motion margin formula.6 Owing to lack of dynamic volumetric imaging, two‐dimensional (2D) cine magnetic resonance imaging (MRI) and 2D portal imaging have been applied to assess tumor motion PDF and its applicability in treatment planning to compensate for the tumor motion.7, 8, 9 As a tumor may not move within a plane,10 2D cine MR imaging may provide incomplete motion data for a mobile tumor and its nearby organs at risk (OARs) for motion‐compensated planning. The 2D portal or fluoroscopic imaging requires implanted fiducials near a mobile tumor as its surrogates. Conventional respiratory‐correlated (RC) 4D computed tomography (4DCT) and recently developed 4DMRI11, 12, 13, 14 only provide a single‐breath composite image series that contain little motion variation, and the single‐breath snapshot of tumor/OAR motions may not represent the patient respiratory motion during treatment.15
Time‐resolved (or dynamic) volumetric four‐dimensional magnetic resonance imaging (TR‐4DMRI) has the potential to provide multi‐breath motion simulation with breathing irregularities for treatment planning.16, 17 However, because of slow physical MR relaxation and large clinical field of views (FOV), it seems impractical to directly acquire TR‐4DMRI images with adequate spatiotemporal resolution.16, 18, 19, 20 In the development of MR‐guided radiotherapy, a hybrid approach was reported to generate TR‐4DMRI based on RC‐4DMRI.21, 22 This method built a patient‐specific motion model based on RC‐4DMRI using the principal component analysis (PCA) and deformable image registration (DIR) and then reconstructed volumetric TR‐4DMRI with the guidance of 2D cine MR images. As the a priori motion model may be limited by RC‐4DMRI image quality, motion range, and motion pattern, the reconstructed TR‐4DMRI provides an approximation to tumor motion.22 Recently, a super‐resolution (SR) approach was reported to reconstruct TR‐4DMRI by combining two complementary image sets with high‐spatial resolution at breath‐hold (BH) and high‐temporal resolution (3D cine) in free‐breathing (FB) using DIR, providing multi‐breath images with motion irregularities.23 This SR‐based method reconstructs TR‐4DMRI by deforming the BH image using low‐resolution 3D cine MR images as guidance without assuming periodic motion, allowing imaging of irregular motion. To reconstruct SR‐based TR‐4DMRI reliably and accurately under clinical conditions, the ability to deform large magnitudes of respiratory motion is critical because lung or liver tumor motion can be up to 4 cm in free‐breathing (FB),10, 24 breathing irregularities may cause greater motions,1, 15 and breath‐hold (BH) can be further away from the FB motion range.25
Deformable image registration has been extensively studied in the past decade for radiation therapy applications, including patient‐specific motion modeling, organ contour propagation, radiation dose mapping, and adaptive radiation therapy.26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37 Among many algorithms, the intensity‐based demons algorithm is useful for single‐modality registration,28, 38 such as TR‐4DMRI reconstruction.23 The demons‐based DIR has been widely implemented in programs, such as MATLAB® (Mathwork, Inc.), ITK (Insight Segmentation and Registration Toolkits),39 and graphical processing unit based codes.32, 35, 36 However, this algorithm has a limited deformable range and often requires other methods to boost its deformable range.40 Reports on prostate, head and neck, and lung patients have studied 1–2 cm deformation magnitude,28, 32, 34, 35, 36, 41 which is at the low range of FB motion (1–4 cm)10, 24 and larger BH displacement (6 cm or greater) between full inhalation (BHI) and full exhalation (BHE).25 Therefore, it is necessary to explore and enhance the DIR dynamic range and robustness to ensure reliable image quality of TR‐4DMRI for multi‐breath motion assessment.
To enhance the deformation range, we introduced a pseudo demons force and applied it to the coarse alignment, followed by the fine‐tuning DIR using the original demons forces in a multi‐resolution approach. A separate displacement vector field (DVF) was used at each resolution level and combined to create the composite DVF via vector operation, prior to reconstructing the TR‐4DMRI image. To demonstrate the enhancement of DIR deformation range, the diaphragm dome alignments were measured in the reconstructed TR‐4DMRI with or without the pseudo demons force. In addition, we introduced a cross‐consistency check (CCC) to cross‐verify the quality of TR‐4DMRI reconstruction by comparing the similarity between two reconstructed images using two opposite‐extreme BH images. Several T1‐mapped 4D images created using the 4D XCAT phantom42 and six subject images (BHI, BHE, and a 3D cine series) acquired under an IRB‐approved protocol were studied to evaluate the new demons pseudo force in TR‐4DMRI reconstruction.
2. Methods and materials
2.A. General description of super‐resolution time‐resolved 4DMRI approach
A T1‐weighted turbo field echo pulse sequence with TE/TR of 1/4 ms, a flip angle of 15°, an acceleration factor of 4 in SENSE parallel imaging, and a factor of 0.8 in partial Fourier approximation, was used to acquire 3D cine low‐resolution FB images (lowR: 5 × 5 × 5 mm3 at 2 Hz) and 3D high‐resolution BH image (highR: 2 × 2 × 2 mm3) using a 3 T MR scanner (Ingenia, Philips Healthcare). The same field of view (FOV) was used for both the low‐ and high‐resolution MR images.
Prior to registration, the 3D cine FB and 3D static BH image intensities were normalized, and the low‐resolution FB images were interpolated to have the same image matrix size as the BH image. The region of interest (ROI) was defined by the union of the two body contours from the moving and static images. A three‐level multi‐resolution DIR was applied with separated DVFs to reconstruct the TR‐4DMRI images (2 × 2 × 2 mm3 and 2 Hz). The registration log file recorded the number of iterations and associated time of DIR at each level of resolution. Additional detailed MR scanning conditions can be found in a previous report.23
2.B. Conventional and modified demons force field
In the demons algorithm,38 image gradient () from moving image (m) was used as the driving force to move the underlying voxels while applying a Gaussian filter thereby “diffusing” nearby voxels to regulate anatomic integrity. A counter demons force () from the static image (s) was introduced to accelerate the deformation.28
| (1) |
where is the total demons force, related to voxel intensity gradient (VIG: ) and voxel intensity difference (VID: |m‐s|), and α is a normalization factor (0.2–0.7).
A pseudo force was introduced to allow the VIG of a voxel to affect the neighboring voxels within a Gaussian cube (gCube: 5 × 5 × 5 voxels) with a weight of the Gaussian distribution profile (σ = 1). The pseudo force () at a voxel (i,j,k∈ROI) was calculated by moving the gCube (; n,m,l = −2,−1,0,1,2) and integrating the forces from the surrounding 124 neighboring voxels (n,m,l∈gCube). The pseudo force direction was determined by DVF directions () of the voxels (i,j,k), and its amplitude was determined by the VIG, VID, and Gaussian profile weight within the gCube (n,m,l). The pseudo force () at the point (i,j,k) and the enhanced force () are expressed as:
| (2) |
| (3) |
where denotes the accumulated force at the point (n,m,l), (z = SI = 1, y = AP = 0, and x = LR = 0) is the directional factor, and is the normalization factor of the p . In this study, and β = 1 were used for simplicity to have an isotropic weight and to balance the contributions from and p , respectively. It is worthwhile to emphasize that the pseudo force strength received by a voxel is proportional to its own VID value, as indicated in Eq. (2).
2.C. Applying multiple DVFs in multi‐resolution DIR
When a separated DVF was applied at each of the multi‐resolution levels, a large deformation was separated into smaller deformation components, thereby reducing the amount of the deformation in each step. The final DVF was calculated from the individual DVF using vector operation. The pseudo demons force (Eqs. 2 and 3) was only applied in the initial low‐resolution fast‐matching alignment, whereas the original demons forces [Eq. (1)] was used in the remaining two levels of resolutions. Fig. 1(a) illustrates how the pseudo force field and the multi‐DVF were implemented using the stopping criteria of VID <10−4 in TR‐4DMRI image reconstruction. In detail, the following demons parameters were used in the multi‐resolution DIR:
Low resolution (8 × 8 × 8 mm3): (fast matching); DVF0(0→1);
Middle resolution (4 × 4 × 4 mm3): onlzy (gross tuning); DVF1(1→2);
High resolution (2 × 2 × 2 mm3): only (fine tuning); DVF2(2→3).
Figure 1.
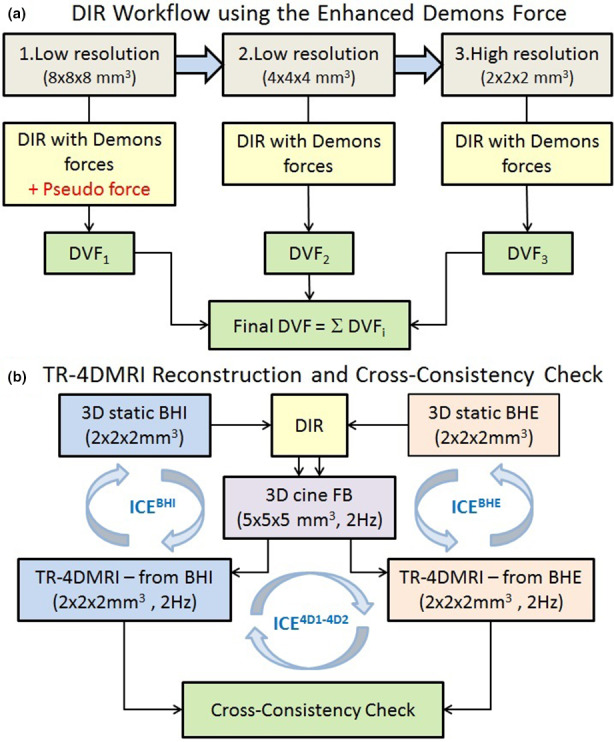
Workflow for reconstruction of time‐resolved four‐dimensional magnetic resonance image (TR‐4DMRI) using enhanced demons DIR and cross‐consistency check (CCC). (a) Multi‐resolution DIR with the pseudo demons force and composite displacement vector field (DVF) to reconstruct TR‐4DMRI and (b) cross‐consistency check for reconstruction of TR‐4DMRI images by deforming two breath‐hold images at full inhalation (BHI) and full exhalation (BHE) to the same 3D cine images in free‐breathing (FB). The inverse consistency error (ICE) is calculated on three occasions. [Color figure can be viewed at wileyonlinelibrary.com]
The final DVF was calculated by the vector operation using the following formula:
| (4) |
For a fair comparison, the same number of iterations (n = 15) was applied at each of the 3‐resolution levels of DIR, while only to the first low‐resolution level had different demons forces: the pseudo force and original force [Fig. 1(a)]. The intermediate images were saved, and the match of the diaphragm was evaluated with normalization to the full displacement (1.0) between the two images. The BHI and BHE images were used to reconstruct two 4DMRI for the comparison [Fig. 1(b)]. The voxel intensity correlation (VIC), defined as the correlation of two voxel intensity arrays (representing two images), was used to assess image alignment quality (0–1.0). Both visual VID image check and quantitative VIC measurements were evaluated.
2.D. Cross‐consistency check (CCC) of DIR
A cross‐consistency check (CCC) was introduced between two SR‐based TR‐4DMRI images reconstructed from two opposite BH images, denoted as BHI→FB←BHE [Fig. 1(b)]. A stopping criterion of ∆<0.0001 was applied. If the DIR was accurate, identical TR‐4DMRI images deformed from BHI and BHE would be expected, namely,
| (5) |
where the two highR BH images were deformed to the lowR FB image from two opposite directions. To quantitate the similarity between two images, the CCC was defined as the ratio of the VIC of the two reconstructed images to the mean VIC of each reconstruction:
| (6) |
| (7) |
The Im and Is denote the voxel intensity of the moving and static images, respectively, and the cov is the covariance and σ is the standard deviation. The CCC should be near unity because two deformed images should be similar, represented by similar VICs. Therefore, the CCC may serve as an indicator for the quality of the TR‐4DMRI reconstruction, whereas CCC <1.0‐ σ or CCC >1.0 + σ (possible outliers) implies a potential problem in one or both reconstructed images and therefore requires further examination. The σ is the standard deviation for the TR‐4DMRI image series. For the CCC evaluation with the use of pseudo demons force, a total of 24 DIRs was conducted and compared.
2.E. Inverse consistency error in CCC DIR approach
As shown in Fig. 1(b), the Inverse consistency error (ICE) was calculated in the following three deformation processes: two DIRs for 4DMRI reconstruction (BHI & FB and BHE & FB), and a DIR between the two reconstructed 4DMRI images (). The operator “⇄” is for inverse DIR operation (→ forward DIR and ← backward DIR). If V=DVF F and U=DVF B represent the forward and backward DVF, respectively, then the ideal DIR should have |U ∘ V| = |V ∘ U| = 0. The ICE F and ICE B can be defined as34, 43:
| (8) |
The ICE can be expressed as
| (9) |
As shown in Fig. 1(b), for each volunteer subject, 12 DIR were performed to compute the ICE values and a total of 72 DIR were performed and compared.
2.F. Verification of enhanced DIR using T1w‐mapped 4D XCAT phantom
A digital anthropomorphic phantom, 4D XCAT (version 2),11, 21, 44 was used to simulate 10 respiratory cycles, which was controlled by the motion curves of the diaphragm and chest wall in the superior‐inferior (SI) and anterior‐posterior (AP) directions, respectively. The intensity of the 4D XCAT phantom was first mapped to produce MRI‐like images, based on clinical T1w MRI. Ten 10‐phase 4D MRI images with SI motion range of 2–8 cm and AP motion range of 0.3–1.2 cm (at the skin) were simulated at a respiratory cycle of 5 s. The full exhalation and full inhalation images with a voxel size of 2 × 2 × 2 mm3 were used to simulate 3D cine MRI by down‐sampling them to 5 × 5 × 5 mm3. Similar DIR evaluations were performed as described below in human subjects. The achievable deformation magnitudes for the original demons force and enhanced demons force were evaluated using the 4D XCAT phantoms. A spherical tumor with a 3.0 cm diameter (Φ = 3.0 cm) and 5.0 cm motion range near the left diaphragm (motion range of 6.0 cm) was generated. The tumor alignment between the reconstructed TR‐4DMRI and the ground truth was evaluated based on the center of mass, volume and DICE similarity index.
2.G. Verification of enhanced DIR in six healthy volunteer study
Six healthy volunteers with both arms up were scanned using a FOV of the thorax and upper abdomen under an IRB‐approved protocol. Two BH images (BHI and BHE) were acquired at full inhalation and full exhalation. Using the image pairs of BHI and BHE of the six subjects, we down‐sampled the images to mimic the low‐resolution FB images and performed 96 DIRs between the BH and FB pairs at the specified conditions, including separate DIRs at each resolution level (x4, x2 and ×1 voxel sizes) with a fixed iteration (n = 15) with or without the pseudo force, and full DIR with a stopping criterion. The diaphragm dome was primarily used to quantitate the enhanced DIR performance and comparison with the original demons algorithm. By deforming both BHI and BHE to two selected extreme FB images, we reconstructed two TR‐4DMRI images for each of 24 cases and compared their similarity using the VIC and CCC.
3. Results
3.A. Enhanced demons force and its application in multi‐resolution optimization
A graphical representation of the voxel‐based magnitudes of the original demons force [Eq. (1)] and enhanced demons force [Eqs. (2) and (3)], together with the VID image between two MRI images are shown in Fig. 2. With the pseudo force (), the enhanced force is boosted around high gradient voxels where high VIDs due to organ motion are present, such as the diaphragm and heart. The enhanced demons force boosts the initial coarse alignment at the diaphragm and heart in comparison to the conventional demons‐based DIR process.
Figure 2.
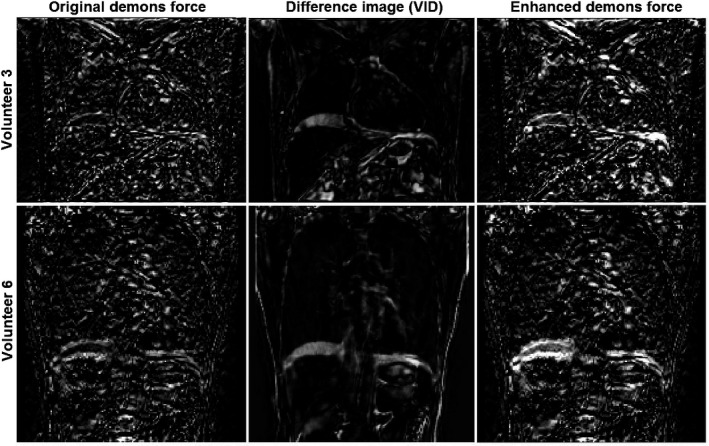
Graphical view of the enhanced demons force (intensity = strength) in two volunteer subjects: the original demons force (left), the difference image with voxel intensity difference (VID) (middle), and the enhanced force (right). The voxel with non‐zero force will be deformed in the direction of the voxel intensity gradient and a Gaussian filter is applied to the displacement vector field in each iteration to regulate the anatomy integrity throughout the optimization.
3.B. Evaluation of modified demons DIR using T1w‐mapped 4D XCAT digital phantom
Figure 3 illustrates the enhancement of the deformation range in 15 iterations at each resolution level using the pseudo demons force, compared with the original demons force. The pseudo force helps to achieve >60% deformation magnitude in 15 iterations, while original demons force can only achieve <20% when the deformation magnitude is >3 cm. The modified demons DIR with the pseudo force can deform beyond 6 cm deformation magnitude.
Figure 3.
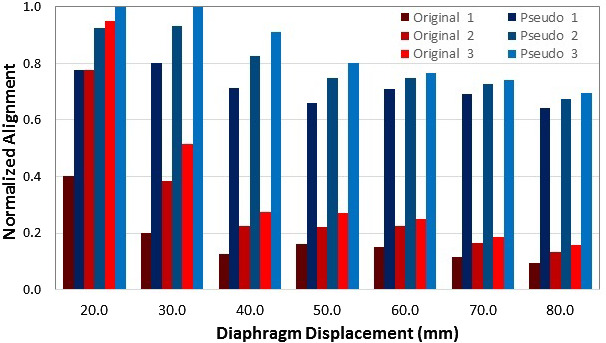
Illustration of the enhancement of the deformation range of the modified demons with the pseudo force (blues) comparing to the original demons force (reds) in the digital T1‐mapped 4D XCAT phantom. The diaphragm domes were used for comparison (full alignment =1.0). 15 iterations were applied to each of the three‐level resolutions. The pseudo force was only applied in the first coarse alignment (blues). The results are the average of DIR from high‐resolution full inhalation (BHI) or full exhalation (BHE) to the low‐resolution images down‐sampled from the opposite BH images.
Figure 4 provides a graphical illustration of the enhanced deformation ability of the pseudo demons force on the T1w‐mapped XCAT phantoms, which succeeded in deforming more than 6 cm displacement at the diaphragm, whereas the original demons force failed at >3 cm displacement. The abdominal misalignment, primarily caused by missing tissue in the full inhalation moving images and the low‐contrast tissue, can be improved by local DIR refinement using the DIR stopping criteria.
Figure 4.
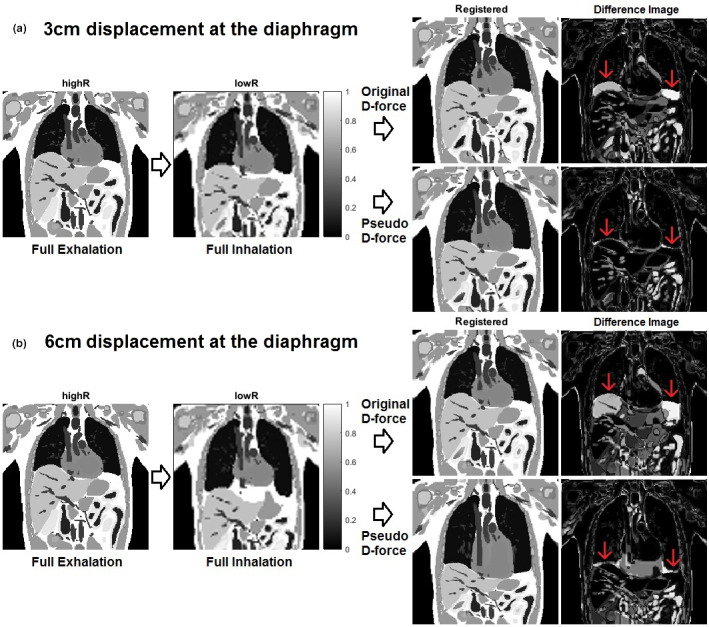
Demonstration of enhanced deformation ability at the diaphragm using the pseudo demons force vs original demons force in the first coarse alignment with 15 iterations. The diaphragm alignment is much improved using the pseudo force, compared with using the original force. The alignment of the low‐contrast tissue needs further local refinement at fine resolutions. Note that in the inferior image, the alignment from full exhalation to full inhalation was improved after more iterations with the stopping criteria. (a) 3cm and (b) 6cm displacements at the diaphragm. [Color figure can be viewed at wileyonlinelibrary.com]
The tumor alignment error in the deformed XCAT phantom with 5.0 cm tumor motion (Φ = 3 cm) and 6.0 cm diaphragm motion is 1.3 mm, the tumor volume ratio is 1.02, and the DICE similarity index is 0.84 in reference to the ground truth, suggesting an acceptable image fidelity. Further DIR refinement within the lung can further improve the DICE index to 0.88.
3.C. Comparison between DIR with original and enhanced demons forces in human subjects
Figure 5 demonstrates the results of multi‐resolution DIR with and without the pseudo force in the first low‐resolution level. The deformation enhancement at the diaphragm in level 1 by the pseudo demons force is 208 ± 126% (range: 25%–433%). This fast matching enhances the overall DIR performance, though the pseudo force is only applied in level 1. Five out of six subject images deformed more than half of the full diaphragm displacement in the first resolution level, except for subject 3 (~30% vs 10% or 20%). The enhance formation range observed in human subjects is consistent with the digital phantom study, as discussed above (3.B).
Figure 5.
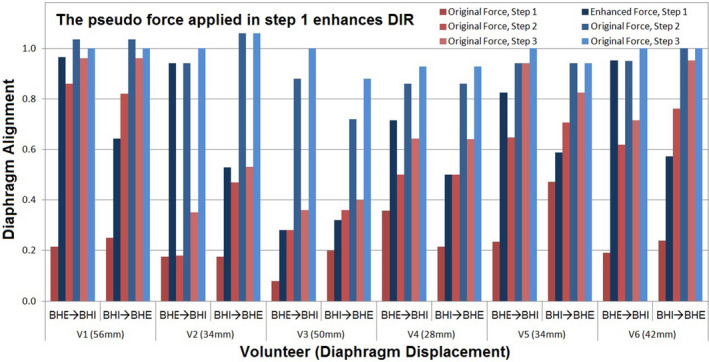
Demonstration of the enhanced deformation range of deformable image registration (DIR) with the pseudo demons force between two extreme breath‐holds (BHI and BHE) in six volunteers. The full diaphragm displacement (28‐56 mm) is normalized to 1.0. The intermediate DIR results with 15 iterations at each resolution level are shown in red (with the original forces) and blue (with the pseudo force). The pseudo force was applied in the first coarse resolution achieving 70% alignment (dark blue) vs 25% alignment otherwise (dark red) on average. Nearly 100% alignment (light red) is achieved with initial pseudo force boost vs 65% alignment otherwise (light blue).
Figure 6 illustrates two visual CCC examples of TR‐4DMRI that resulted from opposite BH images. The diaphragm alignments are almost identical, visually confirming their validity with only mild differences in the VID images. Table 1 tabulates VIC and CCC values among original and deformed BHI and BHE with FB images. It is worthwhile to point out that the CCC value is quite sensitive to mild misalignment as shown in volunteer 3, for which the diaphragm alignment was not complete. This is a patient image specific and Fig. 5 illustrates a similar result. The accuracy of the high‐contrast organ is high, including the diaphragm, heart, and stomach, as shown in Fig. 6. At the diaphragm dome, the accuracy of the alignment is 0.8 ± 1.6 mm.
Figure 6.
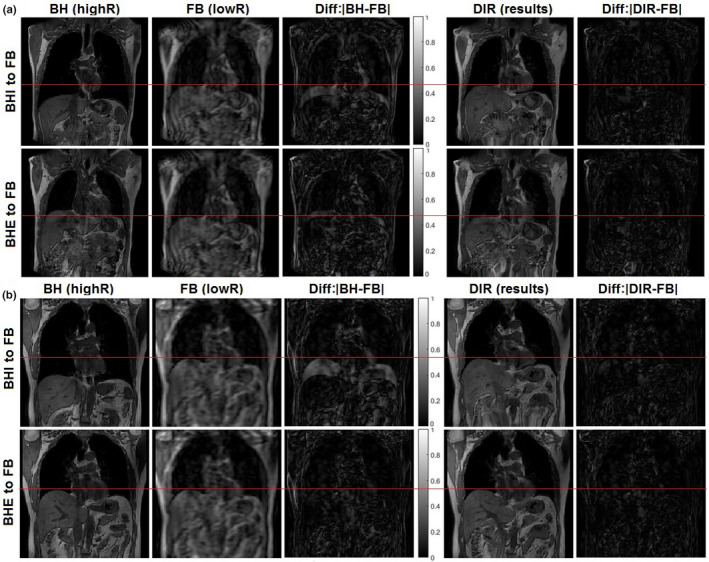
Visual representation of cross‐consistency check (CCC) of the time‐resolved four‐dimensional magnetic resonance image (TR‐4DMRI) of two volunteers (A: v1 and B: v2) using two opposite breath‐hold images at full exhalation (BHE) and full inhalation (BHI). Almost identical diaphragm alignment is achieved between the two deformed images. In (b), the BHE is very close to the full exhalation FB, illustrating that the residual image intensity difference is primarily due to different image resolutions. [Color figure can be viewed at wileyonlinelibrary.com]
Table 1.
Cross‐consistency check (CCC) based on voxel intensity correlation (VIC) in the reconstruction of time‐resolved four‐dimensional magnetic resonance image (TR‐4DMRI) at two extreme free‐breathing (FB) phases near the ends of inhalation (BHI) and expiration (BHE). The initial and final displacements (d) of the diaphragm from breath‐hold (BH) to the FB are shown
| Subject | FB phasea | BHI | BHE | Cross consistencyc | ||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d (mm) | VIC | ICE (mm)b | d (mm) | VIC | ICE (mm) | between 2 TR‐4DMRI | ||||||||
| Pre | Post | Pre | Post | Pre | Post | Pre | Post | VIC | CCC | ICE (mm) | ||||
| 1 | E | 58 | 0 | 0.54 | 0.86 | 1.66 | 2 | 2 | 0.79 | 0.89 | 1.52 | 0.88 | 1.01 | 0.03 |
| I | 24 | 0 | 0.65 | 0.90 | 1.77 | 28 | 4 | 0.71 | 0.88 | 2.74 | 0.90 | 1.02 | 0.09 | |
| 2 | E | 42 | 0 | 0.65 | 0.93 | 1.46 | 8 | 0 | 0.80 | 0.94 | 1.29 | 0.94 | 1.01 | 0.26 |
| I | 20 | 2 | 0.73 | 0.94 | 1.73 | 18 | 2 | 0.82 | 0.93 | 1.01 | 0.95 | 1.01 | 0.29 | |
| 3 | E | 66 | 0 | 0.31 | 0.80 | 2.43 | 16 | 0 | 0.73 | 0.87 | 1.60 | 0.80 | 0.95 | 0.25 |
| I | 40 | 0 | 0.56 | 0.87 | 1.90 | 18 | 2 | 0.55 | 0.87 | 1.32 | 0.86 | 0.99 | 0.16 | |
| 4 | E | 30 | 6 | 0.60 | 0.91 | 2.07 | 8 | 0 | 0.72 | 0.93 | 1.33 | 0.95 | 1.03 | 0.29 |
| I | 28 | 2 | 0.69 | 0.93 | 1.40 | 10 | 0 | 0.74 | 0.93 | 1.88 | 0.96 | 1.03 | 0.14 | |
| 5 | E | 40 | 0 | 0.62 | 0.88 | 0.98 | 8 | 0 | 0.83 | 0.90 | 0.89 | 0.91 | 1.02 | 0.08 |
| I | 34 | 0 | 0.66 | 0.89 | 1.90 | 4 | 0 | 0.83 | 0.90 | 2.58 | 0.92 | 1.02 | 0.12 | |
| 6 | E | 48 | 0 | 0.62 | 0.90 | 0.69 | 2 | 0 | 0.79 | 0.91 | 0.66 | 0.91 | 1.00 | 0.17 |
| I | 32 | 0 | 0.68 | 0.91 | 1.49 | 14 | 0 | 0.74 | 0.91 | 1.05 | 0.92 | 1.01 | 0.18 | |
| Average | 39 | 0.8 | 0.61 | 0.90 | 1.6 | 11 | 0.8 | 0.75 | 0.91 | 1.5 | 0.91 | 1.01 | 0.17 | |
| St Dev | 14 | 1.8 | 0.04 | 0.5 | 8 | 1.3 | 0.02 | 0.6 | 0.04 | 0.02 | 0.08 | |||
4. Discussion
4.A. The pseudo demons force for enhanced DIR deformation range
The pseudo demons force provides a substantial boost to the gradient‐based force field in the fast‐marching alignment. The initial low‐resolution DIR alignment allows the pseudo force to exert a “long distance” impact because of larger voxels. It extends the influence of the image gradient at a voxel to the 124 neighboring voxels with a weighting factor following Gaussian distribution profile. This helps to deform voxels around a voxel with high VIG and VID, similar to the role of the Gaussian filter to the DVF, but up‐front. This pseudo force within a Gaussian cube can increase the mean deformation up‐front with reasonable anatomic integrity, unlike the Gaussian filter applied at the end of each iteration, which pulls back the highly deformed voxels to regulate the anatomic integrity by Gaussian smoothing. Therefore, the pseudo force accelerates the deformation and enhances the deformable range.
However, the pseudo force should only be applied in the initial coarse alignment within the region of interest to avoid excess deformation, causing distortion artifacts. The benefit of using the pseudo force in low‐resolution DIR is that it will reduce computation burden and maintain the “long‐distance” impact. In the high‐resolution DIR, the original demons force provides additional fine‐tuning to complete the DIR. In addition, using a separate DVF at each resolution level and combining multi‐DVF for the final deformation enhances the deformation range, almost equivalent to multi‐DIR processes. As the final DVF is computed prior to image transformation by vector operation using Eq. (4), it avoids repeating image interpolation and thus preserves the image resolution.
In practice, the BHI images may appear outside of the FB range, as a subject tends to inhale more for a breath‐hold, while the BHE is likely within FB range. A 6.6 cm deformation magnitude was observed in volunteer 3 (Table 1). Using the digital phantom, we have demonstrated that the application of the pseudo force deforms >60% magnitude within 15 iterations (Fig. 3). The modified demons DIR achieved accurate alignment on the diaphragm, heart, and stomach with high‐contrast (Figs. 4 and 6, and Table 1). Therefore, the enhanced deformation range makes the reconstruction of TR‐4DMRI a robust process, although in practice, we would try to acquire a BH in the middle of FB motion range. This is the first time to an image has been successfully deformed on such a large scale using the enhanced demons algorithm.
4.B. Cross‐consistency check for TR‐4DMRI reconstruction
To implement the SR‐based TR‐4DMRI technique for a clinical application requires not only a robust DIR method but also an effective indicator of the DIR quality are necessary. The CCC index [Eq. (6)] establishes a self‐consistency check of two independent results so that the results can be automatically cross‐validated by deforming two BH images from opposite directions. The results (shown in Fig. 6 and Table 1) suggest that the CCC index is effective in catching DIR misalignment. In the twelve cases in Table 1, the CCC caught four possible incomplete DIR cases and two were confirmed and then improved with refinement by tightening the stopping criteria. Note that in free‐breathing, the motion range is usually less than 4 cm, therefore, the success rate of reconstruction should be higher. As a comparison, the ICE index could be unreliable if the deformable range is limited. For instance, the ICE may grossly underestimate the error when a DIR deforms only half way forward but can fully deform backward. In fact, the ICE cannot distinguish the results using the original demons and enhanced demons. On the contrary, the CCC is designed to cross‐verify two independent deformations resulting from two opposite directions (BHI and BHE): the probability of a coincidental alignment is small and can be ignored.
In this study, three scenarios of the ICE assessment were also evaluated, as shown in Fig. 1(b) and Table 1. Between the two BHs and FB images, the ICE is about the same (1.6 ± 0.6 mm), whereas it is reduced to 0.17 ± 0.08 mm for the two reconstructed 4DMRI images, about 10 times smaller. This is because the two resultant 4DMRI images are so similar that little deformation is needed, resulting in a small ICE value. This indicates that ICE is dependent on both the DIR method and the initial deformation magnitude. By comparison, the CCC index is independent of deformation magnitude and therefore a useful cross‐verification index of DIR quality.
4.C. Limitation of the pseudo demons force and future direction
Currently, an isotropic Gaussian cube is applied in the pseudo force implementation. Given the knowledge that the respiratory motion is mostly occurring in the superior‐inferior (SI) direction, an anisotropic Gaussian cube with a different Gaussian distribution profile could be used to bias the deformation in the SI direction. Therefore, an up‐front, directional, and long‐distance impact can be established, ensuring a continuous initial deformation. In addition, the weight factor (β in Eq. (3)) could be used to alter the contribution from the pseudo force; when β = 0, Eq. (3) contains only the original demons force. This is an ongoing study for further improvement of the demons DIR algorithm.
Although the pseudo force enhanced the alignment at the diaphragm, which has the highest tissue contrast and largest gradient at the interface, it may not be useful to enhance the alignment of low‐contrast tissues. Therefore, the improvement of low‐contrast tissue alignment is still a challenge and it is currently under investigation. Combining the efforts of both pseudo and original demons forces, the image quality of reconstructed TR‐4DMRI can be reliably ensured. In fact, compared with CT images, T1w MR images provide superior soft‐tissue contrast other than the lungs, facilitating the DIR‐based reconstruction and verification.
Although this study provides an effective approach to increase DIR deformable range beyond 6 cm, in practice we would recommend minimizing the deformation between EOE and EOI using audio or visual breath coaching for BH acquisition. Therefore, two BHI and BHE images within the FB breathing motion range can be acquired, facilitating TR‐4DMRI reconstruction. In general, the smaller the initial deformation magnitude, the less uncertainty would be.
Last, we are recruiting patients for a TR‐4DMRI study under IRB‐approved clinical trials, so that we can evaluate the tumor motion, together with the motions of its surrounding organs. The enhanced deformation range using the pseudo demons force can assist to ensure the robustness of this SR‐based TR‐4DMRI technique to produce high‐quality multi‐breath images for motion‐compensated radiotherapy treatment planning.
5. Conclusion
The introduction of the pseudo demons force in the coarse DIR alignment, together with the multi‐DVF approach, enables the demons algorithm to increase the deformation range (up to 6 cm) for the reconstruction of super‐resolution TR‐4DMRI. In both a digital phantom and six human subjects, the enhancement of the deformation range of the demons DIR is demonstrated at the high‐contrast tissues, while the improvement of low‐contrast tissue is under an ongoing investigation. The cross‐consistency check has the potential to serve as the quality assurance indicator of the TR‐4DMRI reconstruction for clinical applications.
Conflict of interest
Memorial Sloan Kettering Cancer Center has a master research agreement with Philips Healthcare. Part of this work was presented in the AAPM'2017 annual meeting.
Acknowledgments
This research is supported in part by the National Institutes of Health (U54CA137788), the Breast Cancer Research Foundation (BCRF‐17‐193), and the MSK Cancer Center Support Grant/Core Grant (P30 CA008748). The authors would like to thank Dr. Mo Kadbi (Philips Healthcare, MR in Therapy) for support and MRI simulation technologists for help in MRI image acquisition. We thank Mr. Jim Keller for editing this manuscript. We are grateful to all participating volunteers.
References
- 1. Keall PJ, Mageras GS, Balter JM, et al. The management of respiratory motion in radiation oncology report of AAPM Task Group 76. Med Phys. 2006;33:3874–3900. [DOI] [PubMed] [Google Scholar]
- 2. Vergalasova I, Li G, Kelsey CR, Ge H, Huang H, Cai J. Uncertainties of IGRT for lung cancer. In: Cai J, Chang JY, Yin F. Principles and Practice of Image‐Guided Radiation Therapy of Lung Cancer, New York, NY: Taylor & Francis Books, Inc.; 2017. [Google Scholar]
- 3. Lujan AE, Larsen EW, Balter JM, Ten Haken RK. A method for incorporating organ motion due to breathing into 3D dose calculations. Med Phys. 1999;26:715–720. [DOI] [PubMed] [Google Scholar]
- 4. Li JG, Xing L. Inverse planning incorporating organ motion. Med Phys. 2000;27:1573–1578. [DOI] [PubMed] [Google Scholar]
- 5. Li X, Zhang P, Mah D, Gewanter R, Kutcher G. Novel lung IMRT planning algorithms with nonuniform dose delivery strategy to account for respiratory motion. Med Phys. 2006;33:3390–3398. [DOI] [PubMed] [Google Scholar]
- 6. Rit S, van Herk M, Zijp L, Sonke JJ. Quantification of the variability of diaphragm motion and implications for treatment margin construction. Int J Radiat Oncol Biol Phys. 2012;82:e399–e407. [DOI] [PubMed] [Google Scholar]
- 7. Cai J, Read PW, Larner JM, Jones DR, Benedict SH, Sheng K. Reproducibility of interfraction lung motion probability distribution function using dynamic MRI: statistical analysis. Int J Radiat Oncol Biol Phys. 2008;72:1228–1235. [DOI] [PubMed] [Google Scholar]
- 8. Zhang F, Hu J, Kelsey CR, Yoo D, Yin FF, Cai J. Reproducibility of tumor motion probability distribution function in stereotactic body radiation therapy of lung cancer. Int J Radiat Oncol Biol Phys. 2012;84:861–866. [DOI] [PubMed] [Google Scholar]
- 9. Tryggestad E, Flammang A, Han‐Oh S, et al. Respiration‐based sorting of dynamic MRI to derive representative 4D‐MRI for radiotherapy planning. Med Phys. 2013;40:051909. [DOI] [PubMed] [Google Scholar]
- 10. Seppenwoolde Y, Shirato H, Kitamura K, et al. Precise and real‐time measurement of 3D tumor motion in lung due to breathing and heartbeat, measured during radiotherapy. Int J Radiat Oncol Biol Phys. 2002;53:822–834. [DOI] [PubMed] [Google Scholar]
- 11. Cai J, Chang Z, Wang Z, Paul Segars W, Yin FF. Four‐dimensional magnetic resonance imaging (4D‐MRI) using image‐based respiratory surrogate: a feasibility study. Med Phys. 2011;38:6384–6394. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12. Du D, Caruthers SD, Glide‐Hurst C, et al. High‐quality t2‐weighted 4‐dimensional magnetic resonance imaging for radiation therapy applications. Int J Radiat Oncol Biol Phys. 2015;92:430–437. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13. Hu Y, Caruthers SD, Low DA, Parikh PJ, Mutic S. Respiratory amplitude guided 4‐dimensional magnetic resonance imaging. Int J Radiat Oncol Biol Phys. 2013;86:198–204. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14. Li G, Wei J, Olek D, et al. Direct comparison of respiration‐correlated four‐dimensional magnetic resonance imaging reconstructed using concurrent internal navigator and external bellows. Int J Radiat Oncol Biol Phys. 2017;97:596–605. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15. Dhont J, Vandemeulebroucke J, Burghelea M, et al. The long‐ and short‐term variability of breathing induced tumor motion in lung and liver over the course of a radiotherapy treatment. Radiother Oncol. 2018;126:339–346. [DOI] [PubMed] [Google Scholar]
- 16. Li G, Citrin D, Camphausen K, et al. Advances in 4D medical imaging and 4D radiation therapy. Technol Cancer Res Treat. 2008;7:67–81. [DOI] [PubMed] [Google Scholar]
- 17. Plathow C, Ley S, Fink C, et al. Analysis of intrathoracic tumor mobility during whole breathing cycle by dynamic MRI. Int J Radiat Oncol Biol Phys. 2004;59:952–959. [DOI] [PubMed] [Google Scholar]
- 18. Tsao J, Kozerke S. MRI temporal acceleration techniques. J Magn Reson Imaging. 2012;36:543–560. [DOI] [PubMed] [Google Scholar]
- 19. Hollingsworth KG. Reducing acquisition time in clinical MRI by data undersampling and compressed sensing reconstruction. Phys Med Biol. 2015;60:R297–R322. [DOI] [PubMed] [Google Scholar]
- 20. Plathow C, Klopp M, Schoebinger M, et al. Monitoring of lung motion in patients with malignant pleural mesothelioma using two‐dimensional and three‐dimensional dynamic magnetic resonance imaging: comparison with spirometry. Invest Radiol. 2006;41:443–448. [DOI] [PubMed] [Google Scholar]
- 21. Harris W, Ren L, Cai J, Zhang Y, Chang Z, Yin FF. A technique for generating volumetric cine‐magnetic resonance imaging. Int J Radiat Oncol Biol Phys. 2016;95:844–853. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22. Stemkens B, Tijssen RH, de Senneville BD, Lagendijk JJ, van den Berg CA. Image‐driven, model‐based 3D abdominal motion estimation for MR‐guided radiotherapy. Phys Med Biol. 2016;61:5335–5355. [DOI] [PubMed] [Google Scholar]
- 23. Li G, Wei J, Kadbi M, et al. Novel super‐resolution approach to time‐resolved volumetric 4‐dimensional magnetic resonance imaging with high spatiotemporal resolution for multi‐breathing cycle motion assessment. Int J Radiat Oncol Biol Phys. 2017;98:454–462. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24. Li G, Cohen P, Xie H, Low D, Li D, Rimner A. A novel four‐dimensional radiotherapy planning strategy from a tumor‐tracking beam's eye view. Phys Med Biol. 2012;57:7579–7598. [DOI] [PubMed] [Google Scholar]
- 25. Boron WF, Boulpaep EL. Medical Physiology ‐ A Cellular and Molecular Approach. Philadelphia, PA: Elsevier Health Sciences; 2nd Edition, 2012. [Google Scholar]
- 26. Lu W, Chen ML, Olivera GH, Ruchala KJ, Mackie TR. Fast free‐form deformable registration via calculus of variations. Phys Med Biol. 2004;49:3067–3087. [DOI] [PubMed] [Google Scholar]
- 27. Zhang T, Orton NP, Mackie TR, Paliwal BR. Technical note: a novel boundary condition using contact elements for finite element based deformable image registration. Med Phys. 2004;31:2412–2415. [DOI] [PubMed] [Google Scholar]
- 28. Wang H, Dong L, O'Daniel J, et al. Validation of an accelerated ‘demons’ algorithm for deformable image registration in radiation therapy. Phys Med Biol. 2005;50:2887–2905. [DOI] [PubMed] [Google Scholar]
- 29. Brock KK, Dawson LA, Sharpe MB, Moseley DJ, Jaffray DA. Feasibility of a novel deformable image registration technique to facilitate classification, targeting, and monitoring of tumor and normal tissue. Int J Radiat Oncol Biol Phys. 2006;64:1245–1254. [DOI] [PubMed] [Google Scholar]
- 30. Flampouri S, Jiang SB, Sharp GC, Wolfgang J, Patel AA, Choi NC. Estimation of the delivered patient dose in lung IMRT treatment based on deformable registration of 4D‐CT data and Monte Carlo simulations. Phys Med Biol. 2006;51:2763–2779. [DOI] [PubMed] [Google Scholar]
- 31. Rietzel E, Chen GT. Deformable registration of 4D computed tomography data. Med Phys. 2006;33:4423–4430. [DOI] [PubMed] [Google Scholar]
- 32. Sharp GC, Kandasamy N, Singh H, Folkert M. GPU‐based streaming architectures for fast cone‐beam CT image reconstruction and demons deformable registration. Phys Med Biol. 2007;52:5771–5783. [DOI] [PubMed] [Google Scholar]
- 33. Zhang Q, Pevsner A, Hertanto A, et al. A patient‐specific respiratory model of anatomical motion for radiation treatment planning. Med Phys. 2007;34:4772–4781. [DOI] [PubMed] [Google Scholar]
- 34. Yang D, Li H, Low DA, Deasy JO, El Naqa I. A fast inverse consistent deformable image registration method based on symmetric optical flow computation. Phys Med Biol. 2008;53:6143–6165. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35. Samant SS, Xia J, Muyan‐Ozcelik P, Owens JD. High performance computing for deformable image registration: towards a new paradigm in adaptive radiotherapy. Med Phys. 2008;35:3546–3553. [DOI] [PubMed] [Google Scholar]
- 36. Gu X, Pan H, Liang Y, et al. Implementation and evaluation of various demons deformable image registration algorithms on a GPU. Phys Med Biol. 2010;55:207–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37. Brock KK. Results of a multi‐institution deformable registration accuracy study (MIDRAS). Int J Radiat Oncol Biol Phys. 2010;76:583–596. [DOI] [PubMed] [Google Scholar]
- 38. Thirion JP. Image matching as a diffusion process: an analogy with Maxwell's demons. Med Image Anal. 1998;2:243–260. [DOI] [PubMed] [Google Scholar]
- 39. McCormick M, Liu X, Jomier J, Marion C, Ibanez L. ITK: enabling reproducible research and open science. Front Neuroinform. 2014;8:13. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40. Lin M, Chen JH, Mehta RS, et al. Spatial shrinkage/expansion patterns between breast density measured in two MRI scans evaluated by non‐rigid registration. Phys Med Biol. 2011;56:5865–5875. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41. Yim Y, Hong H, Shin YG. Deformable lung registration between exhale and inhale CT scans using active cells in a combined gradient force approach. Med Phys. 2010;37:4307–4317. [DOI] [PubMed] [Google Scholar]
- 42. Panta RK, Segars P, Yin FF, Cai J. Establishing a framework to implement 4D XCAT phantom for 4D radiotherapy research. J Cancer Res Ther. 2012;8:565–570. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43. Bender ET, Tome WA. The utilization of consistency metrics for error analysis in deformable image registration. Phys Med Biol. 2009;54:5561–5577. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44. Ren L, Zhang Y, Yin FF. A limited‐angle intrafraction verification (LIVE) system for radiation therapy. Med Phys. 2014;41:020701. [DOI] [PubMed] [Google Scholar]


