Association Between Sporadic Legionellosis and River Systems in Connecticut

Legionnaires’ disease has been on the rise over the last decade, and the determinants of nonoutbreak cases are not understood. We found that proximity to key river systems and watersheds was associated with increased disease incidence in surrounding zip codes.

Abstract

Background

There has been a dramatic increase in the incidence of sporadic legionnaires’ disease in Connecticut since 1999, but the exact reasons for this are unknown. Therefore, there is a growing need to understand the drivers of legionnaires’ disease in the community. In this study, we explored the relationship between the natural environment and the spatial and temporal distribution of legionellosis cases in Connecticut.

Methods

We used spatial models and time series methods to evaluate factors associated with the increase and clustering of legionellosis in Connecticut. Stream flow, proximity to rivers, and residence in regional watersheds were explored as novel predictors of disease, while controlling for testing intensity and correlates of urbanization.

Results

In Connecticut, legionellosis incidence exhibited a strong pattern of spatial clustering. Proximity to several rivers and residence in the corresponding watersheds were associated with increased incidence of the disease. Elevated rainfall and stream flow rate were associated with increases in incidence 2 weeks later.

Conclusions

We identified a novel relationship between the natural aquatic environment and the spatial distribution of sporadic cases of legionellosis. These results suggest that natural environmental reservoirs may have a greater influence on the spatial distribution of sporadic legionellosis cases than previously thought.

(See the editorial commentary by de Fisman, on pages 188–97.)

Since the first confirmed outbreak in 1976, diagnoses of legionnaires’ disease, or legionellosis, have increased steadily in the United States, often garnering intense media attention during outbreaks [1]. Outbreaks tend to be associated with contaminated cooling towers and potable water sources [2, 3], but the majority of legionellosis cases are not known to be associated with a common exposure. These “sporadic” cases constitute between 3% and 7% of the total burden of community-acquired pneumonia [4, 5] and are particularly important causes of such pneumonia among immunocompromised individuals [6, 7].

The complex ecology and infection process of Legionella complicates the assessment of environmental risk factors and the identification of exposure sources [8]. To infect humans and cause disease, the bacteria must be aerosolized from an aquatic source and then inhaled. Legionella are pervasive in the environment, growing in rivers, lakes, ponds, and estuaries and along ocean coasts. The bacteria grow at temperatures between 25°C and 42°C and can form biofilms in both natural and built aquatic environments [9–12]. Meteorological factors, such as humidity and air temperature, have been linked to increases in sporadic legionellosis and seasonality of the disease [13–15]. In addition, the flooding and accelerated stream flow associated with large precipitation events can potentially disrupt both the structure and composition of river biofilms, dispersing the bacteria and negatively affecting water quality [16, 17].

Despite the ubiquity of Legionella in the environment, regional heterogeneity has been noted in case detection across the United States [9, 18–20] with New England, the Mid-Atlantic and East North Central areas reporting higher incidence [21]. During the past decade, Connecticut has experienced an unexplained increase of community-acquired (sporadic) legionellosis [22]. Given this unexplained increase in cases, it is necessary to identify potential drivers of sporadic cases. In the current study, we used spatial and time series regression models to test specific hypotheses about the relationship between the distribution of cases of legionellosis in Connecticut and proximity to rivers, stream flow, meteorological conditions, and sources of drinking water.

METHODS

Case Identification

In Connecticut, legionellosis is both physician and laboratory reportable to the Connecticut Department of Public Health (DPH) and to the patient’s local health department. Laboratory confirmation of the infection is made through culture, urine antigen testing (detects Legionella pneumophila serogroup 1 only), or paired serology with a ≥4-fold titer rise [23, 24]. Confirmed “legionellosis” refers to both legionnaires’ disease and the milder form of the disease, Pontiac fever. To identify possible common sources of exposure, DPH staff conducted follow-up on all confirmed legionellosis cases by contacting the healthcare provider of record and conducting patient interviews.

Our analyses focused on patients hospitalized during the weeks between 1 January 1999 and 31 December 2015. If cases were not linked to an outbreak during follow-up investigation by public health officials, they were classified as “sporadic” and included in our analyses. All patients were included in the analysis, unless they had an overnight stay at a location with a confirmed outbreak during their exposure period. Along with week of hospitalization, age category, ZIP code of residence, and the drinking water supplier and sources were also available. Incidence rates were calculated as cases per 100000 persons (using 2000 census data) during the 17-year study period. The study was approved by the human investigation committees at Yale University and the Connecticut DPH. Certain data used in this publication were obtained from the Connecticut DPH, and the authors assume full responsibility for analyses and interpretation of these data.

Hydrological Data

The hydrological variables included data from both the natural environment (major rivers and regional watersheds) and built environment (public drinking water supplier and sources) in Connecticut. ZIP codes were assigned to one of Connecticut’s 42 regional watersheds by mapping which watershed the majority of a ZIP code’s area fell (Supplementary Figure S1). The 31 rivers used in the spatial analysis included both large and medium sized rivers. Distance from ZIP code i to river j was calculated as the shortest euclidean distance from the centroid of ZIP code i to river j.

Weekly mean of stream flow for rivers (measured in cubic feet per second) were obtained from daily data from the United States Geological Survey. Stream flow rates were measured at 38 stations along all 34 streams for which data were consistently collected from 1 January 1999 to 31 December 2015. For the time series analysis, data for individual streams were aggregated at the weekly level and then standardized (by subtracting the mean and dividing by the standard deviation). The standardized values for each river were then averaged across all streams to provide an mean weekly stream flow value for the entire state. As part of a secondary analysis, we examined aquatic life use support assessment of the rivers as a proxy for a river’s ecological health (see Supplementary Text for more information).

Meteorological/Climatic Data

Weekly mean of precipitation (in millimeters), relative humidity (as percentages) and temperature (in degrees Celsius) were collected by the National Oceanic and Atmospheric Administration and obtained from the National Climatic Data Center. Temperature and precipitation were recorded daily at 18 stations across the state, and relative humidity was recorded hourly at 4 stations.

Demographic and Testing Data

ZIP code population and area were obtained from the US Census Bureau’s 2000 Summary File 1 for Connecticut and ZIP code density was calculated as population/area [25]. The median age of housing for each ZIP code in 2000 was also collected from the US Census Bureau [26]. Legionella urine antigen testing rates were available by hospital for 2009 only. The proportion of hospitalized pneumonia discharges tested via urine antigen testing was included in all spatial models. Testing proportions were matched to ZIP code through the hospital service area–ZIP code crosswalk provided by the Dartmouth Atlas of Health Care (see Supplementary Text). Hospital service areas were defined as the primary hospital where the greatest proportion of Medicare residents in each ZIP code would be hospitalized (Supplementary Figure S2).

Statistical Methods

Spatial Analysis

Three random effects models were used to estimate the incidence of legionellosis by ZIP code, where the observed number of cases of legionellosis in ZIP code i, Y_i, is assumed to be distributed as a Poisson random variable:

$$Y_{i }|{\lambda }_i~ \text{Poisson}\left({\lambda }_i\right), i=1,\dots ,n,$$

$$\begin{array}{l}\text{ln}\left({\lambda }_i\right)= \ln \left(offse{t}_i\right)+ {\beta }_{0 }+ {\beta }_1\left(\ln \left(densit{y}_i \right)\right)+ {\beta }_2\left(housing age categor{y}_{1 vs 5,i}\right)\\ + {\beta }_3\left(housing age categor{y}_{2 vs 5,i}\right)+ {\beta }_4\left(housing age categor{y}_{3 vs 5,i}\right)\\ + {\beta }_5\left(housing age categor{y}_{4 vs 5,i}\right)+ {\beta }_6\left(ln(proportion\_teste{d}_i)\right)+ u_{0i}\end{array}$$

This model included the log of density in the ZIP code as a measure of urbanization, a categorical median age of housing as a measure of aging infrastructure/plumbing, and the proportion of pneumonia cases tested for Legionella in 2009 by ZIP code [27].

In the first model, the random intercept ($u_{0i}$) was $u_{0i} ~ \text{Ν}\left(0, {\sigma }^2\right)$, and n is the total number of ZIP codes in the analysis (n = 266). In this model, the ZIP codes are treated independently. The second model accounts for spatial correlation in counts from different ZIP codes such that the random intercepts, $u_{0i}$, are modeled using a multivariate normal distribution with spatial covariance structure given as $\text{Cov}\left[u_{0i}, u_{0j}\right]= {\sigma }^2\exp \left(-\frac{d_{ij}}{\alpha }\right)$, where $d_{ij}= c_i-c_j$, $c_i$ are the coordinates of the centroid of ZIP code i, and ||.|| represents the euclidean distance function. The predicted incidence rate from this model was calculated as ${\lambda }_i|offse{t}_i$. This model assumes that ZIP codes separated by shorter distances may be more similar where the range of spatial correlation is controlled by the unknown parameter ±. The third random effects model was constructed to estimate incidence rate ratios for regional watersheds. Instead of using a random intercept for ZIP code, an iid random intercept for regional watershed i was used (similar to model 1).

To evaluate the relationship between cases of legionellosis in ZIP code i and distance to specific rivers j, a fourth model was developed. Model 4 was a Poisson regression without random effects, because this outperformed models with random effects. The log of density, median age of housing, and proportion undergoing urine antigen testing for each ZIP code were included in the model. Variables for proximity to rivers were added to the model in forward fashion and retained in the model if its Akaike information criterion (AIC) value was lowered. Proximity to river variables were dichotomized such that if river j was within d distance of the centroid of a ZIP code I, then proximity equals 1; otherwise, proximity equals 0. Distance d was explored at lengths of 5, 10, and 15 km from ZIP code centroids in univariate analysis for each river and the distance for which a river had the lowest AIC value was the proximity used in the final multivariate model.

Time Series Analysis

Potential covariates were assessed in a Poisson regression model that controlled for secular trends and seasonality, such that

$$Y_t|{\lambda }_t~ \text{Poisson}\left({\lambda }_t\right), t=1,\dots ,n$$

$$\text{ln}\left({\lambda }_t\right)= {\beta }_{0 }+ {\beta }_1\left(wee{k}_t\right)+ {\beta }_2\left(wee{k}_t{}^2\right)+ {\beta }_3\left[\sin \left(2\pi \times \frac{wee{k}_t}{52.25}\right)\right]+ {\beta }_4\left[\cos \left(2\pi \times \frac{wee{k}_t}{52.25}\right)\right]+ {\beta }_5\left(Cova{r}_t\right)$$

where ${\lambda }_t$ is the expected number of cases in a week of a given year and $Cova{r}_t$ is one of the climatic/stream flow variables assessed. Here n (881) is the total number of weeks in the 17 years studied, excluding the first 3 and last 3 (lead and lag) weeks. Variables tested included weekly mean of precipitation, maximum temperature, humidity and stream flow with lags and leads of up to 3 weeks tested for each. All climatic variables were assessed in univariate analysis and only variables that were not collinear in their original (nonlagged) form (assessed in a Spearman rank test with P > .05) were eligible for multivariate analysis. Forward selection of variables was used, and covariates were retained in the multivariate model if they had a P value <.05 and lowered the AIC of the full model. (See Supplementary Text for the R packages and SAS procedures used.)

RESULTS

Epidemiological Characteristics of Legionellosis in Connecticut

Between 1 January 1999 and 31 December 2015, a total of 736 confirmed cases of community-acquired legionellosis cases were reported to the Connecticut DPH. The highest incidence was seen in the ≥65-year age group, with 65.29 cases per 100000 population, whereas no cases were reported among residents aged ≤17 years during the study period. There were 29 cases for which ZIP code was unknown, and these cases were thus excluded from the spatial analysis. Excluded from the time series analysis were 27 cases for which week of hospitalization was unknown. Incidence rate per year shows an increasing trend over time, peaking at 2.41 in 2011 and stabilizing at about 1.70 cases per 100000 thereafter (Table 1).

Table 1.

Demographics of Sporadic Legionellosis Cases in Connecticut, 1999–2015

Population	Cases, N (%)a	Age-Specific Rate or IR
Total	736	…
Overnight exposure
Yes	115 (15.63)	…
No	332 (45.11)	…
Data missing	289 (39.27)	…
Age category, 7		Age-specific rate (per 100000)b
0–17	0	…
18–39	60 (8.15)	6.02
40–64	362 (49.18)	33.53
≥65	307 (41.71)	65.29
Data missing	7 (0.95)	…
Year		IR (per 100000)
1999	18	0.53
2000	18	0.53
2001	14	0.41
2002	19	0.56
2003	28	0.82
2004	24	0.70
2005	35	1.03
2006	58	1.70
2007	45	1.32
2008	51	1.50
2009	55	1.62
2010	55	1.62
2011	82	2.41
2012	55	1.62
2013	64	1.89
2014	58	1.70
2015	57	1.67

^aPercentages may not sum to 100% owing to rounding [25].

^bAge-specific rates were calculated using the US Census Bureau’s 2000 population assessment of Connecticut.

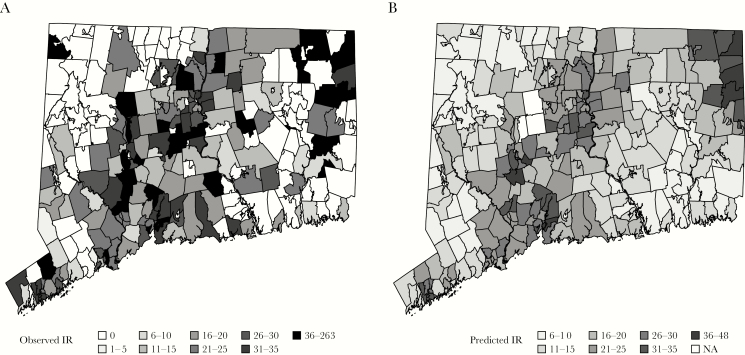
Figure 1 shows the incidence rates by ZIP code, which ranged from 0 (105 ZIP codes never reported a case during the study period) to 263, with notable clustering in urban areas (Figure 1A). The spatial smoothing model confirmed this distinctive spatial pattern of incidence, with high incidence in the northeast and east central regions relative to the statewide adjusted mean (Figure 1B and Supplementary Figure S3) and low incidence in the southeastern part of the state. Incidence was elevated around urban centers (Bridgeport, New Haven, and Hartford) despite controlling for density, median housing age, and testing rates. Three ZIP codes were excluded because they did not have a matching hospital service area to relate to testing practices.

Figure 1.

Observed and predicted incidence rates (IRs) (per 100000) of sporadic legionellosis cases by ZIP code, 1999–2015. A, Observed IR of sporadic legionellosis cases by ZIP code, years 1999–2015. B, Spatially smoothed predicted IR from model 2, which adjusts for density, median housing age, and proportion tested for Legionella in each ZIP code. The spatial smoothing effect is due to the covariance structure, which assumes that ZIP codes near to each other are more similar. NA, not available.

Elevated Incidence Around Key Rivers

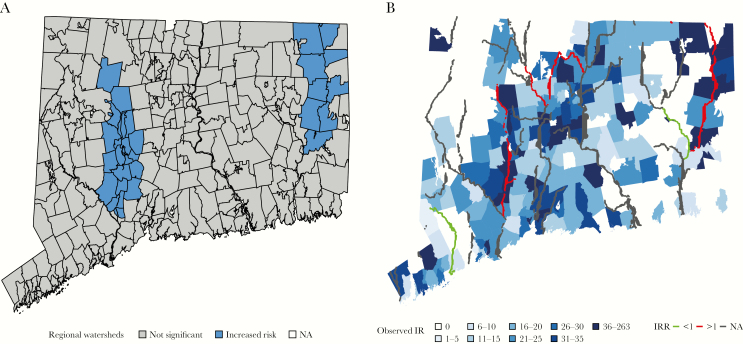
Two regional watersheds (Naugatuck and Quinebaug) were associated with an incidence of disease higher than the statewide adjusted mean (Figure 2A and Supplementary Table S1). Six rivers were associated with statistically significant differences in legionellosis incidence in the surrounding ZIP codes in a multivariate model (Table 2). In multivariate models, ZIP codes within 10 km of the Quinebaug River and the Hockanum Brook were associated with 4.37-fold (95% confidence interval, 2.96–6.44) and 1.71-fold (1.21–2.42) increases in legionellosis (Figure 2B). Close proximity to the Naugatuck and Farmington rivers was also associated with statistically significant increases in legionellosis risk. The Saugatuck and Shetucket rivers were associated with decreased rates of legionellosis. This final multivariate model had the lowest AIC score of all the spatial models explored in this study (Supplementary Table S2). Secondary analysis showed no relationship between the health of a river (aquatic life use support category) and a river’s inclusion in the model (Supplementary Table S3).

Figure 2.

Risk associated with regional hydrology. A, Two watersheds (Naugatuck and Quinebaug) were associated with increased disease in model 3 (random iid intercept for regional watershed) at P < .05. NA, not available. B, ZIP codes shaded according to their observed incidence rates (IR). All 31 rivers are plotted on the map. Those rivers not included in the final multivariate model are shown in gray; those that increased predicted incidence in the surrounding ZIP codes, in red; and those that decreased predicted incidence in the surrounding ZIP codes in green. IRR, incidence rate ratio.

Table 2.

Change in Rates of Legionellosis Associated With Proximity to Rivers

River/Brook	Univariate IRR (95% CI) by Distance from River or Brook			Multivariate Model (Model 4)
	<5 km	<10 km	<15 km
Quinebaug River	2.31 (1.55–3.43)	2.63 (1.83–3.76)a	2.14 (1.52–3.02)	4.37 (2.96–6.44)
Hockanum Brook	2.18 (1.38–3.44)	1.87 (1.36–2.56)a	1.41 (1.13–1.75)	1.71 (1.21–2.42)
Farmington River	0.92 (.61–1.37)	1.15 (.93–1.43)	1.29 (1.07–1.56)a	1.41 (1.15–1.73)
Naugatuck River	1.42 (1.13–1.77)a	1.20 (.98–1.47)	1.22 (1.02–1.45)	1.32 (1.02–1.69)
Saugatuck River	0.56 (.36–.86)	0.50 (.36–.69)a	0.65 (.52–.80)	0.60 (.42–.84)
Shetucket River	0.28 (.09–.90)a	0.80 (.46–1.39)	0.67 (.41–1.10)	0.14 (.04–.45)

Abbreviations: CI, confidence interval; IRR, incidence rate ratio.

^aDistance at which a river/brook had its most significant effect (lowest Akaike information criterion score) in each univariate model; this was also the distance cutoff used in the multivariate river model (model 4).

Of the 707 case patients matched to ZIP codes, 566 were matched to a public water supplier (PWS), and the remaining 137 were assumed to obtain their drinking water from a private well (see Supplementary Text for more information). For 41 of the 161 ZIP codes that experienced ≥1 case, multiple drinking water suppliers provided water to affected ZIP code, either through combinations of multiple PWSs or combinations of PWS and private well water. Secondary analysis did reveal a higher proportion of case patients residing within watersheds with an elevated incidence (Naugatuck and Quinebaug) used private well water (31.40%), compared with case patients living in watersheds without a significant association (17.01%; P < .001) (Table 3).

Table 3.

Association Between Water Supplier and Watershed

Water Supplier	Cases, No. (Column %)a		P Value (χ2 Test)
	Watersheds Positively Associated (Naugatuck, Quinebaug)	Watersheds Not Associated
Private well water	38 (31.40)	99 (17.01)	<.001
Municipal water	83 (68.60)	483 (82.99)

^aPercentages may not sum to 100% owing to rounding. The 4 cases assigned to multiple public water suppliers were excluded from analysis.

Association Between Incidence of Legionellosis and Meteorological Factors and Stream Flow

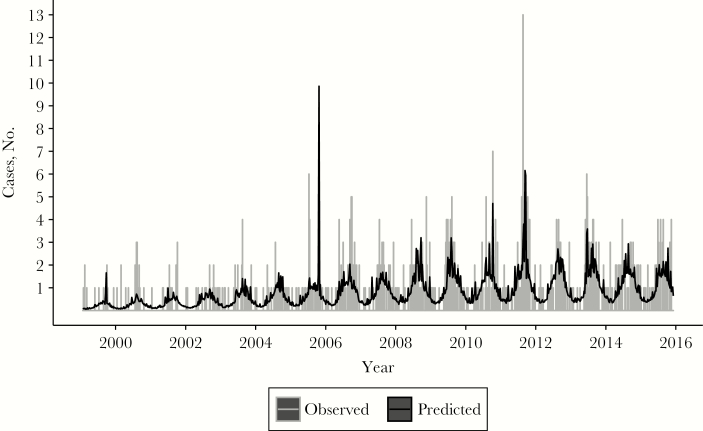
Finally, we evaluated the association between the weekly incidence of legionellosis and different lags and leads of climatic variables and stream flow. For precipitation, humidity and stream flow, a lag of 2 weeks was most predictive of incidence (Supplementary Figure S4). Precipitation was associated with the greatest risk of sporadic disease, with every 5-mm average increase in rainfall over a week being associated with a 48% increased risk of legionellosis 2 weeks later (Table 4 and Figure 3). Table 4 shows that a 5% average increase in relative humidity and a 1–standard deviation average increase in stream flow over a period of a week were also predictors of disease 2 weeks later in univariate analysis. Increasing temperature was associated with a decrease in disease rates, most prominently at a 1-week lag. No combinations of variables in a multivariate analysis created a model fit equal to or better than that of precipitation alone.

Table 4.

Association Between Meteorological/Stream Flow Variables and Legionellosis

Variable	IRR (95% CI)a
5-mm increase in precipitation (2-wk lag)b	1.48 (1.38–1.59)
5% increase in relative humidity (2-wk lag)	1.24 (1.17–1.31)
1-SD increase in stream flow (2-wk lag)	1.26 (1.18–1.35)
5°C increase in maximum air temperature (1-wk lag)	0.81 (0.70–0.93)

Abbreviations: CI, confidence interval; IRR, incidence rate ratio; SD, standard deviation.

^aIRRs corresponding to the most significant lag period for each variable. IRRs were calculated from the univariate Poisson regression for each meteorological variable at each lead/lag period.

^bA 5-mm increase in precipitation with a 2-week lag had the lowest Akaike information criterion (AIC) score in the univariate analysis. See Supplementary Figure S4B for the complete list of corresponding AIC scores.

Figure 3.

Precipitation 2 weeks earlier as a predictor of weekly case patient hospitalizations. Data represent observed (gray) and predicted (black) cases of legionellosis by week in Connecticut, determined using a Poisson regression model with covariates for week, week squared, yearly sine and cosine terms, and precipitation (with a 2-week lag).

DISCUSSION

This study analyzed a variety of environmental predictors of legionellosis, revealing a relationship between incidence and the proximity of ZIP codes to specific rivers and watersheds. While previous work by Ng et al [28] has shown that changes in watershed hydrology can predict cases over time, these results suggest that environmental reservoirs may have a greater influence on the spatial distribution of sporadic legionellosis cases than previously thought.

There are a number of plausible explanations for the association between elevated incidence of legionellosis and proximity to rivers. These possibilities can broadly be divided into (1) direct exposure to aerosolized river water and (2) contamination of drinking water supplies in an area. Legionella could be aerosolized directly from river water by several mechanisms. Some power plants make use of river water as part of the cooling process. Although there are regulations on the temperature of both the water entering and the water discharged from a power plant, these temperatures are still warm enough to promote the growth the Legionella within plant cooling towers, and at least one outbreak of pneumonia has been linked to a power plant cooling tower [29–32]. Likewise, sewage treatment plants can aerosolize bacteria during their treatment process, and a study by the Environmental Protection Agency noted high antibody prevalence rates (23% seroconverted) among persons residing within 1.6 km of sewage treatment plants [33].

These explanations would require more knowledge regarding the exact location of residence and movement patterns of case patients in relation to these industries. Direct aerosolization might also occur after rain events owing to increased turbidity of the river water. Finally, a study by Sakamoto et al [34] put forth the hypothesis that car tires aerosolize Legionella after rain events, thereby increasing its presence in the environment during warm, wet weather.

Individuals could also be exposed to Legionella at their residence via contaminated aerosolized potable water. The spatial clustering present around certain river systems and within watersheds could then be related to localized contamination of surface water or ground water source that case patients are exposed to either through private wells or inadequately treated municipal water systems [35]. The subsequent increase in cases after rainfall events could results from disruption of sediments or biofilms and release of the bacteria, which might strain water treatment plants or contaminate ground water sources [35]. Studies of tap and groundwater samples have shown that, despite water treatment, Legionella can still be isolated from drinking water and groundwater and that its presence can fluctuate over time [36]. Data on drinking water disruptions, contamination of well water and aquifers, and ZIP code-level data on the proportion of residents with private well water would be necessary to build on these hypotheses.

Although we did control for population density, median age of housing, and testing rates in 2009, there could be other demographic factors that were not appropriately captured in our model and are associated with rivers, such as aging industrial infrastructure (eg, cooling towers) [37]. We did not have access to each year’s proportion of pneumonia discharges tested for Legionella, which could prove an issue if testing rates drastically fluctuate by hospital over time. Using the proportion tested does not provide information on the severity of disease being tested. It is possible that some hospitals test infrequently but test only high-risk patients and therefore have a higher case-capture rate.

We also explored the role of the drinking water suppliers and water quality of the rivers as possible explanations for the relationship with rivers. The aquatic life use support assessment did not explain a river’s association with increased disease, which could be due to the inability of this metric to capture the intricacies of a river’s capacity to harbor and spread pathogenic Legionella [38–40]. Because not all case patients in each ZIP code obtained their water from the same PWS, PWS was not analyzed as a predictor of ZIP code incidence rate in our models. Although previous studies have noted private water supply as a risk factor for legionellosis [41, 42], the higher proportion of private well water among case patients in high-risk watersheds seen in our study could be confounded by the lack of municipal water supply in more rural areas of the state. Neither the Environmental Protection Agency nor the state of Connecticut require or regulate the testing of residential private well water, which could allow for the accumulation of Legionella and biofilms if owners do not adequately test and properly maintain their own wells [43].

These analyses also confirmed previous findings of a temporal relationship between climatic conditions and the incidence of legionellosis, but the exact mechanisms behind this association remain to be delineated [13–15]. An increase in cases 2 weeks after increases in precipitation and humidity aligns with the estimated 2–10-day incubation period for legionellosis [44]. These results showed that increases in temperature had a protective effect on cases at all lags, but it is likely that any single week of temperature is not predictive; rather, consecutive weeks of warmer weather are predictive [45]. Although we were limited by the availability of stream temperature data, it is also likely that warming stream temperatures could be predictive of increases in cases during the summer months. It is probable that stream flow did not perform as well as precipitation in the model because rivers have a certain capacity to handle excess rainfall, which could explain the tendency of stream flow to underestimate cases (Supplementary Figure S5).

The current study has important limitations, including availability of patient information and changing trends in diagnostic measures. Patients reporting out-of-state travel during the exposure period were not excluded because this information was not routinely collected until 2007. Exclusion of these potential travel-related cases did not alter the spatial distribution for cases occurring after 2007, and high-incidence watersheds were not more likely to have travel-related cases, indicating little correlation between potential travel-related exposure and case patient residence (Supplementary Table S4). Information on workplace location was not available, but if patients were exposed at the workplace this could alter the spatial pattern seen in this analysis.

Future analysis will need to focus on the association between precipitation events and the presence (and density) of Legionella in natural hydrological systems and determine whether such an association accounts for the spatial clustering around river systems seen in this study. Further research is also needed to determine mechanisms by which Legionella aerosols are disseminated from natural hydrological systems. Due to the relationship between legionellosis, precipitation, humidity, and the optimal growth of Legionella in warm waters, investigation into the potential influence of changes in climatic factors on sporadic cases of disease may also be necessary when making predictive models [46].

Supplementary Data

Supplementary materials are available at The Journal of Infectious Diseases online. Consisting of data provided by the authors to benefit the reader, the posted materials are not copyedited and are the sole responsibility of the authors, so questions or comments should be addressed to the corresponding author.

Notes

Financial support. This work was supported by the Yale Climate Change and Health Initiative through a grant from the Overlook International Foundation and by the National Center for Emerging and Zoonotic Infectious Diseases at the Centers for Disease Control and Prevention through a gift from the Overlook Emerging Infections Program.

Potential conflicts of interest. All authors: No reported conflicts of interest. All authors have submitted the ICMJE Form for Disclosure of Potential Conflicts of Interest. Conflicts that the editors consider relevant to the content of the manuscript have been disclosed.