Standard errors and confidence intervals for variable importance in random forest regression, classification, and survival

Abstract

Random forests is a popular nonparametric tree ensemble procedure with broad applications to data analysis. While RF’s widespread popularity stems from its prediction performance, an equally important feature is that it provides a fully nonparametric measure of variable importance (VIMP). A current limitation of VIMP however is that no systematic method exists for estimating its variance. As a solution, we propose a subsampling approach that can be used to estimate the variance of VIMP and for constructing confidence intervals. The method is general enough that it can be applied to many useful settings, including regression, classification, and survival problems. Using extensive simulations we demonstrate the effectiveness of the subsampling estimator and in particular find that the delete-d jackknife variance estimator, a close cousin, is especially effective under low subsampling rates due to its bias correction properties. These two estimators are highly competitive when compared to the .164 bootstrap estimator, a modified bootstrap procedure designed to deal with ties in out-of-sample data. Most importantly, subsampling is computationally fast, thus making it especially attractive for big data settings.

1 | INTRODUCTION

Random forests (RF)¹ is a popular tree-based learning method with broad applications to machine learning and data mining. RF was originally designed for regression and classification problems, but over time the methodology has been extended to other important settings. For example, random survival forests (RSF)^{2, 3} extends RF to right-censored survival and competing risk settings (see also Hothorn et al. ⁴ and Zhu and Kosorok⁵ for other tree-ensemble approaches to survival analysis). Two guiding principles are at the core of RF’s success. One is the use of deep trees. Another is injecting randomization into the tree growing process. First, trees are randomly grown by using a bootstrap sample of the data. Secondly, random feature selection is used when growing the tree. Thus, rather than splitting a node using all variables, the node is split using the best candidate from a randomly selected subset of variables. The purpose of this two-step randomization is to decorrelate trees, which encourages low variance for the ensemble due to bagging.⁶ When combined with the strategy of using deep trees, which is a bias reduction technique, this reduces generalization error and results in superior performance for the ensemble.

While RF’s popularity stems from its prediction performance, an equally important feature is that it provides a fully non-parametric measure of variable importance (VIMP).^{1, 2, 7, 8, 9} VIMP allows users to identify which variables play a key role in prediction, thus providing insight into the underlying mechanism for what otherwise might be considered a black-box. We note that the concept of variable importance is not specific to RF and has a long history. One of the earliest examples was CART, ¹⁰ which calculated variable importance by summing the reduction in node impurity due to a variable over all tree nodes. Another approach calculated importance using surrogate splitting (see Chapter 5.3 of Breiman et al.¹⁰).

Early prototypes of RF software developed by Leo Breiman and his student Adele Cutler provided for various options for calculating VIMP.¹¹ One procedure used for classification forests was to estimate VIMP using the forest averaged decrease in Gini impurity (somewhat akin to the node impurity approaches of CART). However, while Gini importance¹² saw widespread initial use with RF, over time it has become less popular.⁸ By far, the most frequently used measure of importance was another measure provided by the Breiman-Cutler software, called permutation importance (sometimes also referred to as Breiman-Cutler importance). Unlike Gini importance which estimates importance using in-sample impurity, permutation importance adopts a prediction based approach by using prediction error attributable to the variable. A clever feature is that rather than using cross-validation, which is computationally expensive for forests, permutation importance estimates prediction error by making use of out-of-bootstrap cases. Recall that each tree is calculated from a bootstrap sample of the original data. The approximately 1 − .632 = .368 left from the bootstrap represents out-of-sample data which can be used for estimating prediction performance. This data is called out-of-bag (OOB) and prediction error obtained from it is called OOB error.¹³ Permutation importance permutes a variable’s OOB data and compares the resulting OOB prediction error to the original OOB prediction error—the motivation being that a large positive value indicates a variable with predictive importance.

Permutation (Breiman-Cutler) Importance.

In the OOB cases for a tree, randomly permute all values of the jth variable. Put these new covariate values down the tree and compute a new internal error rate. The amount by which this new error exceeds the original OOB error is defined as the importance of the jth variable for the tree. Averaging over the forest yields VIMP.

— Measure 1 (Manual On Setting Up, Using, And Understanding Random Forests V3.1)

We focus on Breiman-Cutler permutation importance in this manuscript (for simplicity, hereafter simply refered to as VIMP). One of the tremendous advantages of VIMP is that it removes the arbitrariness of having to select a cutoff value when determining the effectiveness of a variable. Regardless of the problem, a VIMP of zero always represents an appropriate cutoff, as it reflects the point at which a variable no longer contributes predictive power to the model. However, in practice one may observe values close to zero, and the meaning of what constitutes being zero becomes unclear. One way to resolve this is to calculate the variance of VIMP, but this is challenging due to the complex nature of RF. Unfortunately, while the empirical properties of VIMP are well documented,^{14, 15, 16} much less is known about VIMP’s theoretical properties outside of a few studies.^{7, 17}

Given the difficulties of theoretical analysis, an alternative approach is to approximate the distribution of VIMP through some form of resampling. This has been the favored approach used for RF regression for assessing variability of RF predicted values. Methods that have been used include bootstrapping¹⁸ for estimating the variance, and the infinitesimal jackknife¹⁹ and infinite order U-statistics ²⁰ for confidence intervals. These methods however only apply to RF predicted values and not to VIMP which involves prediction error. This greatly complicates matters and requires a more general approach.

For this reason, we base our approach on subsampling, ²¹ a general methodology for approximating the distribution of a complex statistic. Section 3 provides a description of of our subsampling procedure for estimating the variance. Notational framework and a formal definition of VIMP are provided in Section 2. Section 3 begins by introducing a bootstrap solution to be used as a comparison procedure. Interestingly, we find the bootstrap cannot be applied directly due to ties that occur in the OOB data. This is precisely due to the fact that VIMP is prediction error based. We propose a solution to this problem called the .164 bootstrap estimator. The subsampling variance estimator and the delete-d jackknife variance estimator, ²² a close cousin, are described later in Section 3. Sections 4, 5, and 6 consider regression, classification, and survival settings and extensively evaluate performance of the two subsampling methods and the .164 bootstrap estimator. We also show how to construct confidence intervals for VIMP using the estimated variance. The results are very promising for the subsampling methods. Section 7 summarizes our findings and provides practical guidelines for use of the methodology. Some theoretical results for VIMP are provided in the Appendix.

2 | NOTATIONAL FRAMEWORK AND DEFINITION OF VIMP

2.1 | Notation

We assume Y ∈ 𝒴 is the response and X ∈ 𝒳 is the p-dimensional feature where Y can be continuous, binary, categorical, or survival, and X can be continuous or discrete. We assume the underlying problem involves a nonparametric regression framework where the goal is to estimate a functional h(x) of the response given X = x. Estimation is based on the learning data ℒ = {(X₁, Y₁), …, (X_n, Y_n)}, where (X_i, Y_i) are independently distributed with the same distribution ℙ as (X, Y).

Examples of h(x) are:

1. The conditional mean h(x) = 𝔼[Y|X = x] in regression.

2. The conditional class probabilities h(x) = (p₁(x), …, p_K(x)) in a K-multiclass problem, where p_k(x) = ℙ{Y = k|X = x}.

3. The survival function h(x) = ℙ{T^o > t|X = x} in survival analysis. Here Y = (T, δ) represents the bivariate response comprised of the observed survival time T = min(T^o,C^o) and censoring indicator δ = 1{T^o ≤ C^o}, where (T^o,C^o) are the unobserved event and censoring times.

2.2 | RF predictor

As in Breiman,¹ we define a RF as a collection of randomized tree predictors {h(·,Θ_m,ℒ), m = 1, …, M}. Here h(x,Θ_m,ℒ) denotes the mth random tree predictor of h(x) and {Θ_m} are independent identically distributed random quantities encoding the randomization needed for constructing a tree. Note that Θ_m is selected prior to growing the tree and is independent of the learning data, ℒ.

The tree predictors are combined to form the finite forest estimator of h(x),

$$h(\mathbf{x},{\mathrm{\Theta }}_1,\dots ,{\mathrm{\Theta }}_M,\mathcal{L})=\frac{1}{M}\sum _{m=1}^{M}h(\mathbf{x},{\mathrm{\Theta }}_m,\mathcal{L}).$$ (1)

The infinite forest estimator is obtained by taking the limit as M → ∞ and equals

$$h(\mathbf{x},\mathcal{L})={\mathbb{E}}_{\mathrm{\Theta }}[h(\mathbf{x},\mathrm{\Theta },\mathcal{L})].$$ (2)

2.3 | Loss function

Calculating VIMP assumes some well defined notion of prediction error. Therefore, we assume there is an appropriately prechosen loss function ℓ(Y, ĥ) ≥ 0 used to measure performance of a predictor ĥ in predicting h. Examples include:

1. Squared error loss ℓ(Y,ĥ) = (Y − ĥ)² in regression problems.

2. For classification problems, widely used measures of performance are the misclassification error or the Brier score. For the latter, $\ell (Y,\widehat{h})=(1/K){\sum }_{k=1}^K{\left(1\{Y=k\}-{\widehat{p}}_k\right)}^2$, where p̂_k is the estimator for the conditional probability p_k.

3. For survival, the weighted Brier score^{23, 24} can be used. Section 6 provides further details.

The choice of ℓ can be very general and we do not impose any specific conditions on how it must be selected. As described later in Section 3, the conditions needed for our methodology to hold require only the existence of a limiting distribution for VIMP. Although such a limit may be satisfied by imposing specific conditions on ℓ, such as requiring the true function h to yield the minimum value of 𝔼[ℓ(Y, h)], we do not impose such assumptions so as to retain as general an approach as possible.

2.4 | Tree VIMP

Let ℒ^*(Θ_m) be the mth bootstrap sample and let ℒ^**(Θ_m) = ℒ\ℒ^*(Θ_m) be the corresponding OOB data. Write X = (X⁽¹⁾, …, X^(p)) where X^(j) denotes the jth feature coordinate. The permuted value of the jth coordinate of X is denoted by X̃^(j). Substituting this into the jth coordinate of X yields X̃_(j):

$${\stackrel{\sim }{\mathbf{X}}}^{(j)}=(X^{(1)},\dots ,X^{(j-1)},{\stackrel{\sim }{X}}^{(j)},X^{(j+1)},\dots ,X^{(p)}).$$

VIMP is calculated by taking the difference in prediction error under the original X to prediction error under the perturbed X̃^(j) over OOB data. More formally, let I(X^(j),Θ_m,ℒ) denote the VIMP for X^(j) for the mth tree. It follows that

$$I(X^{(j)},{\mathrm{\Theta }}_m,\mathcal{L})=\frac{{\sum }_{i\in {\mathcal{L}}^{\ast \ast }({\mathrm{\Theta }}_m)}\ell (Y_i,h({\stackrel{\sim }{\mathbf{X}}}_i^{(j)},{\mathrm{\Theta }}_m,\mathcal{L}))}{{\sum }_{i\in {\mathcal{L}}^{\ast \ast }({\mathrm{\Theta }}_m)}1}-\frac{{\sum }_{i\in {\mathcal{L}}^{\ast \ast }({\mathrm{\Theta }}_m)}\ell (Y_i,h({\mathbf{X}}_i,{\mathrm{\Theta }}_m,\mathcal{L}))}{{\sum }_{i\in {\mathcal{L}}^{\ast \ast }({\mathrm{\Theta }}_m)}1}.$$ (3)

Note that in the first sum, we implicitly assume Θ_m embeds the additional randomization for permuting OOB data to define ${\tilde{\mathbf{X}}}_i^{(j)}$. Because this additional randomization only requires knowledge of OOB membership, and therefore can be parameterized in terms of Θ, we assume without loss of generality that Θ encodes both the randomization for growing a tree and for permuting OOB data.

Expression (3) can be written more compactly by noting that the denominator in each sum equals the OOB sample size. Let N(Θ_m) be this value. Then

$$I(X^{(j)},{\mathrm{\Theta }}_m,\mathcal{L})=\frac{1}{N({\mathrm{\Theta }}_m)}\sum _{i\in {\mathcal{L}}^{\ast \ast }({\mathrm{\Theta }}_m)}\left[\ell (Y_i,h({\stackrel{\sim }{\mathbf{X}}}_i^{(j)},{\mathrm{\Theta }}_m,\mathcal{L}))-\ell (Y_i,h({\mathbf{X}}_i,{\mathrm{\Theta }}_m,\mathcal{L}))\right].$$

2.5 | VIMP

Averaging tree VIMP over the forest yields VIMP:

$$I(X^{(j)},{\mathrm{\Theta }}_1,\dots ,{\mathrm{\Theta }}_M,\mathcal{L})=\frac{1}{M}\sum _{m=1}^{M}I(X^{(j)},{\mathrm{\Theta }}_m,\mathcal{L}).$$ (4)

An infinite forest estimator for VIMP can be defined analogously by taking the limit as M → ∞,

$$I(X^{(j)},\mathcal{L})={\mathbb{E}}_{\mathrm{\Theta }}[I(X^{(j)},\mathrm{\Theta },\mathcal{L})].$$ (5)

It is worth noting that (4) and (5) do not explicitly make use of the forest predictors (1) or (2). This is a unique feature of permutation VIMP because it is a tree-based estimator of importance.

3 | SAMPLING APPROACHES FOR ESTIMATING VIMP VARIANCE

3.1 | The .164 bootstrap estimator

The bootstrap is a popular method that can be used for estimating the variance of an estimator. So why not use the bootstrap to estimate the standard error for VIMP? One problem is that running a bootstrap on a forest is computationally expensive. Another more serious problem, however, is that a direct application of the bootstrap will not work for VIMP. This is because RF trees already use bootstrap data and applying the bootstrap creates double-bootstrap data that affects the coherence of being OOB.

To explain what goes wrong, let’s simplify our previous notation by writing $I_{n,M}^{(j)}$ for the finite forest estimator (4). Let ℙ_n denote the empirical measure for ℒ. The bootstrap estimator of $\text{Var}(I_{n,M}^{(j)})$ is

$${\text{Var}}^{\ast }(I_{n,M}^{(j)})={\text{Var}}_{{\mathbb{P}}_n}(I_{n,M}^{\ast (j)}).$$ (6)

To calculate (6), we must draw a sample from ℙ_n. Call this bootstrap sample ℒ^*. Because ℒ^* represents the learning data, we must draw a bootstrap sample from ℒ^* to construct a RF tree. Let ℒ^*(Θ^*) denote this bootstrap sample where Θ^* represents the tree growing instructions. This is a double-bootstrap draw. The problem is that if a specific case in ℒ^* is duplicated l > 1 times there is no guarantee that all l cases appear in the bootstrap draw, ℒ^*(Θ^*). These remaining duplicated values are assigned to the OOB data but these values are not truly OOB which compromises the coherence of the OOB data.

Double bootstrap data lowers the probability of being truly OOB to a value much smaller than .368, which is the value expected for a true OOB sample. We can work out exactly how much smaller this probability is. Let n_i be the number of occurrences of case i in ℒ^*. Then,

$$Pr\{i\text{is}\text{truly}\text{OOB}\text{in}{\mathcal{L}}^{\ast }({\mathrm{\Theta }}^{\ast })\}=\sum _{l=1}^{n}Pr\{i\text{is}\text{truly}\text{OOB}\text{in}{\mathcal{L}}^{\ast }({\mathrm{\Theta }}^{\ast })\mid n_i=l\}Pr\{n_i=l\}.$$ (7)

We have

$$\begin{gathered} (n_1,\dots ,n_n)~\text{Multinomial}(n,(1/n,\dots ,1/n)) \\ {n}_i~\text{Binomial}(n,1/n)\asymp \text{Poisson}(1). \end{gathered}$$

Hence, (7) can be seen to equal

$$\sum _{l=1}^n{\left(\frac{n-l}{n}\right)}^{n}Pr\{n_i=l\}\asymp \sum _{l=1}^n{\left(\frac{n-l}{n}\right)}^n\left(\frac{{\mathrm{e}}^{-1}{1}^l}{l!}\right)={\mathrm{e}}^{-1}\sum _{l=1}^n{\left(1-\frac{l}{n}\right)}^n\frac{1}{l!}\asymp {\mathrm{e}}^{-1}\sum _{l=1}^n\frac{{\mathrm{e}}^{-l}}{l!}\asymp \mathrm{.1635.}$$

Therefore, double bootstrap data has a OOB size of .164n.

The above discussion points to a simple solution to the problem which we call the .164 bootstrap estimator. The .164 estimator is a bootstrap variance estimator but is careful to use only truly OOB data. Let ℒ^* = {Z₁ = (X_i1, Y_i1), …, Z_n = (X_in, Y_in)} denote the bootstrap sample used for learning and let ℒ^*(Θ^*) = {Z_i: i ∈ Θ^*} be the bootstrap sample used to grow the tree. The OOB data for the double-bootstrap data is defined as {(X_il, Y_il) ∉ ℒ^*(Θ^*)}. However, there is another subtle issue at play regarding duplicates in the OOB data. Even though {(X_il, Y_il) ∉ ℒ^*(Θ^*)} are data points from ℒ^* truly excluded from the double-bootstrap sample, and therefore technically meet the criteria of being OOB, there is no guarantee they are all unique. This is because these values orginated from ℒ^*, a bootstrap draw, and therefore could very well be duplicated. To ensure this does not happen we further process the OOB data to retain only the unique values.

The steps for implementing the .164 estimator can be summarized as follows.

.164 bootstrap estimator for $\mathbf{Var}(I_{n,M}^{(j)})$.

1. Draw a bootstrap sample ℒ^* = {Z₁ = (X_i1, Y_i1), …, Z_n = (X_in, Y_in)}.

2. Let ℒ^*(Θ^*) = {Z_i: i ∈ Θ^*} be a bootstrap draw from ℒ^*. Use ℒ^*(Θ^*) to grow a tree predictor.

3. Define OOB data to be the unique values in {(X_il, Y_il) ∉ ℒ^*(Θ^*)}.

4. Calculate the tree VIMP, I(X^(j),Θ^*,ℒ^*), using OOB data of step 3.

5. Repeat steps 2–4 independently M times. Average the VIMP values to obtain ${\widehat{\theta }}_n^{\ast (j)}$.

6. Repeat the entire procedure K > 1 times obtaining ${\widehat{\theta }}_{n,1}^{\ast (j)},\dots ,{\widehat{\theta }}_{n,K}^{\ast (j)}$. Estimate $\text{Var}(I_{n,M}^{(j)})$ by the bootstrap sample variance, $(1/K){\sum }_{k=1}^K{({\widehat{\theta }}_{n,k}^{\ast (j)}-\frac{1}{K}{\sum }_{k^{\prime }=1}^K{\widehat{\theta }}_{n,k^{\prime }}^{\ast (j)})}^2$.

3.2 | Subsampling and the delete-d jackknife

A problem with the .164 bootstrap estimator is that its OOB data set is smaller than a typical OOB estimator. Truly OOB data from a double bootstrap can be be less than half the size of OOB data used in a standard VIMP calculation (16.4% versus 36.8%). Thus in a forest of 1000 trees, the .164 estimator uses about 164 trees on average to calculate VIMP for a case compared with 368 trees used in a standard calculation. This can reduce efficiency of the .164 estimator. Another problem is computational expense. The .164 estimator requires repeatedly fitting RF to bootstrap data which becomes expensive as n increases.

To avoid these problems, we propose a more efficient procedure based on subsampling theory.²¹ The idea rests on calculating VIMP over small i.i.d. subsets of the data. Because sampling is without replacement, this avoid ties in the OOB data that creates problems for the bootstrap. Also, because each calculation is fast, the procedure is computationally efficient, especially in big n settings.

3.2.1 | Subsampling theory

We begin by first reviewing some basic theory of subsampling. Let X₁, …, X_n be i.i.d. random values with common distribution P. Let θ̂_n = θ̂(X₁, …, X_n) be some estimator for θ(P), an unknown real-valued parameter we wish to estimate. The bootstrap estimator for the variance of θ̂_n is based on the following simple idea. Let ${\mathbf{P}}_n=(1/n){\sum }_{i=1}^n{\delta }_{X_i}$ be the empirical measure for the data. Let $X_1^{\ast },\dots ,X_n^{\ast }$ be a bootstrap sample obtained by independently sampling n points from P_n. Because P_n converges to P, we should expect the moments of the bootstrap estimator ${\widehat{\theta }}_n^{\ast }=\widehat{\theta }(X_1^{\ast },\dots ,X_n^{\ast })$ to closely approximate those of θ̂. In particular, we should expect the bootstrap variance ${\text{Var}}_{{\mathbf{P}}_n}({\widehat{\theta }}_n^{\ast })$ to closely approximate Var(θ_n). This is the rationale for the variance estimator (6) described earlier.

Subsampling²¹ employs the same strategy as the bootstrap but is based on sampling without replacement. For b:= b(n) such that b/n → 0, let S_b be the entire collection of subsets of {1, …, n} of size b. For each s = {i₁, …, i_b} ∈ S_b, let θ̂_n,b,s = θ̂(X_i1, …, X_ib) be the estimator evaluated using s. The goal is to estimate the sampling distribution of n^1/2(θ̂_n − θ(P)). It turns out that subsampling provides a consistent estimate of this distribution under fairly mild conditions. Let ℚ_n denote the distribution of n^1/2(θ̂_n − θ(P)). Assume ℚ_n converges weakly to a proper limiting distribution ℚ:

$${\mathbb{Q}}_n\stackrel{\mathrm{d}}{⇝}\mathbb{Q}.$$ (8)

Then it follows ²¹ that the distribution function for the statistic n^1/2(θ̂_n − θ(P)) can be approximated by the subsampling estimator

$${\stackrel{\sim }{U}}_{n,b}(x)=\frac{1}{C_b}\sum _{s\in S_b}1\{b^{1/2}({\widehat{\theta }}_{n,b,s}-{\widehat{\theta }}_n)\le x\},$$ (9)

where $C_b=\left(\begin{array}{c}n\\ b\end{array}\right)$ is the cardinality of S_b. More formally, assuming (8) and b/n → 0 for b → ∞, then ${\stackrel{\sim }{U}}_{n,b}(x)\stackrel{\mathrm{p}}{\to }F(x)=\mathbb{Q}[-\infty ,x]$ for each x that is a continuity point of the limiting cumulative distribution function F. The key to this argument is to recognize that due to (8) and b/n → 0, Ũ_n,b closely approximates

$$U_{n,b}(x)=\frac{1}{C_b}\sum _{s\in S_b}1\{b^{1/2}\left({\widehat{\theta }}_{n,b,s}-\theta (\mathbf{P})\right)\le x\},$$

which is a U-statistic²⁵ of order b. See Politis and Romano²¹ for details.

The ability to approximate the distribution of θ̂_n suggests, similar to the bootstrap, that we can approximate moments of θ̂_n with those from the subsampled estimator; in particular, we should be able to approximate the variance. Unlike the bootstrap, however, subsampled statistics are calculated using a sample size b and not n. Therefore to estimate the variance of θ̂_n we must apply a scaling factor to correct for sample size. The subsampled estimator for the variance is (see Radulović²⁶ and Section 3.3.1 from Politis and Romano²¹)

$${\widehat{\upsilon }}_b=\frac{b/n}{C_b}\sum _{s\in S_b}{\left({\widehat{\theta }}_{n,b,s}-\frac{1}{C_b}\sum _{s^{\prime }\in S_b}{\widehat{\theta }}_{n,b,s^{\prime }}\right)}^2.$$ (10)

The estimator (10) is closely related to the delete-d jackknife.²² The delete-d estimator works on subsets of size r = n − d and is defined as

$${\widehat{\upsilon }}_{J(d)}=\frac{r/d}{C_r}\sum _{s\in S_r}{\left({\widehat{\theta }}_{n,r,s}-{\widehat{\theta }}_n\right)}^2.$$

With a little bit or rearrangement, this can be rewritten as

$${\widehat{\upsilon }}_{J(d)}=\frac{r/d}{C_r}\sum _{s\in S_r}{\left({\widehat{\theta }}_{n,r,s}-\frac{1}{C_r}\sum _{s^{\prime }\in S_r}{\widehat{\theta }}_{n,r,s^{\prime }}\right)}^2+\frac{r}{d}{\left(\frac{1}{C_r}\sum _{s\in S_r}{\widehat{\theta }}_{n,r,s}-{\widehat{\theta }}_n\right)}^2.$$

Setting d = n − b, we obtain

$${\widehat{\upsilon }}_{J(d)}=\frac{b/(n-b)}{C_b}\sum _{s\in S_b}{\left({\widehat{\theta }}_{n,b,s}-\frac{1}{C_b}\sum _{s^{\prime }\in S_b}{\widehat{\theta }}_{n,b,s^{\prime }}\right)}^2+\frac{b}{n-b}{\underset{\text{bias}}{\underbrace{\left(\frac{1}{C_b}\sum _{s\in S_b}{\widehat{\theta }}_{n,b,s}-{\widehat{\theta }}_n\right)}}}^2.$$ (11)

The first term closely approximates (10) since b/n → 0, while the second term is a bias estimate of the subsampled estimator. Thus, the delete-d estimator (11) can be seen to be a bias corrected version of (10). Furthermore this correction is always upwards because the bias term is squared and always positive.

3.2.2 | Subsampling and delete-d jackknife algorithms

We can now describe our subsampling estimator for the variance of VIMP. In the following we assume b is some integer much smaller than n such that b/n → 0.

b-subsampling estimator for $\mathbf{Var}(I_{n,M}^{(j)})$.

1. Draw a subsampling set s ∈ S_b. Let ℒ_s be ℒ restricted to s.

2. Calculate $I_{n,M}^{(j)}({\mathcal{L}}_s)$, the finite forest estimator for VIMP using ℒ_s. Let ${\widehat{\theta }}_{n,b,s}^{(j)}$ denote this value.

3. Repeat K > 1 times obtaining ${\widehat{\theta }}_{n,b,s_1}^{(j)},\dots ,{\widehat{\theta }}_{n,b,s_K}^{(j)}$. Estimate $\text{Var}(I_{n,M}^{(j)})$ by $[b/(nK)]{\sum }_{k=1}^K{({\widehat{\theta }}_{n,b,s_k}^{(j)}-\frac{1}{K}{\sum }_{k^{\prime }=1}^K{\widehat{\theta }}_{n,b,s_{k^{\prime }}}^{(j)})}^2$.

The delete-d jackknife estimator is obtained by a slight modification to the above algorithm:

delete-d jackknife estimator (d = n − b) for $\mathbf{Var}(I_{n,M}^{(j)})$.

1. Using the entire learning set ℒ, calculate the forest VIMP estimator $I_{n,M}^{(j)}(\mathcal{L})$. Let ${\widehat{\theta }}_n^{(j)}$ denote this value.

2. Run the b-subsampling estimator, but replace the estimator in step 3 with $\{b/[(n-b)K]\}{\sum }_{k=1}^K{({\widehat{\theta }}_{n,b,s_k}^{(j)}-{\widehat{\theta }}_n^{(j)})}^2$.

4 | RANDOM FOREST REGRESSION, RF-R

4.1 | Simulations

In the following sections (Sections 4, 5, and 6) we evaluate the performance of the .164 bootstrap estimator, the b-subsampling estimator, and the delete-d jackknife variance estimator. We begin by looking at the regression setting. We used the following simulations to assess performance.

1. y = 10 sin(πx₁x₂) + 20(x₃ − 0.5)² + 10x₄ + 5x₅ + ε; {x_j} ~ U(0, 1); ε~ N(0, 1).

2. $y={(x_1^2+{[x_2{x}_3-{(x_2{x}_4)}^{-1}]}^2)}^{1/2}+\epsilon$; x₁ ~ U(0, 100), x₂ ~ U(40π, 560π), x₃ ~ U(0, 1), x₄ ~ U(1, 11); ε ~ N(0, 125²).

3. y = tan⁻¹([x₂x₃ − (x₂x₄)⁻¹]/x₁) + ε; x₁ ~ U(0, 100), x₂ ~ U(40π, 560π), x₃ ~ U(0, 1), x₄ ~ U(1, 11); ε ~ N(0, .1²).

4. $y=x_1{x}_2+x_3^2-x_4{x}_7+x_8{x}_{10}-x_6^2+\epsilon$; {x_j} ~ U(−1, 1); ε ~ N(0, .1²).

5. $y=1\{x_1>0\}+x_2^3+1\{x_4+x_6-x_8-x_9>1+x_{10}\}+exp(-x_2^2)+\epsilon$; {x_j} ~ U(−1, 1); ε ~ N(0, .1²).

6. $y=x_1^2+3x_2^2{x}_{3}exp(-\mid x_4\mid )+x_6-x_8+\epsilon$, {x_j} ~ U(−1, 1); ε ~ N(0, .1²).

7. $y=1\{x_1+x_4^3+x_9+sin(x_2{x}_8)+\epsilon >0.38\}$; {x_j} ~ U(−1, 1); ε ~ N(0, .1²).

8. $y=log(x_1+x_2{x}_3)-exp(x_4{x}_5^{-1}-x_6)+\epsilon$; {x_j} ~ U(0.5, 1); ε ~ N(0, .1²).

9. $y=x_1{x}_2^2{\mid x_3\mid }^{1/2}+\lfloor x_4-x_5{x}_6\rfloor +\epsilon$; {x_j} ~ U(−1, 1); ε ~ N(0, .1²).

10. $y=x_3{(x_1+1)}^{\mid x_2\mid }-{(x_5^2{[\mid x_4\mid +\mid x_5\mid +\mid x_6\mid ]}^{-1})}^{1/2}+\epsilon$; {x_j} ~ U(−1, 1); ε ~ N(0, .1²).

11. $y=cos(x_1-x_2)+{sin}^{-1}(x_1{x}_3)-{tan}^{-1}(x_2-x_3^2)+\epsilon$; {x_j} ~ U(−1, 1); ε ~ N(0, .1²).

12. y = ε; ε ~ N(0, 1).

In all 12 simulations, the dimension of the feature space was set to p = 20. This was done by adding variables unrelated to y to the design matrix. We call these noise variables. In simulations 1–3, noise variables were U(0, 1); for simulations 4–11, noise variables were U(−1, 1); for simulation 12, noise variables were N(0, 1). All features (strong and noisy) were simulated independently. Simulations 1–3 are the well known Friedman 1, 2, 3 simulations.^{27, 6} Simulations 4–11 were inspired from COBRA.²⁸ Simulation 12 is a pure noise model.

The sample size was set at n = 250. Subsampling was set at a rate of b = n^1/2, which in this case is b = 15.8. We can see that practically speaking this a very small sample size and allows subsampled VIMP to be rapidly computed. The value of d for the delete-d jackknife was always set to d = n − b. The number of bootstraps was set to 100 and the number of subsamples was set to 100. Note that this not a large number of bootstraps or subsampled replicates. However, they represent values practitioners are likely to use in practice, especially for big data, due to computational costs.

All RF calculations were implemented using the randomForestSRC R-package.²⁹ The package runs in OpenMP parallel processing mode, which allows for parallel processing on user desktops, as well as large scale computing clusters. The package now includes a dedicated function “ subsample” which implements the three methods studied here. The subsample function was used for all calculations. All RF calculations used 250 trees. Tree nodesize was set to 5 and p/3 random feature selection used (these are default settings for regression). Each simulation was repeated independently 250 times. RF parameters were kept fixed over simulations. All calculations related to prediction error and VIMP were based on squared error loss, ℓ(Y, ĥ) = (Y − ĥ)².

4.2 | Estimating the true finite standard error and true finite VIMP

Each procedure provides an estimate of the $\text{Var}(I_{n,M}^{(j)})$. We took the square root of this obtain an estimate for the standard error of VIMP, ${(\text{Var}(I_{n,M}^{(j)}))}^{1/2}$. To assess performance in estimating the standard error we used the following strategy to approximate the uknown parameter $\text{Var}(I_{n,M}^{(j)})$. For each simulation model, we drew 1000 independent copies of the data, and for each of these copies, we calculated the finite forest VIMP, $I_{n,M}^{(j)}$. The same sample size of n = 250 was used and all forest tuning parameters were kept the same as outlined above. We used the variance of these 1000 values to estimate $\text{Var}(I_{n,M}^{(j)})$. We refer to the square root of this value as the true finite standard error. Additionally, we averaged the 1000 values to estimate $\mathbb{E}[I_{n,M}^{(j)}]=\mathbb{E}[I(X^{(j)},\mathcal{L})]$ We call this the true finite VIMP.

4.3 | Results

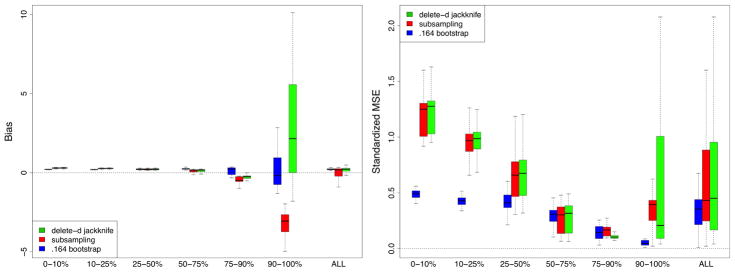
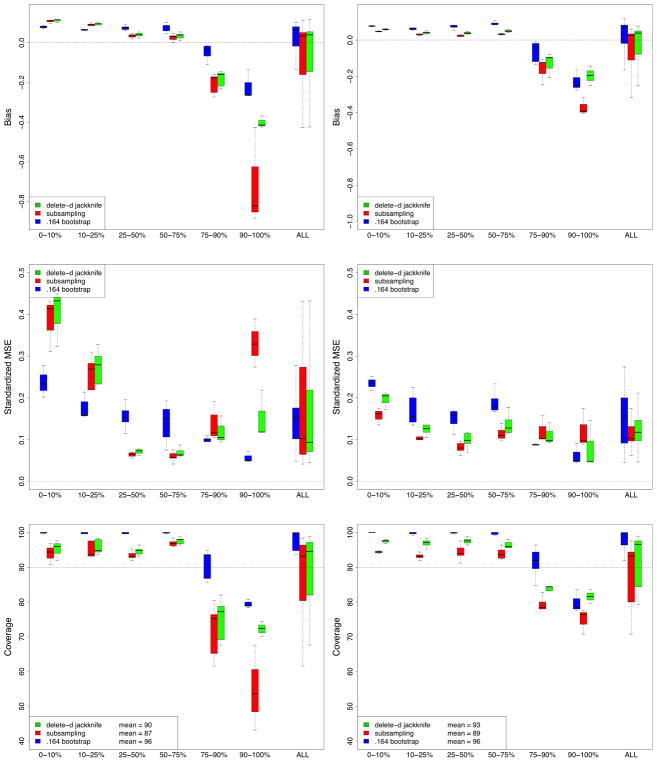
Performance of methods was assessed by bias and standardized mean-squared-error (SMSE). The bias for a method was obtained by averaging its estimated standard error over the 250 replications and taking the difference between this and the true finite standard error. MSE was estimated by averaging the squared difference between a method’s estimated value for the standard error and the true finite standard error. SMSE was defined by dividing MSE by the true finite standard error. In evaluating these performance values, we realized it was important to take into account signal strength of a variable. In our simulations there are noisy variables with no signal. There are also variables with strong and moderately strong signal. Therefore, to better understand performance differences, results were stratified by size of a variable’s true finite VIMP. In total, there were 240 variables to be dealt with (12 simulations, each with p = 20 variables). These 240 variables were stratified into 6 groups based on 10, 25, 50, 75, and 90th percentiles of true finite VIMP (standardized by the Y variance to make VIMP comparable across simulations). Bias and SMSE for the 6 groups are displayed in Figure 1.

FIGURE 1.

Bias and standardized mean-squared-error (SMSE) performance for estimating VIMP standard error from RF-R (RF-regression) simulations. In total there are 240 variables (12 simulations, p = 20 variables in each simulation). These 240 variables have been stratified into 6 groups based on 10, 25, 50, 75, and 90th percentiles of true finite VIMP. Extreme right boxplots labeled “ALL” display performance for all 240 variables simultaneously.

All methods exhibit low bias for small VIMP. As VIMP increases, corresponding to stronger variables, bias for the subsampling estimator increases. Its bias is negative showing that it underestimates variance. The delete-d estimator does much better. This is due to the bias correction factor discussed earlier (see (11)) which kicks in when signal increases. The pattern seen for bias is reflected in the results for SMSE: the delete-d is similar to the subsampling estimator except for large VIMP where it does better. Overall, the .164 estimator is the best of all three methods. On the other hand, it is hundreds of times slower.

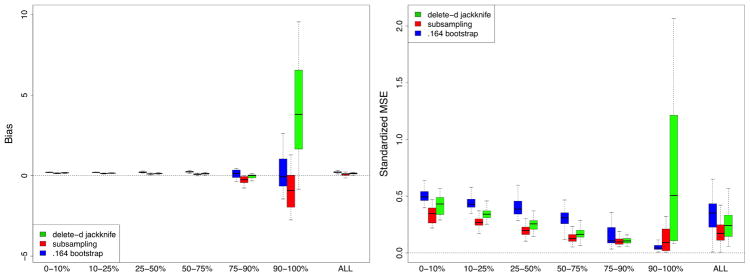
This shows that the delete-d estimator should be used when bias is an issue. However, bias of the subsampling estimator can be improved by increasing the subsampling rate. Figure 2 reports the results from the same set of simulations but using an increased sampling rate b = n^3/4 (b = 62.8). Both estimators improve overall but note the improvement in bias and SMSE for the subsampling estimator relative to the delete-d estimator. Also notice that both estimators now outperform the .164 bootstrap.

FIGURE 2.

Results from RF-R simulations but with increased subsampling rate b = n^3/4. Notice the improvement in bias and SMSE for the subsampling estimator.

4.4 | Confidence intervals for VIMP

The subsampling distribution (9) discussed in Section 3 can also be used to calculate nonparametric confidence intervals.²¹ The general idea for constructing a confidence interval for a target parameter θ(P) is as follows. Define the 1 − α quantile for the subsampling distribution as c_n,b(1 − α) = inf{x : Ũ_n,b(x) ≥ 1 − α}. Similarly, define the 1 − α quantile for the limiting distribution ℚ of n^1/2(θ̂_n − θ(P)) as c(1 − α) = inf{t : F(x) = ℚ[−∞, x] ≥ 1 − α}. Then, assuming (8) and b/n → 0, the interval

$$\left[{\widehat{\theta }}_n-n^{-1/2}{c}_{n,b}(1-\alpha ),\infty \right)$$ (12)

contains θ(P) with asymptotic probability 1 − α if c(1 − α) is a continuity point of F.

While (12) can be used to calculate a nonparametric confidence interval for VIMP, we have found that a more stable solution can be obtained if we are willing to strengthen our asssumptions to include asympotic normality. Let ${\widehat{\theta }}_n^{(j)}=I_{n,M}^{(j)}$ denote the finite forest estimator for VIMP. We call the limit of ${\widehat{\theta }}_n^{(j)}$ as n, M → ∞ the true VIMP and denote this value by ${\theta }_0^{(j)}$,

$${\theta }_0^{(j)}=\underset{n,M\to \infty }{lim}{\widehat{\theta }}_n^{(j)}:=\underset{n,M\to \infty }{lim}{I}_{n,M}^{(j)}.$$

Let ${\widehat{\upsilon }}_n^{(j)}$ be an estimator for $\text{Var}(I_{n,M}^{(j)})$. Assuming asymptotic normality,

$$\frac{{\widehat{\theta }}_n^{(j)}-{\theta }_0^{(j)}}{\sqrt{{\widehat{\upsilon }}_n^{(j)}}}\stackrel{\mathrm{d}}{⇝}\mathrm{N}(0,1),$$ (13)

an asymptotic 100(1 − α) confidence region for ${\theta }_0^{(j)}$, the true VIMP, can be defined as

$${\widehat{\theta }}_n^{(j)}\pm z_{\alpha /2}\sqrt{{\widehat{\upsilon }}_n^{(j)}},$$

where z_α/2 is the 1 − α/2-quantile from a standard normal, Pr{N(0, 1) ≤ z_α/2} = 1 − α/2.

4.5 | Justification of normality

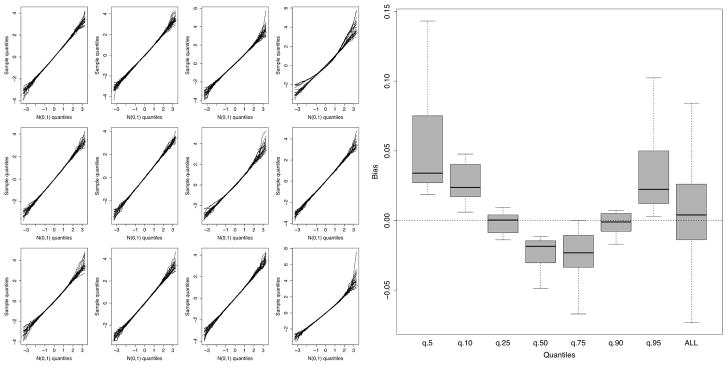
To provide justification for assumption (13), we re-ran our previous simulations 1000 times independently. For each Monte Carlo replication and each simulation model we calculated the finite forest VIMP for a variable and centered it by its mean value from the 1000 simulations and divided this centered value by the standard deviation of the 1000 VIMP values. All experimental parameters were held at the same values as before except for the sample size which was increased to n = 2500. The left-hand side of Figure 3 displays normal quantile plots for standardized VIMP for each of the 12 simulation models. On the y-axis are the quantiles for the standardized VIMP while the x-axis are corresponding N(0, 1) quantiles. The right-hand side displays quantile bias defined as the difference between the quantile for standardized VIMP to the quantile for a standard normal. Values are displayed for 5,10,25,50,75,90,95 percentile values. The results generally confirm that (13) holds. Deviations from normality occur primarily in the tails but these are reasonable and expected in finite sample settings. For example, the median bias is about 0.02 for the 95th percentile. Thus the standardized VIMP quantile differs from the true standard normal value of 1.645 by only a value of 0.02. Also, observe that overall mean bias is near zero (far right boxplot).

FIGURE 3.

Assessing asymptotic normality of VIMP from RF-R simulations. Left-hand figure displays normal quantile plots for standardized VIMP for each of the 12 simulations. Right-hand figure displays bias of VIMP quantiles compared to standard normal quantiles for all 240 variables from all 12 simulations.

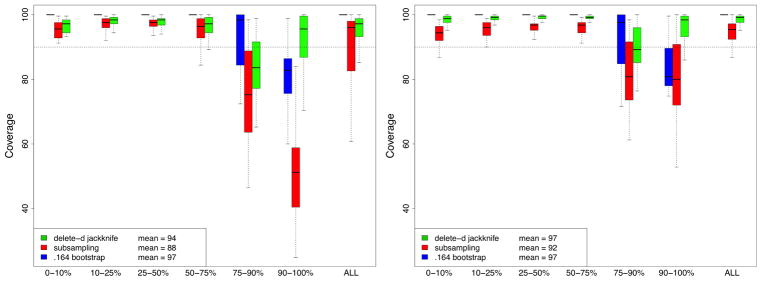
Coverage probabilities for 90% confidence intervals are provided in Figure 4. The left and right figures correspond to simulations of Figures 1 and 2 respectively (recall Figure 2 is based on a larger subsampling rate b = n^3/4). Confidence intervals for the subsampling and delete-d estimators use asymptotic normality. For direct comparison, asymptotic normal bootstrap confidence intervals are also provided. All procedures tend to produce confidence intervals that are too large when VIMP is small (reflected by coverage probabilities exceeding the targeted 90% level). This is actually a good feature as it implies they tend to over-estimate confidence intervals for noisy variables, thereby making them less likely to be selected. For larger VIMP, in the left figure, the subsampling estimator tends to produce intervals that are too small. As mentioned earlier this is because it tends to underestimate the variance. The delete-d estimator performs much better. However, when the subsampling rate is increased (right figure), the subsampling estimator is generally superior to the delete-d estimator. Its overall mean coverage rate is 92 which is much better than the delete-d and bootstrap which achieve coverage rates of 97 which are too high.

FIGURE 4.

Coverage of VIMP 90% asymptotic normal confidence intervals from RF-R simulations. Left and right hand side figures based on subsampling rates b = n^1/2 and b = n^3/4 respectively. Confidence regions for the 240 variables from the 12 simulation experiments have been stratified into 6 groups based on 10, 25, 50, 75, and 90th percentiles of true finite VIMP values.

5 | RANDOM FOREST CLASSIFICATION, RF-C

5.1 | Simulations

The following simulations were used to study performance of methods in the classification problem.

1. Threenorm simulation using mlbench.threenorm from the mlbench R-package.³⁰

2. Two class simulation using twoClassSim from the caret R-package³¹ with 2 factors, 5 linear and 3 non-linear variables.

3. Same as 2, but with a ρ = .75 exchangeable correlation.

4. Same as 2, but with 15 linear variables.

5. Same as 2, but with 15 linear variables and a ρ = .75 exchangeable correlation.

6. RF-R simulation 6 with y discretized into two classes based on its median.

7. RF-R simulation 8 with y discretized into two classes based on its median.

8. RF-R simulation 9 with y discretized into three classes based on its 20 and 75th quantiles.

9. RF-R simulation 10 with y discretized into three classes based on its 20 and 75th quantiles.

10. RF-R simulation 11 with y discretized into three classes based on its 20 and 75th quantiles.

In simulation 1, the feature space dimension was p = 20. Simulations 2–4 added d = 10 noise variables (see the caret package for details). Simulations 6–10 added d = 10 noise variables from a U[−1, 1] distribution. Experimental parameters were set as in RF-R simulations: n = 250; b = {n^1/2, n^3/4}; 100 bootstrap samples; 100 subsample draws. Parameters for randomForestSRC were set as in RF-R except for random feature selection which used p^1/2 random features (default setting). The entire procedure was repeated 250 times.

5.2 | Brier score

Error performance was assessed using the normalized Brier score. Let Y ∈ {1, …, K} be the response. If 0 ≤ p̂_k ≤ 1 denotes the predicted probability that Y equals class k, k = 1, …, K, the normalized Brier score is defined as

$${\text{BS}}^{\ast }=\frac{100K}{K-1}\sum _{k=1}^K{\left(1\{Y=k\}-{\widehat{p}}_k\right)}^2.$$

Note that the normalizing constant 100K/(K − 1) used here is different than the value 1/K typically used for the Brier score. We multiply the traditional Brier score by 100K²/(K − 1) because we have noticed that the value for the Brier score under random guessing depends on the number of classes, K. If K increases, the Brier score under random guessing converges to 1. The normalizing constant used here resolves this problem and yields a value of 100 for random guessing, regardless of K. Thus, anything below 100 signifies a classifier that is better than pure guessing. A perfect classifier has value 0.

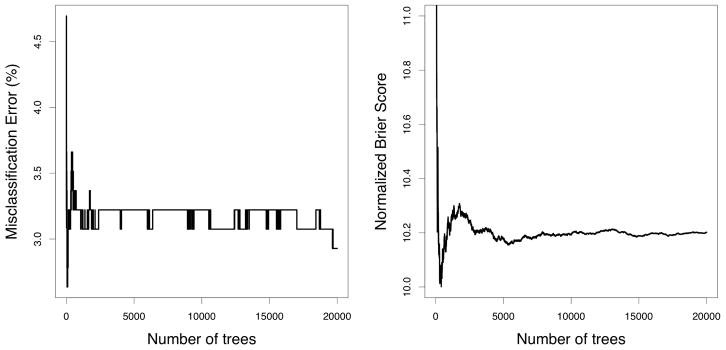
Although misclassification error is the commonly used performance measure in classification problems, it cannot be overstated how much stabler the Brier score is. This stability will naturally lend itself to stabler estimates of VIMP which is why we have chosen to use it. As a simple illustration of this, consider Figure 5 which displays the OOB misclassification rate and OOB normalized Brier score for the Wisconsin breast cancer data from the mlbench R-package. Observe that misclassification error remains unstable even with M = 20, 000 trees.

FIGURE 5.

OOB misclassification error rate versus OOB normalized Brier score for Wisconsin breast cancer data (obtained from the mlbench R-package). Note the fluctuations in misclassification error even after 20,000 trees in contrast to the stable behavior of the Brier score.

5.3 | Results

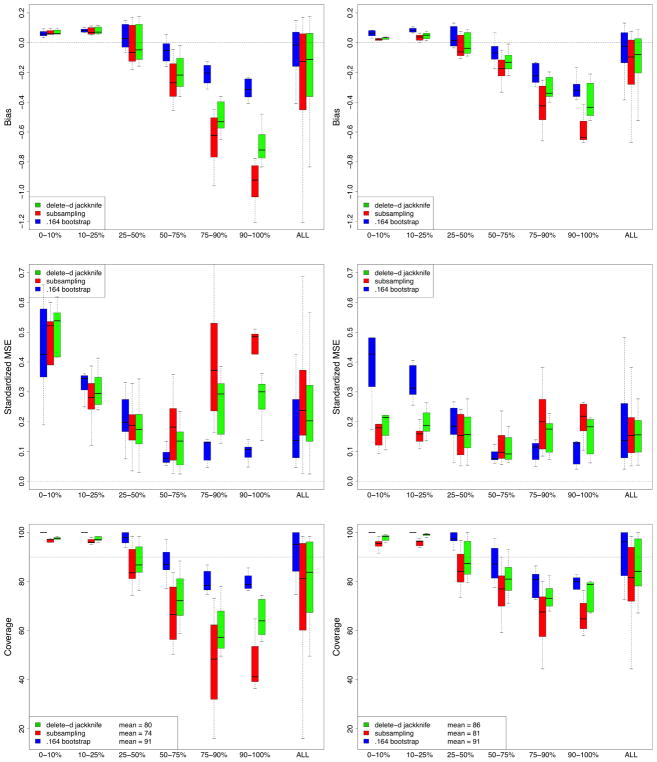
Figure 6 displays the results from the RF-C simulations. Values are displayed as in RF-R. Left and right hand side figures are based on subsampling rates b = n^1/2 and b = n^3/4. The top and middle figures show bias and standardized MSE for estimating the standard error. The bottom figures are coverage probabilities for 90% confidence intervals. VIMP confidence intervals were calculated using asymptotic normality as in RF-R (see the Appendix for justification of normality). The conclusions from Figure 6 are similar to those for RF-R. The delete-d jackknife is more accurate in estimating the standard error for strong variables when the subsampling rate is small, but as b increases, the subsampling estimator improves. Both estimators generally improve with increased b. Note unlike RF-R, coverage probability for the delete-d jackknife is better than the subsampling estimator. This is probably because there are more variables with moderate signal in these simulations.

FIGURE 6.

Results from RF-C (RF-classification) simulations showing performance of subsampling, delete-d jackknife, and .164 bootstrap. Left and right hand side figures are based on subsampling rates b = n^1/2 and b = n^3/4. Top and middle figures display bias and standardized MSE for estimating VIMP standard error. Bottom figure displays coverage for VIMP 90% asymptotic normal confidence intervals. Results have been stratified into 6 groups based on 10, 25, 50, 75, and 90th percentiles of true finite VIMP.

6 | RANDOM SURVIVAL FORESTS, RSF

Now we consider the survival setting. We begin by first defining the survival framework using the notation of Section 2. Following this we discuss two different methods that can be used for measuring prediction error in survival settings. Following this are illustrative examples.

6.1 | Notation

We assume a traditional right-censoring framework. The response is Y = (T, δ), where T = min(T^o, C^o) is the observed survival time and δ = 1{T^o ≤ C^o} is the right-censoring indicator. Here (T^o, C^o) denote the unobserved event and censoring times. Thus δ = 1 denotes an event such as death, while δ = 0 denotes a right-censored case. The target function h is the conditional survival function h(x) = ℙ{T^o > t|X = x}, where t is some selected time point.

6.2 | Weighted Brier score

Let ĥ be an estimator of h. One method for measuring performance of ĥ is the weighted Brier score, ^{23, 24} defined as

$$\text{wBS}(t)={\left(1\{T>t\}-\widehat{h}\right)}^{2}w(t,Y,G),$$

where w(t, Y, G) is the weight defined by

$$w(t,Y,G)=\frac{1\{T\le t\}\delta }{G(T-)}+\frac{1\{T>t\}}{G(t)},$$

and G(t) = ℙ{C^o > t} is the survival function of the censoring variable C^o. Using the notation of Section 2, the loss function ℓ under the weighted Brier score can be written as

$$\ell (Y,\widehat{h})={\left(1\{T>t\}-\widehat{h}\right)}^{2}w(t,Y,G).$$

This assumes G is a known function, but in practice G must be estimated.^{23, 24} Thus if Ĝ is an estimator of G, w(t, Y, G) is replaced by w(t, Y, Ĝ).

6.3 | Concordance index

Harrell’s concordance index³² is another measure of prediction performance that can be used in survival settings. The concordance index estimates the accuracy of the predictor ĥ in ranking two individuals in terms of their survival. A value of 1 represents an estimator that has perfect discrimination, whereas a value of 0.5 indicates performance on par with a random coin toss. This intuitive interpretation of performance has made Harrell’s concordance index very popular and for this reason we will base our analysis on it. Note that because the concordance index is calculated by comparing discordant pairs to concordant pairs, and therefore is very complex, it is not possible to express it in terms of the ℓ-loss function of Section 2. However, this just means that VIMP based on Harrell’s concordance index is not easily described notationally in terms of a formal loss, but this does not pose any problems to the application of our methodology. Permutation VIMP based on Harrell’s concordance index is well defined and can be readily calculated.²

6.4 | Systolic heart failure

For our first illustration we consider a survival data set of n = 2231 cardiovascular patients. All patients suffered from systolic heart failure and all underwent cardiopulmonary stress testing. The outcome was defined as all cause mortality. Over a mean follow-up of 5 years, 742 of the patients died. Patient variables included baseline characteristics and exercise stress test results (p = 39). More detailed information regarding the data can be found in Hsich et al.³³

A RSF analysis was run on the data. A total of 250 survival trees were grown using a nodesize value of 30 with all other parameters set to default values used by RSF in randomForestSRC software. Performance was measured using the C-index defined as one minus the Harrell concordance index.² The delete-d jackknife estimator was calculated using 1000 subsampled values using a b = n^1/2 subsampling rate (b = 47.2). We preferred to use the delete-d jackknife rather than the subsampling estimator because of the low subsampling rate. Also, we did not use the .164 estimator because it was too slow.

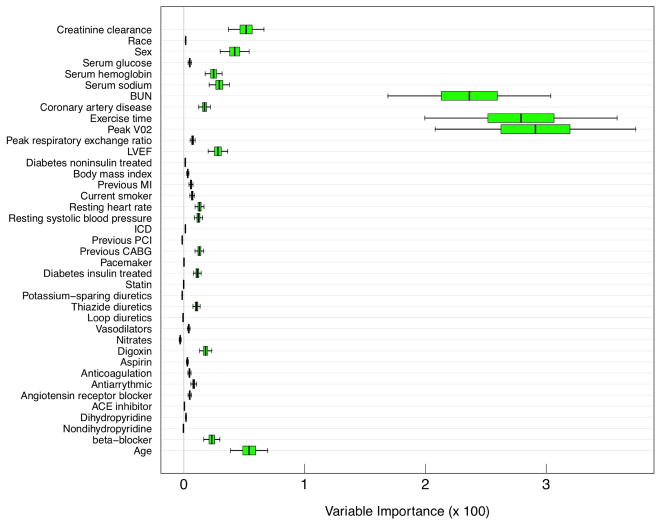
The 95% asymptotic normal confidence intervals are given in Figure 7. VIMP values have been multiplied by 100 for convenient interpretation as percentage. BUN (blood urea nitrogen), exercise time, and peak VO₂ have the largest VIMP with confidence intervals well bounded away from zero. All three variables are known to be highly predictive of heart failure and these findings are not surprising. More interesting, however, are several variables with moderate sized VIMP which have confidence regions bounded away from zero. Some examples are creatinine clearance, sex, LVEF (left ventricular ejection fraction) and use of beta-blockers. The finding for sex is especially interesting because sex is often under appreciated for predicting heart failure.

FIGURE 7.

Delete-d jackknife 95% asymptotic normal confidence intervals from RSF analysis of systolic heart failure data.

6.5 | Survival simulations

Next we study peformance using simulations. We use the three survival simulation models described by Breiman in his 2002 Wald lectures.³⁴ Let h(t, x) be the hazard function for covariate x at time t. Simulations are as follows.

1. h(t, x) = exp(x₁ − 2x₄ + 2x₅).

2. If x₁ ≤ .5, h(t, x) = exp(x₂)1{t ∉ [.5, 2.5]}. If x₁ > .5, h(t, x) = exp(x₃)1{t ∉ [2.5, 4.5]}.

3. h(t, x) = (1 + z₂t) exp(z₁ + z₂t), where z₁ = .5x₁ and z₂ = x₄ + x₅.

In all simulations, covariates were independently sampled from a U[0, 1] distribution. Noise variables were added to increase the dimension to p = 10. Simulation 1 corresponds to a Cox model. Simulations 2 and 3 are non-proportional hazards. Censoring was simulated independently of time in all simulations. Censoring rates were 19%, 15%, and 29% respectively.

RSF was fit using randomForestSRC using the same tuning values as in RF-C simulations (nodesize: 5, random feature selection: p^1/2) Experimental parameters were kept the same as previous simulations. Experiments were repeated 250 times. Results are displayed using the same format as RF-R and RF-C and are provided in Figure 8. The results generally mirror our earlier findings: bias for the subsampling estimator improves relative to the delete-d jackknife with increasing subsampling rate.

FIGURE 8.

Results from RSF simulations showing performance of subsampling, delete-d jackknife, and .164 bootstrap. Left and right hand side figures are based on subsampling rates b = n^1/2 and b = n^3/4. Top and middle figures display bias and standardized MSE for estimating VIMP standard error. Bottom figure displays coverage for VIMP 90% asymptotic normal confidence intervals. Results have been stratified into 6 groups based on 10, 25, 50, 75, and 90th percentiles of true finite VIMP.

6.6 | Competing risk simulations

Here we study performance of the methods in a competing risk setting. For our analysis we use the competing risk simulations from Ishwaran et al.³ Simulations were based on a Cox-exponential hazards model with two competing events. Covariates had differing effects on the hazards. Models included covariates common to both hazards as well as covariates unique to only one hazard. We considered three of the simulations from Section 6.1 of Ishwaran et al.³

1. Linear model. All p covariate effects are linear.

2. Quadratic model. A subset of the p covariate effects are quadratic.

3. Interaction model. Same as 1, but interactions between certain p variables were included.

The feature dimension was p = 12 for simulations 1 and 2, and p = 17 for simulation 3 (i.e. 5 interaction terms were added). Covariates were sampled from both continuous and discrete distributions. Performance was measured using the time truncated concordanace index.³ Without loss of generality we record performance for variables related to event 1 only. RSF competing risk trees were constructed using log-rank splitting with weight 1 on event 1 and weight 0 on event 2 (this ensures VIMP identifies only those variables affecting the event 1 cause). RSF parameters and experimental parameters were identical to the previous simulations. For brevity, results are given in the Appendix in Figure 11. The results mirror our previous findings.

7 | DISCUSSION

7.1 | Summary

One widely used tool for peering inside the RF “black box” is variable importance (VIMP). But analyzing VIMP is difficult because of the complex nature of RF. Given the difficulties of theoretical analysis, our strategy was to approximate the distribution of VIMP through the use of subsampling, a general methodology for approximating distributions of complex statistics. We described a general procedure for estimating the variance of VIMP and for constructing confidence intervals.

We compared our subsampling estimator, and also the closely related delete-d jackknife, ²² to the .164 bootstrap estimator, a modified bootstrap procedure designed to address ties in OOB data. Using extensive simulations involving regression, classification, and survival data, a consistent pattern of performance emerged for the three estimators. All procedures tended to under estimate variance for strong variables and over estimate variance for weak variables. This was especially problematic for the subsamping estimator in low subsampling rate scenarios. The delete-d jackknife did much better in this case due to its bias correction. Both of these methods improved with increasing subsampling rate, eventually outperforming the .164 bootstrap.

7.2 | Computational speed

Overall, we generally prefer the delete-d jackknife because of its better peformance under low subsampling rates, which we feel will be the bulk of applications due to the computational complexity of VIMP. Consider survival with concordance error rates, the most computationally expensive setting for VIMP. The concordance index measures concordance and discordance over pairs of points, a O(n²) operation. With M trees, the number of computations is O(n²M) for a method like the .164 bootstrap. On the other hand, employing a subsampling rate of b = n^1/2 reduces this to O(nM), a factor of n times smaller. The resulting increase in speed will be of tremendous advantage in big data settings.

7.3 | Practical Guidelines

One of the major applications of our methodolgy will be variable selection. Below we provide some practical guidelines for this setting:

1. Use asymptotic normal confidence intervals derived from the delete-d jackknife variance estimator.

2. A good default subsampling rate is b = n^1/2. As mentioned, this will substantially reduce computational costs in big n problems. In small n problems, while this might seem overly aggressive leading to small subsamples, our results have shown solid performance even when n = 250.

3. The α value for the confidence region should be chosen using typical values such as α = .1 or α = .05. Outside of extreme settings such as high-dimensional problems, our experience suggests this should work well.

The above guidelines are only meant to be starting points for the analyst and obviously there will be exceptions to the rules. However, as way of support for these recommendations we did the following variable selection experiment. We re-ran the RF-R simulations of Section 4. Variables were selected using 100(1 − α)% delete-d jackknife asymptotic normal confidence intervals. The true positive rate (TPR) and true negative rate (TNR) was calculated for each simulation and results averaged over 250 independent runs. TPR was defined as the fraction of true signal variables identified. TNR was the fraction of noisy signal variables identified.

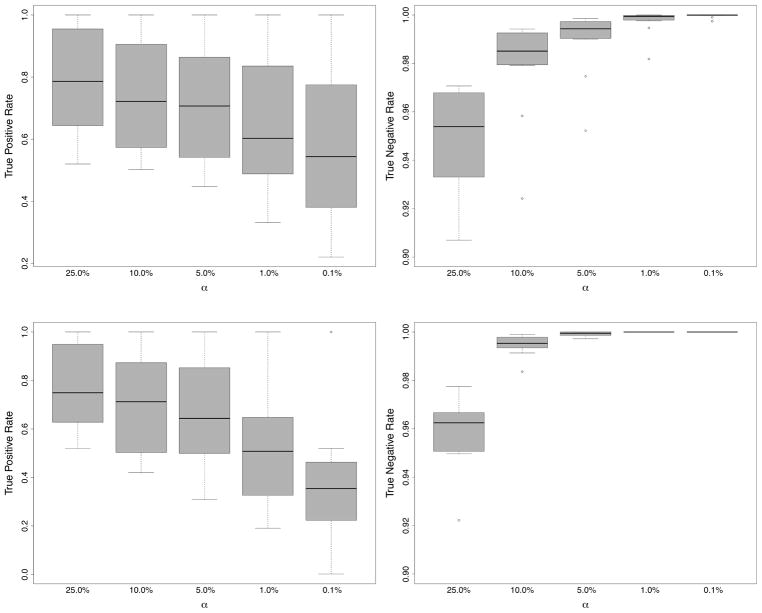
Figure 9 displays the averaged TPR and TNR for each of the 12 simulation experiments under levels of significance α = .25, .1, .01, .001. The top panel was calculated under a subsampling rate b = n^1/2, while the bottom panel used b = n^3/4. A similar pattern for TPR and TNR values is generally observed for both sampling rates: TPR decreases with increasing α; TNR increases with α. For b = n^3/4, TNR rates are slightly better, however for b = n^1/2, TPR rates are slightly better. Thus if the goal is finding true signal the edge goes to b = n^1/2.

FIGURE 9.

Results from variable selection experiment using RF-R simulations of Section 4. Displayed are the true positive rate (TPR) and true negative rate (TNR) for variables selected using 100(1 − α)% delete-d jackknife confidence regions where α = .25, .1, .01, .001. Top and bottom figures are based on subsampling rates b = n^1/2 and b = n^3/4.

Focusing on the top panel corresponding to the recommended n^1/2 subsampling rate, a striking pattern for TPR is that while TPR decreases with α, the decline is fairly slow. This is interesting given the wide range of α values from 25% to 0.1%. These values are extreme and unlikely to be used in practice and yet TPR results remain quite robust. Values for TNR are also fairly robust to α, although TNR values appear relatively too small when α = .25. The value α = .25 is too extreme and creates overly narrow confidence regions causing noisy variables to be misclassified as signal variables. Generally, however, values α = .1, .05, .01 perform very well under both TNR and TPR.

7.4 | Theoretical considerations

The key assumption underlying subsampling is the existence of a limiting distribution (8) for the estimator. However, as discussed earlier, theoretical results for VIMP are difficult to come by and establishing a result like (8) for something as complicated as permuation importance is not easy. As a token, we would like to offer some partial insight into VIMP for the regression case (RF-R), perhaps pointing the way for more work in this area. As shown in the Appendix (see Theorem 1), assuming an additive model $h(\mathbf{X})={\sum }_{j=1}^p{h}_j(X_i^{(j)})$, the population mean for VIMP equals

$$\mathbb{E}[I(X^{(j)},\mathrm{\Theta },\mathcal{L})]=\mathbb{E}\left[{(h_j({\stackrel{\sim }{X}}^{(j)})-h_j(X^{(j)}))}^2\right]+2{\sigma }^2(1-{\rho }_j)+o(1),$$

where ρ_j is a correlation coefficient and h_j is the additive expansion of h attributed to X^(j). For noisy variables, h_j = 0 and ρ_j = 1; thus VIMP will converge to zero. For strong variables, h_j ≠ 0. Our theory suggests that the value of ρ_j will be the same for all strong variables. Therefore for strong variables, except for some constant, VIMP equals the amount that h_j changes when X^(j) is permuted, thus showing that VIMP correctly isolates the effect of X^(j) in the model.

The technical assumptions required by Theorem 1 are provided in the Appendix, however there are two key conditions worth briefly mentioning. One is the use of deep trees in which terminal nodes contain exactly one unique value (replicated values due to bootstrapping are allowed). A second condition is that the forest predictor is L₂-consistent for h. As discussed in the Appendix, this latter assumption is reasonable in our setting and has been proven by Scornet et al.³⁵

It is interesting that the above property for VIMP is tied to the consistency of the forest. We believe in general that properties for VIMP, such as its limiting distribution, will rely on analogous results for the RF predictor. Hopefully in the future these results for VIMP will be proven. At least in the case of RF-R we know that distributional results exist for the predictor. Wager ¹⁹ established asymptotic normality of the infinite forest predictor (assuming one observation per terminal node). Mentch and Hooker ²⁰ established a similar result for the finite forest predictor. See Biau and Scornet ³⁶ for a comprehensive discussion of known theoretical results for RF.

8 | APPENDIX

8.1 | Assessing normality for classification, survival, and competing risk

We applied the same strategy as in RF-R simulations to assess normality of VIMP for RF-C, RSF, and RSF competing risk simulations. Specifically, for each setting we ran simulations 1000 times independently. Experimental parameters were set as before with n = 2500. The finite forest VIMP for a variable was centered by its averaged value from the 1000 simulations. This centered value was then divided by the standard deviation of the 1000 VIMP values. Quantile bias was calculated by taking the difference between the quantile for standardized VIMP to that of a standard normal quantile. Quantile bias is displayed in Figure 10 for the three families.

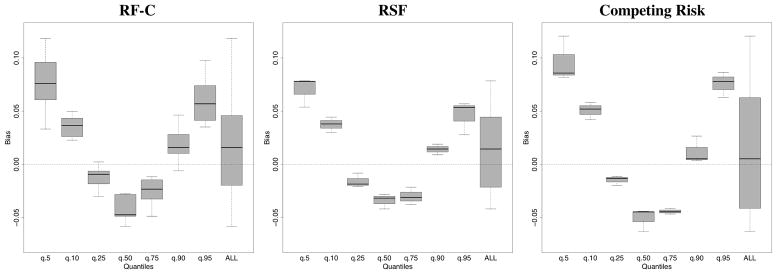
8.2 | Performance results from competing risk simulations

Competing risk simulations from Ishwaran et al.³ were used to assess performance of the subsampling, delete-d jackknife, and .164 bootstrap estimators. Performance was measured using the time truncated concordanace index.³ Analysis focused on variables affecting cause 1 event. RSF competing risk trees were constructed using log-rank splitting with weight 1 on event 1 and weight 0 on event 2. This ensured VIMP identified only those variables affecting event 1. Results are displayed in Figure 11.

FIGURE 10.

Assessing asymptotic normality of VIMP from RF-C, RSF, and RSF competing risk simulations. Figure displays bias of standardized VIMP quantiles compared to standard normal quantiles. Values are displayed for 5,10,25,50,75,90,95 percentile values.

8.3 | Some theoretical results for VIMP in RF-R

Let ${\widehat{\theta }}_n^{(j)}=I(X^{(j)},\mathcal{L})$ be the infinite forest estimator for VIMP (5). We assume the following additive regression model holds

$$Y_i=\sum _{j=1}^p{h}_j(X_i^{(j)})+{\epsilon }_i,i=1,\dots ,n,$$ (14)

where (X_i, ε_i) are i.i.d. with distribution ℙ such that X_i and ε_i are independent and 𝔼(ε_i) = 0, Var(ε_i) = σ² < ∞. Notice (14) implies that the target function h has an additive expansion $h(\mathbf{X})={\sum }_{j=1}^p{h}_j(X^{(j)})$. This is a useful assumption because it will allow us to isolate the effect of VIMP. Also, there are known consistency results for RF in additive models³⁵ which we will use later in establishing our results. Assuming squared error loss, ℓ(Y, ĥ) = (Y − ĥ)², we have

$${\widehat{\theta }}_n^{(j)}={\mathbb{E}}_{\mathrm{\Theta }}\left[\frac{1}{N(\mathrm{\Theta })}\sum _{i\in {\mathcal{L}}^{\ast \ast }(\mathrm{\Theta })}\left[{(Y_i-h({\stackrel{\sim }{\mathbf{X}}}_i^{(j)},\mathrm{\Theta },\mathcal{L}))}^2-{(Y_i-h({\mathbf{X}}_i,\mathrm{\Theta },\mathcal{L}))}^2\right]\right].$$

We will assume the number of OOB cases N(Θ) is always fixed at Round(ne⁻¹), where Round(·) is the nearest integer function. Write N_n for N(Θ). Because this is a fixed value,

$${\widehat{\theta }}_n^{(j)}=\frac{1}{N_n}{\mathbb{E}}_{\mathrm{\Theta }}\left[\sum _{i\in {\mathcal{L}}^{\ast \ast }(\mathrm{\Theta })}\left[{(Y_i-h({\stackrel{\sim }{\mathbf{X}}}_i^{(j)},\mathrm{\Theta },\mathcal{L}))}^2-{(Y_i-h({\mathbf{X}}_i,\mathrm{\Theta },\mathcal{L}))}^2\right]\right].$$

To study ${\widehat{\theta }}_n^{(j)}$ we will evaluate its mean ${\theta }_{n,0}^{(j)}={\mathbb{E}}_{\mathcal{L}}[{\widehat{\theta }}_n^{(j)}]$. For ease of notation, write h_n,i = h(X_i, Θ, ℒ) and ${\stackrel{\sim }{h}}_{n,i}=h({\stackrel{\sim }{\mathbf{X}}}_i^{(j)},\mathrm{\Theta },\mathcal{L})$. Likewise, let h_n = h(X, Θ, ℒ) and h̃_n = h(X̃^(j), Θ, ℒ). We have

$${\theta }_{n,0}^{(j)}=\frac{1}{N_n}\mathbb{E}\left[\sum _{i\in {\mathcal{L}}^{\ast \ast }(\mathrm{\Theta })}\left[{(Y_i-{\stackrel{\sim }{h}}_{n,i})}^2-{(Y_i-h_{n,i})}^2\right]\right]=\mathbb{E}\left[{(Y-{\stackrel{\sim }{h}}_n)}^2-{(Y-h_n)}^2\right],$$

where the right hand side follows because $(\mathbf{X},Y,h_n,{\stackrel{\sim }{h}}_n)\stackrel{\mathrm{d}}{=}({\mathbf{X}}_i,Y_i,h_{n,i},{\stackrel{\sim }{h}}_{n,i})$ if i is OOB (i.e., because the tree does not use information about (X_i, Y_i) in its construction, we can replace (X_i, Y_i) with (X, Y)). Now making using of the representation Y = h(X) + ε, which holds by the assumed regression model (14), and writing h for h(X) and Δ̃_n = h̃_n − h_n,

$${\theta }_{n,0}^{(j)}=\mathbb{E}\left[{(Y-{\stackrel{\sim }{h}}_n)}^2-{(Y-h_n)}^2\right]=\mathbb{E}\left[-2\epsilon {\stackrel{\sim }{\mathrm{\Delta }}}_n+{\stackrel{\sim }{\mathrm{\Delta }}}_n^2+2{\stackrel{\sim }{\mathrm{\Delta }}}_n(h_n-h)\right]=\mathbb{E}\left[{\stackrel{\sim }{\mathrm{\Delta }}}_n^2\right]+2\mathbb{E}\left[{\stackrel{\sim }{\mathrm{\Delta }}}_n(h_n-h)\right],$$ (15)

where in the last line we have used 𝔼(ε) = 0 and that ε is independent of {Δ̃_n, h_n, h}.

FIGURE 11.

Results from competing risk simulations showing performance of subsampling, delete-d jackknife, and .164 bootstrap. Left and right hand side figures are based on subsampling rates b = n^1/2 and b = n^3/4. Top and middle figures display bias and standardized MSE for estimating VIMP standard error. Bottom figure displays coverage for VIMP 90% asymptotic normal confidence intervals. Results have been stratified into 6 groups based on 10, 25, 50, 75, and 90th percentiles of true finite VIMP.

We can see that (15) is driven by the two terms: Δ̃_n and h_n − h. Define integer values n_i := n_i(Θ) ≥ 0 recording the bootstrap frequency of case i = 1, …, n in ℒ^*(Θ) (notice that n_i = 0 implies case i is OOB). By the definition of a RF-R tree, we have

$$h_n=h(\mathbf{X},\mathrm{\Theta },\mathcal{L})=\sum _{i=1}^n{W}_i(\mathbf{X},\mathrm{\Theta })Y_i$$

where ${\{W_i(\mathbf{X},\mathrm{\Theta })\}}_1^n$ are the forest weights defined as

$$W_i(\mathbf{X},\mathrm{\Theta })=\frac{n_{i}1\{{\mathbf{X}}_i\in R(\mathbf{X},\mathrm{\Theta })\}}{\mid R(\mathbf{X},\mathrm{\Theta })\mid }$$

where R(X, Θ) is the tree terminal node containing X and |R(X, Θ)| is the cardinality equal to the number of bootstrap cases in R(X, Θ). Notice that the weights are convex since 0 ≤ W_i(X, Θ) ≤ 1 and

$$\sum _{i=1}^n{W}_i(\mathbf{X},\mathrm{\Theta })=\sum _{i=1}^n\frac{n_{i}1\{{\mathbf{X}}_i\in R(\mathbf{X},\mathrm{\Theta })\}}{\mid R(\mathbf{X},\mathrm{\Theta })\mid }=\sum _{i=1}^n\frac{n_{i}1\{{\mathbf{X}}_i\in R(\mathbf{X},\mathrm{\Theta })\}}{{\sum }_{i^{\prime }=1}^n{n}_{i^{\prime }}1\{{\mathbf{X}}_{i^{\prime }}\in R(\mathbf{X},\mathrm{\Theta })\}}=1.$$

Similarly, we have

$${\stackrel{\sim }{h}}_n=h({\stackrel{\sim }{\mathbf{X}}}^{(j)},\mathrm{\Theta },\mathcal{L})=\sum _{i=1}^n{W}_i({\stackrel{\sim }{\mathbf{X}}}^{(j)},\mathrm{\Theta })Y_i,\text{where}{W}_i({\stackrel{\sim }{\mathbf{X}}}^{(j)},\mathrm{\Theta })=\frac{n_{i}1\{{\mathbf{X}}_i\in R({\stackrel{\sim }{\mathbf{X}}}^{(j)},\mathrm{\Theta })\}}{\mid R({\stackrel{\sim }{\mathbf{X}}}^{(j)},\mathrm{\Theta })\mid }.$$

Therefore,

$${\stackrel{\sim }{\mathrm{\Delta }}}_n(\mathbf{X})=h({\stackrel{\sim }{\mathbf{X}}}^{(j)},\mathrm{\Theta },\mathcal{L})-h(\mathbf{X},\mathrm{\Theta },\mathcal{L})=\sum _{i=1}^n{W}_i({\stackrel{\sim }{\mathbf{X}}}^{(j)},\mathrm{\Theta })Y_i-\sum _{i=1}^n{W}_i(\mathbf{X},\mathrm{\Theta })Y_i.$$

In order to study Δ̃_n in more detail we will assume deep trees containing one unique case per terminal node.

Assumption 1

We assume each terminal node contains exactly one unique value. That is, each terminal node contains the bootstrap copies of a unique data point.

Assumption 1 results in the following useful simplification. For notational ease, write R̃ = R(X̃^(j), Θ) and R = R(X, Θ). Then

$$\begin{gathered} {\stackrel{\sim }{\mathrm{\Delta }}}_n(\mathbf{X})=\frac{1}{\mid \tilde{R}\mid }\sum _{i\in \stackrel{\sim }{R}}{n}_i{Y}_i-\frac{1}{\mid R\mid }\sum _{i\in R}{n}_i{Y}_i \\ =\frac{1}{\mid \stackrel{\sim }{R}\mid }\sum _{i\in \stackrel{\sim }{R}}{n}_{i}h({\mathbf{X}}_i)-\frac{1}{\mid R\mid }\sum _{i\in R}{n}_{i}h({\mathbf{X}}_i)+\frac{1}{\mid \stackrel{\sim }{R}\mid }\sum _{i\in \stackrel{\sim }{R}}{n}_i{\epsilon }_i-\frac{1}{\mid R\mid }\sum _{i\in R}{n}_i{\epsilon }_i \\ =h({\mathbf{X}}_{i(\stackrel{\sim }{R})})-h({\mathbf{X}}_{i(R)})+{\epsilon }_{i(\stackrel{\sim }{R})}-{\epsilon }_{i(R)}, \end{gathered}$$

where i(R̃) and i(R) identify the index for the bootstrap case in R̃ = R(X̃^(j), Θ) and R = R(X, Θ) respectively (note that i(R̃) and i(R) are functions of X and j but this is suppressed for notational simplicity). We can see that the information in the target function h is captured by the first two terms in the last line and therefore will be crucial to understanding VIMP. Notice that if h(X_i(R̃)) ≍ h(X̃^(j)) and h(X_i(R)) ≍ h(X), which is what we would expect asymptotically with a deep tree, then

$$h({\mathbf{X}}_{i(\stackrel{\sim }{R})})-h({\mathbf{X}}_{i(R)})\asymp h({\stackrel{\sim }{\mathbf{X}}}^{(j)})-h(\mathbf{X})=h_j({\stackrel{\sim }{X}}^{(j)})-h_j(X^{(j)}),$$

where the right-hand side follows by our assumption of an additive model (14). This shows that VIMP for X^(j) is assessed by how much its contribution to the additive expansion, h_j, changes when X^(j) is permuted. This motivates the following assumption.

Assumption 2

Assuming a deep tree with one unique value in a terminal node,

$$h({\stackrel{\sim }{\mathbf{X}}}^{(j)})=h({\mathbf{X}}_{i(\stackrel{\sim }{R})})+{\stackrel{\sim }{\xi }}_n(\mathbf{X}),h(\mathbf{X})=h({\mathbf{X}}_{i(R)})+{\zeta }_n(\mathbf{X}),$$

where $\mathbb{E}({\stackrel{\sim }{\zeta }}_n^2)=o(1)$and $\mathbb{E}({\zeta }_n^2)=o(1)$.

This deals with the first two terms in the expansion of Δ̃_n(X). We also need to deal with the remaining term involving the measurement errors, ε_i(R̃) − ε_i(R). For this we will rely on a fairly mild exchangeability assumption.

Assumption 3

ε_i(R̃), ε_i(R) is a finite exchangeable sequence with variance σ².

Finally, a further assumption we will need is consistency of the forest predictor.

Assumption 4

The forest predictor is L₂-consistent, 𝔼 [(h_n − h)²] → 0 where 𝔼[h²] < ∞.

Putting all of the above together, we can now state our main result.

Theorem 1

If Assumptions 1, 2, 3, and 4 hold, then

$${\theta }_{n,0}^{(j)}=\mathbb{E}\left[{(h_j({\stackrel{\sim }{X}}^{(j)})-h_j(X^{(j)}))}^2\right]+2{\sigma }^2(1-{\rho }_j)+o(1),$$

where ρ_j = corr(ε_i(R̃), ε_i(R)).

Note that the asymptotic limit will be heavily dependent on the strength of the variable. Consider when X^(j) is a noisy variable. Ideally this means the tree is split without ever using X^(j). Therefore, if we drop X and X̃^(j) down the tree they will occupy the same terminal node. Hence, R̃ = R and ε_i(R̃) = ε_i(R) and therefore ρ_j = 1. Furthermore, because h_j must be zero for a noisy variable, it follows that ${\theta }_{n,0}^{(j)}=o(1)$ . Thus, the limit is zero for a noisy variable. Obviously, this is much different than the limit of a strong variable which must be strictly positive because h_j ≠ 0 and ρ_j < 1 for strong variables.

Proof

By (15), we have ${\theta }_{n,0}^{(j)}=\mathbb{E}[{\stackrel{\sim }{\mathrm{\Delta }}}_n^2]+2\mathbb{E}[{\stackrel{\sim }{\mathrm{\Delta }}}_n(h_n-h)]$. We start by dealing with the second term, 𝔼[Δ̃_n(h_n − h)]. By the Cauchy-Schwartz inequality,

$$\mathbb{E}\left[{\stackrel{\sim }{\mathrm{\Delta }}}_n(h_n-h)\right]\le \mathbb{E}\left[\mid {\stackrel{\sim }{\mathrm{\Delta }}}_n\mid \mid h_n-h\mid \right]\le \sqrt{\mathbb{E}\left[{\stackrel{\sim }{\mathrm{\Delta }}}_n^2\right]}\sqrt{\mathbb{E}\left[{(h_n-h)}^2\right]}.$$

By Assumption 4, the right-hand side converges to zero if $\mathbb{E}[{\stackrel{\sim }{\mathrm{\Delta }}}_n^2]$ remains bounded. By Assumption 2, and the assumption of an additive model (14),

$${\stackrel{\sim }{\mathrm{\Delta }}}_n(\mathbf{X})=h_j({\stackrel{\sim }{X}}^{(j)})-h_j(X^{(j)})-{\overline{\zeta }}_n(\mathbf{X})+{\zeta }_n(\mathbf{X})+{\epsilon }_{i(\stackrel{\sim }{R})}-{\epsilon }_{i(R)}.$$

Assumption 4 implies h (and therefore h_j) is square-integrable. Assumption 3 implies that ε_i(R̃), ε_i(R) have finite second moment and are square-integrable. Therefore squaring and taking expectations, and using $\mathbb{E}({\stackrel{\sim }{\zeta }}_n^2)=o(1)$ and $\mathbb{E}({\zeta }_n^2)=o(1)$, deduce that

$$\mathbb{E}[{\stackrel{\sim }{\mathrm{\Delta }}}_n{(\mathbf{X})}^2]=\mathbb{E}\left[{(h_j({\stackrel{\sim }{X}}^{(j)})-h_j(X^{(j)}))}^2\right]+2\mathbb{E}\left[(h_j({\stackrel{\sim }{X}}^{(j)})-h_j(X^{(j)}))({\epsilon }_{i(\stackrel{\sim }{R})}-{\epsilon }_{i(R)})\right]+\mathbb{E}\left[{({\epsilon }_{i(\stackrel{\sim }{R})}-{\epsilon }_{i(R)})}^2\right]+o(1).$$

By exchangeability, 𝔼[g(X)ε_i(R̃)] = 𝔼[g(X)ε_i(R)] for any function g(X). Hence,

$$0=\mathbb{E}\left[(h_j({\stackrel{\sim }{X}}^{(j)})-h_j(X^{(j)})){\epsilon }_{i(\stackrel{\sim }{R})}\right]-\mathbb{E}\left[(h_j({\stackrel{\sim }{X}}^{(j)})-h_j(X^{(j)})){\epsilon }_{i(R)}\right]=\mathbb{E}\left[(h_j({\stackrel{\sim }{X}}^{(j)})-h_j(X^{(j)}))({\epsilon }_{i(\stackrel{\sim }{R})}-{\epsilon }_{i(R)})\right].$$

Appealing to exchangeability once more, we have

$$\mathbb{E}[{({\epsilon }_{i(\stackrel{\sim }{R})}-{\epsilon }_{i(R)})}^2]=\mathbb{E}[{\epsilon }_{i(\stackrel{\sim }{R})}^2]+\mathbb{E}[{\epsilon }_{i(\stackrel{\sim }{R})}^2]-2\mathbb{E}[{\epsilon }_{i(\stackrel{\sim }{R})}{\epsilon }_{i(R)}]=2{\sigma }^2(1-{\rho }_j),$$

where ρ_j = corr(ε_i(R̃), ε_i(R)). Therefore we have shown

$$\mathbb{E}[{\stackrel{\sim }{\mathrm{\Delta }}}_n{(\mathbf{X})}^2]=\mathbb{E}\left[{(h_j({\stackrel{\sim }{X}}^{(j)})-h_j(X^{(j)}))}^2\right]+2{\sigma }^2(1-{\rho }_j)+o(1),$$

which verifies boundedness of $\mathbb{E}[{\stackrel{\sim }{\mathrm{\Delta }}}_n^2]$ and that ${\theta }_{n,0}^{(j)}=\mathbb{E}[{\stackrel{\sim }{\mathrm{\Delta }}}_n^2]+o(1)$.

The conditions needed to establish Theorem 1 are fairly reasonable. Assumption 2 can be viewed as a type of continuity condition for h. However, it is also an assertion about the approximating behavior of the forest predictor h_n. It asserts that all features X within a terminal node have h(X) values close to one another, which can be seen as an indirect way of asserting good local prediction behavior for the tree. Thus, Assumption 2 is very similar to Assumption 4. The latter assumption of consistency is reasonable for deep trees under an additive model assumption. Scornet et al.³⁵ established L₂-consistency of RF-R for additive models allowing for the number of terminal nodes to grow at rate of n (see Theorem 2 of their paper). For technical reasons their proof replaced bootstrapping with subsampling and required X to be uniformly distributed, but other than this their result can be seen as strong support for our assumptions.