Abstract
Objective
The goal of this study was to compare several parameters, including wall shear stress (WSS) and flow pattern, between unruptured and ruptured anterior communicating artery (ACoA) aneurysms using patient-specific aneurysm geometry.
Methods
In total, 18 unruptured and 24 ruptured aneurysms were analyzed using computational fluid dynamics (CFD) models. Minimal, average, and maximal wall shear stress were calculated based on CFD simulations. Aneurysm height, ostium diameter, aspect ratio, and area of aneurysm were measured. Aneurysms were classified according to flow complexity (simple or complex) and inflow jet (concentrated or diffused). Statistical analyses were performed to ascertain differences between the aneurysm groups.
Results
Average wall shear stress of the ruptured group was greater than that of the unruptured group (9.42% for aneurysm and 10.38% for ostium). The average area of ruptured aneurysms was 31.22% larger than unruptured aneurysms. Simple flow was observed in 14 of 18 (78%) unruptured aneurysms, while all ruptured aneurysms had complex flow (p<0.001). Ruptured aneurysms were more likely to have a concentrated inflow jet (63%), while unruptured aneurysms predominantly had a diffused inflow jet (83%, p=0.004).
Conclusion
Ruptured aneurysms tended to have a larger geometric size and greater WSS compared to unruptured aneurysms, but the difference was not statistically significant. Flow complexity and inflow jet were significantly different between unruptured and ruptured ACoA aneurysms.
Keywords: Aneurysm, Anterior communicating artery aneurysm, Computational fluid dynamics, Wall shear stress, Flow pattern
INTRODUCTION
Sudden rupture of cerebral aneurysms can cause subarachnoid hemorrhage, which is associated with serious morbidity and mortality [11,27]. Because prediction of aneurysm rupture risk is challenging, researchers have investigated and compared features of unruptured and ruptured aneurysms with hemorrhagic sequelae in order to identify characteristics of a ruptured aneurysm that may permit early detection [7,29]. In particular, the anterior communicating artery (ACoA) is known to have diverse configurations and complex flow conditions in the anterior circulation. Research on ACoA aneurysms is important because these lesions account for 25% of all cerebral aneurysms, according to previous studies [1,2,10].
The precise mechanism of aneurysm rupture is not yet clearly defined [30], but both morphological [15] and hemodynamic [28] parameters are believed to be associated factors. In one previous study, aneurysm area was only considered as a morphological parameter in the statistical comparison between unruptured and ruptured aneurysm groups, and no statistical difference was shown between the two groups [17]. Other work suggests that additional morphological characteristics, including aspect ratio, should be considered, rather than judging the risk of aneurysm rupture using aneurysm area alone [15,23]. Several authors have noted that hemodynamic factors such as wall shear stress (WSS) play an important role in the formation, pathogenesis, and rupture of cerebral aneurysms [3,14,18,20]. Because WSS impacts endothelial cell function, understanding WSS is important in determining risk of aneurysm rupture [19,28]. According to Meng et al.’s study [19], whether high WSS or low WSS affects the growth and rupture of aneurysms is still controversial. Both high and low WSS have a respective effect on the aneurysm rupture. Impinging jet of flow pattern could be formed through the high WSS of aneurysm, and disturbed f low could be observed with low WSS of aneurysm. However, as the geometry of the aneurysm changes, flow pattern could be also affected. Like the “high-versus-low WSS” controversy, the effect of morphological parameters and hemodynamic factors on aneurysm rupture has been studied respectively [19]. However, their correlations have not been widely investigated. For example, Lu et al. [17] used size of aneurysm and WSS to show the risk of aneurysm rupture between unruptured and ruptured aneurysm groups, but any correlation between the morphological and hemodynamic factors was not suggested.
Thus, the purpose of this study was to identify morphological and hemodynamic factors relating to ACoA aneurysms and compare blood f low patterns between unruptured and ruptured groups using a computational fluid dynamics (CFD) model. We examined WSS and f low patterns, such as f low complexity and inflow jet, in unruptured and ruptured aneurysm groups. Statistical correlations between morphological parameters (height, ostium diameter, aspect ratio, and area of aneurysm) and average WSS at the aneurysm were analyzed in relation to the causes and risk of aneurysm rupture.
MATERIALS AND METHODS
Patient selection
ACoA aneurysm, which has a complex flow characteristic, was chosen in the present study. A total of 47 patients with ACoA aneurysms treated at the Chonbuk National University Hospital were included. Between October 2015 and July 2017, 23 unruptured and 24 ruptured ACoA aneurysms were diagnosed with rotational cerebral angiography. Five patients with unruptured aneurysms had a bilateral symmetrical inlet, and they were excluded from the study sample. Thus, the final sample of this study consisted of 18 unruptured and 24 ruptured aneurysms. Among 42 patients, there were 13 patients with daughter sac, 10 patients with lobular contour, and three patients with aneurysmal bleb. The patients in these two aneurysm groups had similar mean ages, 60 for the unruptured aneurysm group and 59 for the ruptured aneurysm group (Table 1). All patients were evaluated for the presence of neurovascular diseases or subarachnoid hemorrhage. Institutional Review Board of Chonbuk National University Hospital approved this retrospective study.
Table 1.
Morphological variables for the unruptured and ruptured aneurysms
| Unruptured (n=18) | Ruptured (n=24) | p-value | |
|---|---|---|---|
| Age (years) | 60±11 | 59±11 | 0.23 |
| Height of aneurysm (mm) | 3.67±1.51 | 4.12±1.90 | 0.40 |
| Ostium diameter (mm) | 5.06±1.02 | 5.25±1.49 | 0.60 |
| Aspect ratio | 0.72±0.27 | 0.78±0.29 | 0.46 |
| Aneurysm area (mm2) | 70.42±33.60 | 92.41±66.94 | 0.57 |
Values are presented as mean±standard deviation
Preparation of vascular model
All image acquisitions were made using rotational cerebral angiography (Axiom Artis dBA; Siemens Medical Solutions, Erlangen, German). A source image was obtained from rotational cerebral angiography with a 1.5 degree rotation for 29 frames per second during an 8 second scan. For each patient, 3D rotational angiographic data in DICOM format was converted into a 3D model using Materialise Mimics software (version 20.0; Materialise NV, Leuven, Belgium). We performed a cropping operation to segment the geometric model, and unnecessary branches were removed. All patient-specific models were smoothed prior to making geometric measurements for modeling and analysis.
Morphologic analysis
The height of the aneurysm dome and the ostium diameter were measured using a reconstructed patient-specific 3D model. The maximum length from the center of ostium to the dome of aneurysm was defined as aneurysm height. As suggested from the previous studies, the ostium diameter was obtained using an ostium cross-section, and the longest diameter in the cutting plane was defined as the ostium diameter [23,26]. The aneurysm height was divided by the ostium diameter to obtain the aspect ratio. The area of the aneurysm was calculated from the surface of the reconstructed aneurysm dome [14,16,31].
Hemodynamic modeling
Patient-specific 3D models were imported into COMSOL Multiphysics (version 5.2a; COMSOL Inc., Burlington, MA, USA) to create a mesh for CFD simulations. COMSOL Multiphysics was used to solve the f low-governing Navier-Stokes equation and the equation of continuity (equations [1] and [2]). In both equations, u represents the flow velocity. In equation (2), indicates the rate of change of velocity with time, ρ denotes the density, p represents the pressure, and μ indicates the fluid viscosity [13].
Blood flow was assumed to be laminar. The fluid properties of blood were considered to be incompressible with a density of 1066 kg/m3. A constant (Newtonian) dynamic viscosity was used with 0.0035 Pa·s. Because of insufficient information on wall thickness and aneurysm elasticity, the vessel wall was assumed to be rigid with a no-slip condition [8,21]. Using the aneurysm inlet area for each patient, the same physiologic average flow rate of 2.6 mL/s was used for the inlet boundary condition. Zero pressure was set for the outlet boundary condition, due to the lack of specific blood f low information [12,21]. Four cardiac cycles were simulated for numeric stability, and the second cycle was used for the results [4]. The CFD results were obtained at end-diastole to clearly show the difference in tendency between unruptured and ruptured aneurysm groups.
Flow pattern analysis
Flow patterns were evaluated for flow complexity and inflow jet. Flow complexity was then classified as either simple or complex depending on the number of recirculation regions. Simple flow complexity was defined as containing only one recirculation region. Complex flow complexity was defined as including two or more recirculation regions [8]. For analysis, the number of unruptured or ruptured aneurysms with either simple or complex flow was counted.
According to the concentration of the inflow jet as it entered the dome of aneurysm, the inflow jet was classified as either concentrated or diffused inflow jet. By definition, a concentrated inflow jet flows directly toward the tip of aneurysm. In contrast, a diffused inflow jet quickly spreads laterally as soon as the blood flow enters the aneurysm dome and flows along the wall of aneurysm [4]. For statistical comparison, the numbers of aneurysms in the unruptured and ruptured groups with either diffused or concentrated inflow jet were counted.
Statistical analyses
The minimal, average, and maximal WSS for both aneurysm and ostium were calculated (Table 2). The independent two-sample test was used for normal distribution variables to observe significant differences between the two aneurysm groups. For non-normal distribution variables, a Mann-Whitney rank sum test was employed to compare variations between unruptured and ruptured aneurysm groups. To identify any correlations between average WSS at the aneurysm and morphological features, the Pearson correlation coefficient was analyzed. The χ2 (Pearson uncorrected) test was used for the differences between simple and complex flow parameters of the two groups. The inflow jet was statistically analyzed for differences between unruptured and ruptured aneurysms. If the p value was less than 0.05, the results were considered statistically significant.
Table 2.
Comparison of hemodynamic variables between unruptured and ruptured aneurysms
| Unruptured (n=18) | Ruptured (n=24) | p-value | |
|---|---|---|---|
| Aneurysm | |||
| Minimal wall shear stress (Pa) | 3.25±1.53 | 3.56±3.77 | 0.43 |
| Average wall shear stress (Pa) | 5.94±3.02 | 6.50±7.81 | 0.50 |
| Maximal wall shear stress (Pa) | 20.22±10.89 | 22.47±24.84 | 0.54 |
| Ostium | |||
| Minimal wall shear stress (Pa) | 5.72±2.41 | 6.14±4.67 | 0.98 |
| Average wall shear stress (Pa) | 10.11±4.51 | 11.16±9.00 | 0.98 |
| Maximal wall shear stress (Pa) | 31.89±15.16 | 34.42±27.10 | 0.93 |
Values are presented as mean±standard deviation
RESULTS
Morphological comparison between unruptured and ruptured aneurysms
In Table 1, the observed morphological characteristics of the unruptured and ruptured aneurysm groups are shown. In general, the measured parameters had slightly higher values in the ruptured aneurysm group. The mean height of the unruptured aneurysm group was 12.26% smaller than that of the ruptured aneurysm group. In addition, the mean area of the ruptured aneurysms was 31.22% greater than that of unruptured aneurysms. Although, mean values of height, ostium diameter, aspect ratio, and aneurysm area tended to show differences between unruptured and ruptured groups, none of the differences achieved statistical significance.
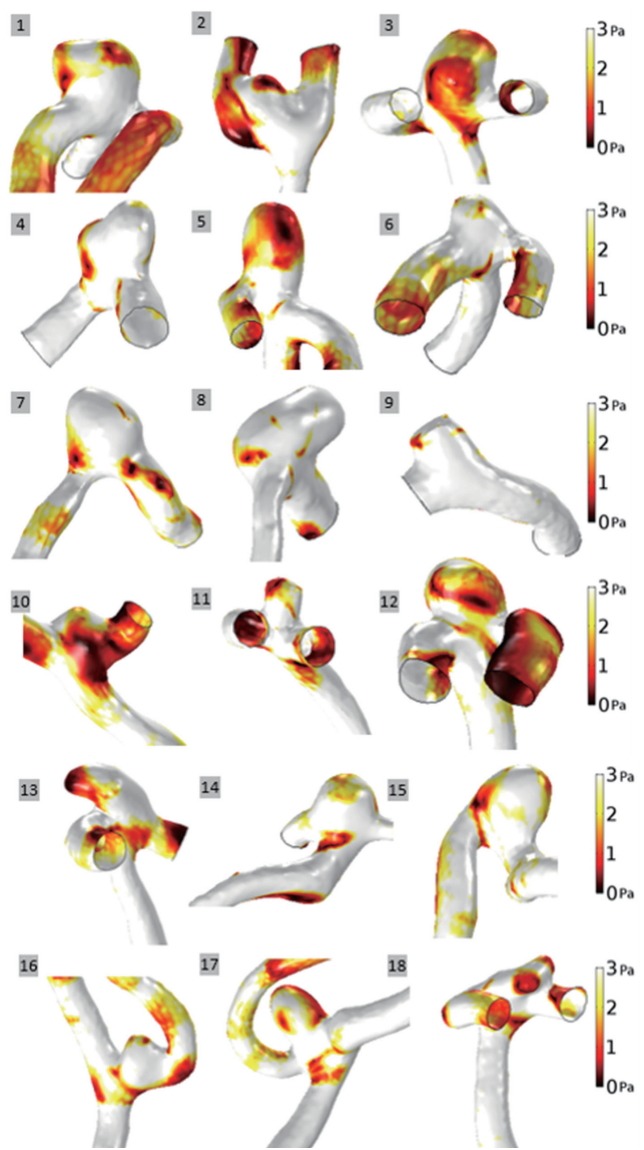
In Figs. 1 and 2, the WSS distributions for 18 unruptured and 24 ruptured aneurysms at end-diastole are shown. The shape and size parameters of the 18 unruptured aneurysm domes were variable (Fig. 1). Similarly, the shape and size of 24 ruptured aneurysm domes were also diverse (Fig. 2).
Fig. 1.
The wall shear stress distributions for 18 unruptured aneurysms at end-diastole.
Fig. 2.
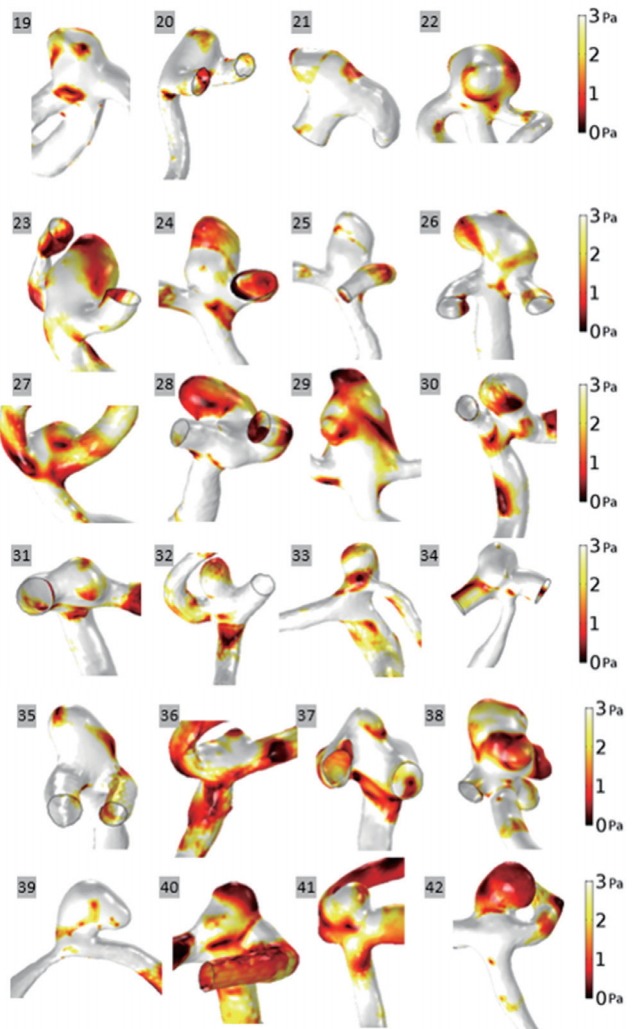
The wall shear stress distributions for 24 ruptured aneurysms at end-diastole.
WSS distributions
WSS values for both unruptured and ruptured aneurysm groups at end-diastole are represented with a scale bar which ranged from 0 to 3 Pa (Figs. 1 and 2). There was a tendency for aneurysms to have lower WSS values than arteries. In aneurysms, decreased WSS was focused at the tip or distributed around the entire dome. For example, decreased WSS was observed at the tip of the aneurysms: unruptured aneurysm No. 9 and ruptured aneurysm No. 35. In contrast, decreased WSS was found over the entire aneurysm dome in several instances: unruptured aneurysms Nos. 3 and 5, and ruptured aneurysms Nos. 24, 28, and 42. When unruptured and ruptured aneurysms were compared, unruptured aneurysms had a smooth and regular shape, whereas ruptured aneurysms had irregular shapes. Moreover, decreased WSS appeared at irregular regions of ruptured aneurysms, Nos. 29 and 38.
Quantitative comparison of WSS values
Minimal, average, and maximal WSS values were obtained to quantitatively compare the difference between unruptured and ruptured aneurysms. Minimal WSS was defined as the smallest value observed during the cardiac cycle, and maximal WSS was defined as the greatest value noted during the cardiac cycle. The average WSS was obtained as the mean value noted during the cardiac cycle. WSS values for both aneurysm groups are shown in Table 2. Overall, the minimal, average, and maximal WSS values of the ruptured group were higher than those of the unruptured group for both aneurysm and ostium measurements. At the aneurysm, the mean of minimal WSS values of the ruptured aneurysm group was 9.53% higher than that of the unruptured aneurysm group. Similarly, at the aneurysm, the mean of the average WSS of the ruptured aneurysm group was 9.42% higher than that of the unruptured aneurysm group. In the ruptured group, the mean of the maximal WSS was 11.12% higher than the unruptured group. However, the differences between the unruptured and ruptured groups for minimal, average, and maximal WSS values were not statistically significant.
At the ostium, average WSS was used to quantitatively compare WSS values between unruptured and ruptured groups. The average WSS at the ostium was obtained by calculating the WSS along the circumferential wall of aneurysm neck. The mean of minimal WSS values of the ruptured aneurysm group was 7.34% greater than values of the unruptured aneurysm group. The mean of average WSS values of the ruptured aneurysm group was 10.38% greater than the values of the unruptured aneurysm group. The mean of the maximal WSS value was 7.93% greater in the ruptured aneurysm group. None of these differences were found to be statistically significant.
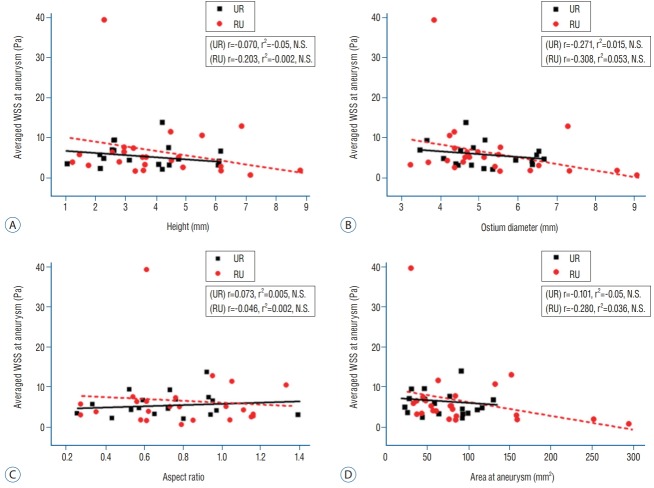
Morphological factors versus average WSS at aneurysms
Fig. 3 shows the interaction between hemodynamic and morphological parameters. We used the average WSS to indicate the overall trend of hemodynamic changes, and it was correlated with morphological factors. With the exception of the aspect ratio, morphological factors tended to show an increase as the average WSS decreased. However, as a result of linear regression analysis, this tendency was not statistically significant. For example, no correlation between average WSS and ostium diameter was observed in unruptured (r=-0.271 and r2=0.015) or ruptured aneurysms (r=-0.308 and r2=0.053) (Fig. 3B).
Fig. 3.
Scattergram with regression analysis of average WSS at unruptured and ruptured aneurysms. Average WSS at unruptured and ruptured aneurysms did not correlate with the height (A), ostium diameter (B), aspect ratio (C), or area of the aneurysms (D). WSS : wall shear stress, UR : unruptured aneurysm, RU : ruptured aneurysm, N.S. : not significant.
Flow patterns
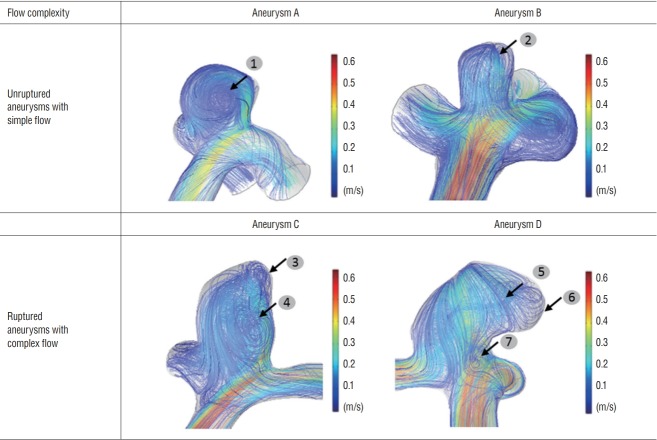
We counted the number of aneurysms exhibiting each flow pattern, and the statistical results of our flow complexity and inflow jet analysis are shown in Table 3. Of the 18 unruptured aneurysms, 14 aneurysms (78%) exhibited a simple flow, and four aneurysms showed a complex flow. All ruptured aneurysms showed a complex flow. Two examples are shown for each f low complexity in Fig. 4, which also shows the f low streamline and velocity profile. The velocity of unruptured and ruptured aneurysms at end-diastole was represented with a scale bar ranged from 0 to 0.6 m/s. The point where the recirculation occurred was indicated with an arrow.
Table 3.
Statistical analyses of flow patterns
| Unruptured | Ruptured | χ2 | p-value | |
|---|---|---|---|---|
| Flow complexity | 28.000 | <0.001 | ||
| Simple | 14 | 0 | ||
| Complex | 4 | 24 | ||
| Inflow jet | 8.823 | 0.004 | ||
| Diffused | 15 | 9 | ||
| Concentrated | 3 | 15 |
Fig. 4.
Representative cases of aneurysms with flow complexity. Top row (aneurysm A and B), unruptured aneurysms with simple flow; bottom row (aneurysm C and D), ruptured aneurysms with complex flow; recirculation zone marked with number and arrow. Two recirculation areas were involved in aneurysm C, and three recirculation zones were observed in aneurysm D.
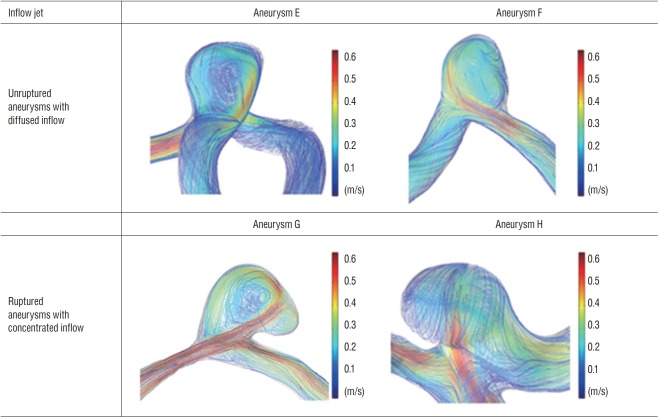
In Table 3, the numbers of aneurysms with either diffused or concentrated inflow jet were summarized. For unruptured aneurysms, 15 of 18 aneurysms (83%) showed diffused inflow, and the remaining three aneurysms showed a concentrated inf low jet. In contrast, 15 of 24 ruptured aneurysms (62%) showed a concentrated inflow jet. In Fig. 5, two examples of each inf low jet at end-diastole are shown using the velocity profile (ranged from 0 to 0.6 m/s) with the flow streamline. The examples of unruptured aneurysms with diffused inflow jet were shown as aneurysm E and F, and the examples of ruptured aneurysms with concentrated inflow jet were indicated as aneurysm G and H. Our analysis on flow complexity and inflow jet between two aneurysm groups revealed statistically significant differences with p <0.001 and p =0.004, respectively. Table 3 also shows the χ2 values which supported the significant differences between the two groups.
Fig. 5.
Representative cases of aneurysms with inflow jet. Top row (aneurysm E and F), unruptured aneurysms with diffused inflow; bottom row (aneurysm G and H), ruptured aneurysms with concentrated inflow. In aneurysm E and F, the flow spread immediately after blood flow entered. In aneurysm G and H, concentrated inflow was observed when the blood entered the dome of aneurysm.
DISCUSSION
Due to the variety of cerebral aneurysms and lack of information on aneurysm formation, there is limited understanding regarding the process of aneurysm pathogenesis [12]. In this study, we examined hemodynamic, morphological, and flow patterns between unruptured and ruptured ACoA aneurysms. There are four major findings of the present study. First, ruptured aneurysms tended to have higher WSS than unruptured aneurysms, although statistical significance was not reached. Second, ruptured aneurysms tended to have larger geometric size compared to unruptured aneurysms, although the differences did not achieve statistical significance. Third, no statistical correlation between the hemodynamic factor of WSS and various morphological factors was observed. Lastly, unruptured and ruptured aneurysms had significantly different flow complexity and inflow jet values.
Higher WSS for ruptured aneurysms
WSS is known to act parallel to the vessel wall and induces molecular biological responses. In addition, WSS is closely related to the formation of cerebral aneurysms by inducing deterioration of the blood vessel wall [22]. In this study, we compared the WSS between unruptured and ruptured aneurysms and found that domes of ruptured aneurysms tended to have higher minimal, average, and maximal WSS in comparison to domes of unruptured aneurysms (Table 2). A trend toward higher WSS was also observed at the ostium level in ruptured aneurysms compared to unruptured aneurysms. The mean values of WSS of ruptured aneurysms tended to be greater than those of unruptured aneurysms, but the differences were not statistically significant. We theorized that the lack of statistical significance was due to the small group size in our study.
Whether ruptured aneurysms have increased or decreased WSS in comparison to unruptured aneurysms still remains controversial [19]. Several previous studies have suggested that a ruptured aneurysm is associated with higher mean WSS [2,15], and that a region with maximal WSS appears around the point where the aneurysm rupture occurs [24]. Chien et al. [5] found that ruptured aneurysms had significantly higher WSS in the aneurysm sac compared to unruptured aneurysms. We conclude that further studies using larger groups are required to confirm the hypothesis that ruptured aneurysms have increased WSS compared to unruptured aneurysms.
Morphological and hemodynamic factors in aneurysm rupture
From previous work, WSS and aneurysm size ratio are known to be closely related. Xiang et al. [28] found that as the size ratio increases, the decreased WSS region becomes larger. Moreover, the flow pattern becomes more complex as the size ratio increases. In the present study, four morphological factors (height, ostium diameter, aspect ratio, and area of aneurysm) and the hemodynamic factor of average WSS at the aneurysm were measured to analyze the correlation between morphological and hemodynamic features. Although overall tendencies were observed, no statistical correlations were found (Fig. 3). According to our previous research on posterior communicating artery aneurysms, for ruptured aneurysms, the smallest aneurysm size had the highest WSS, and the lowest WSS was found in the largest ruptured aneurysm. Although the anatomic location was different, the present study of ruptured ACoA aneurysms showed the same pattern of WSS in relation to aneurysm size. The largest ruptured aneurysm (291.60 mm2) had the smallest WSS (0.93 Pa), and the smallest ruptured aneurysm (30.64 mm2) had the largest WSS (39.73 Pa). Interestingly, this tendency was not observed for unruptured aneurysms.
However, in the present study, the results of WSS were not statistically significant due to insufficient number of patients. Although there is a possibility that statistically insignificant results of morphological factors may have affected the insignificance of CFD results, there are a number of studies that explain no correlation between the significance of morphological factors and CFD results. For example, Xu et al. [30] compared morphological and hemodynamic factors between unruptured and ruptured aneurysm groups. In morphological comparison, the difference between two groups was not statistically significant. However, in hemodynamic comparison, the difference between two groups was statistically significant [30]. Therefore, it might be concluded that hemodynamic factors are independent of the morphological factors.
Flow patterns in aneurysms
Flow pattern, such as flow complexity, is known to be one of the most important risk factors in aneurysm rupture. Previous CFD studies have examined parameters such as stability, complexity of flow pattern, impingement region, and concentrated inf low jet in attempts to determine the risk of aneurysm rupture [2,4,8]. Sforza et al. [25] was able to examine images of aneurysms just one hour before they ruptured and found that the ruptured aneurysms were closely associated with complex flow and a concentrated inflow jet. Xiang et al. [28] confirmed that ruptured aneurysms had a more complex flow and more recirculation zones than unruptured aneurysms. Fukazawa et al. [8] also showed that a recirculation zone with low velocity was found near the rupture point where the decreased WSS was observed. In the present study, two or three recirculation zones were found at the ruptured aneurysm. As shown in Fig. 4, the point of occurrence was as follows : 1) the tip of the aneurysm where reduced WSS occurs, 2) the center of the aneurysm dome, and 3) the ostium. We found that a ruptured aneurysm was more likely to have complex flow and a concentrated inflow jet.
In our study, all 24 ruptured aneurysms had complex flow, but unruptured aneurysms could have either simple flow (14 of 18) or complex flow (4 of 18). Even though complex flow and concentrated inflow jet are the main characteristics of the ruptured group, these features also might be found in the unruptured group, as shown in Table 3. Because there is a possibility that unruptured aneurysms can rupture, it is not strange that unruptured aneurysms have features of ruptured aneurysms. One previous author has shown, however, that compared to the complex flow of a ruptured aneurysm, the recirculation zone of an unruptured aneurysm was smaller and had a less dense inflow jet [4].
The flow pattern was also classified according to the morphological characteristics (daughter sac, lobular contour, and aneurysmal bleb). In particular, complex flow was significantly observed in daughter sac (p =0.011). The concentrated and diffused inflow jet showed no significant difference. We conclude that further studies are required to elucidate the primary cause and possible mechanisms of flow patterns related to aneurysm rupture and morphological characteristics.
Consideration during CFD analyses
This study had some limitations. First, when measuring the morphological factors, a deviation might occur depending on how the 3D geometry model is rotated. Therefore, the measurements of height of aneurysm and ostium diameter may have caused deviations in calculating aspect ratio, which might have resulted in statistically insignificant differences between unruptured and ruptured aneurysms. Second, although 3D rotational angiography was used to accurately obtain the shape of Acom aneurysms, only dominant A1 flow images could be obtained. The bilateral flow, the characteristics of Acom aneurysm, could not be reflected in 3D image. Third, patient-specific geometry was used for the analyses, but patient-specific boundary conditions were not used in the study because obtaining boundary conditions, i.e., flow velocity, flow rate, or inlet and outlet pressure, for each patient was difficult due to the ACoA location. This difference might have caused a deviation in the analysis results. Moreover, patientspecific flow rate could not be obtained because the patients with ruptured aneurysms were in emergency situations. Fourth, the CFD simulations were analyzed based on the assumption that blood behaves as Newtonian flow. Due to a linear relationship between shear stress and shear rate, Newtonian blood f low has a constant viscosity value. In contrast, non-Newtonian blood is a shear-thinning f luid, in which blood viscosity varies depending on shear rate [6,9]. Thus, flow analyses should have been done using patient-specific, non-Newtonian blood viscosity. In future research, patient-specific CFD simulations will be analyzed using non-Newtonian viscosities obtained for each patient. Lastly, there was no statistically significant association between average WSS and any of the morphological parameters, which we postulate is due to the small number of patients in our study. Further studies are needed to see if the trends noted in this comparison can reach significance with larger groups. However, as shown in Table 3, highly significant differences between unruptured and ruptured aneurysm groups were noted for both flow complexity and inflow jet.
CONCLUSION
Ruptured aneurysm had higher average WSS and larger geometric size of an aneurysm in this study. However, a comparison between average WSS and morphological parameters, including height, ostium diameter, aspect ratio, and area of aneurysm, did not achieve statistical significance. Our analysis of f low pattern has shown that ruptured aneurysms had complex f low and concentrated inf low jet, whereas unruptured aneurysms tended to have simple flow and a diffused inflow jet.
Acknowledgments
This research was supported by Basic Science Research Program (NRF-2016R1D1A3B03935132, NRF-2016R1C1B2014747, and NRF-2017R1A4A1015681) by the National Research Foundation of Korea (NRF) funded by the Ministry of Education.
Footnotes
No potential conflict of interest relevant to this article was reported.
INFORMED CONSENT
This type of study does not require informed consent.
References
- 1.Castro MA, Putman CM, Cebral JR. Patient-specific computational fluid dynamics modeling of anterior communicating artery aneurysms: a study of the sensitivity of intra-aneurysmal flow patterns to flow conditions in the carotid arteries. AJNR Am J Neuroradiol. 2006;27:2061–2068. [PMC free article] [PubMed] [Google Scholar]
- 2.Castro MA, Putman CM, Sheridan MJ, Cebral JR. Hemodynamic patterns of anterior communicating artery aneurysms: a possible association with rupture. AJNR Am J Neuroradiol. 2009;30:297–302. doi: 10.3174/ajnr.A1323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Cebral JR, Castro MA, Burgess JE, Pergolizzi RS, Sheridan MJ, Putman CM. Characterization of cerebral aneurysms for assessing risk of rupture by using patient-specific computational hemodynamics models. AJNR Am J Neuroradiol. 2005;26:2550–2559. [PMC free article] [PubMed] [Google Scholar]
- 4.Cebral JR, Mut F, Weir J, Putman CM. Association of hemodynamic characteristics and cerebral aneurysm rupture. AJNR Am J Neuroradiol. 2011;32:264–270. doi: 10.3174/ajnr.A2274. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Chien A, Tateshima S, Castro M, Sayre J, Cebral J, Viñuela F. Patientspecific flow analysis of brain aneurysms at a single location: comparison of hemodynamic characteristics in small aneurysms. Med Biol Eng Comput. 2008;46:1113–1120. doi: 10.1007/s11517-008-0400-5. [DOI] [PubMed] [Google Scholar]
- 6.Errill EW. Rheology of blood. Physiol Rev. 1969;49:863–888. doi: 10.1152/physrev.1969.49.4.863. [DOI] [PubMed] [Google Scholar]
- 7.Fan J, Wang Y, Liu J, Jing L, Wang C, Li C, et al. Morphological-hemodynamic characteristics of intracranial bifurcation mirror aneurysms. World Neurosurg. 2015;84:114–120.e2. doi: 10.1016/j.wneu.2015.02.038. [DOI] [PubMed] [Google Scholar]
- 8.Fukazawa K, Ishida F, Umeda Y, Miura Y, Shimosaka S, Matsushima S, et al. Using computational fluid dynamics analysis to characterize local hemodynamic features of middle cerebral artery aneurysm rupture points. World Neurosurg. 2015;83:80–86. doi: 10.1016/j.wneu.2013.02.012. [DOI] [PubMed] [Google Scholar]
- 9.Gijsen FJ, van de Vosse FN, Janssen JD. The influence of the non-Newtonian properties of blood on the flow in large arteries: steady flow in a carotid bifurcation model. J Biomech. 1999;32:601–608. doi: 10.1016/s0021-9290(99)00015-9. [DOI] [PubMed] [Google Scholar]
- 10.Horiuchi T, Tanaka Y, Hongo K. Surgical treatment for aneurysmal subarachnoid hemorrhage in the 8th and 9th decades of life. Neurosurgery. 2005;56:469–475. doi: 10.1227/01.neu.0000153926.67713.b8. discussion 469-475. [DOI] [PubMed] [Google Scholar]
- 11.Jansen IG, Schneiders JJ, Potters WV, van Ooij P, van den Berg R, van Bavel E, et al. Generalized versus patient-specific inflow boundary conditions in computational fluid dynamics simulations of cerebral aneurysmal hemodynamics. AJNR Am J Neuroradiol. 2014;35:1543–1548. doi: 10.3174/ajnr.A3901. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jou LD, Lee DH, Morsi H, Mawad ME. Wall shear stress on ruptured and unruptured intracranial aneurysms at the internal carotid artery. AJNR Am J Neuroradiol. 2008;29:1761–1767. doi: 10.3174/ajnr.A1180. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Kojima M, Irie K, Fukuda T, Arai F, Hirose Y, Negoro M. The study of flow diversion effects on aneurysm using multiple enterprise stents and two flow diverters. Asian J Neurosurg. 2012;7:159–165. doi: 10.4103/1793-5482.106643. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Le WJ, Zhu YQ, Li MH, Yan L, Tan HQ, Xiao SM, et al. New method for retrospective study of hemodynamic changes before and after aneurysm formation in patients with ruptured or unruptured aneurysms. BMC Neurol. 2013;13:166. doi: 10.1186/1471-2377-13-166. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Lin N, Ho A, Charoenvimolphan N, Frerichs KU, Day AL, Du R. Analysis of morphological parameters to differentiate rupture status in anterior communicating artery aneurysms. PLoS One. 2013;8:e79635. doi: 10.1371/journal.pone.0079635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Lin N, Ho A, Gross BA, Pieper S, Frerichs KU, Day AL, et al. Differences in simple morphological variables in ruptured and unruptured middle cerebral artery aneurysms. J Neurosurg. 2012;117:913–919. doi: 10.3171/2012.7.JNS111766. [DOI] [PubMed] [Google Scholar]
- 17.Lu G, Huang L, Zhang XL, Wang SZ, Hong Y, Hu Z, et al. Influence of hemodynamic factors on rupture of intracranial aneurysms: patientspecific 3D mirror aneurysms model computational fluid dynamics simulation. AJNR Am J Neuroradiol. 2011;32:1255–1261. doi: 10.3174/ajnr.A2461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Ma B, Harbaugh RE, Raghavan ML. Three-dimensional geometrical characterization of cerebral aneurysms. Ann Biomed Eng. 2004;32:264–273. doi: 10.1023/b:abme.0000012746.31343.92. [DOI] [PubMed] [Google Scholar]
- 19.Meng H, Tutino VM, Xiang J, Siddiqui A. High WSS or low WSS? Complex interactions of hemodynamics with intracranial aneurysm initiation, growth, and rupture: toward a unifying hypothesis. Am J Neuroradiol. 2014;35:1254–1262. doi: 10.3174/ajnr.A3558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Metaxa E, Tremmel M, Natarajan SK, Xiang J, Paluch RA, Mandelbaum M, et al. Characterization of critical hemodynamics contributing to aneurysmal remodeling at the basilar terminus in a rabbit model. Stroke. 2010;41:1774–1782. doi: 10.1161/STROKEAHA.110.585992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Morales HG, Larrabide I, Geers AJ, Aguilar ML, Frangi AF. Newtonian and non-Newtonian blood flow in coiled cerebral aneurysms. J Biomech. 2013;46:2158–2164. doi: 10.1016/j.jbiomech.2013.06.034. [DOI] [PubMed] [Google Scholar]
- 22.Papaioannou TG, Karatzis EN, Vavuranakis M, Lekakis JP, Stefanadis C. Assessment of vascular wall shear stress and implications for atherosclerotic disease. Int J Cardiol. 2006;113:12–18. doi: 10.1016/j.ijcard.2006.03.035. [DOI] [PubMed] [Google Scholar]
- 23.Raghavan ML, Ma B, Harbaugh RE. Quantified aneurysm shape and rupture risk. J Neurosurg. 2005;102:355–362. doi: 10.3171/jns.2005.102.2.0355. [DOI] [PubMed] [Google Scholar]
- 24.Russell JH, Kelson N, Barry M, Pearcy M, Fletcher DF, Winter CD. Computational fluid dynamic analysis of intracranial aneurysmal bleb formation. Neurosurgery. 2013;73:1061–1068. doi: 10.1227/NEU.0000000000000137. discussion 1068-1069. [DOI] [PubMed] [Google Scholar]
- 25.Sforza DM, Putman CM, Scrivano E, Lylyk P, Cebral JR. Blood-flow characteristics in a terminal basilar tip aneurysm prior to its fatal rupture. AJNR Am J Neuroradiol. 2010;31:1127–1131. doi: 10.3174/ajnr.A2021. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Skodvin TØ, Johnsen LH, Gjertsen Ø, Isaksen JG, Sorteberg A. Cerebral aneurysm morphology before and after rupture: nationwide case series of 29 aneurysms. Stroke. 2017;48:880–886. doi: 10.1161/STROKEAHA.116.015288. [DOI] [PubMed] [Google Scholar]
- 27.Taylor TN. The medical economics of stroke. Drugs 54 Suppl. 1997;3:51–57. doi: 10.2165/00003495-199700543-00008. discussion 57-58. [DOI] [PubMed] [Google Scholar]
- 28.Xiang J, Natarajan SK, Tremmel M, Ma D, Mocco J, Hopkins LN, et al. Hemodynamic-morphologic discriminants for intracranial aneurysm rupture. Stroke. 2011;42:144–152. doi: 10.1161/STROKEAHA.110.592923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Xiang J, Tutino VM, Snyder KV, Meng H. CFD: computational fluid dynamics or confounding factor dissemination? The role of hemodynamics in intracranial aneurysm rupture risk assessment. AJNR Am J Neuroradiol. 2014;35:1849–1857. doi: 10.3174/ajnr.A3710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Xu J, Yu Y, Wu X, Wu Y, Jiang C, Wang S, et al. Morphological and hemodynamic analysis of mirror posterior communicating artery aneurysms. PLoS One. 2013;8:e55413. doi: 10.1371/journal.pone.0055413. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Zeng Z, Kallmes DF, Durka MJ, Ding Y, Lewis D, Kadirvel R, et al. Hemodynamics and anatomy of elastase-induced rabbit aneurysm models: similarity to human cerebral aneurysms? AJNR Am J Neuroradiol. 2011;32:595–601. doi: 10.3174/ajnr.A2324. [DOI] [PMC free article] [PubMed] [Google Scholar]