A Novel Classification Method using Effective Neural Network and Quantitative Magnetization Transfer Imaging of Brain White Matter in Relapsing Remitting Multiple Sclerosis

Abstract

Background:

Quantitative Magnetization Transfer Imaging (QMTI) is often used to quantify the myelin content in multiple sclerosis (MS) lesions and normal appearing brain tissues. Also, automated classifiers such as artificial neural networks (ANNs) can significantly improve the identification and classification processes of MS clinical datasets.

Objective:

We classified patients with relapsing-remitting multiple sclerosis (RRMS) from healthy subjects using QMTI and T1 longitudinal relaxation time data of brain white matter, then the performance of three ANN-based classifiers have been investigated.

Materials and Methods:

The input features of ANN algorithms, including multilayer perceptron (MLP), radial basis function (RBF) and ensemble neural networks based on Akaike information criterion (ENN-AIC) were extracted in the form of QMTI and T1 mean values from parametric maps. The ANNs quantitative performance is measured by the standard evaluation of confusion matrix criteria.

Results:

The results indicate that ENN-AIC-based classification method has achieved 90% accuracy, 92% sensitivity and 86% precision compared to other ANN models. NPV, FPR and FDR values were found to be 0.933, 0.125 and 0.133, respectively, according to the proposed ENN-AIC model. A graphical representation of how to track actual data by the predictive values derived from ANN algorithms, was also presented.

Conclusion:

It has been demonstrated that ENN-AIC as an effective neural network improves the quality of classification results compared to MLP and RBF.In addition, this research provides a new direction to classify a large amount of quantitative MRI data that can help the physician in a correct MS diagnosis.

Introduction

MS is an autoimmune neurological disorder, which affects the central nervous system (CNS) and leads to progressive disability in young adults. The main feature of MS disease is the presence of focal demyelinated lesions referred to as plaques and are visualized on conventional MRI images [1,2]. Currently, attention is mainly focused on advanced MRI techniques by which they more accurately reveal the underlying pathological substrates occurred in lesions and normal appearing CNS tissues [3]. The use of methods such as diffusion-weighted and diffusion-tensor imaging (DWI and DTI), proton MRI spectroscopy (MRS), quantitative magnetization transfer imaging (QMTI), functional MRI (fMRI), relaxometry and myelin water fraction (MWF) measurements are considered as promising tools with high sensitivity and specificity to determine the microscopic progression of pathologies in the brain parenchyma and the spinal cord [4-6].

QMTI is one of these advanced MRI methods based on the interactions between free protons in the water environment and protons bound to macromolecular structures found mostly in the myelin membrane [7]. It has been proven that QMTI provides an indirect assessment of tissue matrix integrity in the course of disease evolution [8,9].

The ability of this technique to quantify the myelin content is mainly expressed by the MTR which is a global measurement .It has been proven that other MT parameters including Ksat and T1_sat along with the measurement of T1 longitudinal relaxation time have a better performance of the detecting neuron degeneration process [10,11]. Investigating the extent of microscopic lesion burden in the normal appearing white matter (NAWM) using QMTI-T1 parameters allows more precise monitoring of pathological abnormalities such as inflammation, demyelination, gliosis, edema, remyelination and axonal loss. technique allows for a better assessment of therapeutic interventions [12,13].

On the other hand, researchers have always been interested in discovering patterns of prediction and scientific relationships in a large volume of data. Data mining by utilizing methods from statistics, neural networks and machine learning on the sophisticated database can effectively turn them into functional information [14]. One of the most important approaches in the field of data mining is the classification of data that has led to the introduction of various types of classifiers including: support vector machines (SVM), Bayesian classifier, K-nearest neighbor (KNN) method, artificial neural networks and genetic classifiers [15-17]. This way, with the given quantitative MRI datasets obtained from brain tissues, the need to use automatic classification methods is felt more than ever [18]. ANNs with the ability to model highly nonlinear systems with unknown or complex relationships between their inputs can provide a classification decision for existing data with less sensitivity to noise and outliers [19] The objective of this paper is to investigate the utility of three ANN algorithms, including MLP, RBF and ENN-AIC to classify RRMS patients from healthy subjects. This approach is generally based on: (1) feature extraction to extract QMTI-T1 parameters that distinguish pathological white matter tissues from healthy ones; (2) RRMS and healthy subjects’ classification to construct three automated classifiers based on ANNs along with evaluating and comparing their performance. We also focus mainly on the effective neural network model based on the AIC, which is used in ENN design to optimize this classifier. Although similar studies have been carried out using ANNs on the MRI data of the brain [20,21] and especially in the context of ANNs for MS lesion segmentation [22-24], to the best of our knowledge, this is the first work introducing ANN models as reliable classifiers in the field of QMTI and T1 relaxometry.

Material and Methods

The objective of this research is to determine the status of the subjects in terms of RRMS and healthy based on QMTI-T1 measurements and the use of ANN algorithms. For this purpose, three different types of neural networks were used and their performance was compared with each other to determine the highly precise classifier. General analysis flow of this ANNs-based classification is divided into five main steps: image acquisition, Image pre-processing, image processing-feature extraction, classification and evaluation (Figure 1).

Figure1.

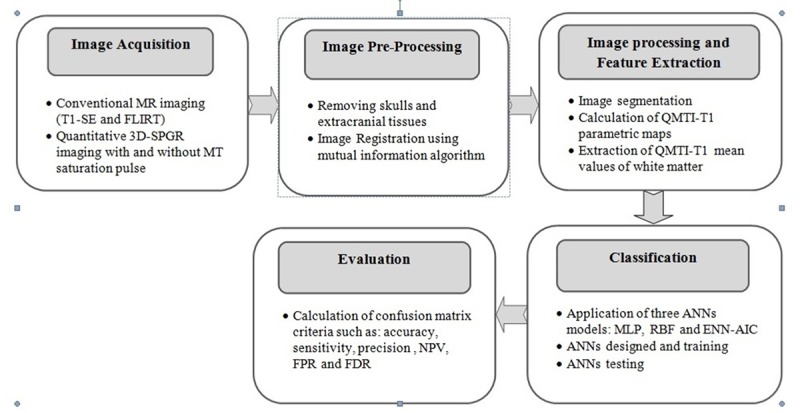
A general block diagram of the ANNs based classification procedure

Patients and MR Data Acquisition

The dataset from MR imaging of healthy controls and patients with clinically definite RRMS from the neurological research center of Tehran University of Medical Science were studied. The participants’ demographics are also reported in Table 1. The study was approved by the local ethics committee at Imam Hospital, department of radiology and imaging in Tehran, Iran.

Table 1.

Participants’ Demographics.

	Male/Female	Age	Mean EDSS Values	Mean Disease Duration (years)	Number of MS Plaques
Healthy Controls	9/21	30 (21-41)	------	------	------
RRMS Patients	11/19	30.2 (20-45)	2	5	134

MR imaging was performed with a 1.5 Tesla MR whole body GE-MRI imager using the standard transmit/receive quadrature head coil. Conventional MR imaging protocols included T1 weighted spin echo (T1-SE) (400ms/9ms/1 [TR/TE/excitation]) and FLAIR (9000ms/95ms/2140ms TR/TE/TI]) were obtained. Two series of 3D spoiled gradient echo in steady state (SPGR) pulse sequences were acquired with/without MT saturation pulse and used for T1 longitudinal relaxation time measurement and QMTI analysis. The characteristics of these two 3D-SPGR pulse sequences are respectively as follows:

Two series of four 3D-SPGR scans with TR/TE = 27ms/5ms and variable flip angles of α = 5°, 15°, 30° and 60°, one with MT pulse operation and another one without it were acquired. MT saturation pulse was 1.6 KHz below the free water frequency with the Fermi envelope of 8 ms duration and 670° pulse power. Both quantitative and clinical MR images covered the same volume of the brain along the axial plane with identical geometric parameters (FOV = 25cm, matrix size 256×192, slice thickness = 4mm, without any gap and number of slices = 27). The information was obtained on a thick slab of the brain parenchyma consisting of twenty-seven consecutive slices with a thickness of 4mm, covering almost the entire brain, especially those areas of white matter that MS plaques and myelin membrane destruction appears predominantly there. The total examination time for both clinical and quantitative imaging was about 20 minutes.

Image Pre-processing

The image preprocessing was conducted as follows: (1) removal of skulls and other tissues from both quantitative and clinical data sets (2) the image motion correction by registering images on a reference pattern. High T1 contrast and acceptable SNR in 3D-SPGR pulse sequence are obtained when the excitation flip angle is held comparable to TR [25]. Therefore, among eight 3D-SPGR data sets, the set of 3D-SPGR images with a flip angle of 30° and TR=27ms without MT saturation pulse was selected as reference images for the registration process. Then, all clinical and quantitative data sets were registered to this reference template using the mutual information registration tool in FSL software.

Image Processing

Image Segmentation

Masks generation representing brain white matter, gray matter and CSF was provided based on high T1 contrast 3D-SPGR reference images under flip angle of 30° and TR=27ms without MT saturation pulse. Only white matter masks were used to calculate QMTI-T1 mean values from parametric maps (Figure 2). For patients, MS plaques were identified as a region of interest (ROI) by an experienced radiologist on FLAIR and T1-weighted scans. Afterwards, the pixels belonging to the plaques were removed from the white mater masks in each RRMS patient, resulting in a pure NAWM volume.

Figure2.

A sample of white matter masks for a healthy subject

QMTI-T1 Maps Calculation

T1 and T1_sat maps reconstruction on a pixel basis approach was performed using 3D-SPGR images at flip angles of α = 5°, 15°, 30°, 60° with constant TR parameter under MT saturation pulse off and on, respectively (Figure 3 (b, c)). A fitting procedure according to Eqs 1 and 2 are applied to the 3D-SPGR measured signal intensities at different flip angles to estimate T1 and T1_sat values as follows:

Figure3.

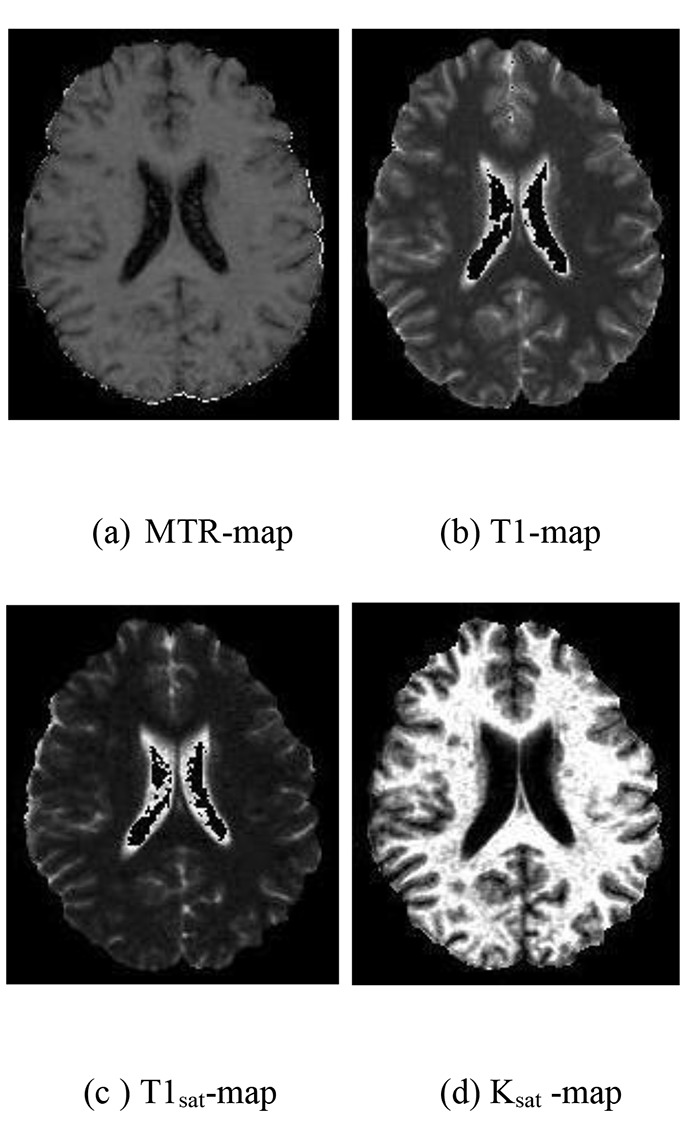
QMTI-T1 parametric maps for a RRMS patient

$\mathrm{SI}=M_0(1-e^{\mathrm{-TR}/\mathrm{T1}})[\mathrm{sin\; \alpha }/(1-{\mathrm{cos\; \alpha e}}^{\mathrm{-TR}/\mathrm{T1}}\left)\right]$ (1)

M0 in Eq.1 should be replaced by Msat/M0 and T1 parameter should be changed to T1_sat for T1_sat map calculation.

$\mathrm{SI}=\frac{M_S}{M_0}(1-e^{\mathrm{-TR}/\mathrm{T1}}\mathrm{sat})[\mathrm{sin\; \alpha }/(1-{\mathrm{cos\; \alpha e}}^{\mathrm{-TR}/\mathrm{T1}}\mathrm{sat}\left)\right]$ (2)

MTR maps were calculated using registered images with and without MT saturation pulse at flip angle 5° according to the following equation: MTR=[M₀-M_S)/M₀]×100 (3)

M0 and MS are the signal intensities of the particular pixel in the absence and presence of MT saturation pulse, respectively (Figure 3).

K_sat maps (Figure 3) were derived using a pixel by pixel analysis from the MTR and T1_sat maps with the below expression:

K_SAT=MTR/T1_SAT (4)

Feature Extraction

At first, the average of each of the MT parameters and T1 relaxation time value was assigned to the total volume of segmented white matter. Later, the input features of the classification algorithms under ANN were calculated and extracted in the form of mean values of MTR, K_sat, T1_sat and T1 relaxation time from parametric maps (Table 2).

Table 2.

Training data set for ANNs modeling.

Sample Numbers	MTR (%)	Ksat (s-1)	T1sat (ms)	T1 (ms)	RRMS and normal Definition for ANN modelsRRMS:50Normal: 0
1	55.05	1.495	385.10	635.14	0
2	55.80	1.381	355.38	694.62	0
3	55.09	1.497	361.62	645.50	0
4	52.10	1.095	428.66	760.56	50
5	54.68	1.205	390.55	698.15	50
6	53.35	1.408	496.22	826.52	50
7	54.66	1.182	466.02	774.27	50
8	55.27	1.174	433.15	760.95	50
9	55.52	1.419	394.74	656.10	50
10	54.60	1.089	484.22	775.40	50
11	53.27	1.210	482.05	790.67	50
12	54.78	1.405	458.29	715.42	50
13	54.84	1.333	421.21	724.17	50
14	52.02	1.179	454.94	732.42	50
15	52.42	1.070	388.95	695.55	50
16	52.01	1.090	487.33	780.03	50
17	55.58	1.322	397.88	689.30	50
18	54.88	1.400	392.40	687.29	50
19	53.20	1.202	453.02	772.46	50
20	56.38	1.409	390.74	692.77	0
21	56.18	1.431	384.60	672.85	0
22	55.90	1.493	366.65	644.80	0
23	55.40	1.385	390.85	695.67	0
24	56.41	1.425	358.27	632.17	0
25	56.14	1.430	385.11	645.95	0
26	56.01	1.458	378.80	657.43	0
27	56.02	1.421	387.33	638.75	0
28	56.47	1.478	383.20	660.64	0
29	56.00	1.478	373.80	641.18	0
30	54.75	1.422	379.67	646.99	0
31	54.92	1.271	496.85	788.45	50
32	55.05	1.319	427.60	711.51	50
33	52.05	1.077	425.33	730.78	50
34	52.08	1.0335	396.76	691.20	50
35	54.80	1.320	424.37	692.50	50
36	52.47	1.072	490.40	854.47	50
37	54.82	1.185	455.08	743.68	50
38	54.85	1.415	491.41	855.37	50
39	53.30	1.091	493.71	824.51	50
40	52.01	1.315	468.00	727.15	50
41	54.55	1.085	462.05	770.47	50
42	52.12	1.180	450.95	778.62	50
43	55.04	1.276	436.16	714.40	50
44	53.77	1.326	488.45	866.25	50
45	55.00	1.498	359.37	631.82	0
46	55.15	1.388	395.82	690.52	0
47	55.18	1.398	392.74	685.43	0
48	55.27	1.441	375.86	665.63	0
49	55.60	1.448	366.16	630.11	0
50	55.90	1.454	374.82	686.25	0
51	55.56	1.488	384.80	687.20	0
52	55.82	1.391	388.76	688.80	0
53	55.02	1.458	370.58	627.22	0
54	55.47	1.447	352.15	690.25	0
55	55.11	1.459	373.66	659.28	0
56	56.03	1.460	375.68	674.67	0
57	56.06	1.411	360.55	674.82	0
58	55.00	1.427	366.00	675.74	0
59	56.23	1.436	378.75	661.31	0
60	56.05	1.427	383.35	691.65	0

Using Artificial Neural Networks

An ANN is a mathematical model which has the same function as a biological neuron and depending on the system complexity, is composed of several neuron layers with weighted interconnections. These weights can be changed and optimized by a training algorithm, consequently, the neural network behaves appropriately in modelling nonlinear statistical data [26,27]. Since the relationship between pathological changes in brain tissue and RRMS is nonlinear and unknown, neural networks can help diagnose the disease. In this study, three kinds of ANNs were utilized as classifiers for RRMS diagnosis which will be referred as follows:.

Multilayer Perceptron (MLP) Neural Network

One of the main existing neural models is the MLP model that simulates the behavior of the brain network and the propagation of the signal in it. MLP algorithm can have several hidden layers in addition to the input and output ones for which neurons connected to all neurons of previous and subsequent layers in each layer; nonetheless, there is no connection between neurons of a same layer. It trains a neural network based on a kind of supervised learning technique which is known as back propagation. MLP is widely used for pattern classification, recognition, prediction and approximation [28].

Radial Basis Function (RBF) Neural Network

RBF neural networks have the same pattern as MLP, with a difference in which RBF algorithm, neurons as processor elements are focused on a particular position which is modelled through radial functions. RBF neural networks often have a quick learning and preparation processes and are more regulated by focusing neurons on a specific functional range. They have many uses, including function approximation, time series prediction, classification and system control [29,30].

Ensemble Neural Network based on Akaike Information Criterion (ENN-AIC)

An ensemble neural network is made up of a limited number of component neural networks which are all trained independently; each component creates an output data from the input data sets. Afterwards, to get a better result, these output data are combined together. In this way, the generalization capability for an artificial neural network model becomes possible. ENNs depend on the diversity and accuracy of the component networks which can provide the correct outputs based on highly non-linear experimental data. The main approach of the ENN is to reduce the mean square error (MSE) of each component neural network, which can lead to a complicated ENN and an increase in computing time as well as over-fitting [31,32]. In order to overcome these problems, an ensemble neural network model can be provided based on AIC. The AIC determines an optimal model among several competing models and estimate its relative quality for a given dataset. The AIC application for ENN is such that it initially reduces the error of each ANN component and then adjusts their contributions to the ENN by using the AIC-based weighting [33]. Three assumptions are considered as follows: firstly, datasets extracted from one main process, secondly, the sufficient sample size, and finally multivariate normal distribution of parameter estimators. Based on these criteria, AIC looks for a model that more precisely fits to the truth [34].

Neural Networks Designing and Training

A total of 60 samples was collected and analyzed. Each sample consisted of three mean values for QMTI parameters (MTR, Ksat and T1_sat) and one mean value associated with T1 longitudinal relaxation time parameter. Datasets were prepared by healthy subjects and RRMS patients’ image acquisition and used as the ANNs training-testing datasets (Table 2). Practically only 50 of 60 samples were used in practice to train and test the ANN models. The output of the neural network was set to 50 for the RRMS patients and zero for the healthy subjects.

The data were divided into two groups, which included data related to the training of the neural networks and data related to the testing of the neural networks. First, a training dataset was used to adjust the weights. Then, the test dataset was used to evaluate its performance. To train the neural network, the data obtained from QMTI and T1 relaxometry for brain white matter were divided into six parts of ten. Then, each time, 5 parts for training and 1 part for the test were given to the neural networks. This process was performed for 60 healthy and patient data (Table 3). We considered the threshold of 25 for determination. If the propagation value obtained from the neural network was greater than 25, it was considered as RRMS patient and if less, it was considered healthy.

Table 3.

Training-Testing Partition Pairs.

Partition Pairs	Training Set	Testing Set
1	Partition {1,2,3,4,5}	Partition {6}
2	Partition {1,2,3,4,6}	Partition {5}
3	Partition {1,2,3,5,6}	Partition {4}
4	Partition {1,2,4,5,6}	Partition {3}
5	Partition {1,3,4,5,6}	Partition {2}
6	Partition {2,3,4,5,6}	Partition {1}

Results

This research has developed an approach to classify RRMS patients from healthy subjects by using QMTI-T1 dataset. Initially, features were extracted by analyzing QMTI-T1 data of normal and pathologic white matter. Then, three ANN models including MLP, RBF and ENN-AIC were applied to these QMTI-T1 features derived from each sample. The estimated Output Labels of each model for existing samples are given in Table 4.

Table 4.

Estimated Output Labels from MLP, RBF and ENN-AIC models for participants

Sample Numbers	MLP	RBF	ENN-AIC	Normal and Patient definition
1	-0.01451	-0.00658	-4.6E-05	0
2	0.00181	0.02574	0.006129	0
3	-0.05406	-0.00960	-0.00062	0
4	-0.02341	0.11096	0.022492	50
5	-0.09248	0.04496	42.68706	50
6	-0.06720	0.19317	38.40058	50
7	-0.05528	0.13914	49.96256	50
8	-0.00923	0.67417	51.84795	50
9	-0.07156	0.32359	39.46159	50
10	50.00000	0.14848	29.73741	50
11	12.50000	36.36364	40.61062	50
12	12.50000	53.63630	15.36948	50
13	50.00000	29.62500	55.06200	50
14	50.00000	36.38080	40.60829	50
15	50.00000	28.63400	43.06204	50
16	12.50000	36.20730	37.20354	50
17	12.50000	29.07280	40.61062	50
18	49.94840	34.60870	34.57622	50
19	12.50000	30.86960	27.73782	50
20	35.21211	28.69410	0.61062	0
21	3.66E-13	2.2E-06	18.22890	0
22	38.55434	-7.9E-07	16.59923	0
23	35.16543	34.84458	31.81818	0
24	42.21847	-7.9E-07	21.68982	0
25	42.21760	44.44444	13.75943	0
26	42.21847	-7.7E-07	12.80289	0
27	42.21847	44.44444	1.935599	0
28	42.21847	42.94037	5.987599	0
29	42.21847	-5.88861	22.68833	0
30	51.38184	44.44441	13.81829	0
31	10.08353	33.75715	50.00000	50
32	30.34264	16.79689	28.57143	50
33	30.34264	20.05657	45.05263	50
34	10.08353	20.05657	21.05263	50
35	30.34264	16.79698	49.99518	50
36	10.08353	19.21221	41.78947	50
37	30.34264	16.79689	28.57370	50
38	50.45523	30.86669	21.05263	50
39	51.38184	16.79689	28.57143	50
40	50.00007	33.75715	50.00000	50
41	50.00021	49.98613	47.82543	50
42	50.00007	48.22301	52.05172	50
43	50.00021	47.85065	38.72384	50
44	4.68E-05	52.68255	29.15772	50
45	49.99978	1.862144	1.55265	0
46	49.96495	43.07934	22.05158	0
47	0.44288	43.07933	5.16500	0
48	18.00028	1.86214	17.36665	0
49	0.000238	-1.37591	9.94998	0
50	2.655436	-0.00012	32.05158	0
51	2.598292	0.00620	12.51167	0
52	0.00268	-0.03770	11.66926	0
53	-1.8E-05	0.01030	6.23249	0
54	2.59829	-0.15340	5.11669	0
55	2.59829	-0.06380	6.69258	0
56	-1.8E-05	-0.26530	0.87901	0
57	0.00111	-0.19170	9.25879	0
58	2.59829	-0.15700	15.87901	0
59	2.59829	-0.02220	6.23249	0
60	0.00041	-0.20450	17.90100	0

The performance of the proposed ANN algorithms for the best classification task was evaluated in terms of confusion matrix criteria such as accuracy, sensitivity and precision together with Negative Predictive Value (NPV), False Positive Rate (FPR) and False Discovery Rate (FDR). Precision is ,moreover, recognized under the name of the Positive Predictive Value (PPV). Higher accuracy, sensitivity, precision and NPV together with lower FPR and FDR indicate good classification of RRMS patients from healthy volunteers. The summary of the ANNs performance is shown in Table 5. Their equations are as follows:

Table 5.

Confusion matrix measurements of three ANN algorithms.

	MLP		RBF		ENN-AIC
	RRMS	Normal	RRMS	Normal	RRMS	Normal
RRMS	16	14	16	14	26	4
Normal	11	19	8	22	2	28
Accuracy	0.583		0.633		0.900
Sensitivity	0.592		0.666		0.928
Precision (PPV)	0.533		0.533		0.866
NPV	0.633		0.733		0.933
FPR	0.424		0.388		0.125
FDR	0.466		0.466		0.133

$\mathrm{Accuracy}=\frac{\mathrm{TP+TN}}{\mathrm{TP+TN+FP+FN}}$ (5)

$\mathrm{Snsetivity}=\frac{\mathrm{TP}}{\mathrm{TP+FN}}$ (6)

$\mathrm{Precision(PPV)}=\frac{\mathrm{TP}}{\mathrm{TP+FP}}$ (7)

$\mathrm{NPV}=\frac{\mathrm{TN}}{\mathrm{TN+FN}}$ (8)

$\mathrm{FPR}=\frac{\mathrm{FP}}{\mathrm{FP+TN}}$ (9)

$\mathrm{FDR}=\frac{\mathrm{FP}}{\mathrm{FP+TP}}$ (10)

Where, TP is true positive and denote the number of patient subjects correctly classified, FP is false positive and denotes the number of patient subjects that is misclassified as normal, TN is true negative and denotes the number of normal subjects that are correctly classified as not belonging to RRMS class, FN is false negative and denotes the number of normal subjects that are misclassified as RRMS patients. The accuracy value determines the ability of ANNs in cases of diagnosis and classification. The sensitivity value represents how much the ANNs are able to correctly select the RRMS patients and the precision value describes the reproducibility of predictions made by ANNs over time. The performance analysis of the proposed classification techniques is also down by plotting graphs of accuracy, sensitivity, precision (PPV), NPV, FPR and FDR (Figure 4 and Figure 5).

Figure4.

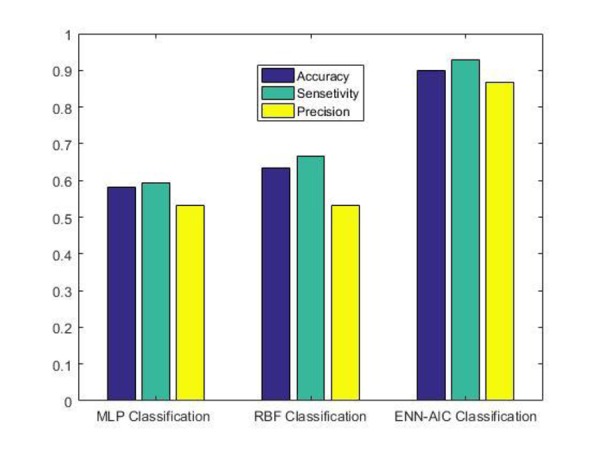
Comparative analysis graphs for accuracy, sensitivity and precision (PPV)

Figure5.

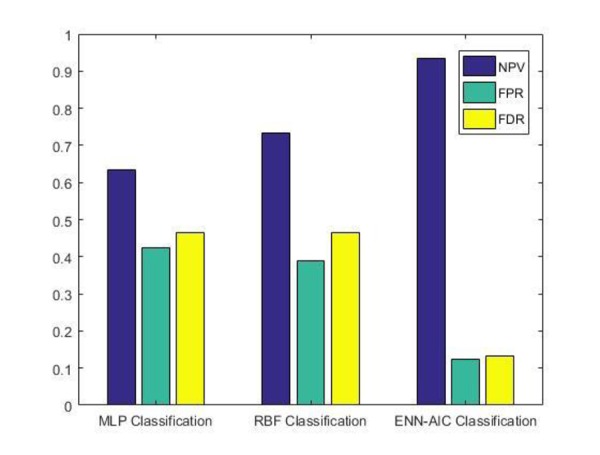
Comparative analysis graphs for NPV, FPR and FDR

In Figure 6, the determination graphs are given for 60 samples. The yellow line displays the actual data for healthy and RRMS subjects. It can be seen that the green line associated with ENN-AIC, has been able to track the actual data and estimates them. The red and blue lines, which indicate the performance of the RBF and MLP neural networks, are less accurate in real data estimation.

Figure6.

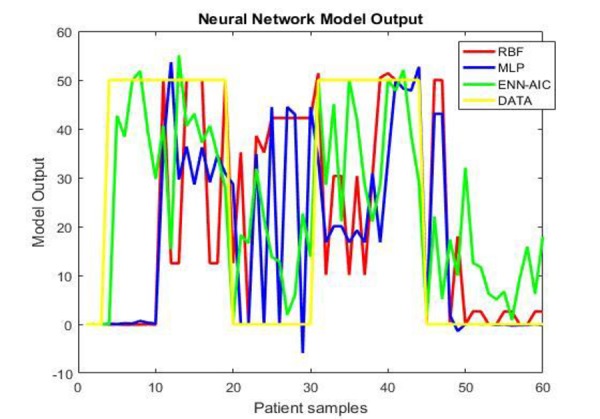
Comparison of actual data and the corresponding determination values of the three ANN algorithms for normal and patient datasets

Discussion

In this paper, the diagnosis and classification of RRMS patients from healthy subjects based on the QMTI-T1 dataset and the use of three different ANN algorithms were presented. The differences in white matter QMTI parameters including MTR, K_sat, T1_sat and T1 longitudinal relaxation time between healthy subjects and patients with RRMS were utilized as selected features under supervision of an experienced radiologist. Next, these four features are fed as inputs to the developed ANN-based classifiers. The performance of ENN-AIC algorithm, as an effective neural network model is also evaluated by comparing its classification results with other traditional classifiers which use the RBF- and MLP-based algorithms.

We investigated previous studies on improving MS diagnosis using MRI data and ANN- based classification methods. ANNs have been widely used to introduce the best automated methods for MS lesion segmentation to measure lesions load and determine the extent of disease burden to brain parenchyma [35-37]. Temporal connectives processing along with the identification and classification of human brain regions for decision making in fMRI have also been investigated with the help of ANN methods [38]. However so far, ANN has not been used to diagnose and classify MS patients based on QMTI-T1 data.

In general, the performance of ANNs is promising, but the results of this study indicate that the ENN-AIC model could identify a high percentage of RRMS subjects with more precision. The comparison results demonstrate that ENN-AIC algorithm as an effective neural network performed the best among all three proposed ANN models in terms of accuracy, sensitivity and precision. According to the results obtained in Table 5, it can be seen that ENN-AIC has obtained the classification accuracy of 0.900 compared with other classifiers as the case of RBF giving 0.633 as well as in the case of MLP giving 0.583. In the case of sensitivity, it was obtained 0.928 for ENN-AIC, 0.666 for RBF and 0.592 for MLP. For precision, the result of ENN-AIC is 0.866, RBF is 0.533 and 0.533 for MLP. Table 5 also reveals NPV, FPR and FDR scores for all the evaluated ANN algorithms. As expected, ENN-AIC performs the best obtaining of 0.933, 0.125 and 0.133 for NPV, FPR and FDR, respectively.

The graphical representation for evaluating the performance of three proposed ANNs models in Figure (6), implies that ENN-AIC algorithm corresponding to green line is able to track and estimate actual data more correctly. After that, RBF and MLP algorithms are arranged respectively. There are two reasons to explain why ENN-AIC model performs better. First, AIC determines the best component network weights and second, ranks them within ENN. This way, it helps to find the optimal ANN architecture [39].

The findings of previous studies suggest that QMTI-T1 parameters can detect the disease progression by quantitatively assessing the microscopic changes and neural degenerative processes in normal appearing white matter. However, ANNs improve the RRMS diagnostic precision using these QMTI-T1 measurements.

In the future, the use of an effective neural network model based on QMTI-T1 parameters can be generalized to clinical detection of other CNS diseases, such as Alzheimer’s and stroke. Decision support systems can also be designed in the form of ANN software based on the quantitative information obtained from various MRI modalities. These systems make patient identification more reliable and promote patient satisfaction.

Conclusion

It was demonstrated that ENN-AIC model introduces a more valid classifier for RRMS patients from healthy subjects. By increasing the accuracy of ANN function, the probability of disease false detection is reduced, which helps to follow the patient condition using the dataset of advanced MRI techniques.