Decision modelling for economic evaluation of liver transplantation

Abstract

As the gap between a shortage of organs and the immense demand for liver grafts persists, every available donor liver needs to be optimized for utility, urgency and equity. To overcome this challenge, decision modelling might allow us to gather evidence from previous studies as well as compare the costs and consequences of alternative options. For public health policy and clinical intervention assessment, it is a potentially powerful tool. The most commonly used types of decision analytical models include decision trees, the Markov model, microsimulation, discrete event simulation and the system dynamic model. Analytic models could support decision makers in the field of liver transplantation when facing specific problems by synthesizing evidence, comprising all relevant options, generalizing results to other contexts, extending the time horizon and exploring the uncertainty. For modeling studies of economic evaluation for transplantation, understanding the current nature of the disease is crucial, as well as the selection of appropriate modelling techniques. The quality and availability of data is another key element for the selection and development of decision analytical models. In addition, good practice guidelines should be complied, which is important for standardization and comparability between economic outputs.

Core tip: This overview focuses on providing an understanding of decision modelling approaches and their application to liver transplantation, outlining the major characteristics of decision analytic models as well as the individual strengths and weaknesses of several main techniques for modelling. We believe decision modelling may be able to provide tools by bringing all evidence from other studies together and comparing the costs and consequences of alternative options to reach a decision. It is a particularly powerful tool for public health policy and clinical intervention assessment.

INTRODUCTION

The improvement of immunosuppression, innovation of splitting technique and growing clinical experience in liver transplantation have increased the utilization of available donor organs and survival rates[1,2]. Nevertheless, the crisis of organ shortage is subsisting. In 2013, 5921 livers were donated for transplantation in the US, while 12407 patients were waiting for an appropriate donor[3]. In 2016, 1567 patients received liver grafts, while 1704 remained on the waiting list in eight European countries[4]. The situation in Germany has been under particularly increasing pressure due to publicly discussed transplant scandals. Furthermore, the gap between donated organs and the necessity of transplants has been widening due to regulatory issues highlighting the relevance of public trust[5]. In 2011, 1191 liver transplantations were performed in Germany, but 1792 patients were listed for liver transplantation[6]. Although living donation and split-liver transplantation have been established to relieve the shortage of organs, the immense demand for liver grafts constantly increases[7-10]. Managing this widening gap remains a major challenge both ethically as well as economically. Decision modelling, based on real clinical and economic data, might provide the tools to overcome these challenges.

Due to this scarcity, every available donor liver should be allocated in a manner that maximizes its utility, urgency and equity. Required resources, funding and coverage by health care insurance for transplant systems need reliable information based on validated economic models to support political and practical decisions. The recent liver allocation system has been urgently confined in the past two decades, and prioritizes candidates by the Child-Turcotte-Pugh score or Model for End-Stage Liver Disease (MELD) score and its adaptions[11]. However, MELD scores and similar systems lack the predictive power for short- and long-term outcome of liver transplantation[12], in addition to the consideration of utility and transplant benefit. Furthermore, care management interventions and extensive treatment of liver transplant recipients are commonly required and consume considerable financial healthcare resources[13]. Therefore, selection and evaluation in this lifesaving procedure is an important topic in health economics[14].

Economic evaluation involves different aspects of transplantation. Evaluations of donor organ quality, recipient characteristics, as well as strategies for organ allocation demand an economically-based decision evaluation. Considerations of alternative therapies other than transplantation, as well as adequate immunosuppression therapy regimes after transplantation, require intensive evaluation. In addition, comorbidities and complications play an important role in the estimation of the cost-effectiveness of transplantation[13].

Decision analytical models combine information from various sources to assess the implications of different decisions, and could therefore generalize evidence from other contexts when local data and studies are unavailable. This sets them apart from statistical models[15]. Furthermore, when randomized clinical trials (RCT) cannot be performed due to practical or ethical issues, the power of decision analytical models lies in their ability to generate results without primary data[16]. This review focuses on providing an understanding of decision modelling approaches and their application to liver transplantation.

WHAT IS DECISION MODELLING?

Decision analytic modelling uses mathematical relationships to define a series of consequences that derive from a set of options[17]. Although it shares a common theoretical foundation with statistic models and has a close association with Bayesian statistics[18], the key feature of decision analytic modelling accounts for the variability and uncertainty in all possible decisions. Moreover, it combines evidence from other studies like clinical-, cost- and health-related quality of life (QOL) data as utility values and compares the cost and consequences of alternative options. This generates a framework to reflect on the key differences of possible end points from all the alternative options in terms of cost and effect. It is thus a powerful tool for public health policy and clinical intervention assessment.

Even though the methods of decision analysis have been applied to medicine for over 40 years, their rather modest impact on real-world decision-making[19] has only recently been on the rise. To illuminate decision analytic models, we introduce the most commonly used types of models: Decision trees, the Markov model, microsimulation, discrete event simulation and the system dynamic model, illustrating how decision analytical models perform in the context of liver transplantation.

Decision trees

A decision tree model is recognized as the simplest structural decision analytical model and represents both the clinical decision procedure as well as consequential results in aggregate levels[15,20]. All clinical outcomes of patients in a decision tree model are visualized as a series of decision nodes and follow pathways with probabilities for each respective branch.

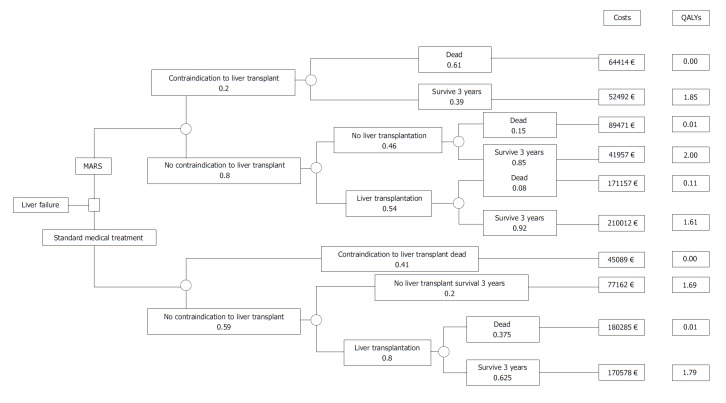
An example is given by Kantola et al[21] in Figure 1. This study was designed to determine cost-utility of molecular adsorbent recirculating system treatment in acute liver failure. The square node at the start of the tree represents the decision between alternative treatment strategies. The circular chance node shows the possible alternative events for a patient. Pathways (the “branches”) following each node represent a series of alternative events, which are mutually exclusive. Probabilities show the likelihood of certain events, multiplying along the nodes and branches to estimate the overall probability of reaching the distinct outcome. Probabilities for all events assessed sum up to a total of one.

Figure 1.

Decision tree for determining the short-term cost-utility of treatment in acute liver failure. Choice between strategies (decision node) and occurrence of chance events (chance node). Kantola et al[21]. MARS: Molecular adsorbent recirculating system.

Following these branches and nodes, a total cost can be derived for the distinct combination of therapy options and compared to the potential benefit, such as in this case Quality Adjusted Life Years. Nevertheless, interpretation needs to account for clinical reason and include a careful discussion when assessing the most beneficial choice for combining therapies.

The simplicity and transparency of decision trees are their main advantages and may illustrate which possible set of options may be most promising. However, decision tree models can be very complex when used to model complicated long-term prognoses[18]. In other words, when they are used to model a chronic disease, decision trees can have numerous lengthy pathways representing recurring events, which is very time-consuming to analyze and interpret.

Markov models

Markov models are commonly used to provide a framework that represents sequences of events as a large number of complexity modelling options over time. Certain events lead to different health states (patients with different probabilities of transitioning from one state to another) given a defined period of time (cycle length). They commonly include large numbers of complexity modelling options. The number of states and the association among them are pre-defined in accordance with the decision problem, as well as the transition probabilities and cycle length[17,22].

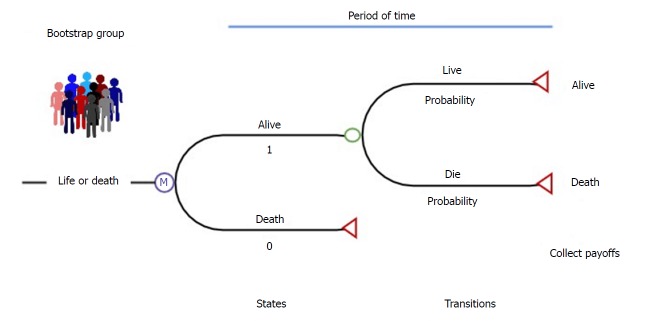
Sarasin and his colleagues[23] showed an example of using Markov models to compare the gain of life expectancy and the cost-effectiveness of living and deceased donor liver transplantation in Figure 2. Each patient starts at the state of “cirrhosis, hepatocellular carcinoma (HCC), with no contraindications to cadaveric liver transplantation”. With this initial state of health, they can then make a transition into several other states with different probabilities for each transition state for each defined, discrete time interval or cycle. They also might stay in their current state. The chances of transferring between different states are a set of defined transition probabilities derived from the appropriate transaction of longitudinal research data. Lengths of these cycles (one month in this example) depend on the disease or interventions of interest. To end the transition process in this Markov model, an absorbing state “death” was set that the patients obviously cannot leave once reached. Then, the Markov process modeled an integrity profile of both donor and recipient life expectancy over a lifetime-long horizon. The application of this Markov model handled the complexity of patients with early HCC and revealed that living donor liver transplantation is cost-effective compared to deceased donor liver transplantation under certain conditions[23].

Figure 2.

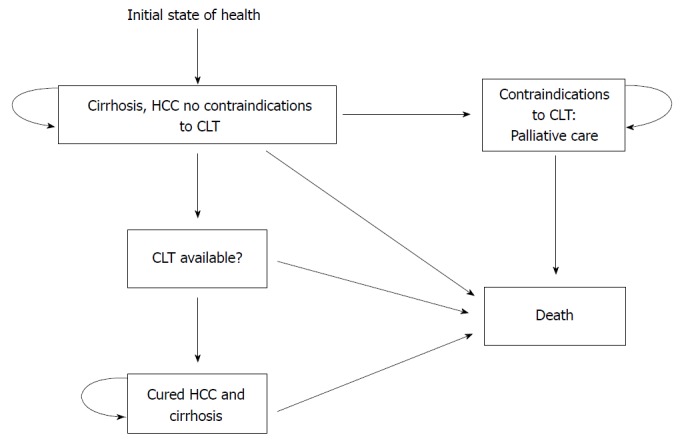
States of health in the decision model. Each square represents a state of health. Straight arrows represent the changes that may occur during each month. Curved arrows mean that the patient may remain in the same state of health. Sarasin et al[23]. HCC: Hepatocellular carcinoma.

A major advantage of Markov models is that they account for time dependency and can model changing probabilities over time. Therefore, Markov models are eligible to analyze chronic and complex conditions and clinical matters[24], such as the transplant field, relatively quickly and easily[13]. The important limitation of Markov models is the “Markov property”, also called “Markov assumption”, which assumes that transition probabilities only depend on the current health status but not on past history. Moreover, the Markov assumption might over-simplify the nature of disease, as it handles patient cohorts homogenously[18]. For higher resolution in this regard, an alternative approach known as patient-leveled simulation can be applied.

Patient level simulation (microsimulation)

The microsimulation model is featured by “individual sampling”, which means to simulate one individual at a time, rather than the whole cohort.

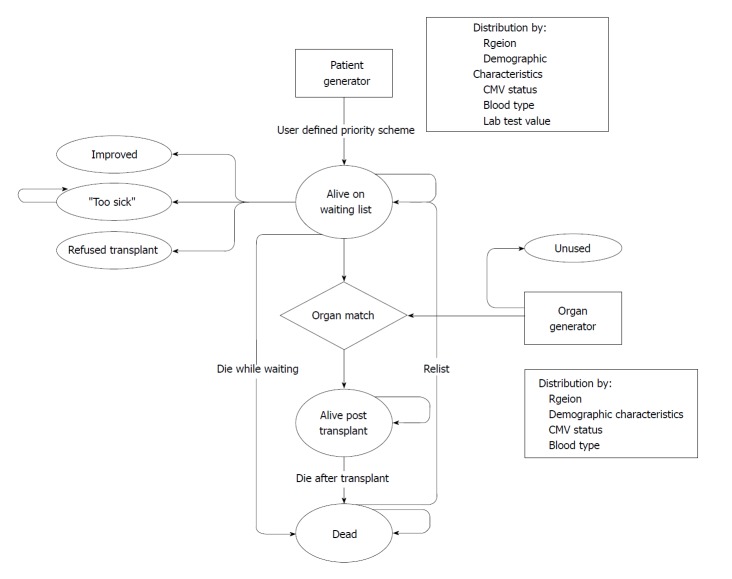
Perkins et al[25] developed a Markov-based microsimulation model to compare results under the present liver allocation policy in the United States (Figure 3). This model simulates how each patient proceeds through the model with the chance of multiple parallel events. One individual case is randomly selected from all patients. The initial state is “alive”. Patients can enter other states based on fixed transition probabilities, which simulate events in one cycle (three months in this study) until reaching the state “death”. This study modeled the changes of the allocation policy, which demonstrated the survival benefit for the patients who have a MELD score ≤ 14 from transplantation, among the highly diverse patient population in the waiting list. The results appear more reliable than models based on aggregated data and could also be validated.

Figure 3.

Simple example of a Markov microsimulation model. Perkins et al[25].

The advantage of microsimulation models is flexibility, in regards to different patterns of disease processes and intervention, because these models keep track of each individual’s history[19]. Moreover, it can be useful when accumulating the history of each patient to determine the different transitions, costs and health benefits. However, there are also disadvantages in using microsimulation: First, outcome effective determinants in patients’ history demand more detailed data, which challenge simply structured database research. Secondly, the simulation and computation of patient level simulation are time-consuming. Consequentially, the uncertainty assessment is not flexible when compared with other types of decision analytic models.

Discrete event simulations

Discrete event simulations (DES) can represent the competition for resources and investigate the changes in stochastic systems[26,27], and are mainly used to evaluate health care systems. The capacity and utility of allocation systems have previously been assessed before and after policy changes[28-31]. Another example reported by Shechter et al[26] is a biologically-based discrete-event simulation model, which represents the biological progression of end stage liver disease (ESLD) and examines the impact of changing allocation policies on this issue. The model was comprised of five modules: The patient generator, organ generator, pretransplant natural history, matching algorithm, and post-transplant survival (Figure 4). DES allows different modules to run independently, as this study shows, where pre-transplant history and allocation policy stand in parallel and individual patient attributes may influence the pathway, costs and outcomes. Unlike patient-level simulation models, DES is appropriate to model situations where constraints on resources could affect treatment options[15,32].

Figure 4.

Model structure for patients entering the liver transplantation program. Shechter et al[26].

DES has several methodological advantages compared to other commonly used models, because it simulates the time until the next event for a given patient, which reduces the amount of time required for model construction and interim computations[18]. The output is not limited to survival only, but also allows estimations of event counts and sub-group analyses[33]. Moreover, statistical processing tools for relevant input parameters can be deployed. In contrast, structural complexity is the most prominent disadvantage of DES, which makes it difficult to apply to clinical research[34]. The complicated structure also makes computations more extensive, in regards to time and resources compared to Markov models when dealing with the same decision problem[35].

System dynamic models

System dynamic models allow modeling interactions within a population and with their environment over time; hence, they are especially suited for studies related to infectious diseases. The theoretic background of a system dynamic model is that complex behaviors of systems are a result of ongoing accumulations of people, resources as well as biological and physiological states[36]. The probabilities of events can change through feedback of such accumulations. To the best of our knowledge, there is no application example of systematic dynamic models in the context of liver transplantation. However, examples of kidney[37] and corneal[38] transplantation showed that the predicted number of transplantations are consistent with observed results, which indicates the potential usefulness of system dynamic models for this field.

The advantage of system dynamic models is the information on interactions between individuals, which may quantify the impact of intervention on outcomes more accurately. Disadvantages are similar to DES, where information and interaction on individual level exponentially increase the complexity of model structure, computational burden, as well as lower transparency more than Markov models[19].

HOW DECISION ANALYTIC MODELLING CAN BE USED IN THE FIELD OF LIVER TRANSPLANTATION

Decision analytic models, in contrast to statistical models, incorporate decision-making into analysis[19]. Established in economic evaluations within other fields, decision analytic models in liver transplantation aim to inform decision-makers in two main areas: Decision analysis and measurement[18]. There are several aspects in which decision analytical modelling could help decision-makers in this field.

Combining different sources of evidence

In concordance with the principle of evidence-based medicine, decision-making on the basis of economic evaluation also requires the use of all accessible evidence related to the intervention effectiveness[39]. A decision analytical model offers a logic framework for the integration of data from very different sources, such as clinical trials, observational studies, insurance claim databases, case registries, public health statistics, and preference surveys[40]. In addition, more parameters related to resource utilization and utilities like unit cost, health-related QOL and preferences of patients are important evidence in economic evaluation[18]. This series of non-clinical indicators complement clinical data within the framework of decision analytics and support a much more complete picture of expectations from various parties involved. In particular, the specific data for patients with ESLD should also be organized into informative resources. Cillo et al[41] recommend a prospective assessment, which will substantially help decision analysis and support the decision-making process[42].

Comprising relevant options

In most instances, a single study cannot compare all the relevant alternative options for treatment paths for diseases such as ESLD. Decision-makers might therefore be challenged by a lacking comparison of all potentially effective interventions. New techniques like network meta-analysis extend the concept of indirect comparison by including multiple pairwise comparison information from clinical trials to constitute a network of evidence[43,44]. However, system dynamic models are more eligible to combine different types and sources of evidence, like clinical trials and patient questionnaires, and therefore adds fundamental information to the shared decision-making process.

Applying results to other context/subgroups

The differences between patient subgroups can, for example, derive from either baseline characteristics like age, gender, comorbidity severity or variations in the healthcare context. The application of findings from one context can be difficult to transfer to other situations. Cucchetti et al[45] performed a study to measure the risk of age for salvaging transplantation in patients resected for HCC. A Markov model was developed to quantify the effect of patient’s age above Milan criteria. Next, the risk of resection at two or three years below the age limit could be evaluated. The clinical evidence may not be able to show the difference between subgroups in heterogeneous patients over a long horizon[46]. However, in this research, the reduction of life expectancy of hepatic resection in different patient groups was clearly shown using a decision model.

Extending the time horizon

Many of the interventions for liver transplant patients require long time periods, and the weight of personal value added by these therapy options takes a long time for patients to assess. Therefore, models that evaluate the benefits of interventions for patients should cover sufficient time horizons. Long-term consequences, as well as costs of alternative options and interventions, are substantially affected by time. Even lifetime horizons are often needed for many models and are almost always required for models in which options have different time-varying survival rates[40]. Decision models offer the framework to include the effect and cost over time by adding respective results, and can evaluate the effects of main interventions beyond primary data sources and their continuous treatment effects[40].

Exploring the uncertainty

A key interest in liver transplantation is weighing the probabilities of risk and success between different options, especially in organ resource allocation and the decision of appropriate time-point selection for certain interventions. Not only are patients affected, but so are other potential organ recipients. Transplantation itself is not a definitively curing option, but leads to a life-long immunosuppressive treatment. Population variation, parametric imprecision as well as modelling selections and other aspects challenge predictive modelling, with uncertainty in different layers[47]. Clinical and economic data accessibility and validity also contribute to this uncertainty[16].

In the face of these challenges, decision modelling methods are not only for reflecting this uncertainty but also to assess their influence so that the decision-makers can make choices with the relevant possibilities known. Analyses estimating the uncertainty due to parameters of interest is the most common approach to perform in modeling, which could be represented via deterministic sensitivity analysis (DSA) or probabilistic sensitivity analysis (PSA)[48]. In DSA, parameters in modelling are specified as multiple point estimates, and are varied manually to test the sensitivity of modeling results. In PSA, model inputs are specified as a distribution and varied to predefined probability distributions accordingly.

Along with the probabilistic analysis mentioned above, expected value of perfect information analysis is argued to be the most appropriate presentational technique for representing decision uncertainty. Jay and colleagues[49] showed the cost-effectiveness of organ donation after cardiac death versus after brain death. This novel sensitivity analysis represents both the probability of whether a decision is appropriate and its consequence, which is important for comparing the incremental net benefits under different accessibilities with the information of probabilities.

KEY POINT IN DECISION ANALYTICAL MODEL DEVELOPMENT

Understanding the nature of disease history

Model construction should combine efforts from multiple parties, including clinical and economic experts as well as decision-makers from the context of interest, and make best utilization of all available evidence. Neither the modeler nor the clinician alone can complete the task that conceptualizes an accuracy-simplicity balanced model. The accuracy of the model depends on whether the structure accounts for all important events or transitions and probabilities[25]. A thorough understanding of the disease is crucial for defining the possible health states in the model as well as capturing the occurrence of clinical events beyond follow-up[50].

Model characteristics and techniques

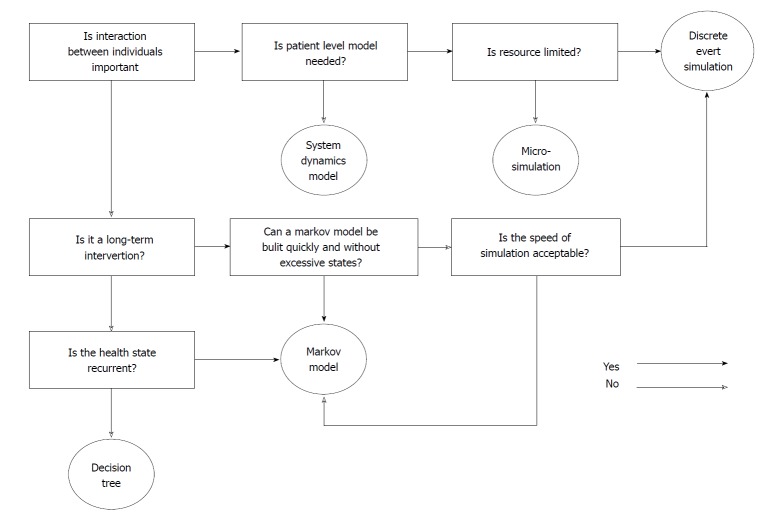
The key consideration of decision analytical model selection is the acceptance of the modelling technique, model “error”, model appropriateness, dimensionality, and ease and speed of model development[32]. Decision trees are typically used when the process is not complicated, the recurrence of disease is not important and the time frame is short. Markov models are more feasible when simple chronic interventions are conducted. When the interaction is important, discrete event time and system dynamics could construct a more comprehensive and interactive system, but the development time and cost may significantly increase[51].

Figure 5 shows a flow chart for selecting the appropriate decision models based on the mentioned summaries and guidelines recommended by Barton et al[15] and Cooper et al[32].

Figure 5.

Scheme of selecting the appropriate model type.

Data quality and availability

The quality and availability of data is another key element for the selection and development of decision analytical models. Without sufficient and high quality data, the development of models will be difficult and result in low validity. As discussed above, synthesizing evidence is one of the most important fields that decision analytical modelling could help with during economic evaluation. In general, the information needed as input parameters for economic evaluation is derived from different kinds of data sources[52], including RCT, observational studies, secondary data analysis (e.g., Meta-analysis) and expert opinions[50]. For topics of interest in liver transplantation, ethical considerations may additionally constrain the option of performing RCT. Therefore, data from published literature needs to be consolidated and considered in this context. In particular, reviews and reports from both the European Liver Transplant Registry, Organ Procurement and Transplantation Network as well as the Scientific Registry of Transplant Recipients database are valuable sources.

However, the consolidated data may cause incorrect estimations of parameters within the models, especially when multiple inputs are derived from single publications. In this situation, individual data from electronic medical databases or re-analysis of available published individual level data will be more appropriate. When several studies provide results on the same parameters of interest, researchers usually need to combine different results using meta-analytical methods[53] or adopt the results reported in meta-analyses. When potential biases in the original research or meta-analyses are handled appropriately, the inclusion of these results might increase uncertainty, which will be noted when constructing the model. Although expert opinion is the least preferable data source due to its subjectivity, it may still play an important role in the evaluation of cost and resource use when other sources of evidence are absent[54].

Good practice guidelines for modelling

The development of decision analytical models is a sophisticated task requiring the modelers to have sufficient experience, as well as the ability to evaluate, present and interpret the model’s output. The complexity of the clinical pathway for complex interventions such as liver transplantation and the differences of health care environments between transplant centers and countries (e.g., organ availability, allocation strategy, financial assistance for transplantation, post-transplant management and the consequential influence on QOL) challenge even the most experienced modeler to develop a model of economic outcomes of interest[51]. The best practice guidelines have therefore been significantly improving the process of model development, which is important for standardizing and comparing economic outputs.

The International Society for Pharmaco-economics and Outcomes Research Task Force group published a series of guidelines on good practice standards for modeling research, which set the standards for modeling practice[48,55-60]. However, these very detailed guidelines may not be well-understood in practice when performing a modeling study for the first time. To bridge this gap, Rautenberg et al[61] developed a beginner’s guide to support modelers alongside the development of decision analytical cost-effectiveness models. This guide is especially helpful for researchers who are interested in utilizing this economic evaluation instrument, which is an easy-to-use practical guideline recommended for elementary modelers to initiate studies in this field.

CONCLUSION

This review demonstrates the major characteristics of decision analytic models (Table 1) as well as the individual strengths and weaknesses of several main techniques for modelling. Decision trees are fit for disease interventions without relapse or recurrence. Markov models are suitable for interventions for chronic conditions involving recurring events over time. When individual level information is important, microsimulation models should be considered. If interactions between individuals are of importance, discrete event time models are suitable for simulation of the interaction of resource allocation. Dynamic models are fit to simulate the spread of infectious diseases.

Table 1.

Summary of types of decision models in liver transplantation

Model type	Model description	Type of scenario most suited for
Decision tree	Clinical outcomes are modelled as a series of decision nodes and follow pathways with probabilities for each respective branch.	Disease without relapse or recurrence.
Markov model	Represents sequences of events that lead to different health states with different probabilities of transitioning from one state to another over a defined period of time.	Chronic conditions involving recurrent events over time.
Microsimulation	Simulates one individual patient proceeding through the model with the chance of multiple parallel events.	Individual level information is important.
Discrete event simulation	Represents the competition for resources and investigates the changes in stochastic systems.	Interactions of resource allocation between individuals are of importance.
System dynamic model	Modeling interactions within a population and with their environment over time.	Spread of infectious diseases.

Besides this, choosing the best depends on advanced understanding of the disease and its related interventions. Inter-professional cooperation is likely needed to combine methodological and clinical knowledge into a purposeful model. Furthermore, data availability and quality must be taken into account, which is as important as the definition and measurement of critical model components. The availability, weight and information of details for interventions, alternatives, target populations, health outcomes and time horizons have to be considered when conceptualizing the model. This is in regards to the modelling technique, model appropriateness and both the ease and speed of model development.

This framework of methods guides the analysis and interpretation of various data sources that further conclusions and a more advanced understanding of various elements and aspects of liver transplantation.