Identification of cell types from single-cell transcriptomes using a novel clustering method

Abstract

Motivation: The recent advance of single-cell technologies has brought new insights into complex biological phenomena. In particular, genome-wide single-cell measurements such as transcriptome sequencing enable the characterization of cellular composition as well as functional variation in homogenic cell populations. An important step in the single-cell transcriptome analysis is to group cells that belong to the same cell types based on gene expression patterns. The corresponding computational problem is to cluster a noisy high dimensional dataset with substantially fewer objects (cells) than the number of variables (genes).

Results: In this article, we describe a novel algorithm named shared nearest neighbor (SNN)-Cliq that clusters single-cell transcriptomes. SNN-Cliq utilizes the concept of shared nearest neighbor that shows advantages in handling high-dimensional data. When evaluated on a variety of synthetic and real experimental datasets, SNN-Cliq outperformed the state-of-the-art methods tested. More importantly, the clustering results of SNN-Cliq reflect the cell types or origins with high accuracy.

Availability and implementation: The algorithm is implemented in MATLAB and Python. The source code can be downloaded at http://bioinfo.uncc.edu/SNNCliq.

Contact: zcsu@uncc.edu

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

The recent advance of single-cell measurements has deepened our understanding of the cellular heterogeneity in homogenic populations and the underlying mechanisms (Kalisky and Quake, 2011; Pelkmans, 2012; Raser and O'Shea, 2004). With the rapid adaption of single-cell RNA-Seq techniques (Saliba et al., 2014), enormous transcriptome datasets have been generated at single-cell resolution. These datasets present a tremendous opportunity and challenge to the computational biology community for their analysis to reveal new insights into many biological problems, for example, to elucidate cell types in complex tissues. A straightforward approach to this problem would be to partition the cells into well-separated groups via clustering techniques, so that cells (data points) in the same group exhibit similar gene expression levels (attributes). However, the high variability in gene expression levels even between cells of the same type (Buganim et al., 2012; Guo et al., 2010; Hashimshony et al., 2012; Shalek et al., 2013) can confound this seemly straightforward clustering approach. In addition, single-cell RNA-Seq data is generally in tens of thousands dimensions, which can substantially further complicate the clustering problem. In particular, usually only a few out of 1000 genes are significantly differentially expressed in distinct cell types. Consequently, when clustering on the whole transcriptome, many genes would be regarded as irrelevant attributes and may even impede the identification of cell types.

It has been claimed that for a broad range of data distributions, the conventional similarities (such as Euclidean norm or Cosine measure) become less reliable as the dimensionality increases (Beyer et al., 1999). The reason is that all data become sparse in high-dimensional space and therefore the similarities measured by these metrics are generally low between objects (Beyer et al., 1999). Accordingly, many clustering methods based on these measures are not effective enough for high-dimensional data with few objects. An alternative similarity measure utilizes the ranking induced by a specified primary similarity. One commonly used secondary similarity is based on the notion of shared nearest neighbor (SNN), which takes into account the effect of surrounding neighbor data points. More specifically, the similarity between a pair of data points is a function of their intersection of the fixed-sized neighborhoods determined by the primary measure (e.g. Euclidean norm). It has been demonstrated that in high dimensionality, SNN measures are more robust and result in more stable performances than the associated primary measures (Houle et al., 2010). SNN techniques have been successfully applied to some clustering problems (Ertöz et al., 2003; Guha et al., 2000; Jarvis and Patrick, 1973). Inspired by these earlier applications, we define a new similarity between two data points based on the ranking of their shared neighborhood.

By representing data as a similarity graph in which nodes correspond to data points and weighted edges represent the similarities between data points, the clustering task can be achieved through partitioning the graph into homogeneous and well-separated subgraphs. That is, the nodes in the same subgraph have high interconnectivity, while nodes from different subgraphs have few connections in between. Several graph theory-based algorithms have been applied to clustering problems in earlier studies. One of the best-known graph-theoretic divisive clustering methods first finds the minimal spanning tree, and then splits the tree by removing inconsistent edges with weights larger than the average in neighborhood (Zahn, 1971). Another algorithm called Chameleon first divides a graph into several subsets via a multilevel procedure, and then repeatedly combines these subsets to the ultimate clustering solution (Karypis et al., 1999). However, the partitioning schemes used in these methods all require a prior knowledge of the number of subsets to be produced or the sizes of the partitions. Some other approaches avoid this problem by making assumptions about when to stop the recursive partition. For example, the highly connected subgraph (HCS) clustering method (Hartuv and Shamir, 2000) defines a cluster as a HCS with a connectivity (the minimum number of edges to be removed to disconnect a graph) above half the number of nodes. The method iteratively cuts an unweighted graph using the minimum-cut algorithm until such subgraphs are produced. However, the algorithm produces many singletons for a sparse graph, although it includes a singleton adoption step. Besides, it does not separate clusters completely for certain data structures in our hand (see later).

To overcome the limitations of these existing algorithms, we developed a quasi-clique-based clustering algorithm inspired by our earlier work (Zhang et al., 2009) to identify tight groups of highly similar nodes that are likely to belong to the same genuine clusters. Combining this algorithm with the SNN-based similarity measure, our method called SNN-Cliq is able to automatically determine the number of clusters in the data. Moreover, it can identify clusters of different densities and shapes, which is considered to be one of the hardest issues in clustering problems. Additionally, it requires few input parameters and finding a valid parameter setting is generally not hard. Most importantly, SNN-Cliq shows great advantages over traditional methods especially in clustering high-dimensional single-cell gene expression datasets.

2 Methods

By incorporating the concept of SNN in similarity measures, we model data as an SNN graph, with nodes corresponding to data points (e.g. vectors of gene expression levels of individual cells) and weighted edges reflecting the similarities between data points. We then find the ultimate clustering solution by using graph-theoretic techniques to cluster the sparse SNN graph. The SNN-Cliq is carried out in the following steps and is schematically shown in Supplementary Figure S1.

2.1 Construct an SNN graph

We first compute a similarity matrix using Euclidean distance (other suitable measures can also be used instead) between pairs of data points (e.g. a point is a cell and the distance between points is calculated using the vectors of gene expression levels in the cells). Next, for each data point x_i, we list the k-nearest-neighbors (KNN) using the similarity matrix, with x_i itself as the first entry in the list. To construct an SNN graph, for a pair of points x_i and x_j, we assign an edge e(x_i, x_j) only if x_i and x_j have at least one shared KNN. The weight of the edge e(x_i, x_j) is defined as the difference between k and the highest averaged ranking of the common KNN:

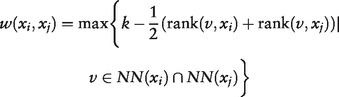(1)

where k is the size of the nearest neighbor list, and rank(v, x_i) stands for the position of node v in x_i’s nearest neighbor list NN(x_i). Note that a closer neighbor v is higher ranked but the value of rank(v, x_i) is lower. For example, rank(x_i, x_i) = 1 because x_i is ordered first in x_i’s nearest neighbor list.

Therefore, this SNN graph captures the similarity between two nodes in terms of their connectivity in the neighborhood. In other words, unlike the primary similarity, in our measure, the similarity between two nodes needs to be confirmed by their closeness to other nodes (common nearest neighbors). The rationale behind SNN is that the ranking of nodes is usually still meaningful in high-dimensional space though the primary similarity might not (Houle et al., 2010). The ranking of shared neighbors of two nodes in a genuine cluster is expected to be high, thus leading to a highly weighed edge. In contrast, the ranking of shared neighbors of two nodes from different clusters is expected to be low, resulting in a lowly weighted edge. Moreover, SNN graphs are usually sparse, thus allowing for scaling to large datasets.

2.2 Identify clusters in the SNN graph

In a recent application, we proposed an algorithm for graph partition by finding maximal cliques (Zhang et al., 2009). A maximal clique is a complete (fully connected) subgraph that is not contained in a larger clique. Although enumerating all the maximal cliques in a graph is an NP-hard problem, maximal cliques associated with each node can be efficiently found by a heuristic approach (Zhang et al., 2009). However, cliques are rare in SNN graphs due to the general sparsity. We instead search for quasi-cliques, which are dense enough but not necessarily complete. Our graph clustering method consists of two steps. Firstly, we extract local maximal quasi-cliques associated with each node in the subgraph induced by the node. We then construct clusters through merging these quasi-cliques and assigning nodes to unique clusters.

2.2.1 Find quasi-cliques in the SNN graph 

Given an SNN graph, we use a greedy algorithm to find a maximal quasi-clique associated with each node (Supplementary Fig. S2). First, for a subgraph S induced by a node v (S consists of v, all its neighbor nodes and associated edges), we find a dense quasi-clique in S. To this end, for each node s in S, we compute a local degree d as the number of edges incident to s from the other nodes in S. We select the s_i with the minimum degree d_i among all the nodes in S and remove s_i from S if d_i/|S| < r, where |S| is the size of the current subgraph S and r is a predefined threshold (r ϵ (0, 1]). We then update d for the remaining nodes and repeat the process until no more nodes can be removed. If the final subgraph S contains more than three nodes, i.e. |S| ≥ 3, we call it the quasi-clique for v.

After all possible quasi-cliques are found, we eliminate redundancy by deleting quasi-cliques that are completely included in other quasi-cliques. The parameter r defines the connectivity in the resulting quasi-cliques. A higher value of r would lead to a more compact subgraph, while a lower value of r would result in a less dense subgraph. One can try different values of r to explore the cluster structures or optimize the results, but we found that when r = 0.7 the method performed well in all of the problems tested (see later). In fact, because of the following merging step, adjusting r in a certain range would not lead to substantial differences in the results.

2.2.2 Identify clusters by merging quasi-cliques

We identify clusters in the SNN graph by iteratively combining significantly overlapping subgraphs starting with the quasi-cliques. For subgraphs S_i and S_j, the overlapping rate O_i,j is defined as the size of their intersection divided by the minimum size of S_i and S_j:

$$O_{i,j}=\frac{|S_i\cap S_j|}{\min (|S_i|,|S_j|)}$$ (2)

We initialize the set of subgraphs to be all the quasi-cliques and merge S_i and S_j if O_{i, j} exceeds a predefined threshold m [m ϵ (0, 1)]. In all the applications in this article, we set m to 0.5. After each merging, we update the current set of subgraphs and recalculate pairwise overlapping rates if necessary. This process is repeated until no more merging can be made, and the final set of subgraphs is our identified clusters. Since a subgraph may overlap with multiple other subgraphs and merging in different orders may lead to distinct results, we give high priority to the pair with the largest total size |S_i| + |S_j|. In this way, a larger cluster is promised and would not likely be split into small ones.

2.2.3 Assign nodes to unique clusters

The iterative merging stops when no pairs of clusters have an overlapping rate greater than m. However, the clusters may still have small overlaps, resulting in some nodes appearing in multiple clusters. However, for many problems such as clustering single-cell transcriptomes that we intend to address in this article, one would prefer a ‘hard clustering’ (each data point belongs to exactly one cluster) over a ‘fuzzy clustering’ (each data point can belong to more than one clusters). To this end, for each candidate cluster C that the target node v is in, we calculate a score measuring the proximity between C and v, defined as the averaged weights on the edges incident to v from nodes in C:

$$\text{Score}\left(C,v\right)=\frac{\text{1}}{|C|}{\displaystyle \sum _{i=\text{1}}^{|C|}w}\left(c_i,v\right)$$ (3)

where c_i is a node in C. Then, we assign v to the cluster with the maximum score and eliminate v from all the other candidate clusters. The assignation will change the cluster composition and may produce clusters with less than three nodes. In this circumstance, these data points are considered to be singletons. However, we did not observe such cases in our applications.

2.3 Time complexity of the algorithm

The most time-consuming step of SNN-Cliq is to construct the SNN graph, which requires O(n²) time, where n is the number of data points. Despite this, this step can be still fast for single-cell transcriptome dataset, since n is usually quite small compared with the number of variables (genes/transcripts). The time complexity for finding a quasi-clique induced by a node is O(d_v²), where d_v is the degree of the node. Since d_v is usually much smaller than n in a sparse SNN graph, the entire cost of finding quasi-cliques for n nodes is bounded by O(n). Moreover, this step can be easily accelerated by parallelization, since there is no data dependency in the process of finding quasi-cliques associated with each node. The merging step does not scale with n and is rather faster, since the overlaps of quasi-cliques only account for a small portion and are related to the cluster structures rather than n.

3 Results

3.1 Performance on synthetic datasets

First, we illustrated the effect of the parameters on SNN graphs and clustering results using a synthetic two dimensional (2D) dataset consisting of six perceptually distinct groups (2 high-dense, 2 mid-dense and 2 low-dense clusters) [Fig. 1(A–C)]. The dataset was generated manually by randomly placing points on a 2D space, and then the coordinates were retrieved. The class labels were given according to an intuitively good clustering way. Figure 1(A–C) show the resulting SNN graphs for k = 5, 8 and 10. With the increase in k from 5 (Fig. 1A) to 8 (Fig. 1B), more edges were present in the SNN graph, connecting nodes in the same or from different clusters. However, in spite of the differences in the SNN graphs, clustering outputs stayed the same (six clusters). When k became even greater than the average size of the clusters (k = 10 in Fig. 1C), the method started to combine similar clusters in the low- to mid-dense regions. We further systematically evaluated k on a wide range (k = 3–25) (Fig. 2A). The minimum value of a valid k is three, because a node needs at least two other neighbors to form a quasi-clique. When k was too large (k ≥ 9), clusters might not be thoroughly separated; on the other hand, when k was too small (k = 3 and 4), a genuine cluster might be split into parts (Fig. 2A). These results demonstrate that SNN-Cliq is relatively robust with respect to the changes in k to a certain extent. A valid choice of k depends on both the size and density of data. In general, a large and high-density dataset usually requires a relatively high k value compared with a sparse and low-density dataset. The parameters r and m both control the compactness of subgraphs, thus can be used to adjust the granularity of resulting clusters [Fig. 2(B–E)]. Altering r or m usually has the same effect. As shown in Figure 2(B–E), the correct clustering could be achieved by many different combinations of k, r and m settings; however, when r = 0.7 and m = 0.5 the method had a higher tolerance to changes in k. Therefore, in the following applications we set r = 0.7 and m = 0.5.

Fig. 1.

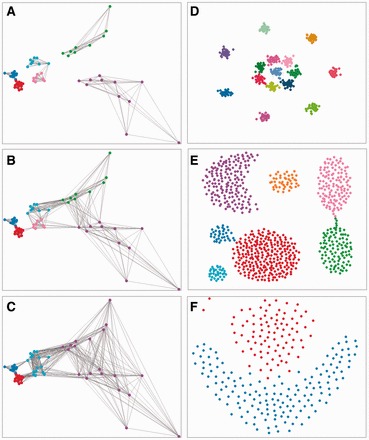
(A–C) SNN graphs constructed with k = 5 (A), 8 (B) and 10 (C) for a synthetic 2D dataset containing six perceptual clusters with high-, mid- and low- densities. Edge weights are not shown for clarity. (D–F) Performance of SNN-Cliq on three synthetic 2D datasets with distinct structures. Dataset are from (Veenman et al., 2002) (D), (Gionis et al., 2007) (E) and (Fu and Medico, 2007) (F). Data points grouped in the same cluster by the algorithm are shown in the same color

Fig. 2.

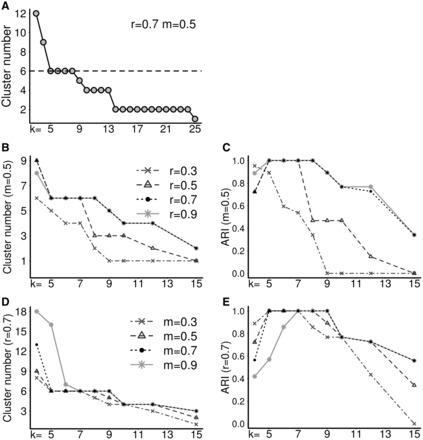
The effects of parameters on the clustering results of the synthetic dataset shown in Figure 1A. (A) The number of clusters detected as a function of k. (B–E) The number of clusters and ARI (see Supplementary Text for how it is calculated) at different parameter settings

To demonstrate the applicability of SNN-Cliq, we tested it on several datasets with distinct structures presented in Figure 1(D–F). The dataset shown in Figure 1D is composed of 15 similar 2D Gaussian clusters that are positioned in rings (Veenman et al., 2002). With k = 15–35, we obtained the same correct clustering result as the original paper did (Veenman et al., 2002). The dataset shown in Figure 1E contains clusters of arbitrary shapes and clusters connected by narrow bridges (Gionis et al., 2007). SNN-Cliq successfully determined the seven clusters as long as k = 20–30. In contrast, applying HCS (from the RBGL package in R) (Carey et al., 2011) to the SNN graphs failed to break the bridges, although a wide range of k was tested (Supplementary Fig. S3A). The dataset shown in Figure 1F consists of two clusters with hardly defined border and shape, which represents a difficult case of clustering (Fu and Medico, 2007). Nonetheless, SNN-Cliq successfully separated the two distinct groups by breaking the bordering area with k = 25, which agrees with an intuitively good clustering for this dataset. In contrast, using HCS on the SNN graph failed to give a result compliant with visual intuition (Supplementary Fig. S3B).

3.2 Performance on single-cell transcriptome datasets

It is generally believed that different cell types in multicellular organisms express distinct sets of genes, as is often manifested by traditional cell-population based assays. However, it has been shown that individual cells of the same type display inevitable cell-to-cell variations due to the stochastic nature of biochemical processes (Kalisky and Quake, 2011; Pelkmans, 2012). Such variability, also referred to as ‘noise’, makes the identification of the type of a cell on the basis of its transcriptome non-trivial. Moreover, as the small copy number of RNA molecules in a cell may lead to random loss of transcripts during library preparations, there is a notable technical noise in single-cell transcriptomes (Brennecke et al., 2013). Therefore, we want to know whether or not individual cells could be grouped according to their cell types using the measured transcriptomes. We tested SNN-Cliq for such capability using three single-cell RNA-Seq datasets generated by different techniques in a variety of cell types in human and mouse (Deng et al., 2014; Ramsköld et al., 2012; Yan et al., 2013). In the original papers, the authors have clustered the cells by hierarchical clustering or projected the cells onto the first two principal components derived from a principal component analysis. Although these analyses revealed general relationships between cells, they lacked a clear grouping description of cells. To extend these studies and explore the valuable data further, we shall present the cell clustering results obtained by SNN-Cliq and compare them with those of two widely used clustering algorithms. One is K-means (MacQueen, 1967), a partition-based clustering technique that is suitable for spherical shaped clusters of similar sizes and densities. Another is Density-Based Spatial Clustering of Applications with Noise (DBSCAN) (Ester et al., 1996), which clusters density-connected points and discards as noise the points having less than a user defined number (MinPts) of neighbors in a given radius (Eps). In addition, we shall compare our quasi-clique-based method with HCS in partitioning SNN graphs.

3.2.1 Human cancer cells

The first dataset was generated by Ramsköld et al. (2012) using a single-cell RNA-Seq protocol called Smart-Seq, which significantly improved read coverage across transcripts. The dataset includes transcriptomes of human embryonic stem cells hESC (n = 8), putative melanoma CTCs (n = 6) isolated from peripheral blood, melanoma cell lines SKMEL5 (n = 4) and UACC257 (n = 3), prostate cancer cell lines LNCap (n = 4) and PC3 (n = 4) and bladder cancer cell line T24 (n = 4). We downloaded the normalized gene expression levels in reads per kilobase of transcript per million mapped reads (RPKM) from the Gene Expression Omnibus (GEO) database. Since technical variability in the measurements of gene expression levels becomes pronounced for lowly expressed genes due to random loss of transcripts (Ramsköld et al., 2012), excluding such genes before analysis could enhance the reliability of results. As suggested by the original paper, we used genes with an averaged RPKM ≥ 20 for the analysis, involving 3582 genes. To reduce the effects of highly expressed genes, we log-transformed the RPKMs, i.e. log₂(x + 1). The gene expression variability is illustrated in Supplementary Figure S4. Because of the small number of cells in the dataset, we set k = 3; r and m are at default values (r = 0.7, m = 0.5). As shown in Figure 3A, SNN-Cliq yielded six clusters, with five clusters each corresponding to a unique cell type and one cluster including cells of SKMEL5 and UACC257. However, both SKMEL5 and UACC257 are melanoma cell lines and the difference between them should be relatively small.

Fig. 3.

Comparison of the clustering results from different algorithms on the human cancer cell dataset (Ramsköld et al., 2012) (A), human embryonic cell dataset (Yan et al., 2013) (B) and mouse embryonic cell dataset (Deng et al., 2014). In the heatmap, each row stands for an individual cell; each column corresponds to the clustering result produced by one of the four methods. Cells that are grouped in the same cluster by a method are displayed in the same color in the column. Cells that are treated as noise or singletons by the method are shown in black in the column. The embryo origins of cells from the same stage are distinguished by the first number in the cell names

To compare our quasi-clique-based method with HCS in partitioning SNN graphs, we applied HCS on the same SNN graph. As shown in Figure 3A, HCS discarded four (shown in black) of the six CTC cells as singletons. To compare our entire algorithm with other methods in capturing the cell types, we applied K-means from MATLAB and DBSCAN from Python module scikit-learn-0.15.0 (Pedregosa et al., 2011) to the log-transformed RPKMs, also with Euclidean norm as the similarity measure. Although K-means was preformed with the correct parameter (K = 7), the clusters found were either formed by cells of multiple types or a portion of cells of a certain type (Fig. 3A). For example, CTC and SKMEL5 cells were all in one cluster, while hESC cells were partitioned into two different clusters. To give DBSCAN some advantages, we tried different sets of parameters (MinPts, Eps) and reported the one giving the best result (MinPts = 3, Eps = 150). However, DBSCAN only found two different clusters; one cluster agreed with the type hESC and the other cluster was a mixture of six cell types (Fig. 3A). We further compared these methods using three external evaluation measures, Purity, Adjusted Rand Index (ARI) and F₁ score (see Supplementary Text for how they are calculated). As shown in Figure 4A, the performance of SNN-Cliq was better than the other methods in all the three measures.

Fig. 4.

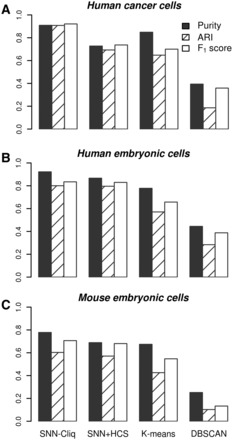
Evaluation of clustering algorithms by external validation measures, Purity, ARI and F₁ score. The gold standard of classes is determined by cell types or developmental stages. For mouse embryonic cell dataset, gold standard also considers the library preparation technique (Smart-Seq or Smart-Seq2)

3.2.2 Human embryonic cells

The second dataset was produced by Yan et al. (2013) using a single-cell RNA-Seq approach that showed high sensitivity and reproducibility. The dataset includes transcriptomes of human oocytes and cells in early embryos at seven crucial developmental stages: metaphase II oocyte (n = 3), zygote (n = 3), 2-cell-stage (n = 6), 4-cell-stage (n = 12), 8-cell-stage (n = 20), morula (n = 16) and late blastocyst at hatching stage (n = 30). For each stage, 2 to 3 embryos were used. We applied SNN-Cliq with the same parameterization as before (k = 3, r = 0.7 and m = 0.5) to the log-transformed RPKMs of 19 591 known RefSeq genes with RPKM > 0.1 in at least one cell. As shown in Figure 3B, SNN-Cliq successfully clustered the cells from the same developmental stages, except for a few cells being mixed into neighboring stages, i.e. two morula cells were placed in the 8-cell-stage cluster and four 4-cell-stage cells were placed in the 2-cell-stage cluster. SNN-Cliq partitioned the 8-cell-stage cells into three different clusters. Intriguingly, the splitting reflects their distinct embryo origins (embryo 1, 2 and 3), as cells from the same embryo form their own cluster. It indicates the notable differences between individual embryos at this developmental stage. Similarly, the morula cells were split into different clusters for the two embryos. Interestingly, morula cells from Embryo 2 were further partitioned into two clusters, indicating that heterogeneous expression patterns and possible cell differentiations might have occurred at this stage.

Applying HCS to the SNN graph yielded very similar results to our graph clustering method (Fig. 3B). However, it failed to recover the 2-cell-stage because most cells at this stage were discarded as singletons (shown in black in Fig. 3B). Although K-means was conducted with the correct parameter (K = 7), it lumped all the cells from oocyte, zygote and 2-cell-stage into a single cluster, and failed to differentiate morula and 8-cell-stage (Fig. 3B). The results given by DBSCAN (MinPts = 5, Eps = 150) were not compliant with the cell identities in most of the cases; furthermore, a large number of cells, in particular the late blastocyst cells, were assigned to noise (Fig. 3B). Evaluations using objective measures also show that SNN-Cliq outperformed the other methods (Fig. 4B).

3.2.3 Mouse embryonic cells

The last dataset was generated by Deng and colleagues (Deng et al., 2014) using Smart-Seq (Ramsköld et al., 2012) or its updated form Smart-Seq2 (Picelli et al., 2013). The dataset consists of transcriptomes for individual cells isolated from mouse (CAST/EiJ x C57BL/6J) embryos at different preimplantation stages. We obtained RPKMs for a total of 135 cells from GEO, including zygote (n = 4), early 2-cell-stage (n = 8), mid 2-cell-stage (n = 12), late 2-cell-stage (n = 10), 4-cell-stage (n = 14), 8-cell-stage (n = 37) and 16-cell-stage (n = 50). A total of 19 703 RefSeq genes with RPKM > 0.1 in at least one cell were included for the analysis. We conducted SNN-Cliq with the same parameter setting as before (k = 3, r = 0.7 and m = 0.5). SNN-Cliq successfully recovered zygote, early 2-cell, mid 2-cell, late 2-cell and 4-cell stages with only few misclassification, i.e. a late 2-cell-stage cell and a 16-cell-stage cell were placed in wrong clusters (Fig. 3C). However, the 8-cell and 16-cell stages could not be differentiated. It is interesting to note that nine cells at 8-cell stage were separated into another cluster instead of being lumped in the 8- to16-cell cluster. Surprisingly, a closer look into their RNA-seq protocols reveals that the libraries of these nine cells were exclusively prepared by Smart-Seq2, while all the other libraries were prepared by Smart-Seq (recorded in GSE45719). Thus the separation might be at least partially caused by the technical variations of different library preparation protocols. Applying HCS to the same SNN graph yielded similar results to ours in many aspects (Fig. 3C). However, the entire zygote stage was missing because of the singleton problem. Both K-means (K = 7) and DBSCAN (MinPts = 3, Eps = 130) could not separate cell stages effectively; multiple stages were often jointed together. In addition, DBSCAN produced too many noise cells. Again, SNN-Cliq outperformed the other methods in all the three evaluation criteria (Fig. 4C).

4 Discussion

In single-cell transcriptome analysis, it is often desired to group individual cells based on their gene expression levels, so that each group corresponds to a cell type with specific functions. Such analysis could help to characterize cell compositions in tissues and distinguish developmental stages, thereby leading to a better understanding of the physiology and pathology of the tissues and the developmental process. An ideal clustering method for genome-wide single-cell data should be able to distinguish cell types from highly noisy gene expression levels due to the unavoidable biological and technical variations. Aimed at this goal, we have presented a clustering algorithm SNN-Cliq based on a new SNN graph and quasi-clique finding techniques (the novelty of SNN-Cliq is described in Supplementary text).

SNN-Cliq possesses some notable features worthy of noting. First, it has low polynomial complexity [O(n²)] and is efficient in practice. Therefore, it is fast enough to handle large datasets, including the ever-increasing number of single-cell transcriptome datasets in a foreseeable future. Second, SNN-Cliq does not require users to specify the number of clusters to be produced; instead, it automatically determines the cluster number in a dataset. Third, it is easy to use in terms of parameter settings. We have demonstrated that finding a valid value of k is usually not hard and altering k in a certain range will not largely affect the results for many clustering problems. To allow more flexibility, SNN-Cliq provides two granularity parameters r for finding quasi-cliques and m for merging clusters, which can fine-tune the clustering outputs.

SNN-Cliq has outstanding performance on both the synthetic and real experimental datasets evaluated. Since the algorithm does not make any assumptions on the structure of clusters, it can handle data with various shapes and densities as demonstrated on the three synthetic datasets. Furthermore, the evaluation on single-cell RNA-seq datasets clearly demonstrates that SNN-Cliq could generate desirable solutions with high accuracy and sensitivity, outperforming the other algorithms tested [Fig. 4(A–C)]. For instance, for the human cancer cell dataset, SNN-Cliq can detect more cell types than the other methods. For the human and mouse embryo datasets, the clustering of embryonic cells according to their developmental stages can be explained by the extensive changes in gene expression over time during early embryonic development. In both human and mouse, the switch from maternal to embryonic genome control is marked by rapid clearance of maternally inherited transcripts and activation of embryonic genome-derived transcription (Telford et al., 1990). In human, the maternal-zygotic transition occurs during the 4-cell to 8-cell stage (Yan et al., 2013). Compared with the vast changes of gene expression over time, the expression patterns are generally homogeneous between cells from the same developmental stage (Supplementary Fig. S4). In mouse preimplantation development, two major waves of de novo transcription occur before the 8-cell stage. One corresponds to the maternal-zygotic transition at the 2-cell stage; another mid-preimplantation activation occurs during the 4-cell to 8-cell stage, preparing for the overt morphological changes in subsequent stages (Hamatani et al., 2004). During the 8-cell to 16-cell stage, embryos embark on compaction and establishment of cellular contact, followed by lineage differentiation at blastocyst stage (Wang et al., 2004). The cell-to-cell variability at this phase revealed by the correlation heatmap (Supplementary Fig. S4) is consistent with the embryo’s need to develop increasingly diverse cells. However, a relatively small number of genes undergo expression changes between the 8-cell and 16-cell stages (Hamatani et al., 2004; Wang et al., 2004), which may explain the lump of the two stages into one cluster. In addition to detecting the cell stages, SNN-Cliq can recognize cells that were isolated from different embryos and cells that were generated by different library preparation protocols. In particular, SNN-Cliq does not discard data points in regions of low density, as other methods often do by treating them as noise or singletons.

Funding

This work was supported by the UNC Charlotte Faculty Research Grant (1-11227) and the National Science Foundation (EF0849615 and CCF1048261).

Conflict of Interest: none declared.