Predicting regulatory variants with composite statistic

Abstract

Motivation: Prediction and prioritization of human non-coding regulatory variants is critical for understanding the regulatory mechanisms of disease pathogenesis and promoting personalized medicine. Existing tools utilize functional genomics data and evolutionary information to evaluate the pathogenicity or regulatory functions of non-coding variants. However, different algorithms lead to inconsistent and even conflicting predictions. Combining multiple methods may increase accuracy in regulatory variant prediction.

Results: Here, we compiled an integrative resource for predictions from eight different tools on functional annotation of non-coding variants. We further developed a composite strategy to integrate multiple predictions and computed the composite likelihood of a given variant being regulatory variant. Benchmarked by multiple independent causal variants datasets, we demonstrated that our composite model significantly improves the prediction performance.

Availability and Implementation: We implemented our model and scoring procedure as a tool, named PRVCS, which is freely available to academic and non-profit usage at http://jjwanglab.org/PRVCS.

Contact: wang.junwen@mayo.edu, jliu@stat.harvard.edu, or limx54@gmail.com

Supplementary information: Supplementary data are available at Bioinformatics online.

1 Introduction

Interpreting functions of non-coding regulatory variants is an important topic in current genetics study because the majority of the variants discovered by genome-wide association studies (GWASs) and large-scale cancer whole-genome sequencing studies are located in the non-coding regulatory regions (Li et al., 2016; Melton et al., 2015). Thus, evaluating and prioritizing the functional impact of regulatory variants, especially for their roles in disease pathogenicity and applications in personalized medicine, are major challenges in current human genetics.

With the accumulation of functional genomics data, computational methods have been developed to predict and prioritize non-coding regulatory variants (Kellis et al., 2014). Strategies such as supervised learning trained on different gold standard datasets as well as defined scoring scheme have been widely used to distinguish functional/pathogenic variants from neutral ones. Available tools, such as CADD (Kircher et al., 2014), GWAVA (Ritchie et al., 2014), Funseq (Khurana et al., 2013), Funseq2 (Fu et al., 2014), GWAS3D (Li et al., 2013a), SuRFR (Ryan et al., 2014), DANN (Quang et al., 2015) and fathmm-MKL (Shihab et al., 2015), can achieve satisfactory performances based on different levels of functional annotations and causality assumptions. However, current methods either performed poorly or acted inconsistently compared with in vivo saturation mutagenesis of enhancer region (Kircher and Shendure, 2015). To systematically assess the performance and consistency of current methods, comprehensive evaluations are needed using different genome-wide benchmark datasets. In addition, computing and querying prediction results from separate algorithm/database/web server is a time-consuming process. Resources which can integrate pre-calculated prediction scores for prevalent algorithms will benefit the functional annotation of regulatory variants. Furthermore, it has been demonstrated that combining multiple algorithms significantly outperforms each single measurement in prioritizing disease-causing non-synonymous single nucleotide variants (Dong et al., 2015; Li et al., 2015) and positively selected loci (Grossman et al., 2010), which implies potential effectiveness in non-coding regulatory variants prioritization.

In this study, we first compiled genome-wide prediction scores from eight tools that prevalently used in predicting non-coding regulatory variants. We observed significant inconsistence among these investigated predictions. To borrow the potential complementarities and strengths of different tools, we used a composite strategy to integrate multiple predictions and compute the composite likelihood of a given variant being causal in gene regulation. We demonstrated that our method significantly improved the performance of regulatory variants prediction and prioritization in several independent benchmark datasets.

2 Methods

2.1 Variant prediction scores collection and processing

We downloaded genome-wide pre-computed prediction scores from five algorithms including four scores (CADD, DANN, Funseq2, fathmm-MKL) for all possible SNPs in the human reference genome (GRCh37) and one score (GWAVA) for all the 1000 Genomes Project alleles (Genomes Project et al., 2012). Other tools didn’t provide pre-calculated files and only supported known variants, we therefore obtained predictions from execution of corresponding programs. For Funseq, we ran the program for all the 1000 Genomes Project variants under germline and the non-coding analysis parameter setting. For GWAS3D, we calculated the prioritization scores for all 1000 Genomes biallelic variants. For SuRFR, we ran the software for 1000 Genomes variants under the ‘ALL’ model. We finally constructed a resource for functional prediction scores of non-coding SNPs from the above eight prevalent methods (Supplementary Table S1).

2.2 Construction of causal and control regulatory variants training datasets

We compiled a disease-causal or functional regulatory variants dataset by combining four different resources: (i) the Human Gene Mutation Database (HGMD) (Stenson et al., 2014) public dataset used by GWAVA [regulatory mutations from the April 2012 release of HGMD that were downloaded from Ensembl release 70 (Cunningham et al., 2015)]; (ii) the ClinVar (Landrum et al., 2014) pathogenic variants in the non-coding region compiled by GWAVA; (iii) validated regulatory variants from the OregAnno (Griffith et al., 2008) database; (iv) candidate causal SNPs for 39 immune and non-immune diseases in a recent fine-mapping study (Farh et al., 2015) (highly reliable fine-mapped GWAS SNPs with high-density Immunochip). We merged these datasets and annotated each variant using GENCODE v19 annotation by SNVrap (Li and Wang, 2015). We further filtered out the variants that overlapped with gene coding regions and known splicing sites (Ensembl release 70). To select more effective and less biased control dataset than direct random sampling or region-specific matching, we first retrieved SNPs in high LD with each above collected causal variant (r²>0.8 in EUR population) and each significant GWAS SNPs [P < 5E-8 in GWASdb (Li et al., 2016)]. We then randomly drew control non-coding SNPs (no overlapping with gene coding regions and known splicing sites) outside of the retrieved SNPs, considering matched minor allele frequency (absolute 0.05 deviations).

2.3 Regulatory variant validation dataset

In addition to aforementioned training datasets, we manually curated 81 experimentally validated regulatory variants from recent publications, which served as an independent dataset for causal variants in evaluating existing algorithms and our model. We then sampled frequency-matched background SNPs from the same loci (within 10 kb) of these curated causal variants.

2.4 Composite model

We computed the probability density of the scores from each of the eight tools using causal and control datasets respectively by kernel density estimation. For each test, the empirical distribution of the causal variants approximates the probability that a SNP will have a prediction score s given the causal attribute; in contrast, the distribution of neutral variants approximates the probability that a SNP will have the same prediction score s given the neutral attribute. Thus, assuming the independence between tests, the probability that a causal SNP obtains a set of scores (s₁,…s_n) and the probability that a neutral SNP obtains the same set of scores can be solved as the product of the probability of each score in the causal or neutral condition (n is the number of test). We calculated the Bayes factor (BF) to compare the two probability models, in which the null hypothesis is that the variant is neutral, and the alternative hypothesis is that the variant is causal:

$$\text{BF}={\displaystyle {\prod }_{i=1}^n\frac{P(s_i|\text{casual})}{P(s_i|\text{neutral})}}$$

The probability of the variant being causal is computed as the composite likelihood:

$$P(\text{casual}|S)={\displaystyle {\prod }_{i=1}^n\frac{P(s_i|\text{casual})\times \pi }{P(s_i|\text{casual})\times \text{π+}P(s_i|\text{neutral})\times (1-\pi )}}$$

where S is the observed set of scores, and we used flat prior probability π = 0.5 for the causal probability of each variant. Comparing with conventional logit model and support vector machine, this prior probability can be measured using different perspectives of variant function, such as the evolutionary selection and condition-specific functional elements.

We trained the composite model using our refined training dataset after removing variants with any missing score. For CADD, DANN, Funseq2 and fathmm-MKL, 1000 Genomes Project reference alleles and the first alternative alleles were used to extract prediction score. For some tools with more than one model scores, we adopted CADD C-scores (CADD_Cscore), GWAVA transcription start site (TSS) scores (GWAVA_TSS) and fathmm-MKL non-coding score according to theme relevance and author’s suggestion. We used ten-fold cross validation to evaluate the model performance and investigated the performance fluctuation using the enumerated subset of eight individual tools. In prediction, a position with missing score was replaced by a population mean score for the corresponding test (Supplementary Table S1). Furthermore, we tested the model on the curated independent dataset and three established datasets for human regulatory loci.

2.5 Expression quantitative trait loci fine-mapping data

We collected the uniformly processed expression quantitative trait locus (eQTL) fine-mapping data that was profiled by Brown and colleagues (Brown et al., 2013). They used multi-traits Bayesian linear regression models to jointly test for eQTLs from eleven studies on seven tissues/cell lines (Supplementary Table S2). We downloaded the eQTL SNPs regarding the most highly associated cis-linked SNP within an LD block. To further acquire more significant eQTL SNPs, we applied log₁₀BF cutoff values of 10% FDR for each tissue/cell type. We merged these eQTL SNPs in different tissues/cell lines and generated 33,104 the most likely functional eQTLs with less false positive associations. We also sampled an equal number of frequency-matched background SNPs around nearest TSS of randomly selected genes (within 10 kb).

2.6 Allelic imbalanced SNPs of chromatin accessibility

We downloaded 9456 allelic imbalanced SNPs from a recent study (Maurano et al., 2015) on identification of sequence variants influencing human transcription factor occupancy. These loci exhibited strong imbalance (>70%) at a strict FDR cutoff of 0.1% by quantifying the relative proportion of DNase-seq reads mapping to each allele totaled across all heterozygous cell types. We used the same strategy as in eQTL data process to generate control SNPs.

2.7 DNase I sensitivity quantitative trait loci data

We downloaded 579 DNase I sensitivity quantitative trait locus (dsQTL) SNPs and 28 950 control SNPs from deltaSVM article (Lee et al., 2015). deltaSVM applied stringent rules to determine the most likely causal dsQTL SNPs by restricting a fixed small region (100-bp) to ensure that the changes in DNase I sensitivity were physically linked to SNP loci. For control dataset, deltaSVM randomly selected a larger set of common SNPs (minor allele frequency > 5%) only from the top 5% of DNase I sensitivity sites that had been used to identify dsQTLs in the original study Degner et al. (2012).

2.8 Somatic mutation dataset

We retrieved the COSMIC (Forbes et al., 2015) non-coding somatic SNVs dataset and classified them as single-site recurrent or non-recurrent. We compared the composite likelihoods between the recurrent and non-recurrent somatic dataset using Wilcoxon rank-sum test.

3 Results

3.1 Integrative resources for non-coding regulatory variant functional annotation and prediction

To facilitate the efficient search of non-coding variant prediction scores, we compiled an integrative database from eight latest algorithms on non-coding variant functional prediction and prioritization, comprising CADD, GWAVA, Funseq, Funseq2, GWAS3D, SuRFR, DANN and fathmm-MKL (Supplementary Table S3). The dataset presented prediction scores for around 8.6 billion possible single nucleotide substitutions in the human reference genome (GRCh37) either by integrating pre-computed values or executing available tools. Since methods like Funseq, GWAVA, GWAS3D and SuRFR, didn’t provide precalculated files or only supported known variants or took long execution time for all possible SNPs, we only provided known variants from 1000 Genomes Project biallelic SNPs in current version. We present the prediction scores of each variant using one line encoding instead of three lines encoding for different alleles, which will benefit the query and reduce the storage space. The compressed dataset is available at ftp://jjwanglab.org/PRVCS/v1.1/dbNCFP_whole_genome_SNVs.bgz, which can also be randomly accessed by Tabix (Li, 2011).

Identifying benchmark data of causal regulatory variants and negative control for training model is challenging. To maximally extend data spectrum and avoid bias in later evaluation, we constructed a large and integrative benchmark dataset for non-coding causal variants from HGMD, ClinVar, OregAnno and fine-mapped GWAS of 39 immune and non-immune diseases. After merging and removing variants with missing value, we generated 5247 genome-wide non-redundant variants with reliable causal evidence as the training set, including disease-causal, regulatory-casual and the most likely casual GWAS variants. Annotations showed that these variants are widely spread in non-coding genomic regions (Supplementary Figure S1), and they also cover the full range of allele frequencies (Supplementary Figure S2). This integrative collection might be a reference data for training and evaluating regulatory variant prediction models. We further generated a control dataset (10 times that of the positive data) with matched allele frequency from LD blocks that do not contain casual and disease-associated variants (Table 1). The dataset together with original sources are available on ftp://jjwanglab.org/PRVCS/reference.

Table 1.

The training and testing dataset in the study

Name	Description	No. positive set	No. control
Training dataset	Refined causal SNPs in the non-coding region from different resources including HGMD, ClinVar, OregAnno and fine-mapping causal variant with high density Immunochip	5247	55 923
Curated SNPs	Manually curated experimentally validated regulatory SNPs	81 (76)	156
eQTL SNPs	Uniformly processed fine-mapping eQTL SNPs for eleven studies	33 104 (31 118)	36 540
Allelic imbalanced SNPs	Allelic imbalanced SNPs of chromatin accessibility by a large number of DNase-seq assays	9456 (8592)	9678
dsQTL SNPs	The most likely causal dsQTL SNPs from deltaSVM	579 (559)	28 950 (26 832)

Note: number in bracket is the number of variant with non-missing values for eight tools.

3.2 Existing methods show inconsistent prioritization of non-coding regulatory variants

To measure the statistical dependence of ranked scores among collected algorithms, we performed Spearman’s Rank Correlation (SRC) tests for each pair of algorithms on each of the causal (Fig. 1A) and control (Supplementary Figure S3) datasets. We found that algorithms with similar models or training features have moderate pairwise correlations, such as FunSeq and FunSeq2 (SRC ∼0.5), or CADD, DANN and Fathmm-MKL (SRC ∼0.6). However, algorithms with different pathogenicity/regulatory causality assumptions are weakly correlated (SRC < 0.3). The weak correlations among existing tools might indicate the heterogeneity of training datasets, features used, as well as the difference in algorithmic assumptions.

Fig. 1.

SRC among eight tools for (A) refined causal dataset and (B) curated experimentally validated dataset. Numbers indicate the correlation coefficients; Lines indicate linear fitting; Line range indicates y range with continuous x values (Color version of this figure is available at Bioinformatics online.)

In addition, we manually curated 81 experimentally validated regulatory variants from recent publications (no overlaps with the training dataset), which served as independent data to test prediction performance (Table 1 and Supplementary Table S4). Pairwise SRC of eight algorithms on this curated data still presented weak correlations (Fig. 1B), further suggesting inconsistent predictions among current methods.

3.3 Composite of multiple signals improves casual regulatory variant detection

To take advantage of possible complementarities among different tools, we combined them into a composite likelihood statistic and estimated the probability of the investigated variant being causal. The composite model significantly improved the prediction performance on our refined training dataset (Fig. 2A). The ten-fold cross-validation of our method yielded an Area Under the Curve (AUC) of 0.84 and an average maximal Matthews Correlation Coefficient of 0.41, higher than those of all current tools. Further evaluation on the independent regulatory variants dataset also indicated that the composite model performed better than existing tools (Fig. 2B). We found GWAS_TSS and FunSeq2 consistently outperformed the remaining tools in these two experiments. However, CADD and DANN showed lower AUC, possibly because they were not specially designed to prioritize non-coding regulatory variants.

Fig. 2.

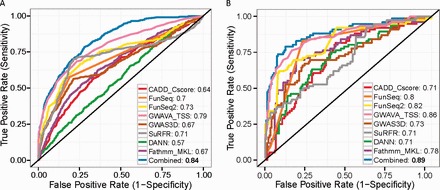
Regulatory variant predictions performance of different methods. (A) ROC curves by ten-fold crossvalidation for CADD, FunSeq, FunSeq2, GWAVA, GWAS3D, SuRFR, DANN, fathmm-MKL and our combined model on our refined training dataset. (B) ROC curves on curated experimentally validated dataset. AUC is shown behind each tool name (Color version of this figure is available at Bioinformatics online.)

Since our training dataset contained SNPs that haven’t been recognized as pathogenic, we here inspect whether our composite model also works well in only pathogenic dataset. We excluded FunSeq, GWAS3D and SuRFR in this test due to many rare variants and variants located in mitochondrial DNA that are not scored by these tools (missing values). 99 pathogenic non-coding SNPs remained with valid scores for CADD, GWAVA, Funseq2, DANN and fathmm-MKL. For these independent pathogenic SNPs, we compared our combined model against two control datasets provided by GWAVA (non-coding variants classified in ClinVar as non-pathogenic and a set of 1000 Genomes Project variants with matched distance to the nearest TSS). We found the combined model (AUC of 0.89) outperformed CADD, GWAVA, Funseq2 and DANN substantially, but worked slightly worse than fathmm-MKL (AUC of 0.90). This may be due to the fact that fathmm-MKL had used these ClinVar pathogenic variants to train their model. (Supplementary Figure S4).

We further investigated whether combining only a subset of the eight methods can achieve better predictive power. Interestingly, many of subset combinations could slightly improve the model performance upon the average AUC of 10-fold cross-validation and rank variance (Supplementary Table S5). The best model consisted of only four tools (CADD_Cscore, GWAVA_TSS, GWAS3D and SuRFR) with an AUC of 0.858 (Supplementary Figure S5). These four tools complement each other by using different learning algorithms and measuring different features such as evolutionary selection, chromatin states, transcription factor binding affinity etc. Although some subset combinations could achieve better performance using cross-validation of training data, we still lack large and independent gold standard to test their stability. Therefore, to make an equitable and unbiased evaluation, we used full combination model in most of comparisons.

3.4 Evaluation of composite model on eQTL, allelic imbalance and dsQTL datasets

Recent advances on large-scale genotyping and genomic/epigenomic sequencing have enabled us to efficiently map QTLs to different molecular phenotypes (Kellis et al., 2014). Here, we utilized three independent human QTLs datasets to further validate the capacity of full composite model in prioritizing regulatory variants underlying different molecular traits of gene regulation. The three datasets include uniformly processed fine-mapping eQTLs on different tissues/cell types, allelic imbalanced loci of chromatin accessibility and deltaSVM refined dsQTLs (Table 1). Our combined model exhibited substantial improvement in predicting eQTLs (AUC of 0.81) and allelic imbalanced loci (AUC of 0.92), while the second best algorithm only achieved AUCs of 0.74 and 0.85, respectively (Fig. 3A and B). For the dsQTLs dataset, although only containing a few hundred positive variants, the combined model received similar performance as FunSeq2 (both for AUC of 0.72), outperforming other algorithms (Fig. 3C). FunSeq2 performed stably as the best method in these assessments for functional QTLs. This is probably due to more regulatory annotation used, such TF motif, distal regulatory elements-gene interaction and regulatory network. Taken together, these experiments strongly demonstrated that our composite model has distinct advantage in prioritizing human functional regulatory variants. All benchmark data are available at ftp://jjwanglab.org/PRVCS/benchmark.

Fig. 3.

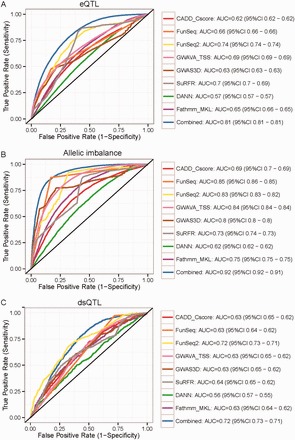
Performance of regulatory QTLs prediction from different methods. ROC curves on (A) eQTLs dataset; (B) allelic imbalanced dataset; (C) dsQTLs dataset (Color version of this figure is available at Bioinformatics online.)

3.5 Evaluation on somatic dataset

We also observed the difference of our composite likelihood between COSMIC recurrent and non-recurrent SNPs. Wilcoxon rank-sum test showed a significant difference (P-value < 2.2 e-16; Supplementary Figure S6). SNPs that occur in more than one COSMIC reported sample had higher likelihood than those that are in single sample. This result suggested that our model is also suitable to prioritize somatic regulatory variants.

3.6 Comparison with unsupervised integrative approach

Most of current methods for regulatory variants prediction rely on the supervised learning strategy. However, a recent approach, Eigen, can integrate different annotations into one measure of functional importance and is based on an unsupervised learning approach (Ionita-Laza et al., 2016). We therefore compared our composite methods with Eigen precomputed non-coding score for four established dataset, including experimental validated SNPs, eQTLs, allelic imbalanced SNPs and dsQTLs. Our results show that our composite method constantly works better than Eigen non-coding score (Supplementary Figure S7) in all four tests.

3.7 PRVCS software

We implemented our model and scoring procedure in JAVA programming language, named PRVCS, which is freely available for academic and non-profit users at http://jjwanglab.org/PRVCS. The software can take either VCF (Danecek et al., 2011) or ANNOVAR (Wang et al., 2010) variant format as input. Our PRVCS Java program takes ∼0.5 h/CPU and 10 GB RAM to score all 1000 Genomes Project variants. We also provided a Tabix Perl wrapper script to facilitate the random access remotely without downloading whole precompiled score dataset.

4 Discussion

In summary, we have addressed several essential problems in the field of regulatory genetic variants prioritization. We provide an integrative and lightweight resource to facilitate the efficient query of prediction scores for current prevalent algorithms. The refined training and benchmark data of regulatory variants could be used to evaluate subsequent methods in the future. The inconsistent prioritization among existing tools impedes the identification of true regulatory variants. Compared with the field of disease-causal non-synonymous variant prediction (Dong et al., 2015; Gonzalez-Perez and Lopez-Bigas, 2011; Li et al., 2013b; Lopes et al., 2012), ensemble methods are urgently needed to predict and prioritize non-coding regulatory variants. Our composite strategy takes advantage of the complementary attributes of individual tools to achieve a better performance.

Identifying the high quality and confident causal regulatory variants training dataset (including functional and pathogenic) and corresponding control is challenging, because the mechanisms of gene regulation are complicated. Regulatory variants could affect many different gene regulation processes such as transcription factor binding, nucleosome positioning, epigenomic modification and non-coding RNA tethering (Kellis et al., 2014). The limited number of experimentally validated regulatory variants impedes the comprehensive and sufficient capture of these regulatory events. For example, there are only a few hundred known causal non-coding variants in ClinVar and OregAnno databases, and these variants are highly region-biased (lots of ClinVar pathogenic variants are co-located; many OregAnno variants are located in the TSS region). Although current massively parallel reporter assay has been applied to investigate the allele effect on gene expression (Patwardhan et al., 2012; Vockley et al., 2015), studies were only carried out on limited chromosome regions and inevitability lost chromatin context. On the other hand, current high-density genotyping arrays and sophisticated fine-mapping strategies enable us to identify the most likely casual variants from large scale GWAS and QTL studies. The most widely used HGMD database has integrated many disease-associated variants (Cassa et al., 2013; Clark et al., 2015). Although we still face difficulty to identify false positive hits from LD proxy of GWAS fine-mapped SNPs, to construct larger and less region-biased training dataset, incorporating the most reliable GWAS/QTL fine-mapping results would be a temporary, practicable solution in the non-coding regulatory variant prediction field. Besides, selecting appropriate control dataset could improve the training model. Comparing with the random/regional sampling, our control selection strategy can avoid the bias of specific region selection (such as promoter) and remove all causal LD blocks that may contain bias of GWAS ascertainment. However, there is still no guarantee that those variants are not functional. Also, some of our control SNPs could locate in the intron region and regulate pre-mRNA processing and splicing. Furthermore, SNPs in the exonic region, which were omitted by our selection, can also regulate the gene expression (Stergachis et al., 2013).

The correlations among the investigated existing methods are from weak to moderate, which might be attributed to the different perspectives and logics of existing algorithms. CADD and DANN applied fixed or nearly fixed human-derived alleles and simulated de novo mutations to train the model, which focus on classifying the deleterious variants from neutral/selected variants. However, our refined training dataset summarized causal variants from a regulatory angle by merging the functional regulatory, deleterious and pathogenic non-coding variants. Therefore, compared with tools trained on HGMD (GWAVA, fathmm-MKL and SuRFR) or under regulatory assumption (GWAS3D, FunSeq and Funseq2), CADD and DANN didn't perform well in most of the evaluations on regulatory QTLs but obtained good performance on ClinVar dataset. This may suggest that our composite method is very suitable to prioritize functional regulatory variants instead of identifying pathogenic non-coding variants using DANN and CADD. In addition, certain annotation features were frequently incorporated into many algorithms, resulting in the similar scoring scheme of specific variants. Clearly, CADD and DANN utilized same feature set and are hence moderately correlated. Also, ENCODE genomic/epigenomic annotations, as well as base-wise evolutionary information [like GERP ++ (Davydov et al., 2010) and phastCons (Siepel et al., 2005)], were substantially adopted in FunSeq, Funseq2, GWAS3D, SuRFR and fathmm-MKL. Interestingly, CADD and fathmm-MKL used different training datasets but correlated well with each other, probably due to large number of shared annotation features. The better performance of our subset combination model than the full model may reflect these redundant or even conflicted relationships among existing tools. Nevertheless, large and independent gold standard is needed to test the correlation of different tools and stability of reduced combination model. Furthermore, for some machine learning-based programs like CADD, DANN, GWAVA and fathmm-MKL, they used training dataset partially overlap with our refined training dataset, so the performance might be inflated in cross validation. Therefore, completely independent and high-quality causal non-coding regulatory variants are needed.