Evaluating large-scale propensity score performance through real-world and synthetic data experiments

Abstract

Background

Propensity score adjustment is a popular approach for confounding control in observational studies. Reliable frameworks are needed to determine relative propensity score performance in large-scale studies, and to establish optimal propensity score model selection methods.

Methods

We detail a propensity score evaluation framework that includes synthetic and real-world data experiments. Our synthetic experimental design extends the ‘plasmode’ framework and simulates survival data under known effect sizes, and our real-world experiments use a set of negative control outcomes with presumed null effect sizes. In reproductions of two published cohort studies, we compare two propensity score estimation methods that contrast in their model selection approach: $L_1$-regularized regression that conducts a penalized likelihood regression, and the ‘high-dimensional propensity score’ (hdPS) that employs a univariate covariate screen. We evaluate methods on a range of outcome-dependent and outcome-independent metrics.

Results

$L_1$-regularization propensity score methods achieve superior model fit, covariate balance and negative control bias reduction compared with the hdPS. Simulation results are mixed and fluctuate with simulation parameters, revealing a limitation of simulation under the proportional hazards framework. Including regularization with the hdPS reduces commonly reported non-convergence issues but has little effect on propensity score performance.

Conclusions

$L_1$-regularization incorporates all covariates simultaneously into the propensity score model and offers propensity score performance superior to the hdPS marginal screen.

Key Messages

• We detail a comprehensive, open-source evaluation framework for propensity score performance.

• L₁ statistical regularization (LASSO) provides improved confounding control as compared with the hdPS for propensity score model selection.

• Using a larger covariate set and including all covariates into the propensity score model produces improved propensity score performance.

• Negative control experiments provide a powerful alternative to simulations in evaluating observational study methods.

• The hdPS marginal screen suffers from covariate interdependence in high-dimensional data.

Introduction

Retrospective observational studies constitute a resource for clinical evidence gathering complementary to randomized controlled trials. However, whereas real-world databases can offer voluminous information on millions of patients, observational studies suffer from obstacles that introduce bias and prevent their more widespread use by the medical community.^1–3 Chief among these is the unknown and non-random treatment assignment process that precludes the cohort balance inherent in randomized studies.

The propensity score (PS), an estimate of treatment assignment probability, is a predominant tool for confounding control in retrospective studies.^4,5 Rich literature addresses best adjustment practices once the PS has already been estimated,^6–10 but relatively few studies evaluate methods for PS estimation.^11,12 Propensity scores are estimated with a classification model, often logistic regression, using pretreatment baseline patient covariates such as demographics and indicators for medical conditions, procedures and drug exposures.⁶ Recent research has questioned the reliability of expert opinion in the traditional approach of manually selecting suspected confounders to include as PS model covariates.¹³ However, the alternative approach, to use all available covariates in the PS logistic model, requires additional model fitting strategies to prevent sparse data bias¹⁴ or entirely non-convergent estimates.

The ‘high-dimensional propensity score’ (hdPS) is a PS model selection approach that selects a fixed number of covariates with highest marginal association with the study outcome.¹⁵ Despite relying on univariate associations in high-dimensional data with likely nonindependent covariates, the hdPS has gained widespread use in pharmacoepidemiology.¹⁶ Other PS model fitting methods include multivariate approaches that incorporate penalties or modifications to the regression objective function.^17–19 In particular, $L_1$-regularization is a workhorse of statistical model selection,²⁰ and has been previously applied to PS estimation.^11,21,22

In this paper, we address the comparative performance of PS estimators in large-scale observational settings in the order of 100 000 subjects and 100 000 unique covariates. We detail a comprehensive framework incorporating synthetic and real-world data experiments for evaluating PS methods, and conduct a comparison of the hdPS with $L_1$-regularization for PS estimation. We provide this framework as an open-source R package [https://github.com/OHDSI/PropensityScoreEvaluation].

Methods

Clinical scenarios

We compare PS methods through reproductions of two previously published retrospective cohort studies using the Truven Health MarketScan Medicare Supplemental and Coordination of Benefits Database. Each study compares two drugs: one designated as the active treatment and the other as the reference. See Supplementary material 1–4, available as Supplementary data at IJE online for full cohort definitions.

The first is a cohort study²³ of new users of anticoagulants, i.e. dabigatran and warfarin initiators in patients with nonvalvular atrial fibrillation. Dabigatran is the active treatment; warfarin is the reference; and intracranial haemorrhage is the outcome of interest. The second is a cohort study²⁴ of new-users of COX-2 inhibitors and traditional nonsteroidal anti-inflammatory drugs (NSAIDs) initiators. We select celecoxib, a representative COX-2 inhibitor, as the active treatment; diclofenac, a representative traditional NSAID, as the reference; and upper gastrointestinal complications as the outcome of interest.

Synthetic framework

Our synthetic approach simulates survival outcomes while preserving characteristics of real-world clinical cohorts. We construct new user cohorts comparing the effect of two drugs on an outcome of interest,²¹ and use the exposure status and baseline covariates from the real data in constructing a Cox proportional hazards model to simulate new survival outcomes. We derive empirical estimates for necessary model components such as baseline survival and censoring functions, and covariate hazard ratio coefficients. Then we perform inverse transform sampling on the subject-specific survival functions.²⁵ See Supplementary material 5, available as Supplementary data at IJE online, for full synthetic framework details. Our approach extends the ‘plasmode’ framework^26,27 by detailing additional distributional forms for the survival and censoring process, proposing additional outcome prevalence adjustment approaches, using an accurate outcome prevalence equation and, most critically, using a non-informative, covariate-free censoring process consistent with the proportional hazards model. We modify the model to simulate under three generative hazard ratios ($1.0, 1.5, 2.0$) and three outcome prevalences ($1\%, 5\%, 10\%$) for $\mathrm{n}\mathrm{i}\mathrm{n}\mathrm{e}$ total simulation settings.

Negative control outcome experiments

In addition to simulations under known hazard ratios, we perform negative outcome control experiments using sets of outcomes believed to be unrelated to the compared treatments, thus having a presumed true hazard ratio of 1.^28,29 Negative control outcomes entirely use real-world data, and when properly specified they provide an estimate of residual systemic bias in a study after controlling for measured confounders. For each study, we identify a set of 50 negative control outcomes using a data-rich algorithm,³⁰ and exclude outcomes that have less than $0.02\%$ prevalence in the combined treatment groups, leaving $49$ negative control outcomes for the Anticoagulants study and $29$ for the NSAIDs study. We produce PS-adjusted treatment effect size estimates for each outcome in the set, and fit the estimates to an empirical null distribution.²⁹ We expect successful PS confounding control to reduce residual bias, and produce a null distribution centred more closely at the presumed null effect. A list of negative outcomes used are given in Supplementary material 6 and 7, available as Supplementary data at IJE online.

Covariates

We use two sets of pretreatment covariates. The first, ‘hdPS Covariates’, is our reproduction of the specific covariates prescribed for the hdPS.¹⁵ The second, ‘OHDSI Covariates’, follows the Observational Medical Outcomes Partnership Common Data Model Version 5 format³¹ and is commonly used in the Observational Health Data Sciences and Informatics (OHDSI) community.³² Both sets of covariates include demographic information (sex, age and treatment initiation index year) and (differently coded) covariates for conditions, procedures and drugs. However, the ‘OHDSI Covariates’ include additional covariate categories and are more expansive than the ‘hdPS Covariates’. Both covariate sets are used to create the synthetic model to create a detailed simulated outcome generative process. See Supplementary material 8, available as Supplementary data at IJE online, for full covariate details.

Propensity score methods

We compare the hdPS to $L_1$-regularization as PS estimation methods. We apply the hdPS to only ‘hdPS Covariates’, and we apply $L_1$-regularization to both covariate sets separately, and to them combined. We include two variations of the hdPS: ‘bias-based hdPS’ that screens covariates based on their apparent relative risk, a measure of confounding on the outcome,³³ and ‘exposure-based hdPS’ that screens based on treatment relative risk.¹² We use default hdPS settings,¹⁵ and fit the resultant logistic regression both without regularization and with $L_1$-regularization, giving seven total compared PS methods (Table 1). The unregularized regression can lead to ‘convergence failures’ that occur due to the PS estimate non-existence.^16,34,35 All regularization penalties are selected through 10-fold cross-validation using large-scale regression tools.³⁶ Using the CohortMethod R package,³⁷ we perform many-to-one PS matching and estimate the treatment hazard ratio using a stratified Cox survival outcome model with treatment as the only covariate. Details regarding the PS adjustment process are given in Supplementary material 9, available as Supplementary data at IJE online.

Table 1.

PS methods evaluated across two real-world studies

PS method	Description
L1-Reg-All	$L_1$-regularization on combined covariates
L1-Reg-OHDSI	$L_1$-regularization on ‘OHDSI Covariates’ only
L1-Reg-HDPS	$L_1$-regularization on ‘hdPS Covariates’ only
bias-hdPS	bias-based hdPS, without regularization
bias-hdPS-Reg	bias-based hdPS, with regularization
exp-hdPS	exposure-based hdPS, without regularization
exp-hdPS-Reg	exposure-based hdPS, with regularization

Metrics

We report standardized difference measures of covariate balance across the PS matched sets, and the c-statistic of the PS models that measures treatment predictive accuracy.^38,39 We report the bias and root mean square error (RMSE) of the estimated hazard ratio from the true hazard ratio, that is known in the simulations and presumed to be $1$ in the negative control experiments. We assess negative control experiment results using fitted Gaussian empirical null distributions that estimate the residual bias distribution.²⁹

Results

Cohorts

The Anticoagulants study contains $72 489$ subjects: $19 768$ new dabigatran users and $52 721$ new warfarin users. There are $98, 118$ unique baseline covariates among all subjects, and the outcome prevalence of intracranial haemorrhage is $0.26\%$. The NSAIDs study contains $121 317$ subjects: $78 695$ new celecoxib users and $42 622$ new diclofenac users. There are $75 425$ unique covariates among all subjects, and the outcome prevalence of upper gastrointestinal complications is $1.81\%$. The ‘OHDSI Covariates’ set is notably larger than the ‘hdPS Covariates’ set in both studies (Table 2). No threshold is used to exclude infrequent covariates.

Table 2.

Number of covariates in each study, by source covariate set. Both sets share same demographics covariates

		Covariates
Study		All	OHDSI	hdPS
Anticoagulants	Full cohorts	98 118	82 281	15 854
	Synthetic model	525	446	83
NSAIDs	Full cohorts	75 425	63 004	12 441
	Synthetic model	530	478	60

Propensity score estimate existence

To explore the robustness of the default hdPS that excludes regularization, we conduct tests for hdPS estimate existence under varied simulation parameters (Supplementary material 10, available as Supplementary data at IJE online). We find that simulations with smaller cohorts and lower outcome prevalence have less likely PS estimate existence (Supplementary Table 1, available as Supplementary data at IJE online). To address this problem, $L_1$-regularization readily promotes model existence for the hdPS.

PS distributions and covariate balance

Although the two studies differ in absolute c-statistic values, they demonstrate a similar ordering of PS methods in order of highest-to-lowest c-statistic: L1-Reg-All, L1-Reg-OHDSI, L1-Reg-HDPS, bias-based hdPS, exposure-based hdPS (Table 3). These trends can be visually appreciated in the PS distributions (Supplementary Figures 1 and 2, available as Supplementary data at IJE online). L1-Reg-All and L1-Reg-OHDSI have much higher c-statistic than the other methods that use only the ‘hdPS Covariates’, suggesting that the larger ‘OHDSI Covariates’ set allows for improved treatment prediction accuracy. Expectedly, increased c-statistic and PS distribution differentiation lead to fewer suitable subjects being included in the matching process (Table 3).

Table 3.

c-statistic of PS methods, and the percentage of cohorts included in the many-to-one matching process

	Anticoagulants study		NSAIDs study
PS method	c-statistic	% Matched	c-statistic	% Matched
L1-Reg-All	0.798	82.5	0.750	91.6
L1-Reg-OHDSI	0.793	83.0	0.750	91.7
L1-Reg-HDPS	0.760	89.2	0.708	95.5
bias-hdPS	0.743	91.3	0.693	96.5
bias-hdPS-Reg	0.742	91.6	0.691	96.7
exp-hdPS	0.737	91.3	N/A	N/A
exp-hdPS-Reg	0.735	91.9	0.678	97.5

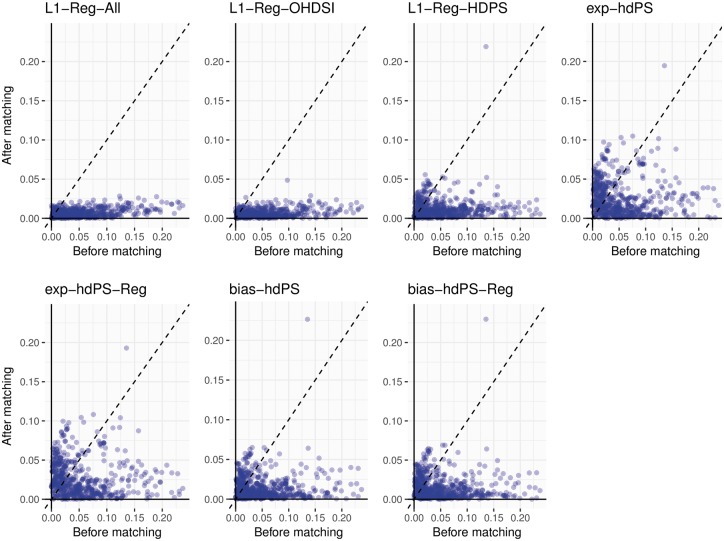
In the simulation experiments, only the synthetic model covariates included in the generative survival model are true confounders that contribute to estimation bias. All PS methods greatly reduce the standardized differences for these covariates for both the Anticoagulants study (Figure 1) and NSAIDs study (Supplementary Figure 3, available as Supplementary data at IJE online). In both studies, the empirical cumulative distribution functions of the PS-adjusted standardized differences reveal a consistent order in performance: L1-Reg-All and L1-Reg-OHDSI provide the best covariate balance, then L1-Reg-HDPS, then bias-based hdPS, and exposure-based hdPS is worst (Supplementary Figures 4 and 5, available as Supplementary data at IJE online). The same relative performance extends to balance among all covariates. Among only hdPS Covariates, L1-Reg-HDPS performs best and exposure-based hdPS worst in both studies, and bias-based hdPS beats L1-Reg-All/L1-Reg-OHDSI in the Anticoagulants study, and vice versa in the NSAIDs study.

Figure 1.

Anticoagulants study: before and after PS matching scatterplot of absolute standardized differences for synthetic model covariates. After matching outlier corresponds to higher frequency of indicator ‘Condition Era Overlapping with Cohort Index: Atrial Fibrillation’ in Warfarin group.

The Anticoagulants study after-matching outlier in Figure 1 is the ‘OHDSI Covariates’ indicator for ‘Condition Era Overlapping with Cohort Index: Atrial Fibrillation’. This covariate identifies patients with presumably active or chronic atrial fibrillation at the time of treatment initiation, who may require the stronger anticoagulation control that warfarin is believed to provide. This complex covariate and likely confounder is absent from the ‘hdPS Covariates’ that only includes simple prior condition indicators, and its imbalance is exacerbated by the PS methods that exclude the larger ‘OHDSI Covariates’ set.

Simulation-hazard ratio estimation

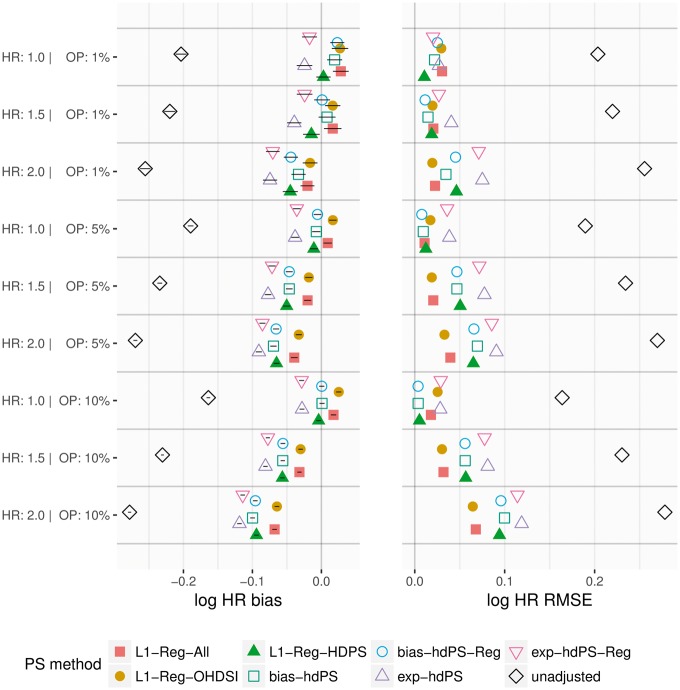
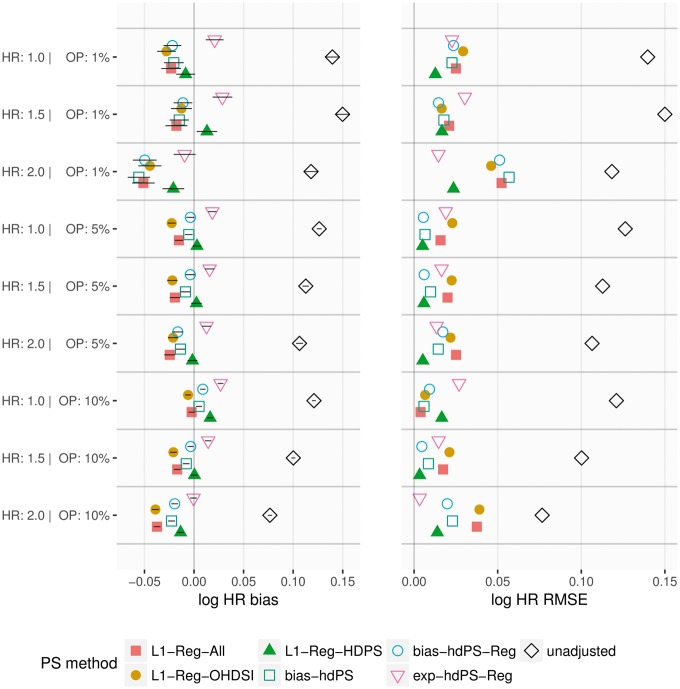
In both studies, the hdPS with and without regularization provide similar simulation results. In the Anticoagulants study (Figure 2), bias-based hdPS and L1-Reg-HDPS provide the lowest RMSE for the $HR=1.0$ simulations, whereas L1-Reg-All and L1-Reg-OHDSI are generally superior for the $HR=1.5$ and $HR=2.0$ simulations. L1-Reg-All and L1-Reg-OHDSI consistently have higher 95% coverage of the true HR than other methods (Supplementary Figure 6, available as Supplementary data at IJE online). In the NSAIDs study (Figure 3), L1-Reg-HDPS provides the lowest RMSE under a majority of simulation parameters, although exposure-based hdPS is best for two of the three $HR=2.0$ simulations. All PS methods have generally high coverage, near or above 90%, and improve substantially on the unadjusted coverage (Supplementary Figure 7, available as Supplementary data at IJE online). In both studies, exposure-based hdPS provides the smallest absolute bias correction relative to unadjusted, and L1-Reg-All/L1-Reg-OHDSI provide the largest. Additionally, as true hazard ratio is increased, there is a strong negative shift in bias that dominates the differences among PS methods.

Figure 2.

Anticoagulants study: bias in log hazard ratio (HR) with one-standard deviation (1-SD) intervals, and associated root mean squared error (RMSE), across 100 simulations under different simulation parameters of true HR and outcome prevalence (OP).

Figure 3.

NSAIDs study: bias in log hazard ratio (HR) with one-standard deviation (1-SD) intervals, and associated root mean squared error (RMSE), across 100 simulations under different simulation parameters of true HR and outcome prevalence (OP).

Negative control-hazard ratio estimation

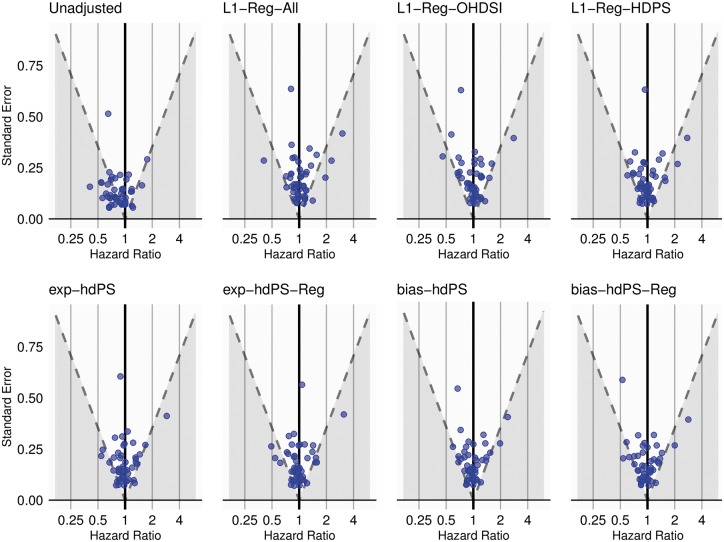
In the absence of residual bias, we expect $95\%$ of negative control estimates to include the presumed hazard ratio of $1$ in their $95\%$ confidence intervals. For the Anticoagulants study, the unadjusted negative control outcomes reveal a clear negative bias that is reduced by all PS methods (Figure 4). The unadjusted coverage of 53% is increased to 80–90%, with L1-Reg-All and L1-Reg-OHDSI providing the highest coverage and exp-hdPS and exp-hdPS-Reg providing the lowest (Table 4). bias-hdPS and exp-hdPS are the most efficient methods as measured by RMSE, and the $L_1$-regularization methods have least biased empirical null distributions, which estimate the residual bias using both the negative control point estimates and their uncertainty. For the NSAIDs study, the unadjusted negative control estimates (Supplementary Figure 8, available as Supplementary data at IJE online) have a higher coverage at 83%, and all PS methods provide between 83% and 88% coverage, except for L1-Reg-OHDSI at 97% (Table 4). L1-Reg-OHDSI provides the most efficient estimates, and L1-Reg-All and bias-hdPS-Reg have least biased null distributions. Both bias-hdPS and exp-hdPS demonstrate degrees of PS estimate non-existence and require regularization for successful model fitting.

Figure 4.

Anticoagulants study: hazard ratio estimates (horizontal axis) and width of 95% confidence interval (via standard error) (vertical axis) for 49 negative control outcomes. Dashed line represents the straight line boundary at where the 95% confidence interval does (above) or does not (below) contain the assumed true hazard ratio of 1.

Table 4.

Results for 49 negative controls in Anticoagulants study and 29 in NSAIDs study

	Anticoagulants				NSAIDs
PS method	Cov	RMSE	Mean	SD	Cov	RMSE	Mean	SD
Unadjusted	0.53	0.325	−0.172	0.216	0.83	0.370	−0.061	0.314
L1-Reg-All	0.88	0.303	0.023	0.108	0.83	0.367	−0.023	0.229
L1-Reg-OHDSI	0.90	0.276	−0.020	0.061	0.97	0.319	−0.087	0.161
L1-Reg-HDPS	0.86	0.275	−0.026	0.089	0.83	0.387	−0.115	0.228
bias-hdPSa	0.86	0.258	−0.037	0.065	0.88	0.347	−0.065	0.135
bias-hdPS-Reg	0.82	0.292	−0.036	0.094	0.83	0.372	−0.039	0.244
exp-hdPSb	0.80	0.268	−0.037	0.113	N/A	N/A	N/A	N/A
exp-hdPS-Reg	0.80	0.284	−0.037	0.096	0.86	0.434	−0.154	0.320

Mean and SD are of the empirical null Gaussian distribution fit to the log hazard ratio estimates.

Cov, coverage of the null effect; RMSE, root mean squared error of log hazard ratio estimates from 0; SD, standard deviation.

^abias-hdPS fails to converge on 12 of 29 outcomes in NSAIDs study.

^bexp-hdPS fails to converge on all 29 outcomes in NSAIDs study.

Discussion

In this study, we conduct synthetic and negative control experiments comparing $L_1$-regularization with the bias- and exposure-based hdPS as PS estimators. We find that $L_1$-regularization and use of a larger covariate set provides the best treatment prediction accuracy and covariate balance, and the exposure-based hdPS provides the worst. However, these differences do not cleanly translate to reduced estimation bias. In simulations, $L_1$-regularization and bias-based hdPS generally outperform exposure-based hdPS under varied simulation parameters. In negative control experiments, PS adjustment provides noticeable improvement over unadjusted in only one of two studies. For that study, $L_1$-regularization provides higher coverage of the null effect size and has least biased empirical null distribution, but the hdPS provided smaller RMSE estimates at the expense of closer to nominal coverage.

We observe a simulation estimation bias towards the null which increases with true hazard ratio and dominates the differences among PS methods. This bias appears in other proportional hazards simulation studies when there is unmeasured confounding in a randomized experiment⁴⁰ and when propensity scores are used for confounding control.¹⁰ In Supplementary material 11, available as Supplementary data at IJE online, we show empirically that this bias arises when there are differences in hazard between matched subjects. Under a proportional hazards simulation model, covariate differences between matched subjects will likely contribute to this bias. By using real-world data, our negative control experiments avoid unnecessary proportional hazards assumptions, and avoid simulation design decisions that can be a source of investigator bias. We believe that negative control experiments can be a valuable tool in addition to simulations for conducting observational studies and evaluating methods.

Bias reduction may be the intended goal of PS adjustment, but alone it is insufficient to judge PS method performance unless assessed on large and robust outcome sets. Outcome-dependent metrics are susceptible to the choice of outcome model and the PS adjustment approach, and methods that work well for one outcome may not for another. Because in this study we are interested in comparing PS estimation methods, metrics such as covariate balance offer an outcome-independent assessment of PS performance. In addition, the c-statistic can also be a reliable outcome-independent indicator of PS performance. We find that the PS methods that produce higher c-statistic also substantially improve covariate balance among true confounders (in the simulation) and among all covariates. Other studies that have questioned the c-statistic as a PS diagnostic^41–44 relied on making marginal changes to a very small simulation model. We reach a different conclusion on the utility of the c-statistic in real-world cohorts that have many thousands of patients and covariates.

A desire to include only ‘true confounders’ in the PS model has motivated the hdPS and other outcome-dependent confounding adjustment methods for PS estimation.^18,45 In addition to noting that these methods violate the unconfoundedness assumption of the potential outcomes framework,⁴⁶ we recommend that outcome-dependent PS estimators be evaluated using control outcomes and not with simulations, as outcomes synthetically generated through a known process can favourably bias outcome-dependent methods in an unrealistic and prophetic fashion. As an extreme example, one could construct the PS model with the exact confounders present in the synthetic model, and thus produce artificially unbiased effect estimates.

Another goal of outcome-dependent propensity scores, and more broadly investigator selected PS models, is to avoid instrumental variables (IVs) that predict treatment but contribute no confounding on the outcome. The potential harmful effects of IVs in inflating estimation bias⁴⁷ and variance⁴⁸ have been shown in theoretical examples and simulation experiments using small models. However, the prevalence of IVs in real-world data is debatable and their identification difficult. In our experiments, the bias-based hdPS that should avoid IVs is not superior to $L_1$-regularized methods that include all available covariates. Comprehensive methods for IV identification and characterization in real-world observational data, and knowledge of the consequences on PS estimator selection, are still lacking and merit further investigation.

The hdPS’s univariate screen for PS model selection suffers from covariate interdependence in large-scale data. We show in Supplementary material 10, available as Supplementary data at IJE online, that hdPS estimate non-existence, or ‘non-convergence’, is a problem in smaller sample sizes and with lower outcome prevalences, corroborating published observations.^34,35 If there is enough covariate interdependence to render the hdPS inoperable in smaller studies, the problem likely persists in larger studies as well, despite algorithm convergence. For example, in our study the explicit selection of marginal treatment associations by the exposure-based hdPS produces the lowest c-statistic among compared PS methods. Inclusion of regularization can promote hdPS convergence but does not noticeably change PS method performance.

A univariate screen is undeniably fast to compute, but modern computational machinery increasingly handles large-scale regressions. For our study with in the order of 100 000 subjects and 100 000 covariates, computing the hdPS completes in minutes, versus reasonable hours for $L_1$-regularization with extensive cross-validation using the Cyclops R package.³⁶ Computer parallelization and future statistical computing advances can further improve large-scale observational analyses, reducing computational burden as a barrier to using appropriate methods.

In this study, we evaluate $L_1$-regularization because of its prior application to PS models and explicit model selection approach that contrasts with that of the widely used hdPS. However, multivariate penalized regression techniques other than $L_1$-regularization exist to address separation and sparse data bias in logistic regression,¹⁹ and there is a wide machine learning literature on binary classification algorithms.⁴⁹ Even though we are using $L_1$-regularization for PS prediction, and not to estimate causal effects, perhaps other methods that do not drop covariates entirely from the PS model may produce improved covariate balance. In particular, log-$F(n,m)$ distribution priors have received positive attention for bias reduction in logistic regression,⁵⁰ and can be implemented in standard regression software through data augmentation. The two distribution parameters are easily interpretable as prior coefficient confidence intervals, perhaps lending peace of mind to the investigator who chooses to fix them instead of performing an expensive parameter search. Our study provides an evaluation framework that can be applied to study log-$F$ priors and other penalized regression methods as PS estimators.

Funding

This work was supported by the National Science Foundation, Division of Information and Intelligent Systems [grant number IIS 1251151], the National Institutes of Health, National Library of Medicine [grant number 1F31LM012636-01] and the Paul and Daisy Soros Fellowships for New Americans.

Conflict of interest: M.A.S. holds a contract grant from Janssen R&D. M.J.S. is an employee and shareholder of Janssen R&D.