Sensitivity of between-study heterogeneity in meta-analysis: proposed metrics and empirical evaluation

Abstract

Background Several approaches are available for evaluating heterogeneity in meta-analysis. Sensitivity analyses are often used, but these are often implemented in various non-standardized ways.

Methods We developed and implemented sequential and combinatorial algorithms that evaluate the change in between-study heterogeneity as one or more studies are excluded from the calculations. The algorithms exclude studies aiming to achieve either the maximum or the minimum final I² below a desired pre-set threshold. We applied these algorithms in databases of meta-analyses of binary outcome and ≥4 studies from Cochrane Database of Systematic Reviews (Issue 4, 2005, n = 1011) and meta-analyses of genetic associations (n = 50). Two I² thresholds were used (50% and 25%).

Results Both algorithms have succeeded in achieving the pre-specified final I² thresholds. Differences in the number of excluded studies varied from 0% to 6% depending on the database and the heterogeneity threshold, while it was common to exclude different specific studies. Among meta-analyses with initial I² > 50%, in the large majority [19 (90.5%) and 208 (85.9%) in genetic and Cochrane meta-analyses, respectively] exclusion of one or two studies sufficed to decrease I² < 50%. Similarly, among meta-analyses with initial I² > 25%, in most cases [16 (57.1%) and 382 (81.3%), respectively) exclusion of one or two studies sufficed to decrease heterogeneity even <25%. The number of excluded studies correlated modestly with initial estimated I² (correlation coefficients 0.52–0.68 depending on algorithm used).

Conclusions The proposed algorithms can be routinely applied in meta-analyses as standardized sensitivity analyses for heterogeneity. Caution is needed evaluating post hoc which specific studies are responsible for the heterogeneity.

Introduction

Assessment of the between-study heterogeneity is an essential component of meta-analysis.¹ Lack of consistency may reflect genuine differences in the design and conduct of the studies (methodological heterogeneity) or in participants, interventions, exposures or outcomes evaluated (clinical heterogeneity).^2,3 Lack of consistency may also herald errors, biases or pure chance. Errors and biases may affect single studies (e.g. quality problems) or research fields at large, e.g. publication and other selective reporting biases.

Sources of heterogeneity need to be carefully examined on a case-by-case basis.⁴ A common approach is to perform sensitivity analyses, where one study is excluded at a time and the impact of removing each of the studies is evaluated on the summary results and the between-study heterogeneity.⁵ Such ‘one-out’ sensitivity analyses can tell us whether the summary effect and heterogeneity are heavily influenced by a particular study. However, it is possible that not one but several studies are primarily responsible for the between-study heterogeneity. One could generalize into sensitivity analyses where many studies are removed, according to some order. Identification of ‘outlying’ studies may also offer some post hoc hints for explaining the reasons of between-study heterogeneity.

Here, we present algorithms that evaluate the change in between-study heterogeneity as one or more studies are excluded sequentially or in combination from the meta-analysis calculations. Our aim is to show how these algorithms can be routinely adopted in meta-analyses as standardized sensitivity analyses for heterogeneity. Accordingly, we have empirically examined their performance in many meta-analyses of clinical trials and genetic epidemiology. Illustrative examples are also discussed in detail.

Methods

Several statistical tests are routinely used to assess overall the extent and statistical significance of heterogeneity. The most common test that examines the null hypothesis that all studies are evaluating the same effect is the Cochran's chi-squared test (Cochran's Q).⁶ The most common metric for measuring the magnitude of the between-study heterogeneity is the I²,⁷ the ratio of Q–df (df: degrees of freedom) over Q. I² is easily interpretable and does not depend on the number of the studies. It ranges between 0% and 100% and is typically considered low for I² < 25%, modest for 25–50%, and large for >50%.⁸

Previous methods have been proposed that examine the relative contribution to heterogeneity of each study in a meta-analysis.^9,10 The standard Galbraith plot is a bivariate radial scatter plot of the inverse of the standard error of each study vs the ratio of the log of the effect size over the respective standard error.⁹ A variant proposed by Baujat et al. plots the contribution of each study to Q as a function of the influence on the overall effect estimate.¹⁰ Here, we have developed algorithms that are based on the I² statistic rather than Q and that allow the removal of more than one studies, if need be.

Specifically, we implemented iterative algorithms to calculate the minimum number of studies that should be omitted to decrease the estimated between-study heterogeneity below a specific threshold . The algorithms are applied to all meta-analyses where the initial estimate of I² is above the . For practical purposes, we use here the traditional threshold of large heterogeneity (I² < 50%, 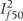) and of modest heterogeneity (I² < 25%, ).

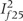The effect size θ and respective standard error SE_θ are used as input data. Very rarely more than one study may have the same input data. Then, the algorithms randomly select one of these similar data sets to be removed first.

Sequential algorithm

In this approach, for a meta-analysis of n studies, we perform n new meta-analyses, where one study is excluded from the calculations each time. The study that is responsible for the largest decrease in I² is dropped and a new set of n−1 studies is created. When two or more studies cause exactly the same decrease in I² by their exclusion, we drop the study with the largest decrease in Q. We continue by successively re-analysing reduced sets of studies and applying the same rule one step before I² decreases below the requested . In the last step there is a chance more than one omitted studies can result in I² dropping below the wanted threshold. We implement two variants of the algorithm: one omits the study that will result in the maximum I² below the desired , while the other omits the study that will result in the minimum possible I² below the desired . Both variants exclude eventually the same number of studies, but the last excluded study may be a different one.

Combinatorial algorithm

The combinatorial algorithm aims to identify clusters of studies whose exclusion can reduce the between-study heterogeneity below the desired threshold. When the exclusion of any single study does not suffice to drop the heterogeneity below the desired threshold, the decrease in the I² is examined by the exclusion of all possible pairs of studies. If no pair exclusion achieves the , we examine the decrease in the I² by the exclusion of all possible triplets of studies, and so forth. At the last step, there are again two variants. If there are more than one set with equal number of excluded studies that decrease I² below the desired , one can choose to omit the set that results in the maximum or minimum I² below .

Sensitivity metrics

The proposed algorithms generate the number of studies that have to be omitted to decrease I² below (k_<50 and k_<25, for the 50% and 25% threshold, respectively). We can also estimate the proportions of studies that need to be excluded, l_<50 = k_<50/n and l_<25 = k_<25/n, respectively. Similarly, one can estimate the proportions based on the sample sizes of the omitted studies vs the total sample size of the meta-analysis aiming for either maximum or minimum I² below .

Databases for empirical evaluation

We applied these algorithms and derived the sensitivity metrics in two datasets of meta-analyses. First, we used a previously described database of 50 meta-analyses of gene-disease associations that had found a nominally statistically significant effect (P < 0.05) by random-effects calculations (DerSimonian and Laird model).¹¹ Large between-study heterogeneity is common in genetic epidemiology.¹²

Second, we used meta-analyses from the Cochrane Database of Systematic Reviews (Issue 4, 2005). We used all systematic reviews where at least one meta-analysis with four or more studies had been conducted and the outcome was binary. Among those, we kept only one meta-analysis per systematic review, the one with highest number of studies; in case of ties, we kept the one with largest sample size.

For all meta-analyses, we recorded the initial number of studies, sample size, and random effects (DerSimonian and Laird) summary effect size [natural logarithm of the odds ratio (OR)] and its standard error, I² and Q (P-value) as well as the sensitivity metrics described earlier. We provide descriptive statistics for the sensitivity metrics for both databases and on differences between the two algorithms. Furthermore, we illustrate the concordance between the initial I² and number and proportion of studies excluded using scatter plots and Spearman correlation coefficients.

Modules

Analyses were conducted in Intercooled STATA 8.2 (College Station, TX, USA) using the metan and hetred modules. The latter module was developed for the purposes of the study and can be downloaded from www.dhe.med.uoi.gr/software.htm and Statistical Software Components (SSC) archive.

Results

Descriptive statistics of meta-analyses for both databases can be found in the Appendix.

Sequential algorithm

In the genetic meta-analyses data set (Table 1), the median number of studies that had to be omitted from the meta-analysis to drop I² below the requested threshold (50% and 25%) was one and two, respectively. In the majority of meta-analyses, excluding one or two studies sufficed [19 (90.5%) for the 50% threshold and 16 (57.1%) for the 25% threshold, Figure 1]. In the two variants of the algorithm (aiming for maximum or minimum I² below ), the excluded studies at the last step were different in 13 (61.9%) and 11 (39.3%) meta-analyses for the 50% and 25% thresholds, respectively.

Table 1.

Sensitivity metrics for heterogeneity, median values (IQR) for the genetic meta-analyses’ database

	Sequential algorithm	Combinatorial algorithm
threshold: 50%	n = 21a
I 2 before exclusion of studies	61.9% (54.1–70.8)
Number of studies excluded	1 (1–2)	1 (1–2)
Proportion of studies excluded	12.5% (7.7–16.7)	12.5% (7.7–16.7)
Proportion of sample size excluded, target of maximum I2 below	11.2% (6.4–17.3)	11.2% (6.4–17.3)
Proportion of sample size excluded, target of minimum I2 below	9.3% (6.4–25.8)	9.3% (6.4–25.8)
I 2 after exclusion of studies, target of maximum I2 below	47% (39.3–49.7)	47.0% (39.3–49.7)
I 2 after exclusion of studies, target of minimum I2 below	38.5% (23.2–47.1)	38.5% (23.2–47.1)
threshold: 25%	n = 28b
I 2 before exclusion of studies	59.1% (48.9–66.9)
Number of studies excluded	2 (1–4)	2 (1–4)
Proportion of studies excluded	17.7% (10.5–24.0)	17.7% (10.6–24.0)
Proportion of sample size excluded, target of maximum I2 below	13.8% (7.8–29.2)	15.9% (7.8–32.3)
Proportion of sample size excluded, target of minimum I2 below	13.2% (7.1–29.2)	11.9% (7.1–21.1)
I 2 after exclusion of studies, target of maximum I2 below	20.6% (4–23.1)	21.5% (4.4–23.2)
I 2 after exclusion of studies, target of minimum I2 below	14.9% (0.7–23.2)	13.7% (0.7–19.6)

^aFor two meta-analyses I² was not able to be dropped <50%.

^bFor 2 meta-analyses I² was not able to be dropped <25%.

Figure 1.

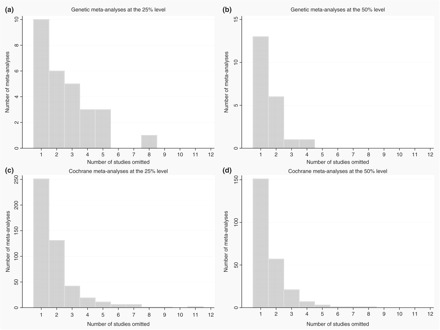
Frequency distribution of excluded studies. (a) Genetic meta-analyses at the 25% level. (b) Genetic meta-analyses at the 50% level. (c) Cochrane meta-analyses at the 25% level. (d) Cochrane meta-analyses at the 50% level

In the Cochrane meta-analyses (Table 2), the median number of studies had to be omitted from the meta-analysis to drop I² < 50% or even 25% was one. Excluding one or two studies sufficed in the vast majority of cases [208 (85.9%) for the 50% threshold and 382 (81.3%) for the 25% threshold, Figure 1]. Different studies were selected for exclusion at the last step, when targeting for maximum or minimum I² below the desired , in 98 (40.5%) and 185 (39.4%) meta-analyses for the 50% and 25% threshold, respectively. Of note, heterogeneity could not be dropped below 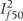or 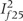in two meta-analyses regardless of how many studies were excluded.

Table 2.

Sensitivity metrics for heterogeneity, median values (IQR) for the Cochrane meta-analyses’ database

	Sequential algorithm	Combinatorial algorithm
threshold: 50%	n = 242a
I 2 before exclusion of studies	65.5% (56.7–74.3)
Number of studies excluded	1 (1–2)	1 (1–2)
Proportion of studies excluded	16.7% (12.0–25.0)	16.7% (12.0–25.0)
Proportion of sample size excluded, target of maximum I2 below	17.5% (8.8–33.7)	17.6% (8.8–37.8)
Proportion of sample size excluded, target of minimum I2 below	18.4% (10.5–35.1)	18.4% (10.5–35.9)
I 2 after exclusion of studies, target of maximum I2 below	40.9% (15.7–47.8)	42.4% (19.1–47.9)
I 2 after exclusion of studies, target of minimum I2 below	30.7% (4.7–43.2)	30.0% (1.3–43.2)
threshold: 25%	n = 470b	n = 466b, c
I 2 before exclusion of studies	51.4% (38.8–65.8)	51.0% (38.6–65.8)
Number of studies excluded	1 (1–2)	1 (1–2)
Proportion of studies excluded	20.0% (11.1–28.6)	20.0% (11.1–28.6)
Proportion of sample size excluded, target of maximum I2 below	19.2% (9.3–33.9)	19.5% (9.3–35.1)
Proportion of sample size excluded, target of minimum I2 below	19.5% (9.4–35.0)	19.5% (9.4–35.3)
I 2 after exclusion of studies, target of maximum I2 below	12.3% (0.0–21.8)	12.7% (0.0–22.4)
I 2 after exclusion of studies, target of minimum I2 below	1.4% (0.0–15.1)	1.0% (0.0–14.7)

^aFor two meta-analyses I² was not able to be dropped <50%.

^bFor two meta-analyses I² was not able to be dropped <25%.

^cFour meta-analyses required excess amount of computational resources and were excluded from analysis.

On average, exclusion of 13% and 17% of the studies in genetic and Cochrane meta-analyses, respectively, sufficed to reach below 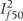; the respective percentages were 18% and 20% for reaching below 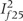(Tables 1 and 2). There was however some diversity across meta-analyses (Tables 1 and 2). The respective percentages were similar, when based on sample size rather than number of studies (Tables 1 and 2).

Differences with the combinatorial algorithm

Results were always very similar and often identical with the use of the combinatorial algorithm (Tables 1 and 2). We will thus focus only on describing the relatively uncommon differences between the two algorithms (Table 3). Differences in the number of studies that had to be excluded occurred in only 0–6% of the meta-analyses, depending on the dataset and desired heterogeneity threshold. Differences in the specific studies to be excluded were somewhat more common and ranged from 11% to 17% when aiming for minimum I² below , and 0% to 29% when aiming for the maximum I² below in the last step.

Table 3.

Differences between sequential and combinatorial algorithm (meta-analyses with two or more excluded studies)

	Different number of studies excluded (%)	Different studies excluded, aiming for maximum I2 below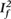 (%)	Different studies excluded, aiming for minimum I2 below (%)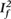
Genetic meta-analyses
50% threshold (n = 8)	0 (0)	0 (0)	1 (11.1)
25% threshold (n = 18)	1 (5.6)	5 (27.8)	2 (11.1)
Cochrane meta-analyses
50% threshold (n = 91)	5 (5.6)	26 (28.6)	15 (16.5)
25% threshold (n = 215)	10 (4.7)	52 (24.2)	33 (15.3)

The combinatorial algorithm was also time-consuming when several studies had to be excluded. A meta-analysis with 38 studies of which seven had to be excluded eventually (requiring almost 16 000 000 meta-analyses), required 86 h in a Intel(R) Pentium(R) 4 CPU 550 3.40 GHz with 1 GB RAM.

Concordance between initial I² estimate and sensitivity metrics

Figure 2 shows the correlation between the estimated initial I² of each meta-analysis and the number of studies that had to be removed to reduce this <50 and 25% (panels A and B, respectively; Cochrane and genetics meta-analyses are combined in both panels) using the sequential algorithm (the results with the combinatorial algorithm are almost identical, as earlier). The Spearman correlation coefficients were 0.65 [(95% confidence interval (CI): 0.58–0.72, n = 263)] and 0.65 (95% CI: 0.60–0.70, n = 498), respectively. The correlation coefficients between the estimated initial I² and the proportion of studies excluded were 0.52 (95% CI: 0.42–0.60, n = 263) and 0.68 (95% CI: 0.62–0.72, n = 498), respectively (Figures 2C and D for 50% and 25% threshold, respectively). When the proportion of sample size was considered, the correlation coefficients were 0.52 (95% CI: 0.42–0.60, n = 263) aiming for minimum and 0.63 (95% CI: 0.55–0.70, n = 263) aiming for maximum I² below of 50%. Targeting for I² below of 25%, the correlation coefficient was 0.58 (95% CI: 0.52–0.64, n = 498) for both minimum and maximum variants.

Figure 2.

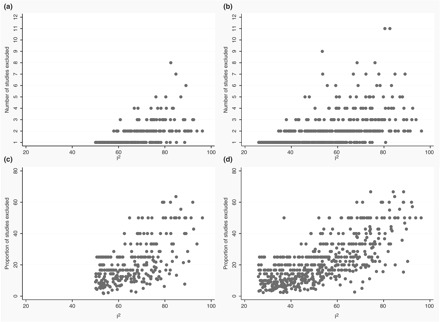
Scatter plots of the number and proportion of excluded studies vs the initial I² The (a) and (b) represent analyses for number of excluded studies using the target threshold of 50 and 25%, respectively. The (c) and (d) represent analyses for proportion of excluded studies using the target threshold of 50 and 25%, respectively

While the average correlation was modestly high, there was considerable variability in the range of k_<50 and k_<25 for a given amount of initial heterogeneity. For example, for initial I² of > 60% the range of k_<50 and k_<25 was 1 to 8 and 1 to 11, respectively. For initial I² between 50% and 60%, the range of k_<50 and k_<25 was 1–2 and 1–9, respectively.

Practical examples

Figure 3A displays a Cochrane meta-analysis with large heterogeneity where the exclusion of a single outlying study decreased significantly the estimated between-study heterogeneity and where a specific plausible explanation for the heterogeneity could be raised. The systematic review¹³ (CD000173) assessed anti-epileptic drugs for the prevention of seizures following acute traumatic brain injury. The specific meta-analysis used in our dataset had six studies and compared anti-epileptic drugs vs standard care for late seizures (Comparison: 02, Outcome: 02 in the specific Cochrane review). The review authors had found significant heterogeneity and stated they should not synthesize the data, nevertheless a figure with an overall estimate was provided. Using OR as the metric of risk, I² was originally 63% (95% CI: 0–83%). Application of our algorithms resulted in omission of one study, resulting in an I² of 19% (95% CI: 0–64%). This study (Pechadre 1991) demonstrated a very large effect of the anti-epileptic treatment (OR 0.09, 95% CI, 0.02–0.39), while the remaining studies showed no benefit, either each one in isolation, or all of them combined (summary OR 1.14, 95% CI, 0.80–1.62). The excluded study was the only one that was not blinded. Lack of blinding could have affected the outcome ascertainment or could have been a marker for other quality deficiencies.¹⁴

Figure 3.

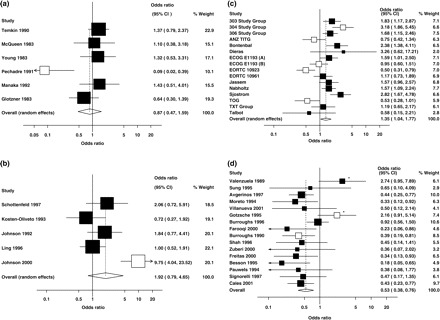
Examples of meta-analyses with very large initial estimate of between-study heterogeneity that required omission of one or several studies for the heterogeneity estimate to decrease <25%. Open boxes represent excluded studies. (a) Cochrane Database ID: CD000173 (one study omitted). (b) Cochrane Database ID: CD002208 (one study omitted). (c) Cochrane Database ID: CD003366 (five studies omitted). (d) Cochrane Database ID: CD000193 (two studies omitted); open boxes represent studies excluded using the sequential algorithm, whereas asterisks denote studies excluded using the combinatorial one

Figure 3B shows an example of a Cochrane meta-analysis with very large initial I², where the exclusion of a single study could also reduce the I² estimate <25%, but where it was more difficult to tell what exactly was different or wrong with the excluded study. The systematic review¹⁵ (CD002208) was about methadone maintenance at different dosages for opioid dependence. The specific meta-analysis used in our dataset had five studies and compared high (60–109 mg/day) vs low (1–39 mg/day) methadone maintenance doses for 17–26 weeks and the outcome was retention rate (Comparison: 01, Outcome: 01, Subgroup: 01 in the specific Cochrane review). In the OR scale, the initial I² was 81% (95% CI: 40–90%). The omission of one study (Johnson 2000) dropped the estimated heterogeneity to 8% (95% CI: 0–70%). This study had shown a very large and statistically significant difference in retention rate (10-fold larger odds with the high vs low dose), while the other four studies had shown no significant difference. The outlier study was the newest one and was the only one that used methadone doses >80 mg/day. However, the review authors also noted that ‘missing samples were considered positive for purposes of analysis’, while this was not mentioned for any of the four other studies. It is difficult to decide whether any of these reasons, or others still not captured and/or not reported by the reviewers, may explain the results of this outlier study vs the others.

Figure 3C shows an example of a meta-analysis with equally large I² that could not be reduced to <25% unless many studies were removed. This Cochrane review¹⁶ (CD003366) compared taxane containing regimens for metastatic breast cancer. The comparison used in this specific dataset was overall effect of taxanes and the outcome overall response among randomized patients (Comparison: 01 Outcome: 03 in the specific Cochrane review). The meta-analysis had 16 studies and I² estimated at 75% (95% CI: 57–84%). The omission of five studies (open boxes in the graph) decreased I² to 17% (95% CI: 0–52%). The same studies were selected for removal in all variants of the sequential or combinatorial algorithm. The reviewers had separated the dataset in subgroups based on the comparison regimen used. This was thought to explain some of the statistical heterogeneity, but actually the largest subgroup (10 studies, single agent taxane vs another agent) had an even larger point estimate of between-study heterogeneity (I² = 83%) than the overall analysis. All five excluded studies were from this subgroup. The reviewers commented also about the low reporting quality of all studies and the differences in the definition of response across trials. Poor reporting may be associated with other flaws and biases that may have affected the estimates of the treatment effect, introducing substantial heterogeneity, but these additional flaws or biases are probably occult and difficult to decipher.

Figure 3D shows an example of a meta-analysis with large I² that both algorithms exclude the same number of studies but different ones. The systematic review (CD000193)¹⁷ assessed somatostatin analogues for acute bleeding oesophageal varices. The comparison we have included in our analysis was ‘somatostatin analogues vs placebo or no treatment’ and the respective outcome ‘number of failing initial haemostasis’ (01/04). This outcome included 16 studies with an I² of 53% (95% CI: 1–72%, using OR as effect estimate). The reviewers stratified the studies as high quality (those with allocation concealment and double-blinding) vs others trial. The high quality trials had less impressive treatment effects for other outcomes such as units of blood transfused and re-bleeding risk and showed no improvement in mortality. The sequential algorithm excluded two studies (first Gøtzshe 1995 and then Burroughs 1996), one of which was a study of high quality. The combinatorial algorithm excluded also two studies (Burroughs 1996 and Valenzuela 1989) neither of which was considered to be of high quality.

Discussion

We have developed and implemented algorithms for sensitivity analyses of between-study heterogeneity in meta-analyses. The different algorithms almost always excluded the same number of studies to reach below a desired heterogeneity threshold. The proposed sensitivity metrics add another useful dimension to the routine examination of between-study heterogeneity, besides the testing of statistical significance and the estimation of the amount of heterogeneity beyond chance (I²). While the number of studies that need to be excluded correlates with the I², the correlation is only modest, thus there is some independent insight to be gained.

Several methods have already been described for exploration of heterogeneity in meta-analysis, as previously reviewed.¹⁸ Some of these methods, such as the traditional Galbraith plot and variants thereof, use graphic presentations to indicate the influence of individual studies.^9,10,19 When only one study causes the extreme heterogeneity, our algorithms pinpoint to the same study as these other methods suggest. However, in situations where the heterogeneity is attributed to several studies, the above methods are either impractical or may yield considerably different inferences. Our algorithms complement the existing methods, given the differences in the analytical approach and objectives. In general, the contribution of a study in the overall heterogeneity is analogous to the squared difference of the study's effect from the overall effect. The exclusion of the first study results in a new overall effect and a new set of outlier studies is created. This is not necessarily the same as before, especially if the exclusion of the first study modifies also substantially the summary effect. Our proposed algorithms overcome this problem: each time a study is omitted, the influence of the remaining studies in overall heterogeneity is automatically reappraised.

Although the different variants of our algorithms exclude almost always the same number of studies to reach below a specific desired heterogeneity threshold, discrepancies in which are the specific studies to be excluded are common. Inferences on which are the specific studies that cause the between-study heterogeneity should be cautious and there is a considerable risk of over interpretation. In one extreme situation, two studies may have identical effects and uncertainty thereof, in which case our algorithms randomly select one of them to be excluded first. In the far more common situation, studies may have minor differences in their contribution to heterogeneity, and the key to understanding heterogeneity may not lie in the one that has the largest estimated contribution based on the observed data. Random noise may change the order of outliers. Moreover, when heterogeneity is explained by patient-level rather than study-level characteristics^20–22 any algorithm that excludes whole studies may not reveal the true reasons for the heterogeneity. Overall, in-depth examination of the characteristics of the excluded studies may be useful in some circumstances. However, this should be seen as an exploratory post hoc evaluation of the sources of heterogeneity.

We should acknowledge that in general exploration of the reasons of heterogeneity is a difficult task in meta-analysis. Sensitivity analyses where studies are subgrouped based on various characteristics are often performed.²³ Subgroups may be selected based on clinical expertise, prior knowledge on the scientific field, or other factors.⁴ Meta-regression for one or multiple factors may serve similar purposes.²⁴ All of these exploratory analyses may suffer from both lack of power and high false-positive rate.^20–22Post hoc selection of the covariates based on subjective interpretation of the already available data can be misleading. The proposed algorithms offer at least an objective approach that is ‘agnostic’, i.e. is not influenced initially by consideration of known specific study characteristics. The important characteristics that contribute to the heterogeneity may be unknown or unrecorded in the examined studies. Meta-analysis of individual-level information may offer a better handle for examining some characteristics, especially patient-level covariates.²⁵ However, such analyses are more difficult, more uncommonly conducted, and often there is insufficient information on covariates of interest.²⁵

We should also acknowledge that heterogeneity in a meta-analysis may vary depending to the effect estimate used, especially for binary outcomes.²⁶ One should have this in mind before investigating any source of inconsistency. Selection of a different metric of effect may result in different studies being excluded.

Another limitation stems from the unavoidable uncertainty in the estimates of I². This metric has some advantages over the Q statistic, in that it can be compared across different meta-analyses with different metrics and different number of studies. However, in the typical meta-analysis where there are only a few studies, poor power may cause substantial uncertainty in the inferences that are based on either Q or I².²⁷ Reducing the amount of heterogeneity below a specific level or even aiming for residual I² = 0% is not reassuring that the remaining studies will be homogeneous. CIs for I² are generally wide, unless many studies exist.²⁸ Our practical examples also demonstrate this uncertainty. Apparent lack of heterogeneity based on the point estimates of I² is not proof of homogeneity. We have recently proposed that presentation of confidence intervals around I² would be useful to promote in the reporting of meta-analyses.²⁸ In this regard, also the selection of the 25% and 50% thresholds should only be seen as a standardized convenience.

Overall, we suggest that our algorithms can be routinely used in meta-analyses with large or moderate estimated heterogeneity to complement existing heterogeneity metrics. Compared with existing methods, the proposed algorithms cater routinely to the possibility of excluding more than one study. The excluded studies offer a starting point for exploring heterogeneity and their selection is made based on purely statistical criteria, potentially avoiding post hoc subjective interpretation of the data. Either the sequential or the combinatorial algorithm can be used. The latter is computationally more demanding when many studies have to be excluded, but in general both algorithms almost always agree on how many studies should be removed. Conversely, great caution is needed in avoiding over-interpreting the data on which specific studies cause heterogeneity and why. The algorithms make this obvious when the two versions exclude different studies, but caution should be applied even when both algorithm versions exclude the same studies.

Appendix

Descriptive of meta-analyses

I ² was estimated to be above 25% in 28 of the 50 (56.0%) genetic meta-analyses and in 472 of the 1011 (46.7%) Cochrane meta-analyses, while values of 50% or higher were seen in 21 (42.0%) and 244 (24.1%), respectively. Appendix Table 1 shows baseline characteristics of the two analysed sets of meta-analyses. Genetic meta-analyses were more heterogeneous, had more studies and larger sample sizes.

Appendix Table 1.

Characteristics of meta-analyses

Characteristic	Genetics (n = 50)	Cochrane (n = 1011)
Number of studies, median (IQR)	13 (8–20)	7 (5–11)
Sample size, median (IQR)	4670 (2823–8761)	1112 (512–2691)
Effect size, median (IQR)a	0.360 (0.257–0.499)	0.371 (0.161–0.827)
Variance, median (IQR)	0.0127 (0.0070–0.0281)	0.0516 (0.0228–0.1246)
I 2, median (IQR)	37.6% (4.6–59.5)	21.1% (0.0–49.7)
0–25%: n (%)	22 (44.0)	539 (53.3)
25–50%: n (%)	7 (14.0)	228 (22.6)
50–75%: n (%)	19 (38.0)	187 (18.5)
75–100%: n (%)	2 (4.0)	57 (5.6)
Q P < 0.10: n (%)	27 (54.0)	350 (34.6)

^aAll effect sizes (presented as natural logarithm of OR) have been coined to be ≥0.