Effective approach to epidemic containment using link equations in complex networks

Assessing the importance of each connection in a network for the spreading of epidemics allows the largest containment up to date.

Abstract

Epidemic containment is a major concern when confronting large-scale infections in complex networks. Many studies have been devoted to analytically understand how to restructure the network to minimize the impact of major outbreaks of infections at large scale. In many cases, the strategies are based on isolating certain nodes, while less attention has been paid to interventions on the links. In epidemic spreading, links inform about the probability of carrying the contagion of the disease from infected to susceptible individuals. Note that these states depend on the full structure of the network, and its determination is not straightforward from the knowledge of nodes’ states. Here, we confront this challenge and propose a set of discrete-time governing equations that can be closed and analyzed, assessing the contribution of links to spreading processes in complex networks. Our approach allows a scheme for the containment of epidemics based on deactivating the most important links in transmitting the disease. The model is validated in synthetic and real networks, yielding an accurate determination of epidemic incidence and critical thresholds. Epidemic containment based on link deactivation promises to be an effective tool to maintain functionality of networks while controlling the spread of diseases, such as disease spread through air transportation networks.

INTRODUCTION

The problem of modeling the spread of a disease among individuals has been studied in depth over many years (1–4). The development of compartmental models, models that divide the individuals among a set of possible states, has given rise to a new collection of techniques that enable, for instance, analysis of the onset of epidemics (5–15) or study of the impact of a vaccination campaign (16–20). Previous studies have relied heavily on a mathematical approach to the study of epidemic spreading (21), and we follow a similar approach here in the same spirit.

The design of effective containment strategies constitutes a major challenge. Measures such as vaccination, improved hygiene, biosecurity, cattle culling, or education to prevent contagions operate on the biological aspects of the disease. On the other hand, isolation or mobility restrictions act on the physical routes or patterns of disease spread, which may transform a local event into a pandemic. Here, we concentrate on the role of the links of the spreading network. For example, if we identify the edges that are more involved in the propagation of a disease, then it is possible to design targeted countermeasures that affect only specific links instead of whole nodes while being more effective. This approach can be illustrated by a hypothetical pandemic disease propagated using the air transportation network: The isolation of one airport is a dramatic measure that is socially and politically difficult to accept and put into practice, but the suspension of only a few connections between selected airports could be more easily assumed and could also achieve a better containment of the disease.

Previous studies have directed their attention mostly toward schemes based on the actuation on single nodes, either randomly or according to node properties such as their degree, betweenness, PageRank, or eigenvector centrality (22–25). Following the same idea, some authors have introduced link removal using properties of the adjacent nodes (degrees or centralities) or of the link itself (edge betweenness) (22, 26, 27). A model of coevolution of epidemics with permanent and temporal link removals was proposed in (28), and methods from optimization and control have been applied to minimize the impact of the epidemics (29–31). The core of what is currently considered to be the optimal approach is built upon finding the minimum set of edges whose removal leads to a maximum decrease in the spectral radius of the network, that is, the largest eigenvalue of the adjacency matrix (27, 32, 33). Because the epidemic threshold is, at first-order approximation of a susceptible-infected-susceptible (SIS) epidemic dynamics, inverse to the spectral radius, it seems the best and more mathematically grounded option. Unfortunately, it turns out to be an NP-complete problem; thus, only heuristics are available for large networks (27).

It must be emphasized that all the previous approaches make use only of the structural characteristics of the network to decide which nodes or edges have to be removed; the characteristics or parameters of the epidemic process are ignored. Even the spectral radius, which is closely related to the epidemic threshold, does not depend on the infection or recovery rates, the expected number of infected neighbors around a certain node, or any other local or global information of the spreading process.

Our proposal concentrates on the role of the links in the spreading of the epidemics, quantifying the importance of each link (34) and thus enabling containment strategies based on their removal. To this end, we first define the epidemic importance of a link as its capacity to infect other individuals once this link has been used to propagate the disease. The determination of this link epidemic importance requires the development of a mathematical model that is able to cope with the infection propagation at the level of links in complex networks. We will show that the proposed model facilitates the determination of the epidemics incidence and threshold with high accuracy. Moreover, the quantification of the epidemic importance of the edges leads to a link removal strategy that, in many cases, outperforms the previous approaches, even those based on minimizing the spectral radius, and also preserves most of the connectivity of the network.

The contributed model is built upon the relationships between the states of nodes connected by links, thus being related to pairwise approximations (35–41). However, our model is microscopic, at the level of individual links as in (40), thus allowing a clear identification of maximally infectious links, but with the additional advantage of being able to easily calculate not only the epidemic threshold but also the incidence of the epidemics and the importance of the links.

RESULTS

Link epidemic importance

Let us consider a discrete-time SIS dynamics that runs on top of a complex network of N nodes and L edges, with adjacency matrix A, and where each node i can be in one of two different states σ_i, either susceptible (S) or infected (I), that is, σ_i ∈ {S, I}. We can say that a link (i, j) between nodes i and j is in state SI if σ_i = S and σ_j = I. The parameters of the SIS dynamics are the infection and recovery probabilities, β and μ, respectively.

Our objective is to find an effective strategy to contain the SIS epidemic process through bond percolation. To determine which link should be removed first, we need a measure of the importance of each link in the spreading of the epidemics. A possible option would be to use the edge importance defined in (34), which accounts for the relative change of the spectral radius when the edge is removed. However, this constitutes an indirect way of containment, because we aim at lowering the incidence of the epidemics as much as possible, whereas the actuation on the spectral radius is directed to increase the epidemic threshold; both are different targets. In addition, the spectral radius only depends on the structure of the network, but not on the epidemic parameters of the process or the participation of the link in the spreading of the disease.

We assume that the system has reached the stationary state, which does not mean that the nodes remain in a certain fixed state, only that the average incidence of the epidemics is basically constant; thus, there is still margin for applying a containment strategy to minimize this incidence. In this regime, we can measure the probabilities of nodes and links in each of the epidemic states, for example, the probability P(σ_i = I) of node i being infected or the joint probability P(σ_i = I, σ_j = S) of link (i, j) being in state IS.

Consider we have a link in state SS or II. In both cases, the next step of the epidemic dynamics is not going to use this link because, in the former, there is no infected node to propagate the disease and, in the latter, both nodes are already infected. Thus, to propagate the epidemics, a link must be in an either SI or IS state. Let us suppose we have a link (i, j) in state IS. First, with probability β, node i can infect node j through this link, changing to state II. Next, infected node j may transmit the disease to some of its neighbors. Thus, if we had removed link (i, j), then we would have cut this path of infections initiated at node i. This means that the larger the expected number of infected neighbors of node j, the largest the impact of removing link (i, j) for the spreading of the epidemics. Note that the degree of j, as well as the probability of its neighbors being susceptible when j is infected, is relevant, because you cannot infect nodes that are already infected. For example, if j is surrounded by many infected nodes, then cutting link (i, j) is not going to have too much effect on the overall incidence of the epidemics. The expected number of infected nodes produced in this way can be expressed as

$${\overline{\mathit{n}}}_{\mathit{i}\mathit{j}}=\mathrm{\beta }\mathit{P}({\mathrm{\sigma }}_{\mathit{j}}=\mathit{S},{\mathrm{\sigma }}_{\mathit{i}}=\mathit{I}){\displaystyle \sum _{\mathit{r}=1}^{\mathit{N}}}{\mathit{A}}_{\mathit{j}\mathit{r}}\mathrm{\beta }\mathit{P}({\mathrm{\sigma }}_{\mathit{r}}=\mathit{S}|{\mathrm{\sigma }}_{\mathit{j}}=\mathit{I})$$ (1)

where P(σ_r = S|σ_j = I) is the conditional probability that node r is susceptible when its neighbor j is infected. Because this measure is asymmetric, and removing an edge affects the propagation of the disease in both directions, we define the link epidemic importance of a link, I_ij, as

$${\mathit{I}}_{\mathit{i}\mathit{j}}={\overline{\mathit{n}}}_{\mathit{i}\mathit{j}}+{\overline{\mathit{n}}}_{\mathit{j}\mathit{i}}$$ (2)

Now, the problem reduces to finding the joint and conditional probabilities for each link, and this is accomplished using our epidemic link equations (ELE). It can be shown that this definition of link epidemic importance has the property of trying to preserve the connectivity of the network (see section S1 and fig. S1), unlike other options such as edge betweenness, which quickly tend to produce a large number of disconnected components, thus hindering the functionality of the network.

Epidemic link equations

To simplify the notation, we first denote the previous joint probability as Φ_ij = P(σ_i = S, σ_j = I); the higher the Φ_ij, the larger the likelihood that the disease propagates from node j to node i. It is worth mentioning that this feature is generally asymmetrical, meaning that the propagation of the illness can be more probable from j to i than the other way around. In the same way, the epidemic is restrained by edges where the nodes are in the same state; thus, it is convenient to define the probabilities ${\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{S}}=\mathit{P}({\mathrm{\sigma }}_{\mathit{i}}={\mathrm{\sigma }}_{\mathit{j}}=\mathit{S})$ and ${\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}=\mathit{P}({\mathrm{\sigma }}_{\mathit{i}}={\mathrm{\sigma }}_{\mathit{j}}=\mathit{I})$ for all pairs of neighboring nodes.

The evolution of the joint probability Φ_ij of one link depends on the probabilities Φ, Θ^I, and Θ^S to the rest of the neighboring links and on the infection rules of the SIS dynamics. Thus, we can write the following equation for each link

$$\begin{array}{c}{\mathrm{\Phi }}_{\mathit{i}\mathit{j}}(\mathit{t}+1)={\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{S}}(\mathit{t}){\mathit{q}}_{\mathit{i}\mathit{j}}(\mathit{t})(1-{\mathit{q}}_{\mathit{j}\mathit{i}}(\mathit{t}))+{\mathrm{\Phi }}_{\mathit{i}\mathit{j}}(\mathit{t})((1-\mathrm{\beta }){\mathit{q}}_{\mathit{i}\mathit{j}}(\mathit{t}))(1-\mathrm{\mu })+\\ \\ {\mathrm{\Phi }}_{\mathit{j}\mathit{i}}(\mathit{t})\mathrm{\mu }(1-(1-\mathrm{\beta }){\mathit{q}}_{\mathit{j}\mathit{i}}(\mathit{t}))\\ +{\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}(\mathit{t})\mathrm{\mu }(1-\mathrm{\mu })\end{array}$$ (3)

where q_ij(t) stands for the probability that a susceptible node i is not infected by any of its neighbors (excluding node j). We have taken into account all the possible changes of state of the nodes i and j. The first term considers the probability that both nodes are in a susceptible state; then, node i remains susceptible, while node j is infected by any of its other neighbors. The second term accounts for both nodes remaining in the same state; node i is not infected by any of its neighbors, and node j is not recovered from the infection. Then, the third term represents the transition in which node i is infected and recovers, while node j is susceptible and is infected by any of its other neighbors. Last, in the fourth term, both nodes are infected, but node i recovers, while node j does not. The asymmetry of probability Φ_ij multiplies the number of equations by two, because, for each link between nodes i and j, we need an equation for Φ_ij(t + 1) and another for Φ_ji(t + 1).

Similarly, we can obtain an expression for probability ${\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}$

$${\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}(\mathit{t}+1)={\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{S}}(\mathit{t})(1-{\mathit{q}}_{\mathit{i}\mathit{j}}(\mathit{t}))(1-{\mathit{q}}_{\mathit{j}\mathit{i}}(\mathit{t}))+{\mathrm{\Phi }}_{\mathit{i}\mathit{j}}(\mathit{t})(1-(1-\mathrm{\beta }){\mathit{q}}_{\mathit{i}\mathit{j}}(\mathit{t}))(1-\mathrm{\mu })+{\mathrm{\Phi }}_{\mathit{j}\mathit{i}}(\mathit{t})(1-\mathrm{\mu })(1-(1-\mathrm{\beta }){\mathit{q}}_{\mathit{j}\mathit{i}}(\mathit{t}))+{\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}(\mathit{t}){(1-\mathrm{\mu })}^2$$ (4)

In this case, we have only L equations, one per link, because of its symmetry. There is no need for extra equations for probability ${\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{S}}$, because the normalization leads to ${\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{S}}=1-{\mathrm{\Phi }}_{\mathit{i}\mathit{j}}-{\mathrm{\Phi }}_{\mathit{j}\mathit{i}}-{\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}$.

q_ij(t) in Eqs. 3 and 4 can be expressed as

$${\mathit{q}}_{\mathit{i}\mathit{j}}(\mathit{t})={\displaystyle \underset{\mathit{r}\ne \mathit{j}}{\prod _{\mathit{r}=1}^{\mathit{N}}}}(1-\mathrm{\beta }{\mathit{A}}_{\mathit{r}\mathit{i}}{\mathit{h}}_{\mathit{i}\mathit{r}})$$ (5)

where h_ij defines the hostility of j against i, that is, the probability that node j is infected when node i is susceptible, h_ij = P(σ_j = I|σ_i = S). The hostility can be obtained in terms of ${\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{S}}$ and Φ_ij as

$${\mathit{h}}_{\mathit{i}\mathit{j}}=\frac{{\mathrm{\Phi }}_{\mathit{i}\mathit{j}}}{{\mathrm{\Phi }}_{\mathit{i}\mathit{j}}+{\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{S}}}$$ (6)

Note that the denominator in Eq. 6 is a property of node i, given that ${\mathrm{\Phi }}_{\mathit{i}\mathit{j}}+{\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{S}}=\mathit{P}({\mathrm{\sigma }}_{\mathit{i}}=\mathit{S})$ for all neighboring nodes j of vertex i.

We call this system of 3L equations and unknowns our ELE model. It can be solved by iteration, starting from any meaningful initial condition, for example, ${\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}(0)={\mathrm{\rho }}_0^2$ and Φ_ij(0) = Φ_ji(0) = ρ₀(1 − ρ₀) (for any 0 < ρ₀ ≤ 1), until a fixed point is found. Apart from the solution where all nodes are susceptible, ${\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{S}}=1$ for all the links, a nontrivial one appears when the system is above the critical value of the epidemic spreading (see Methods for the analytic derivation of the epidemic threshold from ELE model). Last, the incidence of the epidemic process, the average number of infected nodes in the whole system, can be computed as

$$\mathrm{\rho }=\frac{1}{\mathit{N}}{\displaystyle \sum _{\mathit{i}=1}^{\mathit{N}}}\frac{1}{{\mathit{k}}_{\mathit{i}}}{\displaystyle \sum _{\mathit{j}=1}^{\mathit{N}}}{\mathit{A}}_{\mathit{j}\mathit{i}}({\mathrm{\Phi }}_{\mathit{j}\mathit{i}}+{\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}})$$ (7)

where k_i is the degree of node i.

To test the agreement between our approach and empirical simulations, we have analyzed the incidence of the epidemics, ρ, in different synthetic and real network structures, covering the full range of infection probabilities, β (see Fig. 1). The results show a marked agreement between our ELE model and the Monte Carlo simulations and a good prediction of the epidemic threshold for all synthetic and real networks, pointing out the validity of our model to describe the global impact of the epidemics. Note that all networks, except the first one, have a large clustering coefficient, making the determination of the incidence difficult for standard mean field methods because of the effect of dynamical correlations.

Fig. 1. Incidence of the epidemic process ρ as a function of the infection probability β.

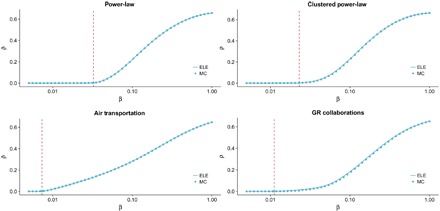
We show the incidence level for the ELE model (solid lines) and for Monte Carlo (MC) simulations (circles). The theoretical epidemic threshold calculated using Eq. 19 is marked with a vertical line. We have made use of two synthetic and two real networks: two scale-free networks (top) with an exponent of 3, one of them with high clustering coefficient; the world air transportation network; and the network of scientific collaborations in the field of general relativity (GR). We have set the recovery rate for all the networks to μ = 0.5 (see Methods for the description of the networks and the details of the MC simulations).

Epidemic containment

Our approach for effective epidemic containment is based on removing the links with the largest link epidemic importance. This is possible once we have solved the ELE model, computing the I_ij for all the links in the network using Eq. 2, which can be expressed as

$${\mathit{I}}_{\mathit{i}\mathit{j}}={\mathrm{\beta }}^2({\mathrm{\Phi }}_{\mathit{j}\mathit{i}}{\displaystyle \sum _{\mathit{r}=1}^{\mathit{N}}}{\mathit{A}}_{\mathit{j}\mathit{r}}\frac{{\mathrm{\Phi }}_{\mathit{r}\mathit{j}}}{{\mathrm{\Phi }}_{\mathit{r}\mathit{j}}+{\mathrm{\Theta }}_{\mathit{r}\mathit{j}}^{\mathit{I}}}+{\mathrm{\Phi }}_{\mathit{i}\mathit{j}}{\displaystyle \sum _{\mathit{r}=1}^{\mathit{N}}}{\mathit{A}}_{\mathit{i}\mathit{r}}\frac{{\mathrm{\Phi }}_{\mathit{r}\mathit{i}}}{{\mathrm{\Phi }}_{\mathit{r}\mathit{i}}+{\mathrm{\Theta }}_{\mathit{r}\mathit{i}}^{\mathit{I}}})$$ (8)

Note that the value of β does not affect the ranking of the links, but we do not remove it from Eq. 8 to preserve the semantics of I_ij. Because the structure of the network changes after each link removal, it is convenient to recalculate the solution of the ELE model to ensure that we really remove the current link with the largest link epidemic importance.

We show the results of our approach for epidemic containment in Fig. 2. For comparison purposes, we also test four additional containment strategies. First, we consider two strategies that only make use of the structure of the network: removal based on maximum edge betweenness (22) and targeting the link with the highest eigenscore, that is, the product of the eigenvector centralities of the nodes connected by the link (27). Then, we consider a measure based on the epidemic process at the level of nodes, the removal of all the links of the node that has the maximum probability of being infected. Last, we carried out a simple random edge removal. As in the case of our strategy, we recalculate all the measures after each removal (see Methods for further details). We have also checked a promising approach based on communicability distances (42); however, the computational costs involved in computing communicability angles and distances for large networks preclude this approach to be used in large networks. For this reason, we have not included results on this one.

Fig. 2. Targeted bond percolation.

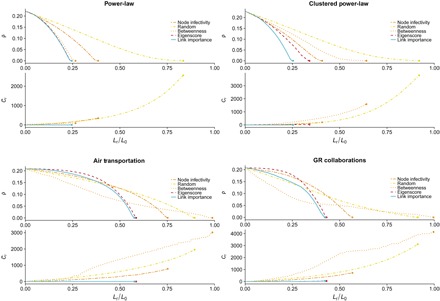
We show the incidence of the epidemics, (ρ), and the number of connected components, (C_r), as functions of the occupation probability, (L_r/L₀), where L₀ is the number of links of the network and L_r is the number of removed edges in the bond percolation process. We compare five different epidemic containment strategies: removing the edges of the node with the highest probability of being infected, P(σ_i = I) (orange dash-dash lines); a random edge removal (yellow dash-dot lines); removing the edge with the highest edge betweenness (light orange dotted lines); targeting the edge with the highest eigenscore (red dashed line); and, last, removing the edge that has the largest link epidemic importance (blue solid line). We apply these processes to the same networks as in Fig. 1 (see Methods). We have set the recovery rate to μ = 0.5 and have chosen the infection probability β such that the stationary incidence of the epidemics is about ρ_ini ≈ 0.2 for all the networks, that is, β = 0.1 for both power-law networks, β = 0.06 for air transportation network, and β = 0.11 for the collaboration network. The dots mark the achievement of total containment.

We observe in Fig. 2 that link epidemic importance leads to the fastest extinction of the epidemics for the four considered networks, and it is the only method that preserves their connectivity (thus, functionality). Note that the strategy based on node infectivity, though better than the random removal, performs poorly for all the networks despite having information about the epidemic process. This means that the use of information at the level of links is crucial to contain the epidemics.

For the power-law network, our approach using link epidemic importance yields the best performance, but the results are very similar to the those obtained using eigenscore and edge betweenness strategies [equivalent results hold for Erdős-Rényi (ER) networks; see fig. S6]. However, when the transitivity of the network is increased, we can see the benefits of using link epidemic importance, both in epidemic containment and on preservation of the connectivity of the network (see figs. S2 and S3 for more details on the containment process for each method).

The effect of the clustering coefficient is also present when we look at the epidemic containment results for the two empirical networks in Fig. 2. Moreover, as in most real networks, the air transportation and the scientific collaboration networks have a significant modular structure. This plays an important role on the epidemic containment process. Here, we can see how the strategy based on edge betweenness apparently performs better when few links are removed because of the fact that links with higher edge betweenness are those connecting different modules (43). When the bond percolation process isolates modules, each module may sustain its own epidemic process, and thus, it may happen that some of the modules are subcritical for the given infection probability β. This will lead to a decrease of the global prevalence of the epidemics at the expense of losing the connectivity of the network. Furthermore, if we look at the prevalence on the giant connected component, an important increase above the initial average number of infected individuals is revealed (see figs. S4 and S5). A consequence of this fragmentation process is the appearance of multiple isolated supercritical components, for which the removal of a link in one of them does not affect the incidence on the other components. As a result, the edge betweenness procedure needs to remove more links to arrive to the total epidemic extinction than any of the other methods, even the random one. For the sake of completeness, we have analyzed two benchmark networks with community structure, obtaining similar results (see figs. S7 and S8).

In Fig. 3 (top), we illustrate the survival links in the air transportation network after 33.3% of the edges have been removed according to our epidemic containment strategy proposal (see fig. S9 for the original network before the containment process). As it is observed, the global connectivity, and thus functionality, of the worldwide connections is preserved (links of the same color are part of the same connected component). In Fig. 3 (bottom), we plot the network after deactivating the same fraction of links (33.3%) using the recursive deactivation of links according to edge betweenness. The edge betweenness containment method, in contrast with our proposal, generates two kinds of components: small or sparsely connected subcritical modules such as the ones in Australia, Africa, or South America, where the epidemics vanishes, and large supercritical communities in Europe, North America, and East Asia, with a large prevalence of the epidemics. This means that, for instance, there is no path to go from London to New York, or from Tokyo to Los Angeles, thus disconnecting the world by air transportation.

Fig. 3. Epidemic containment on the air transportation network.

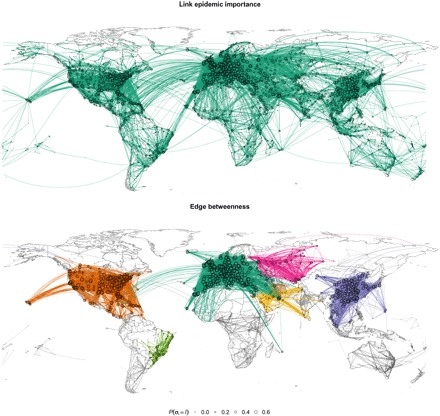
We show the networks after 33.3% of the links have been removed using link epidemic importance (top) and edge betweenness (bottom). Nodes and edges with the same color belong to the same connected component, with subcritical components in gray scale and using darker gray for larger components. The area of the nodes is proportional to their probability of being infected P(σ_i = I) from 0.0 to 0.6. We have set the epidemic probabilities to μ = 0.5 and β = 0.06.

For a better assessment of the performance of the different containment strategies, we show in Fig. 4 their comparison in terms of the required fraction of removed links to attain total containment, L_TC/L₀, when applied to a large set of synthetic networks and epidemic parameters. The results point to a clear advantage of the link epidemic importance method over the node infectivity and random approaches, and better or equal results with respect to edge betweenness and eigenscore. Only eigenscore achieves results comparable to link epidemic importance, with a slight advantage for our method. When applied to a set of 27 real networks (see Methods), the differences between link epidemic importance and eigenscore become more evident, showing again the effectiveness of our approach, but with some exceptions in which eigenscore performs better (see Fig. 5). In addition, we plot in figs. S10 and S11 the comparison of the number of connected components between the different containment strategies, which show the better performance of link epidemic importance to keep the number of components low, with only a few exceptions.

Fig. 4. Fraction of links removed for total epidemic containment on synthetic networks.

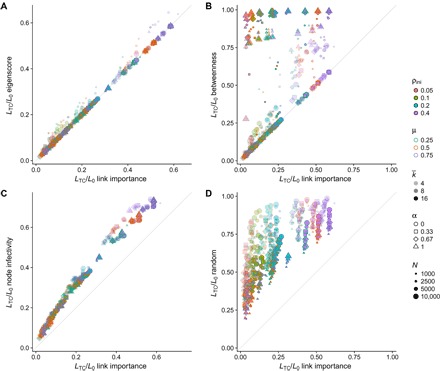
We show the fraction of links that have to be removed to obtain total epidemic containment using link epidemic importance, compared with the fractions for the other four strategies: (A) eigenscore, (B) edge betweenness, (C) node infectivity, and (D) random removal. Each point represents a configuration consisting of a network and a set of epidemic parameters. The networks have been generated with the model in (48), which interpolates between ER (α = 1) and BA networks (α = 0). We use four values of the interpolating parameter: α = 0.0, 0.33, 0.67, and 1.0. These networks are generated in four sizes (N = 1000, 2500, 5000, and 10, 000) and three average degrees (〈k〉 = 4, 8, and 16), thus amounting to 48 different networks. For each network, we apply the five containment strategies for three different values of the recovery probability (μ = 0.25, 0.50, and 0.75) and four values of the infection probability β selected such that, before removing links, the incidence of the epidemics at the stationary state is equal to ρ_ini = 0.05, 0.1, 0.2, and 0.4. Therefore, each plot contains 576 different configurations.

Fig. 5. Fraction of links removed for total epidemic containment on real networks.

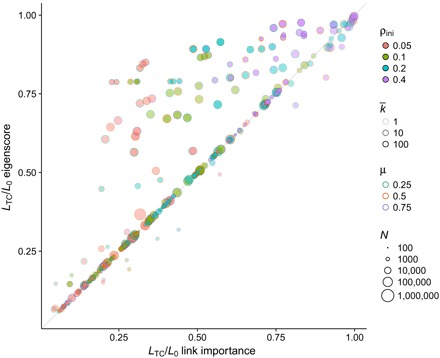
We compare the link epidemic importance and eigenscore methods on a set of 27 real networks selected from the Network Repository (49) (see Methods), with sizes ranging from 410 to 404,719 nodes. The epidemic parameters are the same as in Fig. 4, thus amounting to 324 different configurations.

DISCUSSION

We have presented a methodology for assessing epidemic spreading based on links instead of nodes. The model, named ELE, allows the determination of the epidemic importance of each link in transmitting the disease. The method accounts for the first-order correlations between links, although it could be extended to higher orders, assuming a larger analytical and computational cost. The results are used to develop an epidemic containment strategy built on deactivating recursively the links with the largest link epidemic importance while preserving the connectivity of the full network, that is, avoiding fragmentation. We have validated our proposal in synthetic and empirical networks, comparing with other alternative containment strategies, which show its better performance, with few exceptions. In the empirical case of the worldwide air transportation network, we identify the most important connections between airports for the spreading of epidemics and evaluate the epidemic incidence after its deactivation, considering an SIS epidemic spreading dynamics. Our results open the door to new approaches in the analysis of dynamical diffusive-like models on complex networks at the level of links instead of nodes.

METHODS

Epidemic threshold

The determination of the epidemic threshold was performed by considering a state of the system in which the epidemic incidence is very small (${\mathrm{\Phi }}_{\mathit{i}\mathit{j}},{\mathrm{\Phi }}_{\mathit{j}\mathit{i}},{\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}\ll 1$, for all links); thus, the system of equations can be linearized (see section S2 for full details), resulting in

$${\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}=\mathrm{\beta }(1-\mathrm{\mu }){\mathrm{\Phi }}_{\mathit{i}\mathit{j}}+\mathrm{\beta }(1-\mathrm{\mu }){\mathrm{\Phi }}_{\mathit{j}\mathit{i}}+{(1-\mathrm{\mu })}^2{\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}$$ (9)

$${\mathrm{\Phi }}_{\mathit{i}\mathit{j}}=\mathrm{\beta }{\displaystyle \sum _{\mathit{r}}}({\mathit{A}}_{\mathit{r}\mathit{j}}-(1-\mathrm{\mu }){\mathrm{\delta }}_{\mathit{r}\mathit{i}}){\mathrm{\Phi }}_{\mathit{j}\mathit{r}}+(1-\mathrm{\beta })(1-\mathrm{\mu }){\mathrm{\Phi }}_{\mathit{i}\mathit{j}}+\mathrm{\mu }(1-\mathrm{\mu }){\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}$$ (10)

Here, we removed the dependence on time to emphasize that we are considering the steady state. From Eq. 9, we can write

$${\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}=\frac{\mathrm{\beta }(1-\mathrm{\mu })}{\mathrm{\mu }(2-\mathrm{\mu })}({\mathrm{\Phi }}_{\mathit{i}\mathit{j}}+{\mathrm{\Phi }}_{\mathit{j}\mathit{i}})$$ (11)

Now, calling ${\mathrm{\epsilon }}_{\mathit{i}}={\mathrm{\Phi }}_{\mathit{j}\mathit{i}}+{\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}\ll 1$, which does not depend on node j because P(σ_i = I, σ_j = S) + P(σ_i = I, σ_j = I) = P(σ_i = I), we made the following ansatz

$${\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}=\mathrm{\Upsilon }({\mathrm{\epsilon }}_{\mathit{i}}+{\mathrm{\epsilon }}_{\mathit{j}})$$ (12)

$${\mathrm{\Phi }}_{\mathit{i}\mathit{j}}=\mathit{X}{\mathrm{\epsilon }}_{\mathit{i}}+\mathit{Z}{\mathrm{\epsilon }}_{\mathit{j}}$$ (13)

where ϒ, X, and Z are constants independent of the link. These ansatz include the assumptions of symmetry of ${\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}$ and asymmetry of Φ_ij, respectively. We can determine the constants by substitution in Eq. 11 and using the definition of ε_i, which leads to

$$\mathrm{\Upsilon }=\frac{\mathrm{\beta }(1-\mathrm{\mu })}{\mathrm{\mu }(2-\mathrm{\mu })+2\mathrm{\beta }(1-\mathrm{\mu })}$$ (14)

$$\mathit{X}=-\mathrm{\Upsilon }$$ (15)

$$\mathit{Z}=1-\mathrm{\Upsilon }$$ (16)

Last, we built equations for ε_i by substituting Eqs. 9 and 10 in ${\mathrm{\epsilon }}_{\mathit{i}}={\mathrm{\Phi }}_{\mathit{j}\mathit{i}}+{\mathrm{\Theta }}_{\mathit{i}\mathit{j}}^{\mathit{I}}$ and using the ansatz. The result is

$$\frac{\mathrm{\mu }}{\mathrm{\beta }}{\mathrm{\epsilon }}_{\mathit{i}}={\displaystyle \sum _{\mathit{j}}}{\mathit{B}}_{\mathit{j}\mathit{i}}{\mathrm{\epsilon }}_{\mathit{j}}$$ (17)

where B is a matrix whose elements depend on the adjacency matrix of the network, on ϒ, and on the degrees k_i of the nodes

$${\mathit{B}}_{\mathit{i}\mathit{j}}=(1-\mathrm{\Upsilon }){\mathit{A}}_{\mathit{i}\mathit{j}}-\mathrm{\Upsilon }{\mathit{k}}_{\mathit{i}}{\mathrm{\delta }}_{\mathit{i}\mathit{j}}$$ (18)

δ_ij stands for the Kronecker delta function, which is 1 if i = j and 0 otherwise. If μ/β is an eigenvalue of matrix B, then Eq. 17 has nontrivial solutions. Hence, the onset of the epidemics β_c, the lowest value of β that yields nontrivial solutions of Eq. 17, is given by

$${\mathrm{\beta }}_{\mathit{c}}=\frac{\mathrm{\mu }}{{\mathrm{\Lambda }}_{\text{max}}(\mathit{B})}$$ (19)

where Λ_max(B) is the largest eigenvalue of matrix B. Note that matrix B depends on β and μ; thus, Eq. 19 is implicit for β_c, which can be solved by iteration (see section S3 for a discussion on the determination of the epidemic threshold).

Estimation of the incidence of the epidemic from numerical simulations

The numerical incidence of the epidemics, ρ, is calculated using discrete-time and synchronous Monte Carlo simulations. We made use of the quasistationary (QS) approach (44, 45) to avoid the effect that a large number of realizations end up in the absorbing state with no infected individuals in the system. Basically, the QS method focuses the simulation on active configurations, that is, with one or more infected individuals. Every time the system reaches the absorbing state, this state is replaced by one of the previously stored active states of the system. We kept 50 active configurations with an update probability of 0.20. We gave the systems a transient time of 10⁵ time steps and then calculated ρ as an average over a relaxation time of 2 × 10⁴ time steps.

Networks

In this work, we evaluated our methodology on synthetic and empirical networks. We built a network with power-law degree distribution P(k) ~ k^−γ with exponent γ = 3 and 〈k〉 = 6 using the configuration model. To evaluate the impact of transitivity, we also built another network with the same characteristics of the previous one but with a clustering coefficient of 0.6 using the algorithm of Holme and Kim (46) with a parameter p = 0.8.

We considered also two empirical networks: the air transportation network and the network of scientific collaborations in the field of general relativity. The air transportation network was constructed using data from the website openflights.org, which has information about the traffic between airports updated to 2012. This network accounts for the largest connected component, with 3154 nodes and 18,592 edges (see data file S1). The network of scientific collaborations was obtained from (47); it is composed of 5242 nodes linked by 14,496 edges.

The synthetic networks in Fig. 4 were generated with the model in (48), which interpolates between ER and Barabási-Albert (BA) networks. In this way, we were able to evaluate the performance of the containment strategies on networks with degree distributions that range from Poisson (ER) to power-law (BA). By construction, these networks have no community structure and low transitivity.

The 27 real networks in Fig. 5 were obtained from the Network Repository (49), selecting only the largest connected component. They cover wide ranges of number of nodes (from 410 to 404,719), number of links (from 1043 to 713,319), average degree (between 2.04 and 84.82), average clustering coefficient (from 0.0023 to 0.1105), and assortativity (between −0.88 and 0.64) (see section S4).

Containment process

To perform the deactivation of links, we imposed an adiabatic process: After each removal step, we let the system converge to the meta-stable equilibrium before removing any other link. For a fair comparison between different containment strategies, we removed on each deactivation step as many edges as we have removed using the node infectivity strategy. In the case of the real networks in Fig. 5, we set the maximum number of adiabatic processes to 1000 because of its large computational cost on the largest networks. This means that, if the network has 20,000 links, we removed 20 links at each deactivation step. We considered that we reached total containment when the incidence of the epidemics becomes lower than 1/N. The computational cost of calculating the links to remove for each containment strategy is shown in fig. S13.

SUPPLEMENTARY MATERIALS

Supplementary material for this article is available at http://advances.sciencemag.org/cgi/content/full/4/12/eaau4212/DC1

Section S1. Link epidemic importance and connected components

Section S2. Linearization of the ELE model

Section S3. Epidemic threshold

Section S4. Data description

Fig. S1. Ratio between the link epidemic importance I^A of a link in a subnetwork A and the link epidemic importance I^AB of a link that acts as the only bridge between subnetworks A and B.

Fig. S2. Epidemic containment for a network with 5000 nodes, power-law degree distribution of exponent 3, and average degree 〈k〉 = 6.

Fig. S3. Epidemic containment for a network with 5000 nodes, power-law degree distribution of exponent 3, high clustering coefficient, and average degree 〈k〉 = 6.

Fig. S4. Epidemic containment for the air transportation network.

Fig. S5. Epidemic containment for the general relativity collaborations network.

Fig. S6. Epidemic containment for an ER network with 5000 nodes and average degree 〈k〉 = 6.

Fig. S7. Epidemic containment for a network with 5000 nodes generated with a stochastic block model, with four blocks of 250 nodes, two blocks of 1000 nodes, and one block of 2000 nodes, average degree of 5, and mixing probability of 0.3.

Fig. S8. Epidemic containment for a network with 5000 nodes generated using the LFR algorithm, with average degree of 6, exponent of 3, and mixing probability of 0.1.

Fig. S9. Original air transportation network (top) and the results after a removal of 33.3% of the links using link epidemic importance (middle) and edge betweenness (bottom).

Fig. S10. Comparison of the number of connected components after total containment between the link epidemic importance strategy and the other four methods, calculated for the synthetic networks and parameters as in Fig. 4.

Fig. S11. Comparison of the number of connected components after total containment between the link epidemic importance and eigenscore strategies, calculated for the real networks and parameters as in Fig. 5.

Fig. S12. Graphical representation of the determination of the epidemic threshold.

Fig. S13. Computational time invested for each method to perform a single ranking and removal for BA networks ranging from 100 to 400,000 nodes, averaged over 36 repetitions.

Table S1. Structural characteristics of the 27 real networks obtained from the Network Repository (http://networkrepository.com) and used in Fig. 6 and fig. S11.

Data file S1. Air transportation network data.