emClarity: Software for High Resolution Cryo-electron Tomography and Sub-tomogram Averaging

Abstract

Macromolecular complexes are intrinsically flexible and often challenging to purify for structure determination by single particle cryoEM. Such complexes may be studied using cryo-electron tomography combined with sub-tomogram alignment and classification, which in exceptional cases reaches sub-nanometer resolution, yielding insight into structure-function relationships. Extending this approach to specimens that exhibit conformational or compositional heterogeneity, and that may be present at low abundance, remains challenging. To address this challenge, we developed emClarity (https://github.com/bHimes/emClarity/wiki), a GPU-accelerated image processing package, which features an iterative tomographic tilt-series refinement algorithm using sub-tomograms as fiducial markers and a 3D-samping function compensated, multi-scale Principle Component Analysis classification method. We demonstrate substantial improvements in the resolution of maps and in the separation of different functional states of macromolecular complexes, compared to those generated using current state-of-the-art software.

Introduction

Recent advances in the capabilities of cryo-electron microscopy (cryoEM) have enabled determination of structures approaching atomic resolution. Software tools for the single particle analysis (SPA) of cryoEM data have been developed to probe macromolecular functional dynamics; for example, the maximum-likelihood approach to classification as implemented in cisTEM¹ or RELION². For a sample to be suitable for SPA, it must yield tens to hundreds of thousands³ of particles, purified to high compositional and conformational homogeneity⁴ and subsequently imaged in many different orientations. These conditions are often difficult to realize, especially for the large and dynamic assemblies of biological complexes most relevant to cellular activities⁵. An alternative to SPA, cryo-electron tomography (cryoET), can be used to generate three-dimensional (3D) reconstructions of the specimen.

These reconstructions (tomograms) are typically limited to ~3–4 nm resolution due to the low electron dose used to prevent excessive radiation damage to samples⁶. Additionally, the signal-to-noise ratio (SNR) is not distributed evenly in the tomogram, resulting in anisotropic resolution. This is a consequence of both the increased specimen thickness at high tilt angles and the restricted angular sampling (+/− 60°) known as the “missing-wedge effect⁷“. However, when many copies of a macromolecule are present in a tomogram, they may be extracted in silico, aligned to a common orientation, and averaged using procedures that share many similarities to SPA, which ameliorates the distortions due to the “missing-wedge effect”. One major difference compared to SPA is that the metrics used in the orientation search are biased by the missing-wedge. This bias may be compensated by only considering the regions in Fourier space where both volumes being compared have been measured; the two most common being the constrained cross correlation^8,9 and the constrained Euclidean distance¹⁰.

Obtaining averages of sub-tomograms at resolutions of 15–20 Å is now relatively routine, and is a prerequisite for further classification of the sample into multiple biological states or functional conformations^11,12. Compared to SPA, this is arguably the greatest strength of cryoET and sub-tomogram averaging, because each particle exists as a unique, albeit distorted, 3D reconstruction. This allows for a direct analysis of the 3D variance, the value of which has been discussed extensively^13,14. Despite substantial progress over the last decade, very few structures have been solved at resolutions better than 8 Å using cryoET and sub-tomogram averaging, a critical threshold beyond which flexible fitting approaches to modeling of protein complexes are more reliable^11,15.

We present here a complete set of GPU-accelerated programs called emClarity for enhanced macromolecular classification and alignment for high-resolution tomography, with the aim of routinely reaching beyond the critical sub-nanometer resolution for diverse specimens. We have focused our efforts on those areas of image processing that are likely to yield the greatest improvements, as suggested by empirical observation and theoretical calculations^16,17: accuracy of tilt-series alignment, improved defocus determination and CTF correction, explicit treatment of anisotropic resolution, and more robust classification.

Results

emClarity workflow

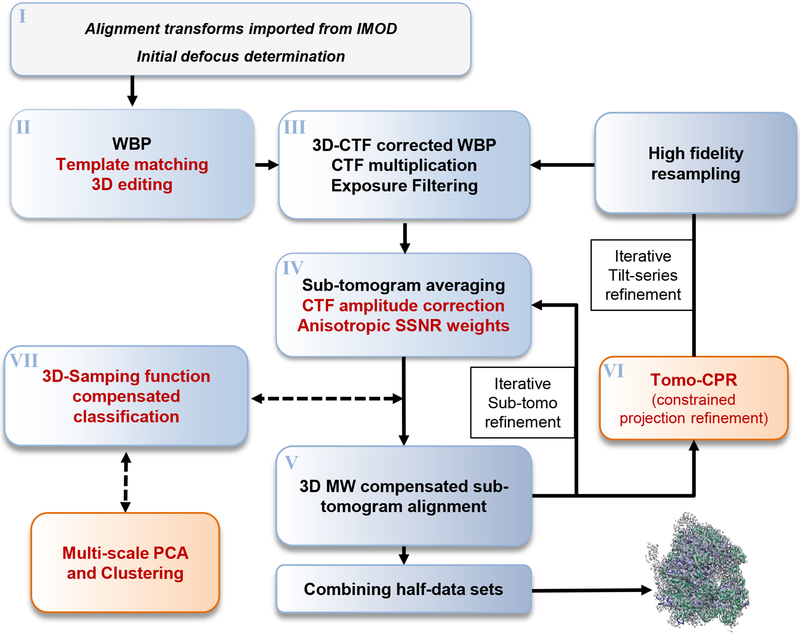
A typical emClarity workflow is illustrated in figure 1, with new features highlighted in red text. Detailed steps are described below. A comparison of features in available sub-tomogram processing packages, including emClarity, PEET, RELION, Dynamo, Jsubtomo, pyTom and Protomo is presented in Supplementary Table 1. Run times for each major operation are presented in Supplementary Table 2, and run times and speed up factors are compared for several popular Nvidia GPUs in Supplementary Figure 1.

Figure 1. The emClarity workflow for sub-tomogram averaging and classification.

The most important improvements introduced in emClarity are highlighted in red text, while novel additions to the process [AU: please clarify if you mean the general workflow for cryo-ET image processing here?] are indicated in orange boxes. Dashed lines indicate optional branches which may be included any number of times during the iterative alignment.

I). Input data

The raw data for emClarity are tilt-series, rather than tomograms, and an initial estimate of the tilt-series alignment parameters—tilt-axis angle, in-plane shifts and rotations, magnification and tilt angle—readily obtained using a separate installation of the IMOD software package¹⁸. For the defocus determination we use periodogram averaging as described previously¹⁹, refined by fitting a 2D astigmatic CTF and using a low pass filtered power spectrum for background subtraction²⁰.

II). Tomogram WBP, template matching with 3D interactive editing

By default, emClarity limits the resolution of the initial tomogram used in template matching to 40 Å to prevent model bias. This also means CTF correction is not needed and traditional weighted back-projection is sufficient to reconstruct these initial tomograms.

Sub-tomogram positions and orientations are chosen by the best scoring locally normalized cross-correlation, as described previously²¹ with two main exceptions. First, our algorithm is optimized to fit in GPU memory. Second, we do not use distribution fitting to estimate the number of false-positives, rather we provide a maximum intensity projection and interface with IMOD’s 3D model editing tools to enable rapid manual cleaning of the results.

III). 3D-CTF corrected WBP

To correct for the defocus gradient along the optical axis (sample thickness), emClarity uses a straightforward version of the “Defocus Gradient Corrected Back Projection”²². The approach has recently been validated and re-named “3D-CTF correction^23,24. To balance accuracy with practical compute time, emClarity determines the acceptable thickness based on the current resolution and defocus (Online Methods). For each slab of this thickness we whiten the power spectrum²⁵, multiply by the determined CTF and filter according to cumulative electron dose²⁶. For tilted images, strips of a width corresponding to the current accepted defocus are extracted from the inverse Fourier transform of the full image multiplied by the respective CTF.

IV). Averaging sub-tomograms, CTF amplitude correction, Anisotropic SSNR weighting

The iterative alignment procedure in emClarity alternates between averaging the sub-tomograms using the current estimate of their orientations, and performing a missing-wedge constrained cross correlation grid search²⁷. In addition to the data volumes, an average is also made of the “3D-sampling function” which is similar to the “weighted 3D CTF model” described in figure 1 of Bharat et al.¹⁰ with the additional consideration of the R-weighting applied during tomogram reconstruction (Online Methods eq 1). To avoid confusion with “3D CTF correction”, we do not adopt the name “3D CTF model”, instead using “3D-sampling function”.

V). 3D-sampling function compensated iterative refinement of sub-tomogram alignment

The iterative refinement procedures commonly used in cryoEM are prone to erroneously fitting noise, known as “over-fitting²⁸“. To minimize over-fitting emClarity divides the data from the beginning into two halves which are kept separate during refinement, the so-called “gold standard” approach²⁹. Additionally, the references used in the constrained search are carefully filtered as follows. In each cycle the SSNR of the average is estimated by the “gold-standard” FSC. A figure-of-merit weighting³⁰ derived from this FSC is then combined with CTF amplitude restoration via our adaption of the post-reconstruction volume normalized single-particle Wiener Filter³¹ (eq 8 in the original paper). Importantly, this adaptation involves an explicitly accounting of the directional anisotropy in the distribution of signal (Online Methods).

The iterative procedure is a local refinement, improving on the initial global alignment obtained during template matching. Importantly, we rotate the noisy particles back into the microscope reference frame for cross-correlation with the reference volume. This allows symmetry to be applied to the particle improving the SNR in the orientation search. This is not possible in SPA, where the particle is a projection and the reference must be rotated to the particle’s orientation, and to our knowledge, is not implemented in any other sub-tomogram averaging package.

VI). Iterative refinement of tilt-series alignment

emClarity implements iterative refinement of the tilt-series alignment by using sub-tomograms as fiducial markers, which we call tomogram constrained-particle refinement (tomoCPR.) It is an approach similar to “particle polishing³²” implemented for SPA in RELION with two primary differences. First, the reference projections we generate for refining the location of the sub-tomogram fiducial markers in the “raw” tilt-series, includes information from neighboring particles as well as non-particle information that is present in the tomograms (Supplementary Figure 2). Second, tomoCPR constrains spatially proximal particles to behave similarly within a given projection, as in SPA, while also requiring them to vary smoothly as a group from projection to projection through the tilt-series. The set of image transformations (shift, in-plane rotation, tilt-angle, and magnification) are fit for a grid of overlapping patches each containing a fixed number of particles, determined by the total molecular weight. The single set of image transformations that minimize the error for all fiducials in a given patch over all projections are solved using IMOD’s tiltalign. As the patches overlap significantly (0.75), the image transformations vary smoothly over neighboring particles.

VII). 3D-sampling function compensated classification

Regions of significant variance across a data set may be visualized by overlaying a 3D “variance map” with the average structure. The “missing-wedge” produces significant artifacts that are specific to the orientation of each particle in the sample, but not necessarily its identity or conformation. Left uncorrected these artifacts obscure meaningful differences among particles, reflected in a diffuse variance across the data set (Supplementary Figure 3 a–c). A previously demonstrated technique for estimating the effect of the “missing-wedge” by using a binary mask, called “wedge masked differences (WMDs)”, was shown to be a good first order correction³³; however, the accuracy of this model breaks down when higher-resolution features are considered (Supplementary Figure 3 d–e). To allow higher-resolution information in the classification, we replace this binary wedge mask with our 3D-sampling function, resulting in a more accurate estimate of the artifacts introduced by the “missing-wedge” (Supplementary Figure 3 g–i). It is worth noting that this does not “fill in” any missing data, rather it estimates what a given particle should look like by distorting the current sub-tomogram average by that particle’s 3D-sampling function, and clusters based on the difference between this expected value and the observed particle.

VIII). Multi-scale clustering

We encode a priori biological information through introducing inter-voxel correlations at biologically relevant length scales, such as ~ 10 Å for alpha-helical density, 18–20 Å for RNA helices or small protein domains, and ~ 40 Å for larger protein domains. This is accomplished by selecting features of given length scale via a bandpass filter. A singular value decomposition is run at each length scale using the native MATLAB function SVD, and the singular vectors describing the greatest variance for each length scale are then concatenated into feature vectors for further clustering. While this approach is similar to existing ideas in multi-scale multi-variate statistical analysis applied in other fields³⁴, because emClarity considers each length scale simultaneously, the approach is capable of providing a richer description of the feature space.

emClarity improves resolution in sub-tomogram averaging

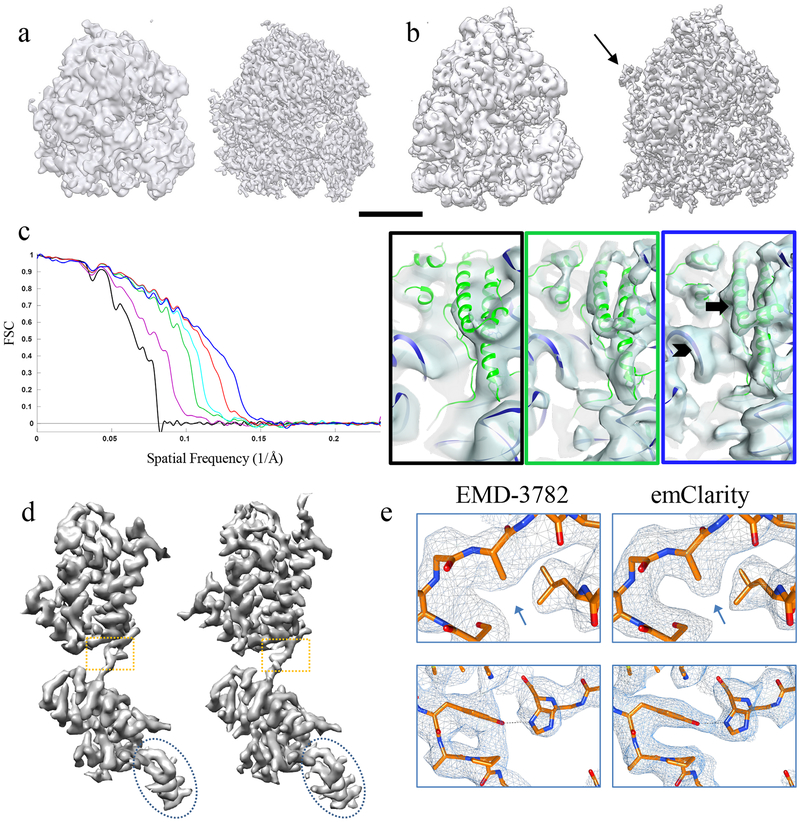
Given the inherent difficulty in working with extremely low SNR cryoEM data, and the sensitivity of the results to optimal selection of parameters, we elected to demonstrate our software using two publicly available data sets from the Electron Microscopy Pilot Image Archive³⁵ (EMPIAR). We show these published/deposited maps, juxtaposed with the maps obtained with emClarity in figure 2. Using emClarity, we obtained a structure at 7.8 Å for the yeast 80s ribosome (EMPIAR-10045) as compared to the structure at 12.9 Å solved using RELION version 1.4 (EMD-3228³⁶) (Figure 2a). For the mammalian 80s ribosome (EMPIAR-10064), we obtained an improvement from 11.2 Å (solved using pyTOM (EMD-3420³⁷)) to 8.6 Å (Figure 2b).

Figure 2. Improvement in resolution of sub-tomogram averaging using emClarity.

(a-b) Comparison of the sub-tomogram average of yeast 80s ribosome (a) and of rabbit 80s ribosome (b) by RELION (EMD-3228) (a, left) or by pyTOM (EMD-3420) (b, left) and by emClarity (right). Arrow points to an additional feature only revealed in emClarity. Scale bar, 100 Å. (c) Cross-FSC between the sub-tomogram averages by emClarity and the SPA cryoEM map (EMD-2275) of yeast 80s ribosome, each accumulating the previous improvement: original orientation parameters from Relion (black), CTF estimation and correction with the optimal exposure filter (magenta), one round of tomo-CPR (green), per-tilt defocus estimation (cyan), consideration of resolution anisotropy (red), and with all features plus alignment in emClarity (blue). Right, representative views of sub-tomogram averages, with the frame color matching the plot colors, and a rigid body docking of yeast 80s atomic model (PDB-47VR). The arrow and chevron highlight the resolved alpha helices and RNA structures, respectively. These experiments were repeated at least three times with nominally identical results. (d) Comparison of the sub-tomogram average of HIV-1 immature CA-SP1 monomer (EMD-3782) (left) and by emClarity (right). (e) Enlarged views of boxed area in d overlaid with a real-space refined model.

To evaluate the relative impact of each of the individual features implemented in emClarity, we incrementally included them into several reconstructions of the yeast 80s ribosome. To control for errors in alignment and perform a one-to-one comparison with EMD-3228, we used precisely the same particles and orientation parameters from the star files that accompany the raw data (EMPIAR-10045). We compare each map to an external reference map derived from SPA (EMD-2275³⁸), via a cross-Fourier Shell Correlation (cross-FSC), starting from the RELION reconstruction as a control (Figure 2c). The results demonstrate the recovery of additional signal from the same data as each subsequent feature is incorporated.

The accuracy of our combined CTF correction approach, including a re-implementation of optimal-exposure filtering and 3D-sampling function based Wiener filtering is reflected in the magenta curve in figure 2c, which shows a substantial improvement over the cross-FSC of the control (black). The largest single improvement comes from the tomoCPR, shown in green (which included optimal-exposure filtering and Wiener filtering as well.) The ribosome sample had very few gold-fiducial markers and limited overlapping density, perhaps accounting for the high impact of tomoCPR. A more modest improvement is obtained by adding in a per-tilt defocus estimation (cyan cross-FSC curve). When we also explicitly consider anisotropy in the SSNR in our adaptation of the single particle Wiener filter, we see another substantial improvement (red cross-FSC curve). The yeast 80s sample had a preferential orientation which is reflected in the FSC-cones and a plot of the angular distribution in supplementary figure 4. The final and highest resolution curve (blue) represents an alignment carried out in emClarity with all features added, illustrating the total impact on the accuracy of orientation determination.

In addition to improved resolution, we observe a density outside the peptide exit tunnel of the ribosome (figure 2b, white arrow) that is present in the map derived with emClarity, but not in the map derived with pyTOM. Finally, we show the density from a peripheral region with a rigidly docked model of the yeast 80s ribosome (PDB-47VR), clearly displaying alpha helices and the RNA structure in the map from emClarity (Figure 2c, blue box), compared to the map from the original publication (Figure 2c, black box).

To test emClarity on a more challenging case, we analyzed an HIV-1 immature Gag particle dataset³⁹ which was recently released (EMPIAR-10164). These data yielded the highest resolution (3.4 Å) sub-tomogram average to date (EMD-3782)²³. Using emClarity, we produced a sub-tomogram average at 3.1 Å resolution (Figure 2d, Supplementary Figure 5). The quality of the density map is clearly manifested in the real-space refinement of the HIV-1 CA structure using Phenix⁴⁰ (Figure 2e).

emClarity improves classification and reveals multiple ribosome functional states

Using multi-scale clustering combined with 3D-sampling function compensated Principal Component Analysis, emClarity helps reveal subtle conformational differences and distinguishes minor populations from noisy and distorted images, as demonstrated with yeast 80s ribosome data from EMPIAR-10045 (Figure 3), and mammalian 80s ribosome data from EMPIAR-10064 (Figure 4).

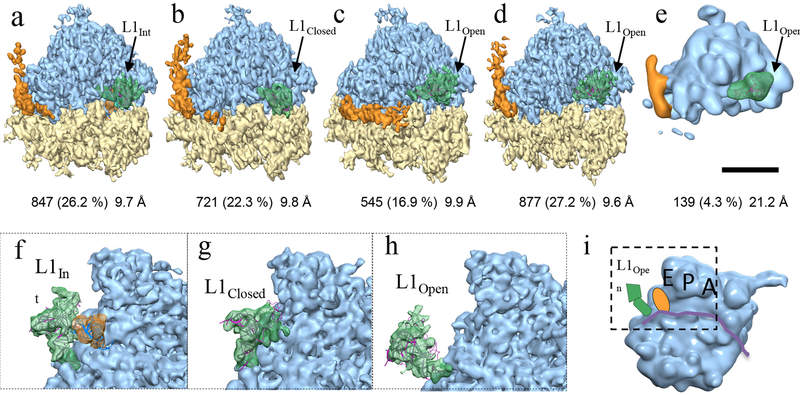
Figure 3. Classification of yeast 80s ribosome (EMPIAR-10045) with 3D-CTF compensated missing-wedge and multi-scale PCA.

(a-e) Four major classes and a minor class contributing 96.9% of sub-tomograms are shown with number and percentage of contributing units and resolution indicated below. The highly dynamic L1 protuberance and RNA expansion-segment 27 are shown in green and orange, respectively. Scale bar, 100 Å. (f-h) Enlarged views, with the small-subunit removed for clarity, of the L1 protuberance (green) in an intermediate position (f, class a), fully closed (g, class b), and fully open (h, classes c-e) respectively. The riboprotein and selected RNA helix components of the L1 protuberance (rpL1,h76,h79 from PDB 3J78) shown in magenta ribbon after rigid body docking into the respective density. (i) A cartoon illustrates the region displayed in (f-h) from the inter-subunit space with the E,P,A sites labelled and L1 (green) E-site tRNA (orange) and mRNA channel (purple ribbon.)

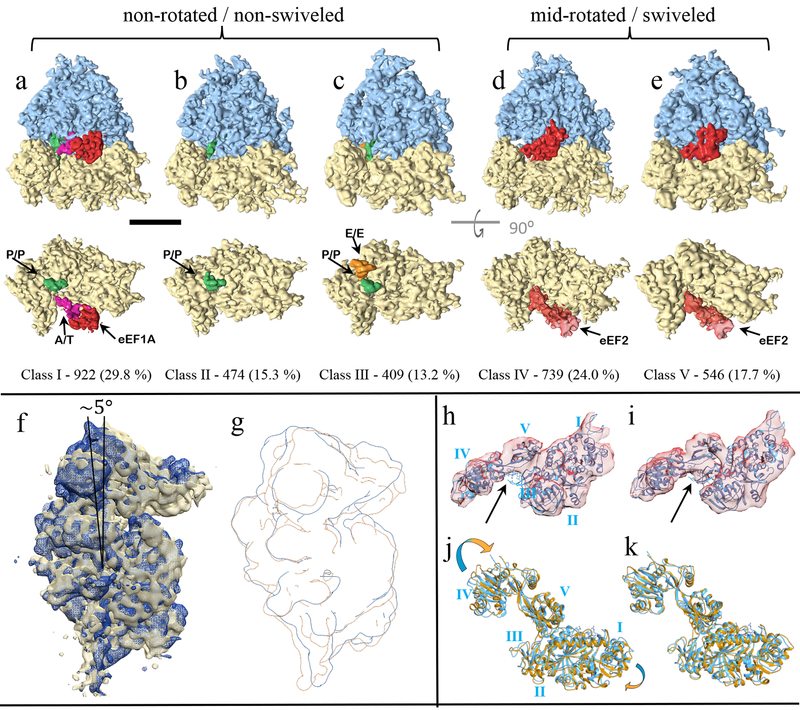
Figure 4. Classification of translating mammalian 80s ribosome with 3D-CTF compensated missing-wedge and multi-scale PCA.

(a-c) Classes I-III represent a post translocational state with the co-factors shown in the lower row from the inter-subunit surface with the 60s subunit removed for clarity. (d-e) Classes IV-V have a mid-rotated 40s and a swiveled head corresponding to a pre-translocational intermediate. Scale bar represents 100 Å. (f-g) Class IV in dark blue overlaid with class III in gold, showing the mid-rotated 40s state. (h-i) MDFF of eeF2 (orange) with the density from class-IV (h) and class-V (i) starting from PDB-4ujo (cyan ribbon). (j-k) The rigid body docking of PDB-4ujo into the density from class IV/V, respectively. Arrows point to this density which is occupied by the antibiotic Sordarin in PDB-4ujo, but is not present in the sample used in this study.

Classification of non-translating Yeast 80s ribosomes

The ribosome is a complex molecular machine composed of RNA and protein which exists in many functional states and interacts with an array of co-factors. The eukaryotic ribosome is composed of two major domains dubbed the large subunit (60s) and small subunit (40s). While the ribosome has a well-conserved catalytic core which mediates the peptidyl transferase reaction⁴¹, it is increasingly subject to more complex regulation in higher organisms resulting in an expanded set of both RNA and protein components. RNA expansion segments are found primarily at the periphery of the ribosome and are typically highly dynamic and difficult to resolve in structural analysis. One good example is es27, an approximately 150 Å RNA helix which predominantly adopts one of two conformations separated by about 90⁰, shown in orange in figure 3a–e. The first situates the end of the RNA helix just outside the peptide exit tunnel on the 60s subunit (es27_pet, figure 3a, b, d, e) and the second points toward the tRNA exit site (es27_L1, figure 3c). This dynamic domain is generally observed in cryoEM maps as a superposition of these two states, as is the case with the currently published results by ML classification in RELION³⁶. A notable exception being ribosomes with accessory complexes bound at the peptide exit tunnel, e.g. Sec61, are known to bias the conformation to the es27_L1⁴².

Another example of a highly dynamic ribosome domain is the L1 stalk – comprised of protein L1, and RNA helices h75, h76 and h79 from the 25s portion of the 60s subunit⁴³ – which moves through ~ 55Å during a translocation cycle. The motions of L1 are well correlated with several defined functional translocational states as observed using single molecule FRET and SPA⁴⁴. Using emClarity, we can discern three of these L1 conformational states isolated from thermal (stochastic) fluctuations of the non-translating yeast 80s ribosome: L1_open, L1_int, and L1_closed shown in green with variable occupancy in the five classes in figure 3. In addition to isolating dynamic states, identifying very sparsely populated classes is a particularly important and challenging task for classification of cryoEM data. We see in figure 3e the dissociated 60s subunit occupying a minor class, only ~4% of the data set or roughly ~140 sub-tomograms. In contrast, the Maximum likelihood approach implemented in RELION found three classes, one designated as a junk class and two relatively indistinguishable classes³⁶. This minor population could only be isolated in the case where feature vectors built from the projection on the principal components from at least three length-scales were simultaneously clustered.

Mammalian 80s ribosome

In contrast to the non-translating yeast specimen, the mammalian ribosomes imaged in EMPIAR-10064 were prepared from clarified rabbit reticulocyte lysate using a buffer low in Mg²⁺ but lacking polyamines, such that cofactors should co-purify excepting perhaps some loss of e-Site tRNA⁴⁵. We extracted 3,090 ribosomes from the four tilt-series deposited as the “mixed-CTEM” data set on EMPIAR, which are collected over a range of defocus values without a phase plate. emClarity identified five predominant classes as shown in figure 4a–e. Three of these classes show ribosomes adopting a non-rotated 40s conformation with variable tRNA eeF1A occupancy (class I-III), while two very similar classes adopted a mid-rotated (~5–6⁰) 40s conformation with eeF2 present (class IV-V).

A rigid body docking of the full 80s mammalian ribosome in the non-rotated POST state from PDB-4UJE⁴⁶ showed very clear agreement with the conformation of the 40s subunit, which combined with the co-factors observed suggest classes II and III are POST trans-locational ribosomes differing in retention of E site tRNA while class I is most similar to the “sampling” state. Classes IV and V both have eeF2 bound and differ in rotation of the 40s subunit of 5.9⁰ and 5.0⁰, respectively (Figure 4f–g). Rigidly docking the 80s yeast structure of eeF2 from PDB-4UJO⁴⁷ into classes IV and V show overall good agreement with their eeF2•sordarin•GDP position and our density. There are differences in domain IV of eeF2 which is known to be dynamic and plays a key role in translocation^48,44. We analyzed these differences qualitatively by comparing the Molecular Dynamics Flexible Fitting (MDFF) model (figure 4h–i) with the docked model solved with Sordarin present (figure 4j–k). The antibiotic Sordarin is highly specific for binding to fungal eeF2 and permits GTP hydrolysis, yet prevents conformational changes that result in subsequent release of eeF2 after translocation⁴⁹. Sordarin is not present in the sample under study, yet there is a pronounced difference in electron density between domains III-V of eeF2 in class V (figure 4i black arrow) that coincides with the Sordarin binding pocket. This density is not present in class IV which also exhibits a rotation of eeF2-domain IV (figure 4j).

Discussion

We have created a set of image processing routines incorporated into the program emClarity, which demonstrated improved accuracy in alignment and image restoration compared to current state-of-the-art approaches. We have aimed to make emClarity as easy to use as possible, limiting user specified parameters to the normal microscope and data collection information, as well as an estimate of the particle’s radius and mass. The user must also select the angular search range, which is something that may be improved in the future.

We demonstrate a powerful approach for image classification in the presence of the “missing-wedge” effect by combining the correction for wedge differences with multi-scale clustering which helps to encode biologically relevant information for the clustering algorithms. Having isolated classes IV and V of the mammalian ribosome ex vivo suggests both that Sordarin binding stabilizes an interaction between eeF2-domian III/V that exists on pathway in functional ribosomes, and that nearby intermediates on the energy landscape not observed in studies using the antibiotic, may be explored and observed by using this approach. In addition to isolating well-resolved class averages with minor populations, and finding nearby minima in the energy landscape, our approach also results in the production of accurate 3D-variance maps.

By highlighting key regions of dynamic behavior, our approach should be useful for direct analysis and the design of complementary biophysical experiments. While these advances in classification are in the pre-processing and dimensionality reduction stage, future work to explore modern approaches in pattern recognition and machine learning, may allow substantial improvement in the technique.

Online Methods

Please refer to “Life Sciences Reporting Summary” for detailed information on experimental design, reagents and software.

Datasets

The datasets used in emClarity processing are from Electron Microscopy Public Image Archive (EMPIAR), including the yeast 80s ribosome (EMPIAR-10045), the mammalian 80s ribosome (EMPIAR-10064), and the HIV-1 immature Gag (EMPIAR-10164).

emClarity programs

emClarity is run from the command line and is easily scripted to run in a manner most suited to a user’s particular project. A text parameter file is used to input project specific details, like microscope parameters, mask dimensions, and angular search ranges. We typically make a copy of the parameter file for each cycle of averaging and alignment, which we refer to as paramC.m, where C refers to the cycle number. The meta-data of each project is tracked in a binary database which named using the “subTomoMeta” parameter. Each tilt-series may have multiple areas slated for reconstruction, tiltN M refers to tilt-series “N” and reconstruction area “M”. A brief description of the major functions (in italic) in emClarity is below:

emClarity init paramN.m

Read in the desired dimensions for each sub-region of each tilt-series to reconstruct, initialize the subTomoMeta (metadata binary.)

emClarity ctf estimate tiltN

estimate the ctf for a given tilt-series N

emClarity reScale mapNameIN mapNameOUT AngPixIN AngPixOUT cpu/GPU

resample a map to a new pixel size, particularly for template matching.

emClarity templateSearch tiltN M reference.mrc symmetry gpuIDX

Reconstruct tomogram M from tilt-seris N without ctf correction, run template matching on GPU # gpuIDX, randomize results at symmetry related positions.

emClarity ctf 3d paramN.m

Run 3d-CTF corrected weighted-back projection.

emClarity avg paramN.m N RawAlignment

Every cycle begins by creating a sub-tomogram average, calculating the “gold-standard” FSC, and weighting the average accordingly while compensating for amplitude attenuation by the CTF to produce references for the alignment.

emClarity alignRaw paramN.m N

Run the alignment

emClarity removeDuplicates paramN.m N

clean out any subtomograms that have drifted to the same position. Not needed every cycle.

emClarity tomoCPR paramN.m N

Run tomogram constrained particle refinement, this is generally done prior to a step down in binning, e.g. bin4 → bin3.

emClarity ctf update paramN.m N

Only needed after a run of tomoCPR, this updates the tilt-series geometry in the subTomoMeta, and also resamples the raw tilt-series applying rotation, shift and magnification scaling all in Fourier space to reduce interpolation losses of high resolution information.

Since the tilt-series alignments are update, and usually also the binning is reduced, a new round of 3D-CTF reconstructions need to be made with.

If classification is to be run, the cycle starts the same, but with the “flgClassification” parameter enabled.

emClarity avg paramN.m N

emClarity pca paramN.m N previousPCA

Run 3D-sampling function compensated PCA at each length scale specified in the “pcaScaleSpace” parameter. The command line argument previousPCA is always zero on the first run. If a random subset (25% or ~3000, whichever is larger) is to be analyzed by setting “Pca_randSubset” then a subsequent round of pca must be run with “previousPCA” set to one in order to project all of the sub-tomograms along the principal component axes.

emClarity cluster paramN.m N

Cluster the data based on selected eigenvectors from the pca step.

emClarity avg paramN.m N Cluster_cls

Notice the last argument (a string) which creates a montage of the class averages selected in the parameter file. Classes with different memberships may be selected.

At the end of processing, the half-sets may be aligned and combined by running:

emClarity avg paramN.m N FinalAlignment

Align and combine half-sets, optionally creating multiple, differently sharpened maps.

Image processing

The alignment and classification procedures are generally identical for all the samples, except for the HIV-1 Gag data, which were not classified and had C6 symmetry applied. All parameters unique to each dataset, including the angular search range and iterations used, are shown in Supplementary Tables 3 and 4. emClarity is only tested on Linux operating systems, and all references to command line operations are to be understood in that manner.

Project set-up and coarse tilt-series alignment:

For each specimen, we make a project directory, which we will refer to generically as “projectDir.” During processing, several sub-directories will be created by emClarity in addition to the user created directories for the raw data, which we recommend calling “rawData” and a folder for the cleaned data that must be named “fixedStacks.”

The HIV-1 Gag data consist of dose fractionated frames, which we aligned using the program “unblur” version 1.0 included in the cisTEM package. The aligned frames were summed and saved without any exposure-based filtering because this is handled later inside emClarity.

All tilt-series were aligned using the default parameters in IMOD version 4.10.12 using the eTomo interface, with the available gold-fiducial markers. For the ribosome datasets, all gold fiducials (~5–7/tilt) were selected, while for the HIV-1 Gag data ~20–30 closest to the protein and distributed on both surfaces of the ice were selected. Local alignments with fixed XYZ global coordinates were run for the HIV-1 Gag data only. After generating the final aligned stack, the gold beads were located using find beads3d. Only the fiducial model describing the location of the beads is needed, so they were not erased. Note: for EMPIAR 10045 the pixel size in the header must be corrected to 2.17 Å prior to beginning. This may be done with the IMOD program alterheader from the command line.

The files describing the projection transformations, any local alignments, and fitted tilt-angles are copied to the fixedStacks directory and renamed.

>$ mv specimen_name_1_fid.xf	projectDir/fixedStacks/tilt1.xf
>$ mv specimen_name_1_fid.tlt	projectDir/fixedStacks/tilt1.tlt
>$ mv specimen_name_1_local.xf	projectDir/fixedStacks/tilt1.local
>$ mv specimen_name_1_erase.fid	projectDir/fixedStacks/tilt1.erase

Additionally, a file listing the tilt-angles in the order they were collected must be created for emClarity to apply an appropriate exposure filter.

projectDir/fixedStacks/tilt1.order

If outlier pixels are removed in IMOD, this “fixed” stack may be moved to projectDir/fixedStacks/tilt1.fixed, otherwise you may just link the raw data.

>$ cd projectDir/fixedStacks

>$ ln -s ../rawData/specimen_name_1.st tilt1.fixed

This is repeated for all tilts-series, of which there are 7, 4, and 41 in the yeast, mammalian, and HIV-1 Gag data sets respectively.

CTF estimation:

The mean defocus at the tilt-axis was then estimated in emClarity for each tilt-series using a 3.5 ± 2.5 μm window covering the range of expected defocus values for all three data sets.

For the HIV-1 Gag data, the per-tilt defocus was determined using “emClarity ctf refine” to produce the power-spectra, which were subsequently fit using ctffind4 with the–amplitude-spectrum input flag and default parameters.

For the yeast ribosome data which have a thin layer of carbon providing extra signal in the power spectrum, the per-tilt defocus values were refined during tomoCPR. To do so, the height of the cross-correlation peak is maximized by scanning through a small range of defocus values as applied to each reference tile⁵⁰.

Selecting sub-regions for further analysis

The selection of sub-regions of each tilt-series for reconstruction are defined by a text file with the minimum and maximum values in x, y, z for each region. The script “recScript2.sh” provided with emClarity was used to first create reconstructions of each tilt-series at a binning of 10 and thickness of 300 covering the full X,Y dimension of the images. Each region is then defined while viewing the reconstruction in IMOD by making an IMOD model with six points per region, xmin, xmax, ymin, ymax, zmin, zmax, in that order.

A second run of “recScript2.sh” creates a projectDir/recon directory and converts these model files into the text files read in by emClarity to be used for the rest of the procedure. These are called tilt1_recon.coords and list the tilt-series base name, number of regions to reconstruct, and for each region the width, first and last slice in y, thickness, x-origin offset and z-origin offset.

The ribosome data were divided on the x-axis into two regions per tilt-series. The HIV-1 Gag data were divided into quadrants. Additionally, the flag “fscGoldSplitOnTomos=1” is set in the parameter file for the HIV-1 Gag data, so that the even/odd half sets are divided based on tomogram, not randomly on sub-tomograms. This is necessary to avoid mixing neighboring particles which would violate the gold-standard hypothesis.

Template matching

References were derived from SPA EMD-3228³⁹ (yeast 80s ribosome), EMD-5592⁵¹ (human 80s ribosome) and EMD-8403 (HIV-1 Gag)⁵² and rescaled to the full pixel size of each data set using “emClarity reScale.” These references were then passed to “emClarity templateSearch” binned to achieve a nominal pixel size ~ 8–12 Å depending on the size of the specimen. All maps and tomograms are automatically low-pass filtered to 40 Å resolution by default in emClarity. Non-CTF corrected tomograms are reconstructed by the templateSearch program as needed for template matching.

The results for the ribosome data set were cleaned manually by comparing the maximum intensity projection maps and the binned tomograms overlaid with an IMOD model showing the x,y,z coordinates of each peak detected.

For the HIV-1 Gag data, emClarity removeNeighbors was used to automatically clean the results based on geometrical restraints. Only peaks that had five neighbors within 100 Å and also oriented within 20˚ were retained, resulting in 179,168 sub-tomograms to start. (This number dropped to 162,213 in the first round of averaging as particles too close to the edge to allow padding by 1.5 x particleRadius were excluded.

Particles with symmetry pose a special challenge to all missing-wedge compensation approaches as any error in the compensation will result in the particle looking different at its symmetry related orientations. To help with this, we randomize the template matching results around each symmetry related orientation, and subsequently only search an angular range small enough to not reach the neighboring positions.

Iterative alignment

Each cycle of alignment is initiated by calculating averages of the two half sets, calculating the gold-standard FSC, and then applying re-weighting each average to generate a FOM weighted reference. These alignments are only for the FSC calculation and are never considered in the updates to the particle orientations in the iterative alignment, as necessary to maintain independence between the two half-sets.

We alternate searching over just the azimuthal and polar angles, and an in-plane search. For each specimen, we started at a binning of chosen to produce a pixel size of ~7–8 Å. Details may be found in Supplementary Table 3 for the ribosome data sets, and Supplementary Table 4 for the HIV-1 gag data. We then go through three rounds of averaging and alignment, followed by removing any positions that may have drifted to overlap using “emClarity removeDuplicates.” We then run a round of tomo-CPR, which requires updating the aligned tilt-series and the 3dCTF corrected tomograms.

>$ emClarity ctf update paramX.m

>$ emClarity ctf 3d paramX.m

This reconstruction is generated at a binning one finer than the previous, and the same pattern was repeated until reaching full sampling.

Classification

The ribosome data for the yeast 80s were classified in a single pass, using three resolution bands 10,18, and 28Å, 36 of the top eigenvalues were saved, and five from each band were selected (parameter Pca_coefficients=[7:11;7:11;1:11])] for clustering via kmeans The class averages were then generated by running emClarity avg paramX.m X cluster_cls

The ribsome data for the mammalian 80s were classified in two passes. First, they were split into groups displaying either a rotated or un-rotated 40s small subunit. To do this, the subTomoMeta file (projectName.mat) was copied to two new files: project_smallSU.mat and project_largeSU.mat. The classes are selected for removal by viewing the class average montage in IMOD, and selecting any point in the region of a given class. These models are then used to remove their contributing members in the subTomoMeta.

>$ emClarity geometry paramX.m X RemoveClasses [X,0,0] STD.

Since both branches of the project access the same raw data, it is convenient to remain in the same project directory, and all subsequent output will be identified by the new subTomoMeta basename.

A subsequent round of classification was run using 12,22,32 Å resolutions. Unlike the yeast 80s which had some Eigen images with clear missing wedge bias, revealed as “streakiness” in the density, the mammalian displayed sufficient true variability to overpower the noise from the missing-wedge bias, and all 36 eigenvectors from each resolution band were used in clustering.

Analysis

Models PDB-3J78 for yeast were rigid body docked in using Chimera.

Models PDB-4UJO for mammalian were docked in using Chimera, in combination with the “Segger” plugin.

Models PDB-5l93 were docked in using Chimera, refined in real-space using Phenix version 1.13-2998-000, and manually edited in COOT version 0.8.9.

Algorithmic details

3D-Sampling Function

$$3DSamplingFunction\equiv S{F}^{3D}={\sum }_{j=1}^S{\sum }_{i=1}^Z{T}^{i,j}|CT{F}_i^{2d}{|}^2{R}^{2d}ExpFilte{r}_i^{2d}$$ eq 1.

The first term in the summation is the combined transformation of projection (i) into the tomogram, and sub-tomogram (j) into the final average. The second term is the normal expression for the CTF limited to third order Seidel aberrations⁵³, the third is the R-weighting, and the fourth is the optimal-exposure filter as defined²⁶, Z is the number of projections in each tilt-series, and S the number of sub-tomograms.

Refinement of tilt-series alignment

Tomo-CPR works by combining the strengths of the 3D-model-based and feature-tracking approaches, while also taking advantage of the robust alignment tools developed for gold-fiducial alignment available in the IMOD package, which must be installed alongside emClarity. Starting with the tomogram (as in the 3D model approach), we additionally replace the density corresponding to our particles of interest at the proper orientation, with a copy of the high SNR sub-tomogram average and then re-project that synthetic tomogram using the IMOD program tilt (Supplementary Figure 2a). This re-projection also includes any local alignments previously determined and allows us to create a reference tilt-series along with a model for each sub-tomogram position in the 2D-projection. This model is used to cut tiles out of the data and reference projections for comparison by cross-correlation, while considering the CTF of the data projection at that point, as well as the structural noise from each particle’s unique environment (Supplementary Figure 2b,c). These refined positions are then used as input to IMOD’s tiltalign as if they were derived from gold fiducials, allowing us to take advantage of local refinement and robust fitting, as described previously⁵⁴. The global changes to the projection geometry are applied to the tilt-series, while the local refinements are taken into consideration when the tomograms are reconstructed on the fly by emClarity. In addition to the importance of considering neighboring particles (Supplementary Figure 2d), additional high-contrast features, like the edge of the carbon foil or other particulate matter are pointed out in supplementary figure 2e, where a thin strip of one of the tomo-CPR references, prior to tiling, is shown.

Statistical optimization of the SNR in the final map

In addition to alternating phase reversals, the CTF also modulates the amplitudes of the data. Several programs for correcting the CTF phase and amplitude modulations directly in the 2D projections of tilted images are available; the two predominant being CTFPLOTTER and CTFPHASEFLIP⁵⁵ included in the IMOD package¹⁸ for measurement and correction respectively, and TOMOCTF¹⁹. Both may be used to restore the amplitudes in the Fourier transforms of individual projections which inevitably amplifies noise in the process⁵⁶. A more attractive approach is to correct the phases on the projections, via multiplication by the CTF, and then to address the amplitudes after building the 3D reconstruction (sub-tomogram average).

The amplitude modulations are compensated using a Wiener filter in both SPA and the adaptation of RELION for sub-tomogram averaging¹⁰. A typical Wiener filter based approach has also been described recently in the structure of the HIV-1 capsid protein³⁹ but is only implemented through “in-house” software. In addition to the CTF and consideration of increasing sample thickness with tilt angle, our 3D-sampling function also takes into consideration the R-weighting that is applied during tomogram reconstruction and is applied via our adaption of the “volume normalized single-particle Wiener (original eq. 8)³¹ We include the original expression, with our nomenclature in eq. s1.

$$F^{SP{W}_t}\left(q_{hkl}\right)=\frac{S{F}^{3D}}{S{F}^{3D}+\frac{f_{particle}}{f_{mask}}\left(\frac{1-FS{C}_{mask}\left(q_{hkl}\right)}{2FS{C}_{mask}\left(q_{hkl}\right)}\right)\left(\frac{1}{n_q}{\sum }_{q\in q_{h\text{'}k\text{'}l\text{'}}}S{F}^{3D}\right)}{F}^{LSQ}\left(q_{hkl}\right)$$ eq s1

The least squares estimate, which is a Wiener filtered reconstruction with an ad-hoc Wiener constant [CITE] is defined below eq s2.

$$F^{LSQ}\left(q_{hkl}\right)=\frac{{\sum }_{j=1}^S{\sum }_{i=1}^Z{T}^{i,j}|CT{F}_i^{2d}{|}^2{R}^{2d}ExpFilte{r}_i^{2d}{F}_i^{2d}}{{\sum }_{j=1}^S{\sum }_{i=1}^Z{T}^{i,j}|CT{F}_i^{2d}{|}^2{R}^{2d}ExpFilte{r}_i^{2d}{F}_i^{2d}+1}$$ eq s2

We have made three major changes to the filter:

1. The 3D-Sampling function is weighted for critically under-sampled regions, where the SSNR estimated by the FSC is less reliable. This is done by:

   1. choosing a minimum acceptable sampling threshold, 0.2 * median (SF^3D != 0)
   2. scaling SF^3D to replace less sampled regions by smoothly transition from this value to some new larger number, chosen by the maximum in the original SF^3D.

2. The FSC, normally calculated over spherical sections is replaced by an anisotropic FSC calculated over conical sections, typically 38, which has been used previously to estimate resolution anisotropy⁵⁷.

3. Finally, the average sampling over spherical shells (final term in the denominator of eq s1) that is used to scale the SSNR estimate to represent the average SSNR in a single sub-tomogram is replaced with a gaussian smoothed version of the 3D-sampling function. Again to account for anisotropy in the sampling.

$$F^{SP{W}_t}\left(q_{hkl}\right)=\frac{|S{F}^{3D}{|}^2}{|S{F}^{3D}{|}^2+\frac{f_{particle}}{f_{mask}}\left(\frac{1-FS{C}_{aniso,mask}\left(q_{hkl}\right)}{2FS{C}_{aniso,mask}\left(q_{hkl}\right)}\right)\left(G\otimes |S{F}^{3D}{|}^2\right)}{F}^{LSQ}\left(q_{hkl}\right)$$ eq s3

3D-sampling function compensated classification

For the special case where sub-tomograms are all oriented similarly, being adsorbed to a lipid monolayer for example, they may be averaged along the direction of their missing wedge and classified in 2D⁵⁸; however, this is obviously of limited interest for most specimen. Another popular approach involves classifying the

constrained-cross-correlation matrix^9,27, however, this can be expensive to calculate and also disregards large amounts of information – discussed in detail in the paper on wedge masked differences (WMDs)³³ on which we further expand and enhance.

The WMDs approach seeks to compensate the missing wedge by forming the difference between a given particle and its expected value. The expected value is estimated to be the global average distorted by the particle’s missing wedge. These are mean centered, normalized to a variance of one, and arranged into a 2D matrix followed by singular-value decomposition (SVD). The binary wedge used in this approach is only a first approximation, and we replace it with our full 3D-sampling function. This correction allows the classification to include higher-resolution details than previously possible, which is a necessary but not sufficient condition to achieve the classification we report. We find that including the highest variance information from three to four discrete length scales at the same time is required to observe each class.